ID: 794 847 5614, PWD: 785453
Vorwort

Die Vorlesung Physik der sozio-ökonomischen Systeme mit dem Computer wurde im Wintersemester 2015/16 das erste Mal gehalten und viele der auf dieser Hauptseite erreichbaren Internetseiten basieren grundsätzlich auf dem damals erstellten Kurs. Das nebenstehende Video (ist in Arbeit!) gibt einen kurzen Überblick der Inhalte der Vorlesung. In der ersten Vorlesung (siehe Zoom Link in der rechten oberen Ecke) werden die Voraussetzungen besprochen, die man benötigt um einen benoteten bzw. unbenoteten Schein mit fünf Creditpoints zu erhalten.
Weiterführende Links

- Zoom Meeting Software
- Online-Lernplatform OLAT
- Online-Lernplatform Lon Capa
- Zusätzliches Angebot: Die von der Goethe-Universität anerkannte studentische Initiative TechAcademy bietet auch in diesem Semester rund 90 Studierenden die Möglichkeit, sich kostenlos Programmierkenntnisse in den Bereichen Data Science und Web Development anzueignen (siehe Anschreiben, Infoabend).
- Zusätzliches Angebot: Das Frankfurter Akademische Schlüsselkompetenz-Training bietet den Studierenden auch in diesem Wintersemester die Möglichkeit, Online-Workshops zu Studienkompetenzen zu besuchen (siehe Flyer, Selbstlernmaterialien).
Physik der sozio-ökonomischen Systeme mit dem Computer
(Physics of Socio-Economic Systems with the Computer)
Vorlesung WS 2021/22
Auch in diesem Semester findet die Vorlesung nur Online statt!
Diese Internetseite fasst die Online-Angebote der Vorlesung Physik der sozio-ökonomischen Systeme mit dem Computer zusammen. Auf der linken Seite finden Sie die einzelnen Vorlesungspräsentationen (pdf-Dateien), Computerprogramme und weiterführende Links. Die Vorlesungstermine (Zoom Meetings, synchrones Lehrangebot) finden jeweils freitags von 15.00-17.00 Uhr statt. An den Online-Übungen können Sie entweder freitags vor (13.30-15.00 Uhr) oder nach der Vorlesung (17:00-18:30 Uhr) teilnehmen (Beginn der Online-Übungen erst am 29.10.2021). Alle Lehrangebote werden mittel der Zoom Meeting Software gemacht und die jeweiligen Zoom-Links sind in der rechten oberen Ecke dieser Internetseite angegeben.
Die Inhalte der Vorlesung gliedern sich in drei Teile (Teil I, Teil II, Teil III), die Sie in der zweiten oberen Spalte einsehen können. Weiteres Zusatzmaterial und diverse Online-Aufgaben sind über die Online-Lernplattformen OLAT und Lon Capa erhältlich (siehe E-Learning).
Weiterführende Literatur
- Schlee, Walter, Einführung in die Spieltheorie, Vieweg 2004
- Hofbauer, Josef, and Karl Sigmund. Evolutionary games and population dynamics. Cambridge university press, 1998
- Martin A. Nowak, Evolutionary Dynamics - Exploring the Equations of Life, 2006
- Albert-Laszlo Barabasi, Network science, Cambridge university press, 2016
- Matthias Hanauske, Evolutionäre Quanten-Spieltheorie im Kontext sozio-ökonomischer Systeme, 2011
- Vorlesungsmaterialien: Neue Entwicklungen in der Evolutionären Spieltheorie (2009)
- Vorlesungsmaterialien: Hochschul-Sommerkurs
Money, Money, Money: Deutschlands Wirtschafts- und Finanzleben (2011)
Vorlesung 1
Bevor wir uns mit den Inhalten der Vorlesung beschäftigen, werden in der Vorlesung 1 einige technische Dinge erläutert.
Während der Vorlesung und in den Übungsstunden werden diverse Anwendungsprogramme (z.B. Maple oder Mathematica) und Simulationsprogramme (Python und Jupyter-Notebooks) von den Studenten selbst ausführt und bearbeitet. Die Teilnehmer der Vorlesung erhalten hierfür ein Account für die Rechner des Instituts für Theoretische Physik (ITP) der Goethe-Universität zu Verfügung gestellt. Mittels dieses Accounts können Sie einen Remote Login auf den Server des ITP machen und die benötigten Programme nutzen. Im Folgenden wird der Remote Login beschrieben und gezeigt wie man das Programm Maple startet. Im Gegensatz zu den Vorlesungen der vergangenen Jahre werden die computerunterstützten Berechnungen in diesem Wintersemester 2020/21 hauptsächlich mittels sogenannter Jupyter Notebooks durchführt.
Wie mache ich einen Remote Login auf den Server des ITP und starte ein der Maple-Worksheets?
Das nebenstehende Video beschreibt die einzelnen Schritte wie man einen Remote Login von einem Linux Betriebssystem zum Server des ITP aufbaut (weiteres siehe Graphical Remote Login with xrdp). Sie benötigen hierzu einen Account für die Rechner des ITP. Mittels des Remote Login können Sie sich durch einen Fernzugriff auf den Desktop des Servers des ITP verbinden und Anwendungsprogramme (z.B. Maple oder Mathematica) oder Simulationsprogramme (z.B. Python und Jupyter-Notebooks) ausführen und auf Ihrem Computer darstellen. Zusätzlich wird am Ende des Videos gezeigt wie man das Passwort des eigenen ITP-Accounts ändert (empfohlen!). Im zweiten Video wird gezeigt, wie man das Computeralgebra-System Maple startet und das Maple-Worksheet Maple Tutorium ausführt.
Einführung in Jupyter Notebooks
In den zugehörigen Übungsgruppen der Vorlesung werden wir die computerunterstützten Berechnungen hauptsächlich mittels sogenannter Jupyter Notebooks durchführen. In Jupyter Notebooks kann man die Programmiersprache Python in einer anwendungsfreundlichen Umgebung nutzen und die berechneten Ergebnisse auch gleich visualisieren. Auf den Computern des ITP kann man Jupyter Notebooks starten, indem man in einem Linux-Terminal den Befehl "jupyter-notebook" eingibt. Einige der in den Vorlesungen behandelten Jupyter Notebooks benutzen spezielle Python Module und Libraries (z.B sympy, siehe SymPy), die man im Linux-Terminal für den Python3-Kernel mittels des Befehls "pip3 install sympy" installieren kann. Da es sich bei den Jupyter Notebooks um eine frei zugängliche Open-Source-Software handelt, kann man diese auch direkt auf dem eigenen Computer/Laptop installieren und benötigt nicht den Umweg mittels des Remote Logins auf den Server des ITP. In der ersten Vorlesung (siehe Folien der 1.Vorlesung) wird kurz besprochen, wie man eine solche Installation durchführt. In der ersten Übungsstunde werden Hilfestellungen zu dem Remote Login und der Installation von Python/Jupiter gegeben und eine einführendes Jupyter Notebook besprochen. Dieses Notebook finden Sie unter dem folgenden Link (IntroJupyter.ipynb) und zu dem html-Export gelangen Sie durch Klicken auf des nebenstehende obere Bild.Weiterführende Links

- Folien der 1.Vorlesung
- Vorlesungsaufzeichnung der 1.Vorlesung (22.10.2021)
- Graphical Remote Login with xrdp
- Weitere Maple Worksheets: Physik mit dem Computer, Physik der sozio-ökonomischen Systeme, Physik der sozio-ökonomischen Systeme (alt), Das begleitende Dreibein, Der harmonische Oszillator mit Dämfung, Der harmonische Oszillator mit Dämfung, Allgemeine Relativitätstheorie mit Maple
- Einführung in die Programmierung mit Python von Dr. Georg Wille (aktuelle Vorlesung WS 21/22)
- Python-Onlinekurs auf Deutsch
- Python 3 documentation
Vorlesung 1
Nach einem kurzen Überblick in die Inhalte der gesamten Vorlesung wird in der ersten Vorlesung werden die Grundlagen der Spieltheorie vorgestellt (siehe Teil I). Im Gegensatz zur Physik, die die Gesetzmäßigkeiten der leblosen Materie/Energie und deren Wechselwirkungen in Raum und Zeit betrachtet, ist der wissenschaftliche Untersuchungsgegenstand der Spieltheorie (das zu erforschende Ding) der Mensch, und wir sind daran interessiert wie dieser sich bei ökonomischen oder sozial relevanten strategischen Entscheidungen verhält. Viele Wirtschafts- und Sozialwissenschaftler betrachten die Spieltheorie als die formale Sprache der ökonomischen Theorie.
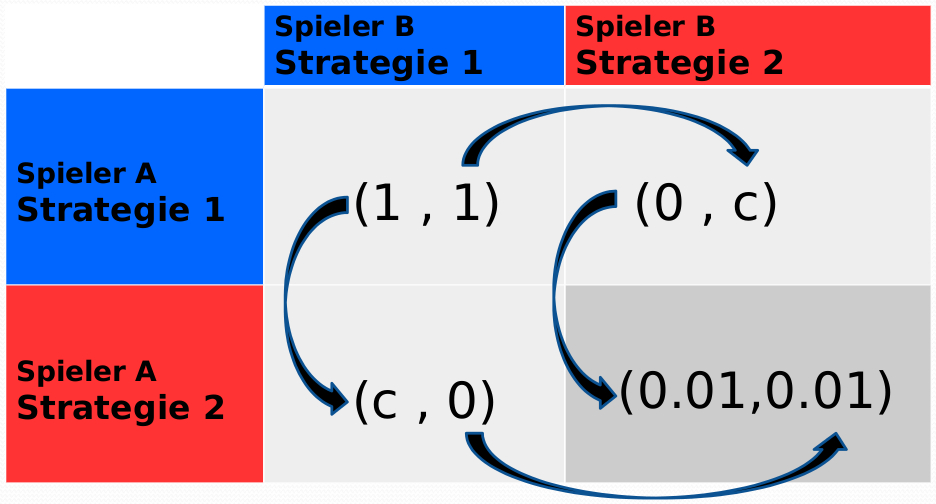
Im Prinzip benötigt man für die formale mathematische Definition eines Spiels lediglich die Angabe dreier Größen: Die Menge ${\bf \cal I}$ der Spieler, die Menge (der Raum) ${\bf \cal {S}}$ der Strategien der Spieler und ihre Auszahlungsfunktion (Präferenzordnungen) ${\bf \cal {\$}}$ (siehe I.1.1 Definition eines Spiels). Es wird der Spielbaum und die Auszahlungsmatrix eines simultanen (2 Personen)-(2 Strategien) Spiels (($2 \times 2$) Spiel) vorgestellt
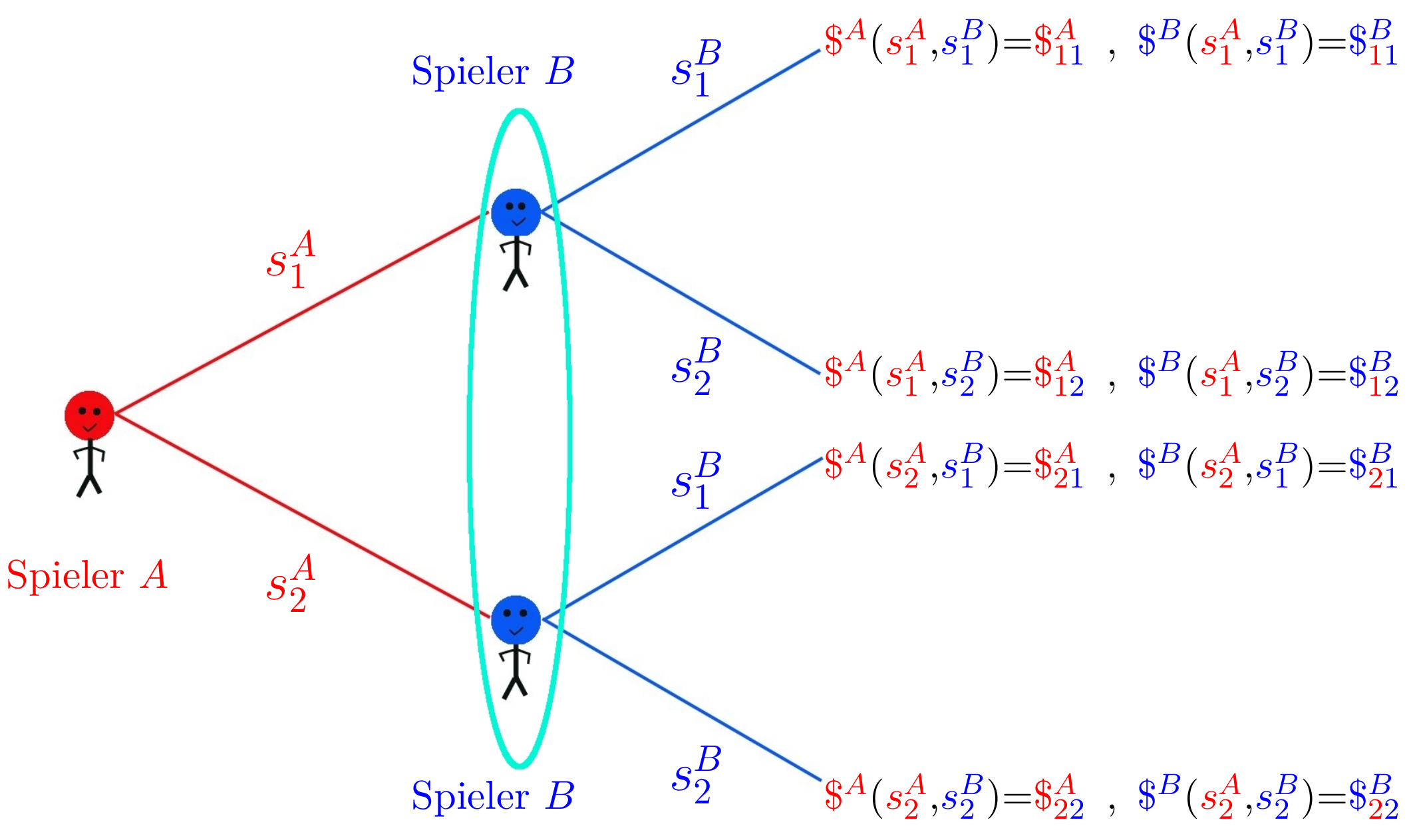
und anhand von mehreren bekannten klassischen Spielen wird das Konzept des Nash-Gleichgewichtes mittels der Bestantwort-Pfeile illustriert (siehe Gefangenendilemma, Hirschjagd- und Angsthasen-Spiel).
Im linken Panel finden Sie neben den Folien der auch mehrere Links zu technischen Dingen, die in der ersten Vorlesung besprochen werden.
Vorlesung 2
Wir betrachten im Folgenden die gemischte Erweiterung eines simultanen (2 Spieler)-(2 Strategien) Spiels in strategischer Form mit Auszahlung. Die Menge der gemischten Strategien des Spielers A (${\bf \tilde{\cal S}}^A$) und B (${\bf \tilde{\cal S}}^B$) kann als eine mathematische Verallgemeinerung der Menge der reinen Strategien (${\bf {\cal S}}^A$ und ${\bf {\cal S}}^B$) verstanden werden. Die einzelnen Elemente der Menge der gemischten Strategien eines Spielers $\mu=A,B$ ($\tilde{{\bf s}}^\mu=(\tilde{s}^\mu_1,\tilde{s}^\mu_2) \in {\bf \tilde{\cal S}}^\mu$) bestehen aus zwei reellwertigen Zahlen ($\tilde{s}^\mu_1 \in [0,1]$ und $\tilde{s}^\mu_2 \in [0,1]$) und können als die Wahrscheinlichkeit des Spielers $\mu$ zur Wahl der Strategie 1 ($\tilde{s}^\mu_1$) bzw. der Strategie 2 ($\tilde{s}^\mu_2$) interpretiert werden. Aufgrund der Normalisierungsbedingung (siehe Nash-Gleichgewichte in gemischten Strategien) $\tilde{s}^\mu_1 + \tilde{s}^\mu_2 =1 \,\, \forall \, \mu=A,B$ setzen wir $x:=\tilde{s}^A_1$ und $y:=\tilde{s}^B_1$, und somit $\tilde{s}^A_2=1-x$ und $\tilde{s}^B_2=1-y$.
Die gemischte Auszahlungsfunktion ${\bf \cal {\tilde{\$}}^\mu}(x,y)$ schreibt sich dann wie folgt
\[
\begin{eqnarray}
&&{\bf \tilde{\cal \$}}^\mu: \left( [0,1] \times [0,1] \right) \rightarrow ℝ \\
&& {\bf \tilde{\cal \$}}^\mu(x,y)=\$^\mu_{11}\, x y + \$^\mu_{12}\, x (1-y) + \$^\mu_{21} (1-x) y + \$^\mu_{22} (1-x) (1-y) \quad .\nonumber
\end{eqnarray}
\]
Ein Spezialfall des Nash-Gleichgewichtes besteht, falls die partielle Ableitung der gemischten Auszahlungsfunktion verschwindet. Man nennt dann ein solches Nash-Gleichgewicht $(x^{\star},y^{\star})$ ein internes Nash-Gleichgewicht bzw. ein Nash-Gleichgewicht in gemischten Strategien.
\[
\begin{eqnarray}
&&\left. \frac{ \partial {\bf \tilde{\cal \$}}^A(x,y)}{\partial x} \right|_{y=y^{\star}}=0 \quad \forall \,\,\, x \in [0,1] \,\,\, , \,\, y^{\star} \in ]0,1[
\nonumber\\
&&\left. \frac{ \partial {\bf \tilde{\cal \$}}^B(x,y)}{\partial y} \right|_{x=x^{\star}}=0 \quad \forall \,\,\, y \in [0,1] \,\,\, , \,\, x^{\star} \in ]0,1[\nonumber
\end{eqnarray}
\]
Beispiel: Das gemischte Nash-Gleichgewicht im Hirschjagd Spiel
In den unten angegebenen Links finden Sie das der Berechnung zugrundeliegende Jupyter Notebook und alternativ das entsprechende Maple Worksheet.
Weiterführende Links
Vorlesung 2
Das Konzept des Nash-Gleichgewichtes wurde in der letzten Vorlesung mittels der Bestantwort-Pfeile an mehreren klassischen Spielen illustriert. In dieser Vorlesung werden die beiden fundamentalen Gleichgewichtskonzepte der Spieltheorie, die dominante Strategien und die Nash-Gleichgewichte, formal mathematisch definiert. Die bisher dargestellten spieltheoretischen Konzepte basierten auf einer diskreten Strategiemenge der Spieler, die sogenannte Menge der reinen Strategien ${\bf \cal{S}}$. Wir erweitern nun die Menge der reinen Strategien ${\bf \cal{S}}$ zur Menge der gemischten Strategien ${\bf \tilde{\cal{S}}}$. Ein solches Spiel bezeichnet man als die gemischte Erweiterung eines simultanen ($N$ Spieler)-($m$ Strategien) Spiels in strategischer Form mit Auszahlung. Gemischte Strategien können als die Wahrscheinlichkeit des Spielers zur Wahl einer reinen Strategie verstanden werden. Es wird eine gemischte Auszahlungsfunktion der Spieler ${\bf \cal {\tilde{\$}}}$ formuliert und die beiden fundamentalen Gleichgewichtskonzepte der Spieltheorie in der gemischten Erweiterung definiert (siehe Nash-Gleichgewichte in gemischten Strategien). Das Konzept des Nash-Gleichgewichtes in gemischten Strategien (internes Nash-Gleichgewicht) wird am Beispiel des Hirschjagd- und Angsthasen-Spiels diskutiert.
Vorlesung 3
Im ersten Teil dieser Vorlesung wird gezeigt, dass sich symmetrische ($2 \times 2$) Spiele in die Spielklassen Dominante Spiele, Koordinationsspiele und Anti-Koordinationsspiele untergliedern lassen. Der zweite Teil befasst sich dann mit einer Einführung in die Evolutionäre Spieltheorie.
Klassifizierung von symmetrischen ($2 \times 2$) Spielen
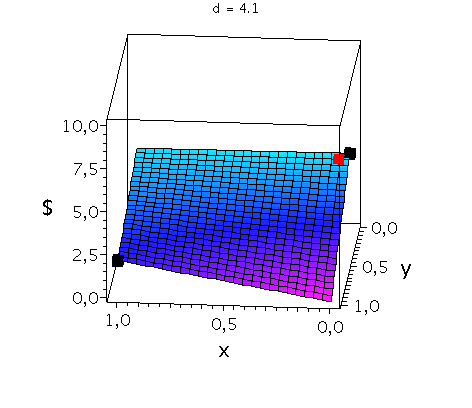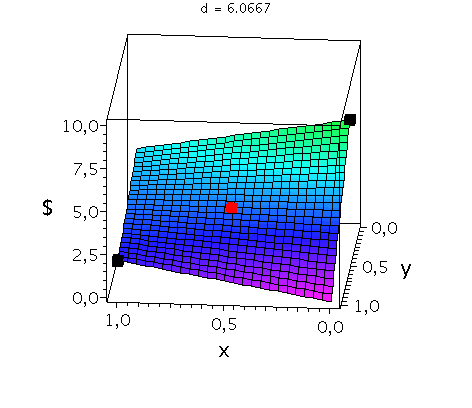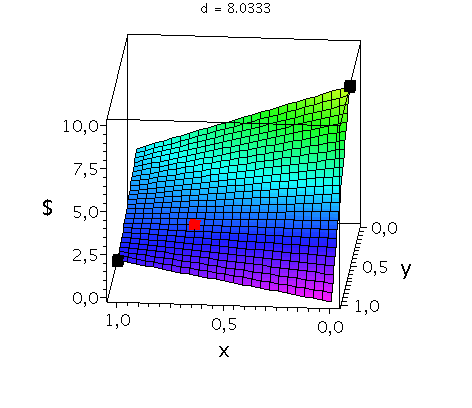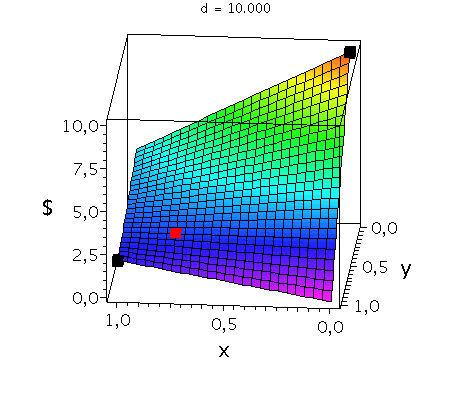
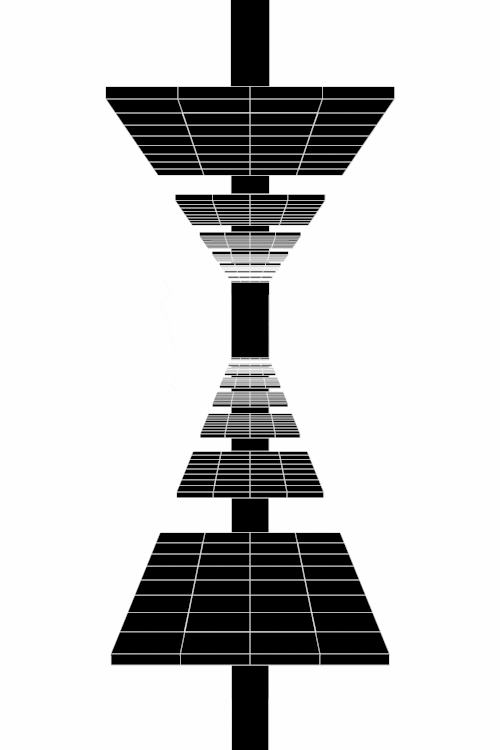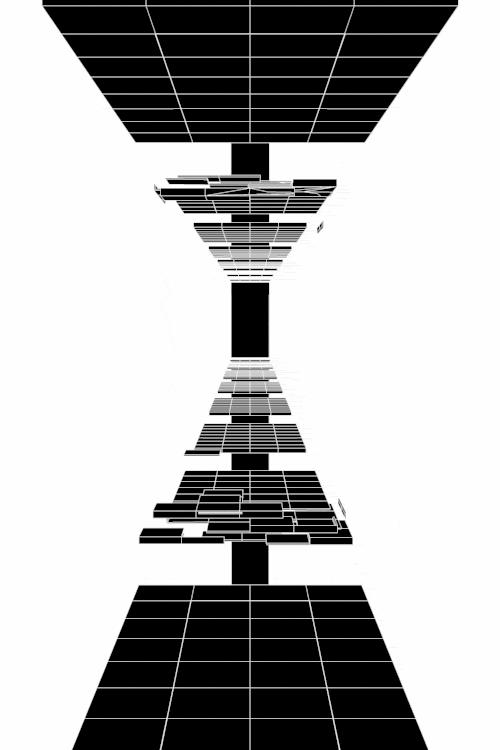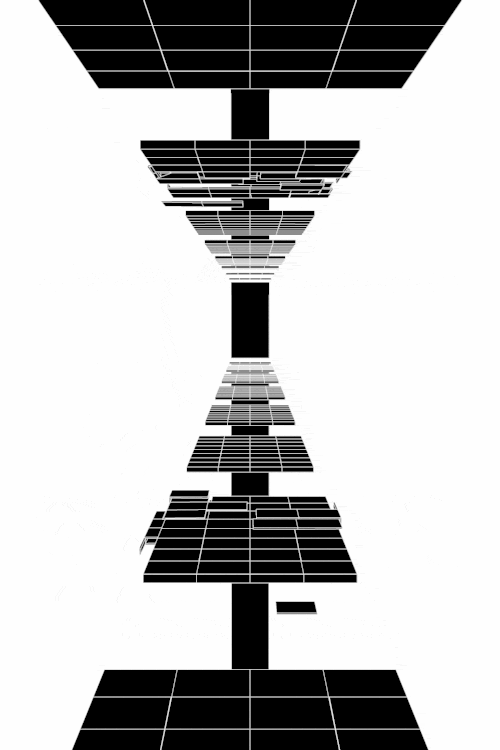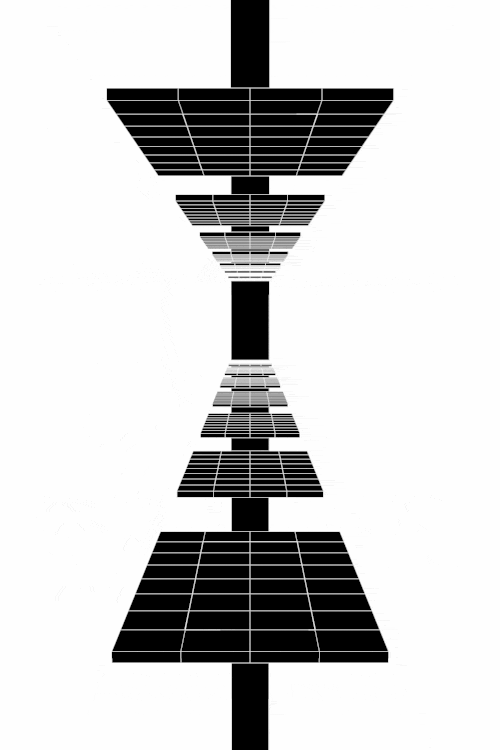
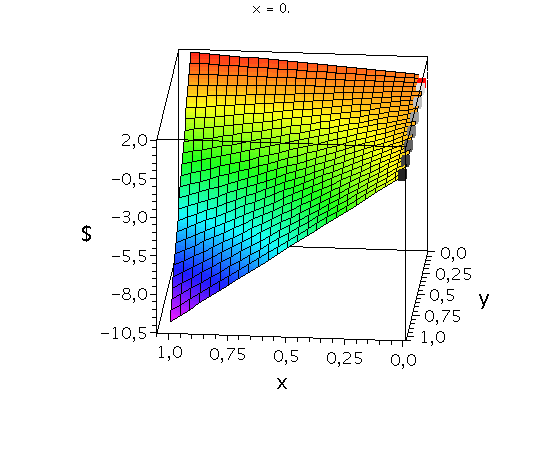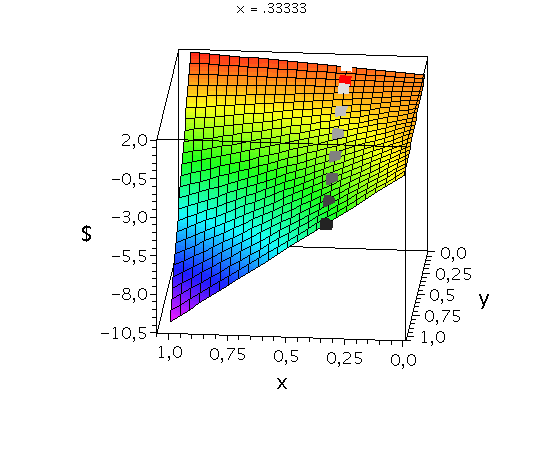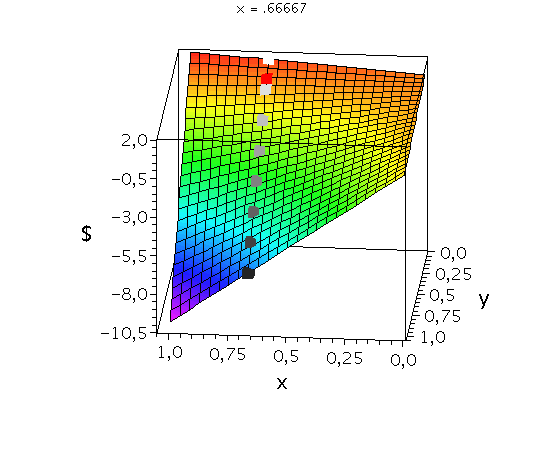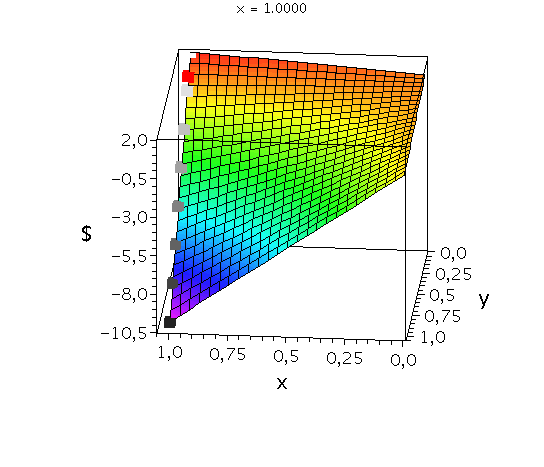
Anhand der Struktur der Nash-Gleichgewichte lassen sich symmetrische ($2 \times 2$) Spiele in drei Klassen untergliedern (siehe Klassifizierung von symmetrischen (2 Personen)-(2 Strategien) Spielen). Spiele der Klasse der Dominanten Spiele (z.B. Gefangenendilemma, Dilemma des Wettrüstens) besitzen nur ein Nash-Gleichgewicht, welches die dominante Strategie des Spiels ist (dominante Strategiekombination bei ${s}^{\dagger}=\left( {s}^{A\dagger}, {s}^{B\dagger} \right) =\left( {s}^{A*}, {s}^{B*} \right)$). Spiele der Klasse der Koordinationsspiele besitzen zwei symmetrische Nash-Gleichgewichte in reinen Strategien (Strategiekombinationen bei $\left( {s}^{A*}, {s}^{B*} \right) = \left( {s}^{A}_1, {s}^{B}_1 \right)$ und $\left( {s}^{A*}, {s}^{B*} \right) = \left( {s}^{A}_2, {s}^{B}_2 \right)$) und ein Nash-Gleichgewicht in gemischten Strategien $\left( \tilde{s}^{A\star},\tilde{s}^{B\star} \right)$, wobei $\tilde{s}^{A\star}=\tilde{s}^{B\star}$. Die Lage des gemischten Nash-Gleichgewichtes hängt von den speziellen Werten der Auszahlungsmatrix ab. Die nebenstehenden Abbildung zeigt die gemischte Auszahlungsfunktion des Spielers A im Hirschjagd-Spiel, wobei der Parameter d, welcher die Hälfte des Verkaufspreises des Hirsches darstellt, kontinuierlich von $d=4.1$ zu $d=10$ variiert wurde. Die beiden schwarzen Rechtecke stellen die Nash-Gleichgewichte in reinen Strategien dar ($\left( x^{*}, y^{*} \right) = \left( 0, 0 \right)$ und $\left( x^{*}, y^{*} \right) = \left( 1, 1 \right)$) und das rote Rechteck zeigt die sich verändernde Lage des gemischten Nash-Gleichgewichtes. Zuletzt, Spiele der Klasse der Anti-Koordinationsspiele (z.B. Angsthasen-Spiel, Chicken Game, Spiel mit dem Untergang) besitzen zwei asymmetrische Nash-Gleichgewichte in reinen Strategien (Strategiekombinationen bei $\left( {s}^{A*}, {s}^{B*} \right) = \left( {s}^{A}_1, {s}^{B}_2 \right)$ und $\left( {s}^{A*}, {s}^{B*} \right) = \left( {s}^{A}_2, {s}^{B}_1 \right)$) und ein Nash-Gleichgewicht in gemischten Strategien $\left( \tilde{s}^{A\star},\tilde{s}^{B\star} \right)$, wobei $\tilde{s}^{A\star}=\tilde{s}^{B\star}$.
Einführung in die Evolutionäre Spieltheorie
Das im rechten Panel dieser Vorlesung dargestellte System von gekoppelten nichtlinearen Differentialgleichungen erster Ordnung beschreibt die evolutionäre Dynamik der deterministischen evolutionären Spieltheorie (Replikatordynamik). Die zeitliche Veränderung der Populationsvektoren $\vec{x}^A(t)=(x^A_1(t), x^A_2(t), ..., x^A_{m_A}(t))$ und $\vec{x}^B(t)=(x^B_1(t), x^B_2(t), ..., x^B_{m_B}(t))$ spiegelt die in der jeweiligen Gruppe vorherrschende Strategiewahl zum Zeitpunkt $t$ wider. In expliziter Formulierung hat die Gleichung das folgende Aussehen: \[ \begin{eqnarray} \frac{d x^A_i(t)}{dt} &=& \left[ \underbrace{\sum_{l=1}^{m_{\small B}} \$^A_{il} \, x^B_l(t)}_{\hbox{Fitness der Strategie i}} - \underbrace{\sum_{l=1}^{m_{\small B}} \sum_{k=1}^{m_{\small A}} \$^A_{kl} \, x^A_k(t) \, x^B_l(t)}_{\hbox{Durchschn. Fitness der Population A}} \right] \, x^A_i(t) \qquad \hbox{(1)} \nonumber \\ \frac{d x^B_j(t)}{dt} &=& \left[ \underbrace{\sum_{l=1}^{m_{\small A}} \$^B_{lj} \, x^A_l(t)}_{\hbox{Fitness der Strategie j}} - \underbrace{\sum_{l=1}^{m_{\small A}} \sum_{k=1}^{m_{\small B}} \$^B_{lk} \, x^A_l(t) \, x^B_k(t)}_{\hbox{Durchschn. Fitness der Population B}} \right] \, x^B_j(t) \quad , \nonumber \end{eqnarray} \] wobei $x^A_i(t), \, i=1, 2, ...,m_{\small A}$ und $x^B_j(t), \, j=1, 2, ...,m_{\small B}$ die Anteile der in den Spielergruppen A und B zur Zeit $t$ gewählten Strategien widerspiegeln und in der Soziobiologie den Frequenzen der Quasispezies entsprechen. Durch eine Beschränkung auf nur zwei Strategien ($m_{\small A}=m_{\small B}=2$) und symmetrische Spiele ($\hat{\bf {\cal \$}}^A = \left( \hat{\bf {\cal \$}}^B \right)^{\!T}$) vereinfacht sich das System der Differentialgleichungen (siehe Die Gleichungen der evolutionären Dynamik und das Jupyter Notebook Evolutionäre Spieltheorie symmetrischer (2x2)-Spiele).Weiterführende Links

- Folien der 3.Vorlesung
- Vorlesungsaufzeichnung der 3.Vorlesung
- Maple Worksheet: Klassifizierung von symmetrischen (2 Personen)-(2 Strategien) Spielen
- View Jupyter Notebook: Evolutionäre Spieltheorie symmetrischer (2x2)-Spiele
- Download Jupyter Notebook: Evolutionäre Spieltheorie symmetrischer (2x2)-Spiele
Vorlesung 3
In dieser Vorlesung werden zunächst die unterschiedlichen Spieltypen der gemischten Erweiterung eines simultanen (2 Spieler)-(2 Strategien) Spiels in strategischer Form mit symmetrischer Auszahlungsmatrix klassifiziert. Abhängig von den gewählten Parametern der Auszahlungsmatrix lassen sich symmetrische ($2 \times 2$) Spiele in drei unterschiedliche Spielklassen gliedern: Dominante Spiele, Koordinationsspiele und Anti-Koordinationsspiele (siehe Klassifizierung von symmetrischen (2 Personen)-(2 Strategien) Spielen oder Martin A. Nowak, Evolutionary Dynamics - Exploring the Equations of Life, 2006 (siehe Seite 49-51)).
Die bisher betrachteten Spiele stellen einfachste spieltheoretische Systeme dar. Eine Ausweitung auf mehr Strategien und mehr Spieler bzw. eine Betrachtung unsymmetrischer, sogenannter Bimatrix-Spiele erweitert den Raum der möglichen Spielklassen. Neben den einmalig gespielten simultanen Spielen können auch wiederholte Spiele in extensiver Form und somit eine zeitabhängige Strategiewahl der Spieler betrachtet werden (siehe z.B. Schlee, Walter, Einführung in die Spieltheorie, Vieweg 2004 (siehe Seite 91-116)), oder kooperative Spiele mittels einer Bildung von Spielerkoalitionen definiert werden (siehe z.B. Schlee, Walter, Einführung in die Spieltheorie, Vieweg 2004 (siehe Seite 117-168)).
Im Folgenden wird das zeitabhängige Strategieverhalten einer Gruppe von Spielern untersucht. Die evolutionäre Spieltheorie betrachtet das zeitliche Verhalten einer ganzen Population von Spieler (unendliche Anzahl von Spielern $N \rightarrow \infty$). Die einzelnen Spieler der Population paaren sich zufällig und spielen ein simultanes ($2 \times m$) Spiel, erhalten ihre erzielten Auszahlungen und paaren sich dann erneut um das gleiche Spiel immer wiederkehrend zu spielen. Gegeben sei die strategische Form eines, zunächst noch unsymmetrischen (2 Personen)-(m Strategien) Spiels $\Gamma$. $x^\mu_i(t)$ ($i=1, 2, ..., m_\mu$ und $\mu=A,B$) seien die zeitabhängigen, gemittelten Anteile der Spieler innerhalb der Spielergruppe $\mu=A,B$, die die Strategie i wählen; sie entsprechen somit einer Art von gemischten Strategie der gesamten Populationsgruppe.
Die zeitliche Veränderung der Populationsvektoren $\vec{x}^A(t)$ und $\vec{x}^B(t)$ spiegelt die in der Gruppe vorherrschende Strategiewahl zum Zeitpunkt $t$ wider und sind durch folgende Differentialgleichung bestimmt (siehe Die Gleichungen der evolutionären Dynamik und Schlee, Walter, Einführung in die Spieltheorie, Vieweg 2004, Seite 169-188)):
\[
\begin{eqnarray}
\frac{d \vec{x}^A}{dt} &=& \hat{\bf x}^A \left( \hat{\bf {\cal \$}}^A\,\vec{x}^B \right) - \left(\left(\hat{\bf {\cal \$}}^A\,\vec{x}^B \right)^T \vec{x}^A \right) \vec{x}^A \nonumber \\
\frac{d \vec{x}^B}{dt} &=& \hat{\bf x}^B \left( \hat{\bf {\cal \$}}^B\,\vec{x}^A \right) - \left(\left(\hat{\bf {\cal \$}}^B\,\vec{x}^A \right)^T \vec{x}^B \right) \vec{x}^B \quad ,\nonumber
\end{eqnarray}
\]
wobei $\hat{\bf x}^\mu:={\rm diag\!}\left( x^\mu_1(t), x^\mu_2(t), ..., x^\mu_{m_\mu}(t) \right)$. Die maßgeblichen Faktoren, die die evolutionäre Entwicklung bestimmen sind der Soziobiologie entnommen und basieren auf Reproduktion, Mutation und Selektion der Strategieentscheidungen. Die zugrundeliegende mathematische Beschreibung und Herleitung der Gleichung lehnt sich an die, in der theoretischen Biologie verwendete, sogenannte Quasispezies-Gleichung (siehe M.A. Nowak, Evolutionary Dynamics - Exploring the Equations of Life, 2006, S: 33) an.
Vorlesung 4
Die Lösungen der im rechten Panel dargestellten Differentialgleichungen der evolutionäre Spieltheorie werden in dieser Vorlesung nummerisch gelöst und die möglichen zeitlichen Entwicklungen der Populationen in Klassen untergliedert. Die entsprechenden Python Programme, Jupyter Notebooks und Maple Worksheets finden Sie weiter unten unter Weiterführende Links.
Evolutionäre symmetrische ($2 \times 2$) Spiele
Evolutionäre unsymmetrische ($2 \times 2$) Spiele (Bi-Matrix Spiele)
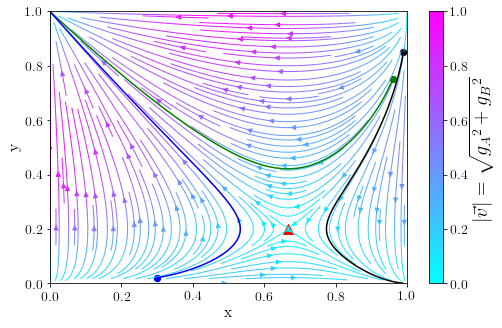
Die im oberen Bereich des rechten Panels dieser Vorlesung dargestellten Gleichungen der Reproduktionsdynamik lassen sich nach Spezifikation der Auszahlungsmatrizen $\hat{\bf {\cal \$}}^A$ und $\hat{\bf {\cal \$}}^B$ auf unterschiedlichste Populationsspiele anwenden. Generell lassen sich evolutionäre unsymmetrische ($2 \times 2$) Spiele in die folgenden drei Spielklassen gliedern: Eckenspiele, Sattelpunktspiele und Zentrumsspiele. Ein Eckenspiel liegt vor, falls zumindest eine der Auszahlungsmatrizen der Spielergruppen eine dominante Struktur hat. Aufgrund der Dominanz der Strategie endet die zeitliche Entwicklung der Populationen, unabhängig von der Anfangsbedingungen, in einer Ecke des x-y Populationsvektor Diagramms - die ESS des Eckenspiels. Ein Sattelpunktspiel liegt vor, falls beide Spielergruppen gleichzeitig ein Koordinationsspiel oder Anti-Koordinationsspiel spielen. Bei einem Sattelpunktsspiel das aus zwei Anti-Koordinationsspielen besteht, existieren zwei ESSs ((x=0,y=1) oder (x=1,y=0)) zu denen sich die Populationsgruppen im Laufe der Zeit entwickeln. Welche dieser evolutionär stabilen Strategien erreicht wird, hängt von der Anfangsstrategiewahl der Population ab. Die nebenstehende Abbildung zeigt die zeitliche Entwicklung von drei Anfangszuständen in einem solchen Eckenspiel. Auch bei sehr ähnlichen Werten der Anfangsstrategiewahl kann es geschehen, dass sich die Population im Laufe der Zeit zu unterschiedlichen Ecken entwickelt (siehe grüne und schwarze Trajektorien). Eine besondere Bedeutung hat der Sattelpunkt des Spiels (siehe rotes Dreieck). Die Position des Sattelpunktes im x-y Diagramm entspricht dem Wert des gemischten Nash-Gleichgewichtes bzw. lässt sich durch die Nullstellen der Funktionen $g_A(x,y)$ und $g_B(x,y)$ bestimmen. Bei einem Zentrumsspielen existiert keine ESS, da die Strategiewahl der Population sich im Laufe der Zeit ständig verändert und um ein Zentrum kreist. Die Position dieses Zentrums im x-y Diagramm entspricht dem Wert des gemischten Nash-Gleichgewichtes bzw. lässt sich durch die Nullstellen der Funktionen $g_A(x,y)$ und $g_B(x,y)$ bestimmen (siehe Evolutionäre Spieltheorie unsymmetrischer (2x2)-Spiele).Weiterführende Links


- Folien der 4.Vorlesung
- Vorlesungsaufzeichnung der 4.Vorlesung
- View Jupyter Notebook: Evolutionäre Spieltheorie symmetrischer (2x2)-Spiele
- Download Jupyter Notebook: Evolutionäre Spieltheorie symmetrischer (2x2)-Spiele
- Download Python Programm: Evolutionäre Spieltheorie symmetrischer (2x2)-Spiele
- View Jupyter Notebook: Evolutionäre Spieltheorie unsymmetrischer (2x2)-Spiele
- Download Jupyter Notebook: Evolutionäre Spieltheorie unsymmetrischer (2x2)-Spiele
- Download Python Programm: Evolutionäre Spieltheorie unsymmetrischer (2x2)-Spiele
- Maple Worksheet: Klassifizierung von symmetrischen evolutionären (2x2)-Spielen
- Maple Worksheet: Evolutionäre Bi-Matrix Spiele
Vorlesung 4
In der vorigen Vorlesung wurden die zugrundeliegenden Differentialgleichungen der evolutionäre Spieltheorie für zeitlich sich wiederholende, unsymmetrische (2 Personen)-(m Strategien) Spiele dargestellt. Wir beschränken uns im Folgenden auf den 2-Strategien Fall ($m_{\small A}=m_{\small B}=2$), lassen jedoch weiter eine Unsymmetrie der Auszahlungsmatrix zu (evolutionäre Bi-Matrix Spiele). Die beiden Komponenten der zweidimensionalen gruppenspezifischen Populationsvektoren lassen sich dann, aufgrund ihrer Normalisierungsbedingung, auf eine Komponente reduzieren ($x^A_2=1-x^A_1$ und $x^B_2=1-x^B_1$). Das zeitliche Verhalten der Komponenten der Populationsvektoren (Gruppe A: $x(t):=x^A_1(t)$ und Gruppe B: $y(t):=x^B_1(t)$) wird in der Reproduktionsdynamik mittels des folgenden Systems von Differentialgleichungen beschrieben: \[ \begin{eqnarray} &&\frac{d x(t)}{dt} \,=\, g_A(x,y) \quad, \quad \frac{d y(t)}{dt} \,=\, g_B(x,y)& \nonumber \\ g_A(x,y) &:=& \left[ \left( \$^A_{11} + \$^A_{22} - \$^A_{12} - \$^A_{21} \right) \,y(t) + \right. \nonumber \\ && + \left. \left( \$^A_{12} - \$^A_{22}\right) \right] \,\left( x(t) - \left( x(t) \right)^2 \right) \nonumber \\ g_B(x,y) &:=& \left[ \left( \$^B_{11} + \$^B_{22} - \$^B_{12} - \$^B_{21} \right) \,x(t) + \right. \nonumber \\ && + \left. \left( \$^B_{12} - \$^B_{22}\right) \right] \,\left( y(t) - \left( y(t) \right)^2 \right) \end{eqnarray} \] In dieser Vorlesung betrachten wir jedoch zunächst die Lösungen der Differentialgleichung für sich wiederholende, symmetrische (2 Personen)-(2 Strategien) Spiele. Aufgrund der Symmetrie des Spiels besteht die betrachtete Population nun nur aus einer Gruppe von ununterscheidbaren Spielern (beschrieben durch den Populationsvektor $x(t)$). Die Replikatordynamik der evolutionäre Spieltheorie vereinfacht sich in diesem Spezialfall auf nur eine nichtlineare Differentialgleichung erster Ordnung: \[ \begin{eqnarray} \frac{d x(t)}{dt} &=& \left[ (\$_{11} - \$_{21}) (x-x^2) + (\$_{12} - \$_{22}) (1-2x+x^2) \right] \, x(t) \nonumber \\ &=:&\,g(x) \end{eqnarray} \] Im linken Panel dieser Vorlesung werden die Lösungen der Differentialgleichungen nummerisch berechnet und analysiert. In Abhängigkeit der zugrundeliegenden Spielklasse des evolutionären Spiels sind unterschiedliche evolutionär stabilen Strategien möglich (siehe Evolutionär stabile Strategien).
Vorlesung 5
Die Lösungen der im rechten Panel dargestellten Differentialgleichung der evolutionäre Spieltheorie von symmetrischen ($2 \times 3$) Spielen wird in dieser Vorlesung nummerisch gelöst und die entstehenden zeitlichen Entwicklungen der Population in 19 Klassen untergliedert. Die entsprechenden Python Programme, Jupyter Notebooks und Maple Worksheets finden Sie weiter unten unter Weiterführende Links. Danach werden die möglichen Anwendungsfelder der evolutionären Spieltheorie an mehreren Beispielen illustriert.
Evolutionäre symmetrische ($2 \times 3$) Spiele
Die Replikatordynamik von symmetrischen ($2 \times 3$) Spielen erlaubt eine Vielzahl von möglichen zeitlichen Entwicklungen der Population. E. C. Zeeman konnte in seinem im Jahre 1980 veröffentlichten Artikel zeigen (siehe E.C. Zeeman, POPULATION DYNAMICS FROM GAME THEORY, In: Global Theory of Dynamical Systems, Springer 1980), dass man evolutionäre, symmetrische (2x3)-Spiele in 19 Klassen einteilen kann. Es gibt Spielklassen, die besitzen lediglich eine evolutionär stabile Strategie und Klassen die sogar drei evolutionär stabile Strategien besitzen. Die untere Animation illustriert die möglichen zeitlichen Entwicklungen der Population an drei dieser Zeeman-Spielklassen. Die weiteren Spielklassen werden in dem folgenden Jupyter Notebook dargestellt: View Jupyter Notebook: Die 19 Klassen der evolutionären symmetrischen (2x3)-Spiele.
Anwendungsfelder der Spieltheorie
Spieltheoretische Konzepte werden in den unterschiedlichsten Fachdisziplinen angewandt und reichen von den Wirtschaftswissenschaften, der Soziologie hin zur Biologie. Der Arbeitskreis des Fachverbandes der Deutsche Physikalische Gesellschaft (siehe DPG-Fachverband: Physik der sozio-ökonomischen Systeme befasst sich mit diesem stark interdisziplinären Forschungsfeld und diverse Anwendungsfelder werden auf den jährlichen Fachtagungen diskutiert. Im Folgenden werden einige Beispiele von Anwendungsfeldern der Spieltheorie und weiterführende Literaturlinks aufgelistet.Anwendungsbeispiele im Bereich der Ökonomie
- Experimentelle Ökonomie am Beispiel des Gefangenendilemmas
- Vertrauen und Fairness in Allgemeingüter Spielen
- Kooperation und Fairness am Beispiel von Markt- und Ultimatum-Spielen
- Die Finanzkrise als Falke-Taube Spiel
- Evolutionäre Dynamik im Öffentliche-Güter-Spiel
- Spieltheorie und Auktionskonzepte (Nobelpreis für Wirtschaftswissenschaften 2020)
- Das Buch von Martin A. Nowak Evolutionary Dynamics - Exploring the Equations of Life, 2006 diskutiert mehrere Anwendungsfelder der evolutionären Spieltheorie im Bereich der Biologie, wie z.B. die evolutionäre Dynamik von Krebs, HIV Infektion und die Evolution der Virulenz.
- Paarungsverhalten einer Eidechsenpopulation als evolutionäres symmetrisches (2x3)-Spiel
- Evolutionäre Entwicklung von Makro-Molekülen
- Das Gefangenendilemma eines RNA-Virus
- Evolution von sozialen Normen
- Evolution der Moral
- Evolution der Sprachentwicklung einer Population
- Das Buch von Martin A. Nowak Evolutionary Dynamics - Exploring the Equations of Life, 2006 diskutiert auch am Ende die Evolution der Sprachentwicklung einer Population.
- Anwendungen in den Politikwissenschaften
- Die Entstehung einer dritten Strategie im Elfmeter-Spiel (Neeskens Effekt)
Weiterführende Links


- Folien der 5.Vorlesung
- Vorlesungsaufzeichnung der 5.Vorlesung
- View Jupyter Notebook: Die 19 Klassen der evolutionären symmetrischen (2x3)-Spiele
- Download Jupyter Notebook: Die 19 Klassen der evolutionären symmetrischen (2x3)-Spiele
- Maple Worksheet: Klassifizierung von symmetrischen evolutionären (2x3)-Spielen
- Maple Worksheet: Äquivalenz der Räuber-Gleichung für N-Populationen mit der Replikatorgleichung der evolutionären Spieltheorie für (N+1)-Strategien
Vorlesung 5
Die in der letzten Vorlesung analysierten evolutionären Spiele waren auf nur zwei reine Strategien beschränkt. Wir betrachten in dieser Vorlesung den Fall, dass eine Population ein wiederholtes (2 Personen)-(3 Strategien) Spiel spielt und beschränken uns dabei auf symmetrische Spiele. Symmetrische ($2\times m$)-Spiele werden durch die folgende Differentialgleichung beschrieben: \[ \begin{equation} \frac{d \vec{x}}{dt} = \hat{\bf x} \left( \hat{\bf {\cal \$}}\,\vec{x} \right) - \left(\left(\hat{\bf {\cal \$}}\,\vec{x} \right)^T \vec{x} \right) \vec{x} \end{equation} \] Aufgrund der Symmetrie der Auszahlungsmatrix $\hat{\bf {\cal \$}} = \hat{\bf {\cal \$}}^A = \left( \hat{\bf {\cal \$}}^B \right)^{\!T}$ kann die zeitliche Entwicklung solcher Spiele durch nur einen Populationsvektor ($\vec{x}(t)=(x_1(t), x_2(t), ..., x_{m}(t))$ beschrieben werden. Wir beschränken uns im Folgenden auf den Fall $m=3$ und setzen die Auszahlungsmatrix wie folgt an: \[ \begin{equation} \hat{\bf {\cal \$}} = \left( \begin{array}{rrr} \$_{11} & \$_{12} & \$_{13}\\ \$_{21} & \$_{22} & \$_{23}\\ \$_{31} & \$_{32} & \$_{33}\\ \end{array} \right) \end{equation} \] Aufgrund der Normalisierungsbedingung des Populationsvektors kann man den Anteil der Population, die z.B. die Strategie 1 ($s_1$) spielen durch die anderen beiden Anteile ausdrücken: $x_1(t)=1 - x_2(t) - x_3(t)$, so dass die Replikatordynamik effektiv ein System von zwei gekoppelten, nichtlinearen Differentialgleichungen erster Ordnung darstellt. Nach Festlegung der Auszahlungsmatrix kann man die zeitliche Entwicklung der Strategiewahl der Population am besten in einem baryzentrischen Dreiecks-Koordinatensystem veranschaulichen, wobei der x-Achsen Wert durch $x:=x_2+x_3/2$ und der y-Achsen Wert durch $y:=x_3$ definiert ist. E. C. Zeeman konnte im Jahre 1980 zeigen, dass man evolutionäre, symmetrische (2x3)-Spiele in 19 Klassen einteilen kann (siehe E.C. Zeeman, POPULATION DYNAMICS FROM GAME THEORY, In: Global Theory of Dynamical Systems, Springer 1980). Im linken Panel dieser Vorlesung werden diese Lösungen in einem Jupyter Notebook nummerisch berechnet und analysiert. Zusätzlich werden im linken Panel mögliche Anwendungsfelder der Spieltheorie vorgestellt.
Vorlesung 6
In dieser und der darauf folgenden Vorlesung werden wir uns mit der Theorie der komplexen Netzwerke befassen (siehe Teil II: Theorie der sozio-ökonomischen Netzwerke). Um die Eigenschaften komplexer Netzwerke beschreiben und analysieren zu können werden wir zunächst die wichtigsten charakteristischen Größen eines Netzwerks darstellen. Danach befassen wir uns mit den zufälligen Netzwerken.
Einführung in die Theorie der komplexen Netzwerke
Ein Netzwerk wird formal mittels graphentheoretischer Größen beschrieben. Wir nehmen im Folgenden zunächst ein ungerichtetes, ungewichtetes Netzwerk bestehend aus einer Knotenart an, wobei $N$ die Anzahl der Knoten und $L$ die gesamte Anzahl der Links (Kanten) des Netzwerks ist. Jeder einzelne Knoten $i$ ($i \in \{1,2,3, ..., N \}$) besitzt eine gewisse Anzahl von Verbindungskanten zu anderen Knoten und die Anzahl dieser Kanten bezeichnet man als den Knotengrad $k_i$ des Knotens. Der durchschnittliche Knotengrad $ {<} k {>} $ eines ungerichteten Netzwerks ist ${<} k {>}=\frac{2 L}{N}$ und die maximale Anzahl möglicher Kanten ($L_{max} $) (ein sogenannter vollständiger Graph) ist $L_{max} =\frac{N (N-1)}{2}$. Eine der wichtigsten Netzwerk-charakterisierenden Größen ist die Verteilungsfunktion der Knotengrade $P(k)=N(k)/N$, wobei $N(k)$ die Anzahl der Knoten mit Knotengrad $k$ beschreibt. Weitere wichtige graphentheoretische Größen werden in dem Jupyter Notebook: Einführung in die Theorie der komplexe Netzwerke behandelt (siehe auch Einführung in die Theorie der komplexen Netzwerke und Albert-Laszlo Barabasi, Network science, Chapter 2 Graph Theory).
Zufällige Netzwerke (random networks)
Kleine Welt Netzwerke (small world networks)
"Kleine Welt"-Netzwerke zeichnen sich durch einen kleinen Wert der durchschnittlichen kürzesten Verbindung zwischen den Knoten des Netzwerkes und einem großen Wert des Clusterkoeffizienten aus. Ein einfaches Modell welches den Übergang von einem Netzwerk mit regulärer Struktur (Gitter-ähnlicher Struktur) über ein "kleines Welt"-Netzwerk hin zu einem zufälligen Netzwerk veranschaulicht, ist das sogenannte Watts-Strogatz Modell: Man startet z.B. mit einer eindimensionalen Gitter-Struktur bestehend aus N Knoten und löscht mit der Wahrscheinlichkeit p die existierenden Kanten und fügt stattdessen neue Kanten in zufälliger Weise hinzu.Weiterführende Links


- Folien der 6.Vorlesung
- Vorlesungsaufzeichnung der 6.Vorlesung
- View Jupyter Notebook: Einführung in die Theorie der komplexe Netzwerke
- Download Jupyter Notebook: Einführung in die Theorie der komplexe Netzwerke
- View Jupyter Notebook: Zufällige komplexe Netzwerke (random networks)
- Download Jupyter Notebook: Zufällige komplexe Netzwerke (random networks)
- View Jupyter Notebook: Kleine Welt Netzwerke (small world networks)
- Download Jupyter Notebook: Kleine Welt Netzwerke (small world networks)
- Download Python Programm: Zufälliges komplexes Netzwerk
- Download Python Programm: Mittelung mehrerer zufälliger komplexer Netzwerke
- Download Python Programm: Kleine Welt Netzwerke (Watts-Strogatz Modell)
Vorlesung 6
Die in der letzten Vorlesungen dargestellten Gleichungen und Lösungen der evolutionären Spieltheorie basierten alle auf der Einschränkung einer vereinfachten zugrundeliegenden Netzwerkstruktur (Netzwerktopologie) der Spieler. Die jeweiligen Spieler der betrachteten Population suchen in jeder Spielperiode einen neuen Spielpartner, wobei sie hierbei zufällig vorgehen (zufälliges Netzwerk) und vom Prinzip her mit jedem Spieler innerhalb der Population potenziell das zugrundeliegende Spiel spielen können (vollständig verbundenes Netzwerk). In Bimatrix Spielen suchen sich die Spieler der Teilpopulation A einen zufälligen Spielpartner aus Gruppe B (bzw. umgekehrt). Betrachtet man sich jedoch real existierende sozio-ökonomische Netzwerke, so zeigt sich, dass diese Annahme oft nicht erfüllt ist. Personen kennen oft nur eine Teilmenge von Spielern innerhalb der Population (kein vollständig verbundenes Netzwerk) und die Wahl der potenziellen Spielpartner erfolgt oft auch nicht nach zufälligen Mustern.
Die Theorie der komplexen Netzwerke ist ein eigenständiges interdisziplinäres Forschungsfeld das seine Anwendung in einer Vielzahl von unterschiedlichen biologischen und sozio-ökonomischen Systemen findet. Da diese Theorie aus dem mathematischen Zweig der Graphentheorie entstanden ist benutzt sie nicht die mathematischen Ausdrücke der Spieltheorie. Man spricht z.B. nicht von Spielern, sondern von Knoten (bzw. Vertices) und die Verbindungen zwischen den Knoten werden als Kanten (bzw. Links) bezeichnet. Die sich zu Beginn des 21. Jahrhunderts rasant entwickelnde Network Science
umfasst Anwendungsfelder wie die sozialen Netzwerke (z.B. berufliche, freundschaftliche und familiäre Kontakte), die Kommunikationsnetzwerke (z.B. Internet, Facebook, Twitter), die Energie- und Stromnetzwerke der Generatoren und Übertragungsleitungen, die neuronalen Netzwerke zur Erklärung der Funktionsweise des Gehirns, die Genen- Proteinen und zellulare Netzwerke und viele weitere Interaktionen zwischen Systemkomponenten.
Formal lassen sich komplexe Netzwerke in verschiedene Typen untergliedern: Netwerke mit nur einer Knotenart oder Netzwerke bestehend aus mehreren Knotenarten, gerichtet und ungerichtet Netzwerke, gewichtete und ungewichtete Netzwerke und zeitlich anwachsende oder abnehmende Netzwerke (näheres siehe Einführung in die Theorie der komplexen Netzwerke).
Die Theorie der komplexen Netzwerke und deren Anwendungsfelder ist in der frei zugängliche Onlineversion des Buches Network Science von Albert-Laszlo Barabasi sehr schön dargestellt und ich empfehle dieses Buch im Besonderen.
Vorlesung 7
In dieser Vorlesung werden die Eigenschaften von exponentiellen und skalenfreien Netzwerken thematisiert und die zugrundeliegenden Prinzipien ihrer Entstehung besprochen.
Exponentielle Netzwerke
Skalenfreie Netzwerke
Weiterführende Links




- Folien der 7.Vorlesung
- Vorlesungsaufzeichnung der 7.Vorlesung
- View Jupyter Notebook: Exponentielle und skalenfreie Netzwerke
- Download Jupyter Notebook: Exponentielle und skalenfreie Netzwerke
- View Jupyter Notebook: Zitations- und Autorennetzwerke
- Download Jupyter Notebook: Zitations- und Autorennetzwerke
- Auf der virtuellen DPG-Tagung 2021 wurden im Fachverband Physik sozio-ökonomischer Systeme die Preisträger des "Young Scientist Award for Socio-and Econophysics" geehrt. Die Vortragsfolien der Preisträger-Vorträge finden sie als .zip-file unter dem folgenden Link: "Quantifying science and art" by Roberta Sinatra, "Multilayer modeling and analysis of complex socio-economic systems" by Manlio De Domenico
- View Jupyter Notebook: Das europäische Stromnetzwerk
- Download Jupyter Notebook: Das europäische Stromnetzwerk
- Das PyPSA-Projekt (Python für Power System Analysis) stellt eine Open-Source-Python-Umgebung für die Modellierung und Analyse komplexer Energie-Netzwerke dar.
- Download Python Programm: Exponentielles Netzwerk







Vorlesung 7
In der vorigen Vorlesung hatten wir die beiden Netzwerk-Klassen der zufälligen und 'kleine Welt' Netzwerke kennengelernt. In dieser Vorlesung befassen wir uns mit den Eigenschaften von exponentiellen und skalenfreien Netzwerken. In exponentiellen und skalenfreien Netzwerken besitzen sehr viele Knoten wenig Kanten und einige wenige Knoten sehr viele Kanten. Im Gegensatz zu zufälligen Netzwerken ist die Verteilungsfunktion der Knotengrade ($P(k)$) somit nicht binomialverteilt, sondern folgt einem anderen mathematischen Verhalten.
Exponentielle Netzwerke entstehen auf natürliche Weise mittels eines zeitlichen Anwachsens der Netzwerkknoten. Betrachtet man z.B. ein Netzwerk, das zunächst nur aus einer geringen Anzahl von Knoten und Kanten besteht und fügt diesem Netzwerk nach und nach weitere Netzwerk Knoten hinzu, wobei man jeden neuen Knoten in zufälliger Weise mit einem der Knoten des bestehenden Netzwerkes verlinkt, so erhält man ein exponentielles Netzwerk (siehe Animation im linken Panel dieser Vorlesung). Die Verteilungsfunktion der Knotengrade bei exponentiellen Netzwerken folgt näherungsweise dem folgenden mathematischen Gesetz: $P(k)=2^{-k}$.
Die Klasse der skalenfreien Netzwerke ist die wohl wichtigste aller Netzwerk-Klassen da diese topologische Eigenschaft in vielen real existierenden Netzwerken realisiert ist (siehe Table 4.1: Albert-Laszlo Barabasi, Network Science). Die Verteilungsfunktion der Knotengrade von skalenfreien Netzwerken wird mathematisch durch eine 'power-law distribution' beschrieben ($P(k)\sim k^{- \gamma}$), wobei viele real existierende komplexe Netzwerke einen Exponenten $\gamma$ im folgenden Wertebereich besitzen $2 < \gamma < 3$. Die Bezeichnung skalenfrei gründet hierbei auf der Eigenschaft, dass eine Umskalierung $k\rightarrow \alpha k$ mit einem beliebigen Faktor $\alpha$ wiederum zu einem Potenzgesetz führt: $P(\alpha k) = \alpha^{- \gamma}k^{- \gamma} \sim k^{- \gamma}$. In skalenfreien Netzwerken existieren einige Knoten die einen sehr großen Knotengrad besitzen (sogenannte Hubs). Die Entstehung solcher Hubs ist aufgrund des Prinzips des 'Preferential Attachment' möglich (siehe linkes Panel dieser Vorlesung).
In den bisher dargestellten komplexen Netzwerken betrachteten wir lediglich eine Knotenart. Multipartite Netzwerke stellen komplexe Systeme dar in denen mehrere Knotenarten miteinander in Verbindung stehen (siehe z.B. Zitations- und Autorennetzwerke).
Da es sich bei dieser Vorlesung um die letzte Vorlesung vor den Weihnachtsfeiertagen handelt (Weihnachtsvorlesung) erzähle ich noch kurz am Ende die kleine Anekdote: Wie ich Prof. Nash kennenlernte
Vorlesung 8
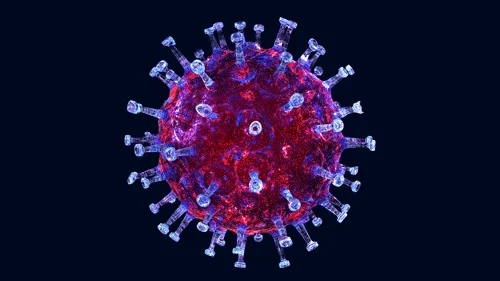
In dieser Vorlesung wird ein aktuelles Anwendungsfeld der Theorie der komplexen Netzwerke, die Ausbreitung eines Krankheitserregers (z.B. COVID-19 Vrius) auf einem komplexen Kontakt-Netzwerk, besprochen. Zunächst werden die Lösungen des deterministischen SIR-Modells (siehe rechtes Panel dieser Vorlesung) vorgestellt und danach die Ausbreitung eines Virus auf einem komplexen Netzwerk simuliert.
Das SIR Modell der Epidemiologie
Die Lösungen des im rechten Panel beschriebene SIR Modells der Epidemiologie hängen sensitiv von den Parametern $<\!\!k\!\!>$, $\beta$ und $\mu$ ab. Durch die Festlegung dieser Parameter ist auch eine weitere wichtige epidemiologische Größe festgelegt, die so genannte Basisreproduktionszahl $ R_0:=\frac{ \beta \, < k >}{ \mu }$. Sie besagt, wie viele Personen von einer infektiösen Person im durchschnittlich angesteckt werden.
Ausbreitung eines Virus auf einem komplexen Netzwerk
Eine bedeutende Einschränkung des deterministischen SIR-Modells der Epidemiologie ist die im Modell angenommene vereinfachte Kontakt-Netzwerkstruktur der Population. Die Ausbreitung eines Krankheitserregers, eines Computervirus im Internet oder eines Gerüchts ("Fake-News") in einem sozialen Netzwerk hängt jedoch stark von der Topologie des zugrundeliegenden komplexen Netzwerkes ab. Im Folgenden wird die epidemische Ausbreitung auf unterschiedlichen Kontakt-Netzwerken mittels simulationsbasierter Ansätze untersucht.Weiterführende Links
- Folien der 8.Vorlesung
- Vorlesungsaufzeichnung der 8.Vorlesung
- View Jupyter Notebook: Ausbreitung eines Virus auf einem komplexen Netzwerk: Das deterministische SIR-Modell
- Download Jupyter Notebook: Ausbreitung eines Virus auf einem komplexen Netzwerk: Das deterministische SIR-Modell
- View Jupyter Notebook: Ausbreitung eines Virus auf einem komplexen Netzwerk: Simulationsbasierte Lösungen
- Download Jupyter Notebook: Ausbreitung eines Virus auf einem komplexen Netzwerk: Simulationsbasierte Lösungen
- Modeling Infectious Diseases in Humans and Animals by Matt J. Keeling and Pejman Rohani
- GLEAM Projekt and GLEAMviz
- Research on Complex Systems, Brockmann Lab
- Covid-19 Mobility Project
- Johns Hopkins University, Coronavirus Resource Center
- Our World in data: Statistics and Research, COVID-19
- Der Beitrag von epidemiologischen Modellen zur Beschreibung des Ausbruchsgeschehens der COVID-19-Pandemie von Priesemann, Meyer-Hermann, Pigeot, and Schöbel (2021)


Vorlesung 8
Die in den letzten beiden Vorlesungen thematisierten Netzwerke spielen eine wichtige Rolle in einer Vielzahl von unterschiedlichen Anwendungsfelder. In dieser Vorlesung wollen wir, aufgrund der aktuellen COVID-19-Pandemie, die Ausbreitung eines Krankheitserregers auf einem komplexen Kontakt-Netzwerk beschreiben und analysieren. Die in dieser Vorlesung vorgestellten mathematischen deterministischen Modelle und Computersimulationen sind allgemein angelegt und können z.B. auch die Ausbreitung eines Computervirus im Internet oder eines Gerüchts ("Fake-News") in einem sozialen Netzwerk beschreiben. Im allgemeinen hängt die Ausbreitung vom jeweiligen Übertragungsmechanismus, der Struktur des zugrundeliegenden komplexen Netzwerkes und von dem Verhalten der Überträger (Knoten, Spieler, Agenten) ab.
Wir betrachten zunächst ein Modell (das Susceptible-Infected-Recovered (SIR) Modell) aus der Epidemiologie, welches die Ausbreitung eines Krankheitserregers, unter gewissen vereinfachten Grundannahmen, in einer analytisch formulierten Differentialgleichung beschreibt (Details siehe z.B. Online-Buch 'Network Science' von Albert-Laszlo Barabasi, Chapter 10: Spreading phenomena)). Im SIR-Modell befindet sich jedes Individuum der betrachteten Population zu jedem Zeitpunkt in einer von drei unterschiedlichen Zuständen: Susceptible (S: Gesunde Personen, die mit dem Virus noch keinen Kontakt hatten), Infected (I: Infizierte Personen, die mit dem Virus Kontakt hatten und andere anstecken können) und Recovered (R: Personen, die infiziert waren aber nicht mehr infektiös sind und sich von der Krankheit erholt haben). Das dem Model zugrundeliegende Kontakt-Netzwerk basiert auf einer 'homogene Massenwirkungsnäherung', die annimmt, dass jede Person mit gleicher Wahrscheinlichkeit mit jeder Anderen in Kontakt treten kann. Man nimmt an, dass ein typisches Individuum im Durchschnitt $<\!\!k\!\!>$ Kontakte hat und dass die Wahrscheinlichkeit, dass die Krankheit in einer Zeiteinheit $\Delta t$ von einem Infizierten auf eine andere Person übertragen wird, mittels des Parameters $\beta$ quantifiziert ist. Zusätzlich können sich infizierte Personen mit einer Wahrscheinlichkeit $\mu$ von der Krankheit erholen/sterben. Die genesenen ("Recovered") Personen betrachtet man als nicht mehr infizierbar (immun) und nimmt zusätzlich an, dass sie auch keine Anderen infizieren können. Man fügt dieser Personengruppe auch die Personen hinzu, die an dem Virus gestorben sind (Removed).
Wir betrachten im Folgenden eine Population aus N Personen. Das dem oben beschriebenen SIR-Modell zugrundeliegende System von Differentialgleichungen lautet:
$$
\begin{eqnarray}
\frac{d s(t)}{dt} &=& -\underbrace{\beta <\!\!k\!\!> i(t) \cdot s(t)}_{\hbox{pro $\Delta t$ neu Infizierte}} \\
\frac{d i(t)}{dt} &=& -\underbrace{\mu \,i(t)}_{\hbox{pro $\Delta t$ Gen. und Gest.}} + \underbrace{\beta <\!\!k\!\!> i(t) \cdot s(t)}_{\hbox{pro $\Delta t$ neu Infizierte}}\\
\frac{d r(t)}{dt} &=& \underbrace{\mu \,i(t)}_{\hbox{pro $\Delta t$ Genesene und Gestorbene}} \quad ,
\end{eqnarray}
$$
wobei $s(t)=\frac{S(t)}{N}$ der Anteil der noch nicht erkrankten Personen, $i(t)=\frac{I(t)}{N}$ der Anteil der infizierten Personen und $r(t)=\frac{R(t)}{N}$ der Anteil der genesenen und gestorbenen Personen darstellt.
Im oberen Teil des linken Panels dieser Vorlesung werden die nummerischen Lösungen dieser Differentialgleichung berechnet und analysiert. Im unteren Teil des linken Panels wird hingegen die Ausbreitung des Krankheitserregers auf einer komplexen Netzwerkstruktur (z.B. räumliches Kontaktgitter, zufälliges, kleine Welt und sklalenfreies Kontakt-Netzwerk) simuliert und mit den Resultaten des deterministischen SIR-Modells verglichen.
Vorlesung 9
In dieser Vorlesung wird zunächst die zeitliche Entwicklung von räumlichen dominanten Spielen, Koordinations- und Anti-Koordinationsspielen simuliert und mit den Lösungen der deterministischen evolutionären Spieltheorie verglichen. Danach wird die zeitliche Entwicklung der Strategienwahl der Population auf unterschiedlichen Netzwerktopologien analysiert.
Dominante räumliche Spiele
Wir betrachten zunächst ein räumliches, leicht dominantes Spiel mit der im rechten Panel angegebenen Auszahlungsmatrix und wählen als Anfangskonfiguration der Strategienwahl der Spielerpopulation eine Konstellation, bei der nur ein Spieler die dominante rote Strategie spielt und alle anderen Spieler die blaue Strategienwahl. Die Simulationen zeigen, dass $\forall 1 < c <1.2$ in der zweiten Spielperiode ein Rechteck aus 9 roten Knoten entsteht, welches aber dann schon in der dritten Spielperiode wieder in einen einzelnen roten Zentrumsknoten übergeht. Die linke untere Abbildung zeigt die räumliche Spielkonstellation zu diesem Zeitpunkt ($c=1.1$), wobei die eingezeichneten $\$$-Werte den erzielten kumulierten Auszahlungswerten der Spieler entsprechen und die kleinen Vierecke innerhalb der großen Vierecke die zukünftige Strategienwahl der Spieler in der nächsten Spielperiode angeben.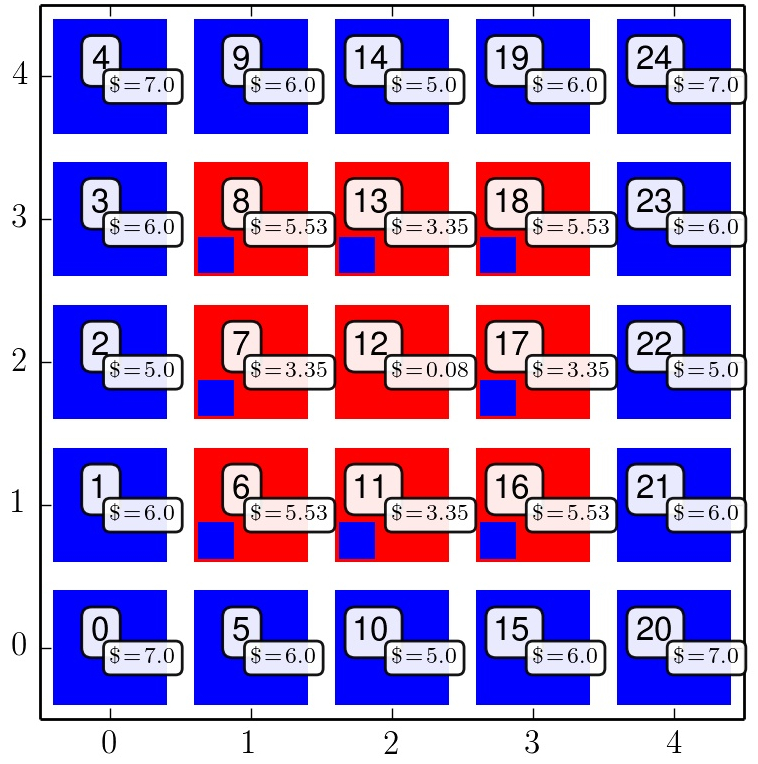
Räumliche Koordinations- und Anti-Koordinationsspiele
Im Jupyter Notebook Evolutionäre räumliche Spiele: Koordinations- und Anti-Koordinationsspiele werden evolutionäre räumliche Spiele simuliert, deren Auszahlungsmatrix der Klasse der Koordinations- bzw. Anti-Koordinationsklasse angehören. Die unten dargestellte Animation zeigt ein räumliches Anti-Koordinationsspiel, wobei eine zufällige Anfangskonfiguration der Strategienwahl der Spielerpopulation benutzt wurde in der ca. $60 \%$ der Spieler die blaue Strategie wählten. Die Animation zeigt, dass sich auch das räumliche Spiel zu einem dynamischen Gleichgewicht entwickelt, wobei der mittlere Wert des simulierten Populationsvektors $x^{\rm SP}(t)$ (schwarze Kurve in der linken Abbildung der Animation) sich nahe dem, von der deterministischen evolutionären Spieltheorie vorhergesagten, gemischten Nash-Gleichgewicht aufhält.
Evolutionäre Spiele auf unterschiedlichen Netzwerk-Topologien
Im Jupyter Notebook Evolutionäre Spiele auf unterschiedlichen Netzwerk-Topologien werden evolutionäre Spiele auf den unterschiedlichen Netzwerkklassen simuliert. Die evolutionäre Entwicklung der Strategienwahl der Spieler wird sowohl auf zufälligen, 'kleine Welt', skalenfreie, als auch auf vollständig verbundene Netzwerkstrukturen simuliert und mit den Resultaten der deterministischen evolutionären Spieltheorie verglichen. Es zeigt sich hierbei, dass die simulierten Spiele auf vollständig verbundene Netzwerken gut mit den Ergebnissen der Replikatordynamik übereinstimmen. Die unten dargestellte Animation zeigt die evolutionäre Entwicklung eines leicht dominanten Spiels ($c=1.66$, siehe rechtes Panel dieser Vorlesung) auf einem skalenfreien Netzwerk. Bei den räumlichen Spielen entwickelte sich die Population zu einem Endzustand bei dem alle Spieler die rote Strategie wählten. Die zeitliche Ausbreitung der roten Strategie auf einem skalenfreien Netzwerk hängt stark von der Anfangskonfiguration ab. In der unten dargestellten Animation wurde eine Anfangskonfiguration gewählt, bei der lediglich der Spieler mit dem größten Knotengrad (der Hub des skalenfreien Netzwerkes) die rote Strategie wählt.Weiterführende Links

- Folien der 9.Vorlesung
- Vorlesungsaufzeichnung der 9.Vorlesung
- View Jupyter Notebook: Evolutionäre dominante räumliche Spiele
- Download Jupyter Notebook: Evolutionäre dominante räumliche Spiele
- View Jupyter Notebook: Evolutionäre räumliche Spiele: Koordinations- und Anti-Koordinationsspiele
- Download Jupyter Notebook: Evolutionäre räumliche Spiele: Koordinations- und Anti-Koordinationsspiele
- View Jupyter Notebook: Evolutionäre Spiele auf unterschiedlichen Netzwerk-Topologien
- Download Jupyter Notebook: Evolutionäre Spiele auf unterschiedlichen Netzwerk-Topologien
- Download Python Programm: Räumliches Spiel (kleines Gitter mit Auszahlungen)
- Download Python Programm: Räumliches Spiel (mittleres Gitter, Walker-Anfangskonfiguration)
- Download Python Programm: Räumliches Spiel (großes Gitter)
Vorlesung 9
Die Verknüpfung der Theorie der komplexen Netzwerke mit der evolutionären Spieltheorie wird in dieser Vorlesung an mehreren Beispielen gezeigt. Die Entscheidungsprozesse der Spieler auf einem komplexen Netzwerk können mittels numerischer, agenten-basierter Computerprogramme simuliert werden.
Wir betrachten zunächst ein evolutionäres räumliches Spiel (siehe Spatial Games), wobei die Spieler einer endlich großen Population auf einem räumlichen Gitter angeordnet und jeder Spieler nur mit seinen nächsten Nachbarn spielen kann (Moore Nachbarschaft). Das zugrundeliegende Netzwerk der Spielerknoten besitzt somit eine reguläre Struktur und im betrachteten 2-dimensionalen Fall spielt jeder Spieler pro Spielperiode mit acht Spielern (Knotengrad $k_i=8\, \forall\, i \in {\cal I}$).
Im linken Panel dieser Vorlesung werden mehrere Jupyter Notebooks und Python Programme vorgestellt, die einerseits die zeitliche Entwicklung dieser räumlichen Spiele unter Verwendung von dominanten, Koordinations- uns Anti-Koordinationsspielen simulieren, andererseits werden auch evolutionäre Spiele auf anderen Netzwerktopologien berechnet und diskutiert ( siehe auch Szabó, György, and Gabor Fath. "Evolutionary games on graphs." Physics reports 446.4-6 (2007): 97-216.).
Vorlesung 10
In dieser Vorlesung behandeln wir die Quanten Spieltheorie. Zunächst wird der mathematische Formalismus eines (2 Personen)-(2 Strategien) Quantenspiels vorgestellt. Danach wenden wir den quantenspieltheoretischen Formalismus auf dominante, Koordinations- und Anti-Koordinationsspiele an. Wir werden sehen, dass wenn die Strategieverschränkung der Spieler nur groß genug ist, können zusätzliche Nash-Gleichgewichte entstehen und zuvor vorhanden Nash-Gleichgewichte verschwinden. Ungünstige, Dilemma-artige Situationen und nicht vorteilhafte evolutionär stabile Strategien können sich ab definierten Verschränkungsbarrieren auflösen.
Der mathematische Formalismus eines (2 Personen)-(2 Strategien) Quantenspiels
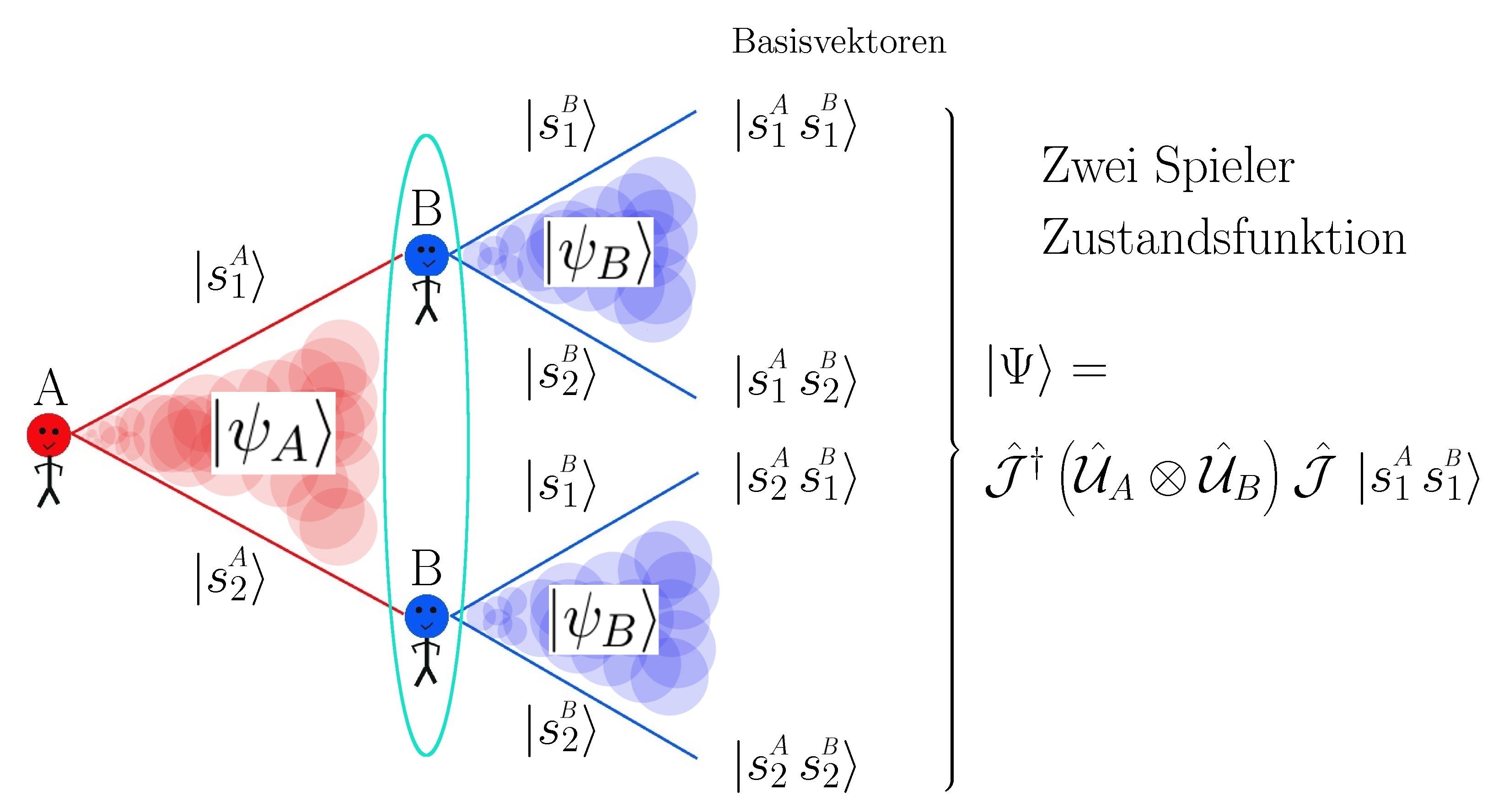
Um die mathematische Beschreibung des quantenspieltheoretischen Modells (siehe rechtes Panel dieser Vorlesung) zu verdeutlichen, wird im Folgenden ein (2 Personen)-(2 Strategien) Quantenspiel betrachtet. In dem Jupyter Notebook Quanten Spieltheorie werden die Entscheidungsoperatoren der Spieler mittels der beiden Entscheidungswinkeln $\theta_{\!\mu}$ und $\varphi_{\!\mu}$ ($\mu=A,B$ für Spieler A und B) wie folgt definiert: \[ \begin{equation} \widehat{U}_\mu(\theta_{\!\mu},\varphi_{\!\mu}) := \left( \begin{array}[c]{cc} e^{i\,\varphi_{\!\mu}} \, \hbox{cos}(\frac{\theta_{\!\mu}}{2})&\hbox{sin}(\frac{\theta_{\!\mu}}{2})\\ -\hbox{sin}(\frac{\theta_{\!\mu}}{2})&e^{-i\,\varphi_{\!\mu}} \, \hbox{cos}(\frac{\theta_{\!\mu}}{2}) \end{array} \right) \quad \forall \quad \theta_{\!\mu} \in{} [0,\pi] \,\, \wedge \,\, \varphi_{\!\mu} \in{} [0,\frac{\pi}{2}] \quad . \end{equation} \] Der Zwei-Spielerzustand $\left| \Psi \right> = \hat{\cal{J}}^\dagger \left( \hat{U}_A \otimes \hat{U}_B \right) \hat{\cal{J}}\, \left| s^A_1 s^B_1 \right>$ ist ein vier komponentiger Spinor, wobei die Basisvektoren dieses vierdimensionalen komplexwertigen Hilbertraumes ${\cal{H}}$ durch die vier möglichen, klassischen Strategienkombinationen (messbaren Eigenzustände des Quantensystems) gebildet werden ($\left| s^A_1 s^B_1 \right>:=(1,0,0,0)$, $\left| s^A_1 s^B_2 \right>:=(0,-1,0,0)$, $\left| s^A_2 s^B_1 \right>:=(0,0,-1,0)$ und $\left| s^A_2 s^B_2 \right>:=(0,0,0,1)$). Um eine mögliche Verschränkung des Zwei-Spielerzustand $\left| \Psi \right>$ zu berücksichtigen, wird der Anfangszustand $\left| \Psi_0 \right> \,=\, \widehat{\mathcal{J}} \left| s^A_1 s^B_1 \right>$ mittels des Verschränkungsoperators $\widehat{\mathcal{J}} := e^{-i \, \frac{\gamma}{2} (\widehat{s_2} \otimes \, \widehat{s_2})}$ verschränkt. Am Ende des Jupyter Notebooks werden die Ergebnisse eines dominanten Spiels mit Dilemma berechnet.
Quantenspiele der Spielklassen: Dominante Spiele, Koordinationsspiele und Anti-Koordinationsspiele
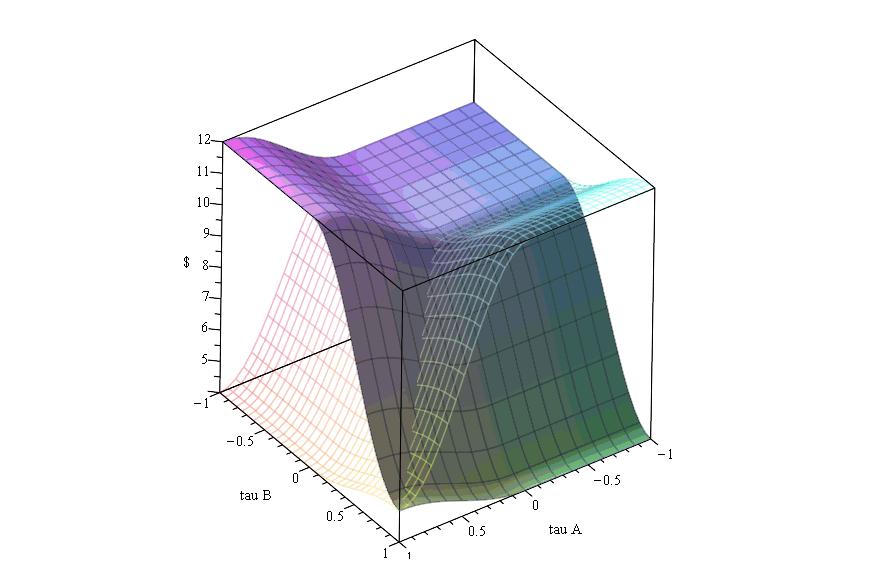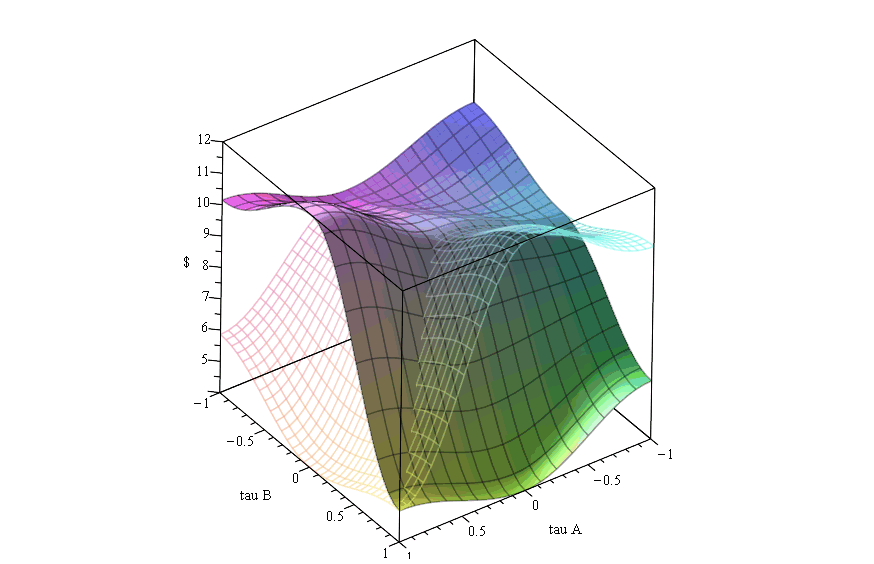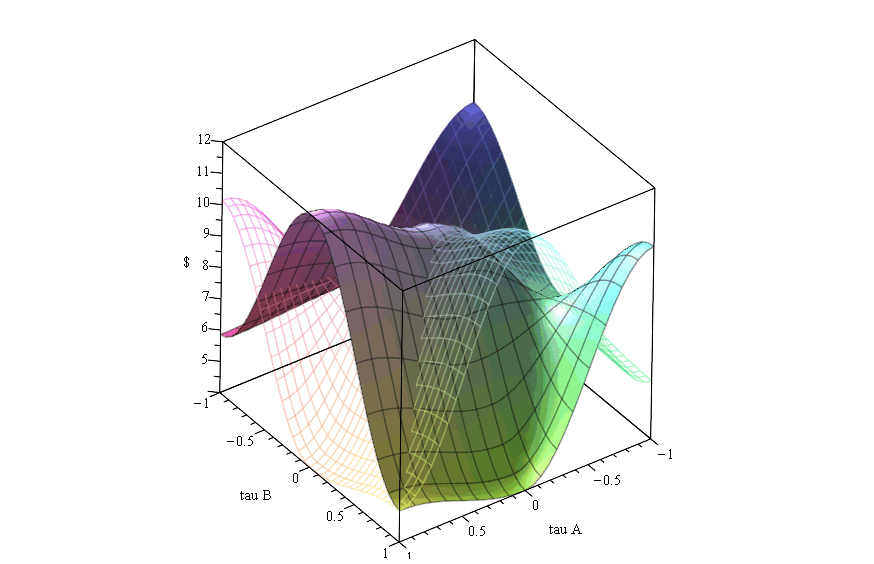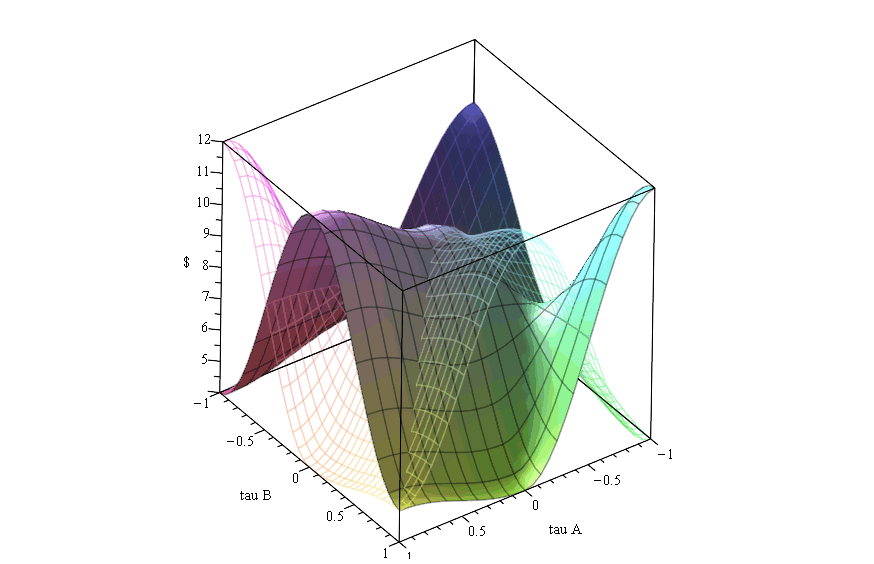
In dem Maple Worksheet Symmetrische (2 x 2) Quantenspiele wird der quantenspieltheoretische Formalismus auf die drei unterschiedlichen Spielklassen von symmetrischen (2 Personen)-(2 Strategien) Spielen angewendet. Zunächst zeigt sich, dass die Resultate der Quantenspiele bei verschwindenden Verschränkungswerten ($\gamma=0$) identisch mit den klassischen Spielen sind. Bei dominanten Spielen mit Dilemma löst sich ab einem definierten Wert der Verschränkung die dominante Strategie auf ($\gamma_1$-Barriere) und ab einer weiteren Grenze ($\gamma_2$-Barriere) entsteht ein neues Nash-Gleichgewicht, bei dem die Spieler dem Dilemma entkommen können. Die nebenstehende Abbildung zeigt die quantentheoretisch erweiterte Auszahlung $\$_A$ des Spielers A (untransparente Fläche) und $\$_B$ des Spielers B (transparente Fläche) als Funktion der reduzierten $s_1$-Quantenstrategien $\tau_A$ des Spielers A und $\tau_B$ des Spielers B in einem dominanten Spiel mit Dilemma, wobei der Verschränkungswert im Bereich $\gamma \in [0,\pi/2]$ variiert wurde. Bei dominanten Spielen ohne Dilemma entstehen keine weiteren Nash-Gleichgewichte und die dominante Strategie bleibt bestehen. Bei Quanten-Koordinationsspielen löst sich das Koordinationsproblem auf, falls der Wert der Verschränkung über der definierten $\gamma_1$-Barriere liegt und die Spieler wählen das symmetrische Gleichgewicht mit der höheren Auszahlung. Erhöht man bei Quanten-Anti-Koordinationsspielen die Verschränkung, so entsteht ab einer definierten $\gamma_2$-Barriere ein zusätzliches symmetrisches Nash-Gleichgewicht.Weiterführende Links


- Folien der 10.Vorlesung
- Vorlesungsaufzeichnung der 10.Vorlesung
- View Jupyter Notebook: Quanten Spieltheorie
- Download Jupyter Notebook: Quanten Spieltheorie
- View Maple Worksheet: Symmetrische (2 x 2) Quantenspiele
- Download Maple Worksheet: Symmetrische (2 x 2) Quantenspiele
- Clusterprojekt ConTrust der Goethe-Universität Frankfurt
Vorlesung 10
Sowohl die deterministische evolutionäre Spieltheorie, als auch die Spieltheorie auf komplexen Netzwerken zeigt, dass die Strategienentwicklung von Populationen sich zu Dilemma-artige Situationen entwickeln können. Die einzelnen Spieler der Population sehen sich (aufgrund der Dilemma-artigen Struktur der Auszahlungsmatrix) gezwungen eine Strategie zu wählen, in der jeder einzelne Spieler und somit die gesamte Population einen geringen Nutzen erhielt, obwohl ein vorteilhafterer Zustand möglich wäre. In dieser Vorlesung betrachten wir die Quantenspieltheorie, die einen speziellen mathematischen Formalismus bereitstellt kooperative Effekte in die Spieltheorie miteinzubeziehen. Die Quantenspieltheorie stellt eine mathematische und konzeptuelle Erweiterung der klassischen Spieltheorie dar. Der Raum aller denkbaren Entscheidungswege der Spieler wird vom rein reellen, messbaren Raum in den Raum der komplexen Zahlen (reelle und imaginäre Zahlen) ausgedehnt. Durch das Konzept der möglichen quantentheoretischen Verschränkung der Entscheidungswege im imaginären Raum aller denkbaren Quantenstrategien können gemeinsame, durch kulturelle oder moralische Normen entstandene Denkrichtungen in die evolutionäre Dynamik mit einbezogen werden. Ist die Strategienverschränkung der Spieler im imaginären Raum der denkbaren Entscheidungswege nur genügend groß, so können zusätzliche Nash-Gleichgewichte auftreten und zuvor existente dominante Strategien sich auflösen.
Vorlesung 11 - 13


Studentische Projekte
Mündliche Prüfung
Die mündlichen Prüfungen werden ebenfalls mittels der Zoom Meeting Software stattfinden, haben eine Dauer von ca. 30 Minuten und Sie dürfen alle auf der Homepage der Vorlesung befindlichen Hilfsmittel verwenden.Prüfungsrelevante Themen
Teil I
Was versteht man unter Spieltheorie? Welche formalen Größen werden für die Definition eines Spiels benötigt? Illustrieren Sie ein simultanes (2 Spieler)-(2 Strategien) Spiel an einem Beispiel (z.B. Gefangenendilemma, Hirschjagd-Spiel, Angsthasen-Spiel (Chicken Game)). Was versteht man unter einer dominanten Strategie? Was ist ein Nash-Gleichgewicht? Illustrieren Sie die Konzepte dominanten Strategie und Nash-Gleichgewicht an zwei Beispielen (z.B. mittels der Bestantwort-Pfeile bei gegebener Auszahlungsmatrix). Was versteht man unter einer gemischten Strategie und was sind reine Strategien? Was ist ein gemischtes Nash-Gleichgewicht und wie berechnet man es mittels der gemischten Auszahlungsfunktion der Spieler? Illustrieren Sie das Konzept des gemischten Nash-Gleichgewichtes mittels der gemischten Auszahlungsfunktion an einem Beispiel (siehe z.B. Hirschjagd-Spiel, Angsthasen-Spiel). In welche drei Klassen lassen sich symmetrische (2 Personen)-(2 Strategien) Spiele untergliedern und wie hängt diese Klassifizierung von der Struktur der reinen und gemischten Nash-Gleichgewichte ab? Was ist der Unterschied zwischen symmetrischen und unsymmetrischen (2 Personen)-(2 Strategien) Spielen? Nennen Sie ein Beispiel eines unsymmetrischen (2 Personen)-(2 Strategien) Spiels (z.B. Kampf der Geschlechter).
Was versteht man unter evolutionärer Spieltheorie? Welche Struktur haben die Differentialgleichung der evolutionären Dynamik (Fitness der Strategie i, durchschnittliche Fitness der Population)? Was versteht man unter dem Populationsvektor $\vec{x}(t)$ (bei Bi-Matrix Spielen $\vec{x}^A(t)$ und $\vec{x}^B(t)$? Wie lauten die Gleichungen für symmetrische und unsymmetrische (2 Personen)-(2 Strategien) Spiele? In welchem Zusammenhang steht die Dynamik bestimmenden Funktion g(x) (bei Bi-Matrix Spielen $g_A(x,y)$ und $g_B(x,y)$) und die Struktur der Nash-Gleichgewichte? Was versteht man unter einer evolutionär stabilen Strategie? Wo befinden sich (nur qualitativ) die evolutionär stabilen Strategien bei symmetrischen dominante Spielen, Koordinationsspielen und Anti-Koordinationsspielen? In welche Spielklassen lassen sich unsymmetrische (2x2)-Spiele (Bi-Matrix Spiele) untergliedern und wie hängt diese Klassifizierung von der Struktur der reinen und gemischten Nash-Gleichgewichte ab? Wie lauten die Gleichungen der evolutionären Dynamik für symmetrische (2 Personen)-(3 Strategien) Spiele und welche evolutionäre Entwicklungen der Population sind hier möglich?
Teil II
Was sind sozio-ökonomische komplexe Netzwerke und in welchen Bereichen finden sie ihre Anwendung? Wie beschreibt man (formal, mathematisch) komplexe Netzwerke? In welche unterschiedlichen Netzwerktypen lassen sich komplexe Netzwerke untergliedern? Mittels welcher Größen lassen sich komplexe Netzwerke charakterisieren? Was versteht man unter der Verteilungsfunktion der Knotengrade $P(k)$ bzw. $N(k)$ und warum ist diese charakteristische Größe wichtig? In welche Netzwerk-Klassen lassen sich komplexe Netzwerke untergliedern? Welche Unterschiede existieren zwischen den Netzwerk-Klassen zufällige Netzwerke , kleine Welt-Netzwerke, exponentielle Netzwerke und skalenfreie Netzwerke. Beschreiben Sie wie man ein komplexes Netzwerk konstruiert und erläutern sie dies an einem Beispiel (benutzen Sie hierbei eines der Python Programme aus der Vorlesung). Beschreiben Sie die Modellierung der Ausbreitung eines Krankheitserregers in einem komplexen Netzwerk (Computervirus im Internet, Gerücht ("Fake-News") in einem sozialen Netzwerk oder Coronavirus in einem Kontakt-Netzwerk) und gehen Sie dabei auf die in der Vorlesung vorgestellten mathematischen deterministischen Modelle und stochastischen Computersimulationen ein. Diskutieren Sie das Susceptible-Infected-Recovered (SIR) Modell aus der Epidemiologie.
Teil III
Was versteht man unter dem Begriff evolutionäre Spieltheorie auf komplexen Netzwerken und in welcher Weise unterscheidet sich diese von der deterministischen evolutionären Spieltheorie? Was versteht man unter evolutionären räumlichen Spielen (spatial games)? Beschreiben Sie die einzelnen aufeinander folgenden Phasen (Schritte) bei einem evolutionären räumlichen Spiel. Vergleichen Sie die zeitliche Entwicklung von räumlichen dominanten Spielen, Koordinations- und Anti-Koordinationsspielen mit den Lösungen der deterministischen evolutionären Spieltheorie. Beschreiben Sie wie man ein evolutionäres Spiele auf einem zufälligen, 'kleine Welt', skalenfreien oder vollständige verbundenen Netzwerk simuliert und diskutieren Sie die Unterschiede der Entwicklung der Population mit den Resultaten der deterministischen evolutionären Spieltheorie. Beschreiben Sie die Grundlagen der Quanten Spieltheorie. Was versteht man unter einem Zwei-Spielerzustand eines simultanen Zwei-Strategien Quantenspiels?
Vorlesung 11 - 13
Studentische Projekte



Die studentischen Projekte können alleine oder in Gruppen (bis zu drei Personen) durchgeführt werden. Under construction ...