Vorwort
Der Titel der Vorlesung ist in Anlehnung eines im Jahre 2001 gegründeten neuen Arbeitskreises/Fachbereiches der Deutsche Physikalische Gesellschaft gewählt worden, welcher sich mit mit der Anwendung und Weiterentwicklung von Methoden der Physik zur Analyse, Modellierung, Simulation und Optimierung von sozio-ökonomischen Systemen befasst (siehe DPG-Fachverband: Physik sozio-ökonomischer Systeme). Die "Physik der sozio-ökonomischer Systeme" ist ein stark interdisziplinäres Forschungsfeld in dem die unterschiedlichen Sprachen der Soziologie, der Wirtschaftswissenschaften, der Biologie, der Physik und der Mathematik aufeinander treffen, um zu beschreiben und zu verstehen, wie sich Menschen untereinander verhalten. Die in den letzten Jahrzenten gefundenen Erkenntnisse sind dabei nicht zwangsläufig nur auf das menschliche Individuum anwendbar, sondern betrachten z.B. auch die Erforschung von biologischen Systemen. In dem Großteil dieser Vorlesung nehmen wir jedoch an, dass der wissenschaftliche Untersuchungsgegenstand, das zu erforschende Ding, der Mensch ist und wir sind daran interessiert wie dieser sich bei ökonomischen oder sozialrelevanten strategischen Entscheidungen verhält. Wir sind demnach auf der Suche nach einer Art von fundamentalen Theorie des menschlichen Verhaltens, ähnlich der physikalischen Elementarteilchen-Theorie und ihrer fundamentalen Wechselwirkungen. Im Gegensatz zur "normalen" Physik, ist man als forschender Wissenschaftler in dem Gebiet der "Physik der sozio-ökonomischer Systeme" selbst ein Teil des zu untersuchenden Gegenstandes und wird somit zwangsläufig mit den eigenen Verhaltensmustern, Denkweisen und Entscheidungsrichtlinien konfrontiert.
Viele Wirtschafts- und Sozialwissenschafter betrachten heutzutage die Spieltheorie als die formale Sprache der ökonomischen Theorie. Die eigene Positionierung im sozialen Umfeld, die Interaktion mit Vorgesetzten, Freunden und dem eigenen Partner, das Verhalten von Firmen- und politischen Entscheidungsträgern kann auch als eine Art von Gesellschaftsspiel angesehen werden (wobei wohl oft die getroffenen Entscheidungen vom individuell erzielten Nutzen dominiert werden). Die zeitliche Veränderung des menschlichen Verhaltens, die evolutionäre Dynamik interagierender Menschengruppen unterliegt gewissen mathematischen Prinzipien, nach denen sich das Leben entwickelte und auch in Zukunft weiter entwickeln wird [1].
Literatur
Albert-Laszlo Barabasi, Network science, Cambridge university press, 2016 [1] Martin A. Nowak, Evolutionary Dynamics - Exploring the Equations of Life, 2006 [2] Schlee, Walter, Einführung in die Spieltheorie, Vieweg 2004 [3] Matthias Hanauske, Evolutionäre Quanten-Spieltheorie im Kontext sozio-ökonomischer Systeme, 2011 [4] Hofbauer, Josef, and Karl Sigmund. Evolutionary games and population dynamics. Cambridge university press, 1998. Vorlesungsmaterialien: Neue Entwicklungen in der Evolutionären Spieltheorie (2009) Vorlesungsmaterialien: Hochschul-SommerkursI.1 Einführung in die Spieltheorie
Im Jahre 1928 veröffentlichte Johann (John) von Neumann eine mathematische Analyse mit dem Titel Zur Theorie der Gesellschaftsspiele. Die Frage, deren Beantwortung die Arbeit von John von Neumann anstrebte lautet: $N$ Spieler ( ${\bf \cal I} = \left\{ 1, 2, ..., N \right\}$ ) spielen ein gegebenes Gesellschaftsspiel $\Gamma$. Wie muss einer dieser Spieler spielen, um dabei ein möglichst günstigstes Resultat zu erzielen? Eine Fußnote innerhalb dieser Arbeit lässt die, von John von Neumann damals schon erkannte, umfassende Anwendung auf ökonomische Fragestellungen erahnen: Es ist das Hauptproblem der klassischen Nationalökonomie: was wird, unter gegebenen äußeren Umständen, der absolut egoistische "homo oeconomicus" tun?. In diesem Kapitel werden die wesentlichen Definitionen und Konzepte der klassischen Spieltheorie vorgestellt, wobei wir uns jedoch zunächst auf das Teilgebiet der sogenannten Simultanen ($N$ Spieler)-($m$ Strategien) Spiele in strategischer Form mit Auszahlung beschränken.
I.1.1 Definition eines Spiels
Die formale mathematische Definition eines solchen Spiels (siehe z.B. [2,3]) benötigt lediglich die Angabe dreier Größen: Die Menge ${\bf \cal I}$ der Spieler, die Menge (der Raum) ${\bf \cal {S}}$ der Strategien der Spieler und ihre Auszahlungsfunktion (Präferenzordnungen) ${\bf \cal {\$}}$. In diesem Unterkapitel wird die allgemeine Definition eines Spiels vorgestellt und das sogenannte Gefangenendilemma als Beispiel behandelt.
I.1.2 Dominante Strategien und Nash-Gleichgewichte
In diesem Unterkapitel werden zwei fundamentale Gleichgewichtskonzepte der Spieltheorie vorgestellt: Das Gleichgewicht in dominanten Strategien und das Nash-Gleichgewicht. Wir beschränken uns hierbei wiederum auf ein simultanes ($N$ Spieler)-($m$ Strategien) Spiel in strategischer Form mit Auszahlung und illustrieren die beiden Gleichgewichtskonzepte mittels der Abbildung der besten Antwort an zwei Beispielen: Dem Gefangenendilemma, welches eine dominante Strategie und ein Nash-Gleichgewicht besitzt und dem sogenannten Hirschjagt-Spiel, das durch zwei symmetrische Nash-Gleichgewichte charakterisiert ist.
I.1.3 Nash-Gleichgewichte in gemischten Strategien
In diesem Unterkapitel werden wir die im Unterkapitel I.1.1 vorgestellte Definition eines Spiels verallgemeinern, indem wir die Menge der reinen Strategien ${\bf \cal{S}}$ zur Menge der gemischten Strategien ${\bf \tilde{\cal{S}}}$ erweitern. Ein solches Spiel bezeichnet man als die gemischte Erweiterung eines simultanen ($N$ Spieler)-($m$ Strategien) Spiels in strategischer Form mit Auszahlung. Ähnlich wie in Unterkapitel I.1.2 werden dann die beiden fundamentalen Gleichgewichtskonzepte der Spieltheorie (dominante Strategien und Nash-Gleichgewichte) in ihrer gemischten Erweiterung definiert. Der Spezialfall eines internen Nash-Gleichgewichts bzw. eines Nash-Gleichgewicht in gemischten Strategien wird vorgestellt werden. Das gesamte Konzept der gemischten Erweiterung wird am Beispiel des Angsthasen-Spiels (Chicken Game) für den Fall eines ($2$ Spieler)-($2$ Strategien) Spiels illustriert.
I.1.4 Klassifizierung von symmetrischen (2 Personen)-(2 Strategien) Spielen
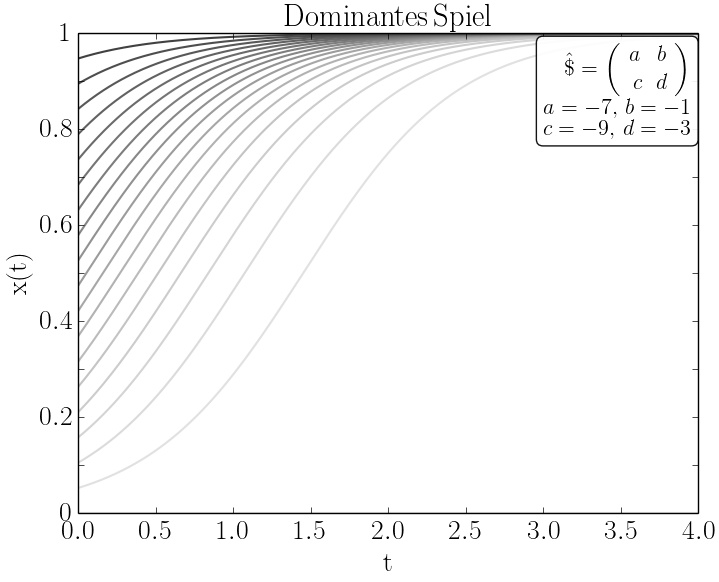
In diesem Unterkapitel werden die unterschiedlichen Spieltypen der gemischten Erweiterung eines simultanen (2 Spieler)-(2 Strategien) Spiels in strategischer Form mit symmetrischer Auszahlungmatrix klassifiziert. Abhängig von den gewählten Parametern der Auszahlunsmatrix lassen sich symmetrische ($2 \times 2$) Spiele in drei unterschiedliche Spielklassen gliedern: Dominante Spiele, Koordinationsspiele und Anti-Koordinationsspiele.
I.1.5 Beispiele weiterer Spieltypen
Die im letzten Unterkapitel betrachtete Spielklassifizierung beschränkte sich auf ein symmetrisches, simultanes ($2 \times 2$) Spiel und stellt somit einer der einfachsten spieltheoretischen Systeme dar. Eine Ausweitung auf mehr Strategien und mehr Spieler bzw. eine Betrachtung unsymmetrischer, sogenannter Bimatrix-Spiele erweitert den Raum der möglichen Spielklassen. Neben den einmalig gespielten simultanen Spielen kann man auch wiederholte Spiele in extensiver Form betrachten und eine zeitabhängige Strategienwahl der Spieler betrachten.
I.2 Evolutionäre Spiele
Dieses Kapitel fasst die wesentlichen Konzepte und die mathematische Formulierung der deterministischen evolutionäre Spieltheorie zusammen. Die evolutionäre Spieltheorie untersucht das zeitliche Verhalten einer großen Anzahl von individuellen Spielern, der sogenannten Population (siehe [1,2,3,4]).
I.2.1 Die Gleichungen der evolutionären Dynamik
In diesem Unterkapitel werden die, die zeitliche Entwicklung des Systems bestimmenden, evolutionären Differentialgleichungen zusammenfassend dargestellt.
I.2.2 Evolutionär stabile Strategien
In diesem Unterkapitel betrachten wir die stationären Lösungen des asymptotischen Verhaltens der gesamten Population und werden ein weiteres fundamentales Gleichgewichtskonzept einführen, das der evolutionär stabilen Strategie (ESS). Am Beispiel des Falke-Taube Spiels verdeutlichen wir das Konzept der evolutionär stabilen Strategie und stellen die entsprechenden Lösungen der zeitlichen Entwicklung der Strategienwahl der Population grafisch dar.
I.2.3 Klassifizierung von symmetrischen, evolutionären (2 x 2) Spielen
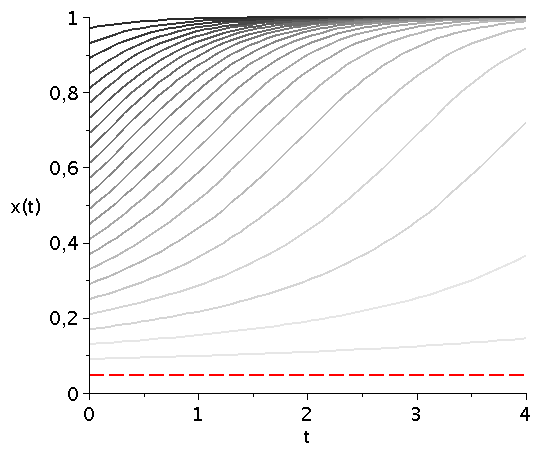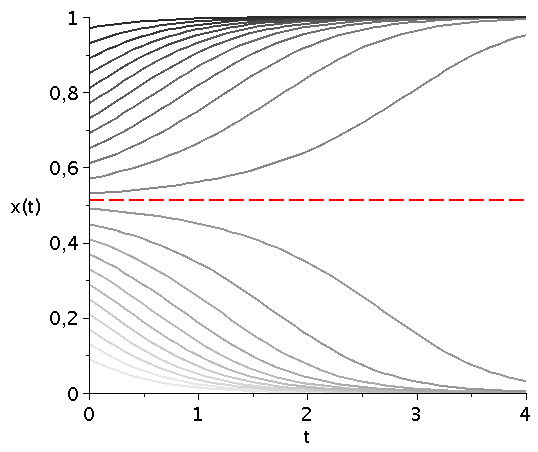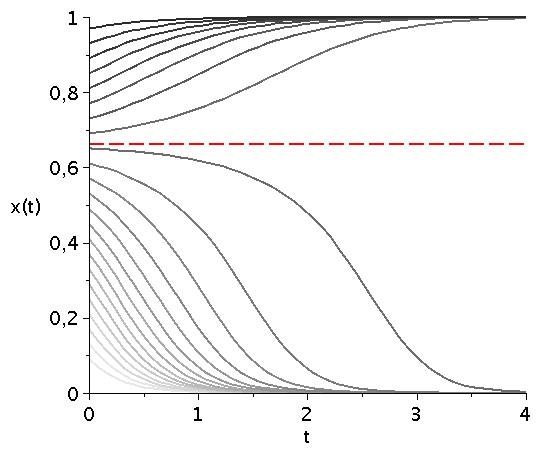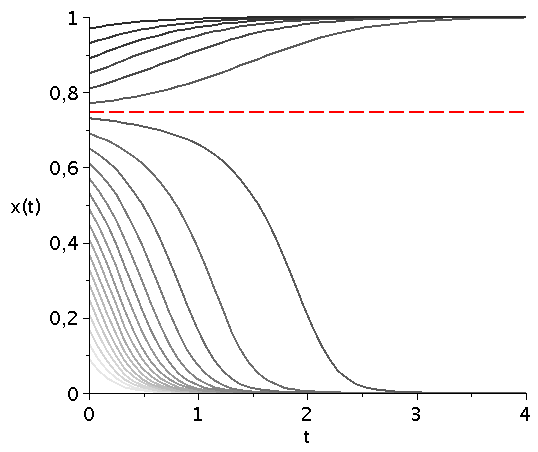
Zeitliche Entwicklung des Populationsvektors x(t) im Hirschjagspiel für mehrere unterschiedliche Anfangspopulationen x(t=0) (graue Kurven). Variiert man den Parameter d (hier d=[4.1,10]), so verschiebt man diese durch das gemischte Nash-Gleichgewicht bestimmte Grenzstrategie (siehe gestrichelte rote Linie).
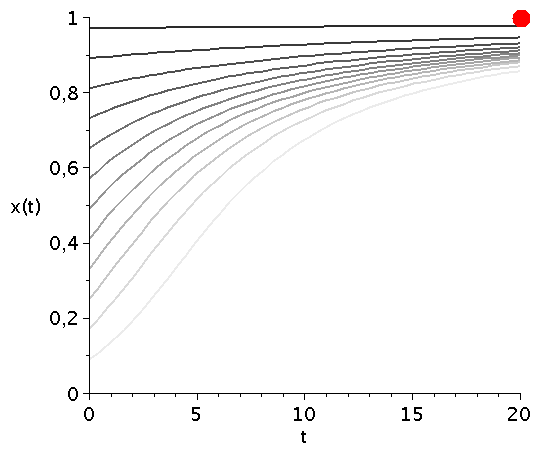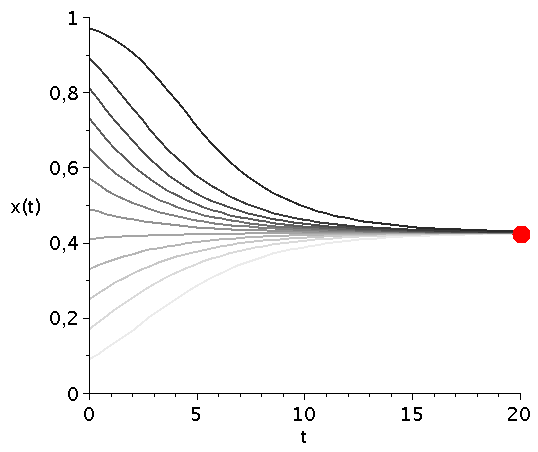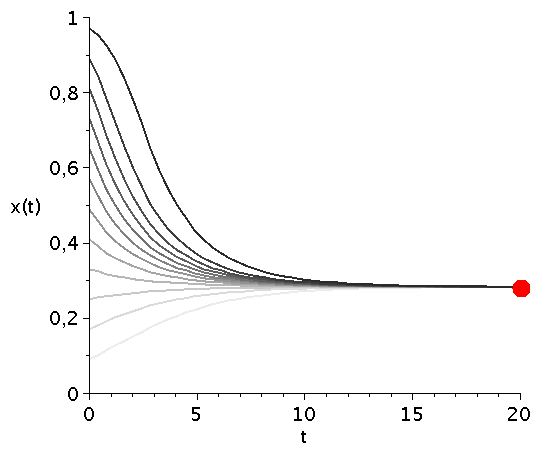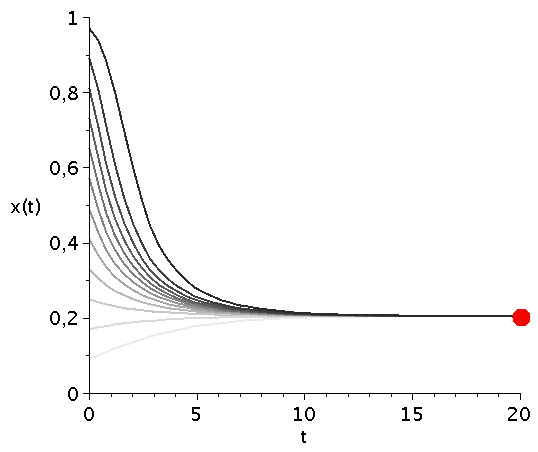
Zeitliche Entwicklung des Populationsvektors x(t) im Falke-Taube Spiel für mehrere unterschiedliche Anfangspopulationen x(t=0) (graue Kurven) bei Variation des Parameters V im Bereich [1,5]. Der rote Punkt mit dem Wert $1/V$ kennzeichnet die evolutionär stabile Strategie des Spiels
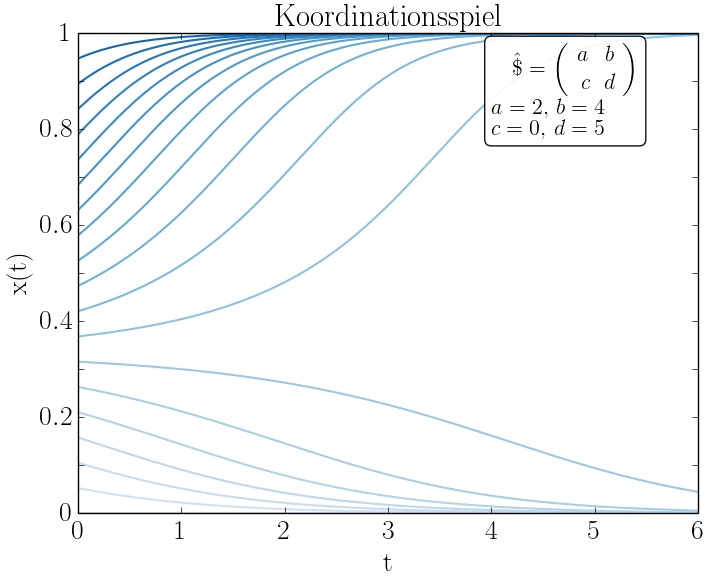
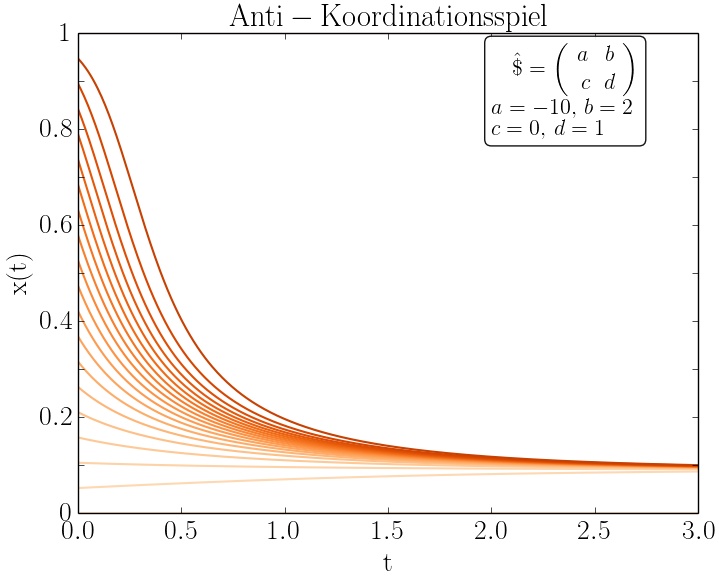
Die dargestellten Gleichungen der Reproduktionsdynamik und die Definition der ESS lassen sich nach Spezifikation der Auszahlungsmatrix $\hat{\bf {\cal \$}}$ auf unterschiedlichste Populationsspiele anwenden. Generell lassen sich symmetrische ($2 \times 2$) Spiele und somit die Differentialgleichungen der Reproduktionsdynamik in drei unterschiedliche Spielklassen gliedern: Dominanten Spiele, Koordinationsspiele und Anti-Koordinationsspiele. Die linke Animation zeigt beispielhaft die Eigenschaften von Koordinationsspiele bei welchen es zwei evolutionär stabile Strategien gibt, und die rechte Abbildung visualisiert die Eigenschaften von Anti-Koordinationsspielen mit nur einer evolutionär stabile Strategie.
I.2.4 Bi-Matrix Spiele
Unsymmetrische ($2 \times 2$) Spiele lassen sich hingegen in die folgenden Spielklassen gliedern: die Eckenspiele (engl.: corner class games ), die Sattelspiele (engl.: saddle class games ) und die Zentrumsspiele (engl.: center class games ). Die Eigenschaften dieser unterschiedlichen Klassen von Spielen sind in dem obigen Link
Die unten dargestellten Animationen stellen das zeitliche Verhalten der Komponenten der Populationsvektoren (Gruppe A: $x(t):=x^A_1(t)$ und Gruppe B: $y(t):=x^B_1(t)$) für drei unterschiedliche Anfangspopulationen-Werte in einem (x,y)-Diagram dar. Die erste Abbildung zeigt ein Eckenspiel, die zweite und dritte Abbildung zeigt zwei unterschiedliche Sattelspiele und die vierte Animation ein Zentrumsspiel.
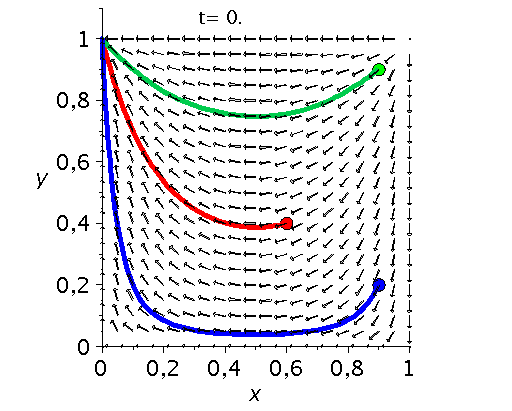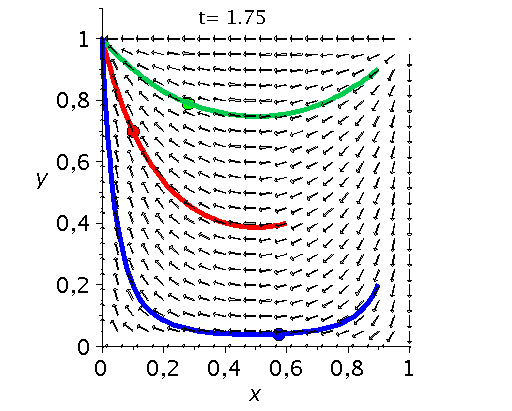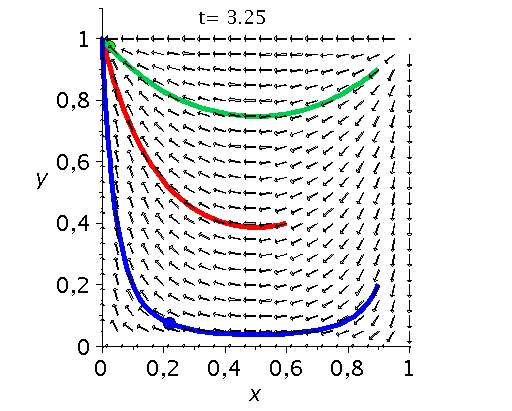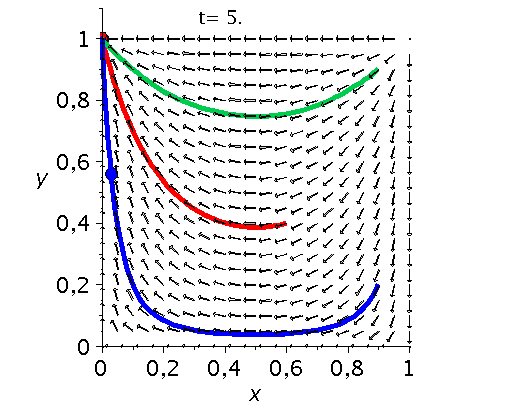
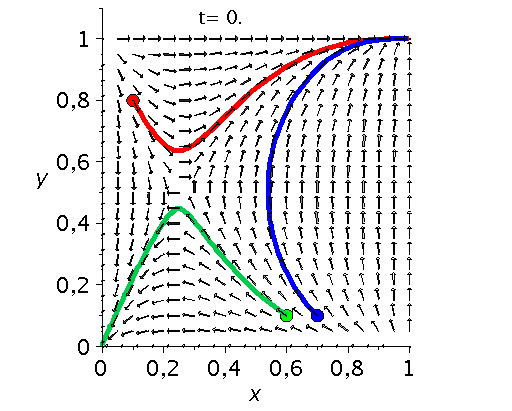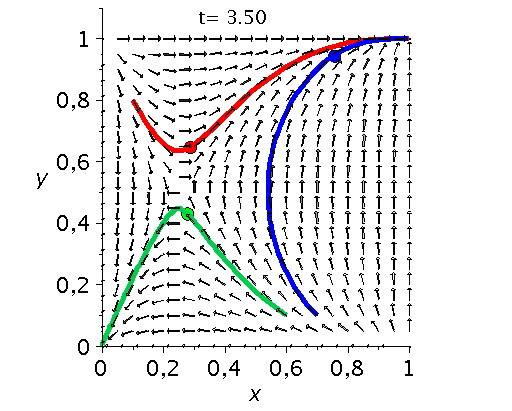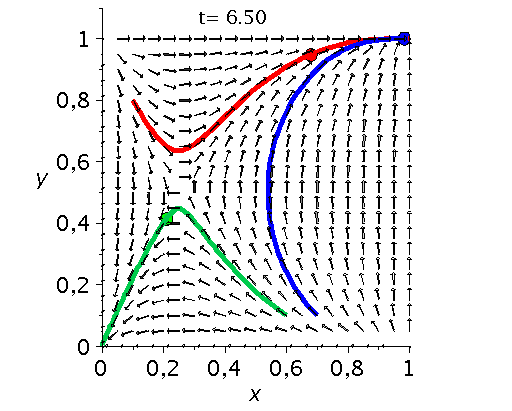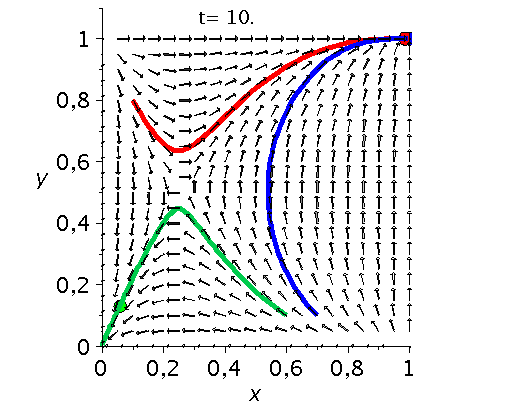
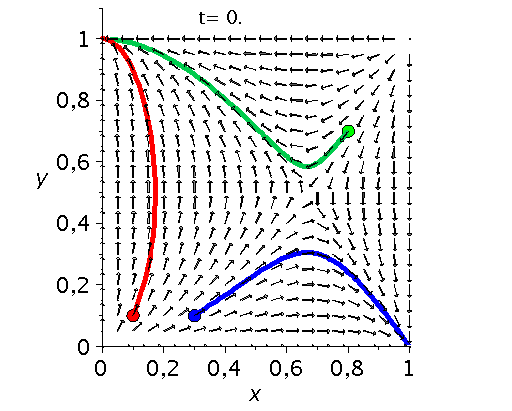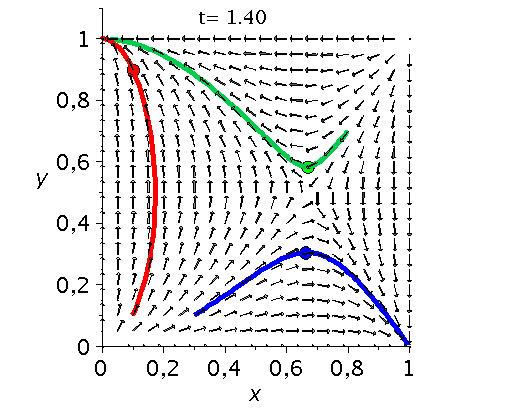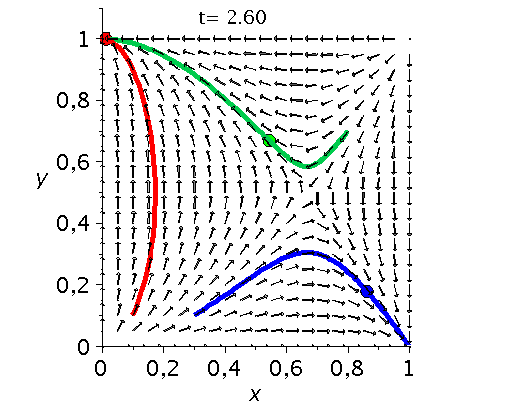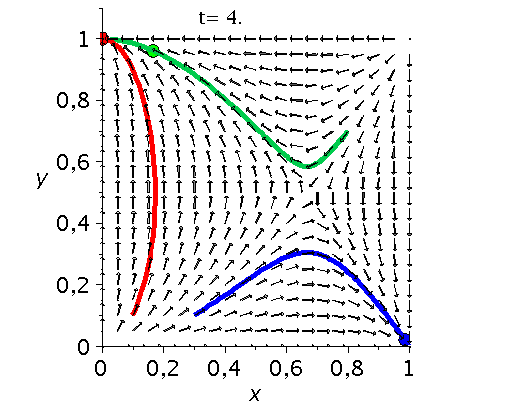
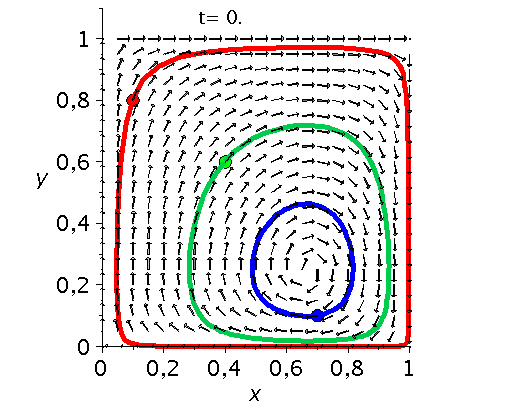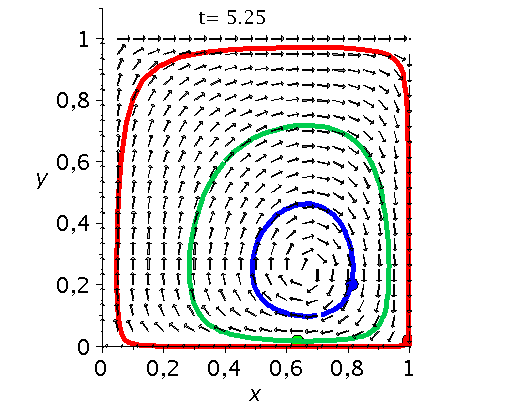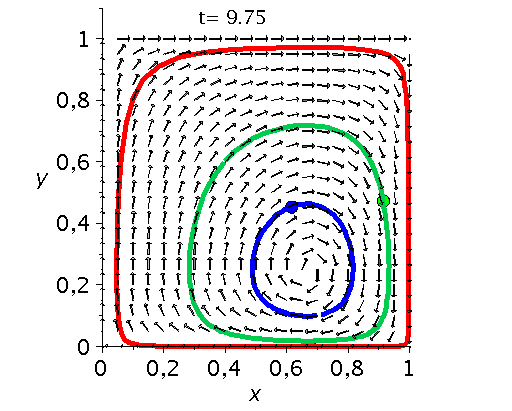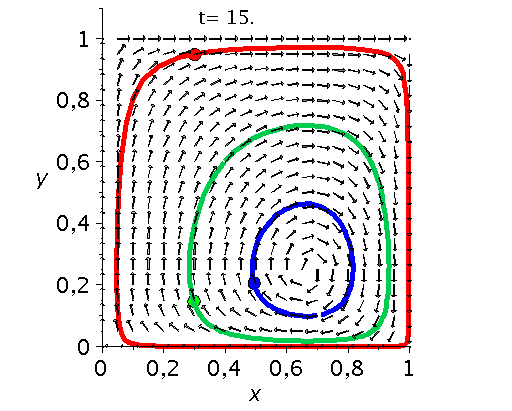
Klassen von unsymmetrische ($2 \times 2$) Spiele: Eckenspiele (links), die Sattelspiele (mitte links/rechs) und die Zentrumsspiele (rechts).
I.2.5 Die Populationsökologie (bzw. Populations-/Evolutionsbiologie) als Anwendungsfeld der evolutionären Spieltheorie
In der Ökologie werden die Beziehungen/Interaktionen von Lebewesen (Organismen) untereinander und zu ihrer unbelebten Umwelt untersucht. Die zeitliche Entwicklung der einzelnen Populationsgrößen ist Gegenstand der Populations- und Evolutionsbiologie, welche ihren mathematische Ansatz in der sogenannten Räuber-Beute-Gleichung (Lotka-Volterra Gleichung) finden. \[ \begin{equation} \frac{d x_i(t)}{dt} = \left( r_i + \sum_{j=1}^{N} b_{ij}\, x_j(t) \right) x_i(t) \end{equation} \] In diesem Unterpunkt wird die Räuber-Beute-Gleichung der theoretischen Biologie behandelt und deren Lösungen am Beispiel für zwei Populationen (N=2, die Populationen sind die Räuber- und Beute Lebewesen) berechnet. Es wird ausserdem ein Bezug zwischen der Räuber-Beute-Gleichung für N-Populationen und der Replikatorgleichung der evolutionären Spieltheorie für N+1 Strategien gezogen. Es wird gezeigt, dass die Räuber-Beute-Gleichung (Lotka-Volterra Gleichung) für N-Populationen sich auf ein evolutionäres Spiel mit N+1 Strategien abbilden lässt (siehe Sigmund/Hofbauer S:77 bzw. Novak "Evolutionary dynamics", p.68). Das unter dem obigen Link einsehbare Maple-Worksheet befasst sich mit dem Räuber-Beute Spiel (Anzahl der Strategien m=3 entspricht N=2 Populationen) und berechnet dessen Lösungen in einem evolutionären, zeitabhängigen Kontext. Ausgangspunkt ist eine allgemeine unsymmetrische Auszahlunsmatrix eines (2 Personen)-(3 Strategien) Spiels. Die Interaktionsmatrix ($b_{ij}$) und die intrinsischen Reproduktions-Sterberaten ($r_i$) sind mit der (2x3)-Spielmatrix des evolutionären Spiels in einer speziellen Weise verknüpft (siehe Sigmund/Hofbauer S:77 bzw. Novak "Evolutionary dynamics", p.68). Die Äquivalenz der Räuber-Beute-Gleichung (Lotka-Volterra Gleichung) mit der Replikatordynamik der evolutionären Spieltheorie repräsentiert eine mathematisch schöne Verbindung zwischen den unterschiedlichen wissenschaftlichen Fachgebieten der theoretischen Ökologie und der evolutionären Spieltheorie.
I.2.6 Python Programmierung evolutionärer Spiele
Dieses Kapitel gibt eine Einführung in die Python Programmierung evolutionärer Spiele. Die numerischen Lösungen der in Teil I.2 dieser Vorlesung erarbeiteten evolutionären Differentialgleichungen werden nun nicht mit der proprietären Software Maple berechnet, sondern unter Verwendung der Programmiersprache
I.2.6.1 Symmetrische, evolutionären (2 x 2) Spielen
Das Verhalten der Spielerpopulation in den drei unterschiedlichen Spielklassen symmetrischer ($2 \times 2$) Spiele (Dominanten Spiele, Koordinationsspiele und Anti-Koordinationsspiele) lässt sich mittels des folgenden Python Skriptes berechnen und grafisch darstellen: Python Skript: evol1.py. In der Vorlesung wird dieses Skript und weitere Variationen des Programms im Detail erläutert. Die untere Abbildung zeigt beispielhaft einige Resultate dieses Python Skriptes.
I.2.6.2 Evolutionäre Entwicklung von Bi-Matrix Spielen
Das Verhalten der Spielerpopulationen A und B in den drei unterschiedlichen Spielklassen unsymmetrischer ($2 \times 2$) Spiele (Eckenspiele (engl.: corner class games ), Sattelspiele (engl.: saddle class games ) und Zentrumsspiele (engl.: center class games )) lässt sich mittels des folgenden Python Skriptes berechnen und grafisch darstellen: Python Skript: bimatrix1.py. In der Vorlesung wird dieses Skript und weitere Variationen des Programms im Detail erläutert. Die untere Abbildung zeigt beispielhaft einige Resultate dieses Python Skriptes.
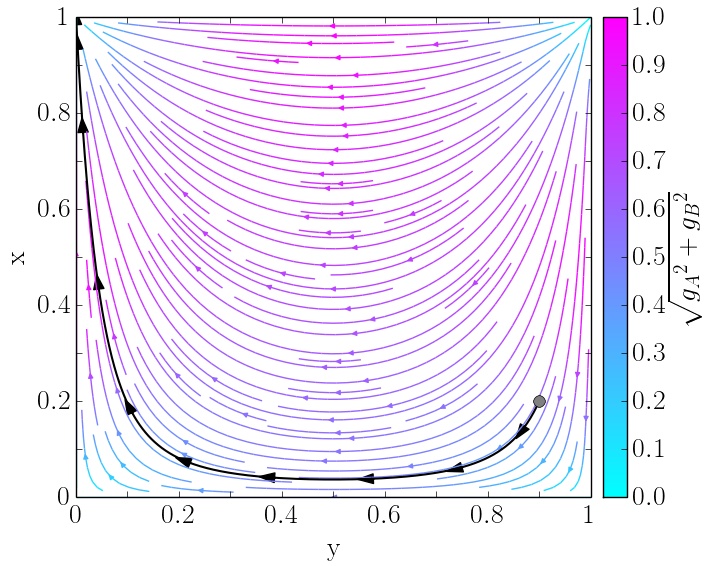
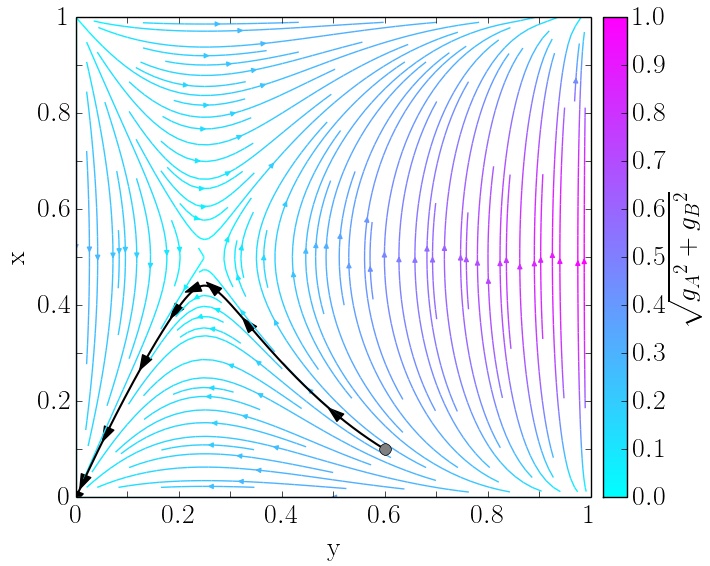
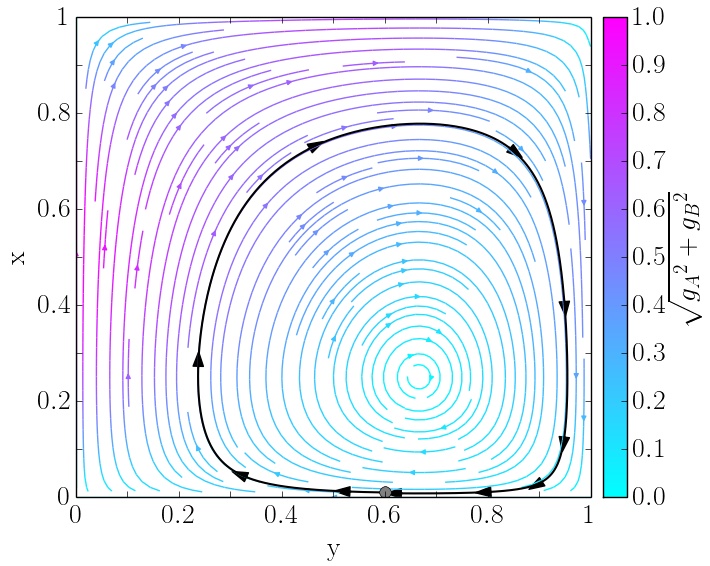
Ergebnisse des Python Skriptes bimatrix1.py: Klassen unsymmetrischer Bi-Matrix Spiele Eckenspiel (links), Sattelspiel (mitte) und Zentrumsspiel (rechts).
I.2.7 Mögliche Projekte im Teil I
Projekt I: Spielklassen symmetrischer (2x3)-Spiele
E. C. Zeeman zeigt in seinem im Jahre 1980 veröffentlichten Artikel, dass man evolutionäre, symmetrische (2x3)-Spiele in 19 Klassen einteilen kann. Es gibt Spielklassen, die besitzen lediglich eine evolutionär stabile Strategie und Klassen die sogar drei evolutionär stabile Strategien besitzen. (siehe E.C. Zeeman, POPULATION DYNAMICS FROM GAME THEORY, In: Global Theory of Dynamical Systems, Springer 1980). Stellen Sie Beispiele dieser Spielklassen mittels eines Python Skriptes dar (benutzen Sie z.B. das Python Skript bimatrix1.py als Vorlage). Das folgende Maple Worksheet kann Ihnen dabei helfen (View Maple Worksheet, Download Maple Worksheet).
Projekt II: Äquivalenz der Räuber-Beute-Gleichung für 2-Populationen mit der Replikatordynamik der evolutionären Spieltheorie für 3 Strategien
Stellen Sie die Äquivalenz der Räuber-Beute-Gleichung für 2-Populationen mit einem evolutionären Spiel mit 3 Strategien mittels eines Maple Worksheets oder eines Python Skriptes dar.