I.2.2 Evolutionär stabile Strategien
Die im vorigen Unterkapitel I.2.1 vorgestellten Differentialgleichungen der evolutionären Dynamik beschreiben die zeitabhängige Entwicklung der Strategienwahl einer ganzen Population von Spielern. Es stellt sich nun die Frage ob es bei vorgegebener Auszahlungsmatrix (Fitness-Matrix) Strategien gibt, zu denen die Population tendiert. In diesem Unterkapitel betrachten wir die stationären Lösungen des asymptotischen Verhaltens des Populationsvektors ($\underset{t \rightarrow \infty}{\hbox{lim}}(\vec{x}(t))$) und werden ein weiteres fundamentales Gleichgewichtskonzept einführen, das der evolutionär stabilen Strategie (ESS). Wir beschränken uns dabei zunächst auf die gemischte Erweiterung eines simultanen ($2$ Spieler)-($2$ Strategien) Spiels in strategischer Form mit Auszahlung (siehe Unterkapitel I.1.3).
Gegeben sei ein allgemeines ($2 \times 2$) Spiel $\Gamma$ (gemischte Auszahlungsfunktionen: ${\bf \tilde{\cal \$}}^A$ und ${\bf \tilde{\cal \$}}^B$).
- $(\tilde{s}^{A\ast},\tilde{s}^{B\ast})$ ist ein Nash-Gleichgewicht des Spiels $\Gamma$
- ${\bf \tilde{\cal \$}}^A(\tilde{s}^A,\tilde{s}^B) \leq {\bf \tilde{\cal \$}}^A(\tilde{s}^{A\ast},\tilde{s}^B) \qquad \forall \quad \tilde{s}^{A} \in r^A(\tilde{s}^{B\ast})\, , \,\,\, \tilde{s}^{B} \neq \tilde{s}^{B\ast}$
${\bf \tilde{\cal \$}}^B(\tilde{s}^A,\tilde{s}^B) \leq {\bf \tilde{\cal \$}}^B(\tilde{s}^{A},\tilde{s}^{B\ast}) \qquad \forall \quad \tilde{s}^{B} \in r^B(\tilde{s}^{A\ast})\, , \,\,\, \tilde{s}^{A} \neq \tilde{s}^{A\ast}$
$r^B(\tilde{s}^{A})$ bzw. $r^A(\tilde{s}^{B})$ ist die Abbildung der besten Antwort des Spielers B auf die Strategie $\tilde{s}^{A}$ bzw. des Spielers A auf die Strategie $\tilde{s}^{B}$. Eine ESS $(\tilde{s}^{A\ast},\tilde{s}^{B\ast})$ des Spiels $\Gamma$ besteht somit, falls diese ein Nash-Gleichgewicht ist (notwendige Bedingung) und zusätzlich (hinreichende Bedingung) die Ungleichungen in b) für alle Strategiekombinationen $(\tilde{s}^{A},\tilde{s}^{B})$ innerhalb der Menge der Bestantwort $r^B(\tilde{s}^{A})$ bzw. $r^A(\tilde{s}^{B})$ erfüllt sind.
Um des Konzept der ESS zu verdeutlichen betrachten wir die zeitliche Entwicklung des strategischen Verhaltens einer ganzen Population in einem wiederholten symmetrischen Spiel. Wie im Unterkapitel I.2.1 dargestellt, wird der Populationsvektors $\vec{x}(t)$ (hier $x(t)$, da nur zwei Strategien) durch folgende Gleichung bestimmt
\[
\begin{equation}
\frac{d x(t)}{dt} = \left[ (\$_{11} - \$_{21}) (x-x^2) + (\$_{12} - \$_{22}) (1-2x+x^2) \right] \, x(t) \, =:\,g(x)
\end{equation}
\]
$x(t)$, der Anteil der Spieler die zum Zeitpunkt $t$ die Strategie $s_1$ spielen, hängt neben der Funktion $g(x)$ von dem Anfangswert $x(t=0)$ ab. In gewisser Weise kann man $x(t)$ als die gemischte Strategie $\tilde{s}$ der gesamten Population ansehen.

Auszahlunsmatrix des Falke-Taube Spiels. Der Parameter $V$ quantifiziert die negative Auszahlung die durch den Kampf zweier Falken entsteht ($V > 1$).
Beispiel: Das Falke-Taube Spiel
Wir betrachten im folgenden ein ($2 \times 2$) Spiel mit symmetrischer Auszahlungsmatrix - das sogenannte Falke-Taube Spiel (siehe z.B. [4], S:57). Wir nehmen an, dass unsere Population aus zwei Arten (zwei Gruppen) besteht: Die Falken, die eine aggressive Spezies repräsentieren und die Tauben, die die friedlich aggierende Populationsart darstellen ($\mu,i=\hbox{Falke,Taube}=F,T$). Wir sind daran interessiert, wie sich der Populationsvektor $x(t)$ mit der Zeit verhält, wobei wir mit $x(t)$ das relative Verhältnis von Falken in der Population definieren (($y(t)=1-x(t)$) stellt somit das relative Verhältnis von Tauben dar). Wenn sich zwei Tauben treffen, so teilen sie friedlich die Ihnen zur Verfügung stehende Auszahlung, der wir im folgenden den Wert 1 zuordnen (somit $\$_{22}=1/2$). Treffen dagegen zwei aggressive Spezies der Population aufeinander, so kämpfen sie um die Auszahlung und ziehen sich unter Umständen Verletzungen zu, die in dem folgenden Auszahlungsansatz mittels des Parameters V berücksichtigt wurde ($\$_{11}=1/2-V/2$). Trifft schliesslich eine Taube auf einen Falken, so flieht die Taube und der Falke erhält die gesamte Auszahlung (somit $\$_{12}=1$ und $\$_{21}=0$). Die nebenstehende Tabelle fasst die jeweiligen Auszahlungen nochmals zusammen.
Wir beschränken uns im folgenden auf den Fall $V > 1$ und man kann leicht mittels der Bestantwort-Pfeile zeigen, dass das Spiel unter diesen Einschränkungen der Klasse der Anti-Koordinationsspiele angehört (für den Fall $V \leq 1$ gehört das Spiel jedoch der Klasse der dominanten Spiel an). Das Falke-Taube Spiel besitzt ein gemischtes Nash-Gleichgewicht bei der Strategienkombination (x,y)=$(\tilde{s}^{A\star},\tilde{s}^{B\star})=(\frac{1}{V},\frac{1}{V})$ und zwei reine, unsymmetrische Nash-Gleichgewicht bei (x,y)=(0,1) und (x,y)=(1,0). Die zeitliche Entwicklung des Populationsvektors $x(t)$ wird durch die folgende Differentialgleichung bestimmt:
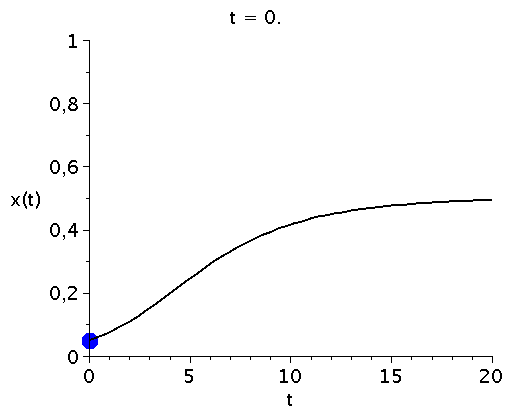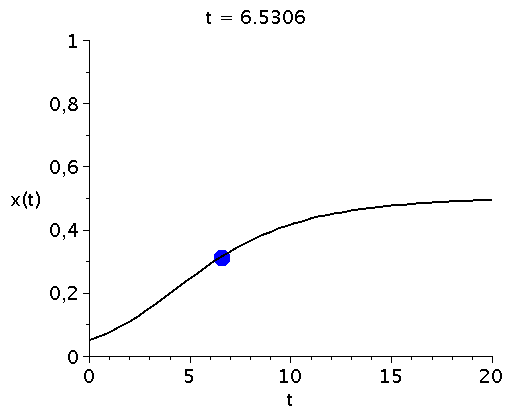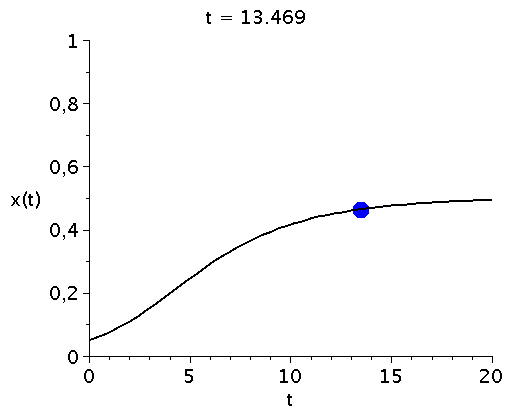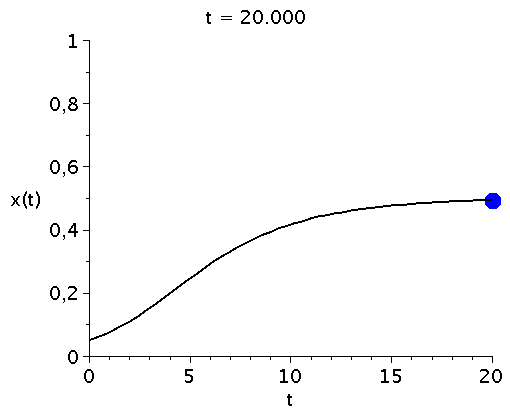
Zeitliche Entwicklung des Populationsvektors x(t) im Falke-Taube Spiel (V=2) bei vorgegebener Anfangspopulation x(t=0)=0.05.
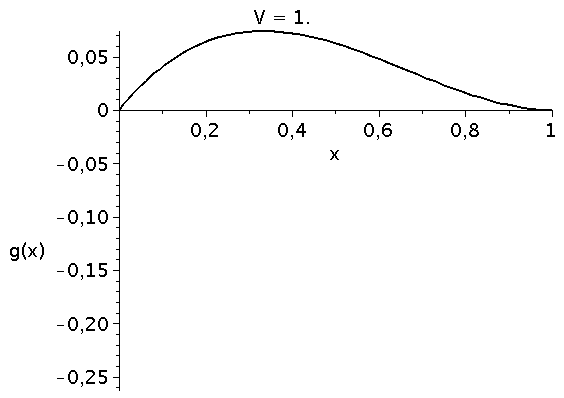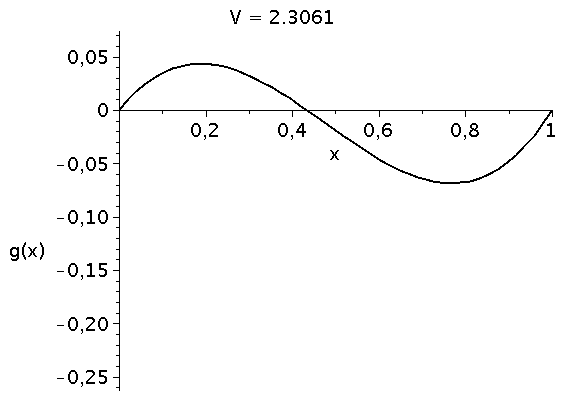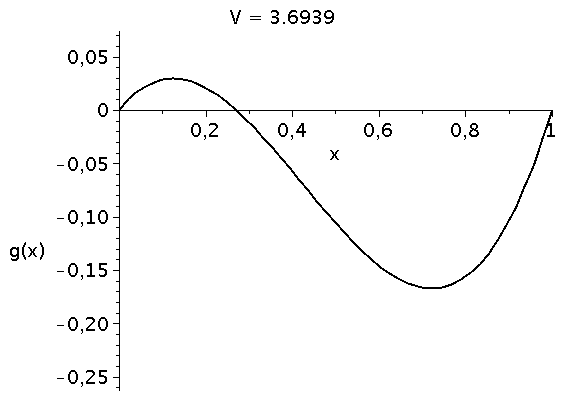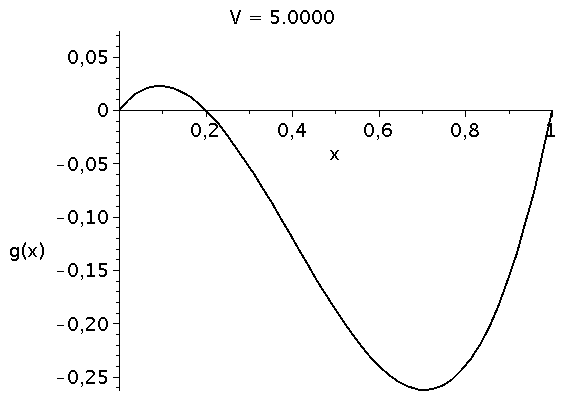
Veränderung der Funktion g(x) bei Variation des Parameters V im Bereich [1,5]. Die interne Nullstelle von g(x) entspricht dem gemischten Nash-Gleichgewicht des Spiels.
\[ \begin{equation} \frac{d x}{dt} = \frac{V}{2} x^3 - \frac{V+1}{2} x^2 + \frac{1}{2} x \, =:\,g(x) \end{equation} \] Die auf der rechten Seite dargestellte Animation zeigt die Funktion g(x) bei Variation des Parameters V im Bereich [1,5]. Die interne Nullstelle der Funktion g(x) entspricht dem gemischten Nash-Gleichgewicht des Spiels ($\frac{d g(x)}{dx}=0 \rightarrow \{0,1/V,1\}$). Die zeitliche Entwicklung des Populationsvektors x(t), d.h. der Anteil der Spieler die zum Zeitpunkt t die Strategie "Falke" spielen, hängt neben der Funktion g(x) von dem Anfangswert x(t=0) ab. Setzt man z.B. x(t=0)=0.05 (entspricht einer Anfangspopulation von 5% Falken und 95% Tauben) und setzt den Parameter V z.B. auf den Wert 2 (V=2) so kann man die Differentialgleichung nummerisch lösen (siehe linke Abbildung). Die durch das gemischte Nash-Gleichgewicht (bzw. die interne Nullstelle der Funktion g(x)) festgelegte gemischte Strategie der Population (1/V) stellt die evolutionär stabile Strategie des Falke-Taube Spiels dar. Unabhängig von der gewählten Anfangszusammensetzung der Population (hier x(t=0)=0.05) entwickelt sich die Population zu einem Zustand der Koexistenz beider Strategien, wobei die für große Zeiten asymptotisch erreichte Populationszusammensetzung durch den Wert des internen gemischten Nash-Gleichgewichts (hier $1/V=1/2$) gegeben ist und die evolutionär stabile Strategie darstellt. Variiert man den Parameter V (hier V=[1,5]), so verschiebt man die evolutionär stabile Strategie (siehe roter Punkt in der unteren Abbildung).
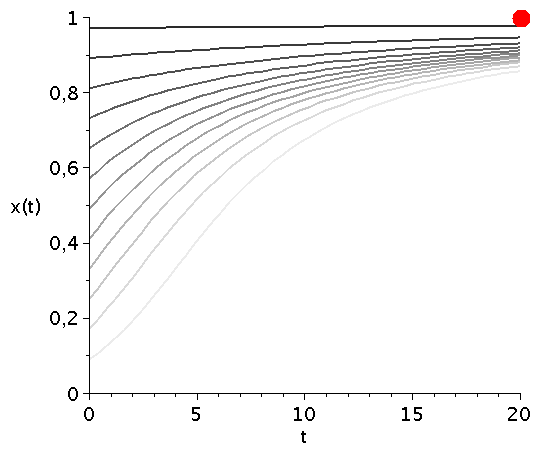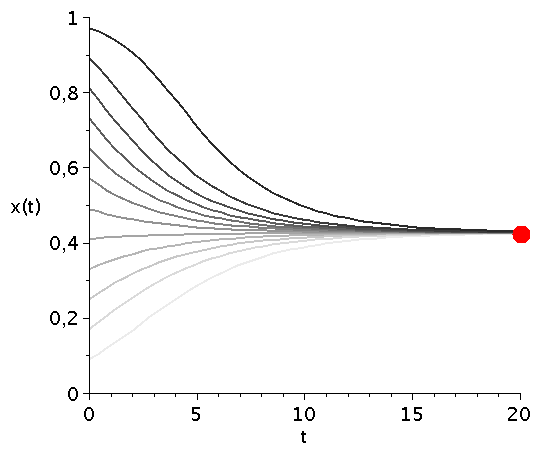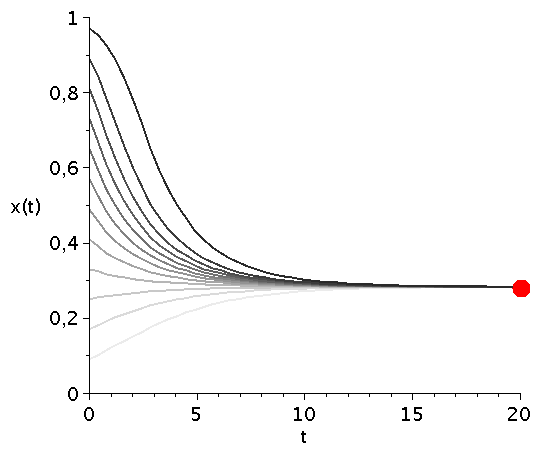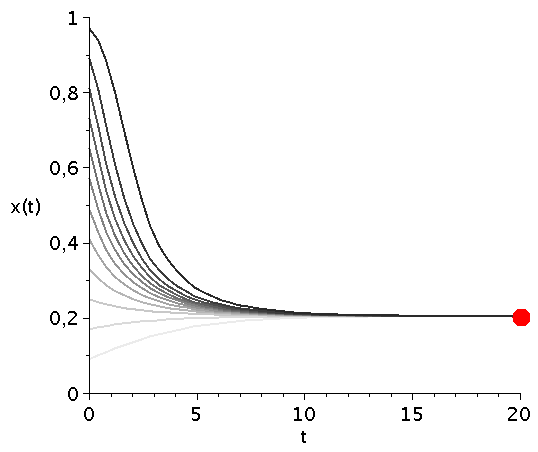
Zeitliche Entwicklung des Populationsvektors x(t) im Falke-Taube Spiel für mehrere unterschiedliche Anfangspopulationen x(t=0) (graue Kurven) bei Variation des Parameters V im Bereich [1,5]. Der rote Punkt mit dem Wert $1/V$ kennzeichnet die evolutionär stabile Strategie des Spiels.
Das Maple-Worksheet: I.2.3 Klassifizierung von symmetrischen, evolutionären (2 x 2) Spielen fasst die dargestellten Ergebnisse zusammen. Einfache Beispiele einer nummerischen Lösung der Differentialgleichungen der evolutionären Dynamik mittels der Skriptsprache Python sind unter den folgenden Links erhältlich: Version 1, Version 2, Version 3