III.1 Evolutionäre Dynamik auf komplexen Netzwerkstrukturen
Die Verknüpfung der Theorie komplexer Netzwerke (siehe Teil II der Vorlesung) mit der evolutionären Spieltheorie (siehe Teil I der Vorlesung) stellt ein vielversprechendes mathematisches Modell dar, welches sowohl der interdisziplinären Grundlagenforschung, als auch der angewandten, empirischen Netzwerkforschung dienen kann. In diesem Kapitel wird die Vorgehensweise einer Miteinbeziehung komplexer Netzwerktopologien in die evolutionäre Spieltheorie beschrieben. Die dann auf einem solchen komplexen Netzwerk ablaufenden Entscheidungsprozesse können in den meisten Fällen lediglich mittels nummerischer, agenten-basierter Computersimulationen veranschaulicht werden.
Viele der in diesem Unterkapitel behandelten Systeme sind dem Buch Martin A. Nowak, Evolutionary Dynamics - Exploring the Equations of Life, 2006 entnommen, welches eine sehr gute und allgemein verständliche Einführung in das Themengebiet der evolutionären Dynamik darstellt. Obwohl der Fokus dieses Buches im Bereich der Evolution von biologischen Systemen liegt (siehe Kapitel 10: HIV Infection, Kapitel 11: Evolution of Virulence, Kapitel 12: Evolutionary Dynamics of Cancer, und Kapitel 13: Language Evolution), sind die Kapitel 1-9 weitgehend allgemein formuliert. Die evolutionäre Dynamik unterschiedlicher Spezien einer Tierart und der Mechanismus wie Tierarten ineinander übergehen wurde von Charles Darwin bereits im Jahre 1840 beschrieben. Im Jahre 1973 stellte John Maynard Smith eine Verbindung zwischen den Populationsgleichungen der Biologie und der evolutionären Spieltheorie her. Das Konzept der Quasi-Spezien (Ensemble von ähnlichen Genomen Sequenzen (Erbgut eines Lebewesens) welches durch einen Prozess der Mutation und Selektion entstanden ist) wurde von Manfred Eigen und Peter Schuster entwickelt (siehe Kapitel 3.3: Martin A. Nowak, Evolutionary Dynamics - Exploring the Equations of Life). Die Struktur der Quasi-Spezien Differentialgleichung ist den Gleichungen der evolutionären Spieltheorie sehr ähnlich (siehe Bild 3.4 und 4.5: Martin A. Nowak, Evolutionary Dynamics - Exploring the Equations of Life). Die evolutionäre Vorteilhaftigkeit einer Genom Sequenz wird hierbei als die Fitness der Quasi-Spezie bezeichnet. Quasi-Spezien entsprechen den Strategien der Spieltheorie und die Fitness kann als der Auszahlungswert einer Strategie aufgefasst werden. Die zeitliche Entwicklung der Quasi-Spezien am Beispiel des Paarungsverhalten von Eidechsen wird z.B. in siehe Sinervo, Barry, and Curt M. Lively. 'The rock-paper-scissors game and the evolution of alternative male strategies.' Nature 380.6571 (1996): 240. analysiert (siehe auch Vorlesung 6). Die evolutionäre Dynamik hängt von der unterliegenden Netzwerkstruktur der beteiligten Akteure ab und skalenfreie Netzwerkstrukturen agieren hier als Verstärker der evolutionären Selektion (siehe Kapitel 8, Evolutionary Graph Theory: Martin A. Nowak, Evolutionary Dynamics - Exploring the Equations of Life). Im folgenden Unterpunkt werden sie sogenannten Spatial Games behandelt (eine ausführliche Einführung findet sich im Kapitel 9: Martin A. Nowak, Evolutionary Dynamics - Exploring the Equations of Life).
III.1.1 Spatial Games: Evolutionäre räumliche Spiele
In diesem Unterpunkt werden die Spieler einer endlich großen Population auf einem räumlichen Gitter angeordnet, wobei jeder Spieler nur mit seinen nächsten Nachbarn spielen kann (Moore Nachbarschaft). Das zugrundeliegende Netzwerk der Spielerknoten besitzt somit eine reguläre Struktur und im betrachteten 2-dimensionalen Fall spielt jeder Spieler pro Spielperiode mit acht Spielern (Knotengrad $k_i=8\, \forall\, i \in {\cal I}$). Wir beschränken uns im folgenden auf symmetrische 2x2-Spiele (siehe Teil I.1.4: Ansatz eines allgemeinen (2 Personen)-(2 Strategien) Spiels mit symmetrischer Auszahlunsmatrix und Parametern a, b, c und d). Die Spielerknoten spielen pro Iteration mit jedem ihrer Nachbarn und am Ende von jedem Zeitschritt vergleichen die Spieler ihren summierten Gewinn/Verlust mit den Nachbarspielern ihres Umfeldes. Ist die Auszahlung eines Spielers höher als der eigene Auszahlungswert, so ändern der Spieler in der nächsten Spielperiode seine Strategie; ist sein eigener Wert der höchste, so bleibt er auch in der nächsten Iteration bei seiner gespielten Strategie.
In dem oberen Link finden Sie eine Beispiel, das an das 9. Kapitel des Buches Martin A. Nowak, Evolutionary Dynamics - Exploring the Equations of Life, 2006 angelehnt ist und ein Gefangenendilemma auf einem räumlichen 2-dimensionalen Gitter beschreibt. In Abhängigkeit der Stärke der Dominanz der Strategie und der Anfangskonfiguration der Strategienwahl der Spieler sind unterschiedliche zeitlichen Entwicklungen der Population möglich. Die nebenstehende Animation zeigt die zeitliche Entwicklung einer speziellen sogenannten Walker-Anfangsbedingung, die nach der Kollission der beiden Walker-Strukturen eine Art explosionsartige Ausbreitung der blauen Strategie verursacht (siehe Python Skript VPSOC-RandomNetwork_evol.py). Das linke obere Diagramm veranschaulicht die zeitliche Entwicklung des Populationsvektors x(t). Obwohl die klassische evolutionäre Spieltheorie vorhersagt (siehe Teil I), dass der Anteil der Spieler die die dominante rote Strategie wählt im Laufe der Zeit kontinuierlich zunehmen sollte und gegen den Wert $\underset{t \rightarrow \infty}{\hbox{lim}}(x(t))=0$ konvergiert, bildet sich bei evolutionären räumlichen Spielen in speziellen Parameterbereichen oft ein dynamischer Gleichgewichtzustand mit $\underset{t \rightarrow \infty}{\hbox{lim}}(x(t))=1/3$ heraus.
III.1.2 Evolutionäre Spiele auf komplexen Netzwerken
Die im vorigen Unterpunkt behandelte Fall eines evolutionären Spiels auf einem räumlichen 2-dimensionalen Gitters mit Mooreschen Nachbarschaft-Kanten stellt ein einfaches Beispiel eines Gefangenendilemma-ähnlichen, evolutionären Spiels auf einer komplexen Netzwerkstruktur dar. Durch eine Veränderung der zugrundeliegenden Netzwerkstruktur (siehe Teil II: zufällige, kleine Welt, exponentiellen und skalenfreien Netzwerke) ist es möglich realistischere, real existierende sozio-ökonomischer Systeme zu simulieren und zu verstehen. Desweiteren behandelte das vorige Unterkapitel lediglich eine Klasse der symmetrischen (2 Personen)-(2 Strategien) Spiele (Klasse der dominanten Spiele) und benutzt eine spezielle, simultane Form der Auswahl der zukünftigen Strategienwahl (Update-Rule). Es kann z.B. gezeigt werden dass ein Spiel auf einem skalenfreien Netzwerk die Herausbildung von Kooperationseffekten begünstigt (siehe z.B. F.C.Santos und J.M.Pacheco, Scale-Free Networks Provide a Unifying Framework for the Emergence of Cooperation, PRL 95, p.098104 (2005)). Weitere Literatur zu diesem Gebiet finden Sie unter dem folgenden Link .
III.1.3 Mögliche Projekte im Teil III
Erstellen Sie ein Python Programm, das ein evolutionäres Spiel auf einem komplexen Netzwerk simuliert. Betrachten Sie unterschiedliche Spielklassen symmetrischer (2 Personen)-(2 Strategien) Spiele und variieren die Struktur des Gitters (z.B. reguläre, vollständig verbundene, zufällige, kleine Welt, exponentiellen und skalenfreien Netzwerke). Zeigen Sie dass im Falle eines vollständig verbundenen Netzwerks einer großen Population von Spielern die Ergebnisse der klassischen evolutionären Spieltheorie reproduziert werden können (siehe Teil I).
III.2 Quanten Spieltheorie
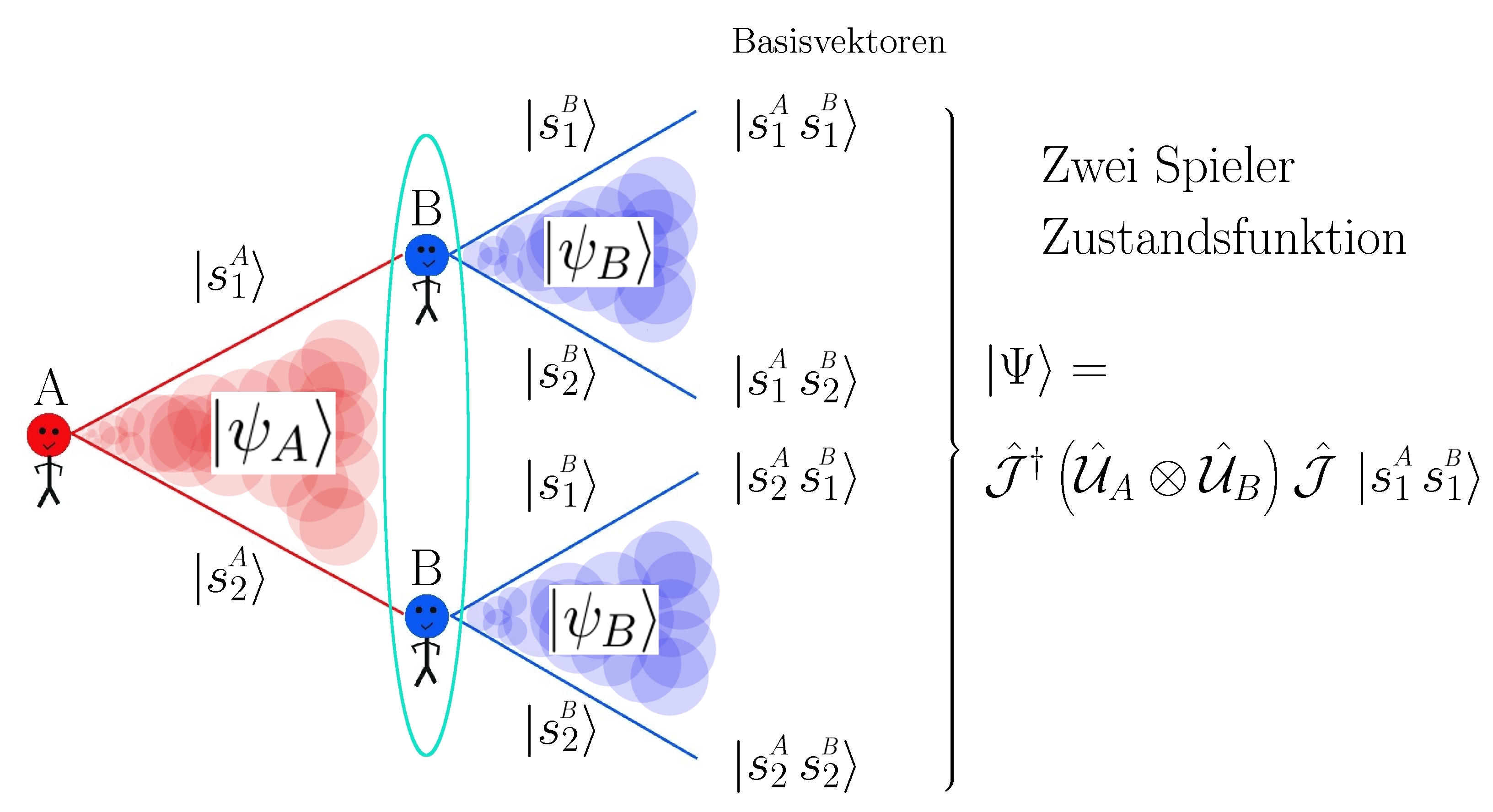
Spielbaum eines (2 Personen)-(2 Strategien) Quantenspiels.
Die Quantenspieltheorie stellt eine mathematische und konzeptuelle Erweiterung der klassischen Spieltheorie dar. Der Raum aller denkbaren Entscheidungswege der Spieler wird vom rein reellen, messbaren Raum in den Raum der komplexen Zahlen (reelle und imaginäre Zahlen) ausgedehnt. Durch das Konzept der möglichen quantentheoretischen Verschränkung der Entscheidungswege im imaginären Raum aller denkbaren Quantenstrategien können gemeinsame, durch kulturelle oder moralische Normen entstandene Denkrichtungen in die evolutionäre Dynamik mit einbezogen werden. Ist die Strategienverschränkung der Spieler im imaginären Raum der denkbaren Entscheidungswege nur genügend groß, so können zusätzliche Nash-Gleichgewichte auftreten und zuvor existente dominante Strategien sich auflösen.
Die Quanten-Spieltheorie beschreibt den Entscheidungszustand eines Spielers $\mu=A,B$, bevor dieser die endgültige Wahl der reinen Strategie getroffen hat, als eine komplexwertige Größe (einen sog. Spinor $\left| \psi \right>_{\!A}$ bzw. $\left| \psi \right>_{\!B}$) in einem zweidimensionalen Zustandsraum, dem sogenannten Hilbertraum ${\cal{H}}_A$ bzw. ${\cal{H}}_B$. Der Zwei-Spielerzustand $\left| \Psi \right>$ ist ein vierkomponentiger Spinor, welcher auf dem gemeinsamen Hilbertraum der Spieler (${\cal{H}}:={\cal{H}}_A \otimes {\cal{H}}_B$) definiert ist. Formal setzt sich dieser aus den Entscheidungsmatrizen (Entscheidungsoperatoren) $\hat{\cal{U}}_A$ bzw. $\hat{\cal{U}}_B$ und der Verschränkungsmatrix (bzw. dem Verschränkungsoperator) $\hat{\cal{J}}$ zusammen (siehe nebenstehenden Abbildung). Die der evolutionären Entwicklung zugrundeliegende Replikatordynamik besitzt in der evolutionären Quantenspieltheorie eine komplexere Struktur und die jeweiligen evolutionär stabilen Strategien können sich, abhängig vom Maß der Verschränkung, abändern.