Teil III.2 Quanten Spieltheorie
Die folgenden Unterkapitel sind meiner Dissertation entnommen. Literaturangaben und weiterführende Darstellungen entnehmen Sie bitte dem Original: Matthias Hanauske, Evolutionäre Quanten-Spieltheorie im Kontext sozio-ökonomischer Systeme, 2011.
Teil III.2.1 Einführung in die Quanten Spieltheorie
Die Annahme des vollständig verbundenen, zufälligen Netzwerks, welches die Grundlage der deterministischen evolutionären Spieltheorie bildet, ist in realen sozialen Netzwerken oft nicht erfüllt. In realen sozialen Netzwerken bilden sich oft weitgehend abgeschlossene Cluster von miteinander verbundenen Spielern, die zu anderen Clustern nur bedingt bzw. selten Kontakt haben. Diese Art von Cluster- bzw. Cliquenbildung kann zu einer unterschiedlichen Ausprägung von sozialen Normen innerhalb der einzelnen Teilgruppen führen. Soziale Normen können sich somit herausbilden, die den einzelnen Spielern neben ihrem homo ökonomischen Interesse auch den Blick auf das Wohl der eigenen Gruppe nahelegen. Eine solche Art von induziertem Gruppeninteresse wird im folgenden mittels des Ansatzes der Quanten-Spieltheorie mathematisch in die deterministischen Gleichungen der evolutionären Spieltheorie eingearbeitet. Die Quantenspieltheorie stellt eine mathematische und konzeptuelle Erweiterung der klassischen Spieltheorie dar. Der Raum aller denkbaren Entscheidungswege der Spieler wird vom rein reellen, messbaren Raum in den Raum der komplexen Zahlen (reelle und imaginäre Zahlen) ausgedehnt. Durch das Konzept der möglichen quantentheoretischen Verschränkung der Entscheidungswege im imaginären Raum aller denkbaren Quantenstrategien können gemeinsame, durch kulturelle oder moralische Normen entstandene Denkrichtungen in die evolutionäre Dynamik mit einbezogen werden. Ist die Strategienverschränkung der Spieler im imaginären Raum der denkbaren Entscheidungswege nur genügend groß, so können zusätzliche Nash-Gleichgewichte auftreten und zuvor existente dominante Strategien sich auflösen.
Die erste formale Beschreibung der Quanten-Spieltheorie wurde im Jahre 1999 von Eisert et al. vorgestellt. Diese oft zitierte Arbeit betrachtet die quantentheoretische Erweiterung eines Gefangenendilemma Spiels und zeigt auf, dass die Spieler dem Dilemma entkommen können, falls der strategische Verschränkungswert oberhalb einer dem Spiel eigenen Grenze liegt. Im selben Jahr (1999) analysierte D. A. Meyer das Penny Flip Spiel und erweiterte dieses mittels quantentheoretischer Konzepte. In seinem Artikel betrachtete er den unrealistischen Fall, dass einer der Spieler das im Spiel benutzte Geldstück in einem überlagerten Quantenzustand positionieren könne und zeigte, dass dieser Spieler stets das Spiel gewinnen wird, falls sein Gegenspieler eine rein klassische Strategie benutzt. Im Jahre 2000 kommentierte S.J. van Enk die Arbeit von D. A. Meyer und zeigte, dass Meyer's Behauptung nicht sonderlich beeindruckend ist, da er nur einem der Spieler einen größeren Strategienraum erlaubt. Im Jahre 2000 wendeten Marinatto $\&$ Weber die quantentheoretischen Konzepte auf das Kampf der Geschlechter (battle of sexes) Spiel an und zeigten, dass durch die Verschränkung der Spielerstrategien ein eindeutiges Gleichgewicht möglich ist. In den folgenden Jahren wurden die quantenspieltheoretischen Konzepte auf weitere Spiele ausgedehnt; so analysierte R.V. Mendes die Quantenversion des Ultimatum Spiels, Hogg et al. betrachteten das Öffentliche Gut Spiel, eine Version des Quanten Koordinationsspiels und analysierten Quanten Auktionen. Benjamin $\&$ Hayden erweiterten im Jahre 2001 den Formalismus der Quanten-Spieltheorie auf mehr als zwei Spieler. Im Jahre 2002 benutzten Piotrowski $\&$ Sladkowsky die quantenspieltheoretischen Konzepte um Eigenschaften im Verhalten von Märkten zu erklären. Im Jahre 2006 analysierten Hanauske et al. das Open Access-Publikationsverhalten wissenschaftlicher Autoren mittels des quantentheoretischen Ansatzes. Bereits im Jahre 2001 wurde das erste Quantenspiel auf einem Quantencomputer realisiert, wobei sich die vorhergesagten Eigenschaften bestätigten. Die Resultate dieser Experimente wurden im Jahre 2007 von A. Zeilinger erneut bestätigt. Die ersten Ansätze einer Anwendung der Quanten-Spieltheorie auf sozio-ökonomische Experimente wurden nach 2007 veröffentlicht. Neben diesen Arbeiten, entwickelte sich im Bereich der Psychologie ein weiterer wissenschaftlicher Forschungszweig, welcher quantentheoretische Konzepte zur Erklärung von experimentellen Daten benutzt. Diese Arbeiten zeigen, dass viele, zunächst nicht erklärbare experimentelle Befunde im Bereich der Psychologie, sich mittels quantenlogischer Konzepte beschreiben lassen.
Teil III.2.2 Mathematischer Formalismus der die Quanten Spieltheorie
Die bei der quantentheoretischen Formulierung benutzten mathematischen Ansätze können grob in zwei Hauptströme gegliedert werden. Der Dichtematrix Ansatz der Quantenspieltheorie (siehe Marinatto $\&$ Weber) und den quanten-informationstheoretischen Ansatz von Eisert et al. Der auf quanteninformationstheoretischen Konzepten aufbauende Ansatz hat einerseits den Vorteil, dass die neu entstehenden Quantenstrategien in einem reduzierten Quanten-Strategienraum visualisiert und interpretiert werden können, andererseits baut der Ansatz die Möglichkeit einer Quantenverschränkung in mathematisch eleganter Weise in die Theorie ein, so dass man die Stärke einer möglichen Strategienverschränkung der Spieler mittels eines zusätzlichen Parameters ($\gamma$) im Modell variieren kann. In den ersten Jahren nach seiner Veröffentlichung wurde der Eisert'sche Ansatz von Benjamin $\&$ Hayden und S.J. van Enk angegriffen und kritisch diskutiert. Die damals erhobenen Vorwürfe stellten sich jedoch im Laufe der Zeit als nicht auf die Eisert'sche Theorie anwendbar heraus. Im Folgenden wird das Konzept der Quanten-Spieltheorie (in der Eisert'schen, quanten-informationstheoretischen Nomenklatur) im Detail beschrieben.
In der Quanten-Spieltheorie kann der Entscheidungszustand der beteiligten Akteure, im Gegensatz zur klassischen Spieltheorie, eine gemeinsame Strategienverschränkung aufweisen. Durch das Konzept dieser möglichen quantentheoretischen Verschränkung der Entscheidungswege im imaginären Raum aller denkbaren Quantenstrategien können gemeinsame, durch kulturelle oder moralische Normen entstandene Denkrichtungen, mit in die klassische Theorie einbezogen werden. Eine der grundlegenden Folgerungen aus einer solchen gemeinsamen Strategienverschränkung ist, dass die beteiligten Akteure eine erhöhte Kooperationsbereitschaft aufweisen, da sie dann eine Optimierung des gemeinsamen Zwei-Spielerzustandes $\left| \Psi \right>$ anstreben.
Um die mathematische Beschreibung eines evolutionären, quantenspieltheoretischen Modells zu verdeutlichen, wird im Folgenden zunächst ein (2 Personen)-(2 Strategien) Quantenspiel betrachtet. Der spieltheoretische, binäre Entscheidungsprozess der Akteure soll durch eine allgemeine Auszahlungsmatrix bestimmt sein (siehe nebenstehende Auszahlungstabelle). Die Quanten-Spieltheorie beschreibt den Entscheidungszustand eines Spielers $\mu=A,B$, bevor dieser die endgültige Wahl der reinen Strategie getroffen hat, als eine komplexwertige Größe (Spinor) in einem zweidimensionalen Zustandsraum, dem sogenannten Hilbertraum ${\cal{H}}_\mu$. Die in dieser Arbeit verwendete mathematische Repräsentation dieses Spinors wird mit Hilfe des Entscheidungsoperators $\widehat{\mathcal{U}}_\mu(\theta_{\!\mu},\varphi_{\!\mu})$ konstruiert, der auf einen Anfangszustand (hier speziell $\left| s^\mu_1 \right>$) wirkt. Ein allgemeiner Entscheidungszustand des Spielers A wird somit wie folgt mathematisch konstruiert:
\begin{eqnarray}
&\left| \psi_A \right>=
\psi^A_1 \left| s^A_1 \right> + \psi^A_2 \left| s^A_2 \right> =
\left(
\begin{array}[c]{c}
\psi^A_1\\
-\psi^A_2
\end{array}
\right) \in {\cal{H}}_A \nonumber&\\
&
\left| s^A_1 \right>=
\left(
\begin{array}[c]{c}
1\\
0
\end{array}
\right)
\, , \,\,
\left| s^A_2 \right>=
\left(
\begin{array}[c]{c}
0\\
-1
\end{array}
\right)
\,\, , \,\,\,
\psi^A_1=e^{i\,\varphi_{\!A}} \, \hbox{cos}(\frac{\theta_{\!A}}{2})
\, , \,\,
\psi^A_2=\hbox{sin}(\frac{\theta_{\!A}}{2})\nonumber&\\
&\left| \psi_A \right>=
\widehat{\mathcal{U}}(\theta_{\!A},\varphi_{\!A}) \left| s^A_1 \right>
=
\left(
\begin{array}[c]{c}
e^{i\,\varphi_{\!A}} \, \hbox{cos}(\frac{\theta_{\!A}}{2})\\
-\hbox{sin}(\frac{\theta_{\!A}}{2})
\end{array}
\right)
\quad
\label{eq1:psiA1}&
\end{eqnarray}
Die reinen Zustände $\left| s^A_1 \right>$ und $\left| s^A_2 \right>$ bilden die Basis des Hilbertraums ${\cal{H}}_A$ des Spielers A und repräsentieren die reinen Strategien $s^A_1$ und $s^A_2$ des Spiels. Der Entscheidungsoperator des Spielers $\mu$ hängt von den beiden Entscheidungswinkeln $\theta_{\!\mu}$ und $\varphi_{\!\mu}$ ab und ist explizit wie folgt definiert:
\begin{equation}
\widehat{\mathcal{U}}_\mu(\theta_{\!\mu},\varphi_{\!\mu}) :=
\left(
\begin{array}[c]{cc}
e^{i\,\varphi_{\!\mu}} \, \hbox{cos}(\frac{\theta_{\!\mu}}{2})&\hbox{sin}(\frac{\theta_{\!\mu}}{2})\\
-\hbox{sin}(\frac{\theta_{\!\mu}}{2})&e^{-i\,\varphi_{\!\mu}} \, \hbox{cos}(\frac{\theta_{\!\mu}}{2})
\end{array}
\right) \quad \forall \quad \theta_{\!\mu} \in{} [0,\pi] \,\, \wedge \,\, \varphi_{\!\mu} \in{} [0,\frac{\pi}{2}] \quad .
\end{equation}
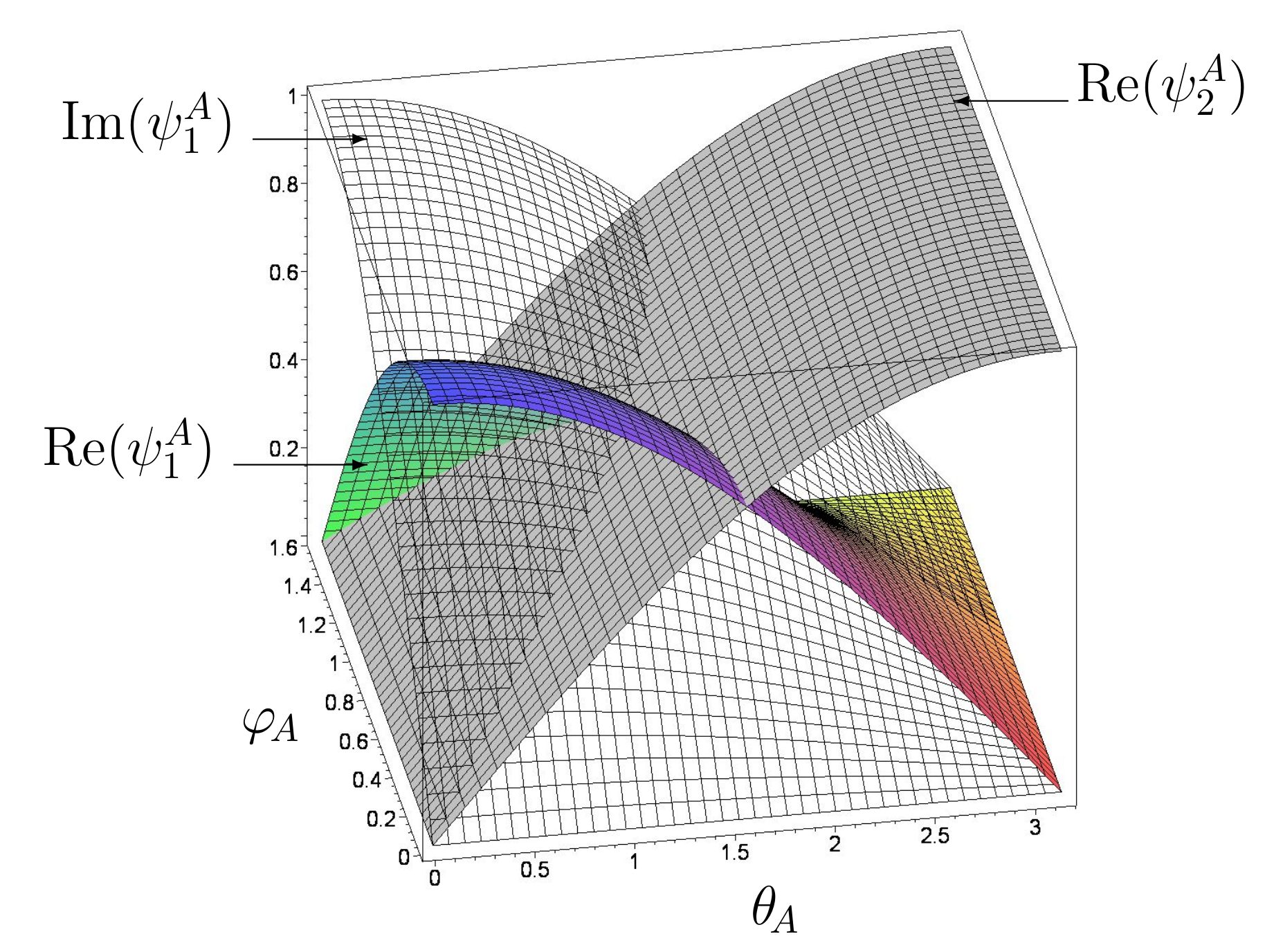
Reellwertige und imaginäre Komponenten des zweidimensionalen Quantenspinors $\left| \psi \right>_{\!A}=\widehat{\mathcal{U}}(\theta_{\!A},\varphi_{\!A}) \left| s^A_1 \right>$ des Spielers A als Funktion der Quantenstrategien $\theta_{\!A}$ und $\varphi_{\!A}$.
Durch die Festlegung der Entscheidungswinkel $\theta_{\!\mu}$ und $\varphi_{\!\mu}$ wählt der Spieler seine Quantenstrategie. Die klassische, reine Strategie $s_1$ legt der Spieler durch die Wahl $\theta=0$ und $\varphi=0$ fest: \begin{equation} \widehat{s_1}:= \hat{{\cal{U}}}(0,0) = \left( \begin{array}[c]{cc} 1&0\\ 0&1 \end{array} \right)\quad, \end{equation} wohingegen die reine Strategie $s_2$ durch $\theta=\pi$ und $\varphi=0$ festgelegt ist: \begin{equation} \widehat{s_2}:= \hat{{\cal{U}}}(\pi,0) = \left( \begin{array}[c]{cc} 0&1\\ -1&0 \end{array} \right)\quad. \end{equation} Zusätzlich zu diesen reinen, klassischen Strategien ist die Quantenstrategie $\widehat{Q}$ wie folgt definiert \begin{equation} \widehat{Q}:= \hat{{\cal{U}}}(0,\pi/2) = \left( \begin{array}[c]{cc} i&0\\ 0&-i \end{array} \right)\quad. \end{equation} Um den Operatorformalismus der Quanten-Spieltheorie und das Konzept der Quantenstrategien besser zu verstehen, veranschaulicht die nebenstehende Abbildung die reellwertigen und imaginären Komponenten $\psi^A_1$ und $\psi^A_2$ des zweidimensionalen Quantenspinors $\left| \psi \right>_{\!A}$ des Spielers A. Die farbige, untransparente Fläche in der Abbildung veranschaulicht den reellwertigen Anteil der ersten Spinorkomponente (Re($\psi^A_1$)), die durchsichtige graue Fläche beschreibt dessen imaginären Anteil (Im($\psi^A_1$)) und die graue undurchsichtige Fläche zeigt den reellwertigen Teil der zweiten Spinorkomponente (Re($\psi^A_2$)) in Abhängigkeit der Winkel $\theta_{\!A}$ und $\varphi_{\!A}$. Da die zweite Spinorkomponente lediglich reellwertige Anteile besitzt veranschaulicht die Abbildung lediglich drei Flächen. Die Menge der klassischen gemischten Strategien des Spielers A (${\bf \tilde{\cal S}}^A = \left\{ \tilde{s}^A_1, \tilde{s}^A_2 \right\}$) ist eine echte Teilmenge des strategischen Hilbertraums des Spielers A (${\cal{H}}_A$) und wird formal realisiert, indem man den Winkel $\varphi_{\!A}$ auf null setzt: \begin{equation} {\bf \tilde{\cal S}}^A = \left\{ \left| \psi \right>_{\!A}=\widehat{\mathcal{U}}(\theta_{\!A},\varphi_{\!A}) \left| s^A_1 \right> \,\, \left| \,\, \varphi_{\!A}\equiv 0 \, , \,\, \theta_{\!A} \in{} [0,\pi] \right. \right\} \subsetneq {\cal{H}}_A \label{eq:psiA_clasical} \quad . \end{equation} In diesem Fall ($\varphi_{\!A}\equiv 0$) verschwinden alle imaginären Anteile des Zustandes $\left| \psi \right>_{\!A}$ und als Folge dessen können die klassischen gemischten Strategien durch Variation des Winkels $\theta \in{} [0,\pi]$ realisiert werden. Für $\varphi_{\!A} > 0$ verschwinden jedoch die imaginären Anteile nicht und diese Art von Quantenstrategien haben kein Pendant in der klassischen Spieltheorie. Da der Entscheidungsoperator auf den reinen Anfangszustand der Strategie $s_1$ wirkt, entstehen mögliche imaginäre Anteile im Zustand $\left| \psi \right>_{\!A}$ lediglich in der ersten Spinorkomponente und man nennt deshalb diese Teilmenge von Quantenstrategien die sogenannten $s_1$-Quantenstrategien. Die quantentheoretische Beschreibung des Entscheidungszustandes des Spielers A kurz vor der definitiven Auswahl und Bekundung der reinen Strategie besitzt demnach im Allgemeinen neben den reellwertigen auch imaginäre Anteile. Bei $s_1$-Quantenstrategien kann sich der Spieler nur im imaginären Raum der ersten Strategie gedanklich bewegen. Eine grundlegende Eigenschaft der gesamten Quantentheorie ist die prinzipielle Unbeobachtbarkeit des Quantenzustandes. Diese Eigenschaft spiegelt sich in der Quanten-Spieltheorie in der Unbeobachtbarkeit des Gedankenprozesses wider. Die einzelnen Inhalte, Gedankenwege und gefühlsauslösende Überlegungen, die während des Entscheidungsprozesses im Gehirn des Spielers (bewusst oder unterbewusst) ablaufenden, können nicht direkt gemessen werden. $s_1$-Quantenstrategien können als der gedankliche Weg während des Entscheidungsprozesses interpretiert werden, welcher vom gedanklichen Ursprung her von der klassischen Strategie $s_1$ startet und hypothetisch, gebunden an die Wünsche und Ängste des Spielers, den Gedankenweg weiterbildet. Aus diesem Grund besitzen die $s_1$-Quantenstrategien (bzw. $s_2$-Quantenstrategien), die speziell bei einer der reinen klassischen Strategien starten ($\{(\theta_{\!A} \equiv 0,\varphi_{\!A}) \mid \varphi_{\!A} \in{} [0,\frac{\pi}{2}] \}$), eine besondere Bedeutung.
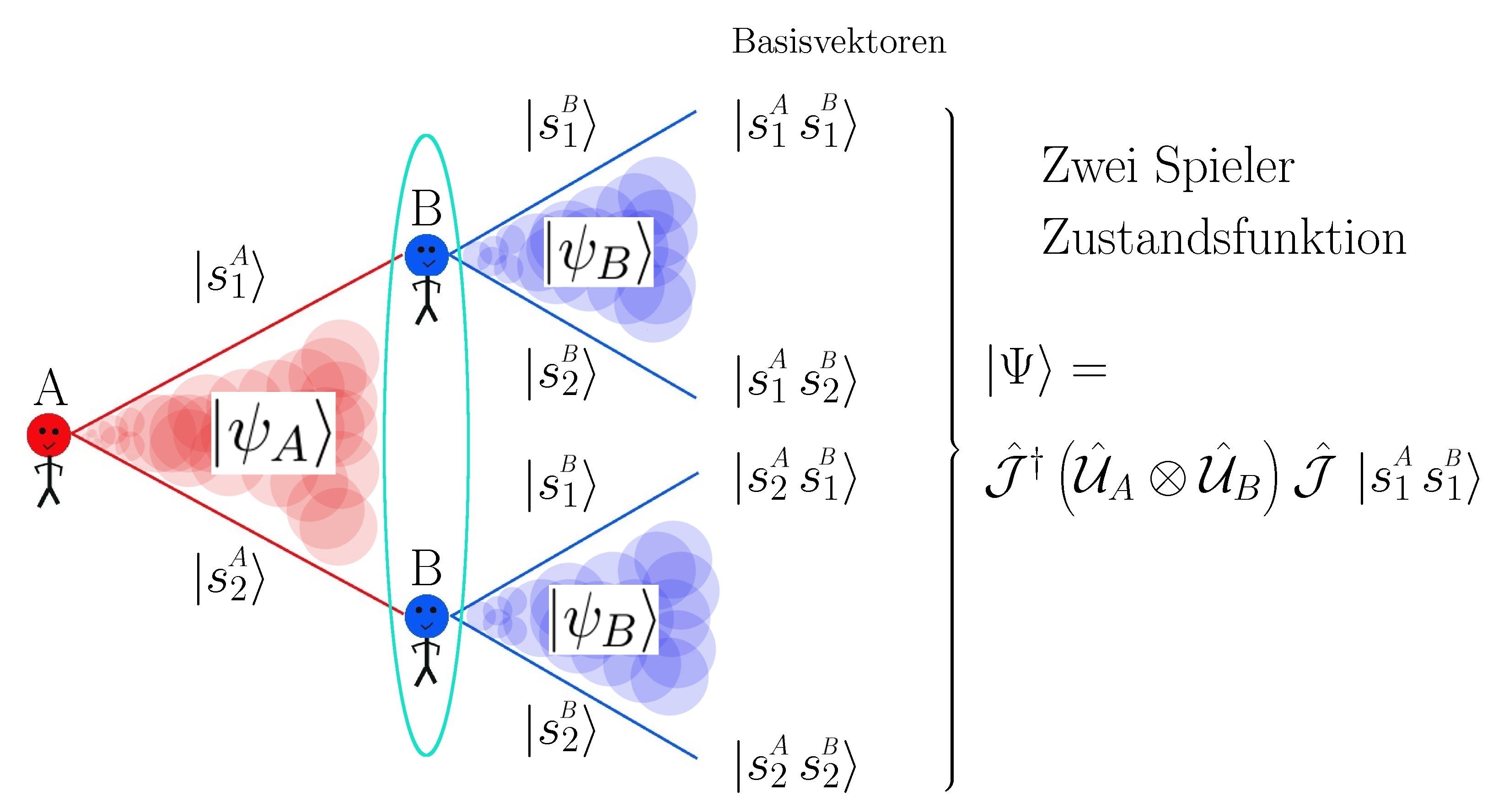
Spielbaum eines (2 Personen)-(2 Strategien) Quantenspiels.
Die quantenspieltheoretische Erweiterung beschreibt somit den Entscheidungszustand eines Spielers A als einen im komplexen Hilbertraum definierten Zustandsvektor. Der Spielbaum eines (2 Personen)-(2 Strategien) Quantenspiels ist in der nebenstehenden Abbildung visualisiert. Der Zwei-Spielerzustand $\left| \Psi \right>$ ist ein vierkomponentiger Spinor, welcher auf dem gemeinsamen Hilbertraum der Spieler (${\cal{H}}:={\cal{H}}_A \otimes {\cal{H}}_B$) definiert ist. Die Basisvektoren dieses vierdimensionalen komplexwertigen Raumes werden durch die vier möglichen, klassischen Strategienkombinationen (messbaren Eigenzustände des Quantensystems) gebildet ($\left| s^A_1 s^B_1 \right>:=(1,0,0,0)$, $\left| s^A_1 s^B_2 \right>:=(0,-1,0,0)$, $\left| s^A_2 s^B_1 \right>:=(0,0,-1,0)$ und $\left| s^A_2 s^B_2 \right>:=(0,0,0,1)$). Der Zwei-Spieler-Anfangszustand $\left| s^A_1 s^B_1 \right>$ bildet sich durch das äußere Produkt der Ein-Spieler Zustände $\left| s^A_1 \right>$ und $\left| s^B_1 \right>$. Die vektorielle Repräsentation der allgemeinen Ein-Spieler Zust"ande $\left| \psi_A \right>$, bzw. $\left| \psi_B \right>$ ist wie folgt durch die Basen der reinen Zustände definiert: \begin{eqnarray} &\left| \psi_A \right>:= \left( \begin{array}[c]{c} \psi^A_1\\ -\psi^A_2 \end{array} \right) = \psi^A_1 \, \left| s^A_1 \right> + \psi^A_2 \, \left| s^A_2 \right>\,, \quad \left| \psi_B \right>:= \left( \begin{array}[c]{c} \psi^B_1\\ -\psi^B_2 \end{array} \right) = \psi^B_1 \, \left| s^B_1 \right> + \psi^B_2 \, \left| s^B_2 \right>& \nonumber\\ &\hbox{wobei:}\quad \left| s^\mu_1 \right> = \left( \begin{array}[c]{c} 1\\ 0 \end{array} \right) \quad \left| s^\mu_2 \right> = \left( \begin{array}[c]{c} 0\\ -1 \end{array} \right)\,, \quad \left| s^A_1 s^B_1 \right>:=\left| s^A_1 \right> \otimes \left| s^B_1 \right> = \left( \begin{array}[c]{c} 1\\ 0\\ 0\\ 0 \end{array} \right)& \end{eqnarray} Der finale Zwei-Spielerzustand eines simultanen Zwei-Strategien-'One Shot'- Quantenspiels wird somit durch den vierkomponentigen Quantenzustand $\left| \Psi \right>$ beschrieben, welcher sich in der Eisert'schen Repräsentation wie folgt aus dem Anfangszustand $\left| \Psi_0 \right> \,=\, \widehat{\mathcal{J}} \left| s^A_1 s^B_1 \right>$ entwickelt \begin{equation} \left| \Psi \right> = \hat{\cal{J}}^\dagger \left( \hat{\cal{U}}_A \otimes \hat{\cal{U}}_B \right) \hat{\cal{J}}\, \left| s^A_1 s^B_1 \right> \, , \quad \left| \Psi_0 \right> \,=\, \hat{\cal{J}} \left| s^A_1 s^B_1 \right> \,=\, \left( \begin{array}{c} \cos\left( \frac{\gamma}{2} \right) \\ \\ 0 \\ \\ 0 \\ \\ i\sin\left( \frac{\gamma}{2}\right) \\ \end{array} \right) \quad , \end{equation} wobei $\hat{\cal{J}}:=(J_{\alpha \beta}), \alpha, \beta=1...4$ die von dem Parameter $\gamma$ abhängige Verschränkungsmatrix (bzw. den Verschränkungsoperator) beschreibt \begin{equation} \widehat{\mathcal{J}} := e^{i \, \frac{\gamma}{2} (\widehat{s_1} \otimes \, \widehat{s_1})} = \left( \begin{array}{cccc} \cos\left( \frac{\gamma}{2} \right) & 0 & 0 & i\sin\left( \frac{\gamma}{2} \right) \\ & & & \\ 0 & \cos\left( \frac{\gamma}{2}\right) & -i\sin\left( \frac{\gamma}{2}\right) & 0 \\ & & & \\ 0 & -i\sin\left( \frac{\gamma}{2}\right) & \cos\left( \frac{\gamma}{2}\right) & 0 \\ & & & \\ i\sin\left( \frac{\gamma}{2}\right) & 0 & 0 & \cos\left( \frac{\gamma}{2}\right) \\ \end{array} \right) \, , \,\, \gamma \in{} [0,\frac{\pi}{2}] \, . \end{equation} $\hat{\cal{U}}_A:=(U^A_{\alpha \beta}), \alpha, \beta=1...2$ und $\hat{\cal{U}}_B:=(U^B_{\alpha\beta}), \alpha, \beta=1...2$ stellen die von den Winkeln $\theta_A, \varphi_A$ und $\theta_B, \varphi_B$ abhängigen Entscheidungsmatrizen (Entscheidungsoperatoren) der Spieler A und B dar.
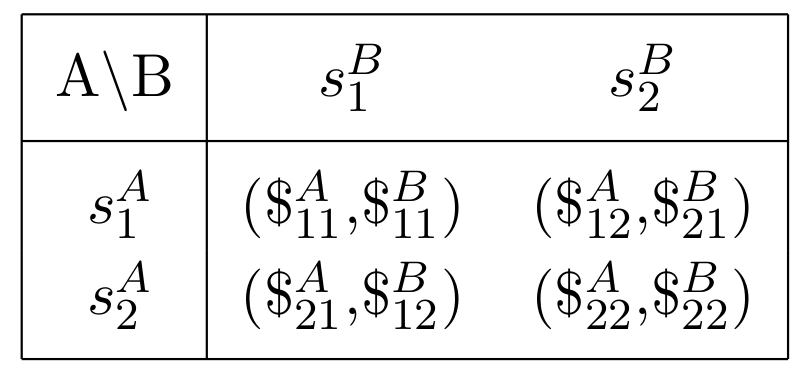
Allgemeine Auszahlungsmatrix eines (2 Personen)-(2 Strategien) Spiels.
Der Erwartungswert der Auszahlungen der Spieler wird zusätzlich durch die Spielmatrix (siehe nebenstehende Auszahlungstabelle) mitbestimmt: \begin{eqnarray} \$_A&=& \$^A_{11}\,P_{1 1} + \$^A_{12}\,P_{1 2} + \$^A_{21}\,P_{2 1} + \$^A_{22}\,P_{2 2} \label{mixedq_payoff}\\ \$_B&=& \$^B_{11}\,P_{1 1} + \$^B_{21}\,P_{1 2} + \$^B_{12}\,P_{2 1} + \$^B_{22}\,P_{2 2} \nonumber\\ \mbox{mit: } && P_{k l}=\left| \, \left< s^A_k \, s^B_l | \Psi \right> \, \right|^2 \,\, , \quad k, l=\left\{ 1, 2 \right\} \nonumber \end{eqnarray} Dieser Erwartungswert der Auszahlungen stellt eine Erweiterung des aus der klassischen Spieltheorie bekannten Konzepts der Auszahlungsfunktion in gemischten Strategien dar. Um die Auswirkungen des quantenspieltheoretischen Konzepts auf die dem Spieler ratsame Wahl der Entscheidung zu untersuchen, wird im Folgenden die Struktur der quantenspieltheoretisch erweiterten gemischten Auszahlungsfunktion untersucht. Im Unterschied zur klassischen Auszahlungsfunktion (${\bf \tilde{\cal \$}}^\mu(\tilde{s}^A,\tilde{s}^B)$, die lediglich von den gemischten Strategien des Spielers A ($\tilde{s}^A$) und des Spielers B ($\tilde{s}^B$) abhängt, hängt die quantentheoretische Erweiterung der Auszahlungsfunktion im Allgemeinen von fünf Parametern ab: Die vier Winkel der Entscheidungsoperatoren ($\theta_A,\varphi_A,\theta_B$ und $\varphi_B$) und der Parameter $\gamma$, welcher die Stärke der Strategienverschränkung quantifiziert.
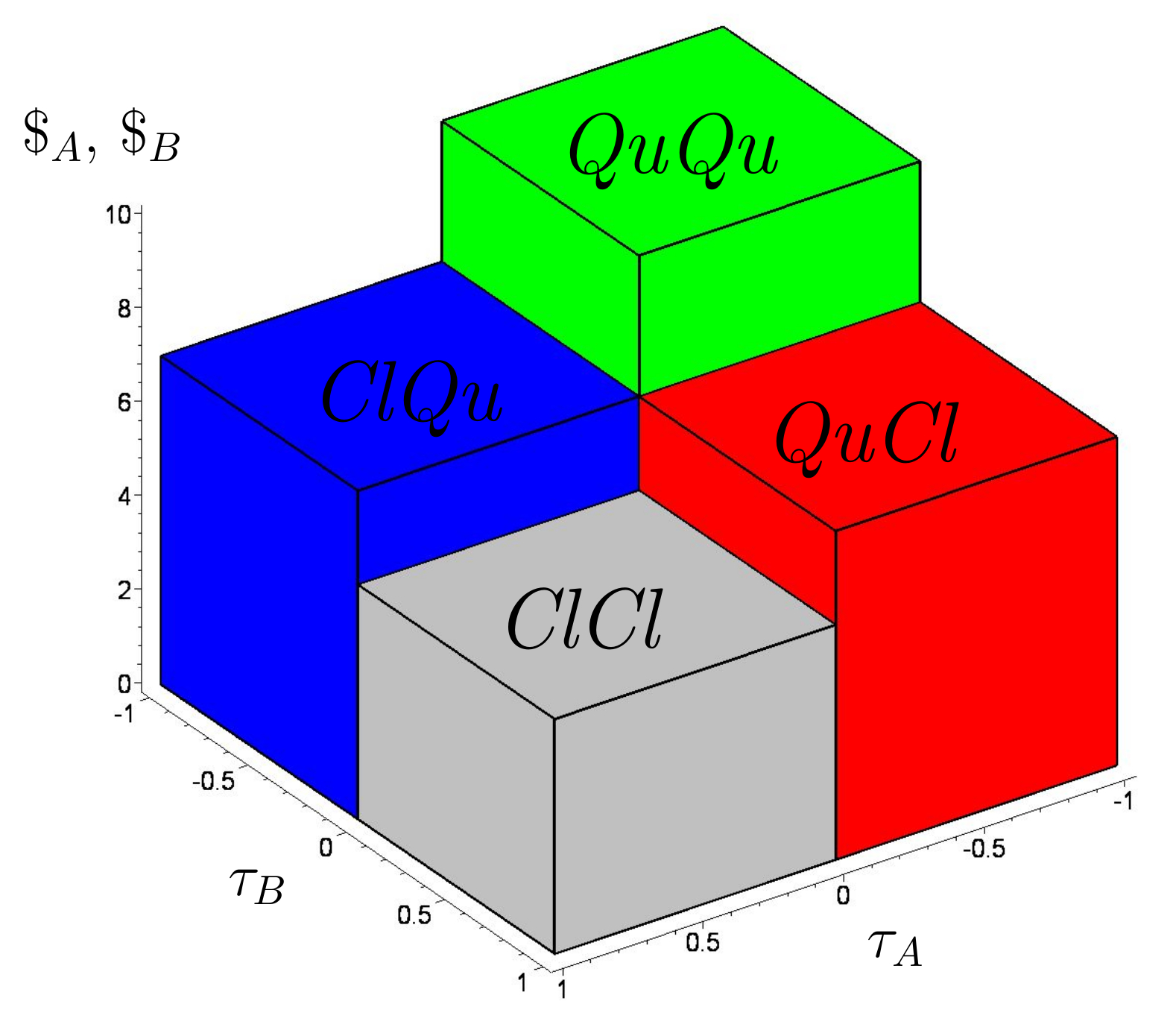
Visualisierungsraum der quantentheoretisch erweiterten Auszahlung $\$$ als Funktion der reduzierten $s_1$-Quantenstrategien $\tau_A$ des Spielers A und $\tau_B$ des Spielers B.
Um die Auszahlungsfunktion dennoch als Fläche in einem dreidimensionalen Raum zu visualisieren, reduziert man deren Abhängigkeiten, indem man einerseits den Verschränkungsparameter $\gamma$ fixiert und die Menge der Quantenstrategien auf diejenigen beschränkt, die vom Ursprung der reinen, klassischen $s_1$-Strategie starten. Die Abhängigkeiten des vierkomponentigen Zwei-Spieler Quantenzustand $\left| \Psi \right>$ werden durch die Einführung zweier neuer Parameter ($\tau_A$ und $\tau_B$) reduziert: $\left| \Psi \right>=\left| \Psi(\theta_A,\varphi_A,\theta_B,\varphi_B) \right> \rightarrow \left| \Psi(\tau_A,\tau_B) \right>$. Die für jeden Spieler wählbaren Entscheidungswinkel $\theta$ und $\varphi$ werden dadurch auf einen einzigen Parameter $\tau \, \in{} [-1,1]$ reduziert. Positive $\tau$-Werte entsprechen den klassischen gemischten Strategien, wohingegen negative $\tau$-Werte Quantenstrategien mit $\theta=0$ und $\varphi>0$ repräsentieren. Der gesamte quantentheoretische Strategienraum wird dadurch in vier separate Regionen unterteilt: in den absolut klassischen Bereich (ClCl: $\tau_A,\tau_B\geq0$), den absoluten Quantenbereich (QuQl: $\tau_A,\tau_B<0$) und in die beiden semi-klassischen Quantenbereiche (ClQl: $\tau_A\geq0 \wedge \tau_B<0$ und QlCl: $\tau_A<0 \wedge \tau_B\geq0$). Durch diese $(\tau_A,\tau_B)$-Repräsentation wird die Menge der möglichen Quantenstrategien auf die folgende Untermenge reduziert: \begin{equation} \underbrace{\{(\tau \, \pi,0) \mid \tau \in{} [0,1] \}}_{\hbox{klassischer Bereich Cl}} \,\,\, \wedge \,\,\, \underbrace{\{(0,\tau \, \frac{\pi}{2}) \mid \tau \in{} [-1,0[ \}}_{\hbox{Quantenbereich Ql}} \end{equation} Die nebenstehende Abbildung stellt die vier Regionen des Visualisierungsraums der quantentheoretischen Auszahlungsfunktion dar. Die absolut klassische Region (ClCl, $\varphi_A, \varphi_B \equiv 0$) befindet sich im vorderen Bereich, die Region in welchem beide Spieler eine Quantenstrategie wählen (QuQl: $\tau_A,\tau_B<0$) ist im hinteren Bereich des Diagramms zu finden und die semi-klassischen Quantenregionen befinden sich seitlich in dem rechten und linken Bereich. Bei der im nächsten Unterkapitel folgenden Diskussion der exemplarischen Beispiele wird dieser Visualisierungsraum benutzt werden, um die Resultate der Quanten-Spieltheorie zu verdeutlichen. Der Eisert'sche Ansatz wurde in der wissenschaftlichen Literatur, in den ersten Jahren nach seiner Veröffentlichung, kritisch diskutiert. Bereits im Jahre 2000 kommentierten beispielweise Benjamin $\&$ Hayden den Eisert'schen Ansatz und behaupteten, dass die benutzte Matrix-Repräsentation der Quanten-Entscheidungsoperatoren der Spieler eine unzulässige Einschränkung darstelle. Definiert man die Quanten-Entscheidungsoperatoren auf einer allgemeinen $SU(2)$-Gruppe, so die Behauptung, dann entstehen keine neuen Nash-Gleichgewichte im Quantenbereich der Strategien. Benjamin $\&$ Hayden begründeten diese Behauptung, indem sie zeigten, dass die beste Antwort auf das von Eisert definierte Quanten Nash-Gleichgewicht ($\widehat{Q}=\hat{{\cal{U}}}(0,\pi/2)$) die zusammengesetzte Entscheidungsoperation ($\hat{{\cal{U}}}(0,\pi/2) \, \hat{{\cal{U}}}(\pi,0)$) ist. Dies ist zwar mathematisch richtig, entspricht jedoch nicht dem Verständnis der in dieser Arbeit benutzten Formalisierung der Quanten-Spieltheorie. Die Einschränkung der Quanten-Entscheidungsoperatoren durch die Matrix-Repräsentation, in Verbindung mit der Reduktion auf $s_1$-Quantenstrategien (bzw. $s_2$-Quantenstrategien) spiegelt die, während des Entscheidungsprozesses durchdachten gedanklichen Pfade des jeweiligen Spielers wider. Zusammengesetzte, simultane Gedankenwege wie ($\hat{{\cal{U}}}(0,\pi/2) \, \hat{{\cal{U}}}(\pi,0)$) würden einem schizophren artigen Gedankenprozess entsprechen, indem der Spieler während des Entscheidungsprozesses in zwei separate Persönlichkeiten (A1 und A2) unterschiedlicher Denkrichtungen geteilt ist ($\widehat{\mathcal{U}}_{A1}(0,\pi/2)$ und $\widehat{\mathcal{U}}_{A2}(\pi,0)$) -- dies ist im Eisert'schen Ansatz nicht möglich. Im Jahre 2002 kommentierten S.J. van Enk $\&$ R. Pike den Eisert'schen quantenspieltheoretischen Ansatz und behaupteten, dass (2 Personen)-(2 Strategien) Quantenspiele äquivalent zu einem klassischen (2 Personen)-(3 Strategien) Spiel seien, wobei die dritte, klassische Strategie der Quantenstrategie $\widehat{Q}$ entsprechen soll. Das Verschwinden der dominanten Strategie im Gefangenendilemma und die Vorteilhaftigkeit der neuen dominanten $\widehat{Q}$-Strategie im (2 Personen)-(3 Strategien) Spiel sei nach van Enk $\&$ Pike nicht beeindruckend, da es sich um unterschiedliche Spiele handelt. Diese Aussage ist nicht richtig, da das zugrundeliegende, beobachtbare Spiel auch in einer quantentheoretisch erweiterten Form ein (2 Personen)-(2 Strategien) bleibt. Die gewählten, beobachtbaren Strategienentscheidungen der Spieler sind auch bei Quantenspielen die beiden reinen Strategien. Die von van Enk $\&$ Pike aufgezeigte Analogie kann man lediglich als pädagogische Veranschaulichung der Quantenstrategie verstehen. Die Vorteilhaftigkeit des durch die $\widehat{Q}$-Strategie erweiterte Strategienraum steigt bei zunehmender Verschränkung der Spielerstrategien. Liegt dieser Verschränkungswert unterhalb einer spieleigenen, definierten Grenze, so können die Spieler die Vorteilhaftigkeit des Gedankenweges $\widehat{Q}$ nicht erkennen und bleiben als Folge dessen im Dilemma des (2 Personen)-(2 Strategien) Spiels gefangen. Liegt die Stärke der Strategienverschränkung jedoch oberhalb der definierten Barriere, so erscheint der Gedankenweg $\widehat{Q}$ ihnen als vorteilhaft. Die neue, dominante Strategie $\widehat{Q}$ stellt jedoch keine real existierende Strategie dar, da diese stets als eine der beiden reinen Strategie beobachtet wird (im Falle des Gefangenendilemmas als kooperierende Strategie).
Teil III.2.3 Symmetrische (2x2)-Quantenspiele
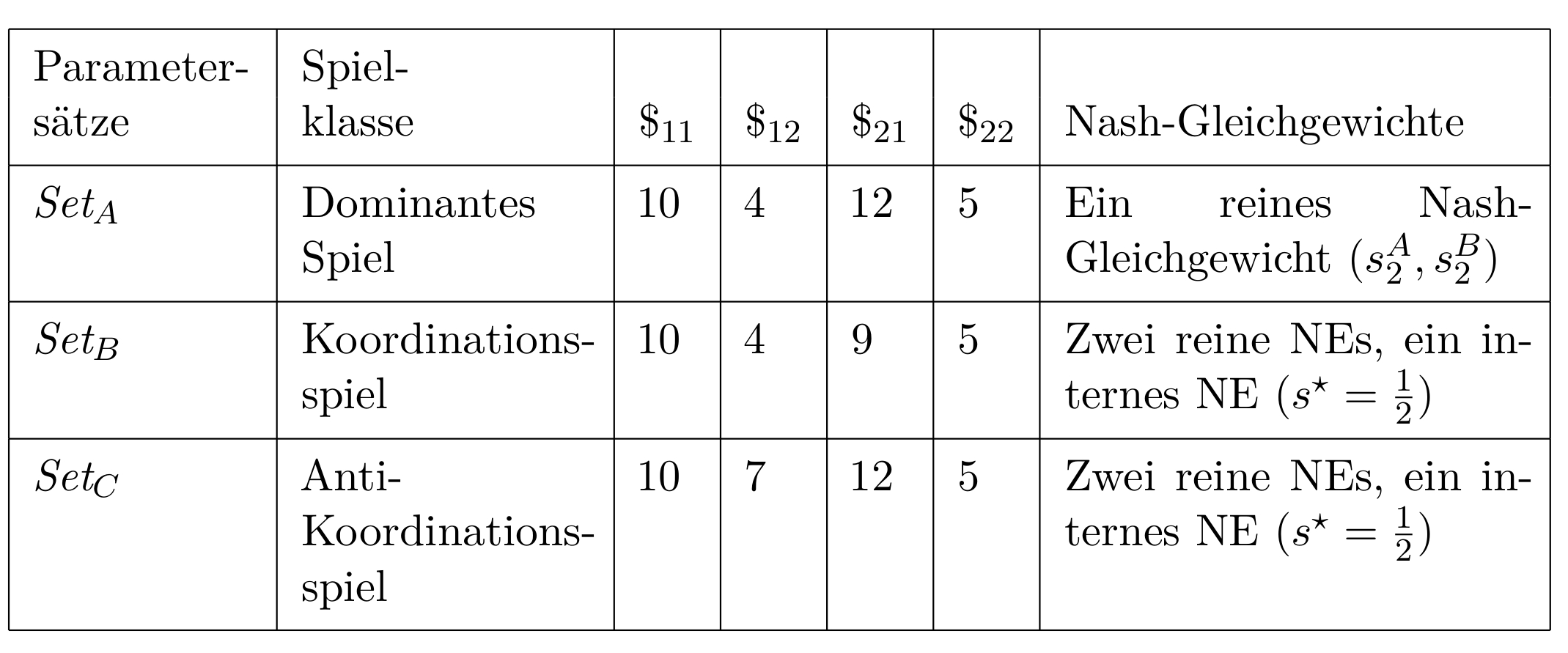
Parameterwerte der drei symmetrischen Beispielspiele.
Symmetrische (2 Personen)-(2 Strategien) Spiele lassen sich formal in drei unterschiedliche Spielklassen separieren (siehe Teil I).
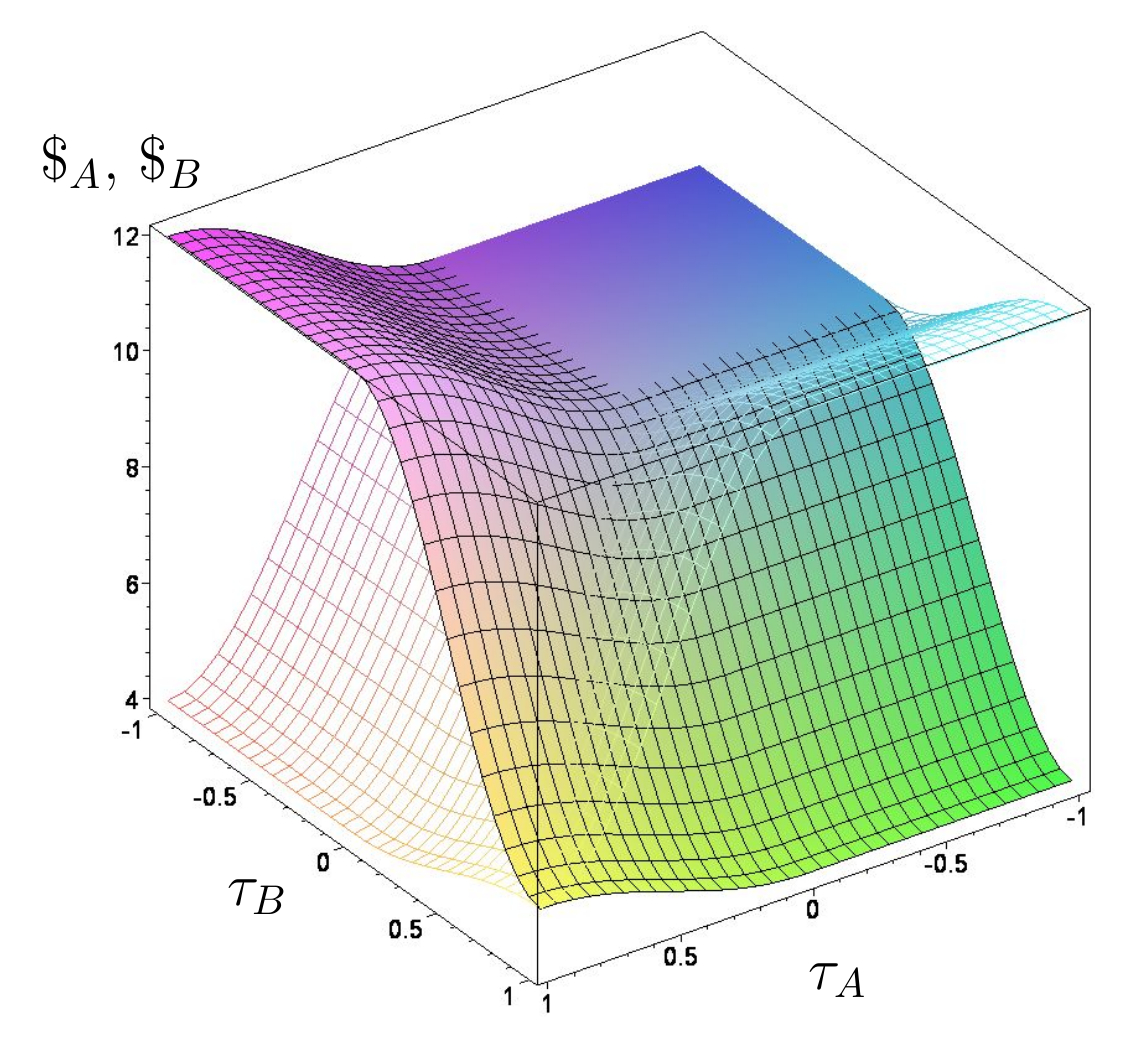
Quantentheoretisch erweiterte Auszahlung $\$_A$ des Spielers A (untransparente Fläche) und $\$_B$ des Spielers B (transparente Fläche) als Funktion der reduzierten $s_1$-Quantenstrategien $\tau_A$ des Spielers A und $\tau_B$ des Spielers B in einem unverschränktem Quantenspiel ($\gamma=0$) unter Verwendung des Parametersatzes Set$_A$.
Dominante Spiele (Set$_A$)
Das durch Parametersatz Set$_A$ definierte Spiel gehört der Klasse der dominanten Spiele an. Das Nash-Gleichgewicht in reinen Strategien befindet sich bei der Strategienkombination, bei welcher beide Spieler die Strategie $s_2$ spielen ($s^A_2,s^B_2$). Die auf der rechten Seite dargestellte Abbildung stellt die quantentheoretisch erweiterte Auszahlung $\$_A$ des Spielers A (untransparente Fläche) und $\$_B$ des Spielers B (transparente Fläche) als Funktion der reduzierten $s_1$-Quantenstrategien $\tau_A$ des Spielers A und $\tau_B$ des Spielers B dar. Als zugrundeliegender Parametersatz wurde Set$_A$ verwendet und die Stärke der Quantenverschränkung der Spielerstrategien wurde auf null gesetzt ($\gamma=0$). Als Visualisierungsraum wurde der in der oberen Abbildung beschriebene reduzierte Raum verwendet, wobei der absolute Quantenbereich QuQu, bei dem beide Spieler eine Quantenstrategie benutzen, im hinteren Teil des Diagramms zu finden ist und die rein klassische Region ClCl nach vorne projiziert wurde. Die Abbildung zeigt deutlich, dass das unverschränkte Quantenspiel identisch mit der klassischen Version des Spiels ist. Im Bereich, in dem beide Spieler eine Quantenstrategie wählen ($\tau_A < 0 \wedge \tau_B < 0$), ist die Auszahlung der Spieler gleich der Auszahlung, als wenn die Spieler die klassische Strategie $s_1$ gewählt hätten ($ \$_A(\tau_A=0,\tau_B=0)=10$, $ \$_B(\tau_A=0,\tau_B=0)=10$). Das Nash-Gleichgewicht des klassischen Spiels ($(s^A_2,s^B_2)$, die dominante Strategie) entspricht den folgenden $\tau$-Werten: $(s^A_2,s^B_2)\hat{=}(\tau_A=1,\tau_B=1)$ und bleibt auch im unverschränkten Quantenspiel bestehen.
Die beiden Diagramme in der linken unteren Abbildung stellen die quantentheoretisch erweiterte Auszahlungsfunktion bei einem mittleren und dem maximalen Verschränkungswert dar. Die Struktur der Auszahlungsflächen innerhalb der vollständig klassischen Region ClCl verändert ihr Erscheinungsbild bei ansteigendem $\gamma$-Wert nicht, wohingegen die anderen Bereiche (ClQu, QuCl und QuQu) durch die Stärke der Verschränkung beeinflusst werden. Bei dem, durch den ansteigenden $\gamma$-Wert verursachten Übergang verschwindet zunächst das ursprüngliche im klassischen Spiel existierende Nash-Gleichgewicht und danach entsteht ein neues Nash-Gleichgewicht bei der Quantenstrategie ($(\widehat{Q},\widehat{Q})\hat{=}(\tau_A=-1,\tau_B=-1)$). Diese beiden separaten Eigenschaften, die bei den $\gamma$-Grenzwerten $\gamma_1$ und $\gamma_2$ entstehen, werden im Folgenden kurz näher erläutert. Für Strategienverschränkungen $\gamma$, die größer sind als die erste $\gamma$-Barriere ($\gamma_1\approx0.361$), ist die beste Antwort des Spielers A auf die $s^B_2\hat{=}(\tau_B=1)$-Strategie des Spielers B nicht mehr die Strategie $s^A_2\hat{=}(\tau_A=1)$, sondern die Quantenstrategie $\tau_A=-1$, da die Auszahlung $\$_A(\tau_A=-1,\tau_B=1)\approx5.05$ für diese Strategie nun größer ist als die Auszahlung im klassischen Nash-Gleichgewicht ($\$_A(\tau_A=1,\tau_B=1)=5$).
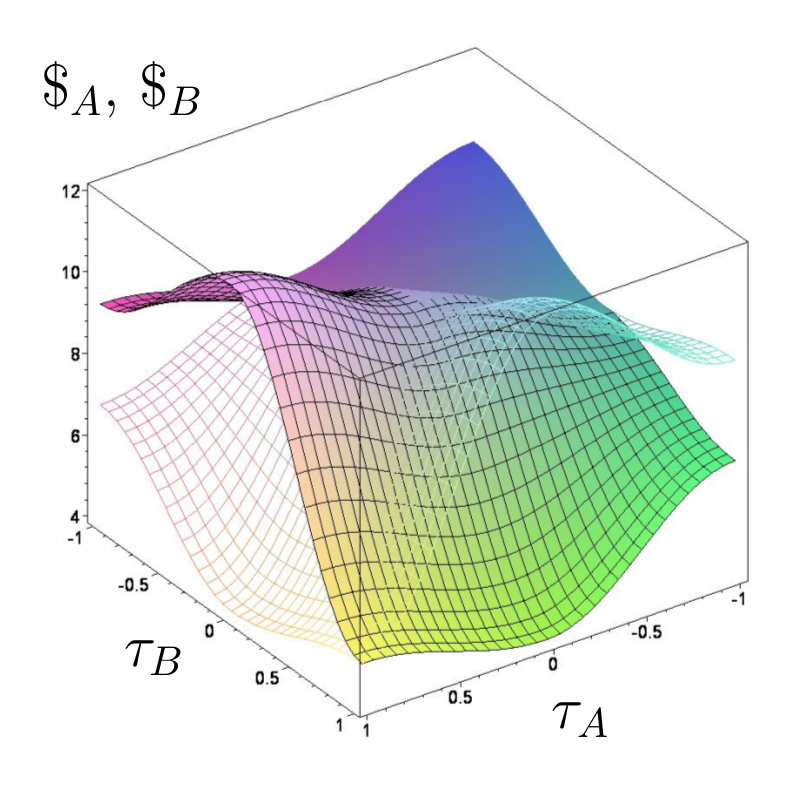
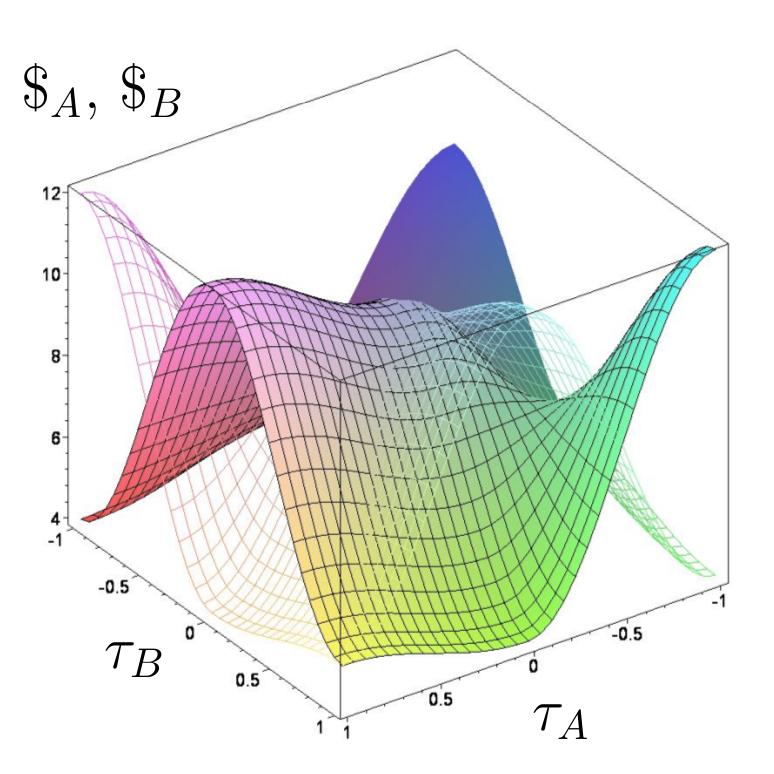
Quantentheoretisch erweiterte Auszahlungsfunktion im Parametersatz Set$_A$. Links: $\gamma=\frac{\pi}{5}$, Rechts: $\gamma=\frac{\pi}{2}$.
Das ursprüngliche Nash-Gleichgewicht verschwindet demnach für $\gamma > \gamma_1$. Ab der zweiten $\gamma$-Barriere ($\gamma_2\approx0.524$) ist die beste Antwort des Spielers A auf die Strategie $\widehat{Q}_B\hat{=}(\tau_B=-1)$ des Spielers B nicht mehr die klassische Strategie $s^A_2\hat{=}(\tau_A=1)$ sondern die Quantenstrategie $\widehat{Q}_A\hat{=}(\tau_A=-1)$, da die Auszahlung $\$_A(\tau_A=1,\tau_B=-1)\approx9.96$ bei einem Wert $\gamma\approx0.524$ niedriger ist als die Auszahlung für den Fall, wenn beide Spieler die Quantenstrategie $\widehat{Q}$ spielen ($\$_A(\tau_A=-1,\tau_B=-1)=10$). Ein neues Nash-Gleichgewicht, welches dann die dominante Strategie des Spiels ist, entsteht demnach für $\gamma > \gamma_2$. Die exakten Werte der beiden $\gamma$-Barrieren können für symmetrische (2 Personen)-(2 Strategien) Quantenspiele analytisch, in Abhängigkeit der Auszahlungsparameter angegeben werden.
Die Resultate zeigen somit, dass durch die quantentheoretische Erweiterung eines Gefangenendilemma-ähnlichen Spiels die Spieler dem Dilemma entkommen können, falls der Wert der Stärke der Verschränkung über einem definierten $\gamma$-Grenzwert liegt. Liegt der $\gamma$-Wert der Strategienverschränkung oberhalb der dem Spiel eigenen $\gamma$-Barriere, so hat sich die klassische dominante Strategie für die Spieler aufgelöst und eine neue vorteilhafte, dominante Strategiekombination ($\widehat{Q}_A,\widehat{Q}_B$) ist für die Spieler entstanden. Da die Projektion dieser dominanten Quantenstrategienkombination ($\widehat{Q}_A,\widehat{Q}_B$) auf den messbaren, realen Raum der klassischen Strategienkombination ($s^A_1,s^B_1$) entspricht, entkommen die Spieler dem Dilemma des Spiels.
Neben diesem exemplarischen Beispiel eines dominanten Quantenspiels können im Allgemeinen die Folgenden Aussagen bewiesen werden: Die quantentheoretische Erweiterung eines dominanten, symmetrischen (2 Personen)-(2 Strategien) Spiels mit Dilemma löst das zugrundeliegende Dilemma des Spiels ab einer definierten $\gamma$-Barriere auf. Die quantentheoretische Erweiterung eines dominanten, symmetrischen (2 Personen)-(2 Strategien) Spiels ohne Dilemma liefert keine weiteren Nash-Gleichgewichte. Die ursprüngliche dominante Strategie des Spiels bleibt auch bei maximaler Strategienverschränkung bestehen.
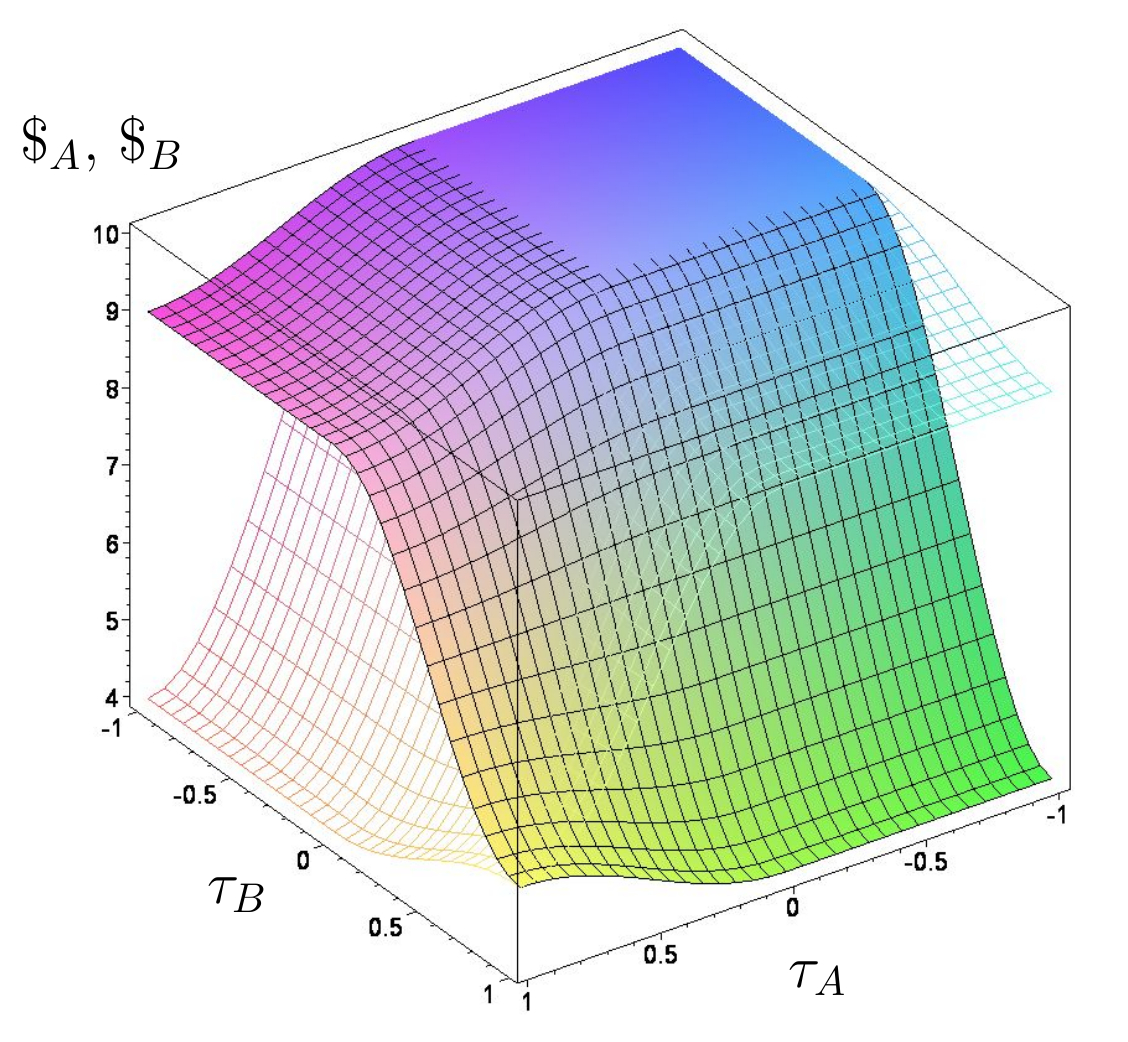
Quantentheoretisch erweiterte Auszahlungsfunktion im Parametersatz Set$_B$ und $\gamma=0$.
Koordinationsspiele (Set$_B$)
Das durch Parametersatz Set$_B$ definierte Spiel gehört der Klasse der Koordinationsspiele an. Im Vergleich zum Set$_A$ hat sich der Wert $\$_{21}$ von $12$ auf $9$ verringert, was den Übergang vom dominanten Spiel hin zu der Klasse der Koordinationsspiele bewirkte. Das Spiel hat nun zwei symmetrische Nash-Gleichgewichte in reinen Strategien (($s^A_1,s^B_1$)$\hat{=}(\tilde{s}^A=1,\tilde{s}^B=1$) und ($s^A_2,s^B_2$)$\hat{=}(\tilde{s}^A=0,\tilde{s}^B=0$)) und ein internes Nash-Gleichgewicht bei der gemischten Strategienkombination ($(\tilde{s}^{A\star},\tilde{s}^{B\star})=(\frac{1}{2},\frac{1}{2})$). Die quantentheoretisch erweiterte Auszahlung $\$_A$ des Spielers A (untransparente Fläche) und $\$_B$ des Spielers B (transparente Fläche) des Parametersatzes Set$_B$ ist in der rechten Abbildung für den unverschränkten Fall ($\gamma=0$) dargestellt. Die Abbildung zeigt wiederum, dass das unverschränkte Quantenspiel des Parametersatzes Set$_B$ identisch mit dem klassischen Koordinationsspiel ist. Falls beide Spieler eine Quantenstrategie wählen ($\tau_A < 0 \wedge \tau_B < 0$), ist deren erzielte Auszahlung gleich dem Fall, in welchem beide Spieler die klassische Strategie $s_1$ spielen ($ \$_A(\tau_A=0,\tau_B=0)=10$), und entspricht der größt möglichen Auszahlung des zugrundeliegenden Koordinationsspiels. Die zwei reinen Nash-Gleichgewichte entsprechen den folgenden $\tau$-Strategien: $(s^A_1,s^B_1)\hat{=}(\tau_A=0,\tau_B=0)$ und $(s^A_2,s^B_2)\hat{=}(\tau_A=1,\tau_B=1)$.
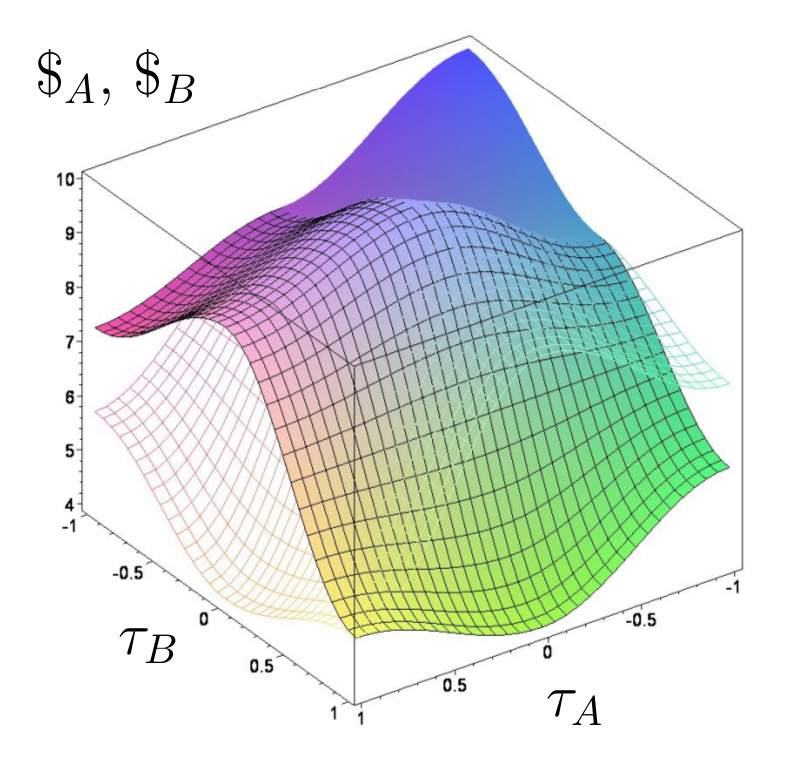
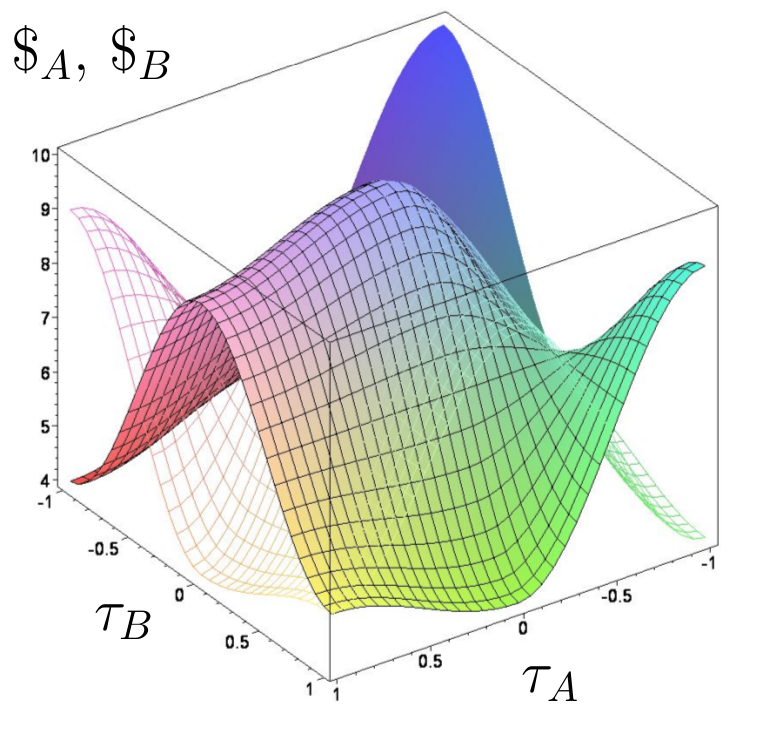
Quantentheoretisch erweiterte Auszahlungsfunktion im Parametersatz Set$_B$. Links: $\gamma=\frac{\pi}{5}$, Rechts: $\gamma=\frac{\pi}{2}$.
Die auf der linken Seite dargestellte Abbildungen zeigen, dass selbst bei minimaler Verschränkung ein neues Nash-Gleichgewicht bei der Quanten-Strategienkombination ($(\widehat{Q},\widehat{Q})\hat{=}(\tau_A=-1,\tau_B=-1)$) entsteht. Formal erhält man dieses Resultat durch die Berechnung der $\gamma_2$-Barriere, die bei Koordinationsspielen rein imaginär ist und somit formal den reellen Wert $\gamma_2=0$ besitzt. Die Auflösung des klassischen, reinen Nash-Gleichgewichts mit geringer Auszahlung $(s^A_2,s^B_2)\hat{=}(\tau_A=1,\tau_B=1)$ im Parametersatz Set$_B$ entsteht bei Verschränkungswerten die oberhalb der $\gamma_1$-Barriere liegen $\gamma > \gamma_1 \approx 0.4636$. In einem evolutionären Koordinationsspiel existiert demnach oberhalb der $\gamma_1$-Barriere nur noch die evolutionär stabile Quantenstrategie, welche projiziert auf die reelle Achse bedeutet, dass die Spieler der Population ausschließlich die $s_1$-Strategie wählen und somit dem Koordinationsproblem des Spiels entkommen. Neben diesem exemplarischen Beispiel eines Quanten-Koordinationspiels kann im Allgemeinen gezeigt werden, dass in einer quantentheoretischen Erweiterung eines symmetrischen (2 Personen)-(2 Strategien) Koordinationspiels das dem Spiel zugrundeliegende Koordinationsproblem ab einer definierten $\gamma$-Barriere verschwindet.
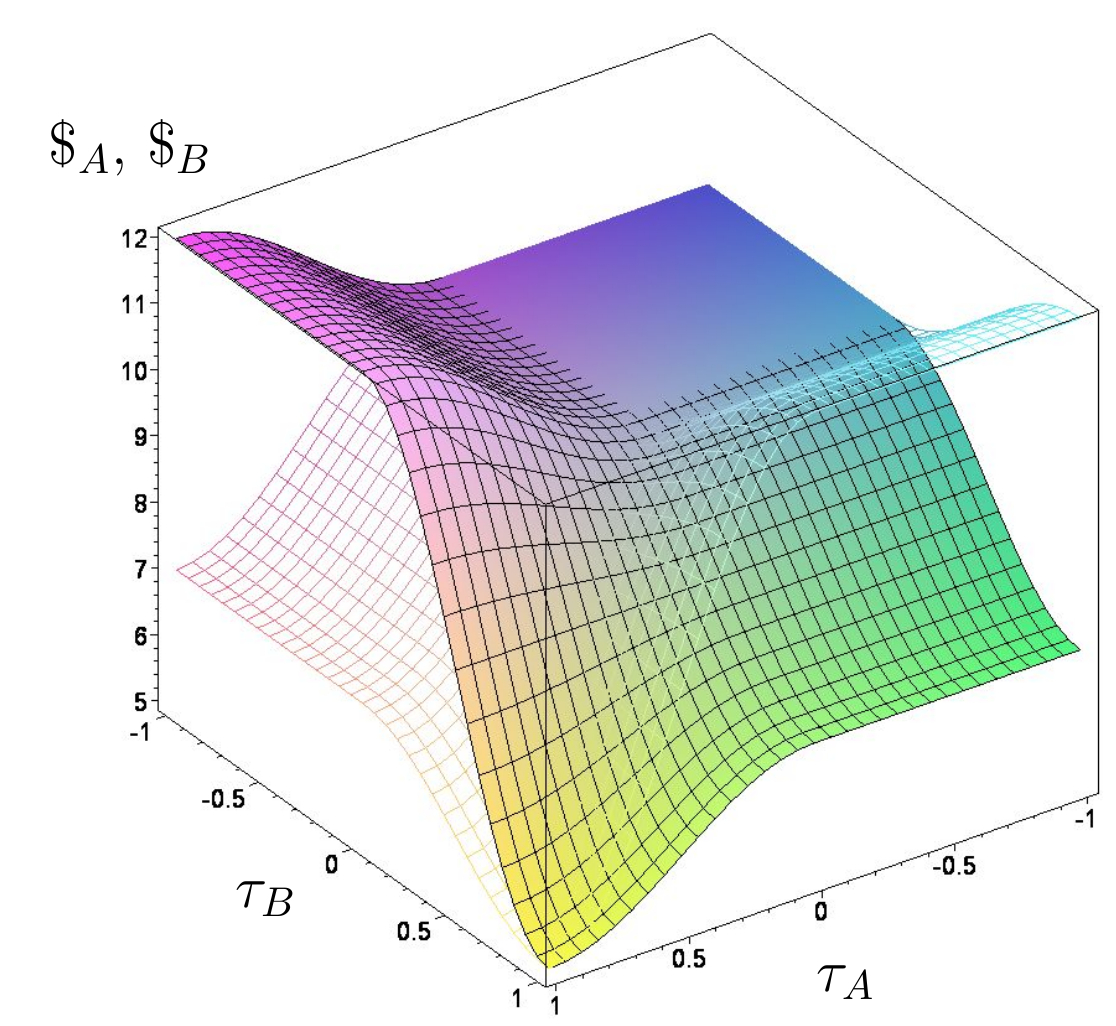
Quantentheoretisch erweiterte Auszahlungsfunktion im Parametersatz Set$_C$ und $\gamma=0$.
Anti-Koordinationsspiele (Set$_C$)
Im Parametersatz Set$_C$ hat sich im Vergleich zum Set$_A$ der Wert $\$_{12}$ von $4$ auf $7$ erhöht, was einen Übergang vom dominanten Spiel hin zu der Klasse der Anti-Koordinationsspiele bewirkte. Das Spiel besitzt nun zwei unsymmetrische Nash-Gleichgewichte in reinen Strategien (($s^A_1,s^B_2$)$\hat{=}(\tilde{s}^A=1,\tilde{s}^B=0$) und ($s^A_2,s^B_1$)$\hat{=}(\tilde{s}^A=0,\tilde{s}^B=1$)) und ein internes Nash-Gleichgewicht bei der gemischten Strategienkombination ($(\tilde{s}^{A\star},\tilde{s}^{B\star})=(\frac{1}{2},\frac{1}{2})$). Die quantentheoretisch erweiterten Auszahlungen der Spieler dieses exemplarischen Anti-Koordinationsspiels sind in der rechten Abbildung für den unverschränkten Fall ($\gamma=0$) dargestellt. Wiederum zeigt die Abbildung, dass der unverschränkte Fall identisch mit dem klassischen Spiel ist. Falls beide Spieler eine Quantenstrategie wählen ($\tau_A < 0 \wedge \tau_B < 0$), ist die erzielte Auszahlung gleich dem Fall, in welchem beide Spieler die klassische Strategie $s_1$ spielen ($ \$_A(\tau_A=0,\tau_B=0)=10$). Die zwei reinen unsymmetrischen Nash-Gleichgewichte des Anti-Koordinationsspiel entsprechen den folgenden $\tau$-Strategien: $(s^A_1,s^B_2)\hat{=}(\tau_A=0,\tau_B=1)$ und $(s^A_2,s^B_1)\hat{=}(\tau_A=1,\tau_B=0)$. Der $\tau^{\star}$-Wert des internen Nash-Gleichgewichts in gemischten Strategien ($s^{\star}$) berechnet sich wie beim Koordinationsspiel zu $\tau^{\star}=\frac{2}{\pi} \hbox{arccos}(\sqrt{\frac{1}{2}})=\frac{1}{2}$.
Die Auszahlungsflächen der linken Abbildung zeigen die Ergebnisse des betrachteten Quanten-Anti-Koordinationsspiels für ein mittelmäßig (linke Seite: $\gamma=\frac{\pi}{5}$) und stark (rechte Seite: $\gamma=\frac{2\,\pi}{5}$) verschränktes Spiel.
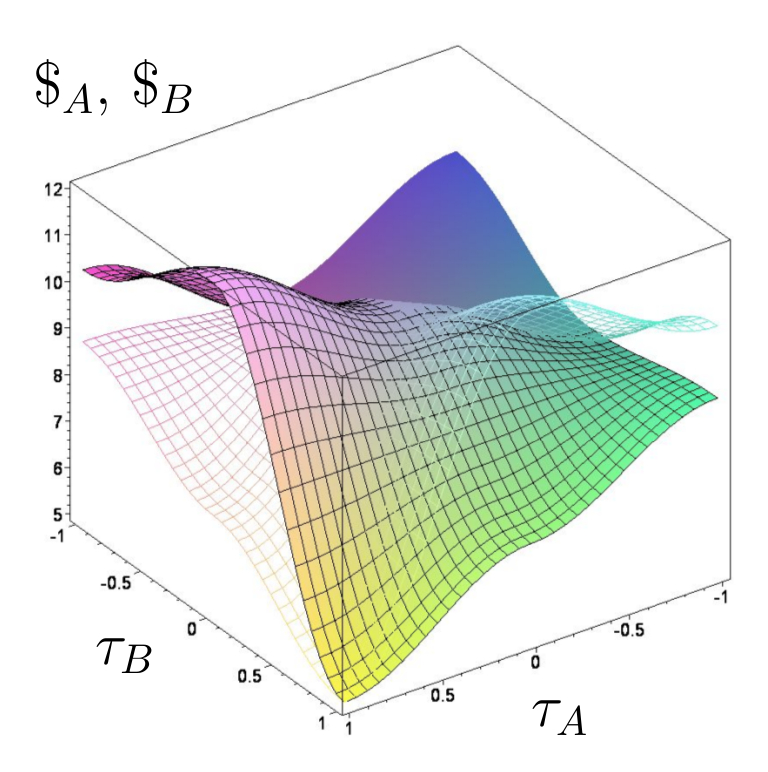
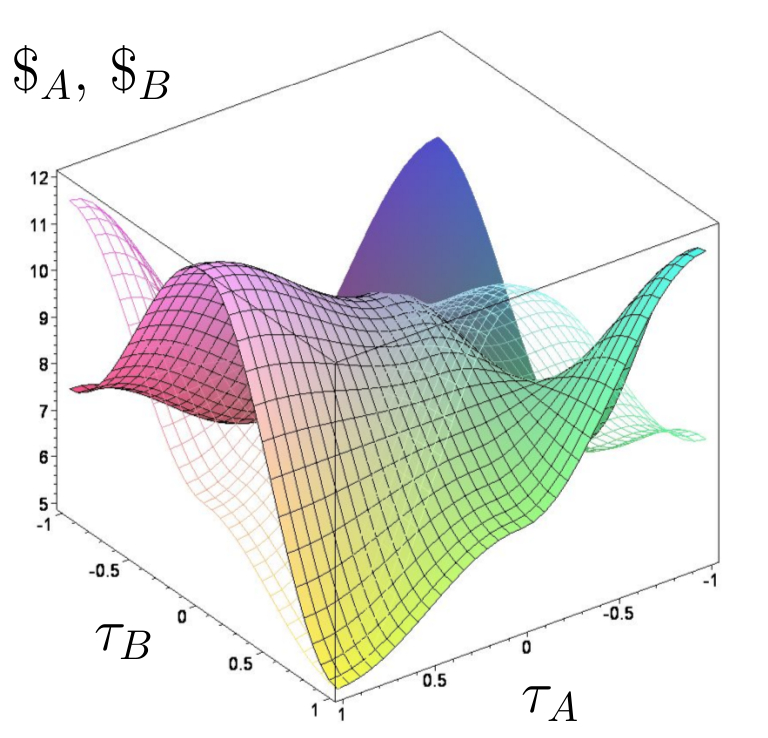
Quantentheoretisch erweiterte Auszahlungsfunktion im Parametersatz Set$_C$. Links: $\gamma=\frac{\pi}{5}$, Rechts: $\gamma=\frac{2\pi}{5}$.
Schon bei minimaler Verschränkung entsteht bei Anti-Koordinationsspiele bei der Strategienkombination $(\tau_A=1,\tau_B=-1)$ bzw. $(\tau_A=-1,\tau_B=1)$ ein neues unsymmetrisches Nash-Gleichgewicht. Formal erhält man dieses Resultat durch die Berechnung der $\gamma_1$-Barriere, die bei Anti-Koordinationsspielen rein imaginär ist, und somit formal den reellen Wert $\gamma_1=0$ liefert. Bei Verschränkungsstärken die höher als die $\gamma_2$-Barriere ($\gamma_2 \approx 0.685$) sind, entsteht bei Anti-Koordinationsspielen (zusätzlich zur klassischen ESS) eine neue evolutionär stabile Quantenstrategie, bei welcher die gesamte Population, auf den reellen Raum projiziert, die $s_1$-Strategie wählt. Neben diesem exemplarischen Beispiel eines Quanten-Anti-Koordinationspiels kann im Allgemeinen gezeigt werden, dass in einer quantentheoretischen Erweiterung eines symmetrischen (2 Personen)-(2 Strategien) Anti-Koordinationspiels ab einer definierten $\gamma$-Barriere eine neue, evolutionär stabile Quantenstrategie entsteht. Welche der beiden evolutionär stabile Strategien in einer dynamischen Populationsentwicklung realisiert wird, ist durch die Struktur der zeitabhängigen, quantentheoretisch erweiterten Differentialgleichungen bestimmt.
Das Maple-Worksheet: Symmetrische (2x2)-Quantenspiele fasst die dargestellten Ergebnisse zusammen.