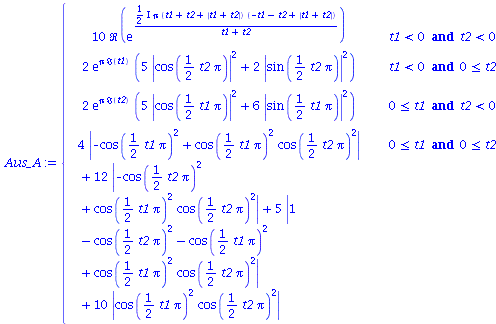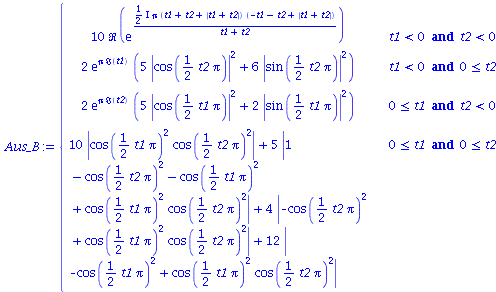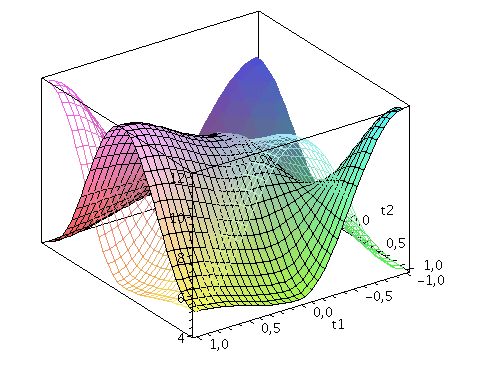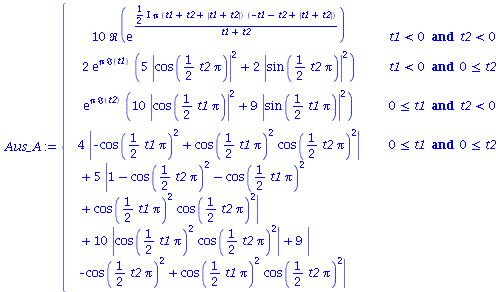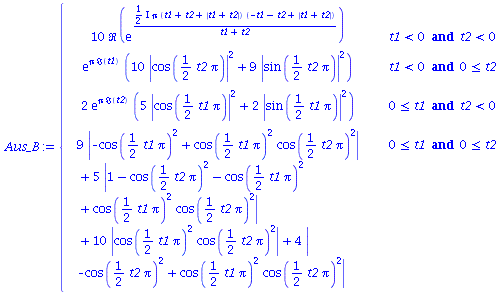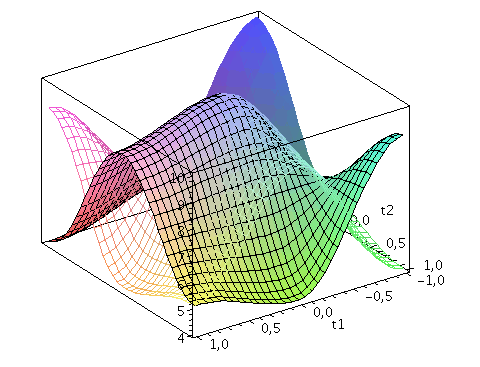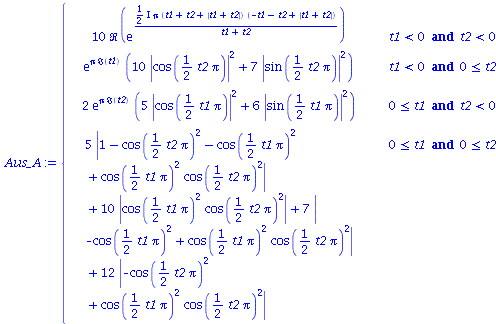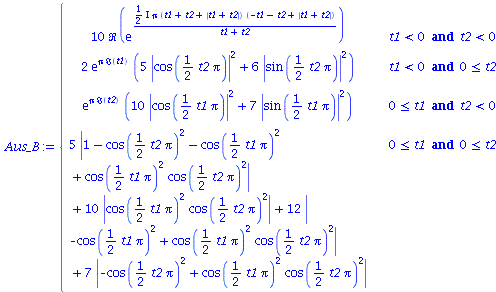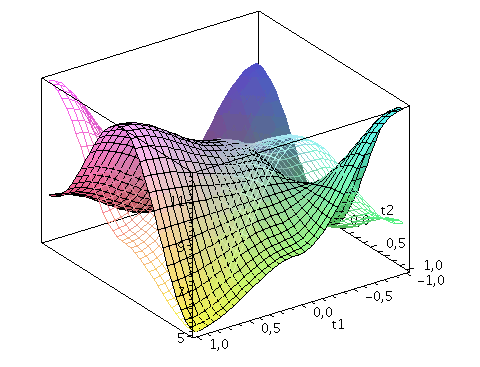Die Quanten Spieltheorie und der verschränkte Zwei-Spieler Zustand 

Dieses Maple-Worksheet illustriert das Konzept der Quanten-Spieltheorie an mehreren Beispielen. 

>	restart: with(linalg): with(LinearAlgebra): with(plots): with(RandomTools): with(networks): with(stats[statplots]): with(plottools): with(ColorTools):

 

Die Quanten-Spieltheorie beschreibt den Entscheidungszustand eines Spielers, bevor dieser die endgültige Wahl der reinen Strategie getroffen hat, als eine komplexwertige Größe (Spinor) in einem zweidimensionalen Zustandsraum, dem sogenannten Hilbertraum. Die in diesem Worksheet verwendete mathematische Repräsentation dieses Spinors wird mit Hilfe des Entscheidungsoperators U konstruiert, der auf einen Anfangszustand wirkt. Die Entscheidungsoperatoren der Spieler A und B sind wie folgt definiert: 

>	UA:=subs({theta=ta,phi=pa},matrix(2,2,[exp(I*phi)*cos(theta/2),sin(theta/2),-sin(theta/2),exp(-I*phi)*cos(theta/2)])); UB:=subs({theta=tb,phi=pb},matrix(2,2,[exp(I*phi)*cos(theta/2),sin(theta/2),-sin(theta/2),exp(-I*phi)*cos(theta/2)]));

 

 

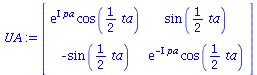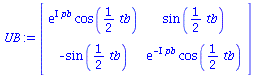	(1.1)

 

Mittels des äusseren Produktes erhält man den gemeinsamen (4x4)-Entscheidungsoperator: 

>	UA_T_UB:=matrix(4,4,[ UA[1,1]*UB[1,1],UA[1,1]*UB[1,2],UA[1,2]*UB[1,1],UA[1,2]*UB[1,2], UA[1,1]*UB[2,1],UA[1,1]*UB[2,2],UA[1,2]*UB[2,1],UA[1,2]*UB[2,2], UA[2,1]*UB[1,1],UA[2,1]*UB[1,2],UA[2,2]*UB[1,1],UA[2,2]*UB[1,2], UA[2,1]*UB[2,1],UA[2,1]*UB[2,2],UA[2,2]*UB[2,1],UA[2,2]*UB[2,2]]);

 

(1.2)

 

Die Zustände der Spieler können miteinander verschränkt sein. Diese Verschränkung wird mathematisch mittels der Verschränkungsmatrix J (bzw. mittels des Verschränkungsoperator) in die Theorie eingearbeitet. Der Verschränkungsoperator hängt von dem Parameter gamma ab, der das Maß der gemeinsamen Verschränkung quantifiziert (gamma=0: keine Verschränkung, gamma=Pi/2: Maximale Verschränkung): 

>

CC:=matrix(4,1,[1,0,0,0]): DD:=matrix(4,1,[0,0,0,1]): CD:=matrix(4,1,[0,-1,0,0]): DC:=matrix(4,1,[0,0,-1,0]): G:=matrix(4,4,[0,0,0,1,0,0,-1,0,0,-1,0,0,1,0,0,0]): Eins:=matrix(4,4,[1,0,0,0,0,1,0,0,0,0,1,0,0,0,0,1]): J:=simplify(subs(x=I*gamma/2,MatrixExponential(Matrix([[0,0,0,1],[0,0,-1,0],[0,-1,0,0],[1,0,0,0]]),x))); JT:=simplify(subs(x=-I*gamma/2,MatrixExponential(Matrix([[0,0,0,1],[0,0,-1,0],[0,-1,0,0],[1,0,0,0]]),x))):

 

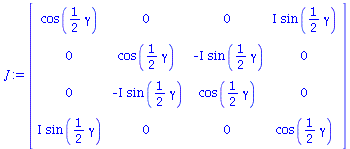(1.3)

 

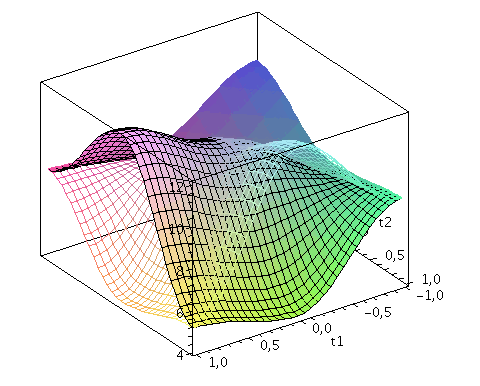
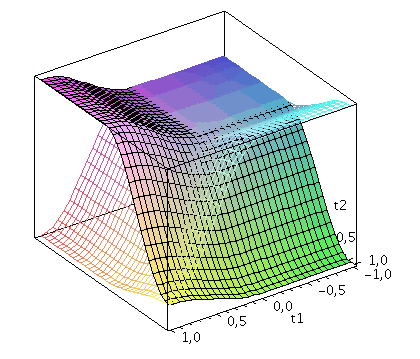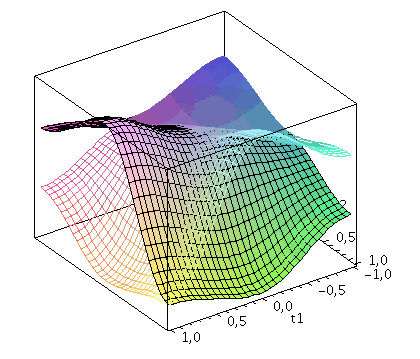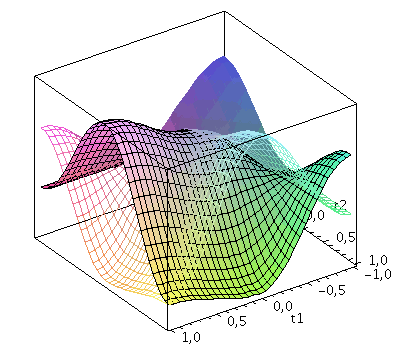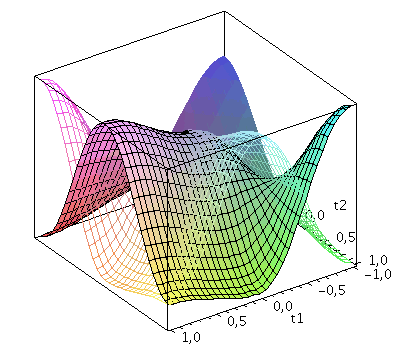
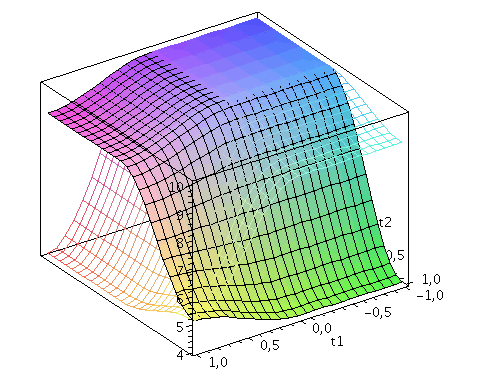
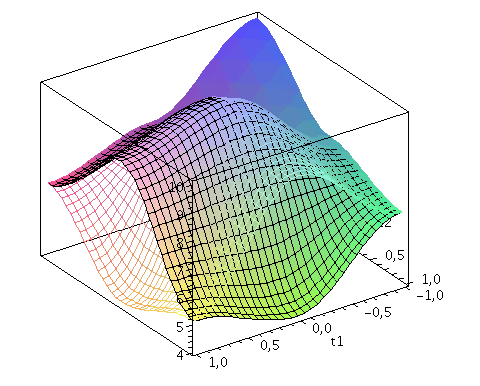
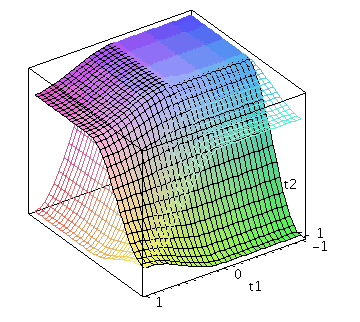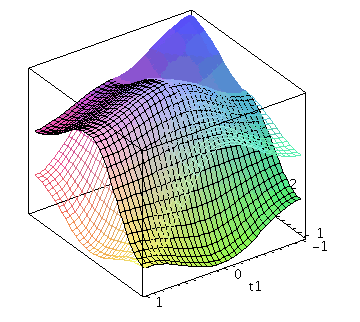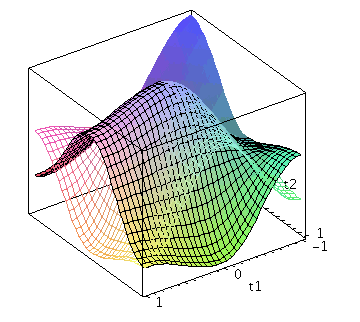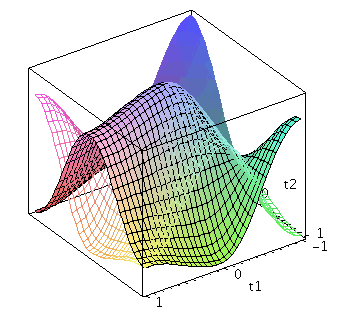
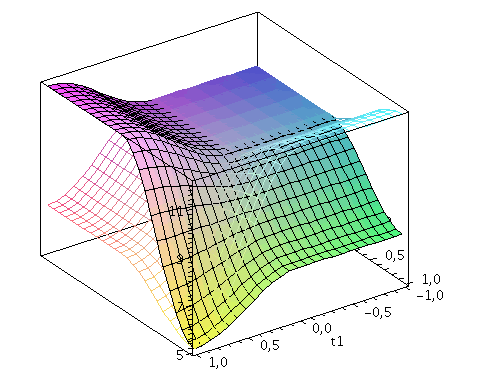
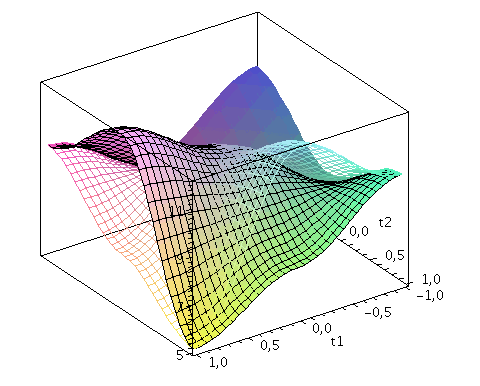
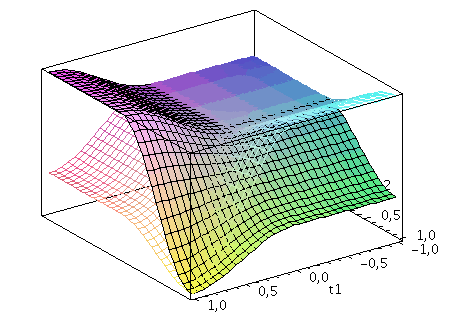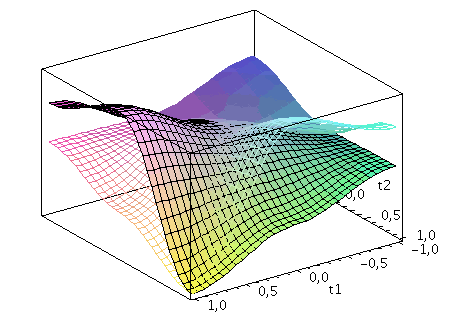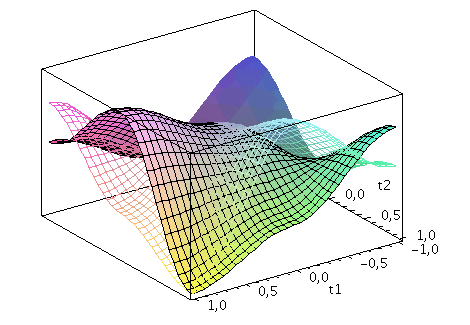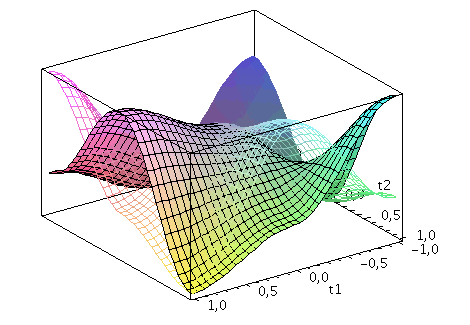
Der Zwei-Spielerzustand ist ein vierkomponentiger Spinor, welcher auf dem gemeinsamen Hilbertraum der Spieler definiert ist. Die Basisvektoren dieses vierdimensionalen komplexwertigen Raumes werden durch die vier möglichen, klassischen Strategienkombinationen (messbaren Eigenzustände des Quantensystems) gebildet ((1,0,0,0), (0,-1,0,0), (0,0,-1,0)$ und (0,0,0,1)). Der finale Zwei-Spielerzustand eines simultanen Zwei-Strategien-'One Shot'- Quantenspiels wird somit durch den vierkomponentigen Quantenzustand beschrieben, welcher sich in der Eisert'schen Repräsentation wie folgt aus dem Anfangszustand (hier CC=(1,0,0,0)) entwickelt: 

>	psi0:=simplify(multiply(subs(x=I*gamma/2,MatrixExponential(Matrix([[0,0,0,1],[0,0,-1,0],[0,-1,0,0],[1,0,0,0]]),x)),CC)): psi_final:=simplify(multiply(subs(x=-I*gamma/2,MatrixExponential(Matrix([[0,0,0,1],[0,0,-1,0],[0,-1,0,0],[1,0,0,0]]),x)),multiply(UA_T_UB,psi0)));

 

(1.4)

 

Der Erwartungswert der Eigenzustände bestimmt sich durch die jeweiligen Aufenthaltswarscheinlichkeitsamplituden bestimmt: 

>	P_CC:=simplify(conjugate(psi_final[1,1])*psi_final[1,1]): P_CD:=simplify(conjugate(psi_final[2,1])*psi_final[2,1]): P_DC:=simplify(conjugate(psi_final[3,1])*psi_final[3,1]): P_DD:=simplify(conjugate(psi_final[4,1])*psi_final[4,1]):

 

Wir nehmen die folgende allgemeine symmetrische Auszahlunsmatrix eines (2 Personen)-(2 Strategien) Spiels an (a, b, c und d sind reelwertige Zahlen) 

>	D_A:=Matrix(2,2,[a,b,c,d]);

 

(1.5)

 

und gewichten diese mit den Wahrscheinlichkeitsamplituden: 

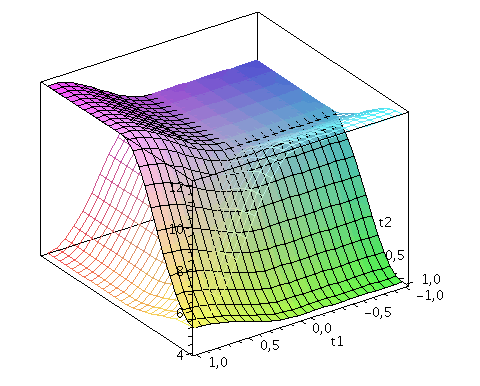
>	Auszahlung_A:=simplify(a*P_CC+d*P_DD+c*P_DC+b*P_CD): Auszahlung_B:=simplify(a*P_CC+d*P_DD+b*P_DC+c*P_CD):

 

Dominante Spiele 

Beispiel SetA: a < c und b < d; Strategie 2 dominiert Strategie 1 im klassischen Spiel 

>	a:=10: b:=4: c:=12: d:=5:

 

Im Unterschied zur klassischen Auszahlungsfunktion, die lediglich von den gemischten Strategien des Spielers A und des Spielers B abhängt, hängt die quantentheoretische Erweiterung der Auszahlungsfunktion im Allgemeinen von fünf Parametern ab: Die vier Winkel der Entscheidungsoperatoren und der Parameter gamma, welcher die Stärke der Strategienverschränkung quantifiziert. Um die Auszahlungsfunktion dennoch als Fläche in einem dreidimensionalen Raum zu visualisieren, reduziert man deren Abhängigkeiten, indem man einerseits den Verschränkungsparameter fixiert und die Menge der Quantenstrategien auf diejenigen beschränkt, die vom Ursprung der reinen, klassischen s1-Strategie starten: 

Separierendes Spiel (Keine Verschränkung) 

>

Aus_A_QQ:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=0,pb=-t2*Pi/2,gamma=0,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_A_QK:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=t2*Pi,pb=0,gamma=0,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_A_KQ:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=0,pb=-t2*Pi/2,gamma=0,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_A_KK:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=t2*Pi,pb=0,gamma=0,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_B_QQ:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=0,pb=-t2*Pi/2,gamma=0,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))): Aus_B_QK:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=t2*Pi,pb=0,gamma=0,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))): Aus_B_KQ:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=0,pb=-t2*Pi/2,gamma=0,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))): Aus_B_KK:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=t2*Pi,pb=0,gamma=0,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))):

 

>

Aus_A:=piecewise(t1<0 and t2<0,simplify(Re(Aus_A_QQ)),t1<0 and t2>=0,simplify(Re(Aus_A_QK)),t1>=0 and t2<0,simplify(Re(Aus_A_KQ)),t1>=0 and t2>=0,simplify(Re(Aus_A_KK))); Aus_B:=piecewise(t1<0 and t2<0,simplify(Re(Aus_B_QQ)),t1<0 and t2>=0,simplify(Re(Aus_B_QK)),t1>=0 and t2<0,simplify(Re(Aus_B_KQ)),t1>=0 and t2>=0,simplify(Re(Aus_B_KK)));

 

 

	(2.1.1)

 

>	Plot1:=plot3d(Re(Aus_A),t1=-1..1,t2=-1..1): Plot2:=plot3d(Re(Aus_B),t1=-1..1,t2=-1..1,style=wireframe): display(Plot1,Plot2,axes=boxed,orientation=[55,55]);

 

 

 

Maximale Verschränkung 

>

setgamma:=Pi/2: Aus_A_QQ:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=0,pb=-t2*Pi/2,gamma=setgamma,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_A_QK:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=t2*Pi,pb=0,gamma=setgamma,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_A_KQ:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=0,pb=-t2*Pi/2,gamma=setgamma,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_A_KK:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=t2*Pi,pb=0,gamma=setgamma,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_B_QQ:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=0,pb=-t2*Pi/2,gamma=setgamma,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))): Aus_B_QK:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=t2*Pi,pb=0,gamma=setgamma,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))): Aus_B_KQ:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=0,pb=-t2*Pi/2,gamma=setgamma,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))): Aus_B_KK:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=t2*Pi,pb=0,gamma=setgamma,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))):

 

>	Aus_A:=piecewise(t1<0 and t2<0,Aus_A_QQ,t1<0 and t2>=0,Aus_A_QK,t1>=0 and t2<0,Aus_A_KQ,t1>=0 and t2>=0,Aus_A_KK): Aus_B:=piecewise(t1<0 and t2<0,Aus_B_QQ,t1<0 and t2>=0,Aus_B_QK,t1>=0 and t2<0,Aus_B_KQ,t1>=0 and t2>=0,Aus_B_KK):

 

>	Plot1:=plot3d(Re(Aus_A),t1=-1..1,t2=-1..1,numpoints=1000): Plot2:=plot3d(Re(Aus_B),t1=-1..1,t2=-1..1,numpoints=1000,style=wireframe): display(Plot1,Plot2,axes=boxed,orientation=[55,55]);

 

 

Partiell verschränktes System 

>

setgamma:=Pi/4: Aus_A_QQ:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=0,pb=-t2*Pi/2,gamma=setgamma,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_A_QK:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=t2*Pi,pb=0,gamma=setgamma,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_A_KQ:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=0,pb=-t2*Pi/2,gamma=setgamma,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_A_KK:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=t2*Pi,pb=0,gamma=setgamma,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_B_QQ:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=0,pb=-t2*Pi/2,gamma=setgamma,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))): Aus_B_QK:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=t2*Pi,pb=0,gamma=setgamma,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))): Aus_B_KQ:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=0,pb=-t2*Pi/2,gamma=setgamma,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))): Aus_B_KK:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=t2*Pi,pb=0,gamma=setgamma,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))):

 

>	Aus_A:=piecewise(t1<0 and t2<0,Aus_A_QQ,t1<0 and t2>=0,Aus_A_QK,t1>=0 and t2<0,Aus_A_KQ,t1>=0 and t2>=0,Aus_A_KK): Aus_B:=piecewise(t1<0 and t2<0,Aus_B_QQ,t1<0 and t2>=0,Aus_B_QK,t1>=0 and t2<0,Aus_B_KQ,t1>=0 and t2>=0,Aus_B_KK):

 

>	Plot1:=plot3d(Re(Aus_A),t1=-1..1,t2=-1..1,numpoints=1000): Plot2:=plot3d(Re(Aus_B),t1=-1..1,t2=-1..1,numpoints=1000,style=wireframe): display(Plot1,Plot2,axes=boxed,orientation=[55,55]);

 

 

Animation 

>

frames:=8: for i from 0 by 1 to frames do setgamma:=i*Pi/(2*frames): Aus_A_QQ:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=0,pb=-t2*Pi/2,gamma=setgamma,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_A_QK:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=t2*Pi,pb=0,gamma=setgamma,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_A_KQ:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=0,pb=-t2*Pi/2,gamma=setgamma,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_A_KK:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=t2*Pi,pb=0,gamma=setgamma,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_B_QQ:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=0,pb=-t2*Pi/2,gamma=setgamma,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))): Aus_B_QK:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=t2*Pi,pb=0,gamma=setgamma,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))): Aus_B_KQ:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=0,pb=-t2*Pi/2,gamma=setgamma,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))): Aus_B_KK:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=t2*Pi,pb=0,gamma=setgamma,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))): Aus_A:=piecewise(t1<0 and t2<0,Aus_A_QQ,t1<0 and t2>=0,Aus_A_QK,t1>=0 and t2<0,Aus_A_KQ,t1>=0 and t2>=0,Aus_A_KK): Aus_B:=piecewise(t1<0 and t2<0,Aus_B_QQ,t1<0 and t2>=0,Aus_B_QK,t1>=0 and t2<0,Aus_B_KQ,t1>=0 and t2>=0,Aus_B_KK): Plot1:=plot3d(Re(Aus_A),t1=-1..1,t2=-1..1,numpoints=1000): Plot2:=plot3d(Re(Aus_B),t1=-1..1,t2=-1..1,numpoints=1000,style=wireframe): Ani[i]:=display(Plot1,Plot2,axes=boxed,titlefont=[TIMES,ROMAN,12],orientation=[55,55]); od:

 

>	display([seq(Ani[i],i=0..frames)],insequence=true,scaling=unconstrained);

 

 

Koordinationsspiele 

Beispiel SetB: a > c und b < d 

>	a:=10: b:=4: c:=9: d:=5:

 

Im Unterschied zur klassischen Auszahlungsfunktion, die lediglich von den gemischten Strategien des Spielers A und des Spielers B abhängt, hängt die quantentheoretische Erweiterung der Auszahlungsfunktion im Allgemeinen von fünf Parametern ab: Die vier Winkel der Entscheidungsoperatoren und der Parameter gamma, welcher die Stärke der Strategienverschränkung quantifiziert. Um die Auszahlungsfunktion dennoch als Fläche in einem dreidimensionalen Raum zu visualisieren, reduziert man deren Abhängigkeiten, indem man einerseits den Verschränkungsparameter fixiert und die Menge der Quantenstrategien auf diejenigen beschränkt, die vom Ursprung der reinen, klassischen s1-Strategie starten: 

Separierendes Spiel (Keine Verschränkung) 

>

Aus_A_QQ:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=0,pb=-t2*Pi/2,gamma=0,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_A_QK:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=t2*Pi,pb=0,gamma=0,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_A_KQ:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=0,pb=-t2*Pi/2,gamma=0,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_A_KK:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=t2*Pi,pb=0,gamma=0,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_B_QQ:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=0,pb=-t2*Pi/2,gamma=0,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))): Aus_B_QK:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=t2*Pi,pb=0,gamma=0,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))): Aus_B_KQ:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=0,pb=-t2*Pi/2,gamma=0,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))): Aus_B_KK:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=t2*Pi,pb=0,gamma=0,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))):

 

>

Aus_A:=piecewise(t1<0 and t2<0,simplify(Re(Aus_A_QQ)),t1<0 and t2>=0,simplify(Re(Aus_A_QK)),t1>=0 and t2<0,simplify(Re(Aus_A_KQ)),t1>=0 and t2>=0,simplify(Re(Aus_A_KK))); Aus_B:=piecewise(t1<0 and t2<0,simplify(Re(Aus_B_QQ)),t1<0 and t2>=0,simplify(Re(Aus_B_QK)),t1>=0 and t2<0,simplify(Re(Aus_B_KQ)),t1>=0 and t2>=0,simplify(Re(Aus_B_KK)));

 

 

	(3.1.1)

 

>	Plot1:=plot3d(Re(Aus_A),t1=-1..1,t2=-1..1): Plot2:=plot3d(Re(Aus_B),t1=-1..1,t2=-1..1,style=wireframe): display(Plot1,Plot2,axes=boxed,orientation=[55,55]);

 

 

 

Maximale Verschränkung 

>

setgamma:=Pi/2: Aus_A_QQ:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=0,pb=-t2*Pi/2,gamma=setgamma,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_A_QK:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=t2*Pi,pb=0,gamma=setgamma,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_A_KQ:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=0,pb=-t2*Pi/2,gamma=setgamma,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_A_KK:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=t2*Pi,pb=0,gamma=setgamma,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_B_QQ:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=0,pb=-t2*Pi/2,gamma=setgamma,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))): Aus_B_QK:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=t2*Pi,pb=0,gamma=setgamma,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))): Aus_B_KQ:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=0,pb=-t2*Pi/2,gamma=setgamma,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))): Aus_B_KK:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=t2*Pi,pb=0,gamma=setgamma,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))):

 

>	Aus_A:=piecewise(t1<0 and t2<0,Aus_A_QQ,t1<0 and t2>=0,Aus_A_QK,t1>=0 and t2<0,Aus_A_KQ,t1>=0 and t2>=0,Aus_A_KK): Aus_B:=piecewise(t1<0 and t2<0,Aus_B_QQ,t1<0 and t2>=0,Aus_B_QK,t1>=0 and t2<0,Aus_B_KQ,t1>=0 and t2>=0,Aus_B_KK):

 

>	Plot1:=plot3d(Re(Aus_A),t1=-1..1,t2=-1..1,numpoints=1000): Plot2:=plot3d(Re(Aus_B),t1=-1..1,t2=-1..1,numpoints=1000,style=wireframe): display(Plot1,Plot2,axes=boxed,orientation=[55,55]);

 

 

Partiell verschränktes System 

>

setgamma:=Pi/4: Aus_A_QQ:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=0,pb=-t2*Pi/2,gamma=setgamma,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_A_QK:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=t2*Pi,pb=0,gamma=setgamma,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_A_KQ:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=0,pb=-t2*Pi/2,gamma=setgamma,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_A_KK:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=t2*Pi,pb=0,gamma=setgamma,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_B_QQ:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=0,pb=-t2*Pi/2,gamma=setgamma,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))): Aus_B_QK:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=t2*Pi,pb=0,gamma=setgamma,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))): Aus_B_KQ:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=0,pb=-t2*Pi/2,gamma=setgamma,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))): Aus_B_KK:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=t2*Pi,pb=0,gamma=setgamma,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))):

 

>	Aus_A:=piecewise(t1<0 and t2<0,Aus_A_QQ,t1<0 and t2>=0,Aus_A_QK,t1>=0 and t2<0,Aus_A_KQ,t1>=0 and t2>=0,Aus_A_KK): Aus_B:=piecewise(t1<0 and t2<0,Aus_B_QQ,t1<0 and t2>=0,Aus_B_QK,t1>=0 and t2<0,Aus_B_KQ,t1>=0 and t2>=0,Aus_B_KK):

 

>	Plot1:=plot3d(Re(Aus_A),t1=-1..1,t2=-1..1,numpoints=1000): Plot2:=plot3d(Re(Aus_B),t1=-1..1,t2=-1..1,numpoints=1000,style=wireframe): display(Plot1,Plot2,axes=boxed,orientation=[55,55]);

 

 

Animation 

>

frames:=8: for i from 0 by 1 to frames do setgamma:=i*Pi/(2*frames): Aus_A_QQ:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=0,pb=-t2*Pi/2,gamma=setgamma,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_A_QK:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=t2*Pi,pb=0,gamma=setgamma,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_A_KQ:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=0,pb=-t2*Pi/2,gamma=setgamma,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_A_KK:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=t2*Pi,pb=0,gamma=setgamma,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_B_QQ:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=0,pb=-t2*Pi/2,gamma=setgamma,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))): Aus_B_QK:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=t2*Pi,pb=0,gamma=setgamma,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))): Aus_B_KQ:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=0,pb=-t2*Pi/2,gamma=setgamma,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))): Aus_B_KK:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=t2*Pi,pb=0,gamma=setgamma,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))): Aus_A:=piecewise(t1<0 and t2<0,Aus_A_QQ,t1<0 and t2>=0,Aus_A_QK,t1>=0 and t2<0,Aus_A_KQ,t1>=0 and t2>=0,Aus_A_KK): Aus_B:=piecewise(t1<0 and t2<0,Aus_B_QQ,t1<0 and t2>=0,Aus_B_QK,t1>=0 and t2<0,Aus_B_KQ,t1>=0 and t2>=0,Aus_B_KK): Plot1:=plot3d(Re(Aus_A),t1=-1..1,t2=-1..1,numpoints=1000): Plot2:=plot3d(Re(Aus_B),t1=-1..1,t2=-1..1,numpoints=1000,style=wireframe): Ani[i]:=display(Plot1,Plot2,axes=boxed,titlefont=[TIMES,ROMAN,12],orientation=[55,55]); od:

 

>	display([seq(Ani[i],i=0..frames)],insequence=true,scaling=unconstrained);

 

 

Anti-Koordinationsspiele 

Beispiel SetB: a < c und b > d 

>	a:=10: b:=7: c:=12: d:=5:

 

Im Unterschied zur klassischen Auszahlungsfunktion, die lediglich von den gemischten Strategien des Spielers A und des Spielers B abhängt, hängt die quantentheoretische Erweiterung der Auszahlungsfunktion im Allgemeinen von fünf Parametern ab: Die vier Winkel der Entscheidungsoperatoren und der Parameter gamma, welcher die Stärke der Strategienverschränkung quantifiziert. Um die Auszahlungsfunktion dennoch als Fläche in einem dreidimensionalen Raum zu visualisieren, reduziert man deren Abhängigkeiten, indem man einerseits den Verschränkungsparameter fixiert und die Menge der Quantenstrategien auf diejenigen beschränkt, die vom Ursprung der reinen, klassischen s1-Strategie starten: 

Separierendes Spiel (Keine Verschränkung) 

>

Aus_A_QQ:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=0,pb=-t2*Pi/2,gamma=0,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_A_QK:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=t2*Pi,pb=0,gamma=0,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_A_KQ:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=0,pb=-t2*Pi/2,gamma=0,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_A_KK:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=t2*Pi,pb=0,gamma=0,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_B_QQ:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=0,pb=-t2*Pi/2,gamma=0,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))): Aus_B_QK:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=t2*Pi,pb=0,gamma=0,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))): Aus_B_KQ:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=0,pb=-t2*Pi/2,gamma=0,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))): Aus_B_KK:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=t2*Pi,pb=0,gamma=0,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))):

 

>

Aus_A:=piecewise(t1<0 and t2<0,simplify(Re(Aus_A_QQ)),t1<0 and t2>=0,simplify(Re(Aus_A_QK)),t1>=0 and t2<0,simplify(Re(Aus_A_KQ)),t1>=0 and t2>=0,simplify(Re(Aus_A_KK))); Aus_B:=piecewise(t1<0 and t2<0,simplify(Re(Aus_B_QQ)),t1<0 and t2>=0,simplify(Re(Aus_B_QK)),t1>=0 and t2<0,simplify(Re(Aus_B_KQ)),t1>=0 and t2>=0,simplify(Re(Aus_B_KK)));

 

 

	(4.1.1)

 

>	Plot1:=plot3d(Re(Aus_A),t1=-1..1,t2=-1..1): Plot2:=plot3d(Re(Aus_B),t1=-1..1,t2=-1..1,style=wireframe): display(Plot1,Plot2,axes=boxed,orientation=[55,55]);

 

 

 

Maximale Verschränkung 

>

setgamma:=Pi/2: Aus_A_QQ:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=0,pb=-t2*Pi/2,gamma=setgamma,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_A_QK:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=t2*Pi,pb=0,gamma=setgamma,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_A_KQ:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=0,pb=-t2*Pi/2,gamma=setgamma,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_A_KK:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=t2*Pi,pb=0,gamma=setgamma,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_B_QQ:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=0,pb=-t2*Pi/2,gamma=setgamma,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))): Aus_B_QK:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=t2*Pi,pb=0,gamma=setgamma,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))): Aus_B_KQ:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=0,pb=-t2*Pi/2,gamma=setgamma,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))): Aus_B_KK:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=t2*Pi,pb=0,gamma=setgamma,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))):

 

>	Aus_A:=piecewise(t1<0 and t2<0,Aus_A_QQ,t1<0 and t2>=0,Aus_A_QK,t1>=0 and t2<0,Aus_A_KQ,t1>=0 and t2>=0,Aus_A_KK): Aus_B:=piecewise(t1<0 and t2<0,Aus_B_QQ,t1<0 and t2>=0,Aus_B_QK,t1>=0 and t2<0,Aus_B_KQ,t1>=0 and t2>=0,Aus_B_KK):

 

>	Plot1:=plot3d(Re(Aus_A),t1=-1..1,t2=-1..1,numpoints=1000): Plot2:=plot3d(Re(Aus_B),t1=-1..1,t2=-1..1,numpoints=1000,style=wireframe): display(Plot1,Plot2,axes=boxed,orientation=[55,55]);

 

 

Partiell verschränktes System 

>

setgamma:=Pi/4: Aus_A_QQ:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=0,pb=-t2*Pi/2,gamma=setgamma,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_A_QK:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=t2*Pi,pb=0,gamma=setgamma,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_A_KQ:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=0,pb=-t2*Pi/2,gamma=setgamma,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_A_KK:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=t2*Pi,pb=0,gamma=setgamma,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_B_QQ:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=0,pb=-t2*Pi/2,gamma=setgamma,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))): Aus_B_QK:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=t2*Pi,pb=0,gamma=setgamma,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))): Aus_B_KQ:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=0,pb=-t2*Pi/2,gamma=setgamma,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))): Aus_B_KK:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=t2*Pi,pb=0,gamma=setgamma,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))):

 

>	Aus_A:=piecewise(t1<0 and t2<0,Aus_A_QQ,t1<0 and t2>=0,Aus_A_QK,t1>=0 and t2<0,Aus_A_KQ,t1>=0 and t2>=0,Aus_A_KK): Aus_B:=piecewise(t1<0 and t2<0,Aus_B_QQ,t1<0 and t2>=0,Aus_B_QK,t1>=0 and t2<0,Aus_B_KQ,t1>=0 and t2>=0,Aus_B_KK):

 

>	Plot1:=plot3d(Re(Aus_A),t1=-1..1,t2=-1..1,numpoints=1000): Plot2:=plot3d(Re(Aus_B),t1=-1..1,t2=-1..1,numpoints=1000,style=wireframe): display(Plot1,Plot2,axes=boxed,orientation=[55,55]);

 

 

Animation 

>

frames:=8: for i from 0 by 1 to frames do setgamma:=i*Pi/(2*frames): Aus_A_QQ:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=0,pb=-t2*Pi/2,gamma=setgamma,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_A_QK:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=t2*Pi,pb=0,gamma=setgamma,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_A_KQ:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=0,pb=-t2*Pi/2,gamma=setgamma,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_A_KK:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=t2*Pi,pb=0,gamma=setgamma,r_A=U1ss,p_A=U1nsns,t_A=U1nss,s_A=U1sns},Auszahlung_A))): Aus_B_QQ:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=0,pb=-t2*Pi/2,gamma=setgamma,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))): Aus_B_QK:=Re(simplify(subs({ta=0,pa=-t1*Pi/2,tb=t2*Pi,pb=0,gamma=setgamma,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))): Aus_B_KQ:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=0,pb=-t2*Pi/2,gamma=setgamma,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))): Aus_B_KK:=Re(simplify(subs({ta=t1*Pi,pa=0,tb=t2*Pi,pb=0,gamma=setgamma,r_B=U2ss,p_B=U2nsns,t_B=U2nss,s_B=U2sns},Auszahlung_B))): Aus_A:=piecewise(t1<0 and t2<0,Aus_A_QQ,t1<0 and t2>=0,Aus_A_QK,t1>=0 and t2<0,Aus_A_KQ,t1>=0 and t2>=0,Aus_A_KK): Aus_B:=piecewise(t1<0 and t2<0,Aus_B_QQ,t1<0 and t2>=0,Aus_B_QK,t1>=0 and t2<0,Aus_B_KQ,t1>=0 and t2>=0,Aus_B_KK): Plot1:=plot3d(Re(Aus_A),t1=-1..1,t2=-1..1,numpoints=1000): Plot2:=plot3d(Re(Aus_B),t1=-1..1,t2=-1..1,numpoints=1000,style=wireframe): Ani[i]:=display(Plot1,Plot2,axes=boxed,titlefont=[TIMES,ROMAN,12],orientation=[55,55]); od:

 

>	display([seq(Ani[i],i=0..frames)],insequence=true,scaling=unconstrained);

 

 

>