II.1 Theorie der sozio-ökonomischen Netzwerke
Eine bedeutende Einschränkung der deterministischen, evolutionären Spieltheorie ist deren zugrundeliegende Netzwerkstruktur (Netzwerktopologie). Die jeweiligen Spieler der betrachteten Population suchen in jeder Spielperiode einen neuen Spielpartner, wobei sie hierbei zufällig vorgehen (zufälliges Netzwerk) und vom Prinzip her mit jedem Spieler innerhalb der Population potentiell das zugrundeliegende Spiel spielen können (vollständig verbundenes Netzwerk). In Bimatrix Spielen suchen sich die Spieler der Teilpopulation A einen zufälligen Spielpartner aus Gruppe B (bzw. umgekehrt). Betrachtet man sich jedoch real existierende sozio-ökonomische Netzwerke, so zeigt sich, dass diese Annahme oft nicht erfüllt ist. Personen kennen oft nur eine Teilmenge von Spielern innerhalb der Population (kein vollständig verbundenes Netzwerk) und die Wahl der potentiellen Spielpartner erfolgt oft auch nicht nach zufälligen Mustern.
II.2 Einführung in die Theorie der komplexe Netzwerke
Die Theorie der komplexen Netzwerke bildet die Grundlage zur Beschreibung einer Vielzahl von unterschiedlichen biologischen und sozio-ökonomischen Systemen. Die mathematische Beschreibung komplexer Netzwerke ist in mehreren Übersichtsartikel (siehe z.B. http://barabasi.com/f/103.pdf, https://arxiv.org/abs/cond-mat/0106144, http://epubs.siam.org/doi/pdf/10.1137/S003614450342480) zusammengefasst (siehe auch Claudius Gros, "Complex and Adaptive Dynamical Systems, a Primer"), wobei im besonderen die frei zugängliche Onlineversion des Buches Network Science von Albert-Laszlo Barabasi zu empfehlen ist.
In dieser auf graphentheoretischen Grundlagen basierenden mathematischen Beschreibung der komplexe Netzwerke werden physikalische bzw. soziale Interaktionen durch Verbindungskanten zwischen den jeweiligen Netzwerkknoten beschrieben. In der Literatur werden grob vier unterschiedliche Netzwerktypen beschrieben -- die zufälligen, die kleine Welt, die exponentiellen und die skalenfreien Netzwerke. Die theoretische Netzwerkforschung befasst sich mit der Entstehung und Beschreibung dieser Netzwerke. Bei einigen Modellnetzwerken können analytische Ergebnisse gewonnen werden. Die Anwendung der Theorie auf real existierende Netzwerkstrukturen ist ebenfalls in den Übersichtsartikeln zusammengefasst. Neben sozialen Netzwerken wie z. B. wissenschaftliche Kollaborationen, Koautorenschaften und Zitationsverflechtungen wissenschaftlicher Artikel, Kommunikationsnetzwerken wie dem Internet und diversen weiteren sozio-ökonomischen Netzwerkstrukturen werden mit Hilfe des mathematischen Modells der komplexen Netzwerke auch biologische Netzwerken wie z.B. neuronale oder Proteinnetzwerke beschrieben und analysiert. Eine kurze Einführung findet sich z.B. auch unter dem folgenden Link: Neue Entwicklungen
in der Evolutionären Spieltheorie: Vorlesungsteil 6
Im folgenden werden die vier unterschiedliche Netzwerktypen im einzelnen beschrieben. Zusätzlich wird die Python Programmierung komplexer Netzwerke vorgestellt. Mittels Python und der Programmbibliothek NetworkX kann man in relativ einfacher Weise die unterschiedlichen Arten von komplexen Netzwerken grafisch darstellen und analysieren.
II.2.1 Zufällige Netzwerke (Random Networks)
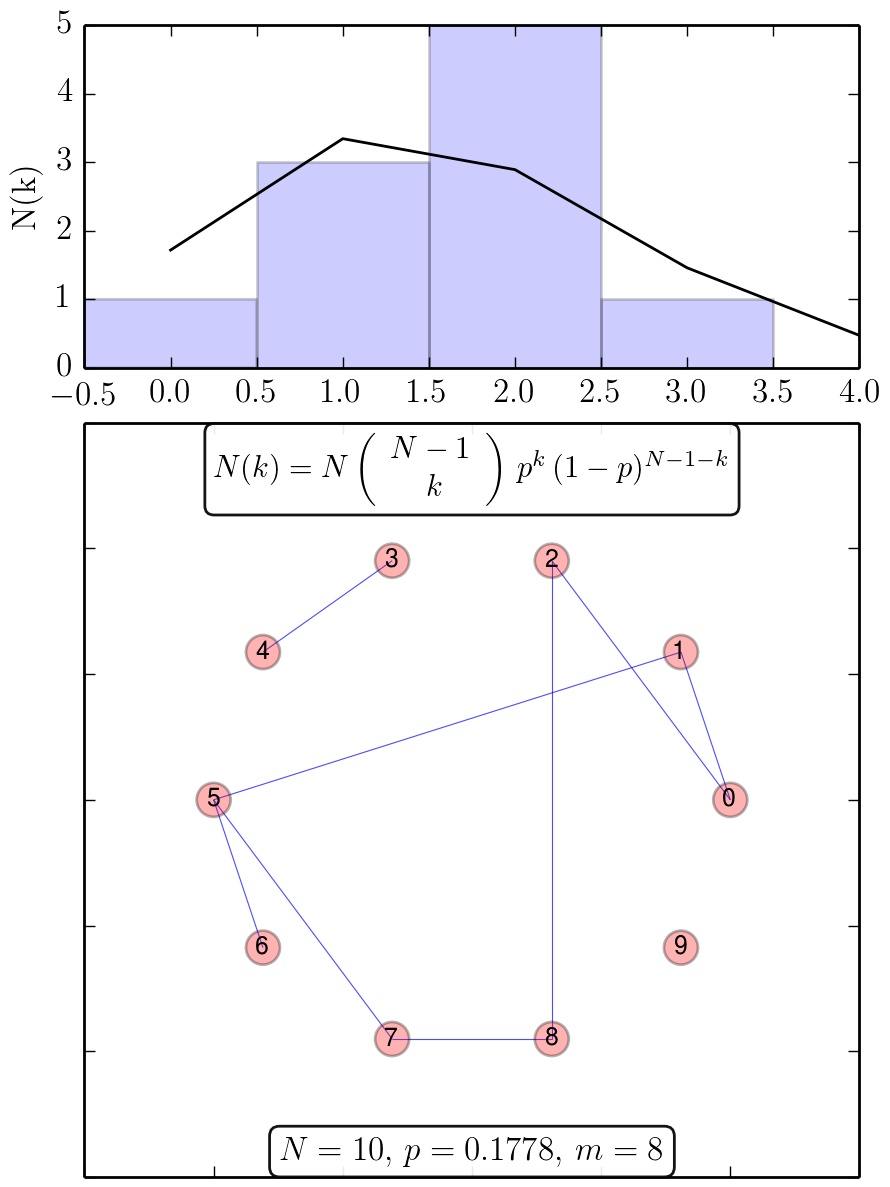
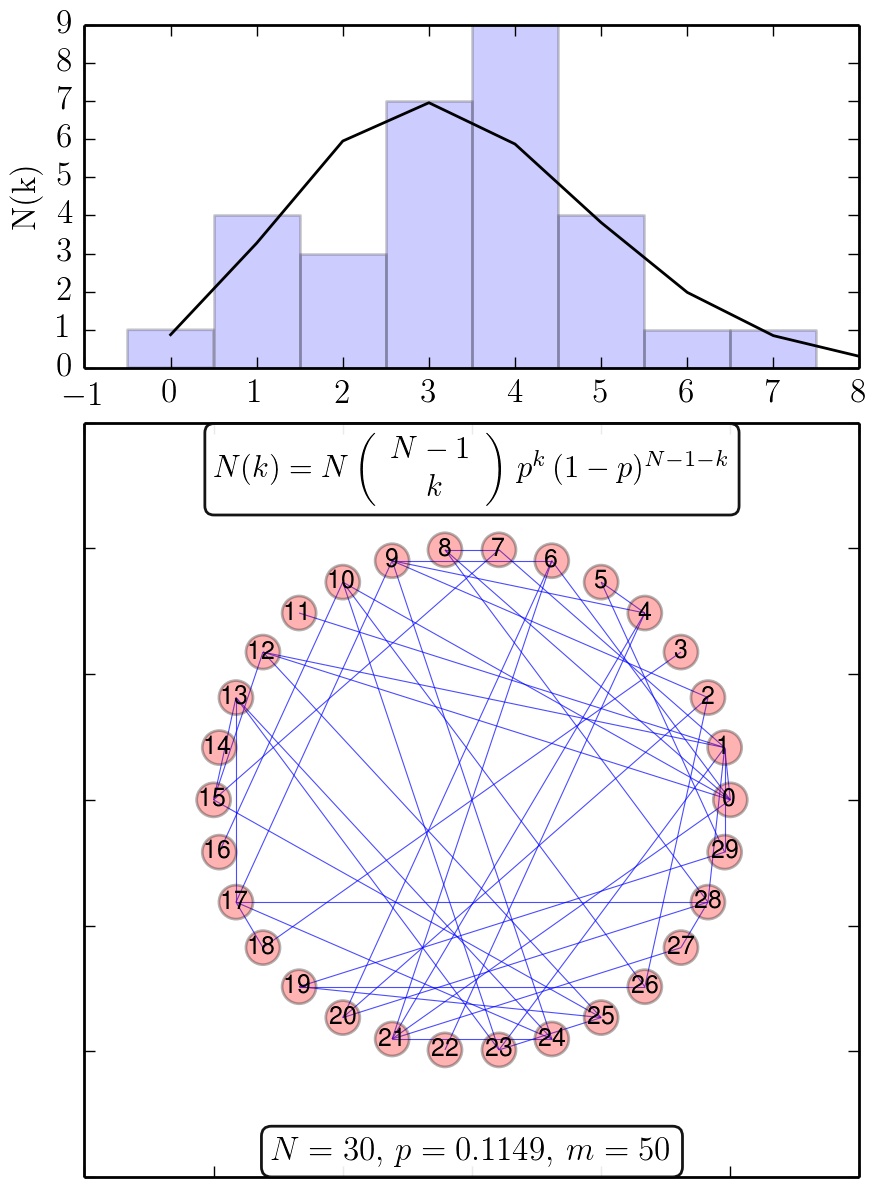
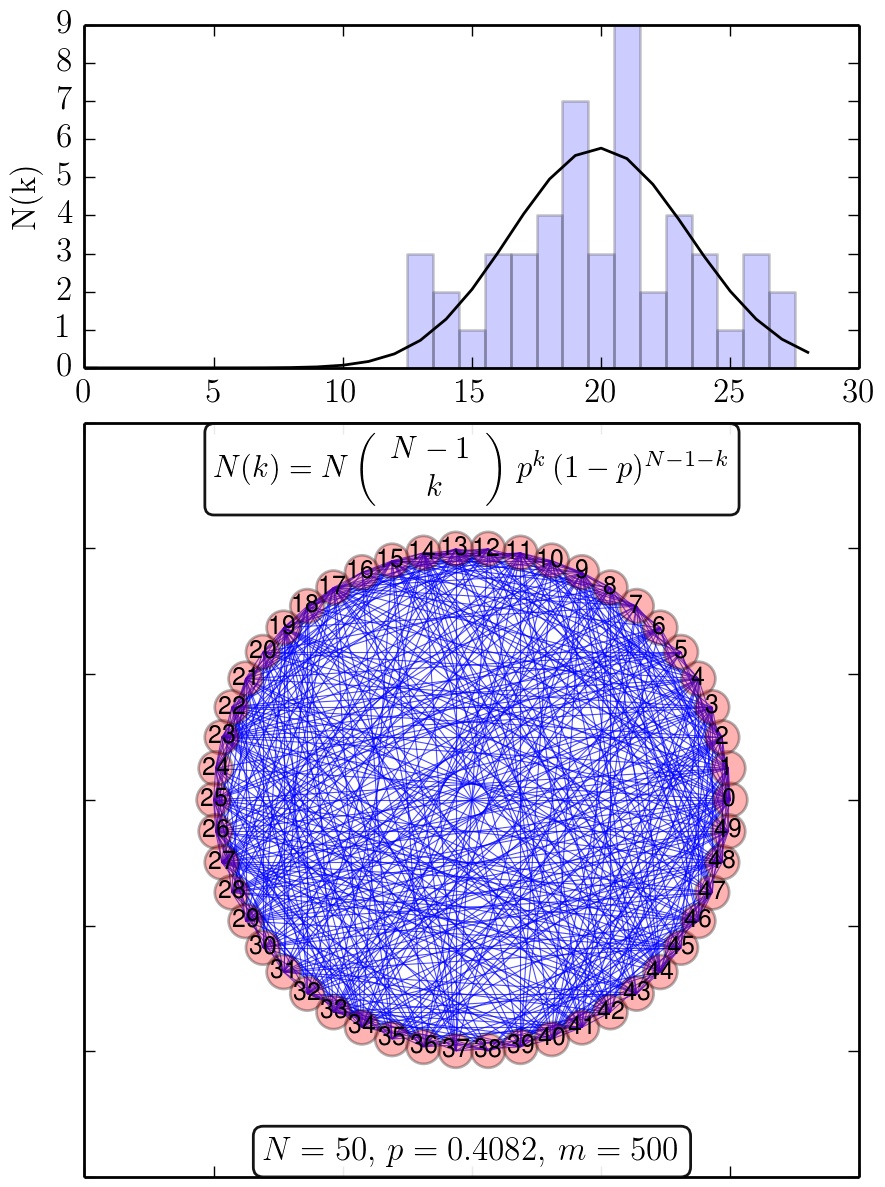
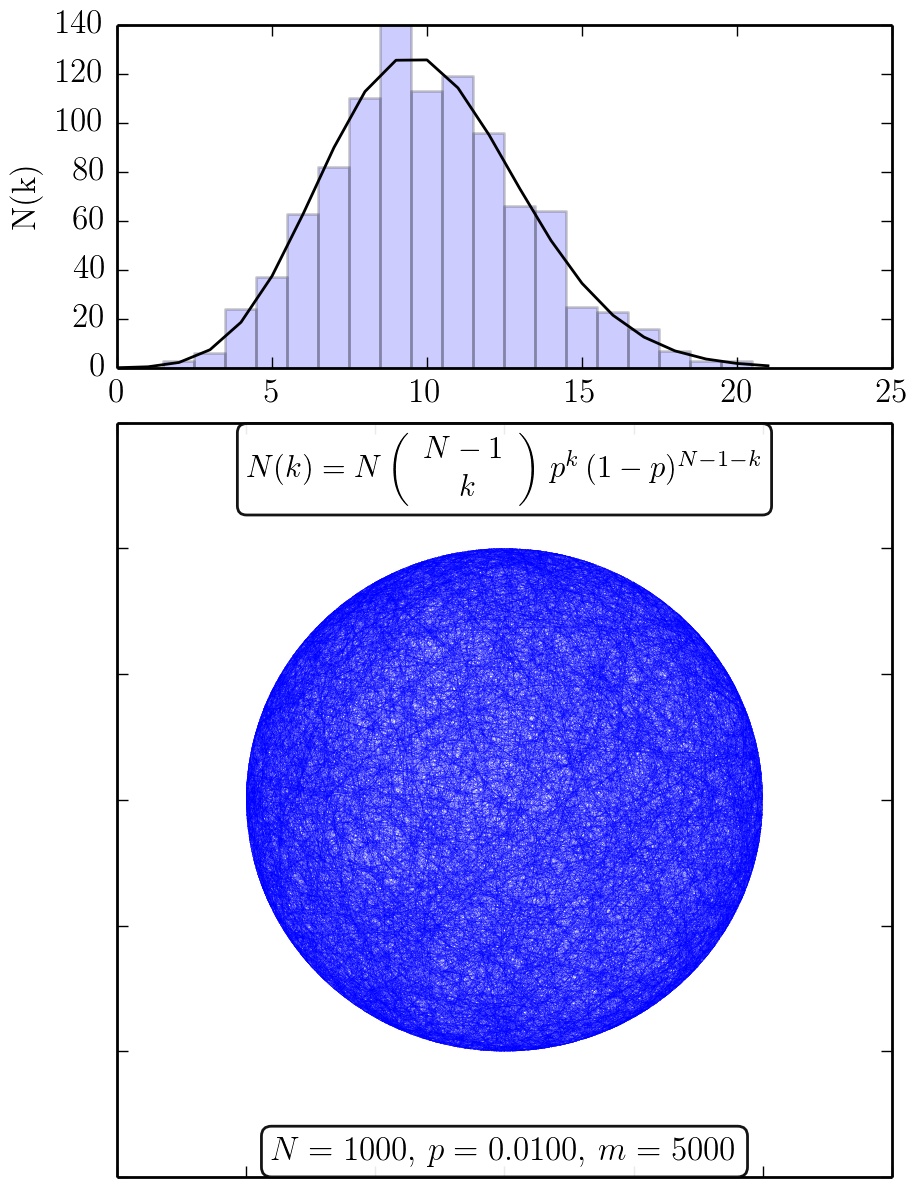
Ergebnisse des Python Skriptes RandomNetwork.py: Zufallsgraph und die zugehörige Verteilungsfunktion der Knotengrade (schwarze Kurve: analytische Verteilung).
Mittelt man über die einzelnen Verteilungsfunktionen P(k) mehrerer zufälliger Netzwerke so ergeben sich die analytisch ermittelten Verteilungsfunktionen (Python Skript VPSOC-RandomNetwork_evol.py).
Die einzelnen Kanten bei zufälligen Netzwerke werden von den Knoten (Spielern) nach einem rein zufälligen Muster ausgewählt. Im Erdos-Renyi Modell (Erdos and Renyi, 1959) werden N Knoten zufällig mit m ungerichteten Kanten verbunden. Die Wahrscheinlichkeit p, das ein Knoten mit dem anderen verbunden ist demnach $p=2m/(N(N-1))$. Die Verteilungsfunktion der Knotengrade $P(k)$ ist binomialverteilt:
\[
\begin{equation}
P(k)=N(k)/N= \left( \begin{array}[c]{cc} N -1 \\ \ k \end{array} \right)\, p^k\,(1-p)^{N-1-k}
\end{equation}
\]
Für große N geht diese Verteilung in die folgende Poisson Verteilungsfunktion über
\[
\begin{equation}
P(k) = \frac{e^{-\bar{k}}\,{\bar{k}}^k}{k!}\quad,
\end{equation}
\]
wobei $\bar{k}=\left< k \right>=p\,(N-1)$ der mittlere Knotengrad im Netzwerk ist (siehe Abb. 3.4 in Chapter 3: Albert-Laszlo Barabasi, Network Science). Die oberen Abbildungen zeigen Ergebnisse des Python Skriptes (Python Skript: RandomNetwork.py) welches einen Zufallsgraph mit N-Knoten und m-Kanten und die zugehörige Verteilungsfunktion $N(k)=N\,P(k)$ der Knotengrade darstellt. Die einzelnen blauen Kästchen des Balkendiagramms stellen die spezifische, zufällig erzeugte Realisierung des Zufallsgraphen dar, wohingegen die schwarze Kurve die analytische Binomialverteilung zeigt. Mittelt man über die einzelnen Verteilungsfunktionen P(k) mehrerer zufälliger Netzwerke, erzeugt man ein Ensemble-Mittelwert der möglichen Realisierungen des Zufallsgraphen. In der nebenstehenden rechten Abbildung ist eine solche Mittelung anhand einer Animation veranschaulicht. Man erkennt deutlich, dass die über mehrere zufällige Netzwerke gemittelte Verteilung (dunkel graue Kästchen) sich der analytische Verteilung (schwarze Kurve) immer mehr annähert.
Eine weitere wichtige Eigenschaft des Netzwerkes ist die relative Größe des größten verbundenen Knotenclusters (Giant component, Hub) $N_G/N$. Zufällige Netzwerke mit kleinem mittlere Knotengrad $\left< k \right> < 1$ besitzen keine ausgeprägte Giant Component ($N_G/N << 1$, subkritischer Bereich) und die einzelnen Knoten des Netzwerkes gliedern sich in viele kleinere zusammenhängende Cluster. Hat der mittlere Knotengrad des Netzwerks jedoch große Werte ($\left< k \right> > 1$), so formt sich eine Giant Component (superkritischer Bereich), die neben den vielen kleineren Clustern koexistiert. Für sehr große Werte ($\left< k \right> > \rm ln(N)$) absorbiert die Giant Component alle Knoten ($N_G/N = 1$, verbundener Bereich); (siehe Abb. 3.7 in Chapter 3: Albert-Laszlo Barabasi, Network Science).
Übergang zwischen einem regulären Netzwerk, einem Kleine Welt Netzwerk und einem zufälligen Netzwerk (Python Skript VPSOC-SmallWorld-Network_evol.py).
II.2.2 Kleine Welt Netzwerke (Small-World Networks)
Kleine Welt-Netzwerke zeichnen sich durch einen kleinen Wert der durchschnittlichen kürzesten Verbindung zwischen den Knoten des Netzwerkes und einem großen Wert des Clusterkoeffizienten aus. Ein einfaches Modell welches den Übergang von einem Netzwerk mit regulärer Struktur (Gitter-ähnlicher Struktur) über ein kleines Welt Netzwerk hin zu einem zufälligen Netzwerk veranschaulicht, wurde von Watts und Strogatz im Jahre 1998 vorgestellt: Im einfachsten Fall startet man hierbei mit einem eindimensionalen Gitter-Netzwerk mit N Knoten, wobei jeder Knoten mit seinen K-nächsten Nachbarn (hier speziell K=2) verbunden ist. Nun löscht man mit der Wahrscheinlichkeit p jede der existierenden Verbindungen (Kanten) und stellt eine neue Kante im Netzwerk in zufälliger Weise her. Für p=0 bleibt die ursprüngliche Gitterstruktur erhalten und für p=1 erzeugt man ein vollständig zufälliges Netzwerk. Watts und Strogatz konnten in ihrem Modell zeigen, dass man schon für kleine p (0 < p << 1) ein kleines Welt-Netzwerk erzeugt, das durch einen kleinen Wert der durchschnittlichen kürzesten Verbindung zwischen den Knoten und einem großen Wert des Clusterkoeffizienten gekennzeichnet ist.
Die linke, nebenstehende Abbildung zeigt eine Animation eines leicht abgeänderten Watts-Strogatz Modells. Zum Zeitpunkt t=0 startet man wiederum mit einer regulären Gitterstruktur (hier N=80, K=2). Zu jedem folgenden Zeitpunkt wird nun zufällig eine Kante im Netzwerk ausgewählt, die in zufälliger Weise neu angeordnet wird. Im Laufe der Zeitentwicklung erkennt man, dass sich die Verteilungsfunktion der Knotengrade immer mehr an die binomialverteilte Funktion des zufälligen Netzwerks annähert (P(k), siehe schwarze Kurve im mittleren Diagramm in der linken Animation). Im oberen Diagramm der linken Animation ist hingegen der normierte Wert des Clusterkoeffizienten ($C_t/C_0$, schwarze Punkte) und der normierte Wert der durchschnittlichen kürzesten Verbindung zwischen den Knoten des Netzwerkes ($l_t/l_0$, rote Punkte) als Funktion des Iterationszeitpunktes t dargestellt. Man erkennt, dass sich $l_t$ schon nach wenigen Iterationsschritten schnell verkleinert - im Bereich $5 < t < 20$ hat das Netzwerk eine klare Kleine Welt-Struktur. Für große Zeiten näher sich das Netzwerk immer weiter einem zufälligen Netzwerk an.
Neben den hier dargestellten Netzwerkeigenschaften von zufällige und klenen Welt Netzwerke findet sich eine ausührliche Darstellung in Chapter 3: Albert-Laszlo Barabasi, Network Science. In der Section 3 (Random Networks) werden die folgenden Fragen im Detail diskutiert: Wie erzeugt man mittels eines mathematischen Algorithmus ein zufälliges Neztwerk (siehe Box 3.2)? Wie sieht die Verteilungsfunktion der Knotengrade in zufällige Neztwerken aus (siehe Image 3.4 Binomial vs. Poisson Degree Distribution)? Vergleich: Real existierende Netzwerke mit zufällige Netzwerken (siehe Image 3.6 Degree Distribution of Real Networks). Die relativen Größe des Hubs (grösster verbundener Knotencluster) hängt von dem durchschnittlichen Knotengrad des Netzwerkes ab. Definition von unterschiedlichen Regimen in zufälligen Netzwerken (subcritical, supercritical, fully connected) (siehe Image 3.7 Evolution of a Random Network). Sind real existierende Netzwerke subcritical, supercritical oder fully connected? (siehe Table 3.1 Are Real Networks Connected? und Image 3.9 Most Real Networks are Supercritical). Definition der kleinen Welt Eigenschaft in komplexen Netzwerken: In the language of network science the small world phenomenon implies that the distance between two randomly chosen nodes in a network is short.. Mittlerer Abstand zwischen zwei Knoten im Netzwerk d bestimmt die Eigenschaft von kleinen Welt Netzwerken (siehe Image 3.10 Six Deegree of Separation und Image 3.11 Why are Small Worlds Surprising? und Table 3.2 Six Degrees of Separation). Der Clusterkoeffizient in real existierenden und zufälligen Neztwerken (siehe Image 3.13 Clustering in Real Networks und Box 3.9 Watts-Strogatz Model).
Zeitlich anwachsendes exponentielles Netzwerk (Python Skript VPSOC-Expontial-Network_evol.py).
II.2.3 Exponentielle Netzwerke (Exponential Networks)
Bei exponentiellen und skalenfreien Netzwerken besitzen sehr viele Knoten wenig Kanten und einige wenige Knoten sehr viele Kanten. Die Verteilungsfunktion der Knotengrade bei exponentielle Netzwerken ist nicht, wie bei zufälligen Netzwerken binomialverteilt, sondern folgt einem exponentiellen Verlauf. Im folgenden wird die Konstruktion eines exponentiellen Netzwerks mittels eines zeitlichen Anwachsens der Netzwerkknoten betracht. Startet man z.B. zur Zeit t=0 mit zwei Knoten die durch eine ungerichtete Kante miteinander verbunden sind und fügt dem Netzwerk in jedem Zeitabschnitt $\Delta t =1$ einen weiteren Knoten hinzu und verbindet diesen in zufälliger Weise mit einem der Knoten des bestehenden Netzwerkes, so entwickelt sich im Laufe der Zeit ein exponentielles Netzwerk (siehe rechte Animation). Die Verteilungsfunktion der Knotengrade nähert sich für große Zeiten dem folgenden exponentiellen Verlauf an: $P(k)=2^{-k}$ (siehe schwarze Kurve in der rechten Animation).
II.2.4 Skalenfreie Netzwerke (Scale-Free Networks)
Eine ausführliche Darstellung der Eigenschaften dieser Netzwerke findet sich in Chapter 4: Albert-Laszlo Barabasi, Network Science. Die Klasse der skalenfreien Netzwerke ist die wohl wichtigste aller Netzwerkklassen da diese topologische Eigenschaft in vielen real existierenden Netzwerken realisiert ist (siehe Table 4.1: Albert-Laszlo Barabasi, Network Science).
Die Verteilungsfunktion der Knotengrade des Internets (WWW, Kanten zwischen Internetseiten, gerichtetes Netzwerk) wird mathematisch durch eine 'power-law distribution' beschrieben ($P(k)\sim k^{- \gamma}$). Die Bezeichnung skalenfrei gründet hierbei auf der Eigenschaft, dass eine Umskalierung $k\rightarrow \alpha k$ mit einem beliebigen Faktor $\alpha$ wiederum zu einem Potenzgesetz führt: $P(\alpha k) = \alpha^{- \gamma}k^{- \gamma} \sim k^{- \gamma}$. In skalenfreien Netzwerken kann man keine Aussage über den erwarteten Knotengrad machen, wenn man in zufalliger Weise einen Knoten aus dem Netzwerk auswählt; dieser kann extrem groß oder sehr klein sein (Was bedeutet 'skalenfrei'? siehe Section 4.4: Albert-Laszlo Barabasi, Network Science). Trägt man ein solches Potenzgesetz $P(k) \sim k^{- \gamma}$ doppelt-logarithmisch auf (y-Achse ln(P), x-Achse ln(k)) so erhält man eine Gerade (ln(P) =$-\gamma$ ln(k)).
In skalenfreien Netzwerken entstehen sehr große Hubs (Hauptunterschied zu zufälligen Netzwerken,
siehe Image 4.4 und 4.5: Albert-Laszlo Barabasi, Network Science. Viele real existierende komplexe Netzwerke zeigen ein skalenfreies Verhalten, wobei der Exponent $\gamma$ meisstens im folgenden Wertebereich zu finden ist: $2 < \gamma < 3$. Skalenfreie Netzwerke mit $\gamma < 3$ besitzen keine sinnvolle interne Knotengradskala. Greift man zufällig einen Knoten aus dem Netzwerk, so kann man seinen Knotengrad nicht vorher einschränken; er kann sehr klein oder sehr sehr groß sein. Die Standardabweichung der Knotengrade divergiert sogar für $N \rightarrow \infty$ (siehe Tabelle 4.1, Image 4.7 und 4.8: Albert-Laszlo Barabasi, Network Science). Man beobachtet die skalenfreie Eigenschaft in vielen unterschiedlichen real existierenden komplexen Netzwerken (siehe Universality, Section 4.5, Box 4.2: Albert-Laszlo Barabasi, Network Science). Es kann zu ultra small world Eigenschaften in skalenfreien Netzwerken kommen; dies ist abhängig vom Exponenten $\gamma$ )siehe Section 4.6: Albert-Laszlo Barabasi, Network Science). Die Größe des Exponenten $\gamma$ hat starke Auswirkungen auf die Netzwerkeigenschaften (siehe Box 4.5: Albert-Laszlo Barabasi, Network Science). Man kann z.B. zeigen, dass skalenfreie Netzwerke mit $\gamma<2$ nicht existieren können (siehe Box 4.6: Albert-Laszlo Barabasi, Network Science). Eine Zusammenfassung der mathematischen Eigenschaften von skalenfreie Netzwerken sindet sich in Box 4.9: Albert-Laszlo Barabasi, Network Science).
Das Barabasi-Albert (BA) Model der skalenfreien Netzwerke stellt eine mathematische Modelierung eines skalenfreien Netzwerkes dar (siehe Chapter 5: Albert-Laszlo Barabasi, Network Science). Im BA-Model werden die folgenden Prinzipien bei der Konstruktion des skalenfreien Netzwerkes benutzt: a) Zeitliches Anwachsen der Knoten und Kanten und b) Preferential Attachment (siehe Section 5.2 und Image 5.2: Albert-Laszlo Barabasi, Network Science). Die mathematische Definition der Konstruktion eines skalenfreien Netzwerkes mittels des Barabasi-Albert Models wird in folgendem link beschrieben: (Box 5.1: Albert-Laszlo Barabasi, Network Science). Die Konstruktion eines skalenfreien Netzwerkes ähnelt der eines exponentiellen Netzwerkes, wobei bei skalenfreien Netzen der zusätzliche Effekt einer erhöhten Verlinkungswahrscheinlichkeit (Preferential Attachment) ein bevorzugtes Anlagern der Netzwerkkanten an attraktivere Knoten bewirkt. Ein Vergleich der Eigenschaften von exponentielle Netzwerke mit skalenfreie Netzwerke findet sich in der Section 5.6: Albert-Laszlo Barabasi, Network Science. Eine Zusammenfassung der mathematischen Eigenschaften von skalenfreie Netzwerken ist in
Box 5.4: Albert-Laszlo Barabasi, Network Science zu finden.
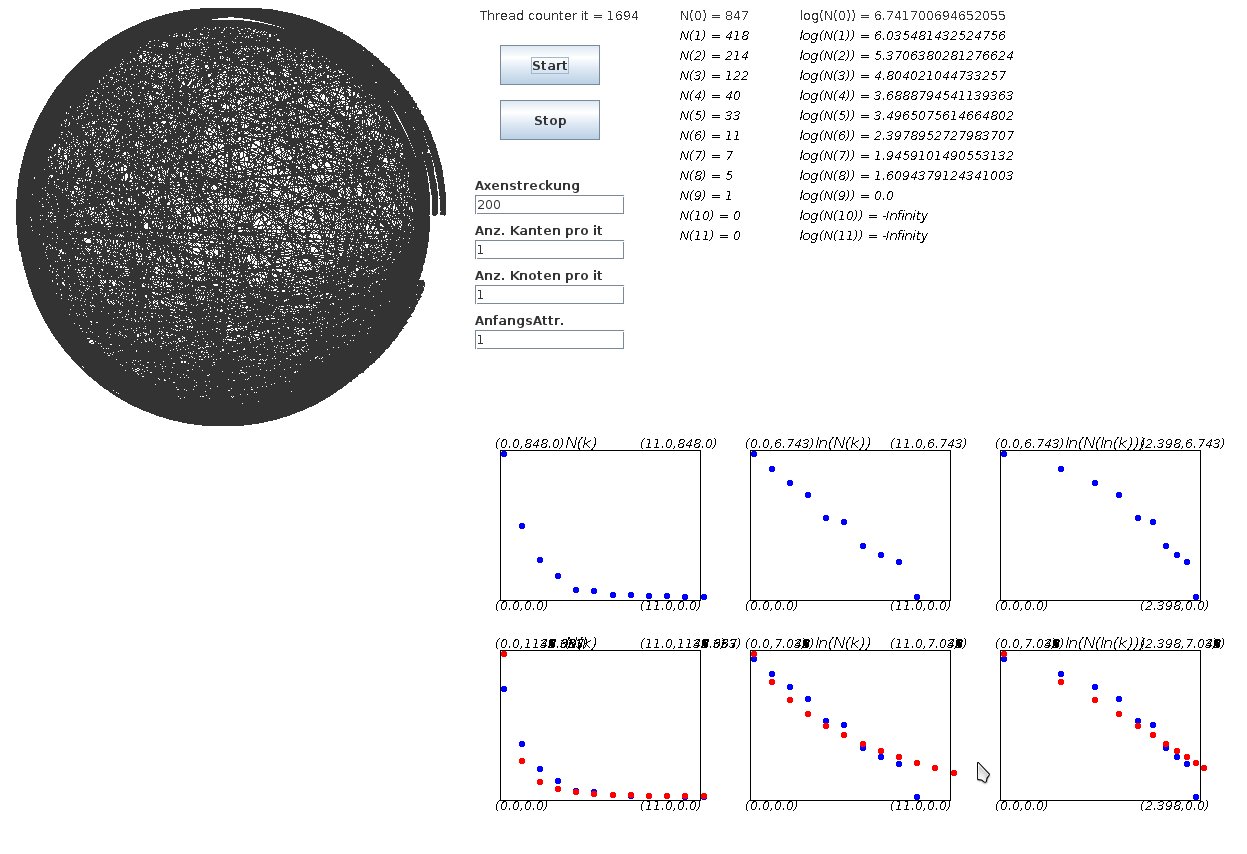
Im Folgenden soll ein Modell der Erzeugung eines skalenfreien Netzwerks beschrieben werden (das sogenannte erweiterte Barabasi-Albert Modell, siehe Dorogovtsev, Mendes, und Samukhin: Structure of Growing Networks: Exact Solution of the Barabasi--Albert's Model). In dem zugrundeliegenden Netzwerkmodell beschränkt man die Komplexität auf drei wesentliche Eigenschaften und lässt sowohl ein zeitliches Anwachsen der Anzahl der Netzwerkknoten, eine Anfangsattraktivität $A^{(0)}$, als auch ein bevorzugtes Anlagern (engl.: preferential attachment) der Netzwerkkanten an attraktivere Knoten zu. Dorogovtsev, Mendes, und Samukhin konnten in diesem Modell zeigen, dass die Verteilung der Anzahl der Verbindungen pro Knoten $P(k)$ analytisch angegeben werden kann. Der von ihnen beschrittene analytische Weg basiert auf dem folgendem Master equation-Ansatz der Verteilungsfunktion $p\left(k_i, i,t\right)$ des Verlinkungsgrades $k_i$ des Netzwerkknotens $i$ zurzeit $t$. \[ \begin{eqnarray} &&p\left(k_i, i,t+1\right) = \Pi\left(k_i,t\right) \, p\left(k_i, i,t\right) + \left[ 1 - \Pi\left(k_i,t\right) \right] \, p\left(k_i-1, i,t\right) +O\left( \frac p{t^2}\right) \nonumber \\ && \Pi\left(k_i,t\right) := \left[ 1-\frac{k_i+A^{(0)}}{\left( 1+\frac{A^{(0)}}{m}\right) t}\right] \, : \, \hbox{Verlinkungswahrscheinlichkeit}\nonumber \\ && m \, : \, \hbox{Anzahl der ausgehenden Verlinkungen pro Knoten} \nonumber \\ && k_i \, : \, \hbox{Anzahl der eingehenden Verlinkungen des Knotens i} \nonumber \\ && A_i:=k_i+A^{(0)} \, : \, \hbox{Attraktivität des Knotens i} \, \, .\label{Gl:1} \end{eqnarray} \] Die Lösung der Gleichung erfolgt mittels Z-Transformation: \[ \begin{equation} p(k_i,i,t)=\frac{\Gamma(k_i+A^{(0)})}{\Gamma(A^{(0)})\, k_i !} \left( \frac{i}{t} \right)^{\frac{A^{(0)}}{ 1+\frac{A^{(0)}}{m}}} \, \left[ 1- \left( \frac{i}{t} \right)^{\frac{1}{1+\frac{A^{(0)}}{m}}} \right]^{k_i} .\label{eq2} \end{equation} \] Für die stationäre Verteilungsfunktion $P(k)=P(k,t \rightarrow \infty)$ der eingehenden Verlinkungen ergibt sich schließlich: \[ \begin{eqnarray} P(k) &=& P(k,t \rightarrow \infty) \quad \mbox{, wobei } \quad P(k,t)=\frac{1}{t}\sum_{i=1}^{t}p(k_i,i,t) \nonumber\\ P(k) &=& \frac{(1+\frac{A^{(0)}}{m}) \, \Gamma(1+\frac{(m+1)\,A^{(0)}}{m}) \, \Gamma(k_i+A^{(0)})}{\Gamma(A^{(0)}) \, \Gamma(k_i+2+\frac{(m+1)\,A^{(0)}}{m})} \label{eq3} \end{eqnarray} \] Unter der Annahme $A^{(0)} + k >> 1$ folgt diese Verteilungsfunktion einem Potenzgesetz \[ \begin{equation} P(k) \approx \frac{(1+\frac{A^{(0)}}{m}) \, \Gamma(1+\frac{(m+1)\,A^{(0)}}{m})}{\Gamma(A^{(0)})} \, \left( k + A^{(0)} \right)^{-\left(2+ \frac{A^{(0)}}{m} \right)} \sim k^{- \gamma} \end{equation} \]
Die linke Abbildung zeigt eine Java-Applet Simulation eines skalenfreien Netzwerkes im erweiterten Barabasi-Albert Modell. Die Verteilungsfunktion der Knotengrade des simulierten Netzwerkes (blaue Punkte) sind zusammen mit der analytischen Verteilung in normaler Darstellung N(k) in logarithmischer Darstellung ln(N)(k) und in doppelt-logarithmischer ln(N)(ln(k)) Form dargestellt.
II.3 Mögliche Projekte im Teil II
Projekt III: Python Programm eines skalenfreien Netzwerkes
Erstellen Sie ein Python Programm das ein skalenfreies Netzwerk im Barabasi-Albert Modell erzeugt (siehe hierzu S:71-73 in http://barabasi.com/f/103.pdf und Section 5.2, Image 5.2 und Box 5.1: Albert-Laszlo Barabasi, Network Science). Vergleichen Sie die Verteilungsfunktion der Knotengrade des simulierten Netzwerkes mit der analytischen Verteilung und stellen beide im Vergleich dar. Lassen Sie sich zusätzlich noch weitere das Netzwerk charakterisierende Größen ausgeben (z.B. Clusterkoeffizient, Wert der durchschnittlichen kürzesten Verbindung zwischen den Knoten des Netzwerkes). Verwenden Sie z.B. als Vorlage das Python Skript VPSOC-Expontial-Network_evol.py.