Teil II.2 Einführung in die Theorie der komplexe Netzwerke
Viele in der Realität vorkommende evolutionäre Spiele werden auf einer definierten Netzwerkstruktur (Topologie) gespielt.
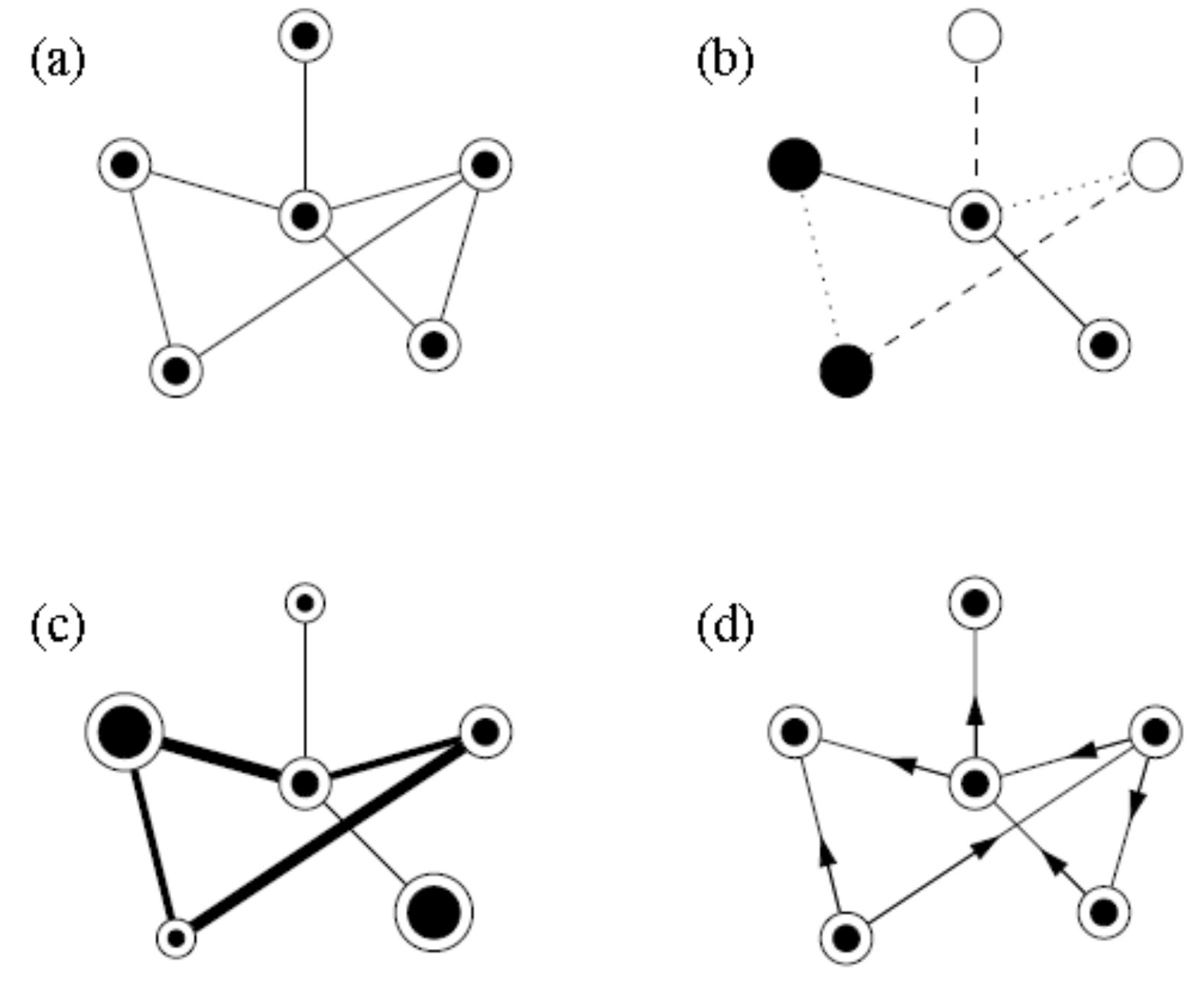
Unterschiedliche Netzwerktypen (credits M.E.J. Newman, The structure and function of complex networks .
Da die Theorie der komplexen Netzwerke aus dem mathematischen Zweig der Graphentheorie entstanden ist benutzt sie nicht die
- Handelt es sich nur um eine Knotenart (Spielergruppe), oder besteht das Netzwerk aus mehreren Knotenarten (z.B. Bi-Matrix Spiele).
- Sind die Kanten (Verbindungslinien zwischen den Knoten) gerichtet oder ungerichtet.
- Besitzen die Kanten zahlenmäßige Gewichtungen oder geben sie einfach an ob ein Knoten mit einem anderen verbunden oder nicht verbunden ist.
- Gibt es zeitliche Veränderungen des Netzwerks; ist die Anzahl der Knoten konstant oder wächst bzw. schrumpft sie im laufe der Zeit.
Die Abbildung auf der rechten Seite zeigt a) ein nicht gerichtetes und ungewichtetes Netzwerk einer einzigen Knotenart, b) ein nicht gerichtetes und ungewichtetes Netzwerk dreier verschiedener Knotenarten, wobei zusätzlich drei verschiedene Kantenarten existieren, c) ein nicht gerichtetes aber gewichtetes Netzwerk; sowohl die Knoten als auch die Kanten des Netzwerks besitzen zahlenmäßige Gewichtungen, d) ein gerichtetes aber nicht gewichtetes Netzwerk; es existiert nur eine Knoten- und gerichtete Kantenart.
- Der Knotengrad $k_i$
Der Knotengrad des Knotens $i$ ist gleich der Anzahl der Kanten die der Knoten $i$ besitzt. Bei gerichteten Netzwerken unterscheidet man zwischen dem eingehenden $k^{\rm in}_i$ und ausgehenden Knotengrad $k^{\rm out}_i$. Bei gewichteten Netzwerken summiert man über die Zahlenfaktoren der gewichteten Kanten. - Der durchschnittliche Knotengrad $ {<} k {>} $
Der durchschnittliche Knotengrad eines ungerichteten Netzwerks ${<} k {>}$ ist gegeben durch ${<} k {>}=\frac{1}{N} \sum_{i=1}^N k_i=\frac{2 L}{N}$, wobei $L=$ die gesamte Anzahl der Links (Kanten) des Netzwerks ist. - Die Nachbarschaftsmatrix (Adjazenzmatrix) $A_{ij}$
Die Nachbarschaftsmatrix des Netzwerkes beschreibt, welche Knoten des Graphen durch eine Kante verbunden sind. Zeigt eine Kante von Knoten j auf den Knoten i, dann ist der zugehörige Matrixwert $A_{ij}=1$, wohingegen ein Eintrag $A_{ij}=0$ bedeutet, dass keine Kante von j nach i zeigt. Bei ungerichteten Netwerken ist die Nachbarschaftsmatrix symmetrisch. Der Knotengrad $k_i$ des Knotens i (bzw. $k^{\rm in}_i$ und $k^{\rm out}_i$ bei gerichteten Graphen) lässt sich mittels der Nachbarschaftsmatrix wie folgt bestimmen: $k_i=\sum_{j=1}^N A_{ij}$ ($k^{\rm in}_i=\sum_{j=1}^N A_{ij}$ und $k^{\rm out}_i=\sum_{j=1}^N A_{ji}$ bei gerichteten Graphen), wobei die gesamte Anzahl der Kanten sich wie folgt bestimmen lässt: $L=\sum_{i,j=1}^N A_{ij}/2$ und die Größe $N$ die Anzahl der Knoten des Netzwerkes bezeichnet. In gewichteten Netztwerken sind die Einträge der Nachbarschaftsmatrix nicht mehr auf Null und Eins beschränkt $A_{ij}=w_{ij}$. - Die Verteilungsfunktion der Knotengrade $P(k)=N(k)/N$
Die Verteilungsfunktion der Knotengrade $P(k)$ (bzw. $N(k)$) ist eine wichtige das Netzwerk charakterisierende Größe. Sie gibt an, wie groß der Anteil an Netzwerkknoten mit Knotengrad k ist. Bei realen (endlichen) Netzwerken ist diese Funktion keine kontinuierliche, sondern eine diskrete Funktion $P(k)\approx P_k$. Bezeichnen wir mit $N_k$ die Anzahl der Knoten mit Knotengrad $k$, so gilt $P_k=\frac{N_k}{N}$. Es gilt $\sum_{k=0}^\infty P_k=1$ und der durchschnittliche Knotengrad berechnet sich wie folgt $ {<} k {>} = \sum_{k=0}^\infty k P_k$ . - Die maximale Anzahl möglicher Kanten $ L_{max} $
Die maximale Anzahl möglicher Kanten in einem ungerichteten Netzwerk (ein sogenannter 'complete graph') besitzt $ L_{max} =\frac{N (N-1)}{2} $ Kanten. Viele real existierende Netzwerke sind dünnbesetzt ($ L {<<} L_{max}$). - Die kürzeste Verbindungstrecke zwischen zwei Knoten $ d_{ij} $
Die Anzahl der Kanten die in einem Verbindungsweg von Knoten $i$ zum Knoten $j$ durchlaufen wird hängt vom gewähten Pfad ab. Die kürzeste Verbindungstrecke $ d_{ij} $ kann hierbei im allgemeinen auf unterschiedlichen Wegen realisiert sein, wobei der Pfad keine Schleifen enthalten darf und sich nicht kreuzen darf. Die Anzahl der kürzeste Verbindungswege $ N_{ij} $ lässt sich mittels der Nachbarschaftsmatrix berechnen. Existieren z.B. Verbindungswege vom Knoten $i$ zum Knoten $j$ mit $ d_{ij}=2 $, so muss die Anzahl der kürzeste Verbindungswege $ N_{ij} = {\sum_{l=1}^N A_{il} A_{jl}} \geq 1$ sein. - Der Clusterkoeffizient $C_i$ bzw. $C$
Der Clusterkoeffizient gibt die Wahrscheinlichkeit an, dass zwei nächste Nachbarn eines Knotens ebenfalls nächste Nachbarn untereinander sind. Für einen speziellen Knoten $i$ berechnet er sich mittels: $C_i=\frac{2L_i}{k_i(k_i-1)}$, wobei $L_i$ die Anzahl der Kanten darstellt, die die nächsten Nachbarn des Knoten i miteinander verbinden. Der globale Wert $C$ des Clusterkoeffizienten ist der Mittelwert aller $C_i$'s ($C = \frac{1}{N} \sum_{i=1}^N C_i \,$) und stellt demnach eine Art von der Enge der Nachbarschaftsbeziehungen des Netzwerks dar. - Durchnittliche Anzahl der $m$-nächsten Nachbarn $z_m$
$z_1$ stellt hierbei den Wert der mittleren Knotenzahl des Netzwerkes dar ($z_1=\left< k \right>$) und $z_2$ die mittlere Anzahl zweiter-nächster Nachbarn ($z_2=\left< k^2 \right>- \left< k \right>$, siehe z.B. Claudius Gros, "Complex and Adaptive Dynamical Systems, a Primer", S:18). - Durchmesser des Netzwerks $l$
Der Durchmesser des Netzwerks gibt die maximale kürzeste Kantenlänge zwischen zwei beliebigen Knoten des Netzwerkes an: $l={\rm log}(N/z_1)/{\rm log}(z_2/z_1)+1\quad$, wobei $N$ die Anzahl der Knoten des Netzwerkes darstellt (siehe z.B. Claudius Gros, "Complex and Adaptive Dynamical Systems, a Primer", S:20). Der Wert $l$ wird auch in einigen Lehrbüchern als $d_{\rm max}$ bezeichnet (siehe Albert-Laszlo Barabasi, Network science, Chapter 2 Graph Theory). - Größter verbundener Knotenclusters $N_G$ (Giant component, Hub)
Die Anzahl der Knoten im größten verbundenen Knotenclusters des Netzwerkes wird mit $N_G$ bezeichnet.
Aufgrund ihrer unterschiedlichen Eigenschaften unterscheidet man die folgenden Netzwerk-Klassen: