III.1.1 Spatial Games: Evolutionäre Spiele auf räumlichen Gitterstrukturen
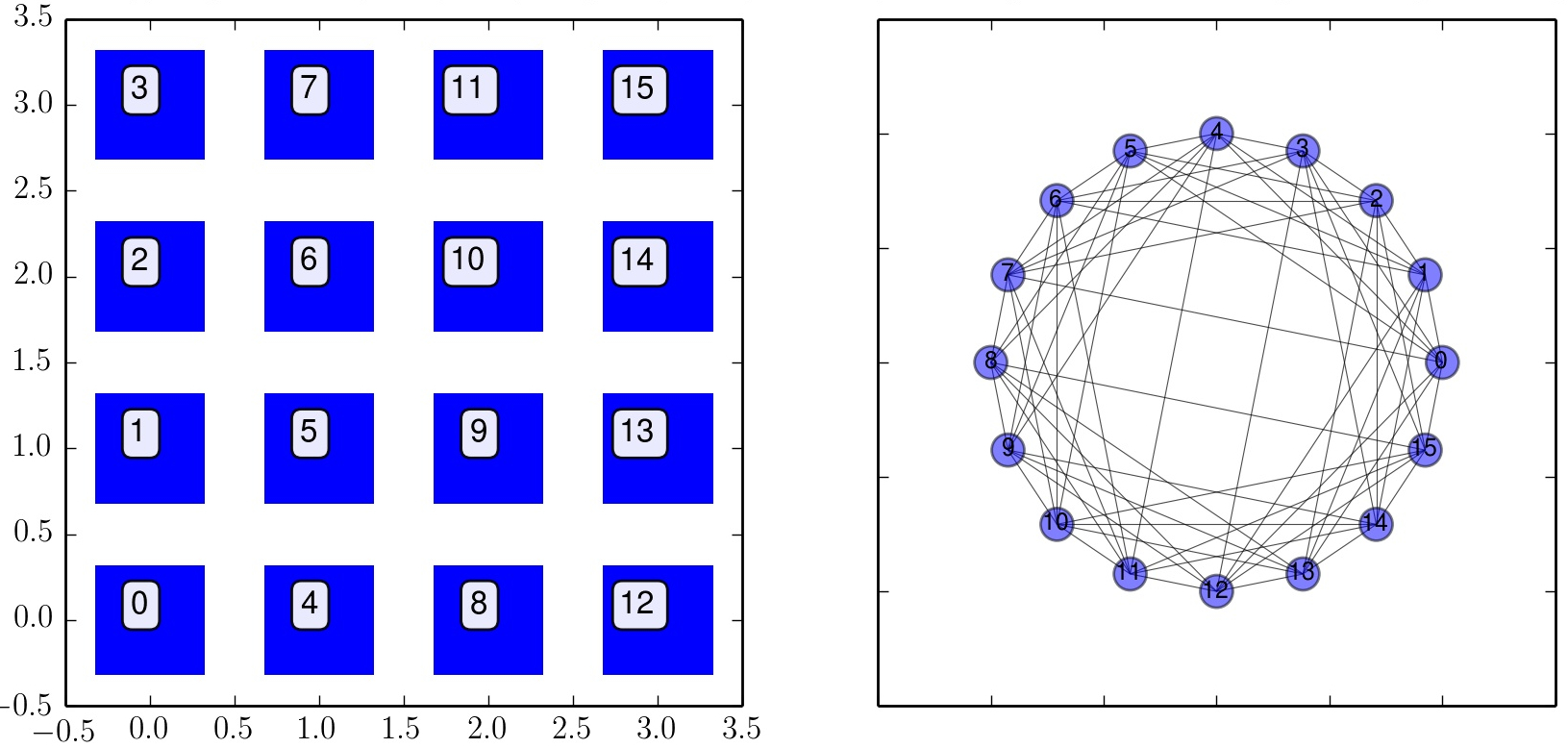
Anordung der 16 Spielerknoten auf einem 2-dimensionealen räumlichen Gitter (links) und das ensprechende Bild der erzeugten Netzwerkstruktur (rechts).
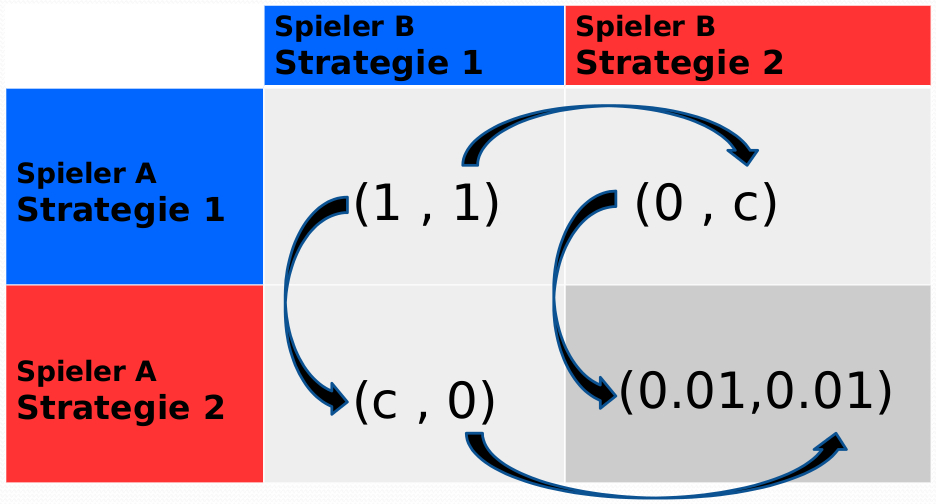
Ansatz eines allgemeinen (2 Personen)-(2 Strategien) Gefangenendilemma-Spiels mit symmetrischer Auszahlunsmatrix (a=1, b=0, c und d=0.01).
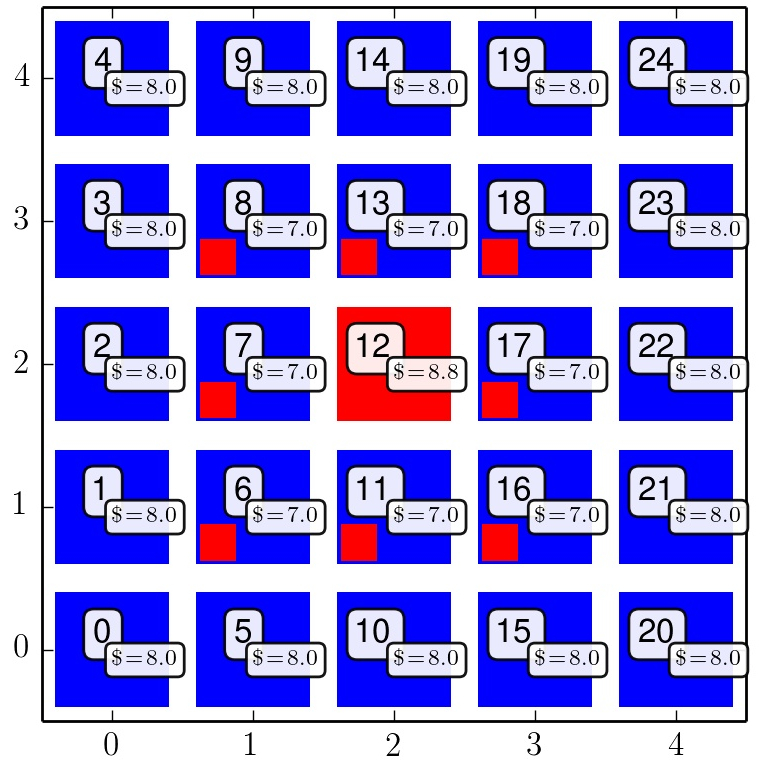
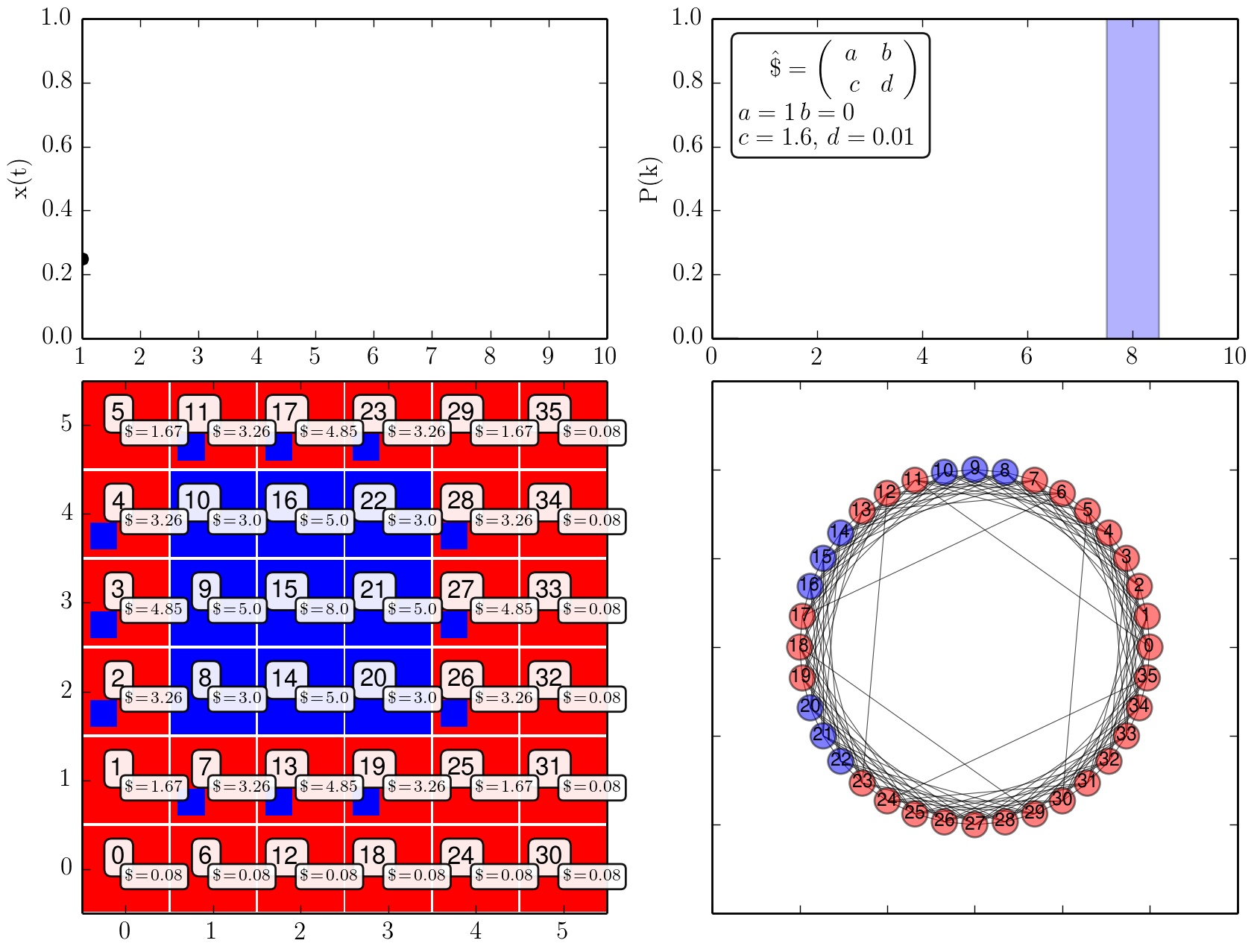
Anfangszustand der Strategienwahl der Spielerpopulation (c=1.1). Die eingezeichneten $\$$-Werte entspechen den in der ersten Spielperiode erzielten kumulierten Auszahlungswerten. Die kleinen Vierecke innerhalb der großen Vierecke geben die zukünftige Strategienwahl des Knotens in der nächsten Spielperiode an.
In diesem Unterpunkt werden die Spieler einer endlich großen Population auf einem räumlichen Gitter angeordnet, wobei jeder Spieler nur mit seinen nächsten Nachbarn spielen kann (Moore Nachbarschaft). Das zugrundeliegende Netzwerk der Spielerknoten besitzt somit eine reguläre Struktur und im betrachteten 2-dimensionalen Fall spielt jeder Spieler pro Spielperiode mit acht Spielern (Knotengrad $k_i=8\, \forall\, i \in {\cal I}$). Die Anordnung und Nummerierung der Spielerknoten auf dem 2-dimensionalen, sowie die entstehende Netzwerkstruktur ist in der nebenstehenden Abbildung für eine Population mit 16 Spielern dargestellt. Wir beschränken uns im folgenden auf symmetrische 2x2-Spiele (siehe Teil I.1.4: Ansatz eines allgemeinen (2 Personen)-(2 Strategien) Spiels mit symmetrischer Auszahlunsmatrix und Parametern a, b, c und d). Die Spielerknoten spielen pro Iteration mit jedem ihrer Nachbarn und am Ende von jedem Zeitschritt vergleichen die Spieler ihren summierten Gewinn/Verlust mit den Nachbarspielern ihres Umfeldes. Ist die Auszahlung eines Spielers höher als der eigene Auszahlungswert, so ändern der Spieler in der nächsten Spielperiode seine Strategie; ist sein eigener Wert der höchste, so bleibt er auch in der nächsten Iteration bei seiner gespielten Strategie.
Das folgende Beispiel ist dem Kapitel 9: Spatial Games des Buches Martin A. Nowak, Evolutionary Dynamics - Exploring the Equations of Life, 2006 entnommen. Wir nehmen im folgenden ein dominantes, symmetrisches 2x2-Spiel mit der nebenstehenden Auszahlungstabelle an. Es handelt sich bei diesem Spiel um eine Version des Gefangenendilemmas, wobei der Parameter $c>1$ die Stärke der Dominanz der Strategie $s_2\hat{=}$Rot über die Strategie $s_1\hat{=}$Blau quantifiziert (siehe Bestantwort-Pfeile in der nebenstehenden Auszahlungstabelle). In der linken Abbildung ist die Anfangskonfiguration der Strategienwahl der Spielerpopulation dargestellt. Zur Zeit t=1 nehmen wir an, dass nur ein Spieler die dominante rote Strategie spielt (Knoten 12) und alle anderen Spieler die blaue Strategienwahl. Nachdem die Spieler mit jedem Spielpartner ihres Umfeldes gespielt haben vergleichen sie ihre Auzahlungen und wählen die zukünftige Strategie (siehe linke Abbildung: kleinen Vierecke innerhalb der großen Vierecke). In Abhängigkeit des Parameters c können nun die folgenden zeitlichen Entwicklungen stattfinden: $\forall c<1.2$ entsteht in der nächsten Spielperiode ein Rechteck aus 9 roten Knoten welches aber dann schon in der dritten Spielperiode wieder in einen einzelnen roten Zentrumsknoten übergeht; $\forall 1.2 < c < 1.4$ entsteht in der nächsten Spielperiode wiederum ein Rechteck aus 9 roten Knoten, in der dritten Spielperiode entsteht ein rotes Kreuz das dann wiederum in den einzelnen roten Zentrumsknoten übergeht; $\forall 1.4 < c < 1.6$ bleibt das in der nächsten Spielperiode entstehende Rechteck aus 9 roten Knoten stabil; $\forall c>1.6$ dehnt sich der Bereich der roten Spieler immer weiter aus, wobei es zu einer dynamischen Fractalbildung, evolutionären Kaleidoskopen und kaotischen Verhalten kommen kann (siehe Animationen im unteren Bereich).
Platziert man jedoch einen einzelnen blauen Spiele (z.B. Knoten 12) in ein Umfeld von roten Spielern, so kann dieser sich nicht durchsetzen und verschwindet in der nächsten Spielperiode. Erst eine Anordnung von 9 blauen knoten kann sich durchsetzen, falls $\forall c < 8/3 \approx 2.667$ und es entstehen wiederum analytische bestimmbare Grenzbereiche des evolutionären Verhaltens des Populationsnetzwerkes in Abhängigkeit des Parameters c (siehe S:153 in Martin A. Nowak, Evolutionary Dynamics - Exploring the Equations of Life, 2006). Die nachfolgenden Abbildungen stellen mehrere mögliche Entwicklungen dar.

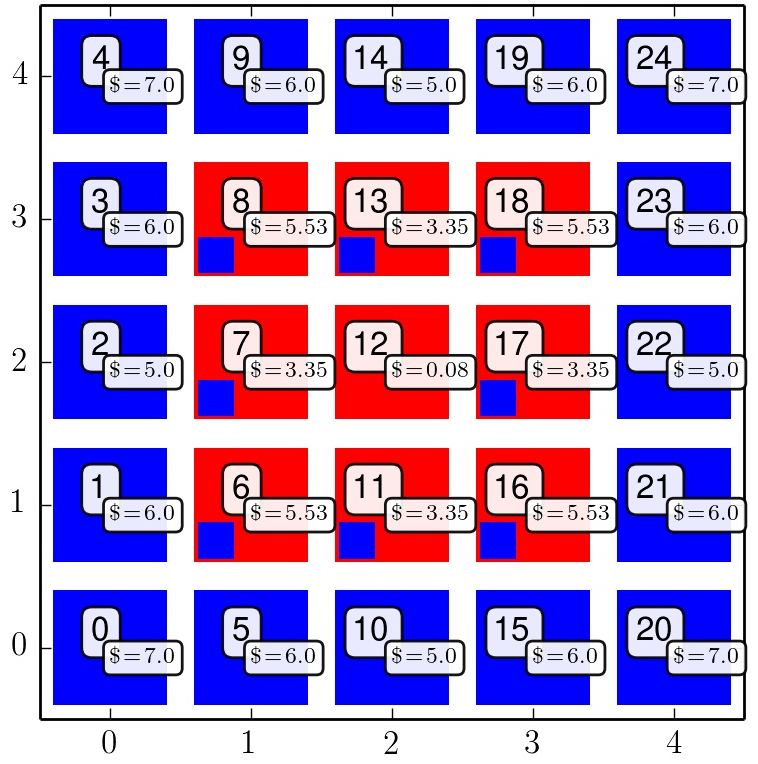

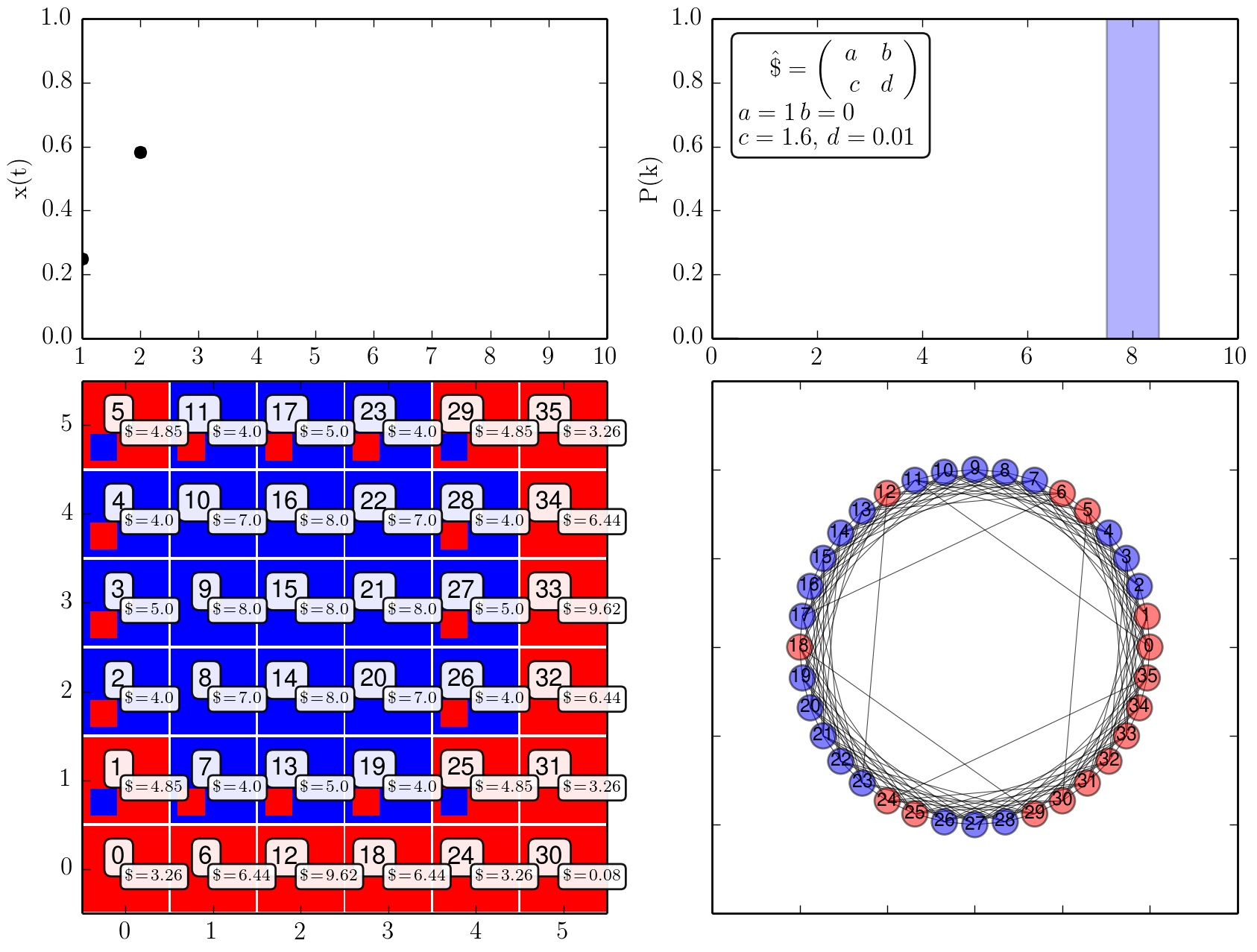
Zeitliche Entwicklung der Strategienwahl der Population (c=1.1). (Python Skript VPSOC7GamesonNetwork_F.py)
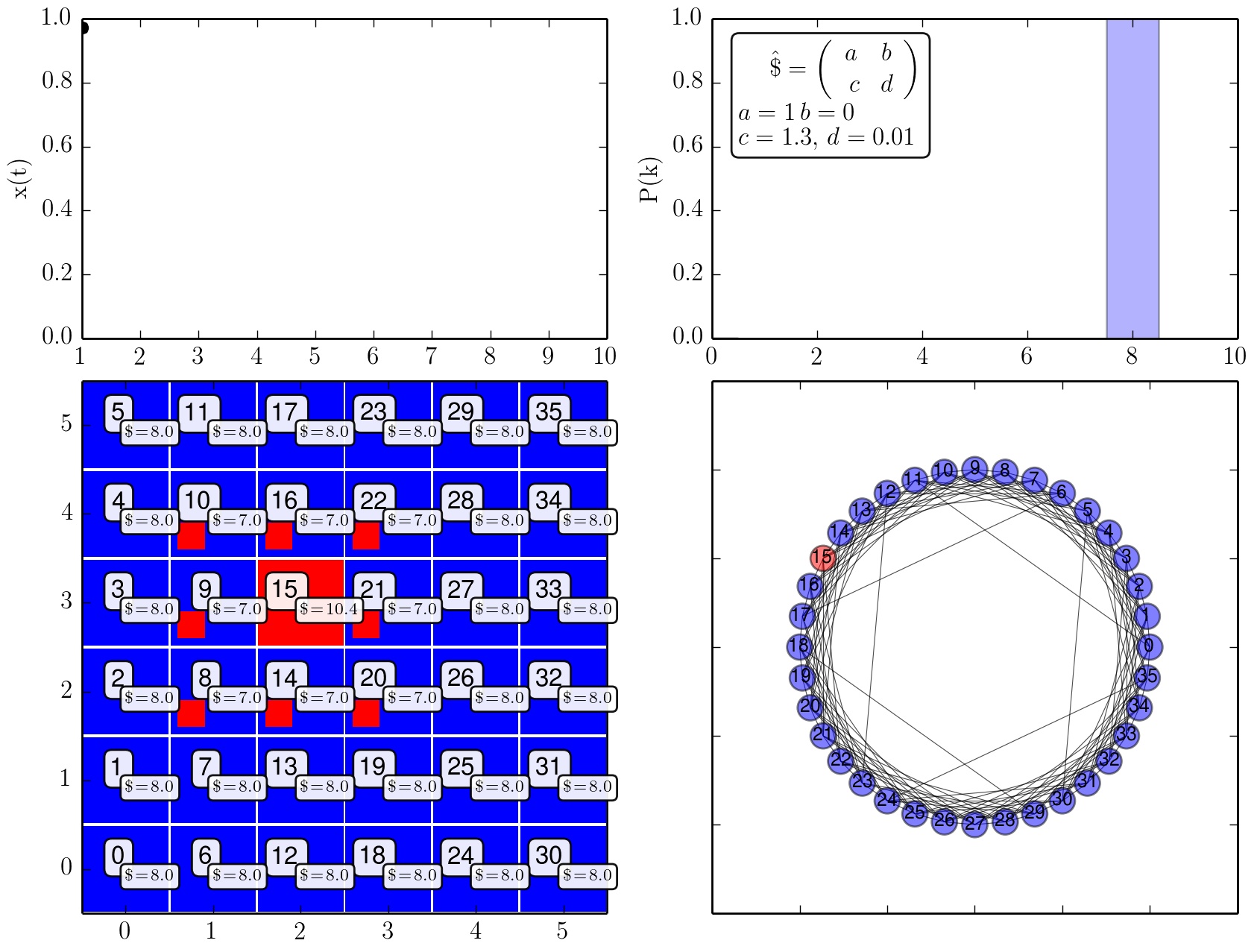
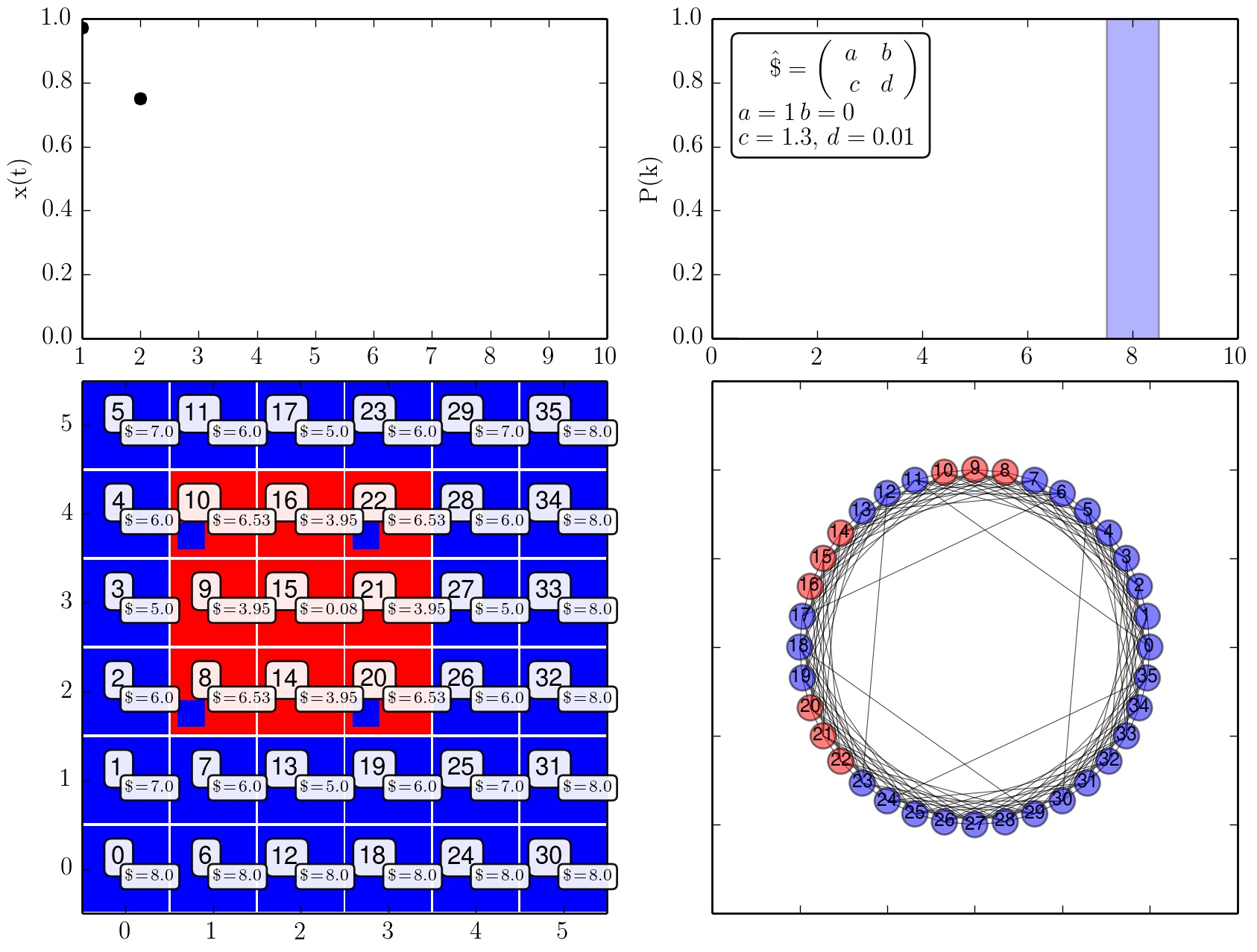
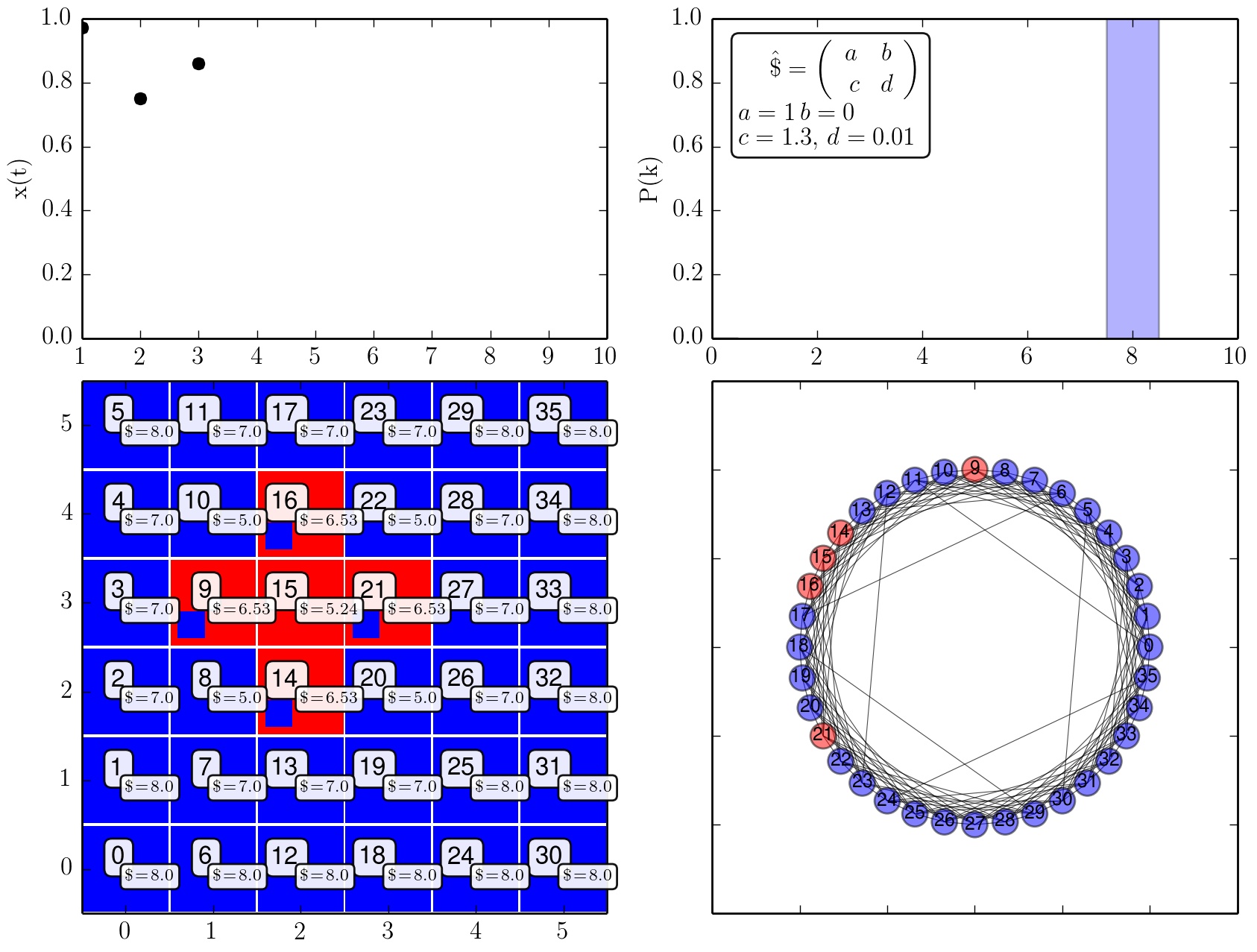
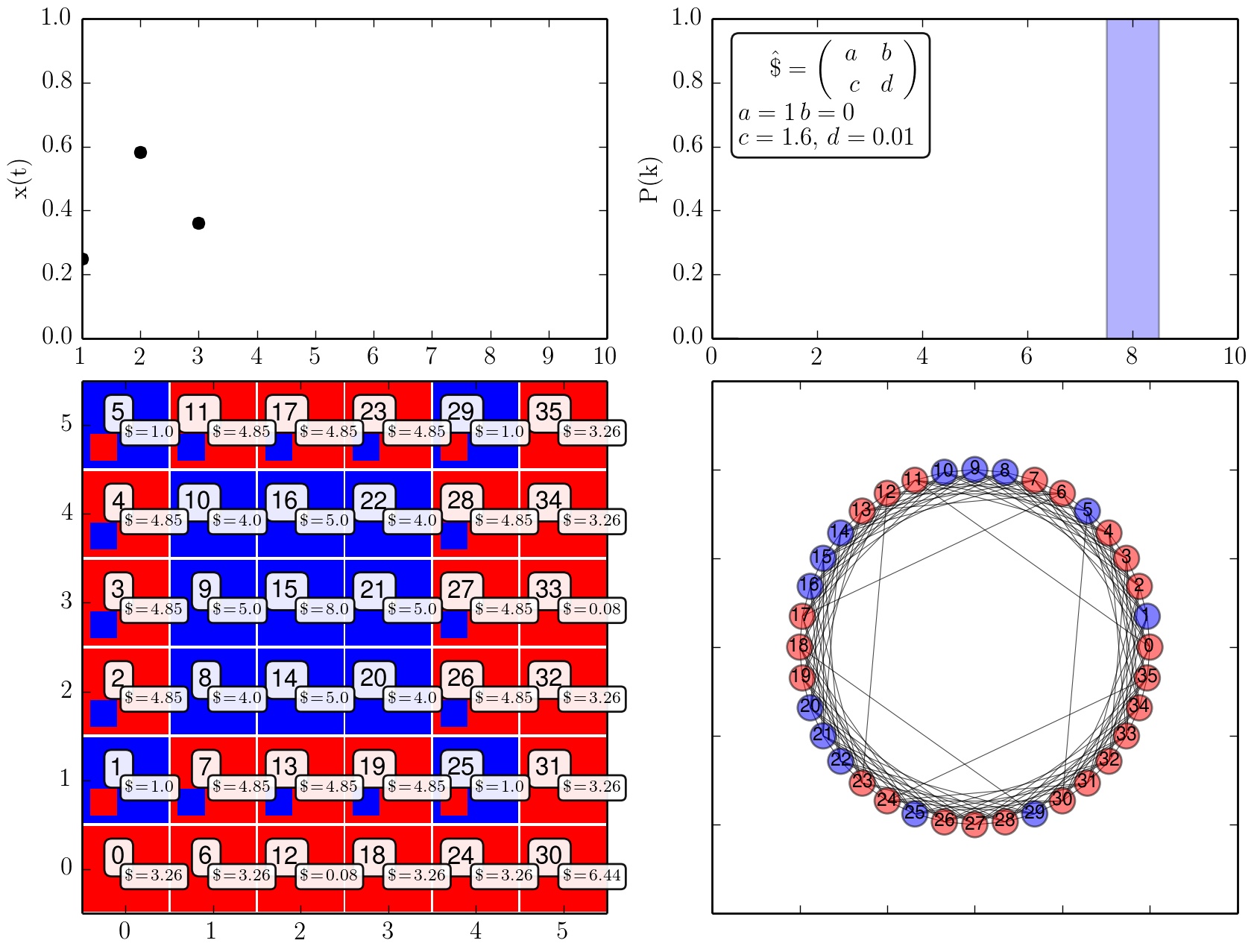
Zeitliche Entwicklung der Strategienwahl der Population (c=1.3).
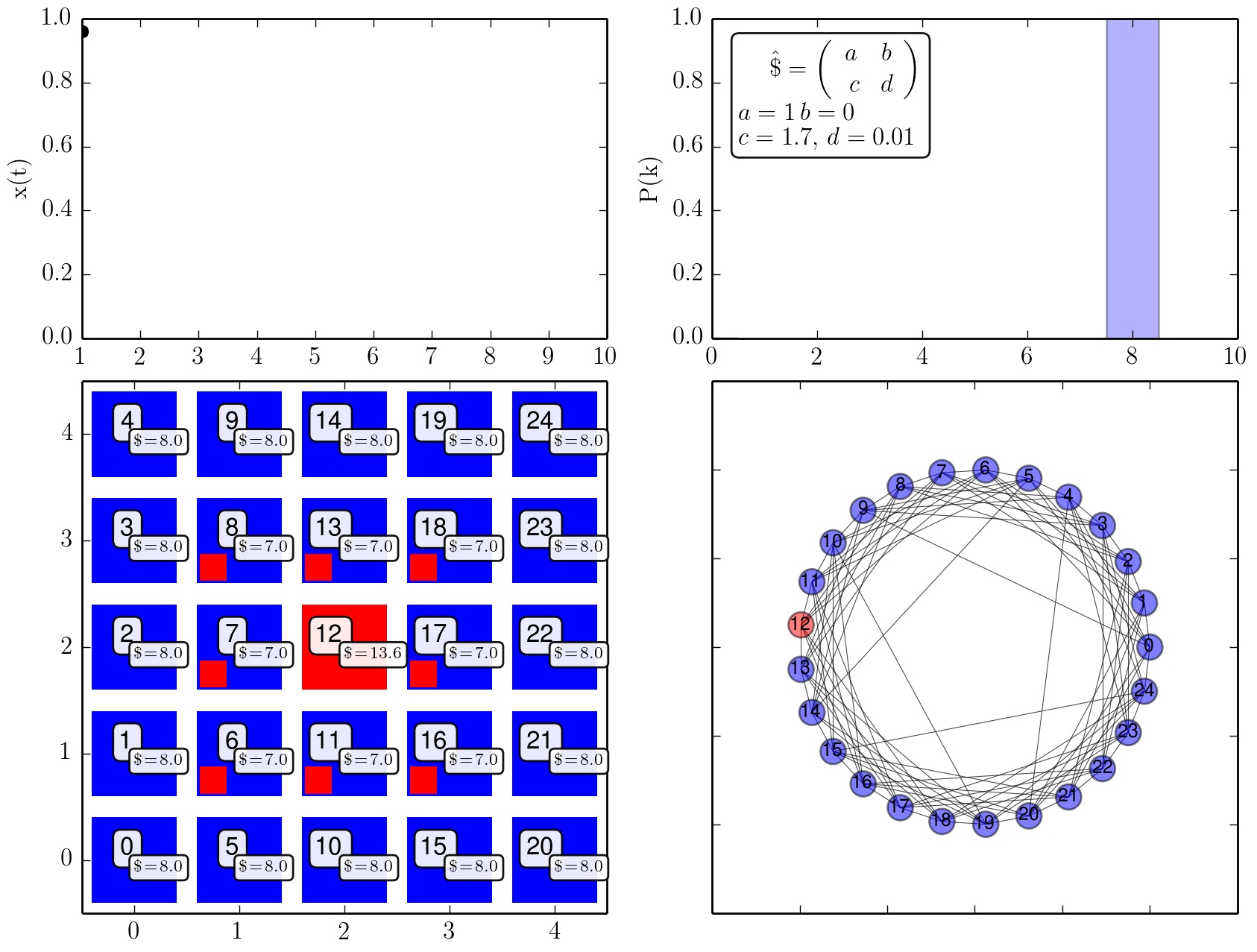
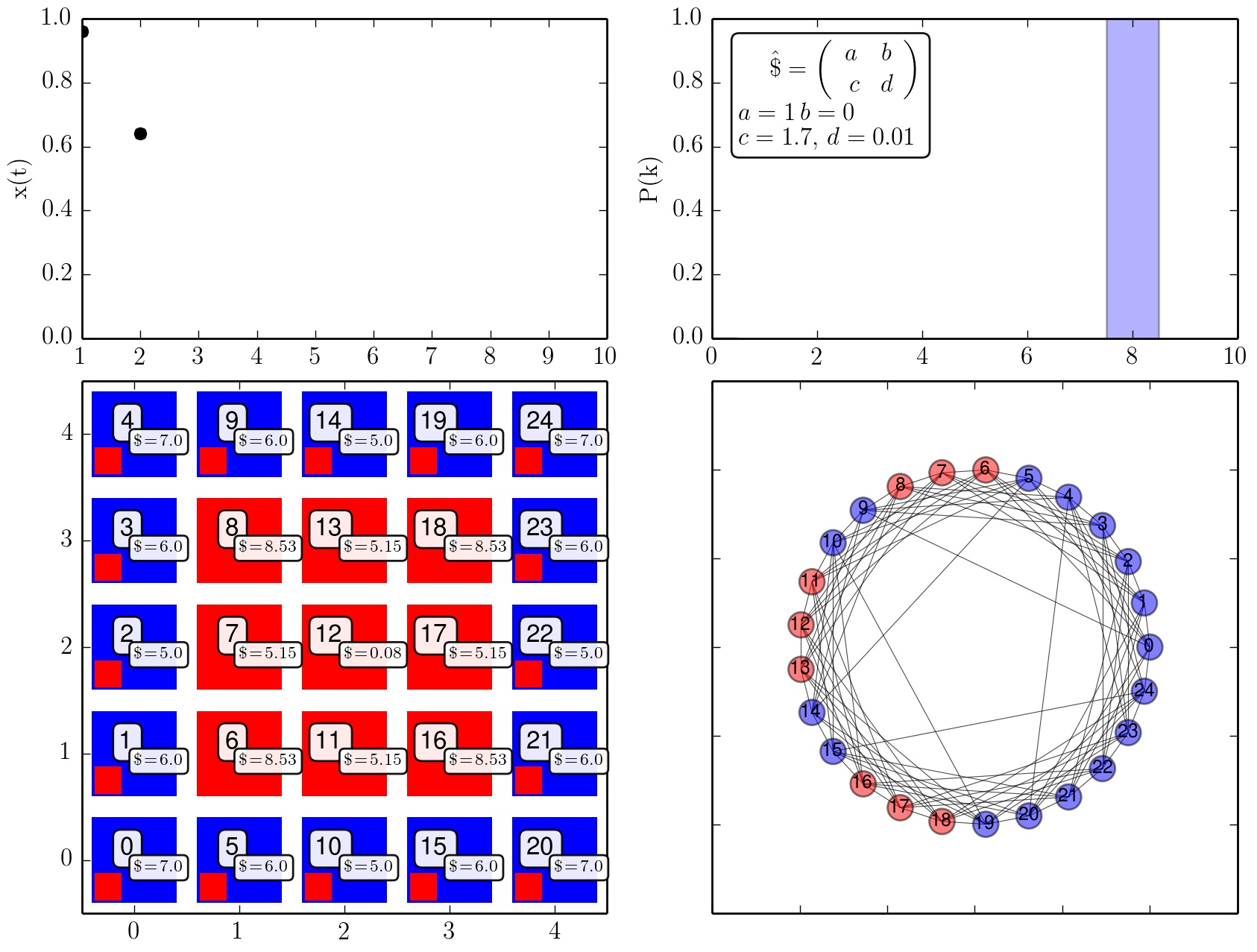
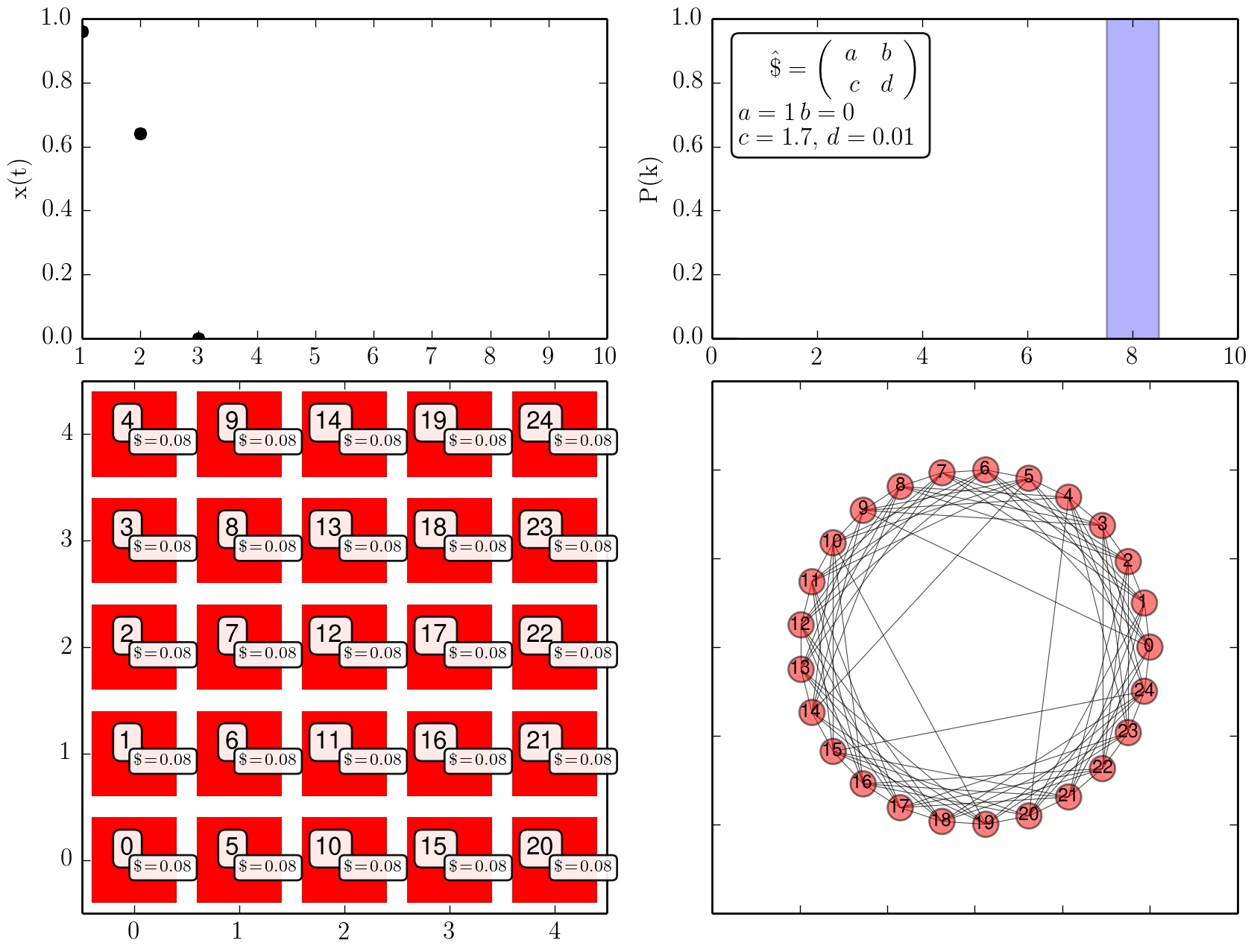
Zeitliche Entwicklung der Strategienwahl der Population (c=1.7).