Klassifizierung von symmetrischen (2 Personen)-(2 Strategien) Spielen

Ansatz eines allgemeinen (2 Personen)-(2 Strategien) Spiels mit symmetrischer Auszahlunsmatrix (a, b, c und d sind reelwertige Zahlen).
In diesem Unterkapitel werden die unterschiedlichen Spieltypen der gemischten Erweiterung eines simultanen (2 Spieler)-(2 Strategien) Spiels in strategischer Form mit symmetrischer Auszahlungmatrix klassifiziert. Die Einteilung lehnt sich an das Buch von Martin A. Nowak, Evolutionary Dynamics - Exploring the Equations of Life, 2006 (siehe Seite 49-51) an, . Eine alternative Klassifizierung findet man z.B. auch in Matthias Hanauske, Evolutionäre Quanten-Spieltheorie im Kontext sozio-ökonomischer Systeme, 2011. Ausgangspunkt ist die neben stehende allgemeine symmetrische Auszahlunsmatrix eines (2 Personen)-(2 Strategien) Spiels (a, b, c und d sind reelwertige Zahlen). Da es sich um eine symmetrische Auszahlungmatrix handelt gilt: $\hat{\bf {\cal \$}}^B = \left( \hat{\bf {\cal \$}}^A \right)^{\!T}$. Abhängig von den gewählten Parametern der Auszahlunsmatrix lassen sich symmetrische ($2 \times 2$) Spiele in drei unterschiedliche Spielklassen gliedern: Dominante Spiele, Koordinationsspiele und Anti-Koordinationsspiele.
Die Klasse der dominanten Spiele ( a > c und b > d bzw. a < c und b < d )
Bei dieser Spielklasse dominiert eine Strategie die andere. Es existiert nur ein reines Nash-Gleichgewicht welches die dominante Strategie des Spiels darstellt. Dieser Fall tritt ein, falls:
a > c und b > d : Strategie 1 dominiert Strategie 2; dominante Strategie bei (x,y)=(1,1).
a < c und b < d : Strategie 2 dominiert Strategie 1; dominante Strategie bei (x,y)=(0,0).
Koordinationsspiele ( a > c und b < d )
Ein Koordinationsspiel existiert, falls die Parameter a, b, c und d der Auszahlungmatrix die folgenden Bedingungen erfüllen: a > c und b < d . Bei dieser Spielklasse existieren drei Nash-Gleichgewichte, ein gemischtes Nash-Gleichgewicht und zwei reine, symmetrische Nash-Gleichgewicht bei (x,y)=(0,0) und (x,y)=(1,1).
Anti-Koordinationsspiele ( a < c und b > d )
Ein Anti-Koordinationsspiel existiert, falls die Parameter a, b, c und d der Auszahlungmatrix die folgenden Bedingungen erfüllen: a < c und b > d . Bei dieser Spielklasse existieren drei Nash-Gleichgewichte, ein gemischtes Nash-Gleichgewicht und zwei reine, unsymmetrische Nash-Gleichgewicht bei (x,y)=(0,1) und (x,y)=(0,1).
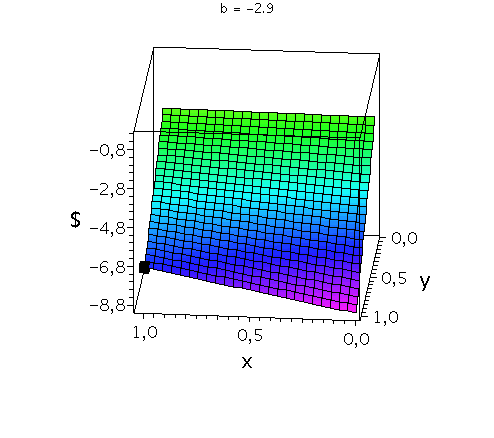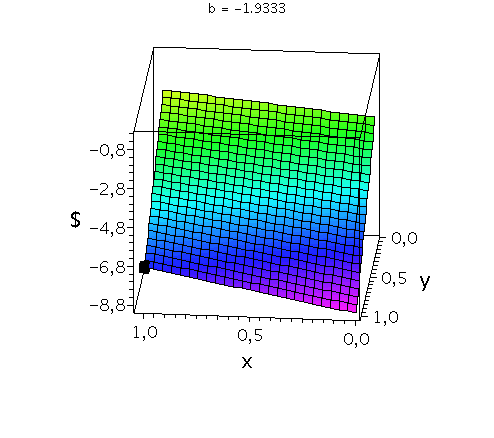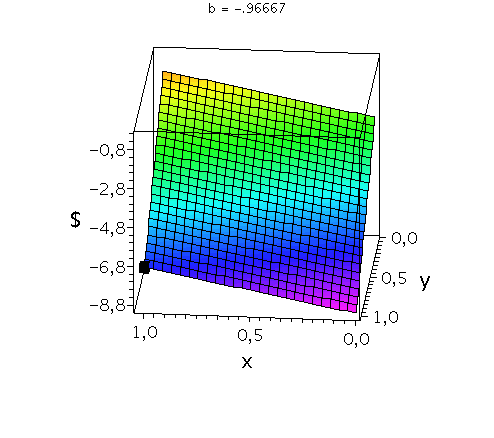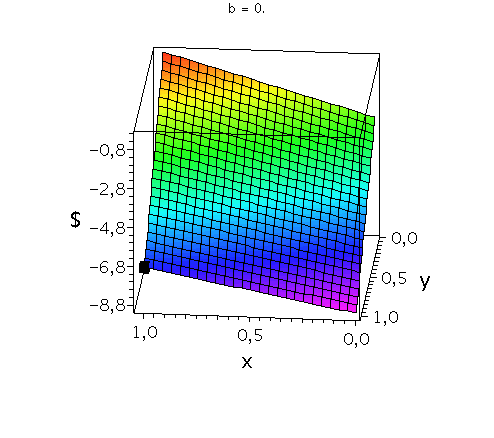
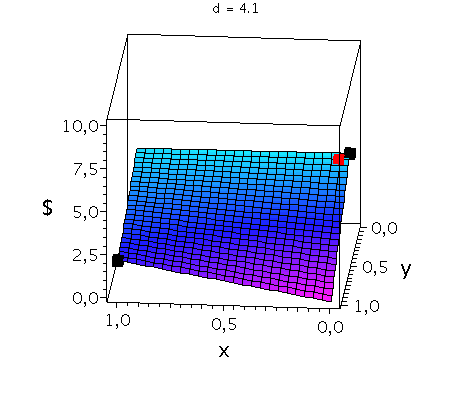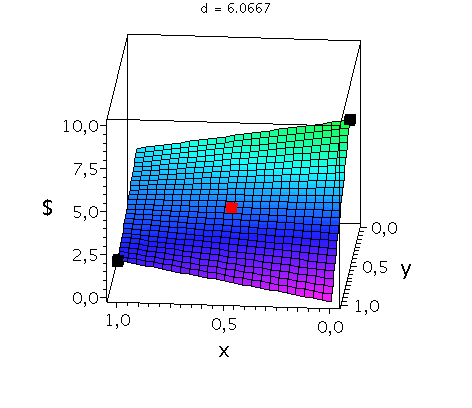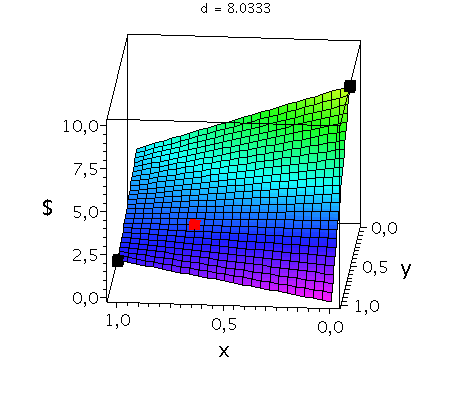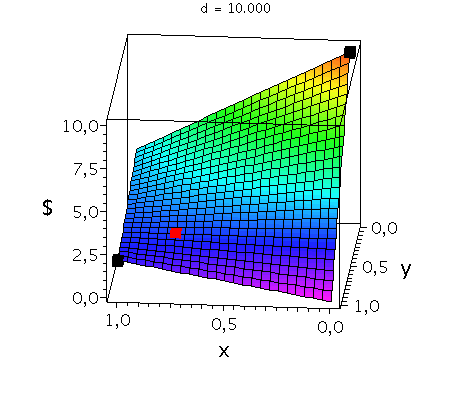
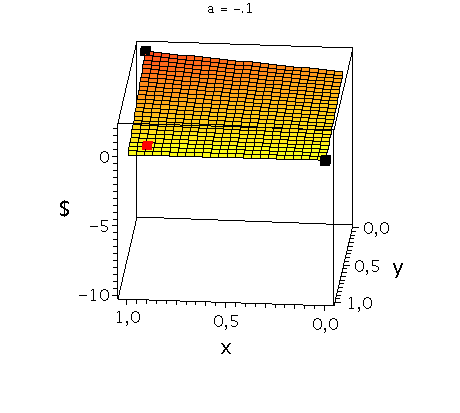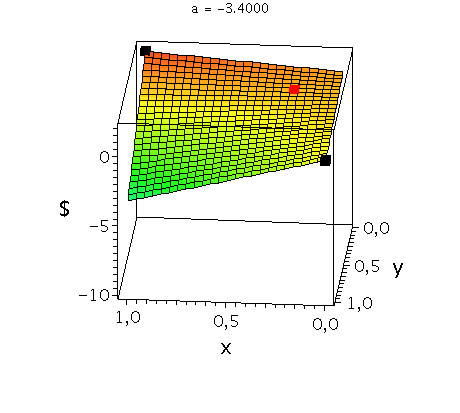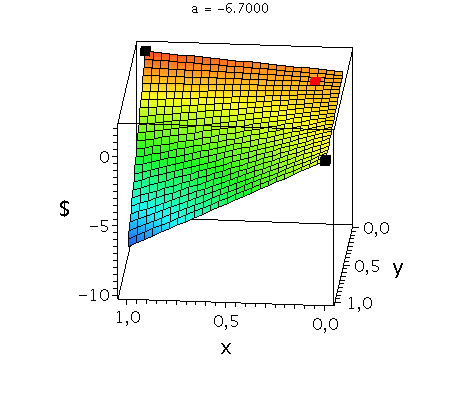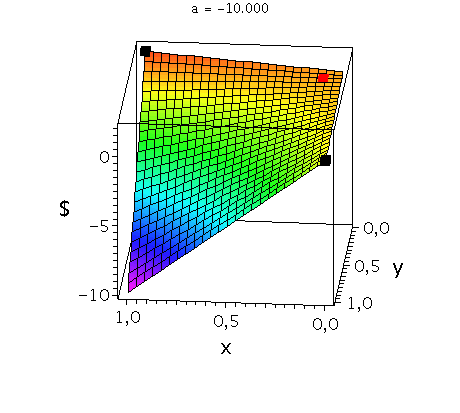
In der unteren Abbildung werden die drei möglichen Spielklassen mittels der gemischten Auszahlungsfunktion des Spielers A verdeutlicht.
Anhand der Struktur der Auszahlungsfläche in der linken Abbildung kann man z.B. die Eigenschaften der dominanten Strategie im Gefangenendilemma verdeutlichen. Die Parameter der Auszahlungsmatrix wurden hierbei auf die folgenden Werte festgelegt a=-7, c=-9 und d=-3, wobei der Parameter b in der linken Animation von -2.9 bis 0 variiert wird. Die Frage lautet: Unter der Annahme das Spieler B eine feste gemischte Strategie y spielt, welche Strategie x sollte Spieler A wählen, so dass er seine Auszahlung maximiert? Nehmen wir an, dass Spieler B die reine Strategie y=0 spielen würde, dann wäre es das Beste für Spieler A die reine Strategie x=1 zu spielen. Nehmen wir dagegen an, dass Spieler B die reine Strategie y=1 spielen würde, dann wäre es das Beste für Spieler A ebenfalls die reine Strategie x=1 zu spielen. Unanbhängig von der Wahl der Startegie des Spielers B, ist Spieler A immer veranlasst die Strategie x=1 zu spielen; (x,y)=(1,1) ist somit die dominante Strategie und das einzige Nash-Gleichgewicht im Gefangenendilemma (siehe schwarzes Rechteck in der linken Animation).
In der mittleren Animation wird die gemischte Auszahlungsfunktion des Spielers A im Hirschjagt-Spiel (Koordinationsspiel: a=2, b=4 und c=0) bei Variation des Parameters d im Bereich 4.1 bis 10 gezeigt. Man erkennt gut, wie sich die Position des gemischten Nash-Gleichgewichts verschiebt (siehe rotes Rechteck), wobei zusützlich die beiden reinen, symmetrischen Nash-Gleichgewichte bei (x,y)=(0,0) und (x,y)=(1,1) bestehen bleiben (siehe schwarze Rechtecke in der mittleren Animation).
In der rechten Animation wird die gemischte Auszahlungsfunktion des Spielers A im Angsthasen-Spiel (Anti-Koordinationsspiel: b=2, c=0, d=1) bei Variation des Parameters a im Bereich -0.1 bis -10 gezeigt. Man erkennt gut, wie sich die Position des gemischten Nash-Gleichgewichts verschiebt (siehe rotes Rechteck), wobei zusätzlich die beiden reinen, unsymmetrischen Nash-Gleichgewichte bei (x,y)=(1,0) und (x,y)=(0,1) bestehen bleiben (siehe schwarze Rechtecke in der rechten Animation).
Die Animationen wurden mit Maple gemacht; das zugehörige Maple-Worksheet finden Sie unter dem folgenden Link: (Klassifizierung von symmetrischen (2 Personen)-(2 Strategien) Spielen: Dominante Spiele, Koordinationsspiele und Anti-Koordinantionsspiele
).