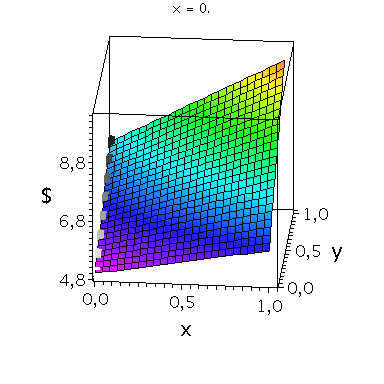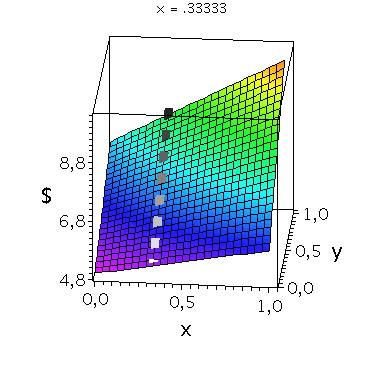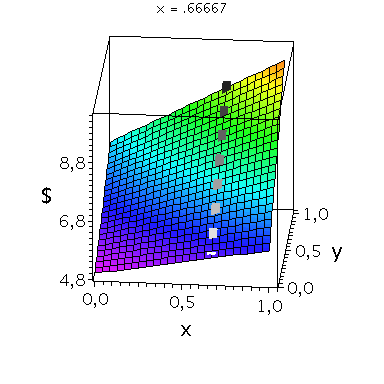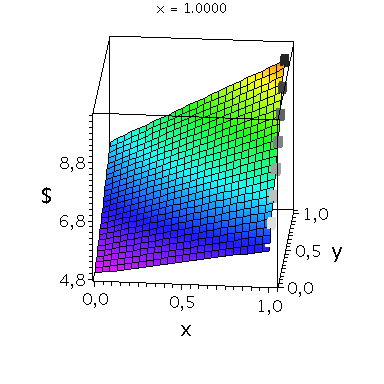Einführung 

In diesem Maple-Worksheet werden die unterschiedlichen Spieltypen der gemischten Erweiterung eines simultanen (2 Spieler)-(2 Strategien) Spiels in strategischer Form mit symmetrischer Auszahlungmatrix klassifiziert. Die Einteilung lehnt sich an das Buch von  Martin A. Nowak, Evolutionary Dynamics - Exploring the Equations of Life, 2006  (siehe Seite 49-51) an. Eine alternative Klassifizierung findet man z.B. auch in Matthias Hanauske, Evolutionäre Quanten-Spieltheorie im Kontext sozio-ökonomischer Systeme, 2011. 

Ausgangspunkt ist die folgende allgemeine symmetrische Auszahlunsmatrix eines (2 Personen)-(2 Strategien) Spiels (a, b, c und d sind reelwertige Zahlen):  

>	restart: with(plots): with(plottools): with(LinearAlgebra): with(ColorTools):

 

Definition der Auszahlunsmatrix für Spieler A: 

>	D_A11:=a: D_A12:=b: D_A21:=c: D_A22:=d: D_A:=Matrix(2,2,[D_A11,D_A12,D_A21,D_A22]);

 

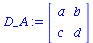(1.1)

 

Da sich das Spiel um ein symmetrisches (2 Personen)-(2 Strategien) Spiel handelt, erhält man die Auszahlunsmatrix für Spieler B durch die transponierte Matrix des Spielers A:  

>	D_B:=Transpose(D_A);

 

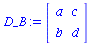(1.2)

 

Unter Verwendung der gemischten Strategien (x,y) lässt sich eine gemischte Auszahlungsfunktion der Spieler wie folgt definieren: 

>	Auszahlungsfunktion_A:=(x,y)->D_A[1,1]*x*y+D_A[1,2]*x*(1-y)+D_A[2,1]*(1-x)*y+D_A[2,2]*(1-x)*(1-y); Auszahlungsfunktion_B:=(x,y)->D_B[1,1]*x*y+D_B[1,2]*x*(1-y)+D_B[2,1]*(1-x)*y+D_B[2,2]*(1-x)*(1-y);

 

 

	(1.3)

 

Die Klasse der dominanten Spiele 

Bei dieser Spielklasse dominiert eine Strategie die andere. Es existiert nur ein reines Nash-Gleichgewicht welches die dominante Strategie des Spiels darstellt. Dieser Fall tritt ein, falls: 

• a > c und b > d : Strategie 1 dominiert Strategie 2; dominante Strategie bei (x,y)=(1,1).

• a < c und b < d : Strategie 2 dominiert Strategie 1; dominante Strategie bei (x,y)=(0,0).

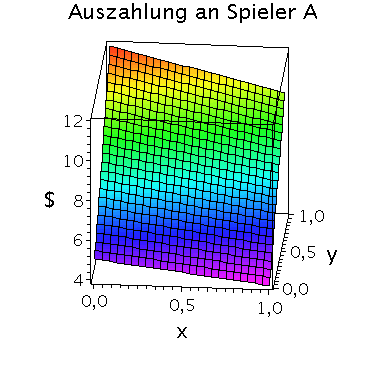
Beispiel: a > c und b > d; Strategie 1 dominiert Strategie 2; dominante Strategie bei (x,y)=(1,1) 

>	a:=10: b:=6: c:=7: d:=5:

 

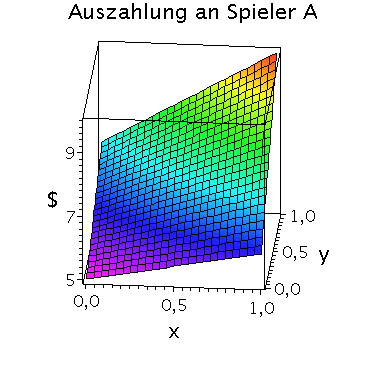
Die gemischte Auszahlungsfunktion des Spielers A besitzt im oben definierten dominanten Spiel das folgende Aussehen: 

>	plot3d(Auszahlungsfunktion_A(x,y),x=0..1,y=0..1,axes=boxed,labels=[x,"y","$"],orientation=[275,65],title="Auszahlung an Spieler A",shading=ZHUE,axesfont=[HELVETICA,13],font=[HELVETICA,15],titlefont=[HELVETICA,16]);

 

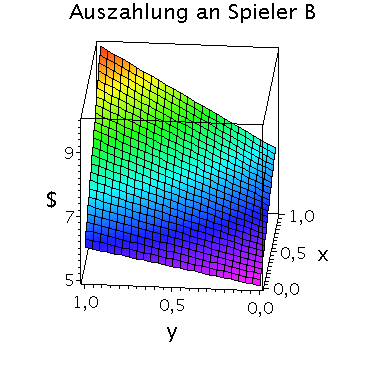
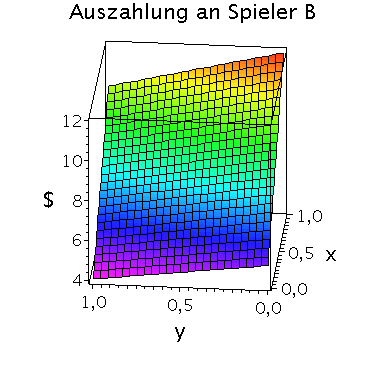
Die gemischte Auszahlungsfunktion des Spielers B sieht wie folgt aus: 

>	plot3d(Auszahlungsfunktion_B(x,y),x=0..1,y=0..1,axes=boxed,labels=[x,"y","$"],orientation=[185,65],title="Auszahlung an Spieler B",shading=ZHUE,axesfont=[HELVETICA,13],font=[HELVETICA,15],titlefont=[HELVETICA,16]);

 

Der Spezialfall des gemischten Nash-Gleichgewichts besteht, falls die partielle Ableitung der gemischten Auszahlungsfläche verschwindet, also 

>	EqGemNashy:=diff(Auszahlungsfunktion_A(x,y),x)=0; EqGemNashx:=diff(Auszahlungsfunktion_B(x,y),y)=0;

 

 

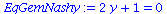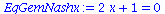	(2.1)

 

Da diese Gleichung keine sinnvolle Lösung besitzt (nur negative gemischte Strategien) existiert in einem dominanten Spiel kein gemischtes Nash-Gleichgewicht. 

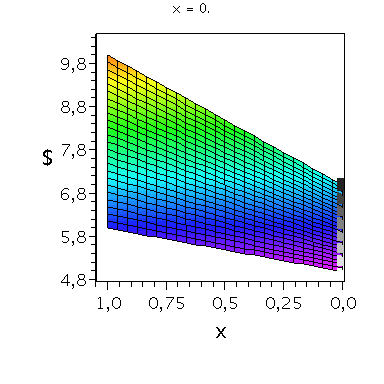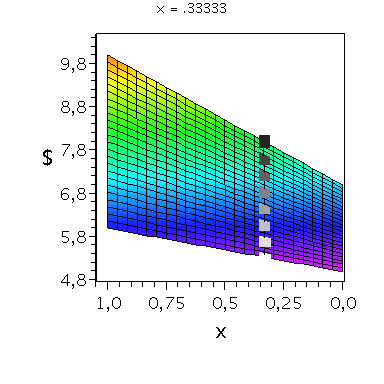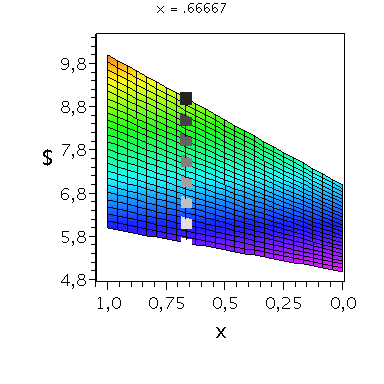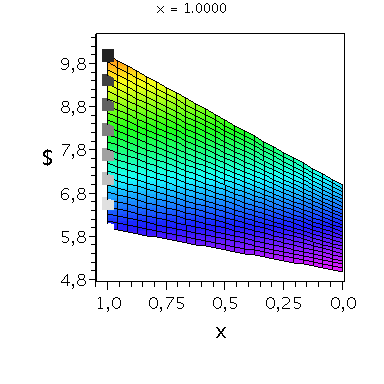
Wir konzentrieren uns zunächst auf die gemischte Auszahlungsfunktion des Spielers A und werden anhand der Struktur der Auszahlungsflächen die Eigenschaften der dominanten Strategie im Spiel verdeutlichen. Die Frage lautet: Unter der Annahme das Spieler B eine feste gemischte Strategie y spielt, welche Strategie x sollte Spieler A wählen, so dass er seine Auszahlung maximiert?  

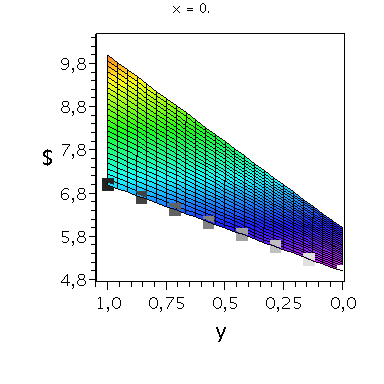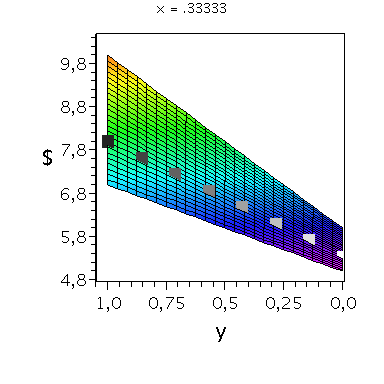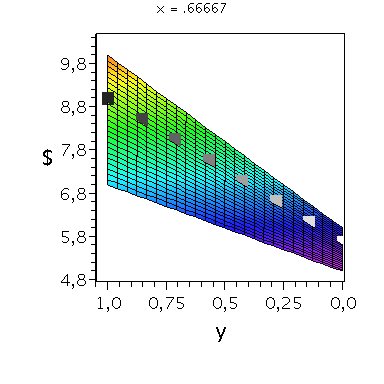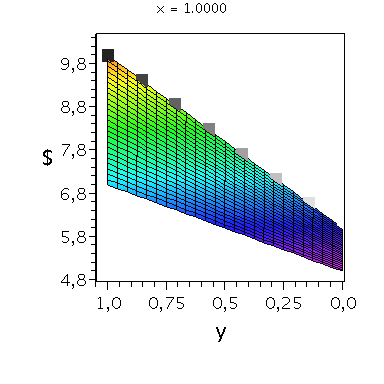
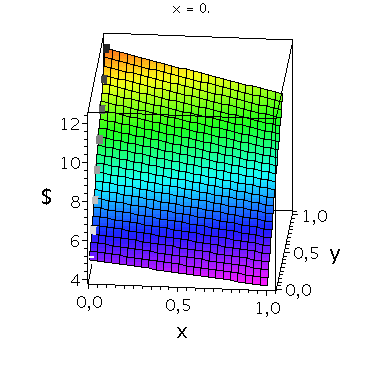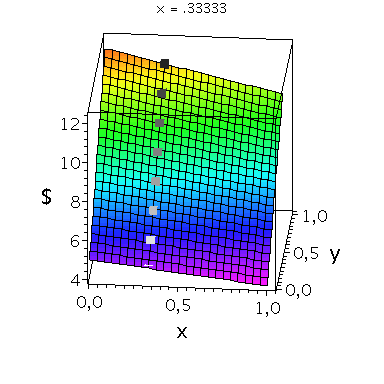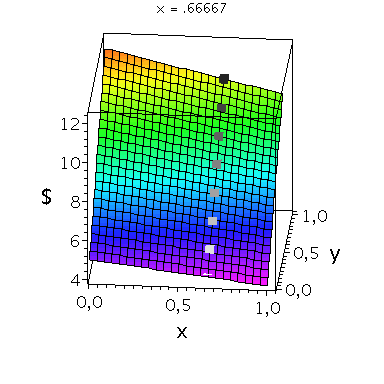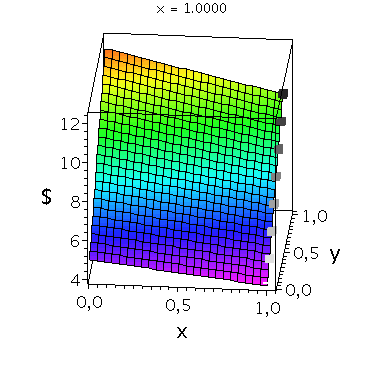
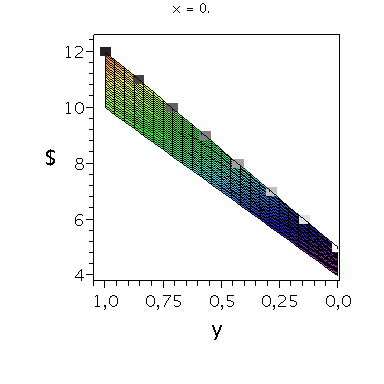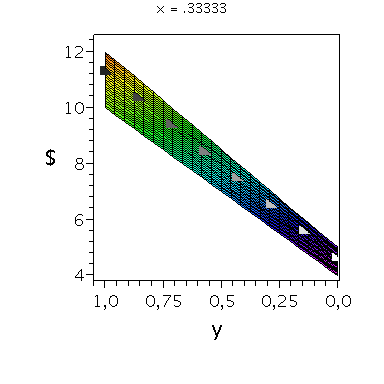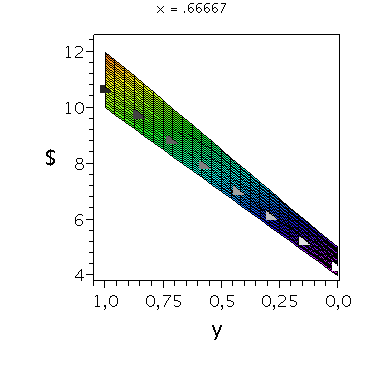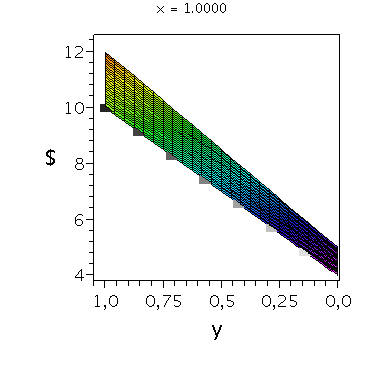
Nehmen wir an, dass Spieler B die reine Strategie y=0 spielen würde, dann wäre es das Beste für Spieler A die reine Strategie x=1 zu spielen (siehe weißes Rechteck in der folgenden Abbildung). 

Nehmen wir dagegen an, dass Spieler B die reine Strategie y=1 spielen würde, dann wäre es das Beste für Spieler A ebenfalls die reine Strategie x=1 zu spielen (siehe schwarzes Rechteck in der folgenden Abbildung). Unanbhängig von der Wahl der Startegie des Spielers B, ist Spieler A immer veranlasst die Strategie x=1 zu spielen (siehe graue Rechtecke in der folgenden Abbildung); (x,y)=(1,1) ist somit die dominante Strategie und das einzige Nash-Gleichgewicht im dominanten Spiel. 

>

PDollarA:=plot3d(Auszahlungsfunktion_A(x,y),x=0..1,y=0..1,axes=boxed,labels=[x,"y","$"],title="Auszahlung an Spieler A",shading=ZHUE,axesfont=[HELVETICA,13],font=[HELVETICA,15],titlefont=[HELVETICA,16]): MinDollar:=5: MaxDollar:=10: Sizecuboid:=0.05: Sizecuboidz:=0.3: anzy:=7: for sety from 0 by 1 to anzy do Ani[sety]:=animate(plots[display], [cuboid([-Sizecuboid/2+x, -Sizecuboid/2+sety/anzy, Auszahlungsfunktion_A(x,sety/anzy)-Sizecuboidz/2], [Sizecuboid/2+x, Sizecuboid/2+sety/anzy, Auszahlungsfunktion_A(x,sety/anzy)+Sizecuboidz/2])], x = 0 .. 1,scaling=constrained, style = patchnogrid,color=RGBToColor([255-round(sety/anzy*220), 255-round(sety/anzy*220), 255-round(sety/anzy*220)])): od: display(PDollarA,seq(Ani[i],i=0..anzy),scaling=unconstrained,view=[-0.01..1.05, -0.01..1.05,0.95*MinDollar..1.05*MaxDollar],orientation=[275,65]); display(PDollarA,seq(Ani[i],i=0..anzy),scaling=unconstrained,view=[-0.01..1.05, -0.01..1.05,0.95*MinDollar..1.05*MaxDollar],orientation=[180,90]); display(PDollarA,seq(Ani[i],i=0..anzy),scaling=unconstrained,view=[-0.01..1.05, -0.01..1.05,0.95*MinDollar..1.05*MaxDollar],orientation=[90,90]);

 

Im folgenden betrachten wir das in der Vorlesung definierte Gefangenendilemma, wobei wir jedoch den Parameter b (Gefängnisstrafe in Jahren für den Gefangenen der gesteht im Falle wenn der andere nicht gesteht) variable. Da es sich um ein dominantes Spiel handeln soll muss in diesem Fall gelten b > -3 . 

>	a:=-7: unassign('b'): c:=-9: d:=-3:

 

Das gemischtes Nash-Gleichgewicht dieses Spiels liefert wieder keine sinnvolle Lösung, da für (b > -3) keine gemischte Strategie im Bereich 0 bis 1 möglich ist: 

>	EqGemNashy:=diff(Auszahlungsfunktion_A(x,y),x)=0: EqGemNashx:=diff(Auszahlungsfunktion_B(x,y),y)=0: GemNashyy:=solve(EqGemNashy,y); GemNashx:=solve(EqGemNashx,x);

 

 

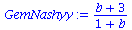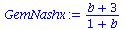	(2.2)

 

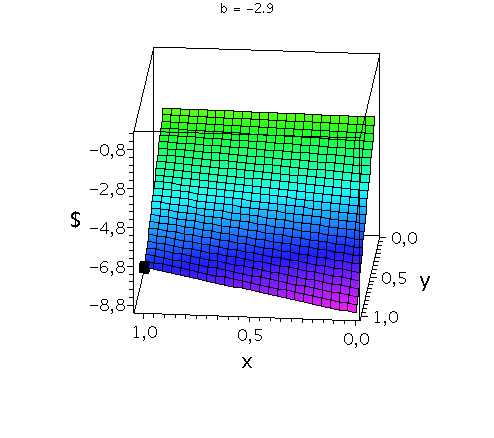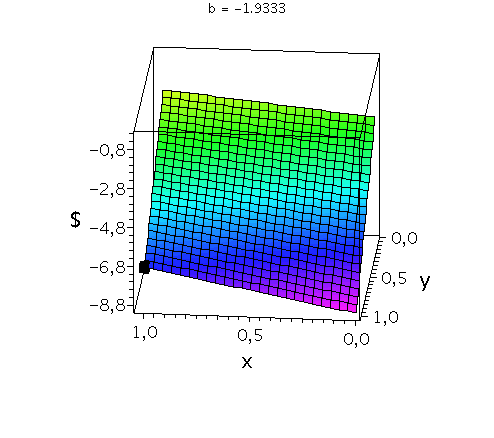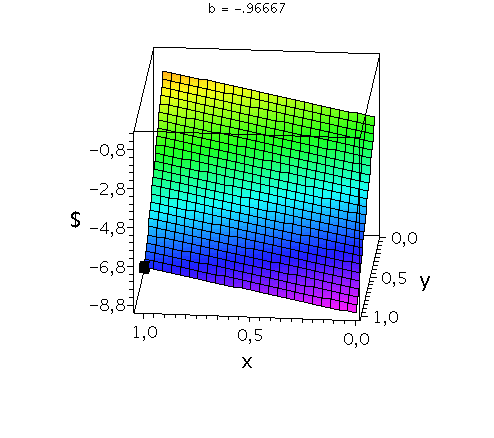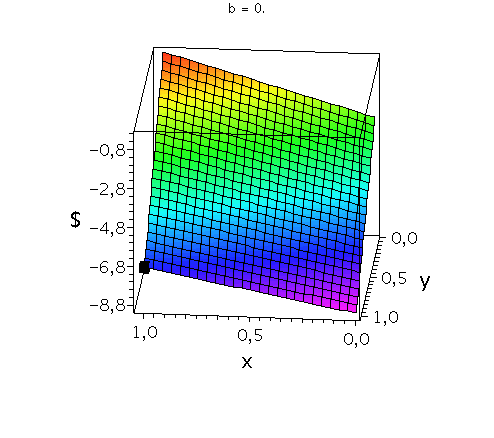
In der folgenden Animation wird die gemischte Auszahlungsfunktion des Spielers A im oben definierten Gefangenendilemma bei Variation des Parameters b im Bereich -2.9  bis 0 gezeigt. Man erkennt gut, wie sich die Position der dominanten Strategie ((x,y)=(1,1); schwarzes Rechteck) nicht verändert. 

>

Sizecuboid:=0.05: Sizecuboidz:=0.43: Ani_reinNash1:=animate(plots[display], [cuboid([-Sizecuboid/2+1, -Sizecuboid/2+1, Auszahlungsfunktion_A(1,1)-Sizecuboidz/2], [Sizecuboid/2+1, Sizecuboid/2+1, Auszahlungsfunktion_A(1,1)+Sizecuboidz/2])], b = -2.9 .. 0,scaling=constrained, style = patchnogrid,color=black):

 

>	Ani2:=animate(plot3d, [Auszahlungsfunktion_A(x,y),x=0..1,y=0..1], b = -2.9 .. 0,axes=boxed,labels=[x,"y","$"],orientation=[95,65],shading=ZHUE,axesfont=[HELVETICA,13],font=[HELVETICA,15]):

 

>	display(Ani_reinNash1,Ani2,scaling=unconstrained);

 

>

 

Beispiel: a < c und b < d; Strategie 2 dominiert Strategie 1; dominante Strategie bei (x,y)=(0,0) 

>	a:=10: b:=4: c:=12: d:=5:

 

Die gemischte Auszahlungsfunktion des Spielers A besitzt im oben definierten Gefangenendilenmma das folgende Aussehen: 

>	plot3d(Auszahlungsfunktion_A(x,y),x=0..1,y=0..1,axes=boxed,labels=[x,"y","$"],orientation=[275,65],title="Auszahlung an Spieler A",shading=ZHUE,axesfont=[HELVETICA,13],font=[HELVETICA,15],titlefont=[HELVETICA,16]);

 

Die gemischte Auszahlungsfunktion des Spielers B sieht wie folgt aus: 

>	plot3d(Auszahlungsfunktion_B(x,y),x=0..1,y=0..1,axes=boxed,labels=[x,"y","$"],orientation=[185,65],title="Auszahlung an Spieler B",shading=ZHUE,axesfont=[HELVETICA,13],font=[HELVETICA,15],titlefont=[HELVETICA,16]);

 

Der Spezialfall des gemischten Nash-Gleichgewichts besteht, falls die partielle Ableitung der gemischten Auszahlungsfläche verschwindet, also 

>	EqGemNashy:=diff(Auszahlungsfunktion_A(x,y),x)=0; EqGemNashx:=diff(Auszahlungsfunktion_B(x,y),y)=0;

 

 

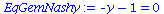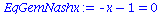	(2.3)

 

Da diese Gleichung keine sinnvolle Lösung besitzt (nur negative gemischte Strategien) existiert im Gefangenendilemma kein gemischtes Nash-Gleichgewicht. 

Wir konzentrieren uns zunächst auf die gemischte Auszahlungsfunktion des Spielers A und werden anhand der Struktur der Auszahlungsflächen die Eigenschaften der dominanten Strategie im Gefangenendilemma verdeutlichen. Die Frage lautet: Unter der Annahme das Spieler B eine feste gemischte Strategie y spielt, welche Strategie x sollte Spieler A wählen, so dass er seine Auszahlung maximiert?  

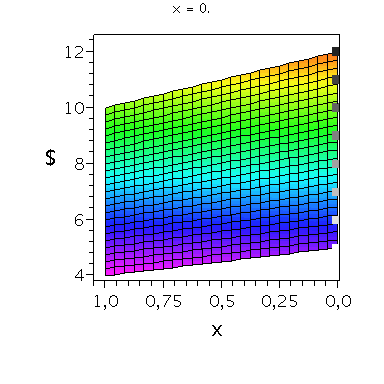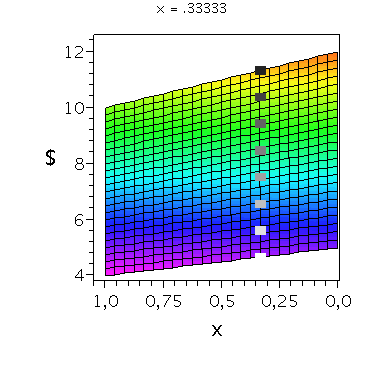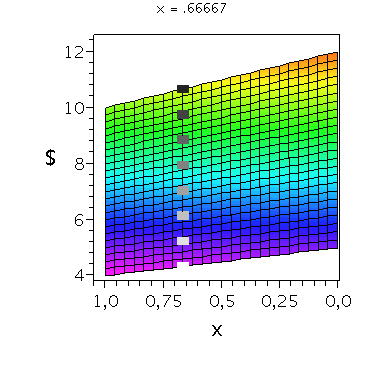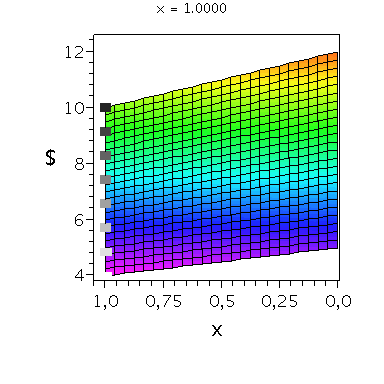
Nehmen wir an, dass Spieler B die reine Strategie y=0 spielen würde, dann wäre es das Beste für Spieler A die reine Strategie x=0 zu spielen (siehe weißes Rechteck in der folgenden Abbildung). 

Nehmen wir dagegen an, dass Spieler B die reine Strategie y=1 spielen würde, dann wäre es das Beste für Spieler A die reine Strategie x=0 zu spielen (siehe schwarzes Rechteck in der folgenden Abbildung). Unanbhängig von der Wahl der Startegie des Spielers B, ist Spieler A immer veranlasst die Strategie x=0 zu spielen (siehe graue Rechtecke in der folgenden Abbildung); (x,y)=(0,0) ist somit die dominante Strategie und das einzige Nash-Gleichgewicht im Gefangenendilemma. 

>

PDollarA:=plot3d(Auszahlungsfunktion_A(x,y),x=0..1,y=0..1,axes=boxed,labels=[x,"y","$"],title="Auszahlung an Spieler A",shading=ZHUE,axesfont=[HELVETICA,13],font=[HELVETICA,15],titlefont=[HELVETICA,16]): MinDollar:=4: MaxDollar:=12: Sizecuboid:=0.05: Sizecuboidz:=0.3: anzy:=7: for sety from 0 by 1 to anzy do Ani[sety]:=animate(plots[display], [cuboid([-Sizecuboid/2+x, -Sizecuboid/2+sety/anzy, Auszahlungsfunktion_A(x,sety/anzy)-Sizecuboidz/2], [Sizecuboid/2+x, Sizecuboid/2+sety/anzy, Auszahlungsfunktion_A(x,sety/anzy)+Sizecuboidz/2])], x = 0 .. 1,scaling=constrained, style = patchnogrid,color=RGBToColor([255-round(sety/anzy*220), 255-round(sety/anzy*220), 255-round(sety/anzy*220)])): od: display(PDollarA,seq(Ani[i],i=0..anzy),scaling=unconstrained,view=[-0.01..1.05, -0.01..1.05,0.95*MinDollar..1.05*MaxDollar],orientation=[275,65]); display(PDollarA,seq(Ani[i],i=0..anzy),scaling=unconstrained,view=[-0.01..1.05, -0.01..1.05,0.95*MinDollar..1.05*MaxDollar],orientation=[180,90]); display(PDollarA,seq(Ani[i],i=0..anzy),scaling=unconstrained,view=[-0.01..1.05, -0.01..1.05,0.95*MinDollar..1.05*MaxDollar],orientation=[90,90]);

 

>

 

Koordinationsspiele 

Wir starten zunächst wieder von einem allgemeinen Spiel einer gemischten Erweiterung eines simultanen (2 Spieler)-(2 Strategien) Spiels in strategischer Form mit symmetrischer Auszahlungmatrix.  

Ein Koordinationsspiel existiert, falls die Parameter a, b, c und d der Auszahlungmatrix die folgenden Bedingungen erfüllen: a > c und b < d . 

Bei dieser Spielklasse existieren drei Nash-Gleichgewichte, ein gemischtes Nash-Gleichgewicht und zwei reine, symmetrische Nash-Gleichgewicht bei (x,y)=(0,0) und (x,y)=(1,1).  

>	restart: with(plots): with(plottools): with(LinearAlgebra): with(ColorTools):

 

Definition der Auszahlunsmatrix für Spieler A: 

>	D_A11:=a: D_A12:=b: D_A21:=c: D_A22:=d: D_A:=Matrix(2,2,[D_A11,D_A12,D_A21,D_A22]);

 

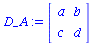(3.1)

 

Da sich das Spiel um ein symmetrisches (2 Personen)-(2 Strategien) Spiel handelt, erhält man die Auszahlunsmatrix für Spieler B durch die transponierte Matrix des Spielers A:  

>	D_B:=Transpose(D_A);

 

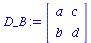(3.2)

 

Unter Verwendung der gemischten Strategien (x,y) lässt sich eine gemischte Auszahlungsfunktion der Spieler wie folgt definieren: 

>	Auszahlungsfunktion_A:=(x,y)->D_A[1,1]*x*y+D_A[1,2]*x*(1-y)+D_A[2,1]*(1-x)*y+D_A[2,2]*(1-x)*(1-y); Auszahlungsfunktion_B:=(x,y)->D_B[1,1]*x*y+D_B[1,2]*x*(1-y)+D_B[2,1]*(1-x)*y+D_B[2,2]*(1-x)*(1-y);

 

 

	(3.3)

 

Der Spezialfall des gemischten Nash-Gleichgewichts besteht, falls die partielle Ableitung der gemischten Auszahlungsfläche verschwindet, also 

>	EqGemNashy:=diff(Auszahlungsfunktion_A(x,y),x)=0; EqGemNashx:=diff(Auszahlungsfunktion_B(x,y),y)=0;

 

 

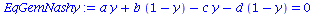	(3.4)

 

Koordinationsspiele haben somit ein gemischtes Nash-Gleichgewicht bei den folgenden Werten der gemischten Strategien: 

>	GemNashyy:=solve(EqGemNashy,y); GemNashx:=solve(EqGemNashx,x);

 

 

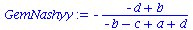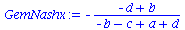	(3.5)

 

Beispiel: Hirschjagt-Spiel 

a > c und b < d 

>	a:=2: b:=4: c:=0:

 

Die Auszahlungsmatrix entspricht dem schon in der Vorlesung besprochenen Hirschjagt-Spiel, wobei der Parameter d, welcher den Verkaufspreis eines Hirsches widerspiegelt, zunächst noch variabel gehalten wurde. Da es sich um ein Koordinationsspiel handel muss jedoch folgende Bedingung gelten: d > 4 . Das gemischtes Nash-Gleichgewicht dieses Spiels befindet sich bei der folgenden Strategienkombination: 

>	GemNashyy:=solve(EqGemNashy,y); GemNashx:=solve(EqGemNashx,x);

 

 

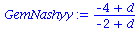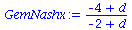	(3.6)

 

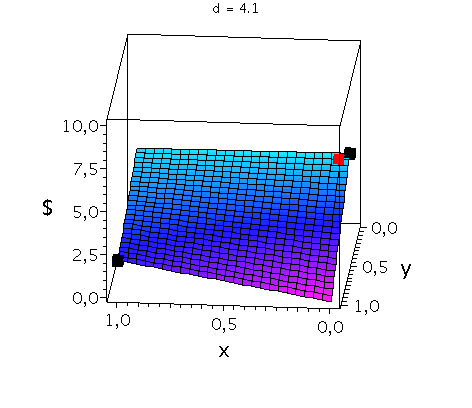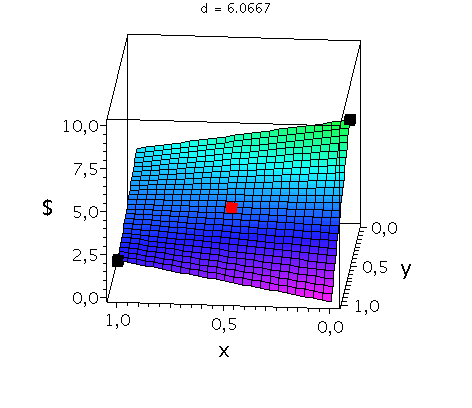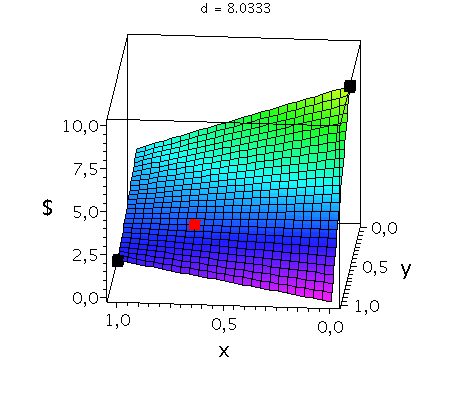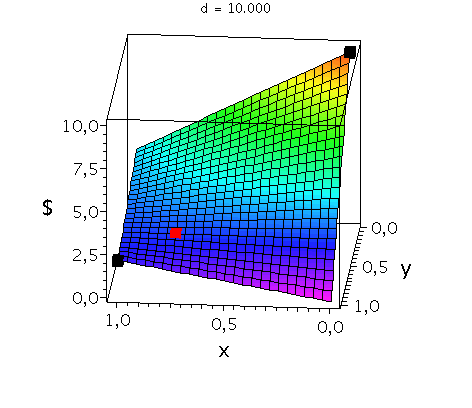
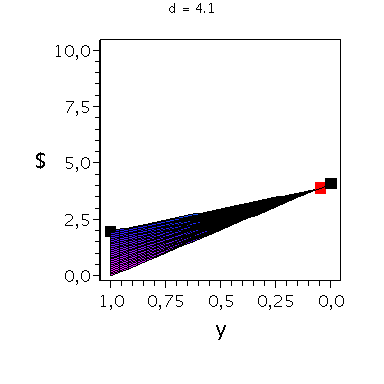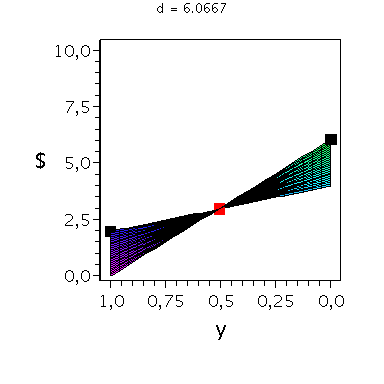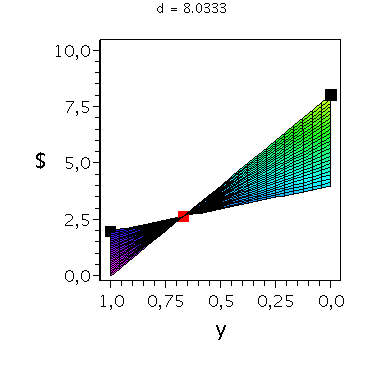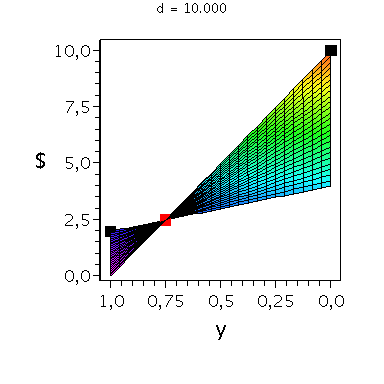
In der folgenden Animation wird die gemischte Auszahlungsfunktion des Spielers A im oben definierten Hirschjagt-Spiel bei Variation des Parameters d im Bereich 4.1 bis 10 gezeigt. Man erkennt gut, wie sich die Position des gemischten Nash-Gleichgewichts verschiebt, wobei zusätzlich die beiden reinen, symmetrischen Nash-Gleichgewichte bei (x,y)=(0,0) und (x,y)=(1,1) bestehen bleiben: 

>

Sizecuboid:=0.05: Sizecuboidz:=0.5: Ani_gemNash:=animate(plots[display], [cuboid([-Sizecuboid/2+GemNashx, -Sizecuboid/2+GemNashyy, Auszahlungsfunktion_A(GemNashx,GemNashyy)-Sizecuboidz/2], [Sizecuboid/2+GemNashx, Sizecuboid/2+GemNashyy, Auszahlungsfunktion_A(GemNashx,GemNashyy)+Sizecuboidz/2])], d = 4.1 .. 10,scaling=constrained, style = patchnogrid,color=red): Ani_reinNash0:=animate(plots[display], [cuboid([-Sizecuboid/2+0, -Sizecuboid/2+0, Auszahlungsfunktion_A(0,0)-Sizecuboidz/2], [Sizecuboid/2+0, Sizecuboid/2+0, Auszahlungsfunktion_A(0,0)+Sizecuboidz/2])], d = 4.1 .. 10,scaling=constrained, style = patchnogrid,color=black): Ani_reinNash1:=animate(plots[display], [cuboid([-Sizecuboid/2+1, -Sizecuboid/2+1, Auszahlungsfunktion_A(1,1)-Sizecuboidz/2], [Sizecuboid/2+1, Sizecuboid/2+1, Auszahlungsfunktion_A(1,1)+Sizecuboidz/2])], d = 4.1 .. 10,scaling=constrained, style = patchnogrid,color=black):

 

>

Ani2:=animate(plot3d, [Auszahlungsfunktion_A(x,y),x=0..1,y=0..1], d = 4.1 .. 10,axes=boxed,labels=[x,"y","$"],orientation=[95,65],shading=ZHUE,axesfont=[HELVETICA,13],font=[HELVETICA,15]): Ani3:=animate(plot3d, [Auszahlungsfunktion_A(x,y),x=0..1,y=0..1], d = 4.1 .. 10,axes=boxed,labels=[x,"y","$"],orientation=[180,90],title="Auszahlung an Spieler A",shading=ZHUE,axesfont=[HELVETICA,13],font=[HELVETICA,15],titlefont=[HELVETICA,16]):

 

>	display(Ani_gemNash,Ani_reinNash0,Ani_reinNash1,Ani2,scaling=unconstrained);

 

>	display(Ani_gemNash,Ani_reinNash0,Ani_reinNash1,Ani3,scaling=unconstrained);

 

>

 

Anti-Koordinationsspiele 

>

 

Wir starten zunächst wieder von einem allgemeinen Spiel einer gemischten Erweiterung eines simultanen (2 Spieler)-(2 Strategien) Spiels in strategischer Form mit symmetrischer Auszahlungmatrix.  

Ein Anti-Koordinationsspiel existiert, falls die Parameter a, b, c und d der Auszahlungmatrix die folgenden Bedingungen erfüllen: a < c und b > d . 

Bei dieser Spielklasse existieren drei Nash-Gleichgewichte, ein gemischtes Nash-Gleichgewicht und zwei reine, unsymmetrische Nash-Gleichgewicht bei (x,y)=(0,1) und (x,y)=(0,1).  

>	restart: with(plots): with(plottools): with(LinearAlgebra): with(ColorTools):

 

Definition der Auszahlunsmatrix für Spieler A: 

>	D_A11:=a: D_A12:=b: D_A21:=c: D_A22:=d: D_A:=Matrix(2,2,[D_A11,D_A12,D_A21,D_A22]);

 

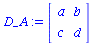(4.1)

 

Da sich das Spiel um ein symmetrisches (2 Personen)-(2 Strategien) Spiel handelt, erhält man die Auszahlunsmatrix für Spieler B durch die transponierte Matrix des Spielers A:  

>	D_B:=Transpose(D_A);

 

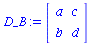(4.2)

 

Unter Verwendung der gemischten Strategien (x,y) lässt sich eine gemischte Auszahlungsfunktion der Spieler wie folgt definieren: 

>	Auszahlungsfunktion_A:=(x,y)->D_A[1,1]*x*y+D_A[1,2]*x*(1-y)+D_A[2,1]*(1-x)*y+D_A[2,2]*(1-x)*(1-y); Auszahlungsfunktion_B:=(x,y)->D_B[1,1]*x*y+D_B[1,2]*x*(1-y)+D_B[2,1]*(1-x)*y+D_B[2,2]*(1-x)*(1-y);

 

 

	(4.3)

 

Der Spezialfall des gemischten Nash-Gleichgewichts besteht, falls die partielle Ableitung der gemischten Auszahlungsfläche verschwindet, also 

>	EqGemNashy:=diff(Auszahlungsfunktion_A(x,y),x)=0; EqGemNashx:=diff(Auszahlungsfunktion_B(x,y),y)=0;

 

 

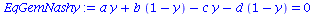	(4.4)

 

Koordinationsspiele haben somit ein gemischtes Nash-Gleichgewicht bei den folgenden Werten der gemischten Strategien: 

>	GemNashyy:=solve(EqGemNashy,y); GemNashx:=solve(EqGemNashx,x);

 

 

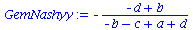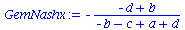	(4.5)

 

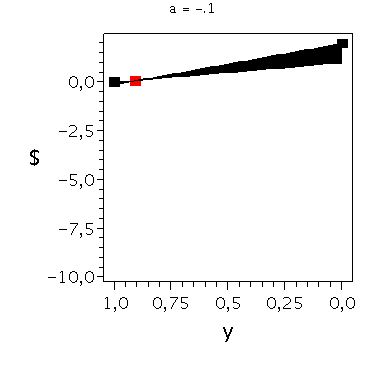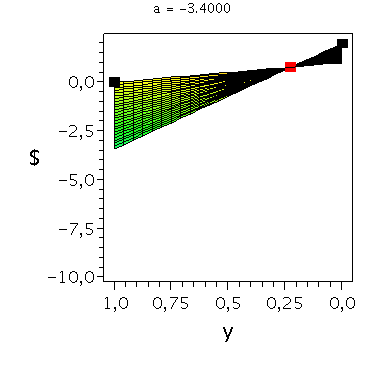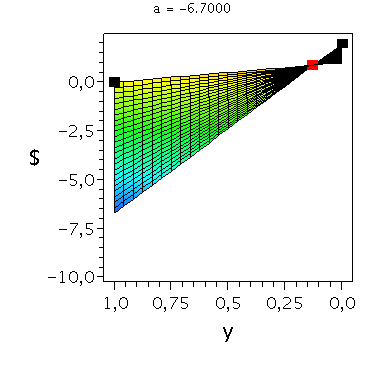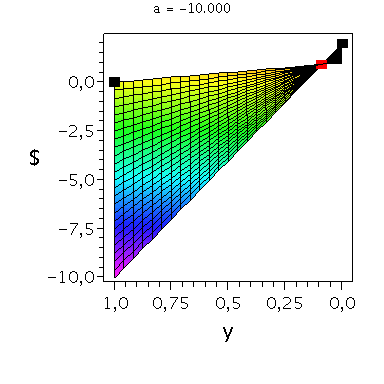
Beispiel: Angsthasen-Spiel 

a < c und b > d 

>	b:=2: c:=0: d:=1:

 

Die Auszahlungsmatrix entspricht dem schon in der Vorlesung besprochenen Angsthasen-Spiel, wobei der Parameter a, welcher die negative Auszahlung widerspiegelt, zunächst noch variabel gehalten wurde. Da es sich um ein Anti-Koordinationsspiel handel muss folgende Bedingung gelten: a < 0 . Das gemischtes Nash-Gleichgewicht dieses Spiels befindet sich bei der folgenden Strategienkombination: 

>	GemNashyy:=solve(EqGemNashy,y); GemNashx:=solve(EqGemNashx,x);

 

 

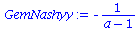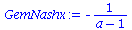	(4.6)

 

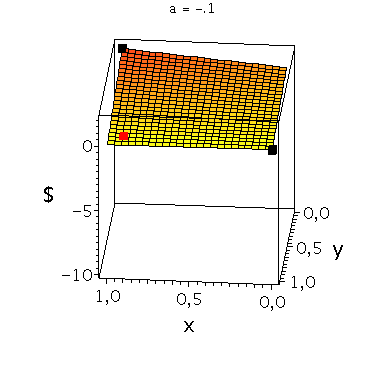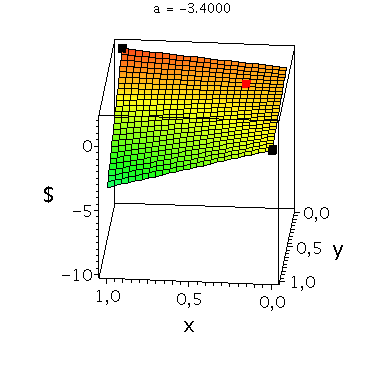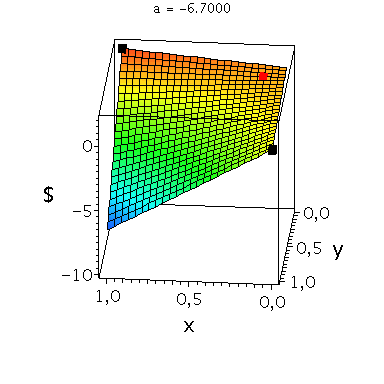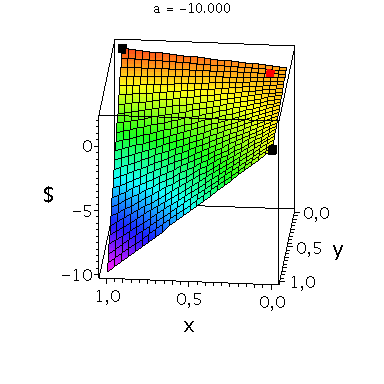
In der folgenden Animation wird die gemischte Auszahlungsfunktion des Spielers A im oben definierten Angsthasen-Spiel bei Variation des Parameters a im Bereich -0.1 bis 10 gezeigt. Man erkennt gut, wie sich die Position des gemischten Nash-Gleichgewichts verschiebt, wobei zusätzlich die beiden reinen, unsymmetrischen Nash-Gleichgewichte bei (x,y)=(1,0) und (x,y)=(0,1) bestehen bleiben: 

>

Sizecuboid:=0.05: Sizecuboidz:=0.5: Ani_gemNash:=animate(plots[display], [cuboid([-Sizecuboid/2+GemNashx, -Sizecuboid/2+GemNashyy, Auszahlungsfunktion_A(GemNashx,GemNashyy)-Sizecuboidz/2], [Sizecuboid/2+GemNashx, Sizecuboid/2+GemNashyy, Auszahlungsfunktion_A(GemNashx,GemNashyy)+Sizecuboidz/2])], a = -0.1 .. -10,scaling=constrained, style = patchnogrid,color=red): Ani_reinNash0:=animate(plots[display], [cuboid([-Sizecuboid/2+0, -Sizecuboid/2+1, Auszahlungsfunktion_A(0,1)-Sizecuboidz/2], [Sizecuboid/2+0, Sizecuboid/2+1, Auszahlungsfunktion_A(0,1)+Sizecuboidz/2])], a = -0.1 .. -10,scaling=constrained, style = patchnogrid,color=black): Ani_reinNash1:=animate(plots[display], [cuboid([-Sizecuboid/2+1, -Sizecuboid/2+0, Auszahlungsfunktion_A(1,0)-Sizecuboidz/2], [Sizecuboid/2+1, Sizecuboid/2+0, Auszahlungsfunktion_A(1,0)+Sizecuboidz/2])], a = -0.1 .. -10,scaling=constrained, style = patchnogrid,color=black):

 

>

Ani2:=animate(plot3d, [Auszahlungsfunktion_A(x,y),x=0..1,y=0..1], a = -0.1 .. -10,axes=boxed,labels=[x,"y","$"],orientation=[95,65],shading=ZHUE,axesfont=[HELVETICA,13],font=[HELVETICA,15]): Ani3:=animate(plot3d, [Auszahlungsfunktion_A(x,y),x=0..1,y=0..1], a = -0.1 .. -10,axes=boxed,labels=[x,"y","$"],orientation=[180,90],title="Auszahlung an Spieler A",shading=ZHUE,axesfont=[HELVETICA,13],font=[HELVETICA,15],titlefont=[HELVETICA,16]):

 

>	display(Ani_gemNash,Ani_reinNash0,Ani_reinNash1,Ani2,scaling=unconstrained);

 

>	display(Ani_gemNash,Ani_reinNash0,Ani_reinNash1,Ani3,scaling=unconstrained);

 

>