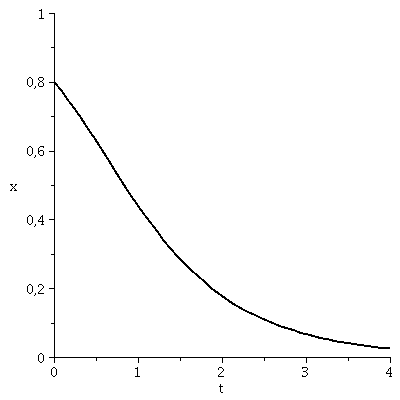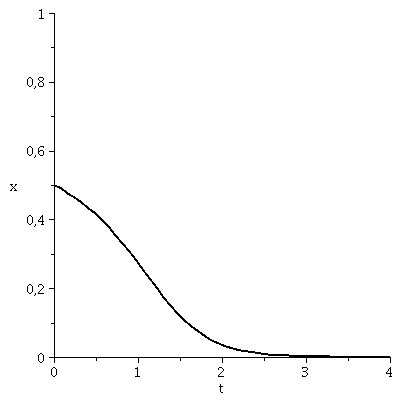Einführung 

Dieses Maple-Worksheet basiert auf dem Maple-Worksheet Spielklassen1.mw und erweitert dieses in einen evolutionären, zeitabhängigen Kontext.Ausgangspunkt ist wiederum die folgende allgemeine symmetrische Auszahlunsmatrix eines (2 Personen)-(2 Strategien) Spiels (a, b, c und d sind reelwertige Zahlen):  

>	restart: with(plots): with(plottools): with(LinearAlgebra): with(ColorTools):

 

Definition der Auszahlunsmatrix für Spieler A: 

>	D_A11:=a: D_A12:=b: D_A21:=c: D_A22:=d: D_A:=Matrix(2,2,[D_A11,D_A12,D_A21,D_A22]);

 

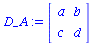(1.1)

 

Da sich das Spiel um ein symmetrisches (2 Personen)-(2 Strategien) Spiel handelt, erhält man die Auszahlunsmatrix für Spieler B durch die transponierte Matrix des Spielers A:  

>	D_B:=Transpose(D_A);

 

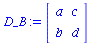(1.2)

 

Unter Verwendung der gemischten Strategien (x,y) lässt sich eine gemischte Auszahlungsfunktion der Spieler wie folgt definieren: 

>	Auszahlungsfunktion_A:=(x,y)->D_A[1,1]*x*y+D_A[1,2]*x*(1-y)+D_A[2,1]*(1-x)*y+D_A[2,2]*(1-x)*(1-y); Auszahlungsfunktion_B:=(x,y)->D_B[1,1]*x*y+D_B[1,2]*x*(1-y)+D_B[2,1]*(1-x)*y+D_B[2,2]*(1-x)*(1-y);

 

 

	(1.3)

 

Die Klasse der dominanten Spiele 

Bei dieser Spielklasse dominiert eine Strategie die andere. Es existiert nur ein reines Nash-Gleichgewicht welches die dominante Strategie des Spiels darstellt. Dieser Fall tritt ein, falls: 

• a > c und b > d : Strategie 1 dominiert Strategie 2; dominante Strategie bei (x,y)=(1,1).

• a < c und b < d : Strategie 2 dominiert Strategie 1; dominante Strategie bei (x,y)=(0,0).

Beispiel: a > c und b > d; Strategie 1 dominiert Strategie 2; dominante Strategie bei (x,y)=(1,1) 

>	a:=10: b:=6: c:=7: d:=5:

 

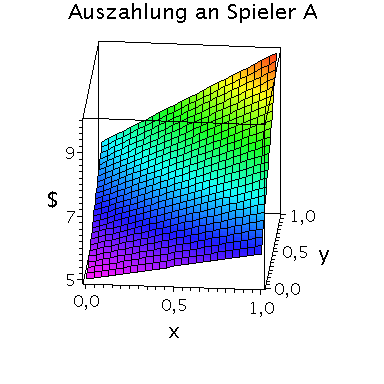
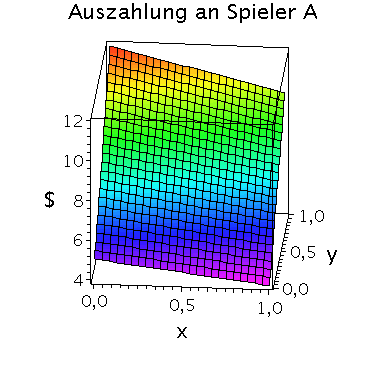
Die gemischte Auszahlungsfunktion des Spielers A besitzt im oben definierten dominanten Spiel das folgende Aussehen: 

>	plot3d(Auszahlungsfunktion_A(x,y),x=0..1,y=0..1,axes=boxed,labels=[x,"y","$"],orientation=[275,65],title="Auszahlung an Spieler A",shading=ZHUE,axesfont=[HELVETICA,13],font=[HELVETICA,15],titlefont=[HELVETICA,16]);

 

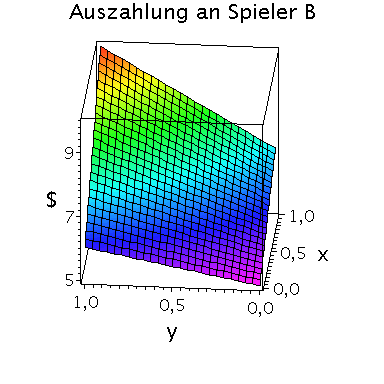
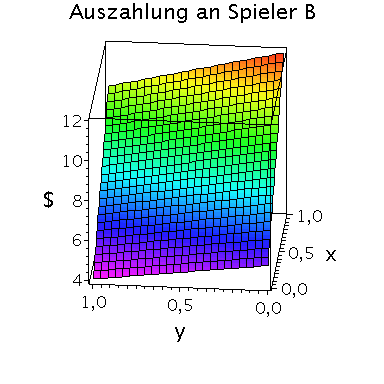
Die gemischte Auszahlungsfunktion des Spielers B sieht wie folgt aus: 

>	plot3d(Auszahlungsfunktion_B(x,y),x=0..1,y=0..1,axes=boxed,labels=[x,"y","$"],orientation=[185,65],title="Auszahlung an Spieler B",shading=ZHUE,axesfont=[HELVETICA,13],font=[HELVETICA,15],titlefont=[HELVETICA,16]);

 

Der Spezialfall des gemischten Nash-Gleichgewichts besteht, falls die partielle Ableitung der gemischten Auszahlungsfläche verschwindet, also 

>	EqGemNashy:=diff(Auszahlungsfunktion_A(x,y),x)=0; EqGemNashx:=diff(Auszahlungsfunktion_B(x,y),y)=0;

 

 

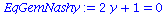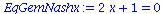	(2.1)

 

Da diese Gleichung keine sinnvolle Lösung besitzt (nur negative gemischte Strategien) existiert in einem dominanten Spiel kein gemischtes Nash-Gleichgewicht. 

Die Differentialgleichung, die die zeitliche Entwicklung des Populationsvektors x(t) beschreibt lautet: 

>	DGL:=diff(x(t),t)=simplify(((D_A11-D_A21)*(x(t)-x(t)^2) + (D_A12-D_A22)*(1-2*x(t)+x(t)^2))*x(t)); g:=simplify(((D_A11-D_A21)*(x-x^2) + (D_A12-D_A22)*(1-2*x+x^2))*x);

 

 

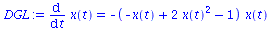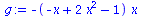	(2.2)

 

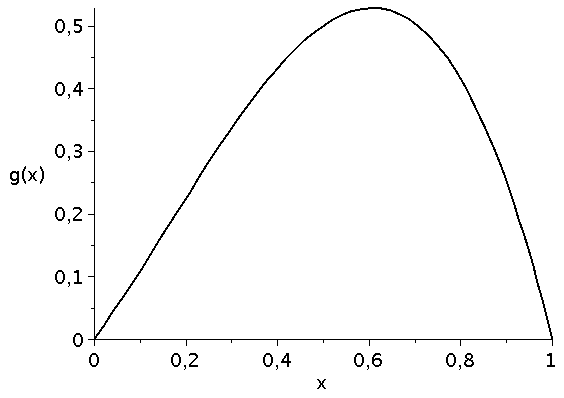
Die die zeitliche Entwicklung bestimmende Funktion g(x) besitzt das folgende Aussehen: 

>	plot(g, x=0..1,color=black,thickness=2,labels=["x","g(x)"],labelfont=[HELVETICA,15],axesfont=[HELVETICA,15],font=[HELVETICA,15]);

 

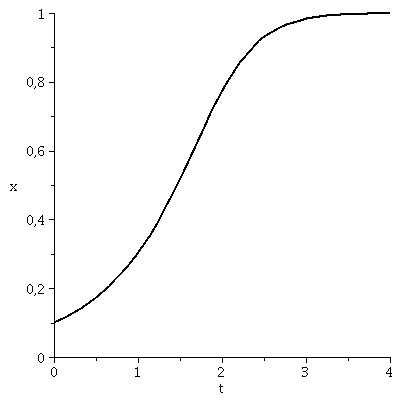
x(t), der Anteil der Spieler die zum Zeitpunkt t die Strategie 1 spielen, hängt neben der Funktion g(x) von dem Anfangswert x(t=0) ab.Setzt man z.B. x(t=0)=0.1 (entspricht einer Anfangspopulation von 10% spielt Strategie 1 und 90% spielt Strategie 2) so kann man die Differentialgleichung wie folgt nummerisch lösen und grafisch darstellen:  

>	x0:=0.10: LoesDGL:=dsolve({DGL,x(0)=x0},x(t),type=numeric):

 

>	tanf:=0: tend:=4: odeplot(LoesDGL,[t,x(t)],tanf..tend,view=[tanf..tend,0..1],thickness=2,color=black);

 

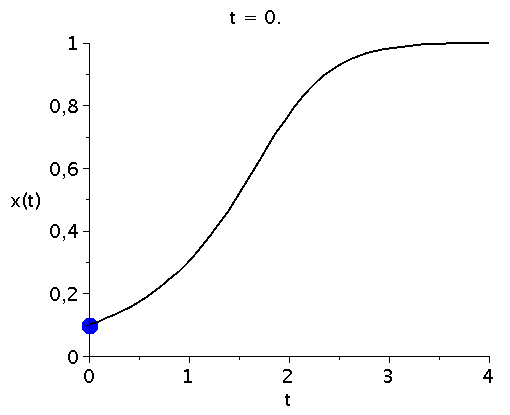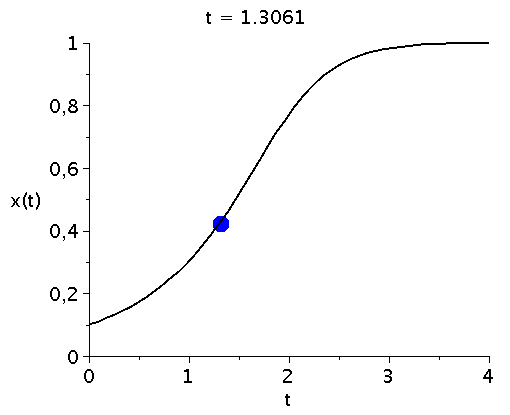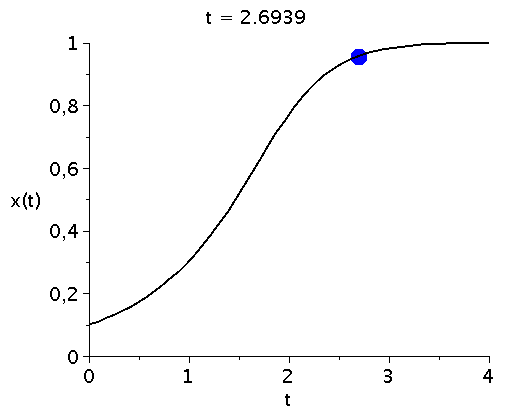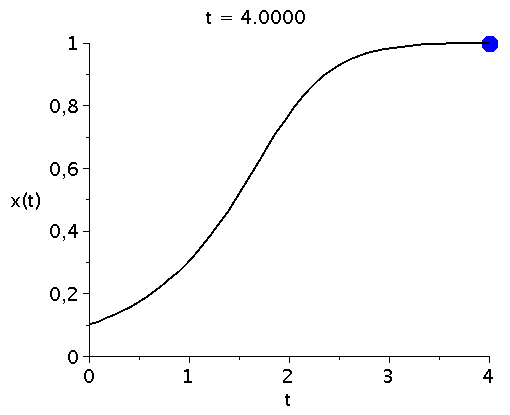
bzw. in einer Animation dargestellt: 

>

ball := proc(t,x) plots[pointplot]([[t,rhs(LoesDGL(x)[2])]],color=blue,symbol=solidcircle,symbolsize=30) end proc: Ani1:=animate(ball, [t,t], t=tanf..tend,view=[tanf..tend,0..1],frames=50): P1:=odeplot(LoesDGL,[t,x(t)],tanf..tend,view=[tanf..tend,0..1],thickness=2,color=black): display(Ani1,P1,labels=["t","x(t)"],labelfont=[HELVETICA,15],axesfont=[HELVETICA,15],font=[HELVETICA,15]);

 

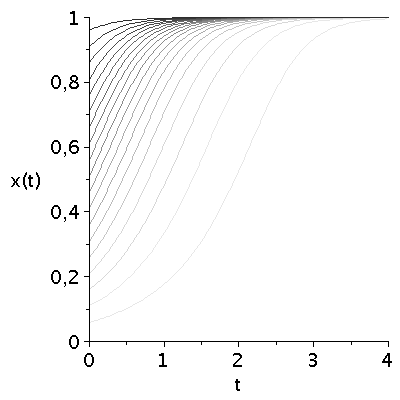
Für unterschiedliche Anfangswerte der Populationszusammensetzung ergibt sich das folgende Bild: 

>	tanf:=0: tend:=4: ii:=0: for x_0 from 0.01 by 0.05 to 0.99 do ii:=ii+1: Loes:=dsolve({DGL,x(0)=x_0},x(t),type=numeric): Plot_FT[ii]:=odeplot(Loes,[t,x(t)],tanf..tend,color=RGBToColor([255-round(x_0*220), 255-round(x_0*220), 255-round(x_0*220)]),view=[tanf..tend,0..1]): end do:

 

>	display(seq(Plot_FT[i],i=1..ii),labels=["t","x(t)"],labelfont=[HELVETICA,15],axesfont=[HELVETICA,15],font=[HELVETICA,15]);

 

Beispiel: a < c und b < d; Strategie 2 dominiert Strategie 1; dominante Strategie bei (x,y)=(0,0) 

>	a:=10: b:=4: c:=12: d:=5:

 

Die gemischte Auszahlungsfunktion des Spielers A besitzt im oben definierten Gefangenendilenmma das folgende Aussehen: 

>	plot3d(Auszahlungsfunktion_A(x,y),x=0..1,y=0..1,axes=boxed,labels=[x,"y","$"],orientation=[275,65],title="Auszahlung an Spieler A",shading=ZHUE,axesfont=[HELVETICA,13],font=[HELVETICA,15],titlefont=[HELVETICA,16]);

 

Die gemischte Auszahlungsfunktion des Spielers B sieht wie folgt aus: 

>	plot3d(Auszahlungsfunktion_B(x,y),x=0..1,y=0..1,axes=boxed,labels=[x,"y","$"],orientation=[185,65],title="Auszahlung an Spieler B",shading=ZHUE,axesfont=[HELVETICA,13],font=[HELVETICA,15],titlefont=[HELVETICA,16]);

 

Der Spezialfall des gemischten Nash-Gleichgewichts besteht, falls die partielle Ableitung der gemischten Auszahlungsfläche verschwindet, also 

>	EqGemNashy:=diff(Auszahlungsfunktion_A(x,y),x)=0; EqGemNashx:=diff(Auszahlungsfunktion_B(x,y),y)=0;

 

 

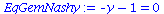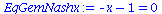	(2.3)

 

Da diese Gleichung keine sinnvolle Lösung besitzt (nur negative gemischte Strategien) existiert im Gefangenendilemma kein gemischtes Nash-Gleichgewicht. 

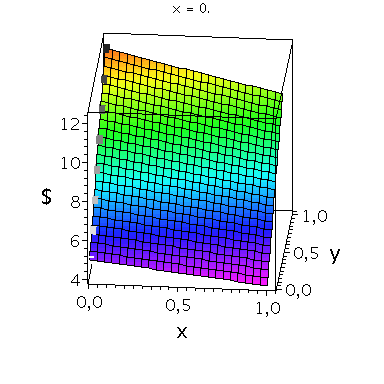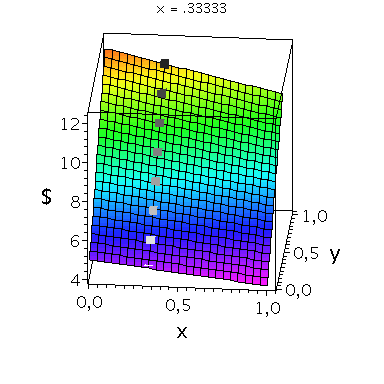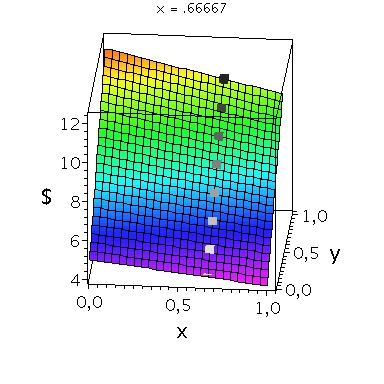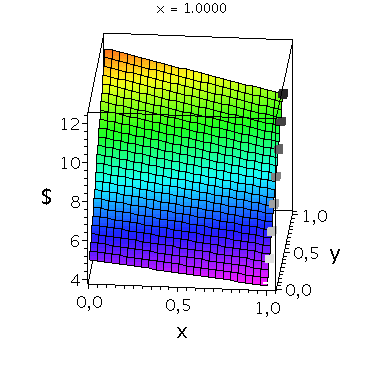
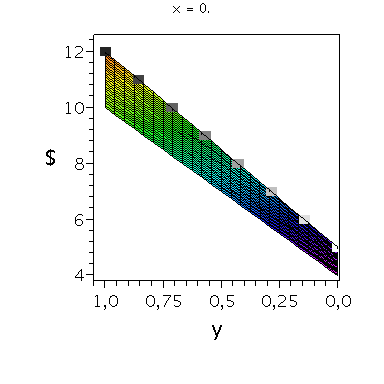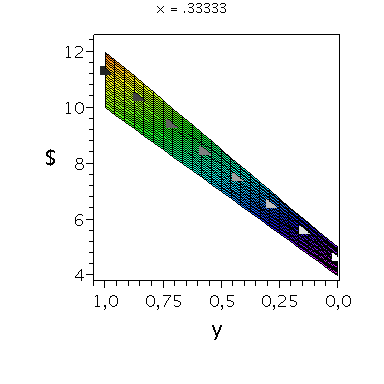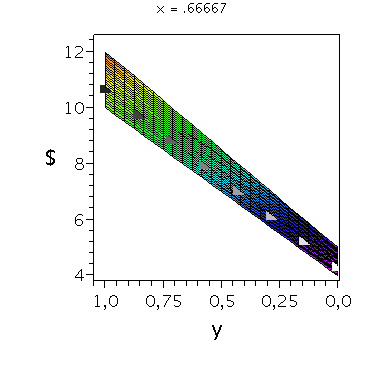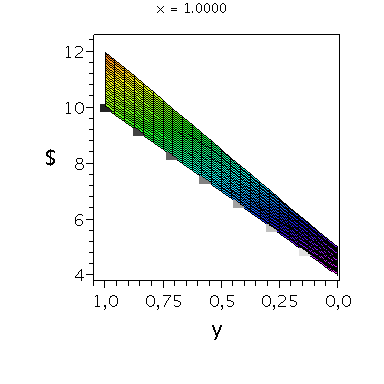
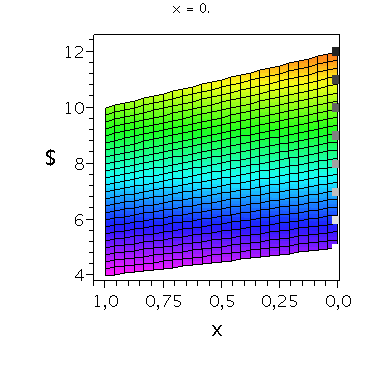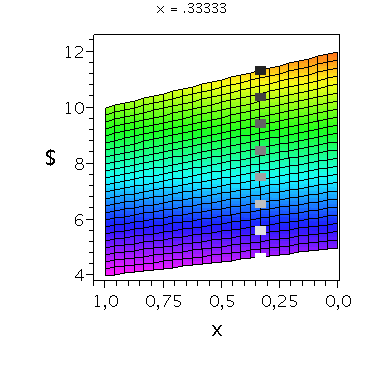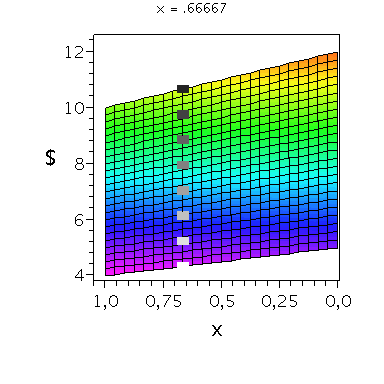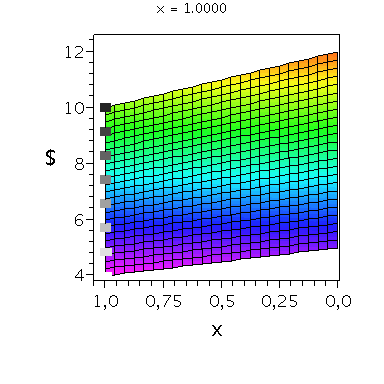
Wir konzentrieren uns zunächst auf die gemischte Auszahlungsfunktion des Spielers A und werden anhand der Struktur der Auszahlungsflächen die Eigenschaften der dominanten Strategie im Gefangenendilemma verdeutlichen. Die Frage lautet: Unter der Annahme das Spieler B eine feste gemischte Strategie y spielt, welche Strategie x sollte Spieler A wählen, so dass er seine Auszahlung maximiert?  

Nehmen wir an, dass Spieler B die reine Strategie y=0 spielen würde, dann wäre es das Beste für Spieler A die reine Strategie x=0 zu spielen (siehe weißes Rechteck in der folgenden Abbildung). 

Nehmen wir dagegen an, dass Spieler B die reine Strategie y=1 spielen würde, dann wäre es das Beste für Spieler A die reine Strategie x=0 zu spielen (siehe schwarzes Rechteck in der folgenden Abbildung). Unanbhängig von der Wahl der Startegie des Spielers B, ist Spieler A immer veranlasst die Strategie x=0 zu spielen (siehe graue Rechtecke in der folgenden Abbildung); (x,y)=(0,0) ist somit die dominante Strategie und das einzige Nash-Gleichgewicht im Gefangenendilemma. 

>

PDollarA:=plot3d(Auszahlungsfunktion_A(x,y),x=0..1,y=0..1,axes=boxed,labels=[x,"y","$"],title="Auszahlung an Spieler A",shading=ZHUE,axesfont=[HELVETICA,13],font=[HELVETICA,15],titlefont=[HELVETICA,16]): MinDollar:=4: MaxDollar:=12: Sizecuboid:=0.05: Sizecuboidz:=0.3: anzy:=7: for sety from 0 by 1 to anzy do Ani[sety]:=animate(plots[display], [cuboid([-Sizecuboid/2+x, -Sizecuboid/2+sety/anzy, Auszahlungsfunktion_A(x,sety/anzy)-Sizecuboidz/2], [Sizecuboid/2+x, Sizecuboid/2+sety/anzy, Auszahlungsfunktion_A(x,sety/anzy)+Sizecuboidz/2])], x = 0 .. 1,scaling=constrained, style = patchnogrid,color=RGBToColor([255-round(sety/anzy*220), 255-round(sety/anzy*220), 255-round(sety/anzy*220)])): od: display(PDollarA,seq(Ani[i],i=0..anzy),scaling=unconstrained,view=[-0.01..1.05, -0.01..1.05,0.95*MinDollar..1.05*MaxDollar],orientation=[275,65]); display(PDollarA,seq(Ani[i],i=0..anzy),scaling=unconstrained,view=[-0.01..1.05, -0.01..1.05,0.95*MinDollar..1.05*MaxDollar],orientation=[180,90]); display(PDollarA,seq(Ani[i],i=0..anzy),scaling=unconstrained,view=[-0.01..1.05, -0.01..1.05,0.95*MinDollar..1.05*MaxDollar],orientation=[90,90]);

 

>

 

Die Differentialgleichung, die die zeitliche Entwicklung des Populationsvektors x(t) beschreibt lautet: 

>	DGL:=diff(x(t),t)=simplify(((D_A11-D_A21)*(x(t)-x(t)^2) + (D_A12-D_A22)*(1-2*x(t)+x(t)^2))*x(t)); g:=simplify(((D_A11-D_A21)*(x-x^2) + (D_A12-D_A22)*(1-2*x+x^2))*x);

 

 

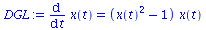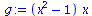	(2.4)

 

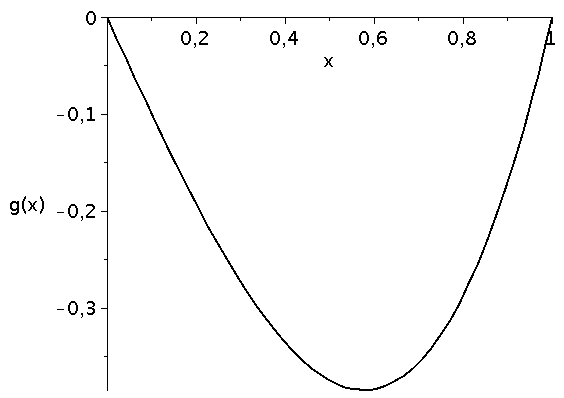
Die die zeitliche Entwicklung bestimmende Funktion g(x) besitzt das folgende Aussehen: 

>	plot(g, x=0..1,color=black,thickness=2,labels=["x","g(x)"],labelfont=[HELVETICA,15],axesfont=[HELVETICA,15],font=[HELVETICA,15]);

 

x(t), der Anteil der Spieler die zum Zeitpunkt t die Strategie 1 spielen, hängt neben der Funktion g(x) von dem Anfangswert x(t=0) ab.Setzt man z.B. x(t=0)=0.8 (entspricht einer Anfangspopulation von 80% spielt Strategie 1 und 20% spielt Strategie 2) so kann man die Differentialgleichung wie folgt nummerisch lösen und grafisch darstellen:  

>	x0:=0.80: LoesDGL:=dsolve({DGL,x(0)=x0},x(t),type=numeric):

 

>	tanf:=0: tend:=4: odeplot(LoesDGL,[t,x(t)],tanf..tend,view=[tanf..tend,0..1],thickness=2,color=black);

 

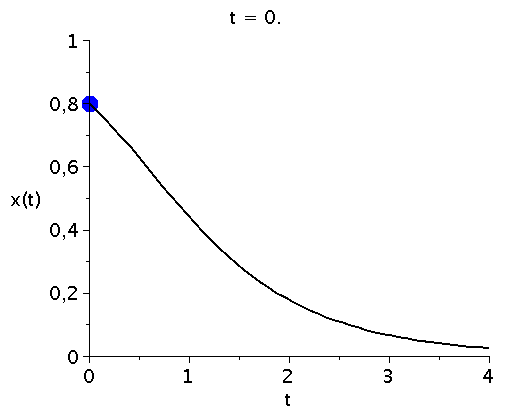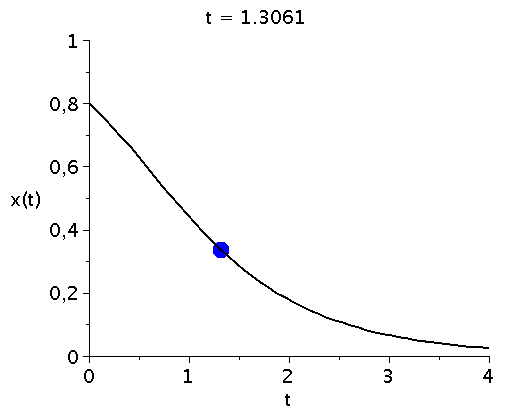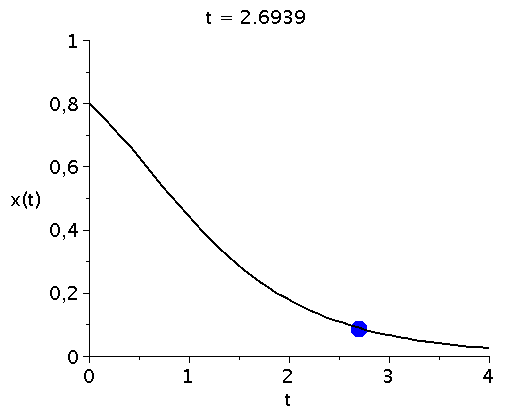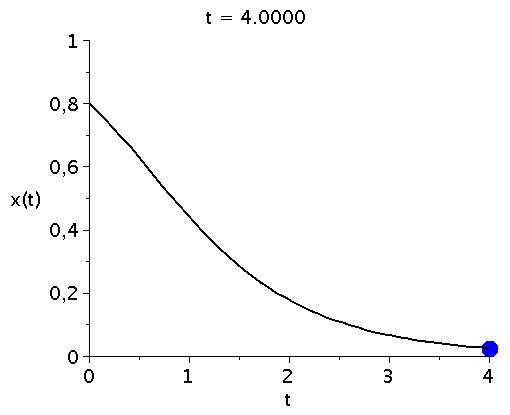
bzw. in einer Animation dargestellt: 

>

ball := proc(t,x) plots[pointplot]([[t,rhs(LoesDGL(x)[2])]],color=blue,symbol=solidcircle,symbolsize=30) end proc: Ani1:=animate(ball, [t,t], t=tanf..tend,view=[tanf..tend,0..1],frames=50): P1:=odeplot(LoesDGL,[t,x(t)],tanf..tend,view=[tanf..tend,0..1],thickness=2,color=black): display(Ani1,P1,labels=["t","x(t)"],labelfont=[HELVETICA,15],axesfont=[HELVETICA,15],font=[HELVETICA,15]);

 

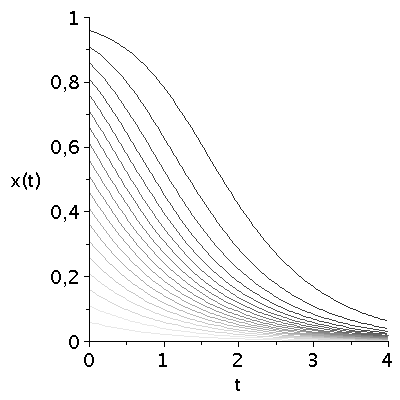
Für unterschiedliche Anfangswerte der Populationszusammensetzung ergibt sich das folgende Bild: 

>	tanf:=0: tend:=4: ii:=0: for x_0 from 0.01 by 0.05 to 0.99 do ii:=ii+1: Loes:=dsolve({DGL,x(0)=x_0},x(t),type=numeric): Plot_FT[ii]:=odeplot(Loes,[t,x(t)],tanf..tend,color=RGBToColor([255-round(x_0*220), 255-round(x_0*220), 255-round(x_0*220)]),view=[tanf..tend,0..1]): end do:

 

>	display(seq(Plot_FT[i],i=1..ii),labels=["t","x(t)"],labelfont=[HELVETICA,15],axesfont=[HELVETICA,15],font=[HELVETICA,15]);

 

Koordinationsspiele 

Wir starten zunächst wieder von einem allgemeinen Spiel einer gemischten Erweiterung eines simultanen (2 Spieler)-(2 Strategien) Spiels in strategischer Form mit symmetrischer Auszahlungmatrix.  

Ein Koordinationsspiel existiert, falls die Parameter a, b, c und d der Auszahlungmatrix die folgenden Bedingungen erfüllen: a > c und b < d . 

Bei dieser Spielklasse existieren drei Nash-Gleichgewichte, ein gemischtes Nash-Gleichgewicht und zwei reine, symmetrische Nash-Gleichgewicht bei (x,y)=(0,0) und (x,y)=(1,1).  

>	restart: with(plots): with(plottools): with(LinearAlgebra): with(ColorTools):

 

Definition der Auszahlunsmatrix für Spieler A: 

>	D_A11:=a: D_A12:=b: D_A21:=c: D_A22:=d: D_A:=Matrix(2,2,[D_A11,D_A12,D_A21,D_A22]);

 

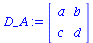(3.1)

 

Da sich das Spiel um ein symmetrisches (2 Personen)-(2 Strategien) Spiel handelt, erhält man die Auszahlunsmatrix für Spieler B durch die transponierte Matrix des Spielers A:  

>	D_B:=Transpose(D_A);

 

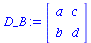(3.2)

 

Unter Verwendung der gemischten Strategien (x,y) lässt sich eine gemischte Auszahlungsfunktion der Spieler wie folgt definieren: 

>	Auszahlungsfunktion_A:=(x,y)->D_A[1,1]*x*y+D_A[1,2]*x*(1-y)+D_A[2,1]*(1-x)*y+D_A[2,2]*(1-x)*(1-y); Auszahlungsfunktion_B:=(x,y)->D_B[1,1]*x*y+D_B[1,2]*x*(1-y)+D_B[2,1]*(1-x)*y+D_B[2,2]*(1-x)*(1-y);

 

 

	(3.3)

 

Der Spezialfall des gemischten Nash-Gleichgewichts besteht, falls die partielle Ableitung der gemischten Auszahlungsfläche verschwindet, also 

>	EqGemNashy:=diff(Auszahlungsfunktion_A(x,y),x)=0; EqGemNashx:=diff(Auszahlungsfunktion_B(x,y),y)=0;

 

 

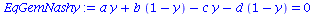	(3.4)

 

Koordinationsspiele haben somit ein gemischtes Nash-Gleichgewicht bei den folgenden Werten der gemischten Strategien: 

>	GemNashyy:=solve(EqGemNashy,y); GemNashx:=solve(EqGemNashx,x);

 

 

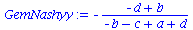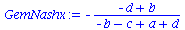	(3.5)

 

Beispiel: Hirschjagt-Spiel 

a > c und b < d 

>	a:=2: b:=4: c:=0:

 

Die Auszahlungsmatrix entspricht dem schon in der Vorlesung besprochenen Hirschjagt-Spiel, wobei der Parameter d, welcher den Verkaufspreis eines Hirsches widerspiegelt, zunächst noch variabel gehalten wurde. Da es sich um ein Koordinationsspiel handel muss jedoch folgende Bedingung gelten: d > 4 . Das gemischtes Nash-Gleichgewicht dieses Spiels befindet sich bei der folgenden Strategienkombination: 

>	GemNashyy:=solve(EqGemNashy,y); GemNashx:=solve(EqGemNashx,x);

 

 

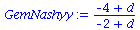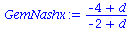	(3.6)

 

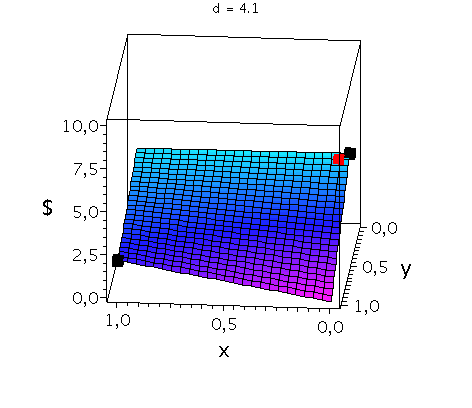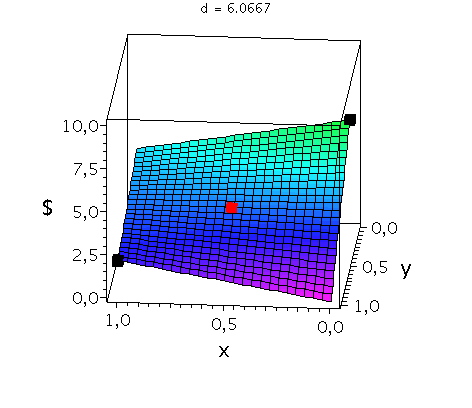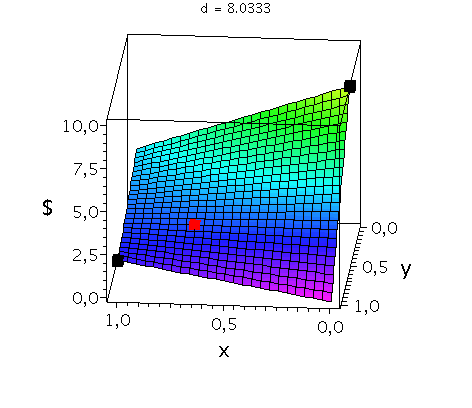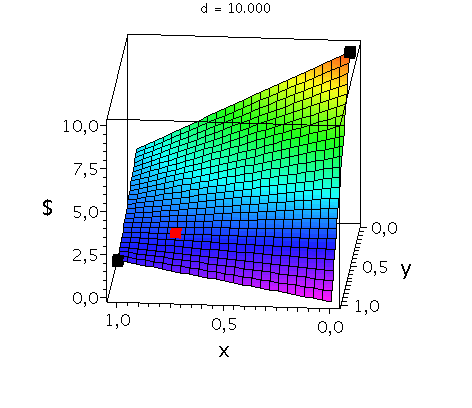
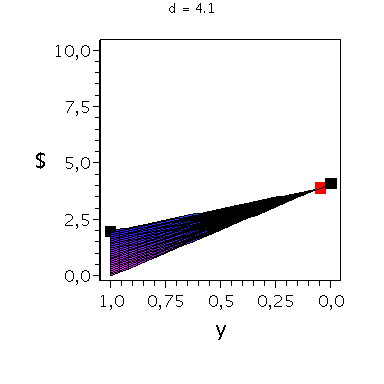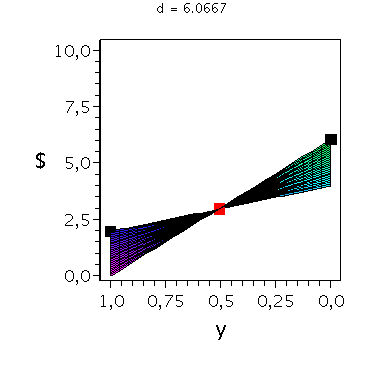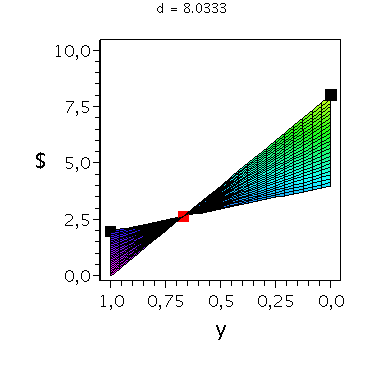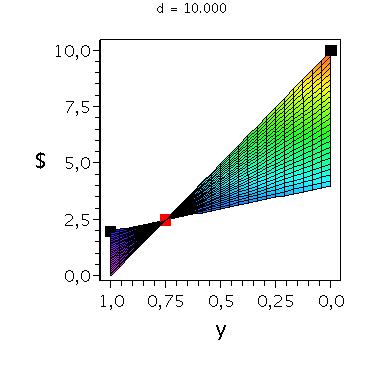
In der folgenden Animation wird die gemischte Auszahlungsfunktion des Spielers A im oben definierten Hirschjagt-Spiel bei Variation des Parameters d im Bereich 4.1 bis 10 gezeigt. Man erkennt gut, wie sich die Position des gemischten Nash-Gleichgewichts verschiebt, wobei zusätzlich die beiden reinen, symmetrischen Nash-Gleichgewichte bei (x,y)=(0,0) und (x,y)=(1,1) bestehen bleiben: 

>

Sizecuboid:=0.05: Sizecuboidz:=0.5: Ani_gemNash:=animate(plots[display], [cuboid([-Sizecuboid/2+GemNashx, -Sizecuboid/2+GemNashyy, Auszahlungsfunktion_A(GemNashx,GemNashyy)-Sizecuboidz/2], [Sizecuboid/2+GemNashx, Sizecuboid/2+GemNashyy, Auszahlungsfunktion_A(GemNashx,GemNashyy)+Sizecuboidz/2])], d = 4.1 .. 10,scaling=constrained, style = patchnogrid,color=red): Ani_reinNash0:=animate(plots[display], [cuboid([-Sizecuboid/2+0, -Sizecuboid/2+0, Auszahlungsfunktion_A(0,0)-Sizecuboidz/2], [Sizecuboid/2+0, Sizecuboid/2+0, Auszahlungsfunktion_A(0,0)+Sizecuboidz/2])], d = 4.1 .. 10,scaling=constrained, style = patchnogrid,color=black): Ani_reinNash1:=animate(plots[display], [cuboid([-Sizecuboid/2+1, -Sizecuboid/2+1, Auszahlungsfunktion_A(1,1)-Sizecuboidz/2], [Sizecuboid/2+1, Sizecuboid/2+1, Auszahlungsfunktion_A(1,1)+Sizecuboidz/2])], d = 4.1 .. 10,scaling=constrained, style = patchnogrid,color=black):

 

>

Ani2:=animate(plot3d, [Auszahlungsfunktion_A(x,y),x=0..1,y=0..1], d = 4.1 .. 10,axes=boxed,labels=[x,"y","$"],orientation=[95,65],shading=ZHUE,axesfont=[HELVETICA,13],font=[HELVETICA,15]): Ani3:=animate(plot3d, [Auszahlungsfunktion_A(x,y),x=0..1,y=0..1], d = 4.1 .. 10,axes=boxed,labels=[x,"y","$"],orientation=[180,90],title="Auszahlung an Spieler A",shading=ZHUE,axesfont=[HELVETICA,13],font=[HELVETICA,15],titlefont=[HELVETICA,16]):

 

>	display(Ani_gemNash,Ani_reinNash0,Ani_reinNash1,Ani2,scaling=unconstrained);

 

>	display(Ani_gemNash,Ani_reinNash0,Ani_reinNash1,Ani3,scaling=unconstrained);

 

>

 

Die Differentialgleichung, die die zeitliche Entwicklung des Populationsvektors x(t) beschreibt lautet: 

>	DGL:=diff(x(t),t)=simplify(((D_A11-D_A21)*(x(t)-x(t)^2) + (D_A12-D_A22)*(1-2*x(t)+x(t)^2))*x(t)); g:=simplify(((D_A11-D_A21)*(x-x^2) + (D_A12-D_A22)*(1-2*x+x^2))*x);

 

 

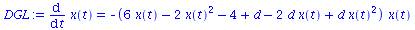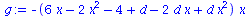	(3.7)

 

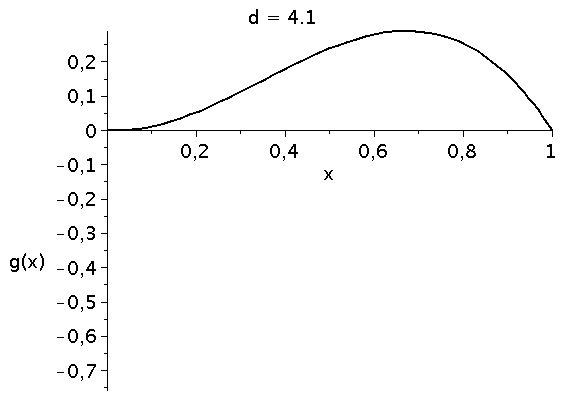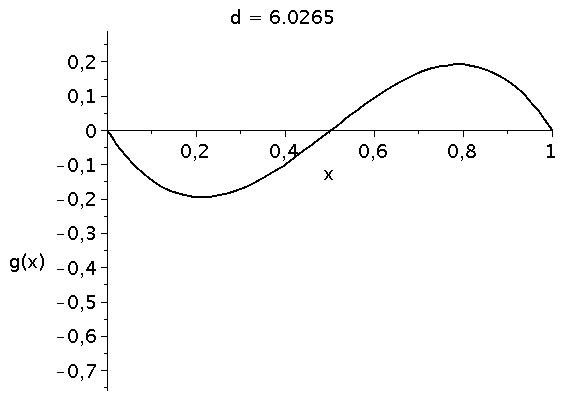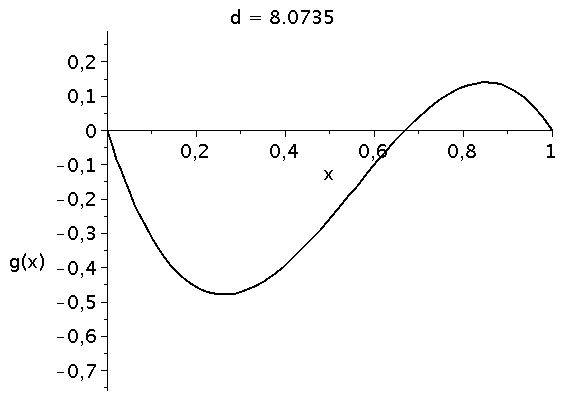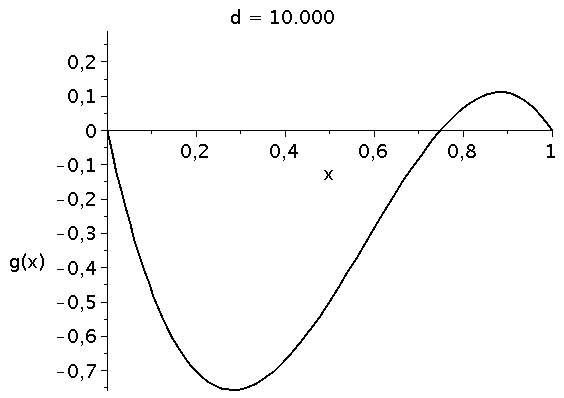
Die die zeitliche Entwicklung bestimmende Funktion g(x) besitzt das folgende Aussehen (Variation des Parameters d im Bereich 4.1 bis 10): 

>	animate(plot, [g, x=0..1,color=black,thickness=2], d=4.1..10,labels=["x","g(x)"],labelfont=[HELVETICA,15],axesfont=[HELVETICA,15],font=[HELVETICA,15],frames=50);

 

Die interne Nullstelle der Funktion g(x) entspricht dem gemischten Nash-Gleichgewicht des Spiels: 

>	solve(g=0,x);

 

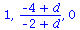(3.8)

 

x(t), der Anteil der Spieler die zum Zeitpunkt t die Strategie "Hasen jagen" spielen, hängt neben der Funktion g(x) von dem Anfangswert x(t=0) ab.Setzt man z.B. x(t=0)=0.5 (entspricht einer Anfangspopulation von 50% "Hasen jagen" und 50% "Hirsch jagen") und setzt den Parameter d auf den Wert 7 (d=7) so kann man die Differentialgleichung wie folgt nummerisch lösen und grafisch darstellen:  

>	x0:=0.50: setd:=7: LoesDGL:=dsolve({subs(d=setd,DGL),x(0)=x0},x(t),type=numeric):

 

>	tanf:=0: tend:=4: odeplot(LoesDGL,[t,x(t)],tanf..tend,view=[tanf..tend,0..1],thickness=2,color=black);

 

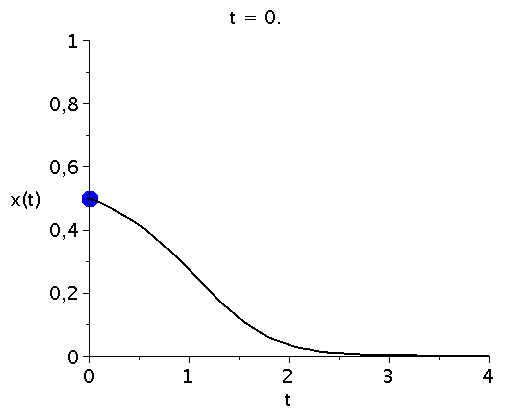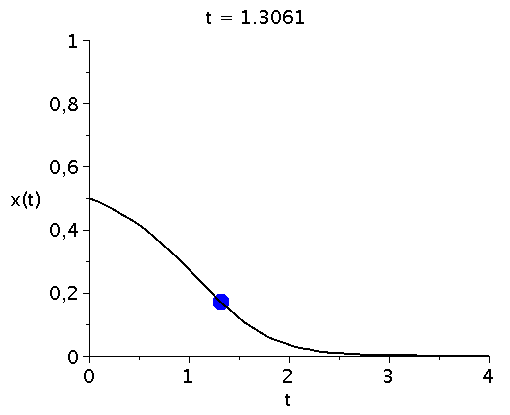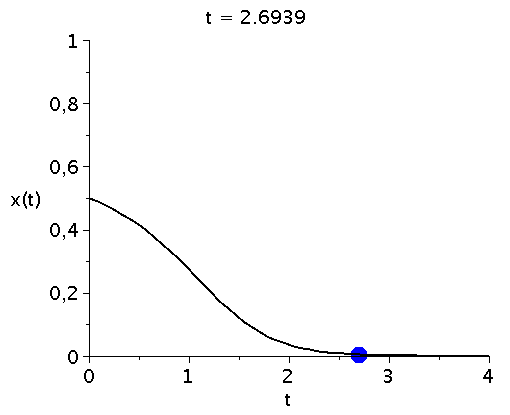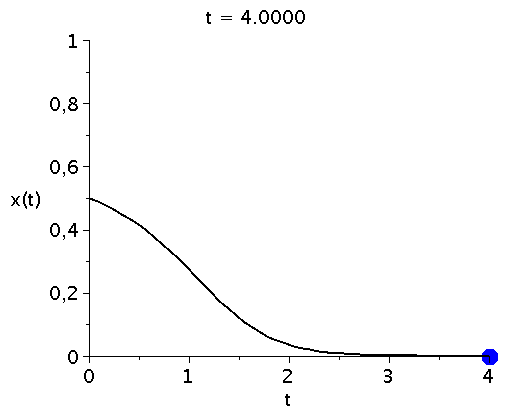
bzw. in einer Animation dargestellt: 

>

ball := proc(t,x) plots[pointplot]([[t,rhs(LoesDGL(x)[2])]],color=blue,symbol=solidcircle,symbolsize=30) end proc: Ani1:=animate(ball, [t,t], t=tanf..tend,view=[tanf..tend,0..1],frames=50): P1:=odeplot(LoesDGL,[t,x(t)],tanf..tend,view=[tanf..tend,0..1],thickness=2,color=black): display(Ani1,P1,labels=["t","x(t)"],labelfont=[HELVETICA,15],axesfont=[HELVETICA,15],font=[HELVETICA,15]);

 

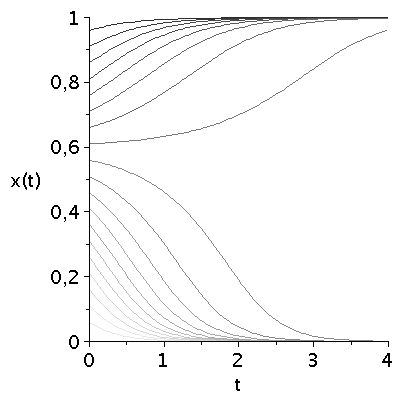
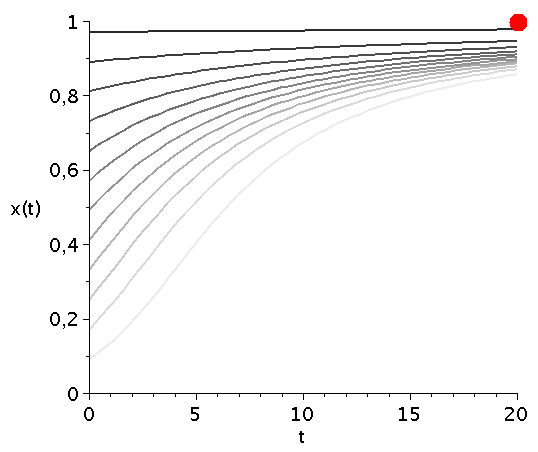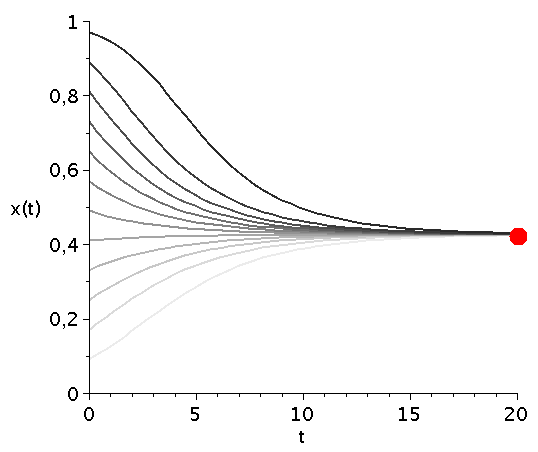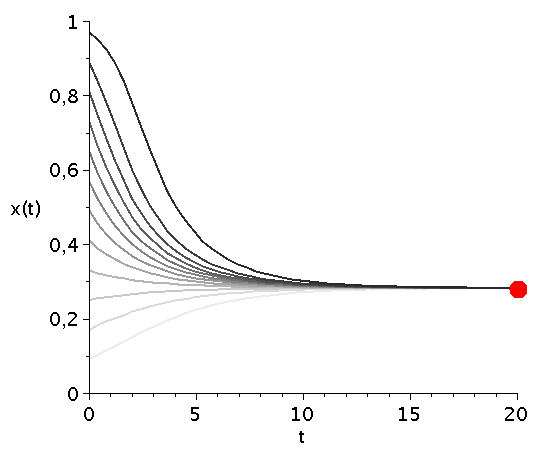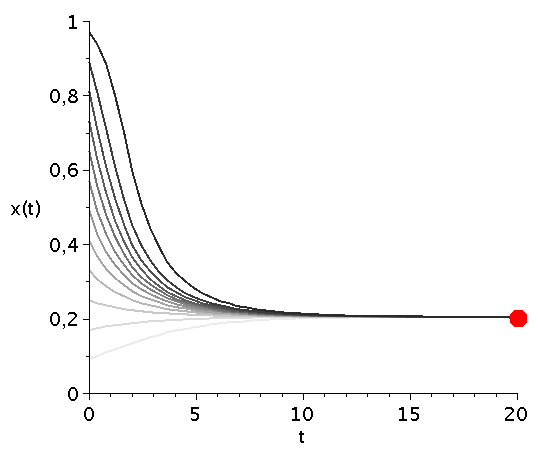
Für unterschiedliche Anfangswerte der Populationszusammensetzung ergibt sich das folgende Bild: 

>	setV:=7: tanf:=0: tend:=4: ii:=0: for x_0 from 0.01 by 0.05 to 0.99 do ii:=ii+1: Loes:=dsolve({subs(d=setd,DGL),x(0)=x_0},x(t),type=numeric): Plot_FT[ii]:=odeplot(Loes,[t,x(t)],tanf..tend,color=RGBToColor([255-round(x_0*220), 255-round(x_0*220), 255-round(x_0*220)]),view=[tanf..tend,0..1]): end do:

 

>	display(seq(Plot_FT[i],i=1..ii),labels=["t","x(t)"],labelfont=[HELVETICA,15],axesfont=[HELVETICA,15],font=[HELVETICA,15]);

 

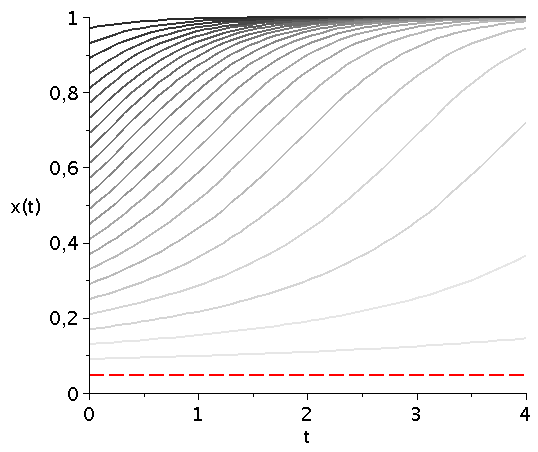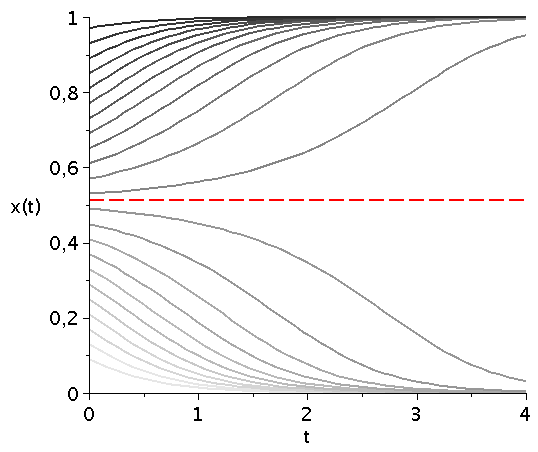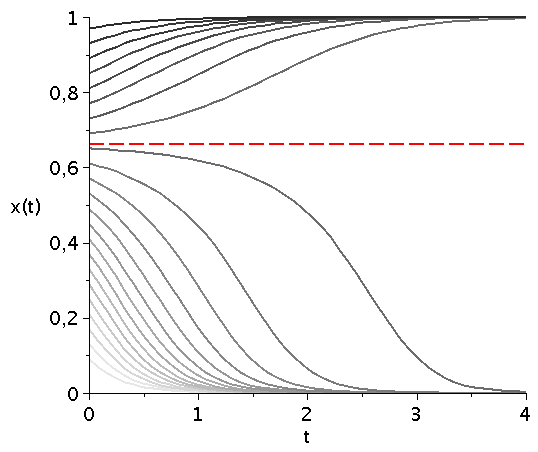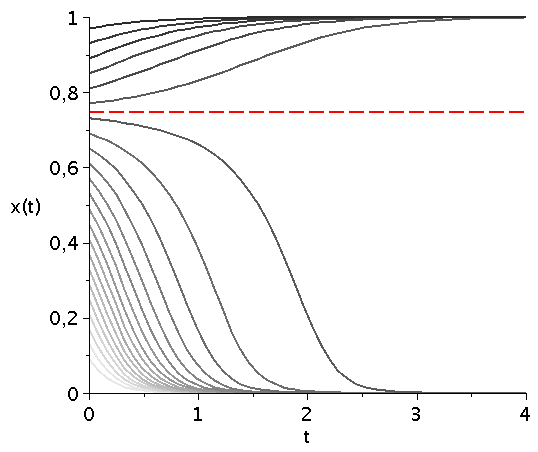
Die durch das gemischte Nash-Gleichgewicht (bzw. die interne Nullstelle der Funktion g(x)) festgelegte gemischte Strategie der Population stellt eine Grenzstrategie im Hirschjagt-Spiels dar. Abhängig von der gewählten Anfangszusammensetzung der Population entwickelt sich das System zu einem Zustand in dem entweder alle Spieler "Hasen jagen" (x=0) bzw. alle "Hirsch jagen" (x=1) wählen. Ist der Wert der gewählten Anfangszusammensetzung größer (bzw. kleiner) als der Wert des gemischten Nash-Gleichgewichts so wird die Strategienwahl der Population im Laufe der Zeit zu x=1 (bzw. x=0) gezogen. 

Variiert man den Parameter d (hier d=[4.1,10]), so verschiebt man diese durch das gemischte Nash-Gleichgewicht bestimmte Grenzstrategie (siehe gestrichelte rote Linie): 

>

tanf:=0: tend:=4: jj:=0: for d_s from 4.1 by 0.2 to 10 do ii:=0: jj:=jj+1: for x_0 from 0.01 by 0.04 to 0.99 do ii:=ii+1: Loes:=dsolve({subs(d=d_s,DGL),x(0)=x_0},x(t),type=numeric): Plot_FT[ii,jj]:=odeplot(Loes,[t,x(t)],tanf..tend,color=RGBToColor([255-round(x_0*220), 255-round(x_0*220), 255-round(x_0*220)]),view=[tanf..tend,0..1],thickness=2): end do: GemNash:=display(line([0,(d_s-4)/(d_s-2)], [4,(d_s-4)/(d_s-2)], color=red, linestyle=dash,thickness=2)): Ani_FT[jj]:=display(seq(Plot_FT[i,jj],i=1..ii),GemNash): end do:

 

>	display(seq(Ani_FT[j],j=1..jj),labels=["t","x(t)"],labelfont=[HELVETICA,15],axesfont=[HELVETICA,15],font=[HELVETICA,15],insequence=true);

 

>

 

>

 

Anti-Koordinationsspiele 

>

 

Wir starten zunächst wieder von einem allgemeinen Spiel einer gemischten Erweiterung eines simultanen (2 Spieler)-(2 Strategien) Spiels in strategischer Form mit symmetrischer Auszahlungmatrix.  

Ein Anti-Koordinationsspiel existiert, falls die Parameter a, b, c und d der Auszahlungmatrix die folgenden Bedingungen erfüllen: a < c und b > d . 

Bei dieser Spielklasse existieren drei Nash-Gleichgewichte, ein gemischtes Nash-Gleichgewicht und zwei reine, unsymmetrische Nash-Gleichgewicht bei (x,y)=(0,1) und (x,y)=(0,1).  

>	restart: with(plots): with(plottools): with(LinearAlgebra): with(ColorTools):

 

Definition der Auszahlunsmatrix für Spieler A: 

>	D_A11:=a: D_A12:=b: D_A21:=c: D_A22:=d: D_A:=Matrix(2,2,[D_A11,D_A12,D_A21,D_A22]);

 

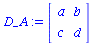(4.1)

 

Da sich das Spiel um ein symmetrisches (2 Personen)-(2 Strategien) Spiel handelt, erhält man die Auszahlunsmatrix für Spieler B durch die transponierte Matrix des Spielers A:  

>	D_B:=Transpose(D_A);

 

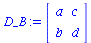(4.2)

 

Unter Verwendung der gemischten Strategien (x,y) lässt sich eine gemischte Auszahlungsfunktion der Spieler wie folgt definieren: 

>	Auszahlungsfunktion_A:=(x,y)->D_A[1,1]*x*y+D_A[1,2]*x*(1-y)+D_A[2,1]*(1-x)*y+D_A[2,2]*(1-x)*(1-y); Auszahlungsfunktion_B:=(x,y)->D_B[1,1]*x*y+D_B[1,2]*x*(1-y)+D_B[2,1]*(1-x)*y+D_B[2,2]*(1-x)*(1-y);

 

 

	(4.3)

 

Der Spezialfall des gemischten Nash-Gleichgewichts besteht, falls die partielle Ableitung der gemischten Auszahlungsfläche verschwindet, also 

>	EqGemNashy:=diff(Auszahlungsfunktion_A(x,y),x)=0; EqGemNashx:=diff(Auszahlungsfunktion_B(x,y),y)=0;

 

 

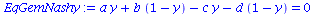	(4.4)

 

Koordinationsspiele haben somit ein gemischtes Nash-Gleichgewicht bei den folgenden Werten der gemischten Strategien: 

>	GemNashyy:=solve(EqGemNashy,y); GemNashx:=solve(EqGemNashx,x);

 

 

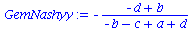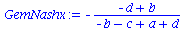	(4.5)

 

Beispiel: Falke-Taube Spiel 

a < c und b > d 

>	a:=1/2-V/2: b:=1: c:=0: d:=1/2:

 

Die Auszahlungsmatrix entspricht dem schon in der Vorlesung besprochenen Falke-Taube Spiel, wobei der Parameter V, welcher die negative Auszahlung verursacht durch die verletzungen während eines Falke-Falke Kampfes, widerspiegelt, zunächst noch variabel gehalten wurde. Da es sich um ein Anti-Koordinationsspiel handel muss folgende Bedingung gelten: a < 0, also V > 1 gelten . Das gemischtes Nash-Gleichgewicht dieses Spiels befindet sich bei der folgenden Strategienkombination: 

>	GemNashyy:=solve(EqGemNashy,y); GemNashx:=solve(EqGemNashx,x);

 

 

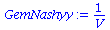	(4.6)

 

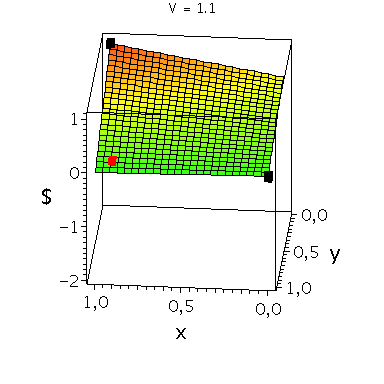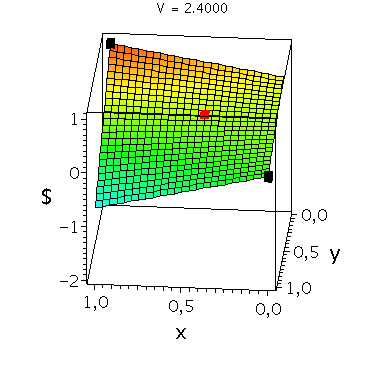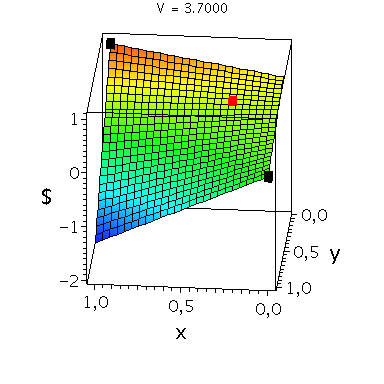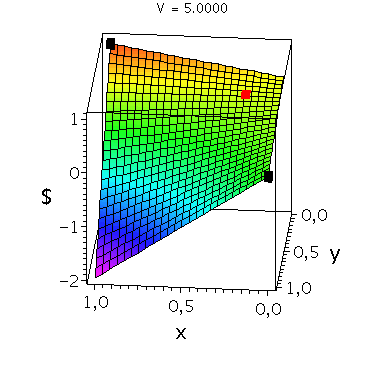
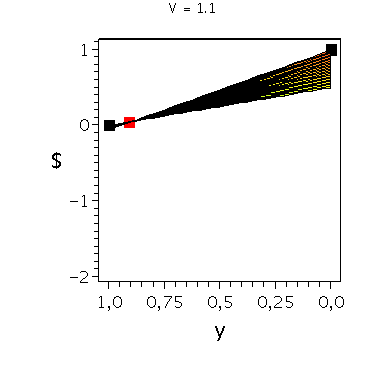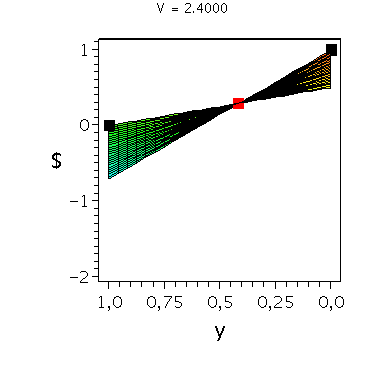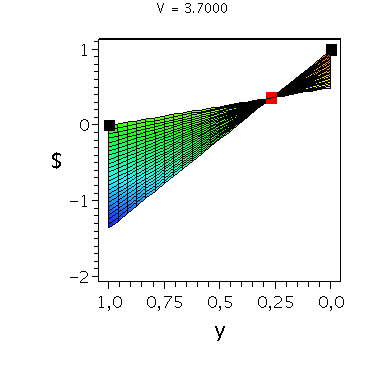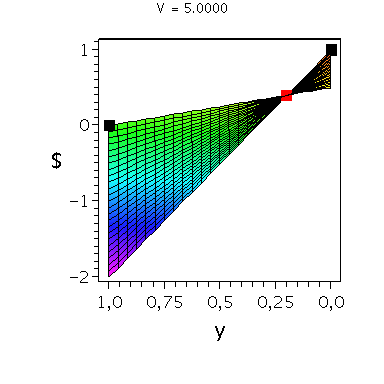
In der folgenden Animation wird die gemischte Auszahlungsfunktion des Spielers A im oben definierten Falke-Taube Spiel bei Variation des Parameters V im Bereich -0.1 bis 10 gezeigt. Man erkennt gut, wie sich die Position des gemischten Nash-Gleichgewichts verschiebt, wobei zusätzlich die beiden reinen, unsymmetrischen Nash-Gleichgewichte bei (x,y)=(1,0) und (x,y)=(0,1) bestehen bleiben: 

>

Sizecuboid:=0.05: Sizecuboidz:=0.15: Ani_gemNash:=animate(plots[display], [cuboid([-Sizecuboid/2+GemNashx, -Sizecuboid/2+GemNashyy, Auszahlungsfunktion_A(GemNashx,GemNashyy)-Sizecuboidz/2], [Sizecuboid/2+GemNashx, Sizecuboid/2+GemNashyy, Auszahlungsfunktion_A(GemNashx,GemNashyy)+Sizecuboidz/2])], V = 1.1 .. 5,scaling=constrained, style = patchnogrid,color=red): Ani_reinNash0:=animate(plots[display], [cuboid([-Sizecuboid/2+0, -Sizecuboid/2+1, Auszahlungsfunktion_A(0,1)-Sizecuboidz/2], [Sizecuboid/2+0, Sizecuboid/2+1, Auszahlungsfunktion_A(0,1)+Sizecuboidz/2])], V = 1.1 .. 5,scaling=constrained, style = patchnogrid,color=black): Ani_reinNash1:=animate(plots[display], [cuboid([-Sizecuboid/2+1, -Sizecuboid/2+0, Auszahlungsfunktion_A(1,0)-Sizecuboidz/2], [Sizecuboid/2+1, Sizecuboid/2+0, Auszahlungsfunktion_A(1,0)+Sizecuboidz/2])], V = 1.1 .. 5,scaling=constrained, style = patchnogrid,color=black):

 

>

Ani2:=animate(plot3d, [Auszahlungsfunktion_A(x,y),x=0..1,y=0..1], V = 1.1 .. 5,axes=boxed,labels=[x,"y","$"],orientation=[95,65],shading=ZHUE,axesfont=[HELVETICA,13],font=[HELVETICA,15]): Ani3:=animate(plot3d, [Auszahlungsfunktion_A(x,y),x=0..1,y=0..1], V = 1.1 .. 5,axes=boxed,labels=[x,"y","$"],orientation=[180,90],title="Auszahlung an Spieler A",shading=ZHUE,axesfont=[HELVETICA,13],font=[HELVETICA,15],titlefont=[HELVETICA,16]):

 

>	display(Ani_gemNash,Ani_reinNash0,Ani_reinNash1,Ani2,scaling=unconstrained);

 

>	display(Ani_gemNash,Ani_reinNash0,Ani_reinNash1,Ani3,scaling=unconstrained);

 

Die Differentialgleichung, die die zeitliche Entwicklung des Populationsvektors x(t) beschreibt lautet: 

>	DGL:=diff(x(t),t)=simplify(((D_A11-D_A21)*(x(t)-x(t)^2) + (D_A12-D_A22)*(1-2*x(t)+x(t)^2))*x(t)); g:=simplify(((D_A11-D_A21)*(x-x^2) + (D_A12-D_A22)*(1-2*x+x^2))*x);

 

 

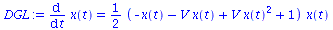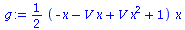	(4.7)

 

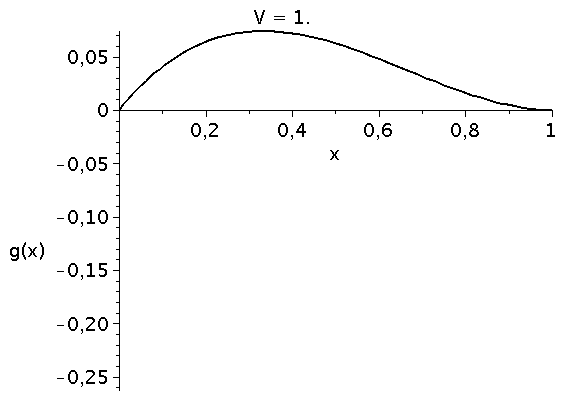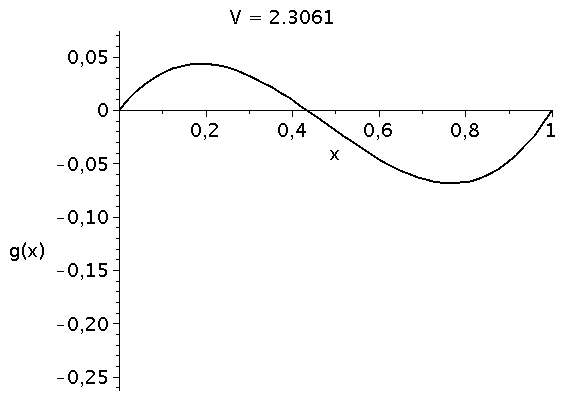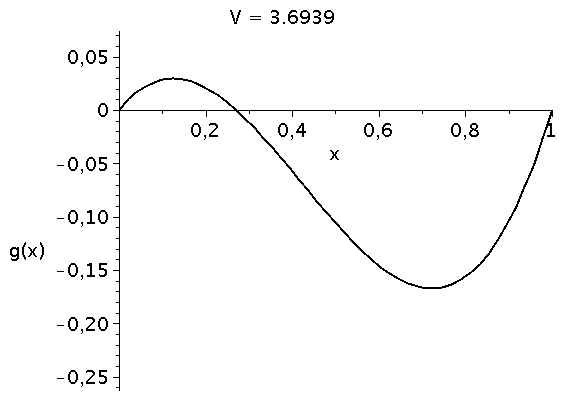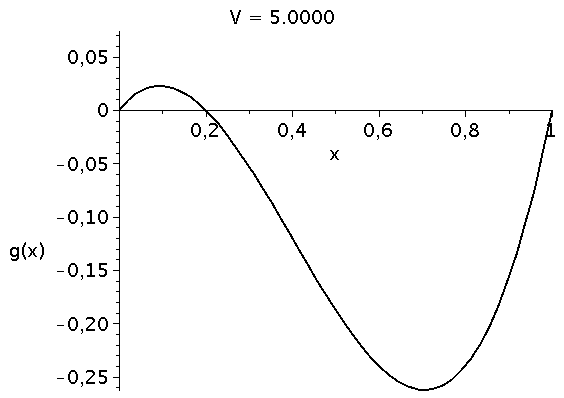
Die die zeitliche Entwicklung bestimmende Funktion g(x) besitzt das folgende Aussehen (Variation des Parameters V im Bereich [1,5]) 

>	animate(plot, [g, x=0..1,color=black,thickness=2], V=1..5,labels=["x","g(x)"],labelfont=[HELVETICA,15],axesfont=[HELVETICA,15],font=[HELVETICA,15],frames=50);

 

Die interne Nullstelle der Funktion g(x) entspricht dem gemischten Nash-Gleichgewicht des Spiels: 

>	solve(g=0,x);

 

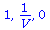(4.8)

 

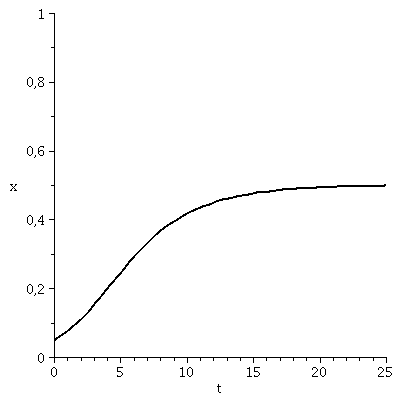
x(t), der Anteil der Spieler die zum Zeitpunkt t die Strategie "Falke" spielen, hängt neben der Funktion g(x) von dem Anfangswert x(t=0) ab.Setzt man z.B. x(t=0)=0.05 (entspricht einer Anfangspopulation von 5% Falken und 95% Tauben) und setzt den Parameter V auf den Wert 2 (V=2) so kann man die Differentialgleichung wie folgt nummerisch lösen und grafisch darstellen:  

>	x0:=0.05: setV:=2: LoesDGL:=dsolve({subs(V=setV,DGL),x(0)=x0},x(t),type=numeric):

 

>	tanf:=0: tend:=25: odeplot(LoesDGL,[t,x(t)],tanf..tend,view=[tanf..tend,0..1],thickness=2,color=black);

 

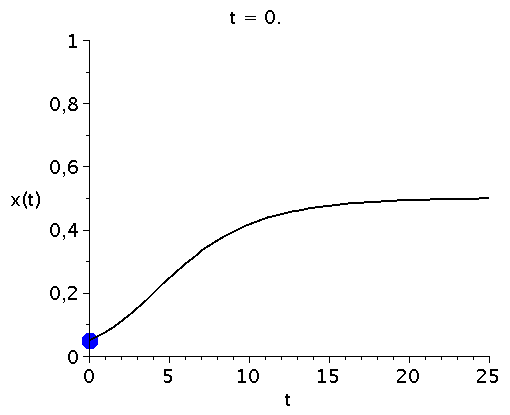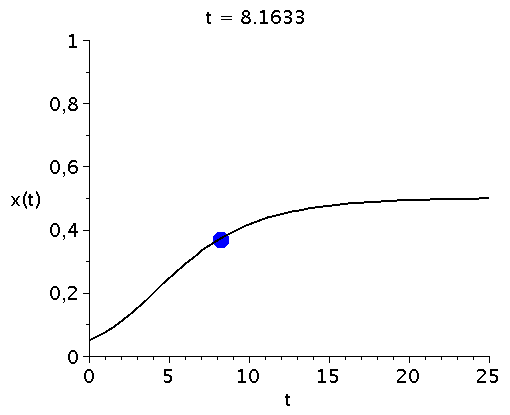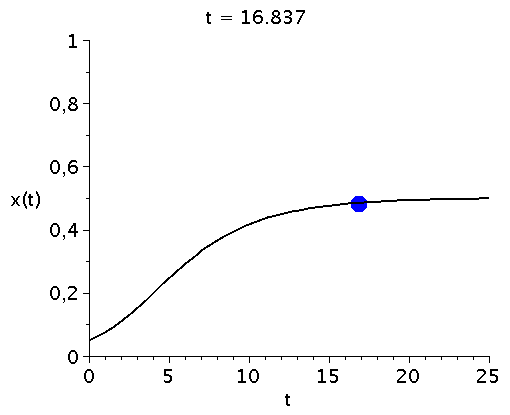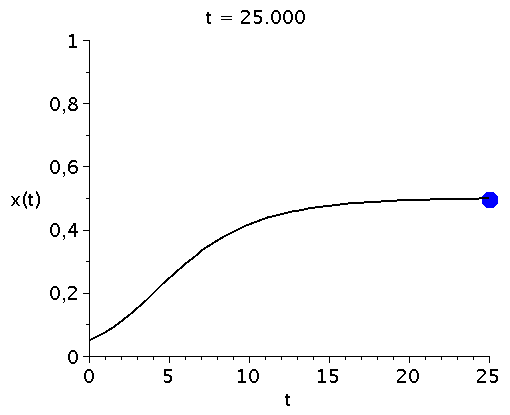
bzw. in einer Animation dargestellt: 

>

ball := proc(t,x) plots[pointplot]([[t,rhs(LoesDGL(x)[2])]],color=blue,symbol=solidcircle,symbolsize=30) end proc: Ani1:=animate(ball, [t,t], t=tanf..tend,view=[tanf..tend,0..1],frames=50): P1:=odeplot(LoesDGL,[t,x(t)],tanf..tend,view=[tanf..tend,0..1],thickness=2,color=black): display(Ani1,P1,labels=["t","x(t)"],labelfont=[HELVETICA,15],axesfont=[HELVETICA,15],font=[HELVETICA,15]);

 

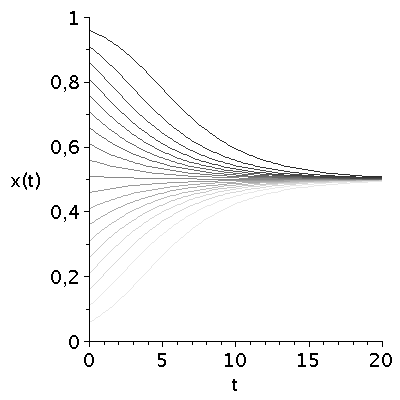
Für unterschiedliche Anfangswerte der Populationszusammensetzung ergibt sich das folgende Bild: 

>

setV:=2: tanf:=0: tend:=20: ii:=0: for x_0 from 0.01 by 0.05 to 0.99 do ii:=ii+1: Loes:=dsolve({subs(V=setV,DGL),x(0)=x_0},x(t),type=numeric): Plot_FT[ii]:=odeplot(Loes,[t,x(t)],tanf..tend,color=RGBToColor([255-round(x_0*220), 255-round(x_0*220), 255-round(x_0*220)]),view=[tanf..tend,0..1]): end do:

 

>	display(seq(Plot_FT[i],i=1..ii),labels=["t","x(t)"],labelfont=[HELVETICA,15],axesfont=[HELVETICA,15],font=[HELVETICA,15]);

 

Die durch das gemischte Nash-Gleichgewicht (bzw. die interne Nullstelle der Funktion g(x)) festgelegte gemischte Strategie der Population (1/V) stellt die evolutionär stabile Strategie des Falke-Taube Spiels dar. Unabhängig von der gewählten Anfangszusammensetzung der Population entwickelt sich das System zu einem Zustand der Koexistenz beider Strategien, wobei die für große Zeiten asymptotisch erreichte Populationszusammensetzung durch den Wert des internen gemischten Nash-Gleichgewichts gegeben ist und die evolutionär stabile Strategie darstellt. 

Variiert man den Parameter V (hier V=[1,5]), so verschiebt man die evolutionär stabile Strategie (siehe roter Kreis): 

>

tanf:=0: tend:=20: jj:=0: for V_s from 1 by 0.15 to 5 do ii:=0: jj:=jj+1: for x_0 from 0.01 by 0.08 to 0.99 do ii:=ii+1: Loes:=dsolve({subs(V=V_s,DGL),x(0)=x_0},x(t),type=numeric): Plot_FT[ii,jj]:=odeplot(Loes,[t,x(t)],tanf..tend,color=RGBToColor([255-round(x_0*220), 255-round(x_0*220), 255-round(x_0*220)]),view=[tanf..tend,0..1],thickness=2): end do: ESS:=plots[pointplot]([[20,1/V_s]],color=red,symbol=solidcircle,symbolsize=30): Ani_FT[jj]:=display(seq(Plot_FT[i,jj],i=1..ii),ESS): end do:

 

>	display(seq(Ani_FT[j],j=1..jj),labels=["t","x(t)"],labelfont=[HELVETICA,15],axesfont=[HELVETICA,15],font=[HELVETICA,15],insequence=true);

 

>

 

>

 

>