I.1.3 Nash-Gleichgewichte in gemischten Strategien
Im Folgenden werden wir die im Unterkapitel I.1.1 vorgestellte Definition eines Spiels verallgemeinern, indem wir die Menge der reinen Strategien ${\bf \cal{S}}$ zur Menge der gemischten Strategien ${\bf \tilde{\cal{S}}}$ erweitern. Ein solches Spiel bezeichnet man als die gemischte Erweiterung eines simultanen ($N$ Spieler)-($m$ Strategien) Spiels in strategischer Form mit Auszahlung.
Die Menge der gemischten Strategien der Spieler ${\bf \cal {\tilde{S}}} = {\cal {\tilde{S}}}^1 \times {\cal {\tilde{S}}}^2 \times ... \times {\cal {\tilde{S}}}^N$ setzt sich aus den einzelnen Mengen der gemischten Strategien der Spieler zusammen. Die Menge der gemischten Strategien des Spielers $\mu \in {\bf \cal I}$ (${\cal {\tilde{S}}}^\mu$) kann als eine mathematische Verallgemeinerung der Menge der reinen Strategien ${\cal {{S}}}^\mu$ verstanden werden, wobei die einzelnen Elemente der Menge der gemischten Strategien des Spielers $\mu$ aus $m_\mu$ reellwertigen Zahlen bestehen, die folgenden Normalisierungsbedingungen unterliegen:
\[
{\cal {\tilde{S}}}^\mu = \left\{ ({\tilde{s}}_1^\mu, {\tilde{s}}_2^\mu, ..., {\tilde{s}}^\mu_{m_\mu}) \mid \sum_{i=1}^{m_\mu} {\tilde{s}}^\mu_i =1 , {\tilde{s}}^\mu_i \geq 0 , i=1, 2, ..., m_\mu \right\}
\]
Die einzelnen Werte ${\tilde{s}}^\mu_i$ können als die Wahrscheinlichkeit des Spielers $\mu$ zur Wahl der Strategie $i$ interpretiert werden. Unter Verwendung der gemischten Strategien lässt sich eine gemischte Auszahlungsfunktion der Spieler wie folgt definieren:
\[
{\bf \cal {\tilde{\$}}} = \left( {\cal {\tilde{\$}}}^1, {\cal {\tilde{\$}}}^2, ... , {\cal {\tilde{\$}}}^N \right) : {\bf \cal {\tilde{S}}} \rightarrow ℝ^N \,, \,\, \hbox{wobei} \quad
{\cal {\tilde{\$}}}^\mu ({\tilde{s}}^1, {\tilde{s}}^2, ... , {\tilde{s}}^N) = \sum_{i_1=1}^{m_1} \sum_{i_2=1}^{m_2} ... \sum_{i_N=1}^{m_N} {\cal \$}^\mu (s_{i_1}^1, s_{i_2}^2, ... , s_{i_N}^N) \prod_{\nu=1}^N {\tilde{s}}_{i_\nu}^\nu
\]
Im folgenden wird das Konzept der gemischten Erweiterung für den Fall eines ($2$ Spieler)-($2$ Strategien) Spiels illustrieren. Die Menge der gemischten Strategien des Spielers A (${\bf \tilde{\cal S}}^A$) und B (${\bf \tilde{\cal S}}^B$) kann als eine mathematische Verallgemeinerung der Menge der reinen Strategien (${\bf {\cal S}}^A$ und ${\bf {\cal S}}^B$) verstanden werden. Die einzelnen Elemente der Menge der gemischten Strategien eines Spielers $\mu=A,B$ ($\tilde{{\bf s}}^\mu=(\tilde{s}^\mu_1,\tilde{s}^\mu_2) \in {\bf {\cal S}}^\mu$) besteht aus zwei reellwertigen Zahlen ($\tilde{s}^\mu_1 \in [0,1]$ und $\tilde{s}^\mu_2 \in [0,1]$) und kann als die Wahrscheinlichkeit des Spielers $\mu$ zur Wahl der Strategie 1 ($\tilde{s}^\mu_1$) bzw. der Strategie 2 ($\tilde{s}^\mu_2$) interpretiert werden. Desweiteren gilt die folgende Normalisierungsbedingung: $\tilde{s}^\mu_1 + \tilde{s}^\mu_2 =1 \,\, \forall \, \mu=A,B$.
Unter Verwendung der Auszahlungsmatrizen des Spielers A ($\hat{\bf {\cal \$}}^A$) und B ($\hat{\bf {\cal \$}}^B$) schreibt sich die gemischte Auszahlungsfunktion des Spielers $\mu=A,B$ wie folgt:
\[
\begin{eqnarray}
&&{\bf \tilde{\cal \$}}^\mu: \left( {\bf \tilde{\cal S}}^A \times {\bf \tilde{\cal S}}^B \right) \rightarrow ℝ \label{Glei:MixedPayoff_general}\\
&&{\bf \tilde{\cal \$}}^\mu((\tilde{s}^A_1,\tilde{s}^A_2),(\tilde{s}^B_1,\tilde{s}^B_2))=\$^\mu_{11} \tilde{s}^A_1 \tilde{s}^B_1 + \$^\mu_{12} \tilde{s}^A_1 \tilde{s}^B_2+\$^\mu_{21} \tilde{s}^A_2 \tilde{s}^B_1+\$^\mu_{22} \tilde{s}^A_2 \tilde{s}^B_2 \nonumber
\end{eqnarray}
\]
Aufgrund der Normalisierungsbedingung vereinfacht sich die gemischte Auszahlungsfunktion wie folgt:
\[
\begin{eqnarray}
&&{\bf \tilde{\cal \$}}^\mu: \left( [0,1] \times [0,1] \right) \rightarrow ℝ \\&& {\bf \tilde{\cal \$}}^\mu(\tilde{s}^A,\tilde{s}^B)=\$^\mu_{11} \tilde{s}^A \tilde{s}^B + \$^\mu_{12} \tilde{s}^A (1-\tilde{s}^B)+\$^\mu_{21} (1-\tilde{s}^A) \tilde{s}^B+\$^\mu_{22} (1-\tilde{s}^A) (1-\tilde{s}^B) \nonumber\label{Glei:MixedPayoff_general1}
\end{eqnarray}
\]
, wobei $\tilde{s}^A:=\tilde{s}^A_1$, $\tilde{s}^B:=\tilde{s}^B_1$, $\tilde{s}^A_2=1-\tilde{s}^A_1$ und $\tilde{s}^B_2=1-\tilde{s}^B_1$.
Ähnlich wie in Unterkapitel I.1.2 werden im Folgenden die beiden fundamentalen Gleichgewichtskonzepte der Spieltheorie (dominante Strategien und Nash-Gleichgewichte) in ihrer gemischten Erweiterung vorgestellt.
Eine Strategienkombination $(\tilde{s}^{A\dagger},\tilde{s}^{B\dagger})$ ist ein Gleichgewicht in dominanten Strategien, wenn die folgenden Bedingungen erfüllt sind:
\[
\begin{eqnarray}
&&\mbox{Gleichgewicht in dominanten Strategien:}\\&&{\bf \tilde{\cal \$}}^\mu(\tilde{s}^{A\dagger},\tilde{s}^{B}) \,\, \geq \,\, {\bf \tilde{\cal \$}}^\mu(\tilde{s}^{A},\tilde{s}^{B}) \quad \forall \,\,\, \mu=A,B \,\, \hbox{und} \,\,\, \tilde{s}^{A}, \tilde{s}^{B} \in [0,1] \nonumber\label{Glei:Dominant_Strategy}
\end{eqnarray}
\]
Eine Strategienkombination $(\tilde{s}^{A*},\tilde{s}^{B*})$ nennt man ein Nash-Gleichgewicht, falls die folgenden Bedingungen erfüllt sind:
\[
\begin{eqnarray}
&&\mbox{Nash-Gleichgewicht:}\label{Glei:Nash_equilibriumaa}\\&&{\bf \tilde{\cal \$}}^A(\tilde{s}^{A*},\tilde{s}^{B*}) \,\, \geq \,\, {\bf \tilde{\cal \$}}^A(\tilde{s}^{A},\tilde{s}^{B*}) \quad \forall \,\,\, \tilde{s}^{A} \in [0,1] \nonumber\\
&& {\bf \tilde{\cal \$}}^B(\tilde{s}^{A*},\tilde{s}^{B*}) \,\, \geq \,\, {\bf \tilde{\cal \$}}^B(\tilde{s}^{A*},\tilde{s}^{B}) \quad \forall \,\,\, \tilde{s}^{B} \in [0,1] \nonumber
\end{eqnarray}
\]
Ein Spezialfall des Nash-Gleichgewichts besteht, falls die partielle Ableitung der gemischten Auszahlungsfläche verschwindet. Man nennt dann ein solches Nash-Gleichgewicht $(\tilde{s}^{A\star},\tilde{s}^{B\star})$ ein internes Nash-Gleichgewicht bzw. ein Nash-Gleichgewicht in gemischten Strategien.
\[
\begin{eqnarray}
&&\mbox{Nash-Gleichgewicht in gemischten Strategien:} \label{Glei:Interior_Nash}\\ &&\left. \frac{ \partial {\bf \tilde{\cal \$}}^A(\tilde{s}^A,\tilde{s}^B)}{\partial \tilde{s}^A} \right|_{\tilde{s}^B=\tilde{s}^{B\star}}=0 \quad \forall \,\,\, \tilde{s}^{A} \in [0,1] \,\,\, , \,\, \tilde{s}^{B\star} \in ]0,1[
\nonumber\\
&&\left. \frac{ \partial {\bf \tilde{\cal \$}}^B(\tilde{s}^A,\tilde{s}^B)}{\partial \tilde{s}^B} \right|_{\tilde{s}^A=\tilde{s}^{A\star}}=0 \quad \forall \,\,\, \tilde{s}^{B} \in [0,1] \,\,\, , \,\, \tilde{s}^{A\star} \in ]0,1[\nonumber
\end{eqnarray}
\]
Veranschaulichung der dominanten Strategie "Gestehe" mittels der Abbildung der besten Antwort im Gefangenendilemma.
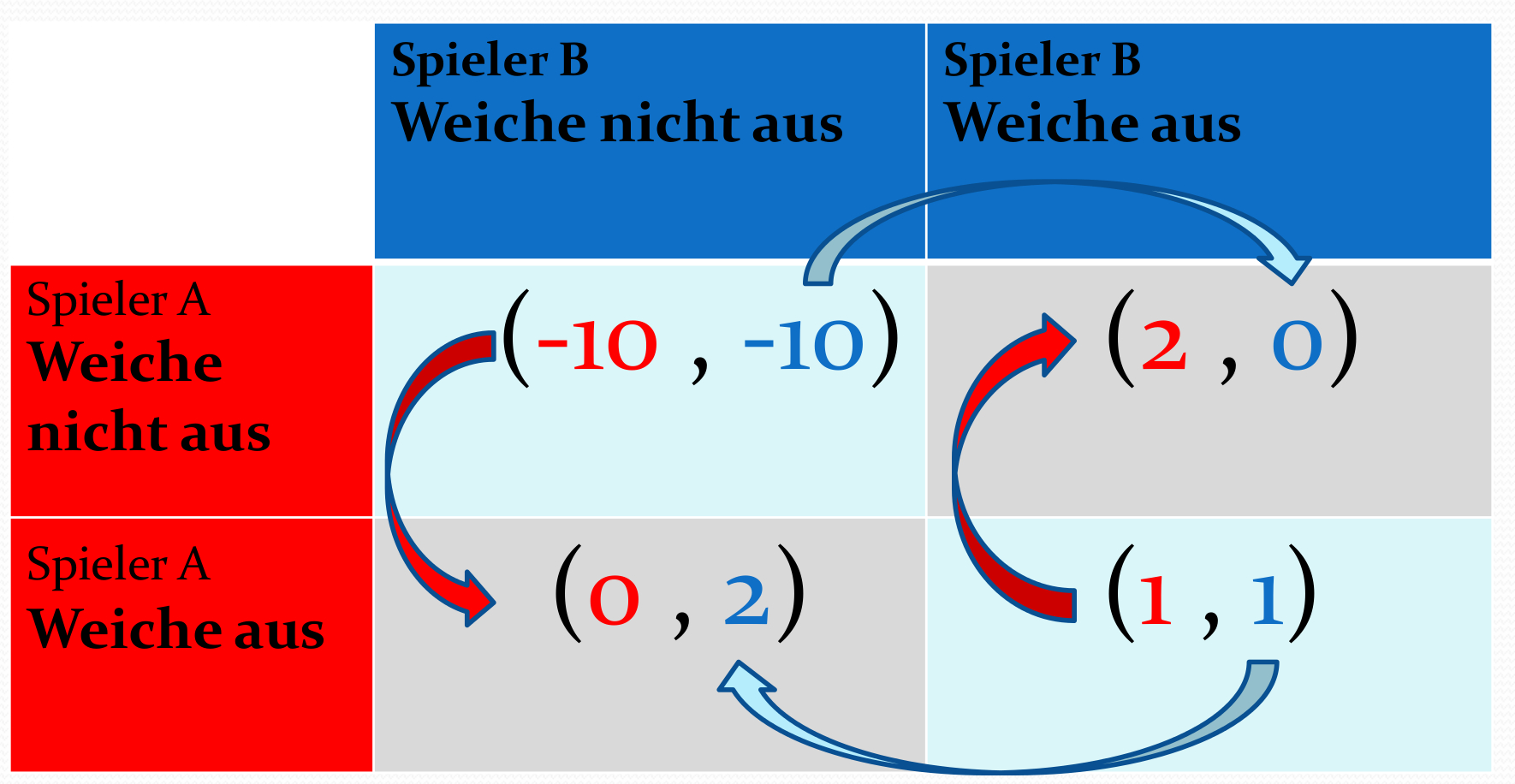
Beispiel: Das Angsthasen-Spiel (Chicken Game)
Das Angsthasen-Spiel ist ein simultanes (2 Personen)-(2 Strategien) Spiel und kann z.B. mittels der folgenden Geschichte illustriert werden (siehe z.B. S.16 in [2]).
"Auf einer einsamen Landstraße in Indien, bei der es nur eine geteerte Fahrbahn gibt, kommen sich zwei Autos mit hoher Geschwindigkeit entgegen. Beide Fahrer stehen nun vor der Entscheidung ob sie dem Anderen die Fahrbahn überlassen und Ausweichen oder mit hoher Geschwindigkeit weiterfahren um zu hoffen, dass der Andere ausweicht." Eine weitere Deutung des Angsthasen-Spiel basiert auf dem Film von Nicholas Ray "Denn sie wissen nicht was sie tun" aus dem Jahre 1955 (mit James Dean): "Jimbo und sein Erzfeind Buzz machen eine Mutprobe und rasen in ihren Autos auf eine Klippe zu. Derjenige ist der Angsthase, der als erster aus seinem Auto herrausspringt."
Die nebenstehende Abbildung zeigt eine mögliche Tabelle der "Auszahlungen" für die Version der aufeinander zusteuernden Autos auf der Landstraße. In dem Fall das keiner der Fahrer ausweicht wurde angenommen, dass es zu einem Unfall mit hoch negativer Auszahlung kommt. Mittels der Bestantwort-Pfeile (siehe Unterkapitel I.1.2) kann man zeigen, dass es in diesem Spiel keine dominante Strategie gibt, sondern zwei anti-symmetrische Nash-Gleichgewicht bei den Strategienkombinationen ${s}^{*} = \left( \hbox{Weiche nicht aus}, \hbox{Weiche aus} \right)$ und ${s}^{*} = \left( \hbox{Weiche aus}, \hbox{Weiche nicht aus} \right)$. Dies sind jedoch lediglich die reinen Nash-Gleichgewichte. Zusätzlich zu diesen existiert jedoch noch ein Nash-Gleichgewicht in gemischten Strategien, wie man wie folgt überprüft: Zunächst erweitern wir den Raum der reinen Strategien und führen die gemischte Strategie $\tilde{s}^A$ des Spielers A und $\tilde{s}^B$ des Spielers B ein, wobei $\tilde{s}^\mu=1$ der reinen Strategie "Weiche nicht aus" und $\tilde{s}^\mu=0$ der reinen Strategie "Weiche aus" entspricht. Unter Verwendung der nebenstehenden Auszahlungstabelle schreibt sich die gemischte Auszahlungsfunktion des Spielers $\mu=A$ wie folgt:
\[
\begin{eqnarray}
{\bf \tilde{\cal \$}}^A(\tilde{s}^A,\tilde{s}^B) &=& -10\, \tilde{s}^A \tilde{s}^B + 2\, \tilde{s}^A (1-\tilde{s}^B)+0 \,(1-\tilde{s}^A) \tilde{s}^B + 1\, (1-\tilde{s}^A) (1-\tilde{s}^B) \\
&=& -11\, \tilde{s}^A \tilde{s}^B + \tilde{s}^A - \tilde{s}^B +1
\end{eqnarray}
\]
Laut der oben angegebenen Bedingung befindet sich ein gemischtes Nash-Gleichgewicht an dem Punkt, bei welchem die partielle Ableitung der gemischten Auszahlungsfläche verschwindet (exemplarisch hier für Spieler A dargestellt):
\[
\left. \frac{ \partial {\bf \tilde{\cal \$}}^A(\tilde{s}^A,\tilde{s}^B)}{\partial \tilde{s}^A} \right|_{\tilde{s}^B=\tilde{s}^{B\star}}=-11\, \tilde{s}^{B\star} +1 \stackrel{!}{=}0 \quad \,\,\, \Rightarrow \,\,\, \tilde{s}^{B\star}=\frac{1}{11}\approx0.091
\]
In gleicher Weise kann man mittels der gemischten Auszahlungsfunktion des Spielers $\mu=B$ zeigen, dass auch $\tilde{s}^{A\star}=\frac{1}{11}$ gilt, so dass das gemischtes Nash-Gleichgewicht bei der gemischten Strategienkombination $(\tilde{s}^{A\star},\tilde{s}^{B\star})=(\frac{1}{11},\frac{1}{11})$ auftritt.
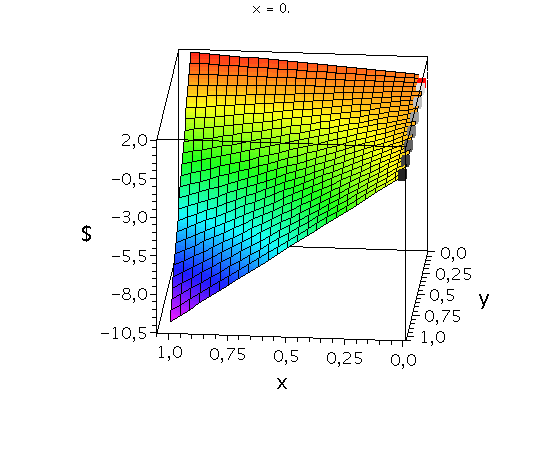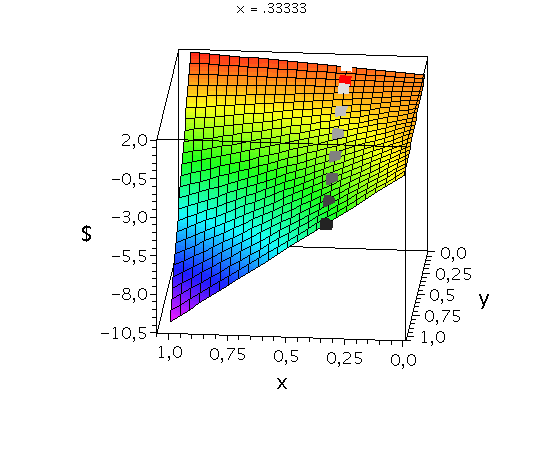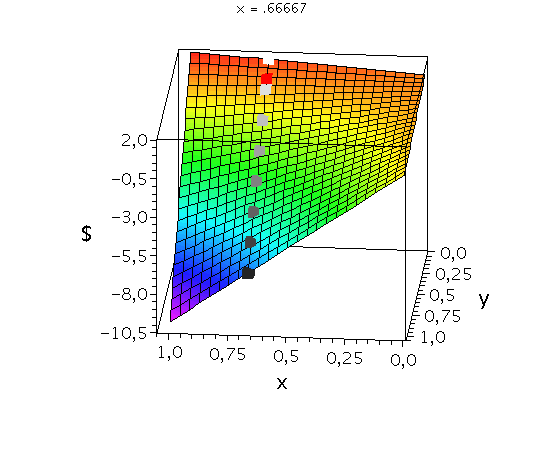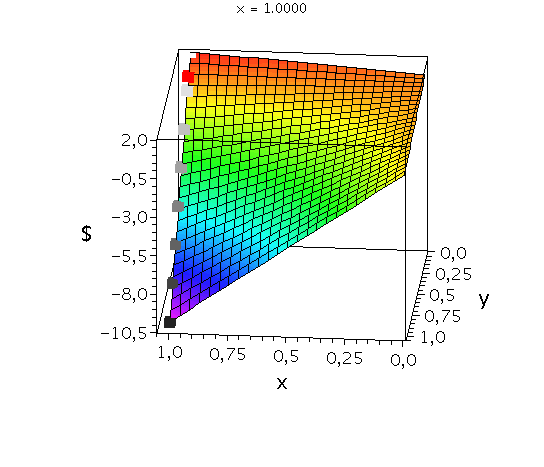
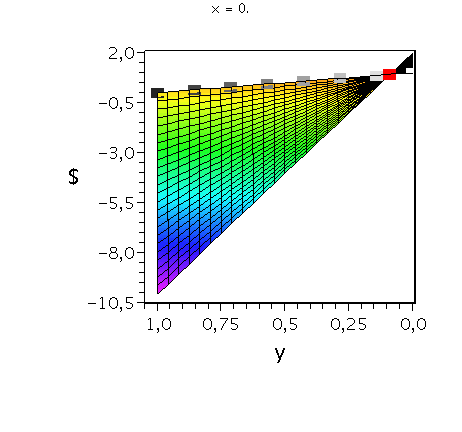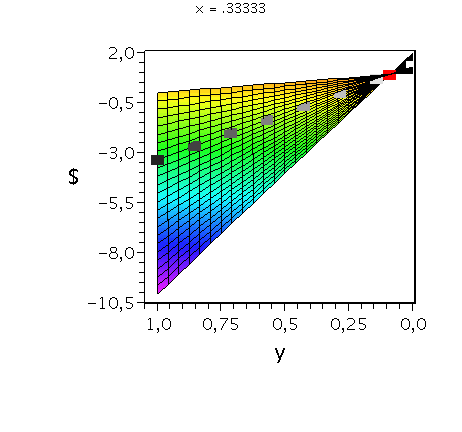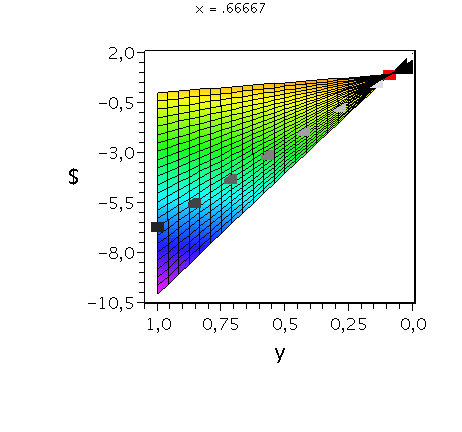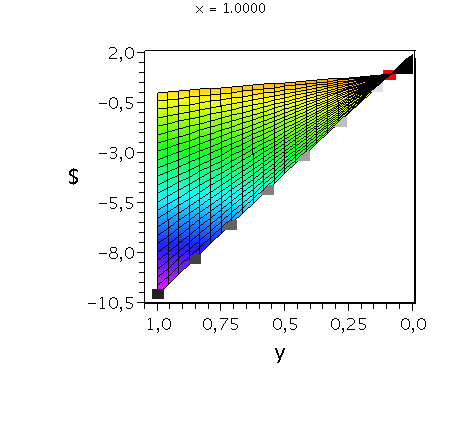
Auszahlungsfunktion des Spielers A. Die animierten Rechtecke zeigen die Veränderung der Auszahlung an Spieler A bei fester gemischter Strategie von Spieler B (${\bf y:=\tilde{s}^B}$=const) und Variation der Strategie von Spieler A (${\bf x:=\tilde{s}^A \in [0,1]}$). Das rote Rechteck veranschaulicht das gemischte Nash-Gleichgewicht.
Wir konzentrieren uns wieder auf die gemischte Auszahlungsfunktion des Spielers A und wollen anhand der Struktur der Auszahlungsfläche die Eigenschaften der reinen und gemischten Nash-Gleichgewichte verdeutlichen. Die Frage lautet: Unter der Annahme das Spieler B eine feste gemischte Strategie y:=$\tilde{s}^B$ spielt, welche Strategie x:=$\tilde{s}^A$ sollte Spieler A wählen, dass er seine Auszahlung maximiert?
Nehmen wir an, dass Spieler B die reine Strategie y=0 spielen würde, dann wäre es das Beste für Spieler A die reine Strategie x=1 zu spielen (siehe weißes Rechteck in den nebenstehenden Abbildungen).
Nehmen wir dagegen an, dass Spieler B die reine Strategie y=1 spielen würde, dann wäre es das Beste für Spieler A die reine Strategie x=0 zu spielen (siehe schwarzes Rechteck in den nebenstehenden Abbildungen).
Da beim gemischten Nash-Gleichgewicht die Steigung in x-Richtung bei festem y=$\frac{1}{11}$ identisch verschwindet verändert sich der Wert der Auszahlung für Spieler A bei Variation von x nicht (siehe rotes Rechteck).
Das Angsthasen-Spiel besitzt somit ein gemischtes Nash-Gleichgewicht bei der Strategienkombination (x,y)=$(\tilde{s}^{A\star},\tilde{s}^{B\star})=(\frac{1}{11},\frac{1}{11})$ und zwei reine, unsymmetrische Nash-Gleichgewicht bei (x,y)=(0,1) und (x,y)=(1,0). Die grauen Rechtecke veranschaulichen das Verhalten der Auszahlungsfunktion bei weiteren festen gemischten Strategien y und Variation von x.
Die Animationen wurden mit Maple gemacht; das zugehörige Maple-Worksheet finden Sie unter dem folgenden Link: (Dominante Strategien und Nash-Gleichgewichte am Beispiel des Gefangenendilemma, Hirschjagt- und Angsthasen-Spiels
).