I.1.2 Dominante Strategien und Nash-Gleichgewichte
Im Folgenden werden zwei fundamentale Gleichgewichtskonzepte der Spieltheorie vorgestellt. Wir beschränken uns wieder auf ein Simultanes ($N$ Spieler)-($m$ Strategien) Spiel in strategischer Form mit Auszahlung. Eine Strategienkombination aller Spieler $s=\left( {s}^1, {s}^2, ..,{s}^N \right) \in {\bf \cal {S}}$ setzt sich aus der gewählten Strategie des $\mu$-ten Spielers ${s}^\mu \in {\cal {S}}^\mu$ und der Strategienkombination aller Spieler mit Ausnahme des $\mu$-ten Spielers $s^{-\mu}:=\left( {s}^1, {s}^2, .., {s}^{\mu-1},{s}^{\mu+1}, ..,{s}^N \right) \in {\bf \cal {S}^{-\mu}}$ zusammen; also $s=\left( s^{\mu}, s^{-\mu} \right) \in {\bf \cal {S}}={\cal {S}}^\mu \times {\cal {S}}^{-\mu}$.
Ein Nash-Gleichgewicht ist demnach eine Strategienkombination, von der aus kein Spieler einen Vorteil erhalten würde, wenn er von seiner Strategie abweichen würde - er würde keine größere Auszahlung erhalten. Es gilt, dass jedes Gleichgewicht in dominanten Strategien auch ein Nash-Gleichgewicht ist. Im folgenden werden die beiden definierten Gleichgewichtskonzepte am Beispiel zweier simultanen ($2$ Spieler)-($2$ Strategien) Spiele illustriert.
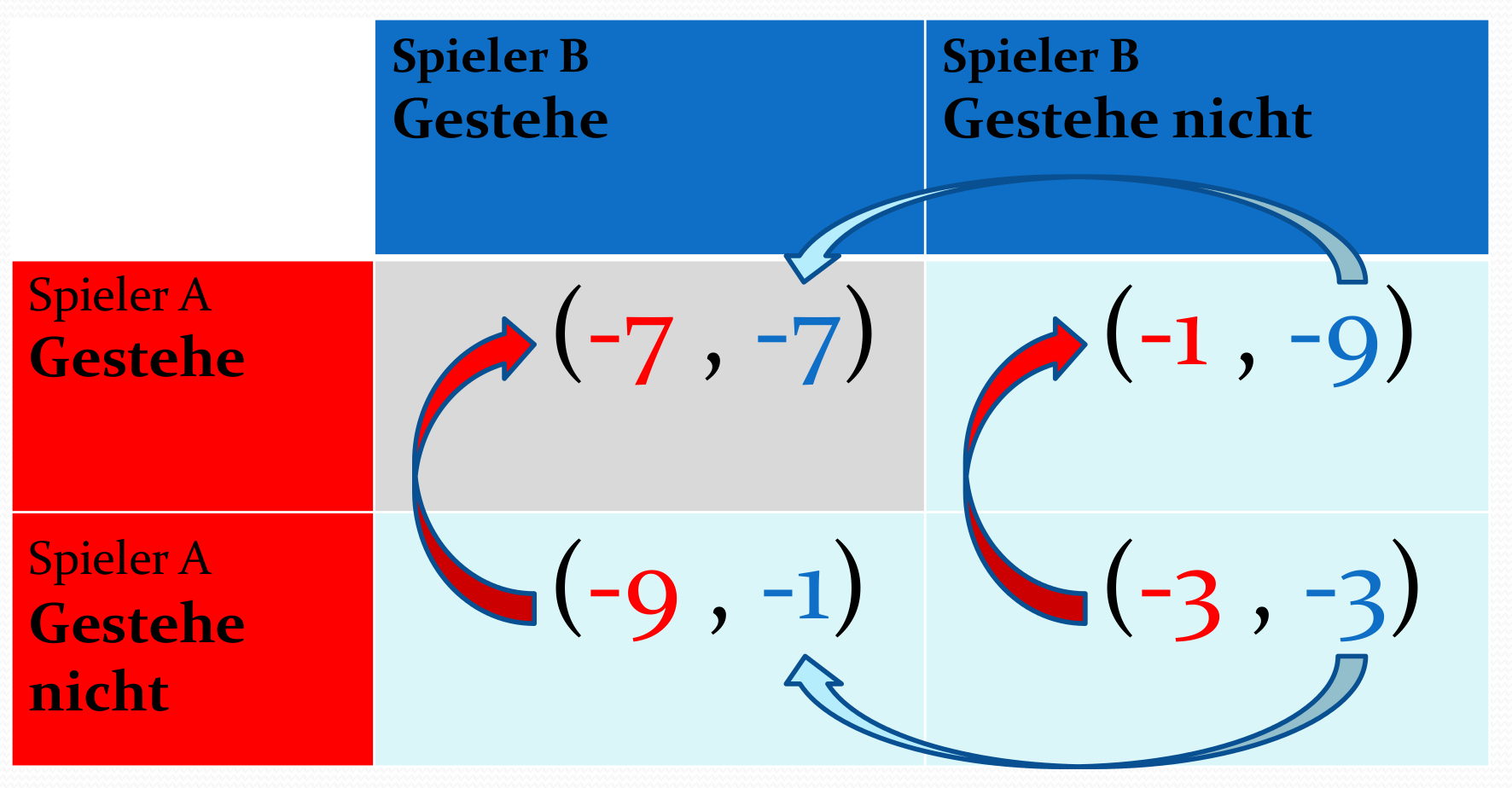
Veranschaulichung der dominanten Strategie "Gestehe" mittels der Abbildung der besten Antwort im Gefangenendilemma.
Beispiel: Das Gefangenendilemma
Das Gefangenendilemma ist ein simultanes (2 Personen)-(2 Strategien) Spiel (Definition siehe Unterkapitel I.1.1 ). Die nebenstehende Abbildung zeigt die Tabelle der "Auszahlungen" (hier die Gefängnisstrafe in Jahren), wobei die roten und blauen Pfeile im Prinzip die Abbildung der besten Antwort der Spieler A (Bonnie) und B (Clyde) visuell darstellen (für eine exakte mathematische Definition der Abbildung der besten Antwort siehe z.B. S:20 in [2]). Die Abbildung der besten Antwort des Spielers A ist hierbei wie folgt zu verstehen: Unter Annahme, dass Spieler B Gesteht, welche Strategie wäre für Spieler A die Vorteilhafteste? Da ${\bf {\cal \$}}^A \left( s^{A\dagger}=\hbox{Gestehe}, s^{B}=\hbox{Gestehe} \right)=-7 \,\, \geq \,\, {\bf {\cal \$}}^A \left( s^{A}=\hbox{Gestehe nicht}, s^{B}=\hbox{Gestehe} \right)=-9$ ist es für Spieler A das beste auch zu Gestehen (der linke rote Pfeil veranschaulicht dies). Dagegen, unter Annahme das Spieler B nicht Gesteht, wäre es das Beste für Spieler A zu Gestehen, da ${\bf {\cal \$}}^A \left( s^{A\dagger}=\hbox{Gestehe}, s^{B}=\hbox{Gestehe nicht} \right)=-1 \,\, \geq \,\, {\bf {\cal \$}}^A \left( s^{A}=\hbox{Gestehe nicht}, s^{B}=\hbox{Gestehe nicht} \right)=-3$ (der rechte rote Pfeil veranschaulicht diese Situation). In gleicher Weise kann man sich die besten Antworten aus der Sicht von Spieler B überlegen (blaue Pfeile). Zusammenfassend erkennt man das im Gefangenendilemma beide Spieler zur Strategie Gestehe gezogen werden und somit eine dominante Strategienkombination bei ${s}^{\dagger}=\left( {s}^{A\dagger}, {s}^{B\dagger} \right) = \left( \hbox{Gestehe}, \hbox{Gestehe} \right)$ auftritt welche auch das einzige Nash-Gleichgewicht des Spiels darstellt; ${s}^{\dagger}={s}^{*}$.
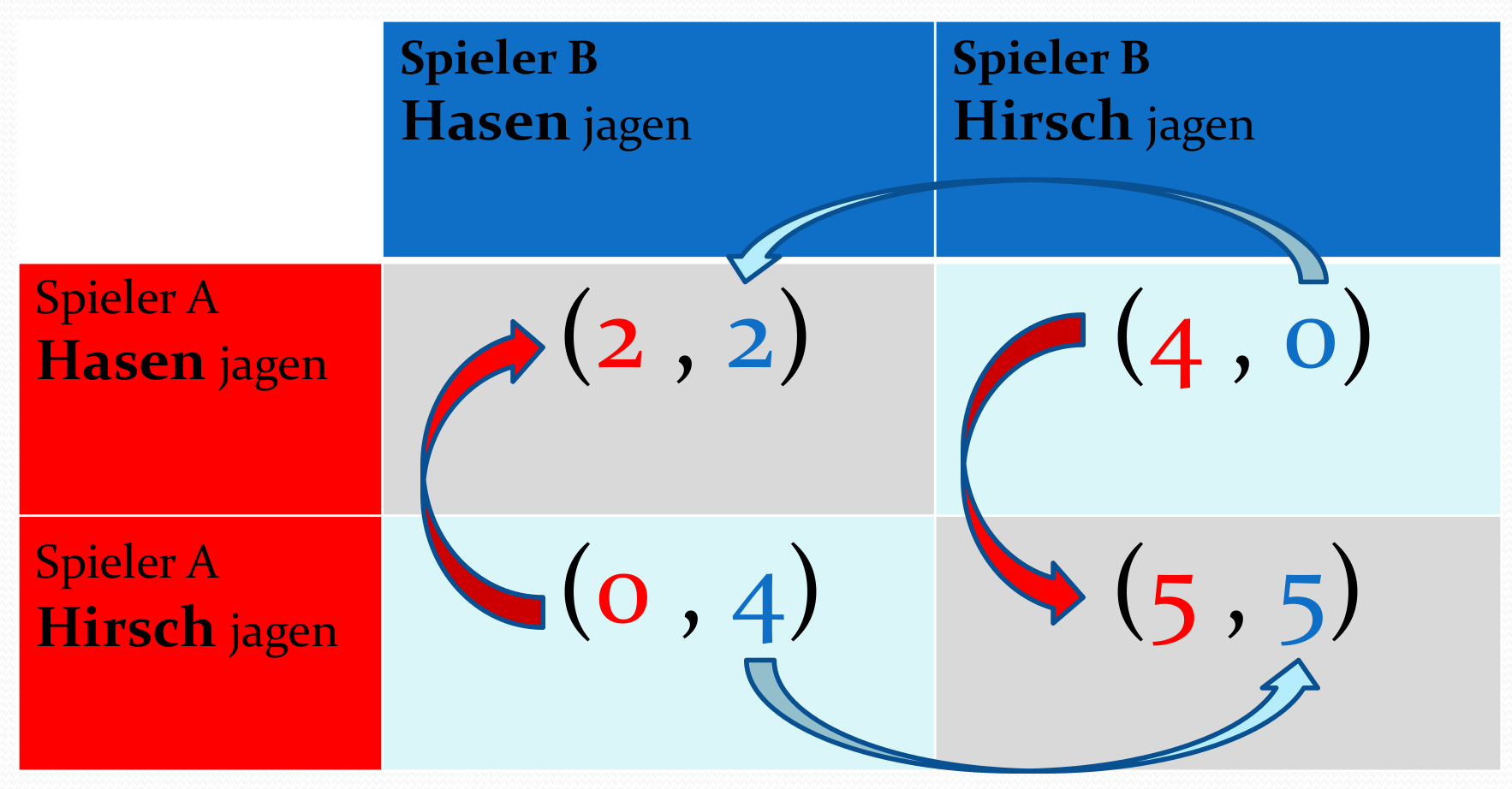
Veranschaulichung der beiden symmetrischen Nash-Gleichgewichte ${\bf {s}^{*} = \left( \hbox{Hasen jagen}, \hbox{Hasen jagen} \right)}$ und ${\bf {s}^{*} = \left( \hbox{Hirsch jagen}, \hbox{Hirsch jagen} \right)}$ mittels der Abbildung der besten Antwort im Hirschjagt-Spiel.
Beispiel: Das Hirschjagt-Spiel (Rousseau)
Ein weiteres bekanntes simultanes (2 Personen)-(2 Strategien) Spiel ist das sogennante Hirschjagt-Spiel von Rousseau:
"Zwei Jägern ist es im Laufe der Jagt gelungen einen Hirsch und vier Hasen einzukreisen. Die Jäger stehen nun vor der Entscheidung die Hasen entkommen zu lassen und gemeinsam den Hirsch zu erlegen oder sofort das Feuer auf die Hasen zu eröffnen. Leider können sich beide Jäger nicht miteinander verständigen oder Informationen austauschen - es handelt sich somit um eine simultane Entscheidung. Entscheiden sich beide dafür den Hirsch zu erlegen, dann hat der Hirsch keine Chance. Einen Hirsch kann man für 10 Goldmünzen verkaufen. Entscheiden sich beide für die Hasenjagt, dann erschiesst jeder Jäger zwei Hasen, für die man jeweils eine Goldmünze bekommt. Entscheidet sich jedoch nur einer für die Hirschjagt, so kann der Hirsch entkommen und derjenige der sich für die Hasenjagt entschieden hat kann alle vier Hasen erlegen."
Die nebenstehende Abbildung veranschaulicht die Auszahlungstabelle und zeigt mittels der Bestantwort-Pfeile, dass es in diesem Spiel keine dominante Strategie gibt, sondern zwei symmetrische Nash-Gleichgewicht bei den Strategienkombinationen ${s}^{*} = \left( \hbox{Hasen jagen}, \hbox{Hasen jagen} \right)$ und ${s}^{*} = \left( \hbox{Hirsch jagen}, \hbox{Hirsch jagen} \right)$. Z.B. ist ${s}^{*} = \left( \hbox{Hasen jagen}, \hbox{Hasen jagen} \right)$ ein Nash-Gleichgewicht, da ${\bf {\cal \$}}^A \left( s^{A*}=\hbox{Hasen jagen}, s^{B}=\hbox{Hasen jagen} \right)=2 \,\, \geq \,\, {\bf {\cal \$}}^A \left( s^{A}=\hbox{Hirsch jagen}, s^{B}=\hbox{Hasen jagen} \right)=0$ und ${\bf {\cal \$}}^B \left( s^{A}=\hbox{Hasen jagen}, s^{B*}=\hbox{Hasen jagen} \right)=2 \,\, \geq \,\, {\bf {\cal \$}}^B \left( s^{A}=\hbox{Hasen jagen}, s^{B}=\hbox{Hirsch jagen} \right)=0$.