I.1.1 Definition eines Spiels

Die formale mathematische Definition eines Simultanen ($N$ Spieler)-($m$ Strategien) Spiels in strategischer Form mit Auszahlung (siehe z.B. [2,3]) benötigt lediglich die Angabe dreier Größen: Die Menge ${\bf \cal I}$ der Spieler, die Menge (der Raum) ${\bf \cal {S}}$ der Strategien der Spieler und ihre Auszahlungsfunktion (Präferenzordnungen) ${\bf \cal {\$}}$.

Ein Spiel $\Gamma := \left( {\bf \cal I}, {\bf \cal {S}} , {\bf \cal {\$}} \right)$ in strategischer Form mit Auszahlung ist hinreichend definiert, wenn die folgenden drei Größen bekannt sind:
  • Menge der Spieler: ${\bf \cal I} = \left\{ 1, 2, ..., N \right\}$
    Die Menge der Spieler ${\bf \cal I}$ kann unter Umständen aus unterschiedlichen Teilmengen bestehen, die ihrerseits unterschiedliche Strategiemengen ${\bf \cal {S}}$ besitzen. In sozio-ökonomischen Netzwerken stellen die Spieler die jeweiligen Knoten des Netzwerkes dar (näheres siehe Teil II).
  • Menge der reinen Strategien der Spieler: ${\bf \cal {S}} = {\cal {S}}^1 \times {\cal {S}}^2 \times ... \times {\cal {S}}^N$
    Jeder Spieler $\mu \in {\bf \cal I}$ besitzt eine eigene Menge an reinen Strategien ${\cal {S}}^\mu = \left\{ {s}_1^\mu, {s}_2^\mu, ..., {s}^\mu_{m_\mu} \right\}$, wobei jede dieser $m_\mu$ Strategien eine für ihn mögliche Entscheidung darstellt.
  • Präferenzordnungen der Spieler, quantifiziert durch eine vektorwertige Auszahlungsfunktion: ${\bf \cal {\$}} = \left( {\cal {\$}}^1, {\cal {\$}}^2, ... , {\cal {\$}}^N \right) : {\bf \cal {S}} \rightarrow ℝ^N$
    Nachdem jeder Spieler (ohne die Entscheidung seiner Mitspieler zu kennen) eine Strategie aus seiner Strategienmenge ${\cal {S}}^\mu$ ausgewählt hat, beurteilt er die entstehende Strategienkombination ${\bf \cal {S}}$ entsprechend seiner Präferenzordnung (Auszahlungsfunktion) ${\cal {\$}}^\mu$.

Um diese formale Definition im einzelnen zu erklären, beschränken sich die folgenden Darlegungen auf den einfachsten Fall des simultanen ($2$ Spieler)-($2$ Strategien) Spiels.


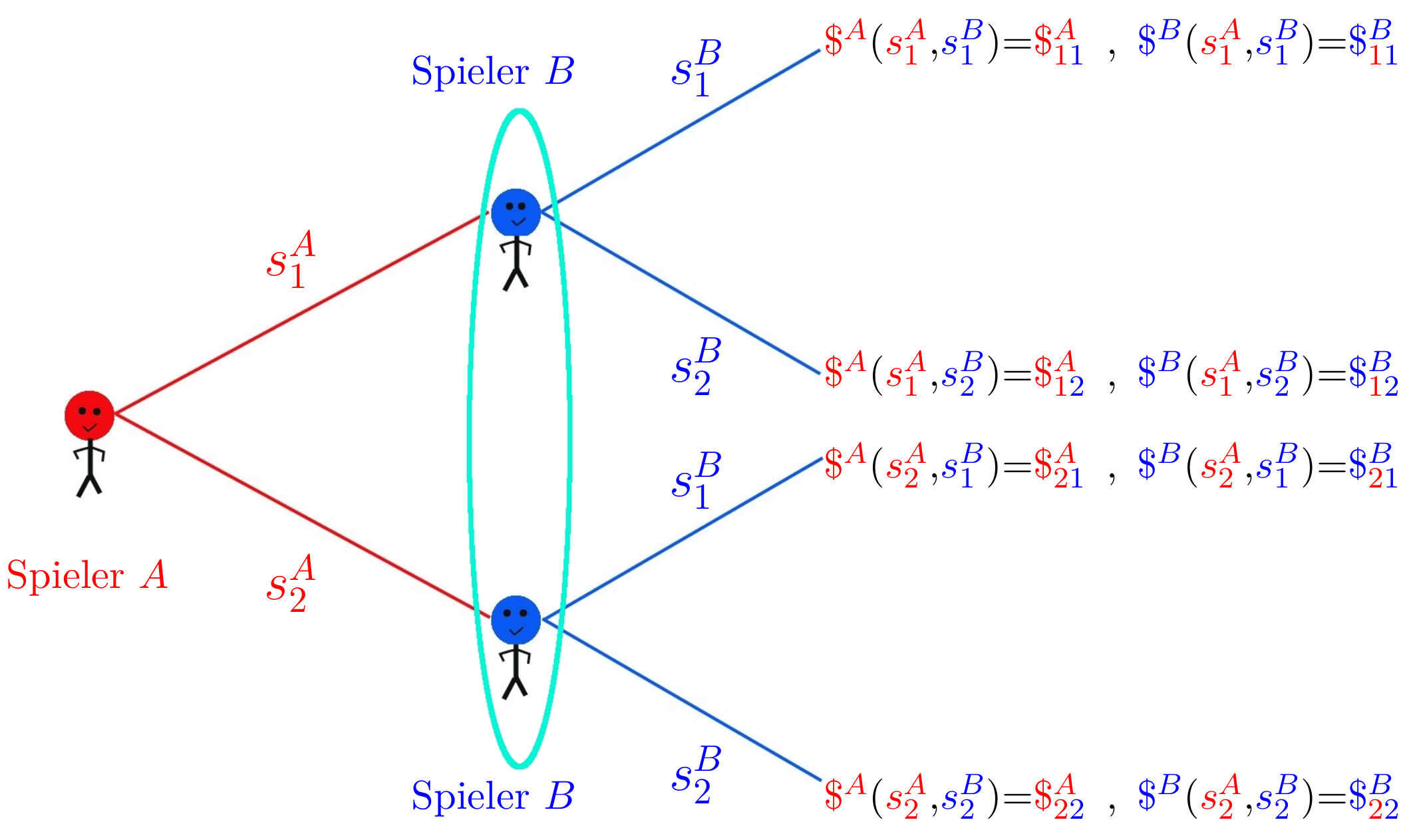
Spielbaum eines (2 Personen)-(2 Strategien) Spiels mit den Auszahlungsfunktionen für Spieler $A$ (${ \bf {\cal \$}}^A$) und Spieler $B$ (${ \bf {\cal \$}}^B$).

Die nebenstehende Abbildung stellt den Spielbaum eines simultanen (2 Personen)-(2 Strategien) Spiels dar. Beide Spieler (Spieler A und Spieler B) treffen die Entscheidung, welche der beiden reinen Strategien ($s_1$ und $s_2$) sie auszuwählen gedenken, zur gleichen Zeit, d.h. beim Zeitpunkt der Entscheidung wissen beide Spieler nicht, welche der Strategien der andere Spieler auswählt. ${\bf \cal {\$}}^\mu$ (mit $\mu= A,\, B$) bezeichnet die Auszahlung, welche den Spielern nach Bekanntgabe ihrer Entscheidung ausgezahlt wird. Die Auszahlungen der vier möglichen Strategienkombinationen werden im folgenden durch die Auszahlungsmatrizen $\hat{\bf {\cal \$}}^\mu$ angegeben. Die oben angegebene Definition vereinfacht sich in einem solchen ($2 \times 2$) Spiel somit wie folgt: \[ \begin{eqnarray} &&\mbox{($2 \times 2$) Spiel: } \nonumber\\&& \Gamma := \left( \left\{ A, B \right\}, {\bf {\cal S}}^A \times {\bf {\cal S}}^B, (\hat{\bf {\cal \$}}^A, \hat{\bf {\cal \$}}^B) \right) \nonumber\\ &&\mbox{Menge der reinen Strategien des Spielers A und B: } \nonumber\\&& {\bf {\cal S}}^A = \left\{ s^A_1, s^A_2 \right\}\, , \,\, {\bf {\cal S}}^B = \left\{ s^B_1, s^B_2 \right\} \nonumber\\ &&\mbox{Auszahlungsmatrix der Spieler A und B: } \nonumber\\&& \hat{\bf {\cal \$}}^A = \left( \begin{array}[c]{cc} \$^A_{11}&\$^A_{12}\\ \$^A_{21}&\$^A_{22} \end{array} \right),\,\, \hat{\bf {\cal \$}}^B = \left( \begin{array}[c]{cc} \$^B_{11}&\$^B_{12}\\ \$^B_{21}&\$^B_{22} \end{array} \right) \nonumber \end{eqnarray} \] Die nebenstehende Abbildung zeigt den Spielbaum eines simultanen (2 Personen)-(2 Strategien) Spiels. Die ovale, türkisene Linie visualisiert den simultanen Charakter des Spiels; ohne diese, wäre der Spielablauf ein sequentieller und Spieler B wüste schon wie sich Spieler A entschieden hätte, bevor er seine Entscheidung trifft. Die vier möglichen Ausgänge des Spiels sind mit unterschiedlichen Auszahlungen an die Spieler verknüpft, wobei diese durch die Auszahlungsmatrizen der Spieler A und B definiert sind.

Beispiel: Das Gefangenendilemma

Das wohl bekannteste Beispiel eines solchen (2 Personen)-(2 Strategien) Spiels ist das sogennante Gefangenendilemma:
"Bonnie und Clyde werden nach einem missglückten Banküberfall geschnappt und in verschiedenen Zellen untergebracht. Wenn beide schweigen kann der Staatsanwalt sie nur wegen verbotenen Waffenbesitzes für drei Jahre hinter Gitter bringen. Verrät jedoch einer den anderen, dann bekommt der Geständige als Zeuge der Anklage nur für ein Jahr hinter Gitter - der Nichtgeständige muss dann aber für neun Jahre ins Gefängnis. Gestehen beide, so müssen sie sieben Jahre absitzen."


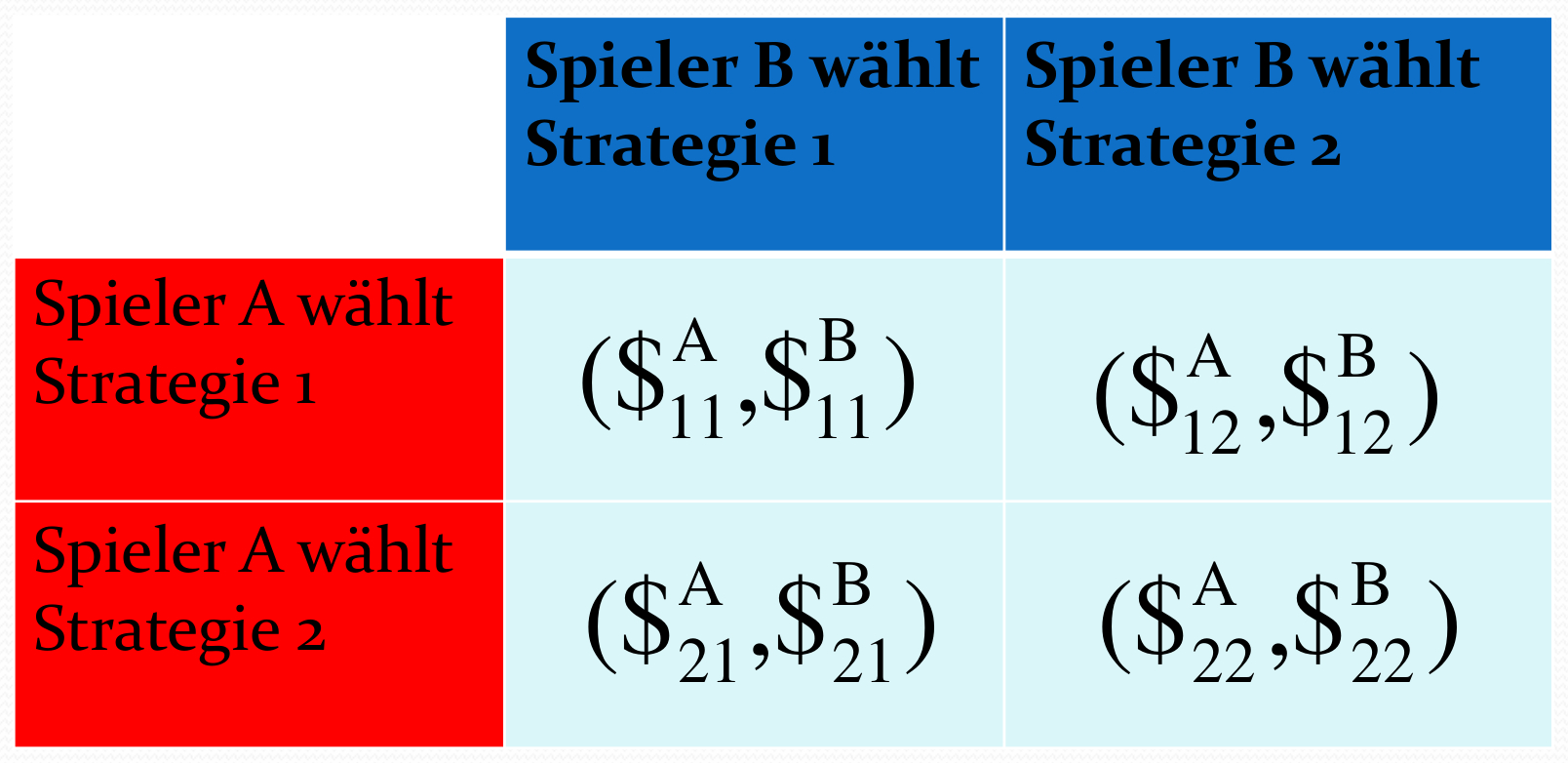
Die durch die Auszahlungsmatrizen der Spieler A und B definierte Auszahlungstabelle.


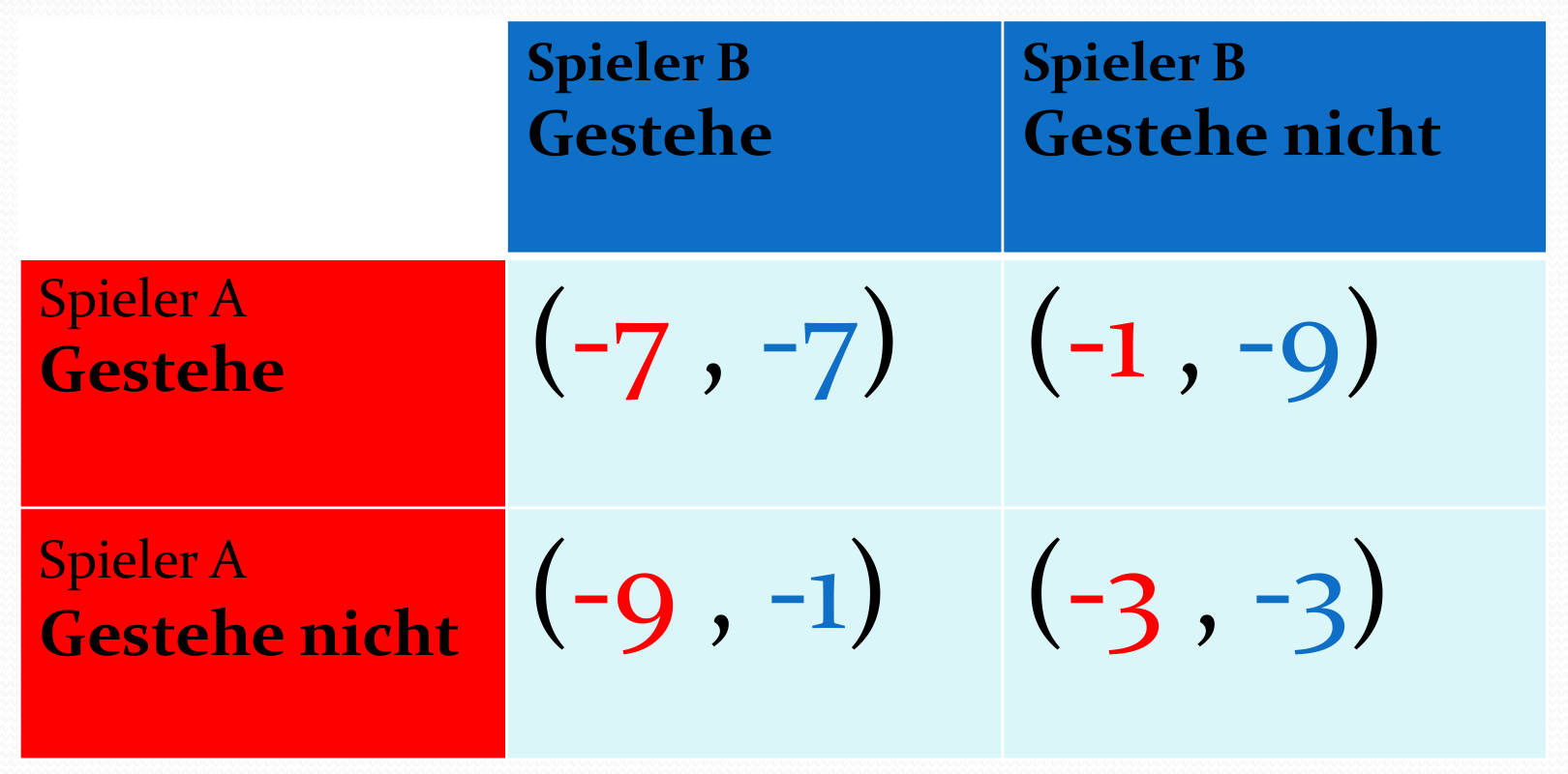
Auszahlungstabelle im Gefangenendilemma.

Es handelt sich bei dieser Entscheidungssituation um ein simultanes (2 Personen)-(2 Strategien) Spiel. Die Menge der Spieler besteht aus "Bonnie und Clyde" (${\bf \cal I} =\left\{ A, B \right\}=\left\{ \hbox{Bonnie}, \hbox{Clyde} \right\}$), die jeweils zwischen den Strategien "Gestehe" und "Gestehe nicht" auswählen können (${\cal S}^A = \left\{ s^A_1, s^A_2 \right\}=\left\{ \hbox{Gestehe}, \hbox{Gestehe nicht} \right\}= \left\{ s^B_1, s^B_2 \right\}={\cal S}^B$). Die durch die Geschichte beschriebene Auszahlungsmatrix der Spieler stellt die Anzahl der Jahre der Gefängnisstrafe als negative Zahlen dar. Es ist üblich die Auszahlungen eines Spiels in Form einer Tabelle anzugeben (siehe nebenstehende Auszahlungstabelle).