BiMatrix1.html

BiMatrix1.mw

Physik der sozio-ökonomischen Systeme mit dem Computer

Physics of Socio-Economic Systems with the Computer

Vorlesung gehalten an der J.W.Goethe-Universität in Frankfurt am Main (Wintersemester 2017/18)

von Dr.phil.nat. Dr.rer.pol. Matthias Hanauske

Frankfurt am Main 22.08.2017

Erster Vorlesungsteil:

Bi-Matrix Spiele

Einführung

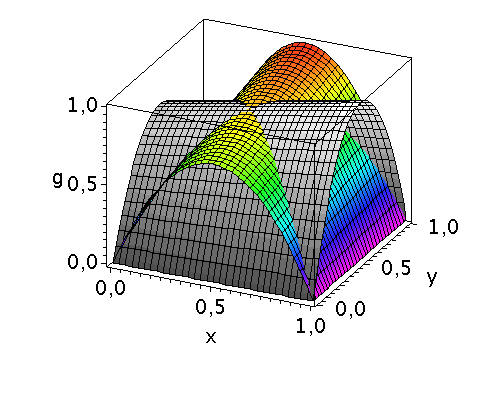
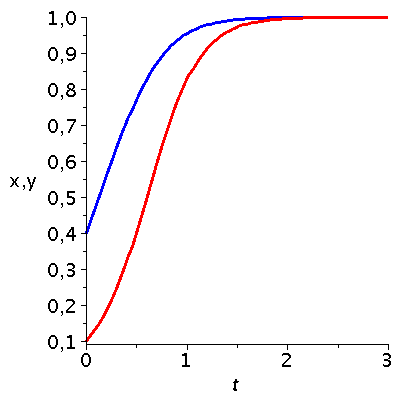
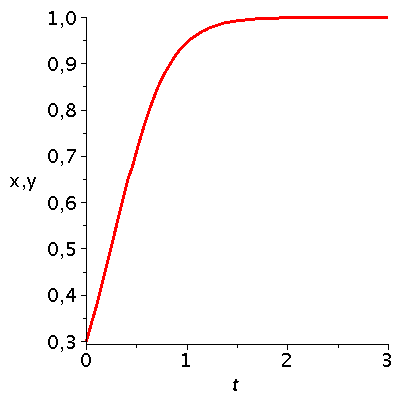
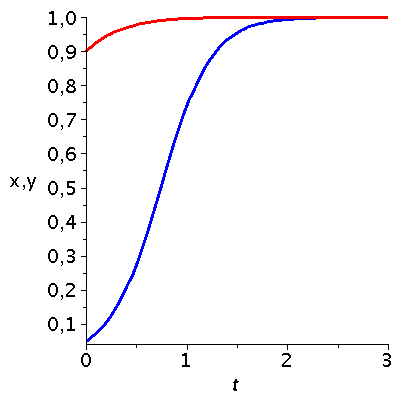
Dieses Maple-Worksheet befasst sich mit Bi-Matrix Spielen und berechnet deren Lösungen in einem evolutionären, zeitabhängigen Kontext.Ausgangspunkt ist eine allgemeine unsymmetrische Auszahlunsmatrix eines (2 Personen)-(2 Strategien) Spiels.

> restart:
with(plots):
with(plottools):
with(LinearAlgebra):
with(ColorTools):
with(StringTools):

Das evolutionäre Spiel besitzt folgendes System von Differentialgleichungen (Strategienanzahl 2):

> Num_Strat:=2:
for i from 1 by 1 to Num_Strat do
Eqx[i]:=Dx[i]=x[i]*(sum(D_A[i,l]*y[l],l=1..Num_Strat) - sum(sum(D_A[k,l]*x[k]*y[l],k=1..Num_Strat),l=1..Num_Strat));
Eqy[i]:=Dy[i]=y[i]*(sum(D_B[l,i]*x[l],l=1..Num_Strat) - sum(sum(D_B[l,k]*x[l]*y[k],k=1..Num_Strat),l=1..Num_Strat));
end do;

(1.1)

Umschreiben des Systems:

> Eqxa[1]:=subs({x[1]=x(t),x[2]=1-x(t),Dx[1]=diff(x(t),t),y[1]=y(t),y[2]=1-y(t)},Eqx[1]);
Eqxa[2]:=subs({x[1]=x(t),x[2]=1-x(t),Dx[2]=diff(1-x(t),t),y[1]=y(t),y[2]=1-y(t)},Eqx[2]);
Eqya[1]:=subs({x[1]=x(t),x[2]=1-x(t),Dy[1]=diff(y(t),t),y[1]=y(t),y[2]=1-y(t)},Eqy[1]);
Eqya[2]:=subs({x[1]=x(t),x[2]=1-x(t),Dy[2]=diff(1-y(t),t),y[1]=y(t),y[2]=1-y(t)},Eqy[2]);

(1.2)

Definition der Auszahlunsmatrix für Spieler A und B:

> D_A:=Matrix(2,2,[D_A11,D_A12,D_A21,D_A22]);

(1.3)

Definition der Auszahlunsmatrix für Spieler B:

> D_B:=Matrix(2,2,[D_B11,D_B12,D_B21,D_B22]);

(1.4)

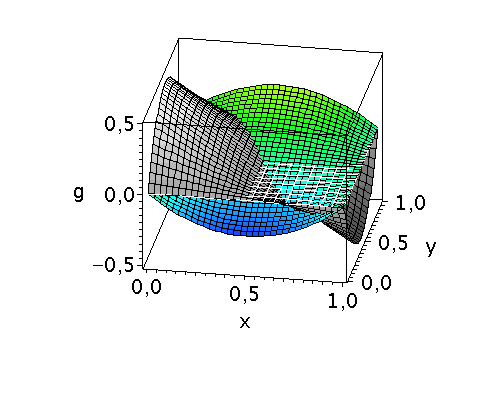
Unter Verwendung der gemischten Strategien (x,y) lässt sich eine gemischte Auszahlungsfunktion der Spieler wie folgt definieren:

> Auszahlungsfunktion_A:=(x,y)->D_A[1,1]*x*y+D_A[1,2]*x*(1-y)+D_A[2,1]*(1-x)*y+D_A[2,2]*(1-x)*(1-y);
Auszahlungsfunktion_B:=(x,y)->D_B[1,1]*x*y+D_B[1,2]*x*(1-y)+D_B[2,1]*(1-x)*y+D_B[2,2]*(1-x)*(1-y);

(1.5)

Klasse der Eckenspiele (Corner Class Games)

Symmetrisches Spiel (Zwei dominante Spiele)

> #Set1us(Set2+Set2)(Do+Do)
D_A11:=10:
D_A12:=8:
D_A21:=6:
D_A22:=5:
D_B11:=10:
D_B12:=6:
D_B21:=8:
D_B22:=5:
print("Matrix Spieler A");
D_A;
print("Matrix Spieler B");
D_B;

(2.1.1)

System der Differentialgleichungen (DGL):

> lhs(Eqxa[1])=collect(simplify(subs({y(t)=x(t)},rhs(Eqxa[1]))),{x(t)});
lhs(Eqya[1])=collect(simplify(subs({x(t)=y(t)},rhs(Eqya[1]))),{y(t)});

(2.1.2)

Die Dynamik bestimmende Funktionen für Spielergruppe A (g_A(x,y), farbige Fläche) und Spielergruppe B (g_B(x,y), graue Fläche):

> P_ga:=plot3d(subs({x(t)=x,y(t)=y},rhs(Eqxa[1])),x=0..1,y=0..1,axes=boxed,orientation=[-65,60],shading=ZHUE,labels=["x","y","g"],numpoints=1000,labelfont=[HELVETICA,15],axesfont=[HELVETICA,15],font=[HELVETICA,15],titlefont=[HELVETICA,16]):
P_gb:=plot3d(subs({x(t)=x,y(t)=y},rhs(Eqya[1])),x=0..1,y=0..1,axes=boxed,orientation=[-65,60],shading=ZGRAYSCALE,style=patch,labels=["x","y","g"],numpoints=1000,labelfont=[HELVETICA,15],axesfont=[HELVETICA,15],font=[HELVETICA,15],titlefont=[HELVETICA,16]):
display(P_ga,P_gb);

Plot

Lösung der DGL für drei unterschiedliche Anfangspopulationen:

> xa0:=0.1:
ya0:=0.4:
xb0:=0.3:
yb0:=0.3:
xc0:=0.9:
yc0:=0.05:
Loes1a:=dsolve({Eqxa[1],Eqya[1],x(0)=xa0,y(0)=ya0},{x(t),y(t)},type=numeric,output=listprocedure);
Loes1b:=dsolve({Eqxa[1],Eqya[1],x(0)=xb0,y(0)=yb0},{x(t),y(t)},type=numeric,output=listprocedure);
Loes1c:=dsolve({Eqxa[1],Eqya[1],x(0)=xc0,y(0)=yc0},{x(t),y(t)},type=numeric,output=listprocedure);

(2.1.3)

Darstellung der zeitlichen Entwicklung der Populationsvektoren:

> tanf:=0:
tenda:=3:
tendb:=3:
tendc:=3:
P1:=odeplot(Loes1a,[t,x(t)],tanf..tenda,color=red,axesfont=[HELVETICA,15],labelfont=[HELVETICA,15],numpoints=100,thickness=3):
P2:=odeplot(Loes1a,[t,y(t)],tanf..tenda,color=blue,axesfont=[HELVETICA,15],labelfont=[HELVETICA,15],labels=[t,"x,y"],numpoints=100,thickness=3):
display(P2,P1);
tanf:=0:
P1:=odeplot(Loes1b,[t,x(t)],tanf..tendb,color=red,axesfont=[HELVETICA,15],labelfont=[HELVETICA,15],numpoints=100,thickness=3):
P2:=odeplot(Loes1b,[t,y(t)],tanf..tendb,color=blue,axesfont=[HELVETICA,15],labelfont=[HELVETICA,15],labels=[t,"x,y"],numpoints=100,thickness=3):
display(P2,P1);
tanf:=0:
P1:=odeplot(Loes1c,[t,x(t)],tanf..tendc,color=red,axesfont=[HELVETICA,15],labelfont=[HELVETICA,15],numpoints=100,thickness=3):
P2:=odeplot(Loes1c,[t,y(t)],tanf..tendc,color=blue,axesfont=[HELVETICA,15],labelfont=[HELVETICA,15],labels=[t,"x,y"],numpoints=100,thickness=3):
display(P2,P1);

Plot_2d

Plot_2d

Plot_2d

Die Darstellung dieser Lösungen des Bi-Matrix Spiels kann man z.B. auch in einem (x,y)-Populationsvektor Diagram veranschaulichen:

> v_norm_max:=0:
tt_schrita:=evalf(tenda/20):
tt_schritb:=evalf(tendb/20):
tt_schritc:=evalf(tendc/20):
vec_lengtha:=tt_schrita:
vec_lengthb:=tt_schritb:
vec_lengthc:=tt_schritc:

> P1a:=odeplot(Loes1a,[x(t),y(t)],tanf..tenda, thickness=5,view=[0..1,0..1],color=red,numpoints=100):
P1b:=odeplot(Loes1b,[x(t),y(t)],tanf..tendb, thickness=5,view=[0..1,0..1],color=COLOR(RGB, .0, 0.8, .3),numpoints=100):
P1c:=odeplot(Loes1c,[x(t),y(t)],tanf..tendc, thickness=5,view=[0..1,0..1],color=blue,numpoints=100):

> kk:=0:
scale_factor:=0.04:
for yy from 0 by 0.05 to 1 do
for xx from 0 by 0.05 to 1 do
vec_sim_1:=simplify(subs({x(t)=xx,y(t)=yy},rhs(Eqxa[1]))):
vec_sim_2:=simplify(subs({x(t)=xx,y(t)=yy},rhs(Eqya[1]))):
v_norm:=sqrt(vec_sim_1^2+vec_sim_2^2):
if (v_norm=0) then v_norm:=0.0001 else end if:
if (v_norm>v_norm_max) then v_norm_max:=v_norm else end if:
#print(v_norm,v_norm_max):
vec_sim_1n:=scale_factor*vec_sim_1/v_norm:
vec_sim_2n:=scale_factor*vec_sim_2/v_norm:
vec_sim:=vector([vec_sim_1n, vec_sim_2n]):
PPzz[kk]:=pointplot([xx,yy], symbolsize=10,symbol=box,view=[0..1,0..1]):
PPzzv[kk]:=arrow([xx,yy], vec_sim, .003, .015, .15, color=COLOR(RGB, v_norm/v_norm_max, v_norm/v_norm_max, v_norm/v_norm_max)):
kk:=kk+1:
end do:
end do:

> PP3:=display(seq(PPzzv[j],j=0..kk-1)):
dim_ball:=0.013:
P_ball_blue:=display(ellipse([rhs(Loes1c(0)[2]),rhs(Loes1c(0)[3])],dim_ball,dim_ball,filled=true,color=blue)):
P_ball_red:=display(ellipse([rhs(Loes1a(0)[2]),rhs(Loes1a(0)[3])],dim_ball,dim_ball,filled=true,color=red)):
P_ball_green:=display(ellipse([rhs(Loes1b(0)[2]),rhs(Loes1b(0)[3])],dim_ball,dim_ball,filled=true,color=COLOR(RGB, .0, 0.8, .3))):

> Vec_blue:=display(arrow([rhs(Loes1c(0)[2]),rhs(Loes1c(0)[3])], [rhs(Loes1c(0.15)[2]),rhs(Loes1c(0.15)[3])], .005, .035, .5, color=blue)):
Vec_red:=display(arrow([rhs(Loes1a(0)[2]),rhs(Loes1a(0)[3])], [rhs(Loes1a(0.15)[2]),rhs(Loes1a(0.15)[3])], .005, .035, .5, color=red)):
Vec_green:=display(arrow([rhs(Loes1b(0)[2]),rhs(Loes1b(0)[3])], [rhs(Loes1b(0.15)[2]),rhs(Loes1b(0.15)[3])], .005, .035, .5, color=COLOR(RGB, .0, 0.8, .3))):

> iii_a:=0:
for tt from 0 by tt_schrita to tenda-2*tt_schrita do
Vec_red[iii_a]:=display(arrow([rhs(Loes1a(tt)[2]),rhs(Loes1a(tt)[3])], [rhs(Loes1a(tt+tt_schrita)[2]),rhs(Loes1a(tt+tt_schrita)[3])], .005, .035, .5, color=red)):
iii_a:=iii_a+1:
end do:

> iii_b:=0:
for tt from 0 by tt_schritb to tendb-2*tt_schritb do
Vec_green[iii_b]:=display(arrow([rhs(Loes1b(tt)[2]),rhs(Loes1b(tt)[3])], [rhs(Loes1b(tt+tt_schritb)[2]),rhs(Loes1b(tt+tt_schritb)[3])], .005, .035, .5, color=COLOR(RGB, .0, 0.8, .3))):
iii_b:=iii_b+1:
end do:

> iii_c:=0:
for tt from 0 by tt_schritc to tendc-2*tt_schritc do
Vec_blue[iii_c]:=display(arrow([rhs(Loes1c(tt)[2]),rhs(Loes1c(tt)[3])], [rhs(Loes1c(tt+tt_schritc)[2]),rhs(Loes1c(tt+tt_schritc)[3])], .005, .035, .5, color=blue)):
iii_c:=iii_c+1:
end do:

> display(seq(Vec_blue[i],i=0..iii_c-1),seq(Vec_green[i],i=0..iii_b-1),seq(Vec_red[i],i=0..iii_a-1),P_ball_red,P_ball_blue,P_ball_green,P1a,P1b,P1c,PP3,axes=normal,labelfont=[HELVETICA,20],axesfont=[HELVETICA,15],font=[HELVETICA,15],labels=[x,y]);

Plot_2d

Es folgt eine Animation die die zeitliche Entwicklung der Lösungen im (x,y)-Diagram visualisiert:

> tend:=1.5:
for tt from 0 by 1 to tend do
Vec_blue[tt]:=display(arrow([rhs(Loes1c(tt*tt_schritc)[2]),rhs(Loes1c(tt*tt_schritc)[3])], [rhs(Loes1c(tt*tt_schritc+vec_lengthc)[2]),rhs(Loes1c(tt*tt_schritc+vec_lengthc)[3])], .005, .035, .5, color=blue)):
Vec_red[tt]:=display(arrow([rhs(Loes1a(tt*tt_schrita)[2]),rhs(Loes1a(tt*tt_schrita)[3])], [rhs(Loes1a(tt*tt_schrita+vec_lengtha)[2]),rhs(Loes1a(tt*tt_schrita+vec_lengtha)[3])], .005, .035, .5, color=red)):
Vec_green[tt]:=display(arrow([rhs(Loes1b(tt*tt_schritb)[2]),rhs(Loes1b(tt*tt_schritb)[3])], [rhs(Loes1b(tt*tt_schritb+vec_lengthb)[2]),rhs(Loes1b(tt*tt_schritb+vec_lengthb)[3])], .005, .035, .5, color=COLOR(RGB, .0, 0.8, .3))):
end do:

> with(StringTools):
Digits := 3:
dim_ball:=0.02:
scale_t:=2:
frames:=20:
for i from 0 by 1 to frames do
P_ani1a[i]:=display(ellipse([rhs(Loes1a(i*tend/frames)[2]),rhs(Loes1a(i*tend/frames)[3])],dim_ball,dim_ball,filled=true,color=red)):
P_ani1b[i]:=display(ellipse([rhs(Loes1b(i*tend/frames)[2]),rhs(Loes1b(i*tend/frames)[3])],dim_ball,dim_ball,filled=true,color=green)):
P_ani1c[i]:=display(ellipse([rhs(Loes1c(i*tend/frames)[2]),rhs(Loes1c(i*tend/frames)[3])],dim_ball,dim_ball,filled=true,color=blue)):
Ptext[i]:=textplot([0.3,1.07, Join(["t=",convert(evalf(i*tend/frames),string)])], align =RIGHT,color=black,font = [TIMES, ROMAN, 15]):
Ani[i]:=display({P1a,P1b,P1c,PP3,P_ani1a[i],P_ani1b[i],P_ani1c[i],Ptext[i]},axesfont=[HELVETICA,17],labelfont=[HELVETICA,17],labels=[x,y]);
od:

> display(seq(Ani[j],j=0..frames),insequence=true,scaling=constrained,view=[0..1,0..1.1]):

Spieler A: Dominantes Spiel , Spieler B: Anti-Koordinationsspiel

> #Set5us(Set3+Set8)(Do+AntiCo)(Pris+AntiCo)
D_A11:=10:
D_A12:=4:
D_A21:=12:
D_A22:=5:
D_B11:=10:
D_B12:=12:
D_B21:=7:
D_B22:=5:

print("Matrix Spieler A");
D_A;
print("Matrix Spieler B");
D_B;

(2.2.1)

System der Differentialgleichungen (DGL):

> lhs(Eqxa[1])=collect(simplify(subs({y(t)=x(t)},rhs(Eqxa[1]))),{x(t)});
lhs(Eqya[1])=collect(simplify(subs({x(t)=y(t)},rhs(Eqya[1]))),{y(t)});

(2.2.2)

Die Dynamik bestimmende Funktionen für Spielergruppe A (g_A(x,y), farbige Fläche) und Spielergruppe B (g_B(x,y), graue Fläche):

> P_ga:=plot3d(subs({x(t)=x,y(t)=y},rhs(Eqxa[1])),x=0..1,y=0..1,axes=boxed,orientation=[-80,60],shading=ZHUE,labels=["x","y","g"],numpoints=1000,labelfont=[HELVETICA,15],axesfont=[HELVETICA,15],font=[HELVETICA,15],titlefont=[HELVETICA,16]):
P_gb:=plot3d(subs({x(t)=x,y(t)=y},rhs(Eqya[1])),x=0..1,y=0..1,axes=boxed,orientation=[-80,60],shading=ZGRAYSCALE,style=patch,labels=["x","y","g"],numpoints=1000,labelfont=[HELVETICA,15],axesfont=[HELVETICA,15],font=[HELVETICA,15],titlefont=[HELVETICA,16]):
P_zero:=plot3d(0,x=0..1,y=0..1,axes=boxed,orientation=[-124,83],color=white,style=wireframe,labels=["","",""],numpoints=300,axesfont=[HELVETICA,15],font=[HELVETICA,15],titlefont=[HELVETICA,16]):
display(P_ga,P_gb,P_zero);

Plot

Lösung der DGL für drei unterschiedliche Anfangspopulationen:

> xa0:=0.6:
ya0:=0.4:
xb0:=0.9:
yb0:=0.9:
xc0:=0.9:
yc0:=0.2:
Loes1a:=dsolve({Eqxa[1],Eqya[1],x(0)=xa0,y(0)=ya0},{x(t),y(t)},type=numeric,output=listprocedure);
Loes1b:=dsolve({Eqxa[1],Eqya[1],x(0)=xb0,y(0)=yb0},{x(t),y(t)},type=numeric,output=listprocedure);
Loes1c:=dsolve({Eqxa[1],Eqya[1],x(0)=xc0,y(0)=yc0},{x(t),y(t)},type=numeric,output=listprocedure);

(2.2.3)

Darstellung der zeitlichen Entwicklung der Populationsvektoren:

> tanf:=0:
tenda:=7;
tendb:=7;
tendc:=12;
P1:=odeplot(Loes1a,[t,x(t)],tanf..tenda,color=red,axesfont=[HELVETICA,15],labelfont=[HELVETICA,15],numpoints=100,thickness=3):
P2:=odeplot(Loes1a,[t,y(t)],tanf..tenda,color=blue,axesfont=[HELVETICA,15],labelfont=[HELVETICA,15],labels=[t,"x,y"],numpoints=100,thickness=3):
display(P2,P1);
tanf:=0:
P1:=odeplot(Loes1b,[t,x(t)],tanf..tendb,color=red,axesfont=[HELVETICA,15],labelfont=[HELVETICA,15],numpoints=100,thickness=3):
P2:=odeplot(Loes1b,[t,y(t)],tanf..tendb,color=blue,axesfont=[HELVETICA,15],labelfont=[HELVETICA,15],labels=[t,"x,y"],numpoints=100,thickness=3):
display(P2,P1);
tanf:=0:
P1:=odeplot(Loes1c,[t,x(t)],tanf..tendc,color=red,axesfont=[HELVETICA,15],labelfont=[HELVETICA,15],numpoints=100,thickness=3):
P2:=odeplot(Loes1c,[t,y(t)],tanf..tendc,color=blue,axesfont=[HELVETICA,15],labelfont=[HELVETICA,15],labels=[t,"x,y"],numpoints=100,thickness=3):
display(P2,P1);

Plot_2d

Plot_2d

Plot_2d

Die Darstellung dieser Lösungen des Bi-Matrix Spiels kann man z.B. auch in einem (x,y)-Populationsvektor Diagram veranschaulichen:

> v_norm_max:=0:
tt_schrita:=evalf(tenda/40):
tt_schritb:=evalf(tendb/40):
tt_schritc:=evalf(tendc/40):
vec_lengtha:=tt_schrita:
vec_lengthb:=tt_schritb:
vec_lengthc:=tt_schritc:

Plot_2d

Es folgt eine Animation die die zeitliche Entwicklung der Lösungen im (x,y)-Diagram visualisiert:

> tend:=5:
for tt from 0 by 1 to tend do
Vec_blue[tt]:=display(arrow([rhs(Loes1c(tt*tt_schritc)[2]),rhs(Loes1c(tt*tt_schritc)[3])], [rhs(Loes1c(tt*tt_schritc+vec_lengthc)[2]),rhs(Loes1c(tt*tt_schritc+vec_lengthc)[3])], .005, .035, .5, color=blue)):
Vec_red[tt]:=display(arrow([rhs(Loes1a(tt*tt_schrita)[2]),rhs(Loes1a(tt*tt_schrita)[3])], [rhs(Loes1a(tt*tt_schrita+vec_lengtha)[2]),rhs(Loes1a(tt*tt_schrita+vec_lengtha)[3])], .005, .035, .5, color=red)):
Vec_green[tt]:=display(arrow([rhs(Loes1b(tt*tt_schritb)[2]),rhs(Loes1b(tt*tt_schritb)[3])], [rhs(Loes1b(tt*tt_schritb+vec_lengthb)[2]),rhs(Loes1b(tt*tt_schritb+vec_lengthb)[3])], .005, .035, .5, color=COLOR(RGB, .0, 0.8, .3))):
end do:

> Digits := 3:
dim_ball:=0.02:
scale_t:=2:
frames:=20:
for i from 0 by 1 to frames do
P_ani1a[i]:=display(ellipse([rhs(Loes1a(i*tend/frames)[2]),rhs(Loes1a(i*tend/frames)[3])],dim_ball,dim_ball,filled=true,color=red)):
P_ani1b[i]:=display(ellipse([rhs(Loes1b(i*tend/frames)[2]),rhs(Loes1b(i*tend/frames)[3])],dim_ball,dim_ball,filled=true,color=green)):
P_ani1c[i]:=display(ellipse([rhs(Loes1c(i*tend/frames)[2]),rhs(Loes1c(i*tend/frames)[3])],dim_ball,dim_ball,filled=true,color=blue)):
Ptext[i]:=textplot([0.3,1.07, Join(["t=",convert(evalf(i*tend/frames),string)])], align =RIGHT,color=black,font = [TIMES, ROMAN, 15]):
Ani[i]:=display({P1a,P1b,P1c,PP3,P_ani1a[i],P_ani1b[i],P_ani1c[i],Ptext[i]},axesfont=[HELVETICA,17],labelfont=[HELVETICA,17],labels=[x,y]);
od:

> display(seq(Ani[j],j=0..frames),insequence=true,scaling=constrained,view=[0..1,0..1.1]):

Klasse der Sattelspiele (Saddle Class Games)

Spieler A: Koordinationsspiel , Spieler B: Koordinationsspiel

> #Set7us(Set4+Set5)(Co+Co)(Co+Co)
D_A11:=10:
D_A12:=4:
D_A21:=9:
D_A22:=5:
D_B11:=10:
D_B12:=7:
D_B21:=4:
D_B22:=5:

print("Matrix Spieler A");
D_A;
print("Matrix Spieler B");
D_B;

(3.1.1)

System der Differentialgleichungen (DGL):

> lhs(Eqxa[1])=collect(simplify(subs({y(t)=x(t)},rhs(Eqxa[1]))),{x(t)});
lhs(Eqya[1])=collect(simplify(subs({x(t)=y(t)},rhs(Eqya[1]))),{y(t)});

(3.1.2)

Die Dynamik bestimmende Funktionen für Spielergruppe A (g_A(x,y), farbige Fläche) und Spielergruppe B (g_B(x,y), graue Fläche):

Plot

Lösung der DGL für drei unterschiedliche Anfangspopulationen:

> xa0:=0.1:#red
ya0:=0.8:
xb0:=0.6:#green
yb0:=0.1:
xc0:=0.7:#blue
yc0:=0.1:
Loes1a:=dsolve({Eqxa[1],Eqya[1],x(0)=xa0,y(0)=ya0},{x(t),y(t)},type=numeric,output=listprocedure);
Loes1b:=dsolve({Eqxa[1],Eqya[1],x(0)=xb0,y(0)=yb0},{x(t),y(t)},type=numeric,output=listprocedure);
Loes1c:=dsolve({Eqxa[1],Eqya[1],x(0)=xc0,y(0)=yc0},{x(t),y(t)},type=numeric,output=listprocedure);

(3.1.3)

Darstellung der zeitlichen Entwicklung der Populationsvektoren:

> tanf:=0:
tenda:=14;
tendb:=14;
tendc:=8;
P1:=odeplot(Loes1a,[t,x(t)],tanf..tenda,color=red,axesfont=[HELVETICA,15],labelfont=[HELVETICA,15],numpoints=100,thickness=3):
P2:=odeplot(Loes1a,[t,y(t)],tanf..tenda,color=blue,axesfont=[HELVETICA,15],labelfont=[HELVETICA,15],labels=[t,"x,y"],numpoints=100,thickness=3):
display(P2,P1);
tanf:=0:
P1:=odeplot(Loes1b,[t,x(t)],tanf..tendb,color=red,axesfont=[HELVETICA,15],labelfont=[HELVETICA,15],numpoints=100,thickness=3):
P2:=odeplot(Loes1b,[t,y(t)],tanf..tendb,color=blue,axesfont=[HELVETICA,15],labelfont=[HELVETICA,15],labels=[t,"x,y"],numpoints=100,thickness=3):
display(P2,P1);
tanf:=0:
P1:=odeplot(Loes1c,[t,x(t)],tanf..tendc,color=red,axesfont=[HELVETICA,15],labelfont=[HELVETICA,15],numpoints=100,thickness=3):
P2:=odeplot(Loes1c,[t,y(t)],tanf..tendc,color=blue,axesfont=[HELVETICA,15],labelfont=[HELVETICA,15],labels=[t,"x,y"],numpoints=100,thickness=3):
display(P2,P1);

Plot_2d

Plot_2d

Plot_2d

Die Darstellung dieser Lösungen des Bi-Matrix Spiels kann man z.B. auch in einem (x,y)-Populationsvektor Diagram veranschaulichen:

> v_norm_max:=0:
tt_schrita:=evalf(tenda/40):
tt_schritb:=evalf(tendb/40):
tt_schritc:=evalf(tendc/40):
vec_lengtha:=tt_schrita:
vec_lengthb:=tt_schritb:
vec_lengthc:=tt_schritc:

Plot_2d

Es folgt eine Animation die die zeitliche Entwicklung der Lösungen im (x,y)-Diagram visualisiert:

> tend:=10:
for tt from 0 by 1 to tend do
Vec_blue[tt]:=display(arrow([rhs(Loes1c(tt*tt_schritc)[2]),rhs(Loes1c(tt*tt_schritc)[3])], [rhs(Loes1c(tt*tt_schritc+vec_lengthc)[2]),rhs(Loes1c(tt*tt_schritc+vec_lengthc)[3])], .005, .035, .5, color=blue)):
Vec_red[tt]:=display(arrow([rhs(Loes1a(tt*tt_schrita)[2]),rhs(Loes1a(tt*tt_schrita)[3])], [rhs(Loes1a(tt*tt_schrita+vec_lengtha)[2]),rhs(Loes1a(tt*tt_schrita+vec_lengtha)[3])], .005, .035, .5, color=red)):
Vec_green[tt]:=display(arrow([rhs(Loes1b(tt*tt_schritb)[2]),rhs(Loes1b(tt*tt_schritb)[3])], [rhs(Loes1b(tt*tt_schritb+vec_lengthb)[2]),rhs(Loes1b(tt*tt_schritb+vec_lengthb)[3])], .005, .035, .5, color=COLOR(RGB, .0, 0.8, .3))):
end do:

> display(seq(Ani[j],j=0..frames),insequence=true,scaling=constrained,view=[0..1,0..1.1]):

Spieler A: Anti-Koordinationsspiel , Spieler B: Anti-Koordinationsspiel

> #Set9us(Set8+Set9)(AntiCo+AntiCo)
D_A11:=10:
D_A12:=7:
D_A21:=12:
D_A22:=5:
D_B11:=10:
D_B12:=12:
D_B21:=9:
D_B22:=5:

print("Matrix Spieler A");
D_A;
print("Matrix Spieler B");
D_B;

(3.2.1)

System der Differentialgleichungen (DGL):

> lhs(Eqxa[1])=collect(simplify(subs({y(t)=x(t)},rhs(Eqxa[1]))),{x(t)});
lhs(Eqya[1])=collect(simplify(subs({x(t)=y(t)},rhs(Eqya[1]))),{y(t)});

(3.2.2)

Die Dynamik bestimmende Funktionen für Spielergruppe A (g_A(x,y), farbige Fläche) und Spielergruppe B (g_B(x,y), graue Fläche):

> P_ga:=plot3d(subs({x(t)=x,y(t)=y},rhs(Eqxa[1])),x=0..1,y=0..1,axes=boxed,orientation=[-140,60],shading=ZHUE,labels=["x","y","g"],numpoints=1000,labelfont=[HELVETICA,15],axesfont=[HELVETICA,15],font=[HELVETICA,15],titlefont=[HELVETICA,16]):
P_gb:=plot3d(subs({x(t)=x,y(t)=y},rhs(Eqya[1])),x=0..1,y=0..1,axes=boxed,orientation=[-140,60],shading=ZGRAYSCALE,style=patch,labels=["x","y","g"],numpoints=1000,labelfont=[HELVETICA,15],axesfont=[HELVETICA,15],font=[HELVETICA,15],titlefont=[HELVETICA,16]):
P_zero:=plot3d(0,x=0..1,y=0..1,axes=boxed,orientation=[-124,83],color=white,style=wireframe,labels=["","",""],numpoints=300,axesfont=[HELVETICA,15],font=[HELVETICA,15],titlefont=[HELVETICA,16]):
display(P_ga,P_gb,P_zero);

Plot

Lösung der DGL für drei unterschiedliche Anfangspopulationen:

> xa0:=0.1:#red
ya0:=0.1:
xb0:=0.8:#green
yb0:=0.7:
xc0:=0.3:#blue
yc0:=0.1:
Loes1a:=dsolve({Eqxa[1],Eqya[1],x(0)=xa0,y(0)=ya0},{x(t),y(t)},type=numeric,output=listprocedure);
Loes1b:=dsolve({Eqxa[1],Eqya[1],x(0)=xb0,y(0)=yb0},{x(t),y(t)},type=numeric,output=listprocedure);
Loes1c:=dsolve({Eqxa[1],Eqya[1],x(0)=xc0,y(0)=yc0},{x(t),y(t)},type=numeric,output=listprocedure);

(3.2.3)

Darstellung der zeitlichen Entwicklung der Populationsvektoren:

> tanf:=0:
tenda:=5;
tendb:=5;
tendc:=5;
P1:=odeplot(Loes1a,[t,x(t)],tanf..tenda,color=red,axesfont=[HELVETICA,15],labelfont=[HELVETICA,15],numpoints=100,thickness=3):
P2:=odeplot(Loes1a,[t,y(t)],tanf..tenda,color=blue,axesfont=[HELVETICA,15],labelfont=[HELVETICA,15],labels=[t,"x,y"],numpoints=100,thickness=3):
display(P2,P1);
tanf:=0:
P1:=odeplot(Loes1b,[t,x(t)],tanf..tendb,color=red,axesfont=[HELVETICA,15],labelfont=[HELVETICA,15],numpoints=100,thickness=3):
P2:=odeplot(Loes1b,[t,y(t)],tanf..tendb,color=blue,axesfont=[HELVETICA,15],labelfont=[HELVETICA,15],labels=[t,"x,y"],numpoints=100,thickness=3):
display(P2,P1);
tanf:=0:
P1:=odeplot(Loes1c,[t,x(t)],tanf..tendc,color=red,axesfont=[HELVETICA,15],labelfont=[HELVETICA,15],numpoints=100,thickness=3):
P2:=odeplot(Loes1c,[t,y(t)],tanf..tendc,color=blue,axesfont=[HELVETICA,15],labelfont=[HELVETICA,15],labels=[t,"x,y"],numpoints=100,thickness=3):
display(P2,P1);

Plot_2d

Plot_2d

Plot_2d

Die Darstellung dieser Lösungen des Bi-Matrix Spiels kann man z.B. auch in einem (x,y)-Populationsvektor Diagram veranschaulichen:

> v_norm_max:=0:
tt_schrita:=evalf(tenda/40):
tt_schritb:=evalf(tendb/40):
tt_schritc:=evalf(tendc/40):
vec_lengtha:=tt_schrita:
vec_lengthb:=tt_schritb:
vec_lengthc:=tt_schritc:

Plot_2d

Es folgt eine Animation die die zeitliche Entwicklung der Lösungen im (x,y)-Diagram visualisiert:

> tend:=4:
for tt from 0 by 1 to tend do
Vec_blue[tt]:=display(arrow([rhs(Loes1c(tt*tt_schritc)[2]),rhs(Loes1c(tt*tt_schritc)[3])], [rhs(Loes1c(tt*tt_schritc+vec_lengthc)[2]),rhs(Loes1c(tt*tt_schritc+vec_lengthc)[3])], .005, .035, .5, color=blue)):
Vec_red[tt]:=display(arrow([rhs(Loes1a(tt*tt_schrita)[2]),rhs(Loes1a(tt*tt_schrita)[3])], [rhs(Loes1a(tt*tt_schrita+vec_lengtha)[2]),rhs(Loes1a(tt*tt_schrita+vec_lengtha)[3])], .005, .035, .5, color=red)):
Vec_green[tt]:=display(arrow([rhs(Loes1b(tt*tt_schritb)[2]),rhs(Loes1b(tt*tt_schritb)[3])], [rhs(Loes1b(tt*tt_schritb+vec_lengthb)[2]),rhs(Loes1b(tt*tt_schritb+vec_lengthb)[3])], .005, .035, .5, color=COLOR(RGB, .0, 0.8, .3))):
end do:

> display(seq(Ani[j],j=0..frames),insequence=true,scaling=constrained,view=[0..1,0..1.1]):

Klasse der Zentrumsspiele (Center Class Games)

Spieler A: Koordinationsspiel , Spieler B: Anti-Koordinationsspiel

> #Set10us(Set4+Set8)(Co+AntiCo)
D_A11:=10:
D_A12:=4:
D_A21:=9:
D_A22:=5:
D_B11:=10:
D_B12:=12:
D_B21:=7:
D_B22:=5:

print("Matrix Spieler A");
D_A;
print("Matrix Spieler B");
D_B;

(4.1.1)

System der Differentialgleichungen (DGL):

> lhs(Eqxa[1])=collect(simplify(subs({y(t)=x(t)},rhs(Eqxa[1]))),{x(t)});
lhs(Eqya[1])=collect(simplify(subs({x(t)=y(t)},rhs(Eqya[1]))),{y(t)});

(4.1.2)

Die Dynamik bestimmende Funktionen für Spielergruppe A (g_A(x,y), farbige Fläche) und Spielergruppe B (g_B(x,y), graue Fläche):

Plot

Lösung der DGL für drei unterschiedliche Anfangspopulationen:

> xa0:=0.1:#red
ya0:=0.8:
xb0:=0.6:#green
yb0:=0.6:
xc0:=0.7:#blue
yc0:=0.1:
Loes1a:=dsolve({Eqxa[1],Eqya[1],x(0)=xa0,y(0)=ya0},{x(t),y(t)},type=numeric,output=listprocedure);
Loes1b:=dsolve({Eqxa[1],Eqya[1],x(0)=xb0,y(0)=yb0},{x(t),y(t)},type=numeric,output=listprocedure);
Loes1c:=dsolve({Eqxa[1],Eqya[1],x(0)=xc0,y(0)=yc0},{x(t),y(t)},type=numeric,output=listprocedure);

(4.1.3)

Darstellung der zeitlichen Entwicklung der Populationsvektoren:

> tanf:=0:
tenda:=13.5;
tendb:=9;
tendc:=11.5;
P1:=odeplot(Loes1a,[t,x(t)],tanf..tenda,color=red,axesfont=[HELVETICA,15],labelfont=[HELVETICA,15],numpoints=100,thickness=3):
P2:=odeplot(Loes1a,[t,y(t)],tanf..tenda,color=blue,axesfont=[HELVETICA,15],labelfont=[HELVETICA,15],labels=[t,"x,y"],numpoints=100,thickness=3):
display(P2,P1);
tanf:=0:
P1:=odeplot(Loes1b,[t,x(t)],tanf..tendb,color=red,axesfont=[HELVETICA,15],labelfont=[HELVETICA,15],numpoints=100,thickness=3):
P2:=odeplot(Loes1b,[t,y(t)],tanf..tendb,color=blue,axesfont=[HELVETICA,15],labelfont=[HELVETICA,15],labels=[t,"x,y"],numpoints=100,thickness=3):
display(P2,P1);
tanf:=0:
P1:=odeplot(Loes1c,[t,x(t)],tanf..tendc,color=red,axesfont=[HELVETICA,15],labelfont=[HELVETICA,15],numpoints=100,thickness=3):
P2:=odeplot(Loes1c,[t,y(t)],tanf..tendc,color=blue,axesfont=[HELVETICA,15],labelfont=[HELVETICA,15],labels=[t,"x,y"],numpoints=100,thickness=3):
display(P2,P1);

Plot_2d

Plot_2d

Plot_2d

Die Darstellung dieser Lösungen des Bi-Matrix Spiels kann man z.B. auch in einem (x,y)-Populationsvektor Diagram veranschaulichen:

> v_norm_max:=0:
tt_schrita:=evalf(tenda/40):
tt_schritb:=evalf(tendb/40):
tt_schritc:=evalf(tendc/40):
vec_lengtha:=tt_schrita:
vec_lengthb:=tt_schritb:
vec_lengthc:=tt_schritc:

Plot_2d

Es folgt eine Animation die die zeitliche Entwicklung der Lösungen im (x,y)-Diagram visualisiert:

> tend:=15:
for tt from 0 by 1 to tend do
Vec_blue[tt]:=display(arrow([rhs(Loes1c(tt*tt_schritc)[2]),rhs(Loes1c(tt*tt_schritc)[3])], [rhs(Loes1c(tt*tt_schritc+vec_lengthc)[2]),rhs(Loes1c(tt*tt_schritc+vec_lengthc)[3])], .005, .035, .5, color=blue)):
Vec_red[tt]:=display(arrow([rhs(Loes1a(tt*tt_schrita)[2]),rhs(Loes1a(tt*tt_schrita)[3])], [rhs(Loes1a(tt*tt_schrita+vec_lengtha)[2]),rhs(Loes1a(tt*tt_schrita+vec_lengtha)[3])], .005, .035, .5, color=red)):
Vec_green[tt]:=display(arrow([rhs(Loes1b(tt*tt_schritb)[2]),rhs(Loes1b(tt*tt_schritb)[3])], [rhs(Loes1b(tt*tt_schritb+vec_lengthb)[2]),rhs(Loes1b(tt*tt_schritb+vec_lengthb)[3])], .005, .035, .5, color=COLOR(RGB, .0, 0.8, .3))):
end do:

> display(seq(Ani[j],j=0..frames),insequence=true,scaling=constrained,view=[0..1,0..1.1]):

Spieler A: Koordinationsspiel , Spieler B: Anti-Koordinationsspiel

> #Set11us(Set4+Set9)(Co+AntiCo)
D_A11:=10:
D_A12:=4:
D_A21:=7:
D_A22:=5:
D_B11:=10:
D_B12:=12:
D_B21:=9:
D_B22:=5:

print("Matrix Spieler A");
D_A;
print("Matrix Spieler B");
D_B;

(4.2.1)

System der Differentialgleichungen (DGL):

> lhs(Eqxa[1])=collect(simplify(subs({y(t)=x(t)},rhs(Eqxa[1]))),{x(t)});
lhs(Eqya[1])=collect(simplify(subs({x(t)=y(t)},rhs(Eqya[1]))),{y(t)});

(4.2.2)

Die Dynamik bestimmende Funktionen für Spielergruppe A (g_A(x,y), farbige Fläche) und Spielergruppe B (g_B(x,y), graue Fläche):

Plot

Lösung der DGL für drei unterschiedliche Anfangspopulationen:

> xa0:=0.1:#red
ya0:=0.8:
xb0:=0.4:#green
yb0:=0.6:
xc0:=0.7:#blue
yc0:=0.1:
Loes1a:=dsolve({Eqxa[1],Eqya[1],x(0)=xa0,y(0)=ya0},{x(t),y(t)},type=numeric,output=listprocedure);
Loes1b:=dsolve({Eqxa[1],Eqya[1],x(0)=xb0,y(0)=yb0},{x(t),y(t)},type=numeric,output=listprocedure);
Loes1c:=dsolve({Eqxa[1],Eqya[1],x(0)=xc0,y(0)=yc0},{x(t),y(t)},type=numeric,output=listprocedure);

(4.2.3)

Darstellung der zeitlichen Entwicklung der Populationsvektoren:

> tanf:=0:
tenda:=14.5;
tendb:=8;
tendc:=6.5;
P1:=odeplot(Loes1a,[t,x(t)],tanf..tenda,color=red,axesfont=[HELVETICA,15],labelfont=[HELVETICA,15],numpoints=100,thickness=3):
P2:=odeplot(Loes1a,[t,y(t)],tanf..tenda,color=blue,axesfont=[HELVETICA,15],labelfont=[HELVETICA,15],labels=[t,"x,y"],numpoints=100,thickness=3):
display(P2,P1);
tanf:=0:
P1:=odeplot(Loes1b,[t,x(t)],tanf..tendb,color=red,axesfont=[HELVETICA,15],labelfont=[HELVETICA,15],numpoints=100,thickness=3):
P2:=odeplot(Loes1b,[t,y(t)],tanf..tendb,color=blue,axesfont=[HELVETICA,15],labelfont=[HELVETICA,15],labels=[t,"x,y"],numpoints=100,thickness=3):
display(P2,P1);
tanf:=0:
P1:=odeplot(Loes1c,[t,x(t)],tanf..tendc,color=red,axesfont=[HELVETICA,15],labelfont=[HELVETICA,15],numpoints=100,thickness=3):
P2:=odeplot(Loes1c,[t,y(t)],tanf..tendc,color=blue,axesfont=[HELVETICA,15],labelfont=[HELVETICA,15],labels=[t,"x,y"],numpoints=100,thickness=3):
display(P2,P1);

Plot_2d

Plot_2d

Plot_2d

Die Darstellung dieser Lösungen des Bi-Matrix Spiels kann man z.B. auch in einem (x,y)-Populationsvektor Diagram veranschaulichen:

> v_norm_max:=0:
tt_schrita:=evalf(tenda/80):
tt_schritb:=evalf(tendb/40):
tt_schritc:=evalf(tendc/40):
vec_lengtha:=tt_schrita:
vec_lengthb:=tt_schritb:
vec_lengthc:=tt_schritc:

Plot_2d

Es folgt eine Animation die die zeitliche Entwicklung der Lösungen im (x,y)-Diagram visualisiert:

> display(seq(Ani[j],j=0..frames),insequence=true,scaling=constrained,view=[0..1,0..1.1]):