Das begleitende Dreibein 

Dieses Beispiel ist angelehnt an die Aufgabe 8.3 des Buches von Walter Greiner, Mechanik (Teil 1) [5. Auflage, 1989, siehe Seite 57-58]. Siehe auch Übungsblatt 3, Aufgabe 2. 

>	restart: with(LinearAlgebra): with(plots):

 

Die betrachtete Trajektorie beschreibt eine Schraubenlinie. 

>	r := < R*cos(omega*t), R*sin(omega*t), b*omega*t>;

 

(1.1)

 

Betrag des Geschwindigkeitsvektors: 

>	VectorNorm(< diff(r[1],t), diff(r[2],t), diff(r[3],t) >,2);

 

(1.2)

 

Man parametrisiert die Raumkurve zunächst nach der Bogenlänge s und benutzt dabei: 

>	Eq_para:=t=solve(s=int(omega*sqrt(R^2+b^2),t),t): Eq_para;

 

(1.3)

 

Raumkurve in natürlicher Parametrisierung: 

>	rs := subs(Eq_para,r);

 

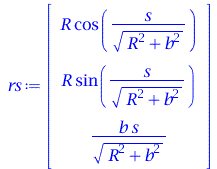(1.4)

 

Tangentialvektor: 

>	T := < diff(rs[1],s), diff(rs[2],s), diff(rs[3],s)>;

 

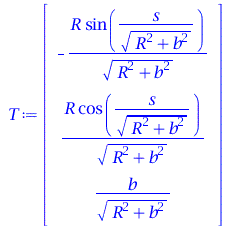(1.5)

 

Normalenvektor:
(Bem.: Die folgenden Ausdrücke,  lassen sich noch sehr vereinfachen!) 

>	rho:=1/VectorNorm(< diff(T[1],s), diff(T[2],s), diff(T[3],s)>,2): N := rho * < diff(T[1],s), diff(T[2],s), diff(T[3],s)>;

 

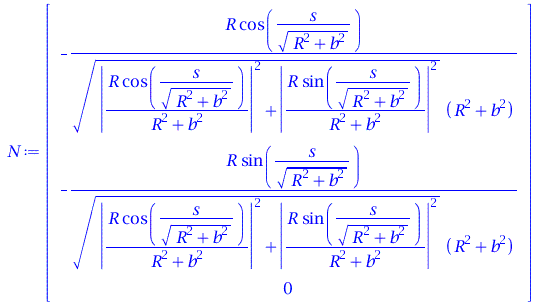(1.6)

 

Binormalenvektor: 

>	B := CrossProduct(T, N);

 

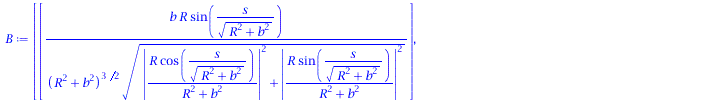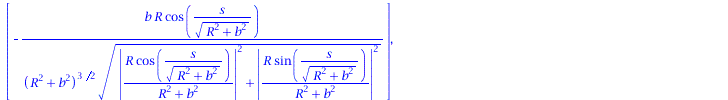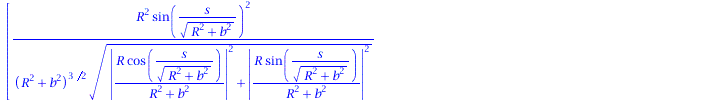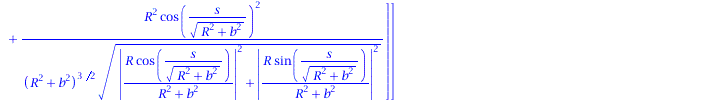(1.7)

 

Ableitung des Binormalenvektors nach der Bogenlänge: 

>	dB := < diff(B[1],s), diff(B[2],s), diff(B[3],s)>; tau:=VectorNorm(dB,2):

 

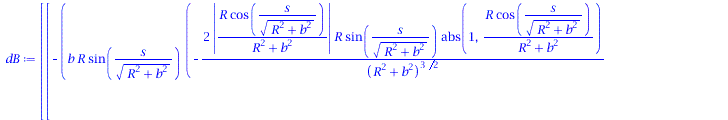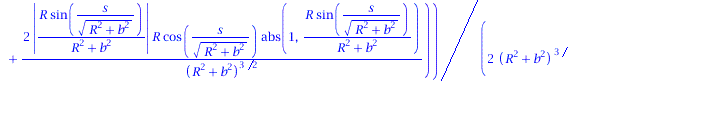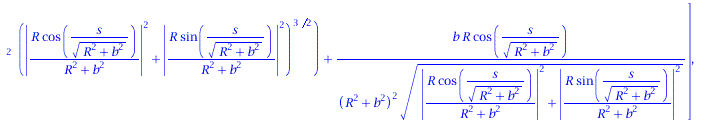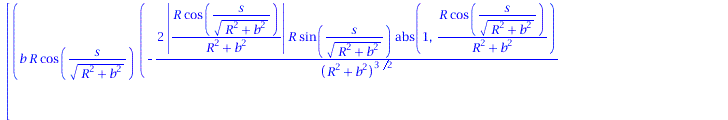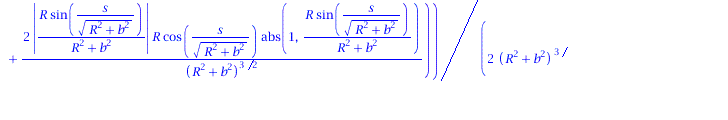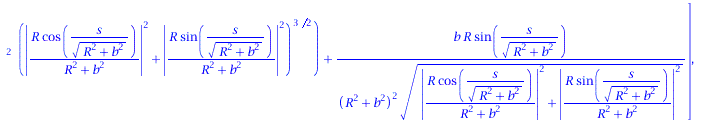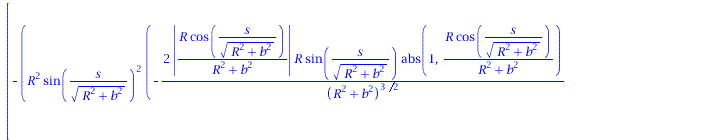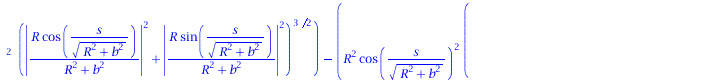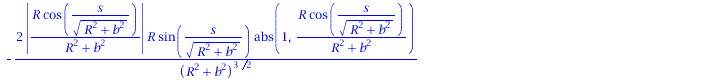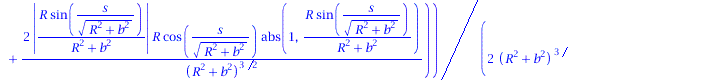(1.8)

 

Ableitung des Normalenvektors nach der Bogenlänge: 

>	dN := < diff(N[1],s), diff(N[2],s), diff(N[3],s)>;

 

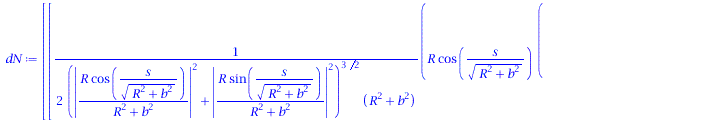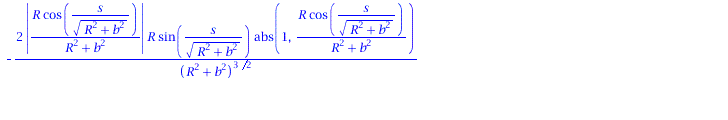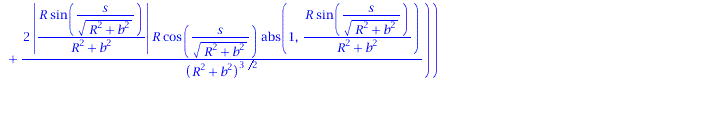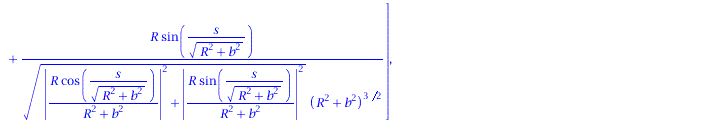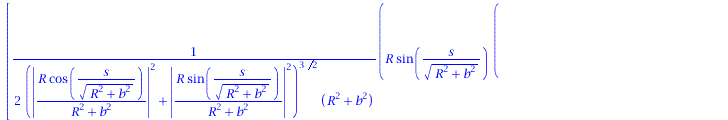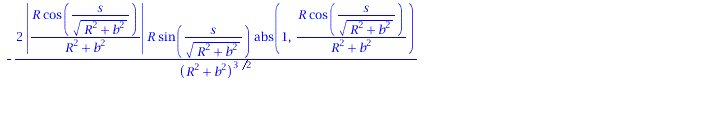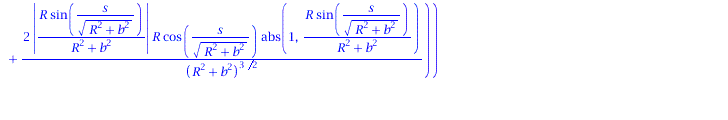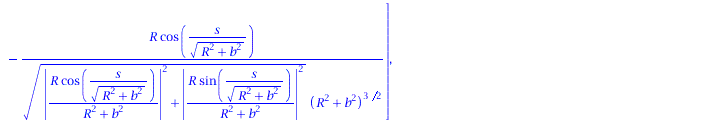(1.9)

 

Im folgenden legen wir die noch freien Parameter wie folgt fest: 

>	R:=1; omega:=1; b:=0.1;

 

 

 

	(1.10)

 

Krümmung der Trajektorie: 

>	kappa=evalf(subs(s=1,1/rho)); evalf(R/(R^2+b^2));

 

 

	(1.11)

 

Torsion der Trajektorie: 

>	evalf(subs(s=1,tau)); evalf(b/(R^2+b^2));

 

 

	(1.12)

 

Die folgende Animation zeigt die Bewegung des begleitenden Dreibeins im Intervall s=[0,15]. Der dünne schwarze Vektor beschreibt den Ortsvektor der Raumkurve, der rote den Tangentialvektor, der blaue den Normalenvektor und der grüne den Binormalenvektor. 

>

frames:=50: s_end:=15: Traj:=spacecurve(rs, s = 0 .. s_end,thickness=3,numpoints=5000): for i from 0 by 1 to frames do AVrs[i]:=arrow( <0,0,0>, subs(s=i*s_end/frames,rs), width = 0.015, head_length = 0.2, color = black): AVT[i]:=arrow( subs(s=i*s_end/frames,rs), subs(s=i*s_end/frames,T), width = 0.04, head_length = 0.2, color = red): AVN[i]:=arrow( subs(s=i*s_end/frames,rs), subs(s=i*s_end/frames,N), width = 0.04, head_length = 0.2, color = blue): AVB[i]:=arrow( subs(s=i*s_end/frames,rs), subs(s=i*s_end/frames,B), width = 0.04, head_length = 0.2, color = green): Ani[i]:=display({AVrs[i],AVT[i],AVN[i],AVB[i],Traj}); od:

 

>	display([seq(Ani[i],i=0..frames)],insequence=true,scaling=constrained,labels=[x,y,z]);

 

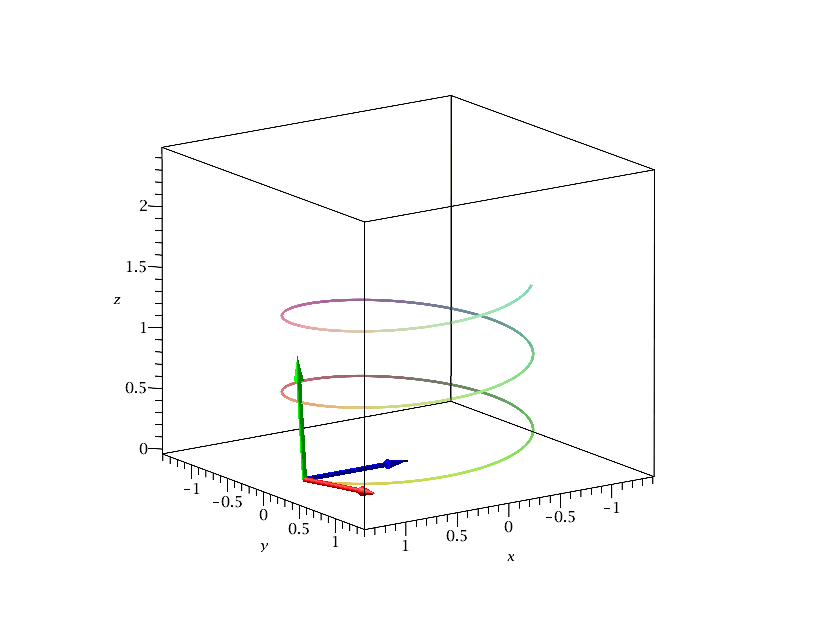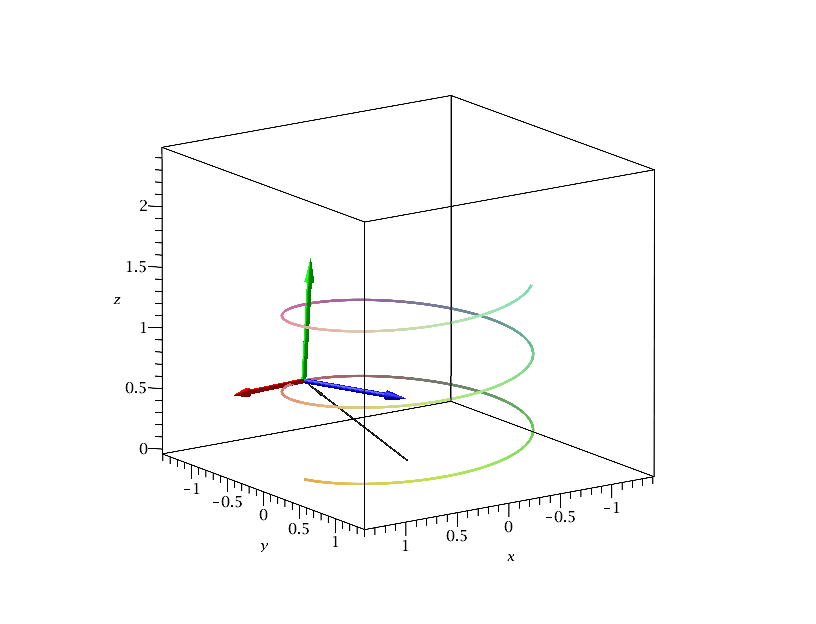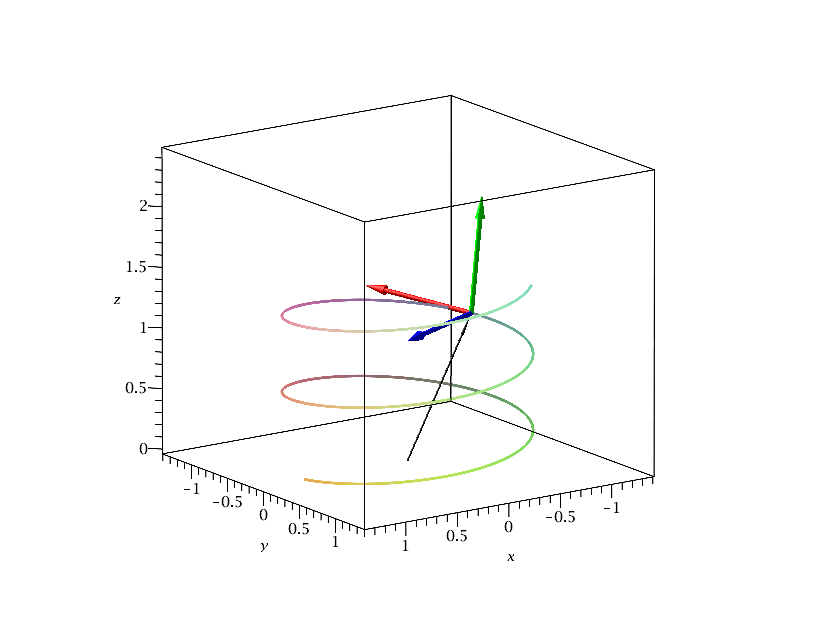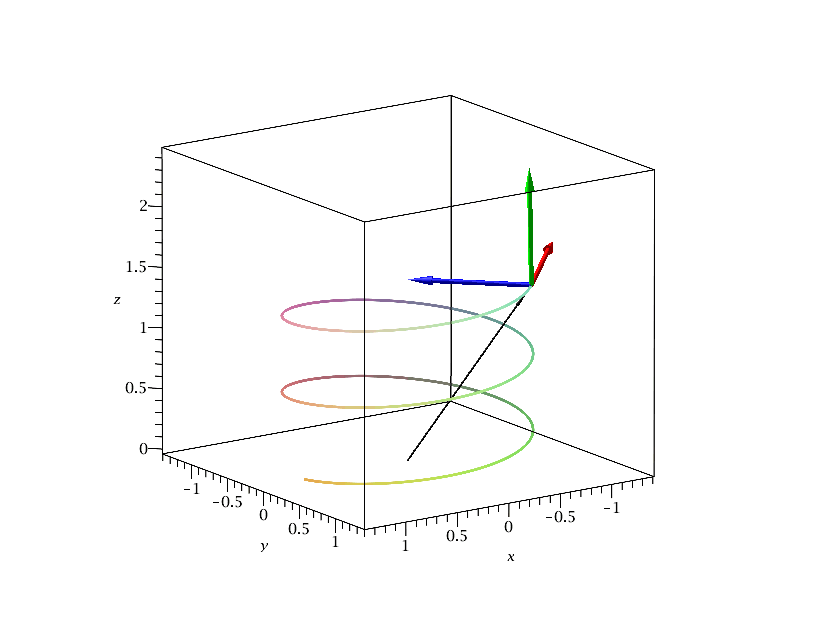Vergrößert man den Parameter b, so erhöht man den Wert der Steighöhe der Bahnkurve, das Herausdrehen der trajektorie aus der (x,y)-Ebene (die Torsion) wird größer und der Wert der Krümmung der Kurve wird veringert:  

>	R:=1; omega:=1; b:=0.5;

 

 

 

	(1.13)

 

Krümmung der Trajektorie: 

>	kappa:=evalf(subs(s=1,1/rho)); evalf(R/(R^2+b^2));

 

 

	(1.14)

 

Torsion der Trajektorie: 

>	evalf(subs(s=1,tau)); evalf(b/(R^2+b^2));

 

 

	(1.15)

 

Die folgende Animation zeigt die Bewegung des begleitenden Dreibeins im Intervall s=[0,15]. Der dünne schwarze Vektor beschreibt den Ortsvektor der Raumkurve, der rote den Tangentialvektor, der blaue den Normalenvektor und der grüne den Binormalenvektor. 

>

frames:=50: s_end:=15: Traj:=spacecurve(rs, s = 0 .. s_end,thickness=3,numpoints=5000): for i from 0 by 1 to frames do AVrs[i]:=arrow( <0,0,0>, subs(s=i*s_end/frames,rs), width = 0.015, head_length = 0.2, color = black): AVT[i]:=arrow( subs(s=i*s_end/frames,rs), subs(s=i*s_end/frames,T), width = 0.04, head_length = 0.2, color = red): AVN[i]:=arrow( subs(s=i*s_end/frames,rs), subs(s=i*s_end/frames,N), width = 0.04, head_length = 0.2, color = blue): AVB[i]:=arrow( subs(s=i*s_end/frames,rs), subs(s=i*s_end/frames,B), width = 0.04, head_length = 0.2, color = green): Ani[i]:=display({AVrs[i],AVT[i],AVN[i],AVB[i],Traj}); od:

 

>	display([seq(Ani[i],i=0..frames)],insequence=true,scaling=constrained,labels=[x,y,z]);

 

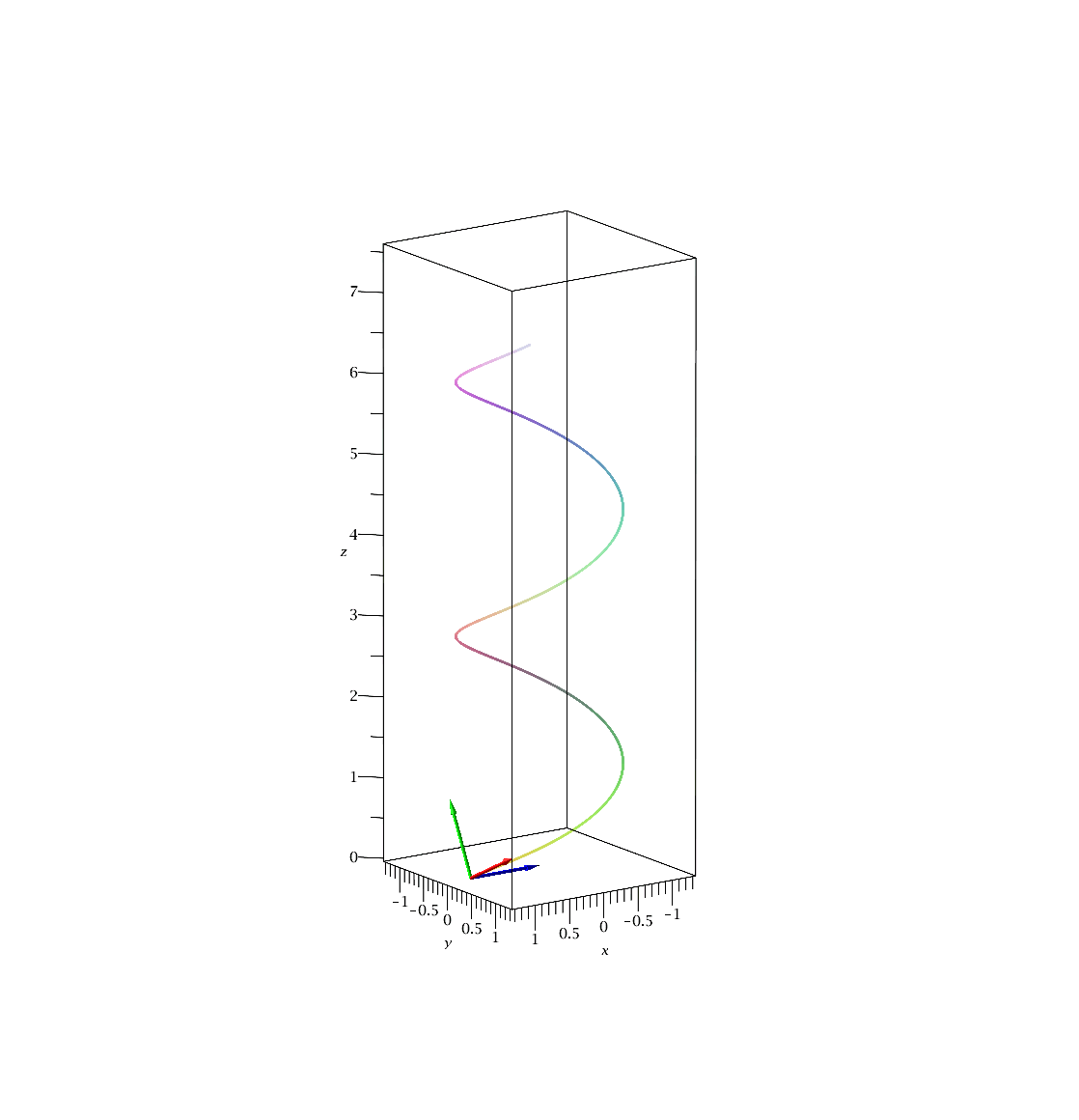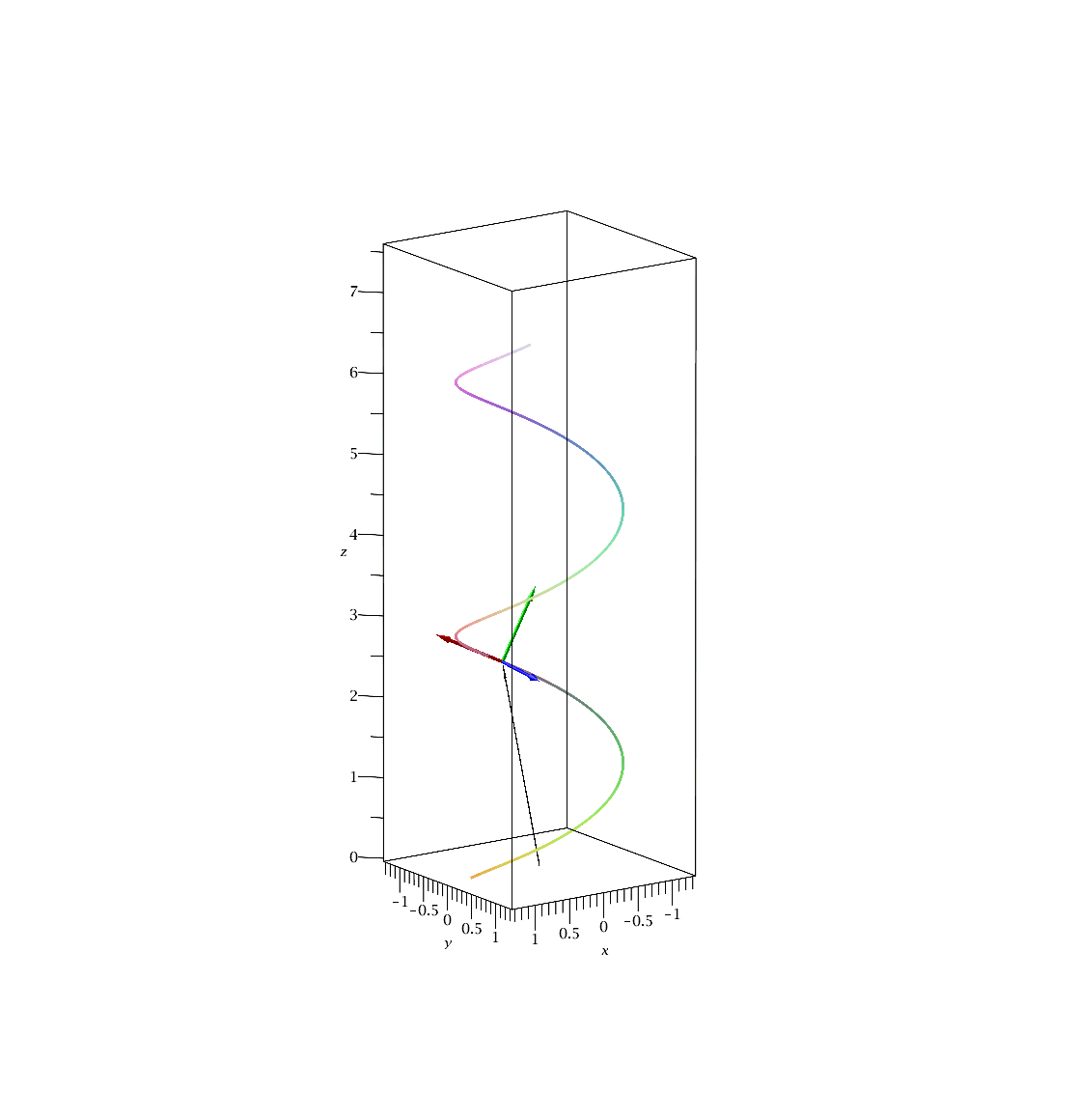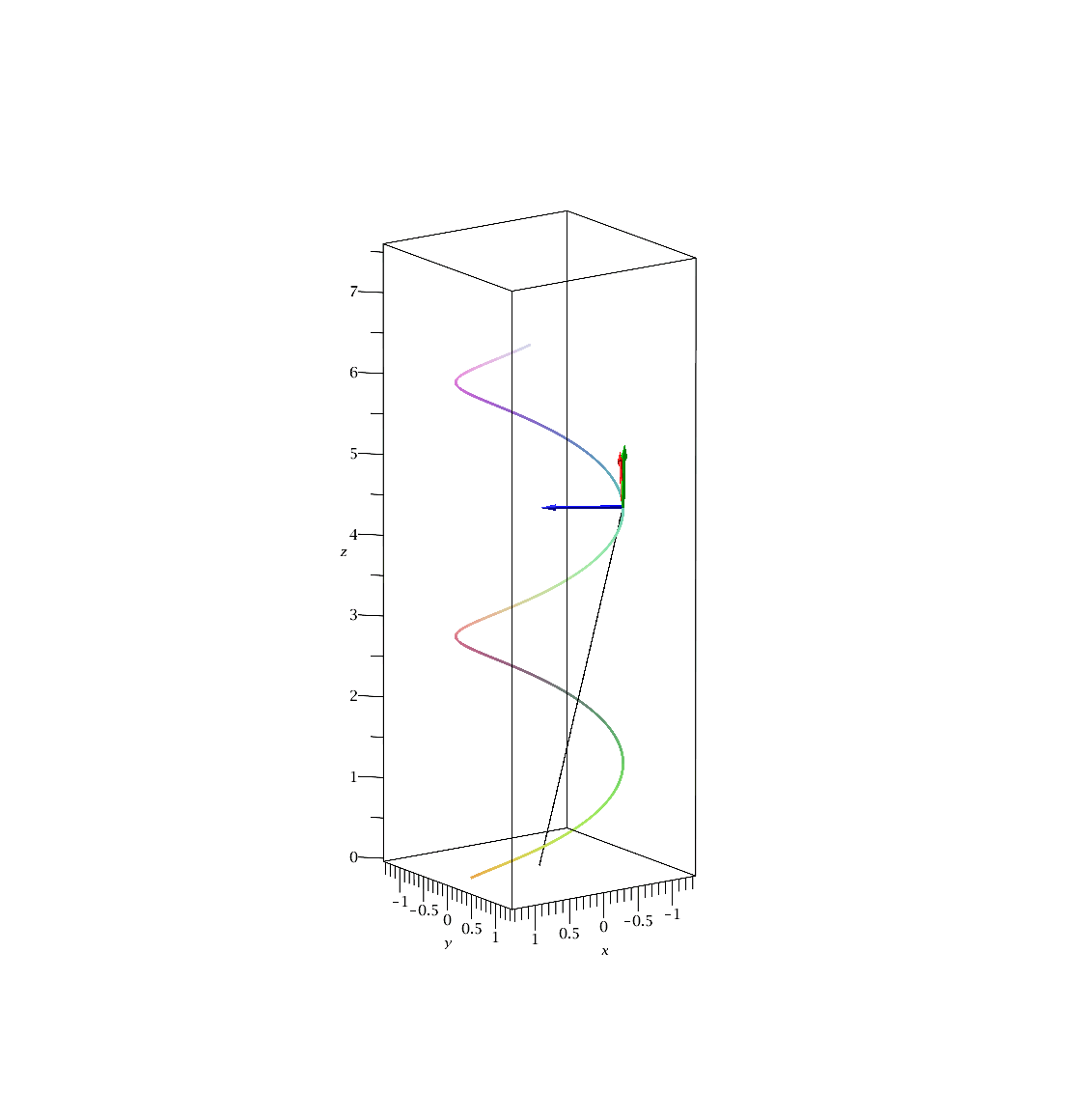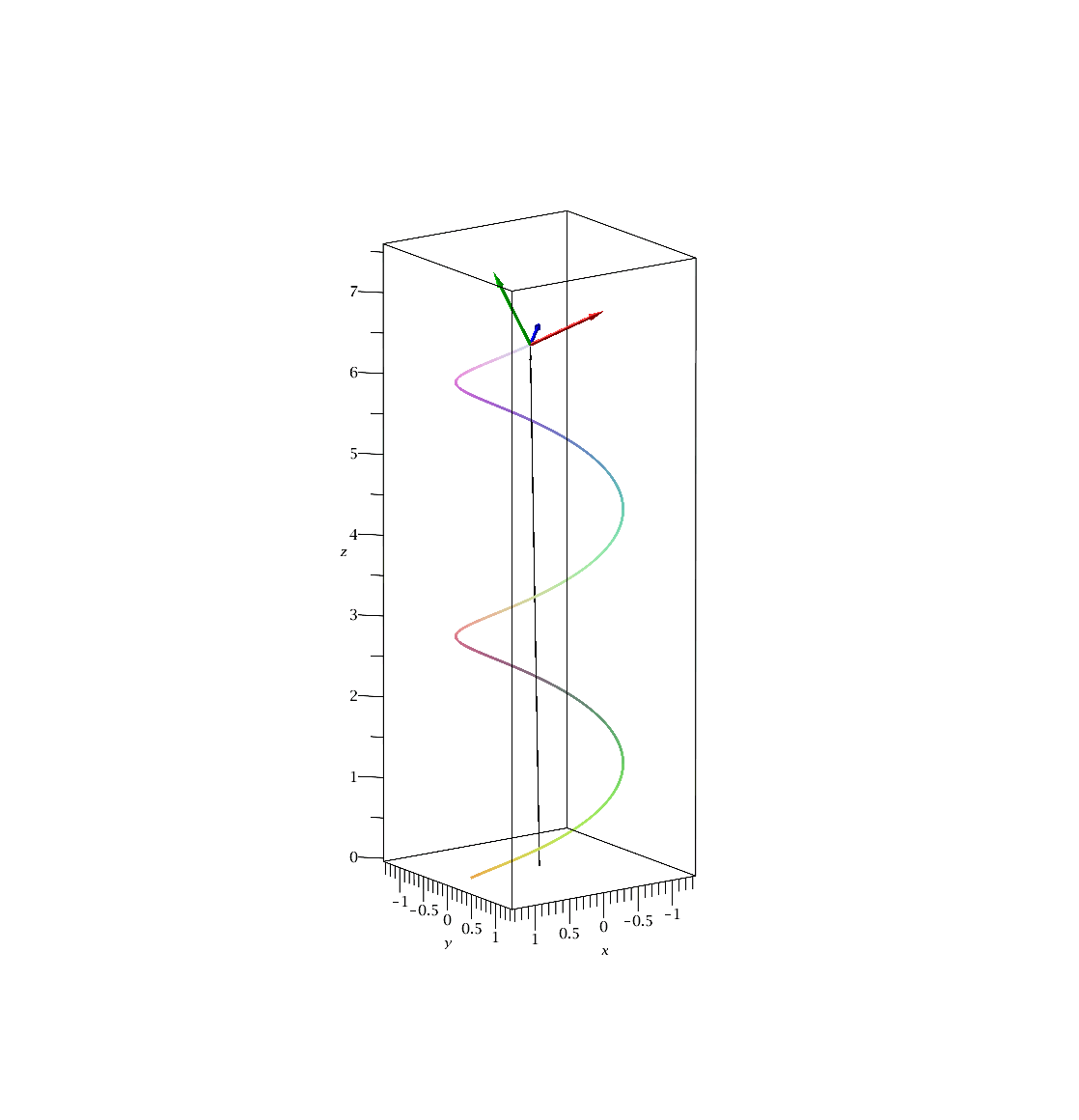Wir überprüfen die 3. Frenetschen Formel (siehe Vorlesungsskript Seite 35, Gleichung (1.71), http://www.th.physik.uni-frankfurt.de/~drischke/Skript_MI_WiSe2016-2017.pdf ) an einem festen Raumpunkt der Bahnkurve (z.B. s=10): 

>

set_s:=10: Traj:=spacecurve(rs, s = 8 .. 11,thickness=3,numpoints=5000): AVT:=arrow( subs(s=set_s,rs), subs(s=set_s,T), width = 0.03, head_length = 0.2, color = red): AVN:=arrow( subs(s=set_s,rs), subs(s=set_s,N), width = 0.03, head_length = 0.2, color = blue): AVB:=arrow( subs(s=set_s,rs), subs(s=set_s,B), width = 0.03, head_length = 0.2, color = green): AVdN:=arrow( subs(s=set_s,rs), subs(s=set_s,dN), width = 0.04, head_length = 0.1, color = "DarkGrey"): AVFrenB:=arrow( subs(s=set_s,rs), subs(s=set_s,tau*B), width = 0.04, head_length = 0.1, color = "DarkGreen"): AVFrenT:=arrow( subs(s=set_s,rs+tau*B), subs(s=set_s,-kappa*T), width = 0.04, head_length = 0.1, color = "DarkRed"): Ani:=display({AVT,AVN,AVB,Traj,AVdN,AVFrenT,AVFrenB}): display(Ani,scaling=constrained,labels=[x,y,z],axes=framed);

 

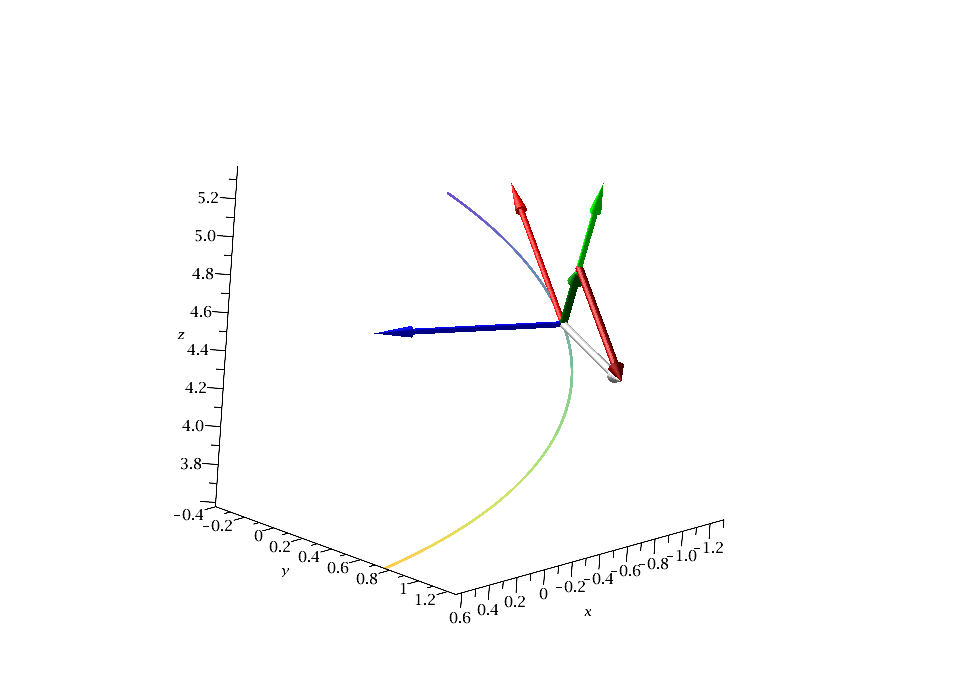Numerische Überprüfung der 3. Frenetschen Formel (Gleichung (1.71)): 

>	evalf(simplify(subs(s=set_s,dN)))=evalf(simplify(subs(s=set_s,tau*B)))-evalf(simplify(subs(s=set_s,kappa*T)));

 

(1.16)

 

Numerische Überprüfung der 2. Frenetschen Formel (Gleichung (1.69)): 

>	evalf(simplify(subs(s=set_s,dB)))=evalf(simplify(subs(s=set_s,-tau*N)));

 

(1.17)

 

Geschwindigkeitsvektor eines Massenpunktes auf der Trajektorie: 

>	diff(r,t); evalf(subs(t=0,VectorNorm(diff(r,t),2)))*evalf(simplify(subs(s=int(omega*sqrt(R^2+b^2),t),T)));

 

 

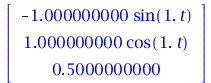	(1.18)

 

Beschleunigungsvektor eines Massenpunktes auf der Trajektorie zur Zeit t=5 (siehe Gleichung Seite S:36). Die Gleichung vereinfacht sich da die zeitliche Ableitung des Geschwindigkeitsbetrages Null ist und somit der Vektor der Beschleunigung nur in Richtung des Normalenvektors zeigt und keinen Beitrag in Tangentialrichtung hat. 

>	evalf(subs(t=5,diff(r,t,t))); evalf(subs(t=5,evalf(subs(t=0,VectorNorm(diff(r,t),2)))^2/(evalf(subs(s=0,rho)))*evalf(simplify(subs(s=int(omega*sqrt(R^2+b^2),t),N)))));

 

 

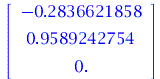	(1.19)

 

Weitere Beispiele von Raumkurven: 

>	restart: with(LinearAlgebra): with(plots):

 

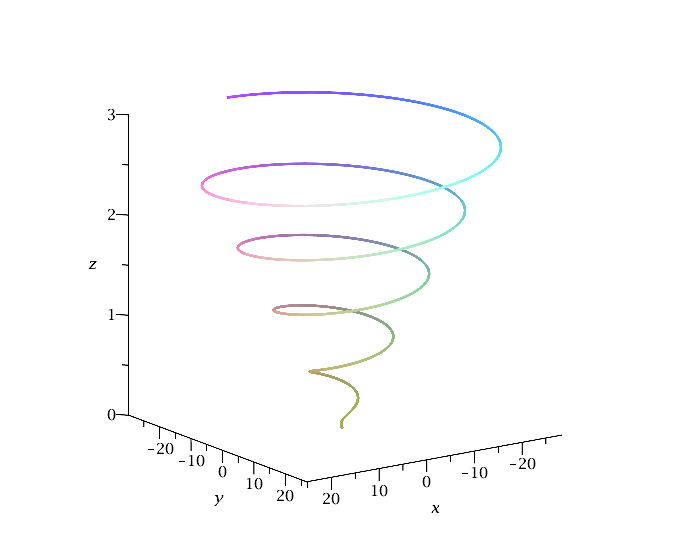
Die folgende Trajektorie beschreibt eine Schraubenlinie deren Radius sich mit der Zeit verändert. 

>	r := < R*t*cos(omega*t), R*t*sin(omega*t), b*omega*t>;

 

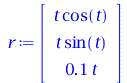(1.20)

 

>	R:=1; omega:=1; b:=0.1; t_end:=30; spacecurve(r, t = 0 .. t_end,thickness=3,numpoints=5000,labels=[x,y,z],axes=framed);

 

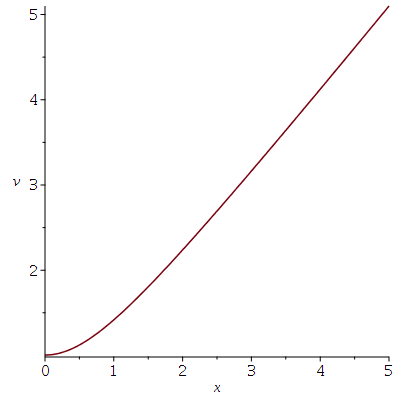
Der Betrag des Geschwindigkeitsvektors eines Massenpunktes auf der Trajektorie ist nun nicht mehr konstant: 

>	VectorNorm(diff(r,t),2); plot(VectorNorm(diff(r,t),2),t=0..5,labels=[x,v]);

 

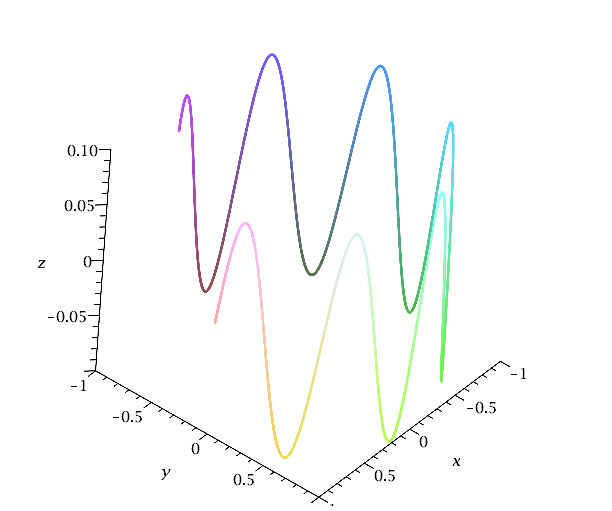
Die folgende Trajektorie beschreibt eine Kreisbewegung mit einem sinusförmigem auf und ab in z-Richtung: 

>	restart: with(LinearAlgebra): with(plots): r := < R*cos(omega*t), R*sin(omega*t), b*sin(Omega*t)>;

 

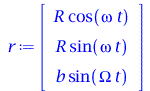(1.21)

 

>	R:=1; omega:=1; b:=0.1; Omega:=8; spacecurve(r, t = 0 .. 5,thickness=3,numpoints=5000,labels=[x,y,z],axes=framed);

 

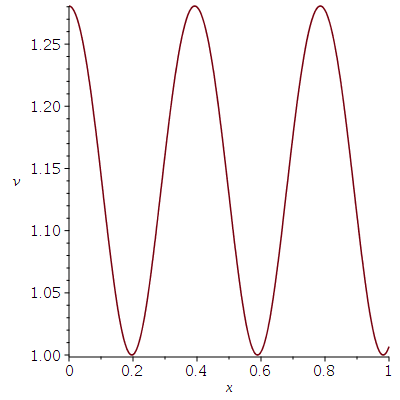
Der Betrag des Geschwindigkeitsvektors eines Massenpunktes auf der Trajektorie ist nun nicht mehr constant: 

>	VectorNorm(diff(r,t),2); plot(VectorNorm(diff(r,t),2),t=0..1,labels=[x,v]);