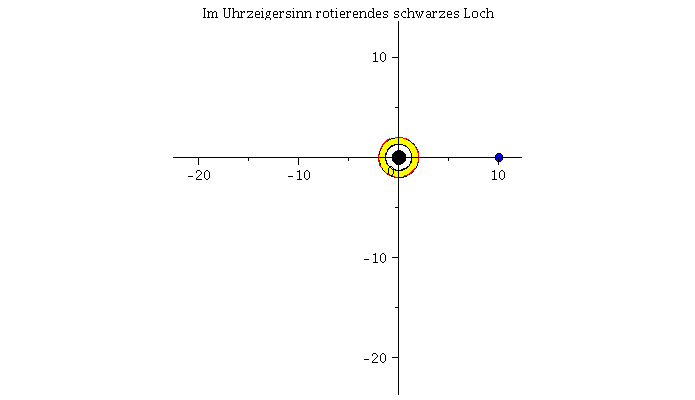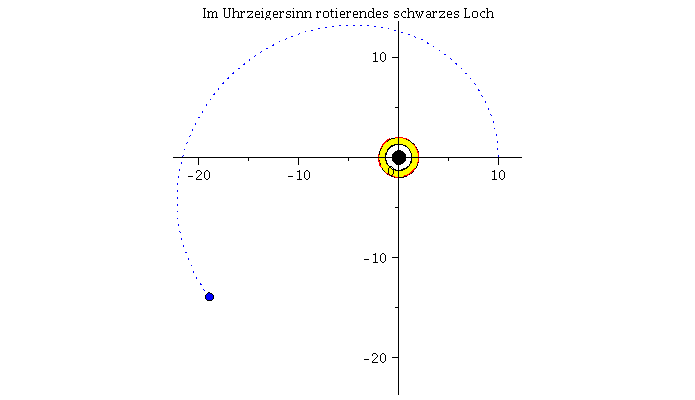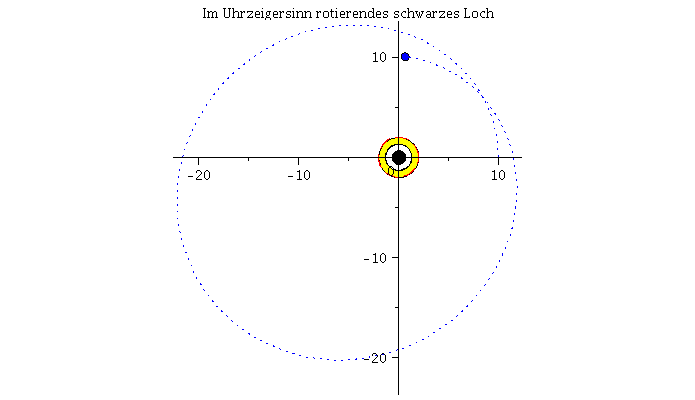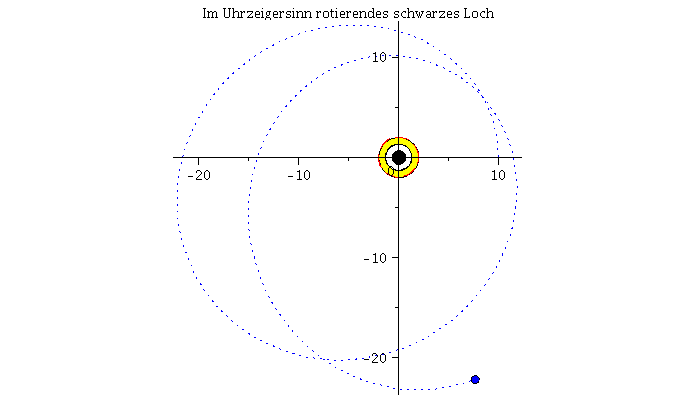Vorwort
Die Vorlesung Allgemeine Relativiätstheorie mit dem Computer wurde im Sommersemester 2016 das erste Mal gehalten und die hier vorliegenden Internetseiten basieren grundsätzlich auf den damals erstellten Seiten. Da sich jedoch innerhalb der letzten drei Jahre das Weltbild der theoretischen Astrophysik grundsätzlich revolutionierte, wird in der aktuellen Version der Vorlesung (SS 2019) auf diese Meilensteine in der Geschichte der Astrophysik speziell eingegangen.
Mittels der Gravitationswellen Detektoren der LIGO/VIRGO Kollaboration, konnten innerhalb der letzten drei Jahre 11 Gravitationswellen aufgespührt werden.

Das erste Bild des schwarzen Lochs im Zentrum unserer Nachbargalaxie M87 wurde mittels des Event Horizon Telescope erstellt, bei dem auch Mitarbeiter der Goethe Universität des BlackHoleCam Teams beteiligt waren.
- 11.04.2019, Frankfurter Allgemeine Zeitung, Titelbild,
Mitten ins Schwarze.
- 11.04.2019, Bild Zeitung,
Darum ist dieser Donut eine Weltsensation!
- 13.04.2019, Titelbild der Zeitschrift Spiegel,
Am Ende von Raum und Zeit, Was uns schwarzer Löcher über die Geheimnisse des Universums verraten.
- 13.04.2019, Zeitschrift Focus,
Portrait eines schwarzen Lochs.
Linke Abbildung: Am 14. September 2015 wurde die erste Gravitationswelle zweier kollidierender schwarzer Löcher experimentell nachgewiesen (siehe GW150914). Mittels der Gravitationswellen Detektoren Ligo und Virgo, konnten mittlerweile 11 Gravitationswellen aufgespührt werden, wobei eine dieser Gravitationswellen von der Kollission zweier Neutronensterne verursacht wurde (GW170817). Da bei diesem Ereignis auch elektromagnetische Begleitstrahlung in allen Frequenzbereichen detektiert wurde, und der ausgesandte Gammablitz mit einer Verzögerung von 1.7 Sekunden auf die Gammastrahlen Sateliten-Teleskope traf, konnte erstmals ein direkter Nachweis einer Neutronenstern Kollission als Ursache der short gamma-ray bursts erbracht werden. Seit 01. April 2019 nimmt die LIGO/VIRGO Kollaboration wieder Daten auf und es wird erwartet, dass sie, mittels der nun noch sensitiveren Gravitationswellendetektoren, ca. ein Ereignis pro Woche aufspühren werden.
Ein wenig mehr als hundert Jahre nachdem Albert Einstein seine Feldgleichungen der Allgemeine Relativiätstheorie der Öffentlichkeit präsentierte, und er damit die Grundlage für Gravitationswellen und schwarzer Löcher formulierte, ist seit einigen Wochen ein weiterer Meilenstein in der Geschichte der Astronomie in aller Munde (erstes Bild eines schwarzen Lochs, siehe rechte Abbildung, YouTube Video).
Einführung
Als Albert Einstein im Jahre 1915 seine Allgemeine Relativiätstheorie der wissenschaftlichen Gemeinschaft vostellte, glaubten noch nicht viele Physiker, dass seine neue Theorie der Raumzeit-Verformung das alte Newtonsche Weltbild der Gravitation ersetzen könne. Heute, ein wenig mehr als hundert Jahre später, triumphiert seine neue Gravitationstheorie und alle experimentellen (zur Zeit möglichen) Überprüfungen der mathematisch sehr anspruchvollen Gleichungen, stimmen mit hoher Genauigkeit mit den Vorhersagen seiner Theorie überein.
Im Teil I dieser Vorlesung werden die Grundlagen der allgemeinen Relativitätstheorie (ART) nochmals kurz wiederholt um dann Themen wie I.2) Das nichtrotierende schwarze Loch, I.3) Weiße Zwerge, Neutronensterne und Quarksterne, I.3) Das rotierende Schwarze Loch und weitere astrophysikalisch/kosmologische Inhalte zu behandeln.
Die grundlegenden Gleichungen der allgemeinen Relativitätstheorie und im besonderen die Einsteingleichung
\[
R_{\mu\nu} - \frac{1}{2} g_{\mu\nu} R ~=~ -8 \pi \, T_{\mu\nu}
\]
und die Geodatengleichung
\[
\frac{d^2 x^\mu}{d\tau^2} + \Gamma^\mu_{\nu \rho} \frac{d x^\nu}{d\tau} \frac{d x^\rho}{d\tau} ~=~ 0
\]
werden als bekannt vorausgesetzt und Studenten die mit dem Tensorformalismus der ART nicht mehr vertraut sind wird geraten die entstandenen Lücken in den ersten Wochen der Vorlesungszeit aufzufrischen. Die griechischen, raumzeitlichen Indices $ \mu, \nu, \rho ... $ laufen von 0..3, wobei, falls nicht anders angegeben, diese den folgenden kartesischen Raumzeitkoordinaten entsprechen: $ x^\mu = \left( x^0, x^1, x^2, x^3 \right) = \left( t, x, y, z \right)$.
Literatur
[1] "Allgemeine Relativitätstheorie" von Torsten Fließbach [2] "Einführung in die Relativitätstheorie" von Ray D'Inverno [3] "General relativity : An introduction for physicists" von M. P. Hobson, G. P. Efstathiou und A. N. Lasenby [4] "Gravity : An introduction to Einstein's general relativity" von James B. Hartle [5] "Relativistic hydrodynamics" von Luciano Rezzolla und Olindo Zanotti [6] "Gravitation" von Charles W. Misner, Kip S. Thorne und John Archibald WheelerTeil I: Analytische Berechnungen und numerische Simulationen in Maple
Einfürung in Maple ( LibreOffice Datei , PDF Datei )
Am Anfang des ersten Teils der Vorlesung wird eine kurze Einfürung in das Computeralgebra-System Maple gegeben.
Im folgenden werden einige grundlegende Größen der allgemeinen Relativitätstheorie am Beispiel der allgemeinen statischen, isotropen Metrik erläutert und aufgezeigt, wie man diese in Maple berechnet. Zunächst wird das "tensor"-Paket eingebunden. Die mit roter Schrift gekennzeichneten Wörter stellen die vom User eingegebenen Befehle dar und die blauen Wörter sind die vom Maple-Program ausgegebenen Größen. Hier werden im speziellen die im "tensor"-Paket neu definierten Befehle ausgegeben. Möchte man die eingegebenen Befehle zwar ausführen, aber nicht ausgeben lassen, so hat man am Ende des Befehls einen Doppelpunkt und kein Semikolon zu schreiben.
1) Grundlegende Größen der ART
Die komplizierten und zeitaufwendigen Berechnungen der tensoriellen Gleichungen der ART können mit Hilfe von Maple erleichtert werden und numerische Simulationen der entstehenden Differentialgleichungen sind ohne viel Aufwand möglich. Im Teil I.1) dieser Vorlesung wird zunächst gezeigt, wie man die grundlegende Größen der allgemeinen Relativiätstheorie im Maple implementiert (Metrik, Christoffelsymbole, Riemann- und Riccitensor, Einsteingleichung, Geodätengleichung, ...).
2) Das nichtrotierende schwarze Loch ( Version 1 , Version 2, Mathematica Notebook der Version 2, Der Merkur-Transit, Das schwarze Loch in M87 (nicht rotierend) )
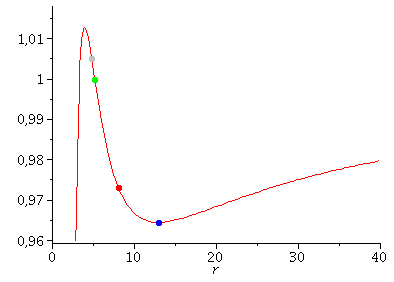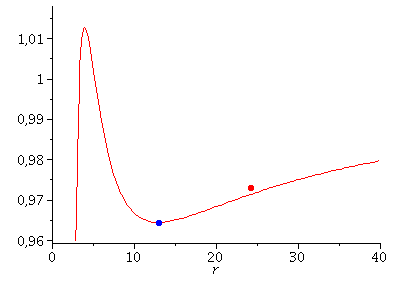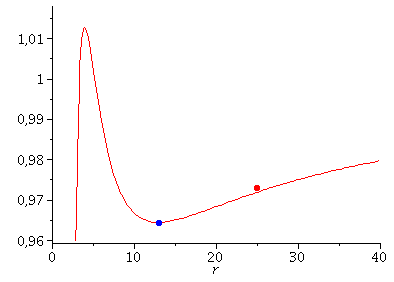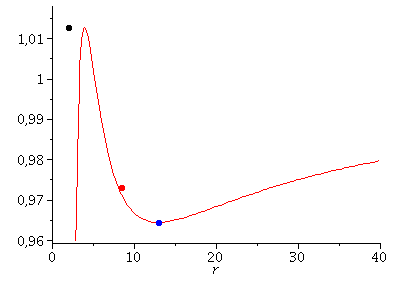
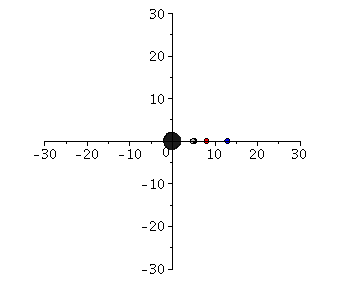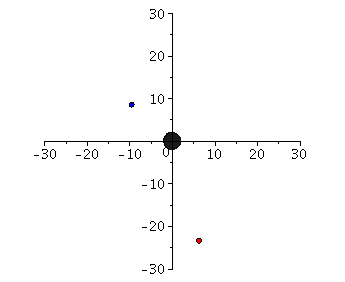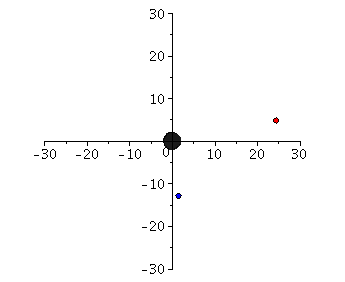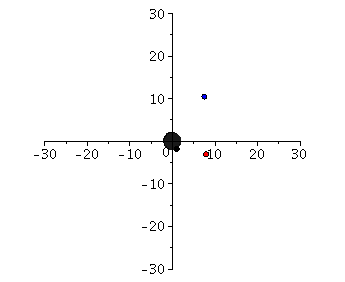
Links: Klassifikation der Bahnbewegungen mittels des effektives Potential Veff(r). Rechts: Trajektorien möglicher Bahnbewegungen um ein nichtrotierendes schwarzes Loch in Schwarzschild-Koordinaten.
Das im Vorwort vorgestellte Bild eines schwarzen Lochs (SL) im Zentrum unserer Nachbargalaxie M87, ist ein erster Versuch, die um ein schwarze Loch entstehende Radiostrahlung mittels eines weltweiten Verbunds von Radiowellenteleskopen sichtbar zu machen. In Kürze (voraussichtlich im Sommer 2019) werden die aufgenommenen Bilder von Sagittarius A*, das schwarze Loch im Zentrum unserer Galaxie, ebenfalls ausgewertet sein, und weitere Bilder in verbesserter Auflösung werden wohl in einigen Jahren folgen.
In beiden Systemen (SL in M87 und Sagittarius A*) kreist Materie in einer Akretionsscheibe um ein supermassives SL und emittiert beim Einfallen Radiowellenstrahlung. Die Bewegung eines Probekörpers (Masse verschwindend klein gegenüber der Masse des schwarzen Lochs) um ein schwarzes Loch ist somit ein astrophysikalisch sehr relevantes Problem. Schon Jahre bevor die ersten Bilder eines SLs entstanden. galt es schon als so gut wie bestätigt, dass im Zentrum unserer Galaxie ein superschweres schwarzes Loch existiert und man verfolgte schon seit Jahrzenten (siehe z.B. R.Genzel et,al.) die Bewegung einzelner sogenannter S-Sterne um dieses Zentrum.
Neben diesen aktuellen Erkenntnissen, gilt die Perihel-Drehung des Merkur als ein, durch die allgemeine Relätivitätstheorie verursachter Effekt. Obwohl die Bewegung der Planenten unseres Sonnensystems um unser Zentralgestirn (die Sonne) ja sicherlich keine Bewegung um ein schwarzes Loch darstellt, können die Gleichungen der Planetenbewegungen in guter Approximation als solche beschrieben werden (siehe Birkov-Theorem). Im Teil I.2) dieser Vorlesung wir die Geodätengleichung in vorgegebener Schwarzschild-Raumzeit behandelt und die möglichen Bahnen von Probekörpern mittels eines definierten effektiven Potentials klassifiziert. Neben den gebundenen kreisförmigen (blau) und eliptischen (rot) Bahnen, den parabolischen (grün) und hyperbolischen (grau) Bahnverläufen ist auch eine durch das schwarze Loch eingefangene Bahn (schwarz: capture orbit) möglich.
Ein Verständnis des Erscheinungsbildes des schwarzen Lochs ist möglich indem man sich grundlegenden Begriffe, wie Ereignishorizont, Photonenspähre und der Orbit der letzten stabilen Kreisbahn um ein SL veranschaulicht (siehe Version 2).
3) Weiße Zwerge, Neutronensterne und Quarksterne ( Version 1 , Version 2: Vergleich mit C++ Resultaten aus Teil II )
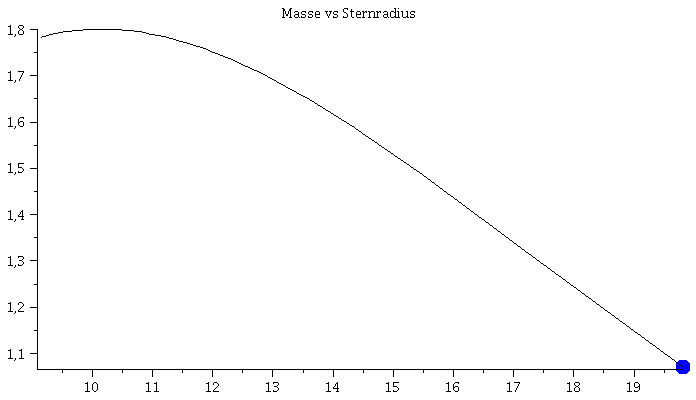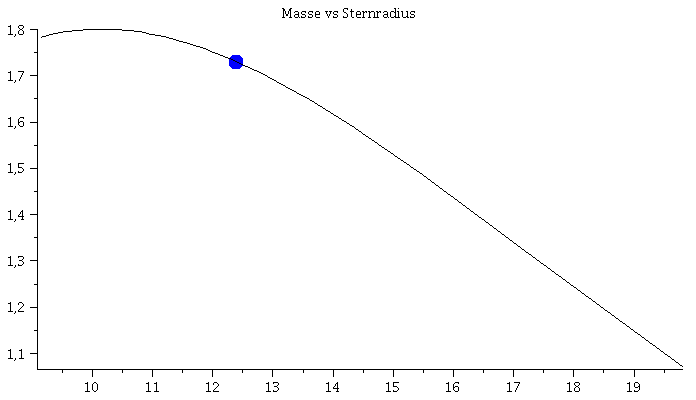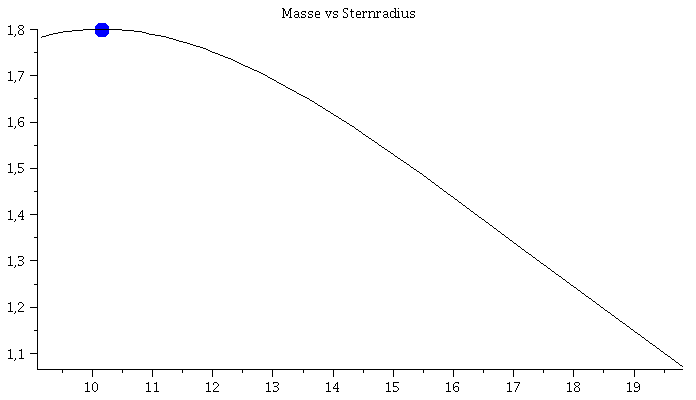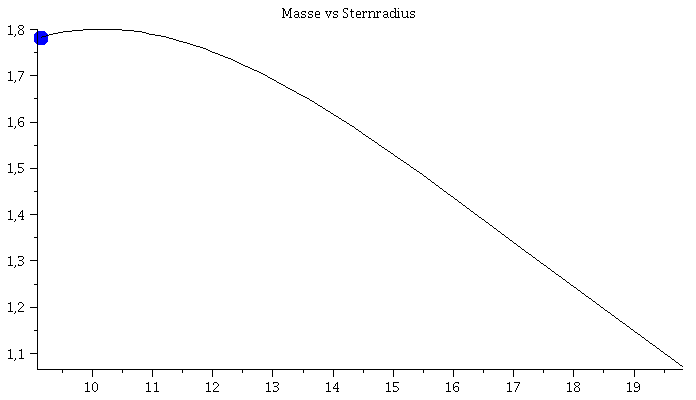
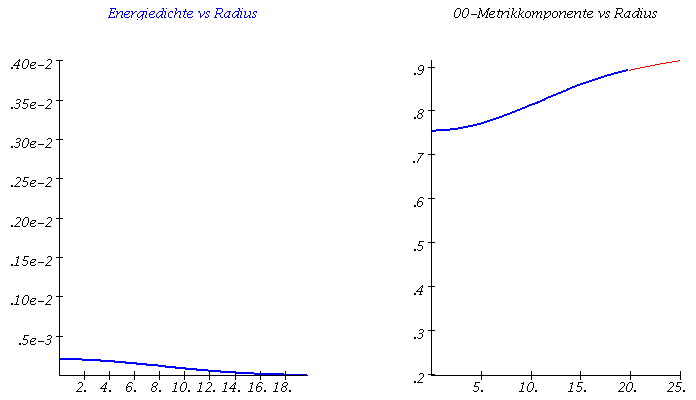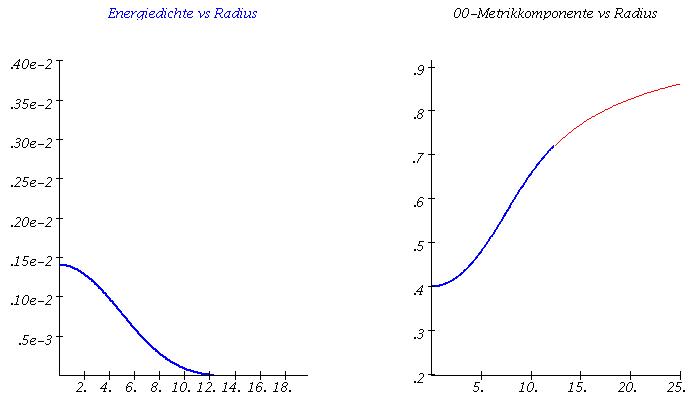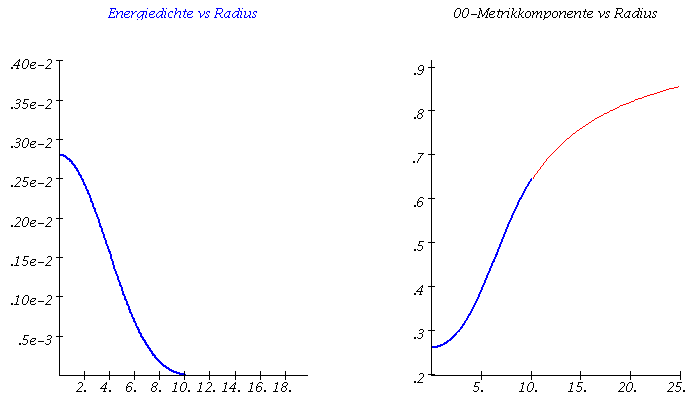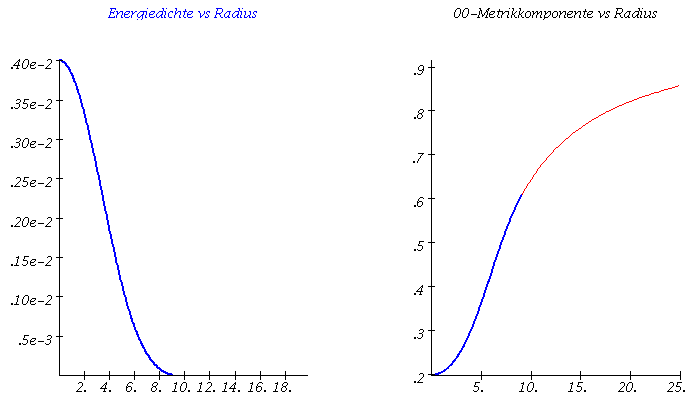
Links: Masse-Radius Beziehung einer Sequenz von Neutronensternen. Rechts: Energiedichteprofil und g00-Metrikkomponente (Innenraum:blau, Aussenraum: rot) als Funktion des Radius r.
Die von den Gravitationswellen Detektoren Ligo und Virgo detektierte Gravitationswelle (GW170817) stammt von einer Kollission zweier Neutronensterne (siehe Vorwort, weiter oben). Neutronensterne sind neben weißen Zwergen und stellaren schwarzen Löchern die möglichen Endzustände des Evolutionsprozesses einer Sonne. Neutronensterne werden in gewaltigen Supernova-Explosionen geboren. Diese faszinierenden stellaren Objekte besitzen lediglich einen Durchmesser von 20 Kilometern, vereinen dort jedoch auf engstem Raum eine Masse von 500 000 Erdmassen. Von den ca. 100 Millionen Neutronensternen die es in unserer Galaxie, der Milchstraße, vermutlich gibt, sind ca. 3000 als Pulsare bekannt. Pulsare sind schnell rotierende Neutronensterne mit einem starken Magnetfeld (bis zu 1011 Tesla), die bevorzugt entlang der Pole elektromagnetische Strahlung aussenden. Einige dieser Neutronensterne, die sogenannten Millisekunden-Pulsare rotieren so schnell, dass sie pro Sekunde mehrere hundert Umdrehungen schaffen. Einige der als Radiopulsare sichtbaren Neutronensterne rotieren in binären Systemen umeinander, wobei der binäre Partner entweder ein normaler Stern, ein weißer Zwerg, ein Planet oder sogar ein weiterer Neutronenstern sein kann. Diejenigen Neutronensterne, die in Zweiersystem umeinander kreisen, veringern ihren Abstand im Laufe der Zeit, da sie Energie durch Aussendung von Gravitationswellen absenden. Kollidieren zwei Neutronensterne miteinander wird eine enorme Energie in Form von Gravitationswellen und eines Gammastrahlen-Blitzes frei gesetzt.
Im Teil I.3) dieser Vorlesung werden die Eigenschaften von Neutronensternen berechnet. Hierbei beschränken wir uns auf nichtrotierende, sich im Gleichgewicht befindende, einzelne, spährisch symmetrische Neutronensterne und vernachlässigen die mögliche Auswirkungen der starken Magnetfelder. In diesem Spezialfall reduziert sich die Einsteingleichung auf die sogenannte Tollmann-Openheimer-Volkov Gleichung, die man dann (bei vorgegebener Zustandsgleichung der Neutronensternmaterie) nummerisch, z.B. mit Maple lösen kann. In der linken Abbildung ist eine Animation dargestellt, die die numerischen Ergebnisse zusammenfasst. Die Gesamtmasse und der Radius des Neutronensterns (links) ändert sich bei Variation des zentralen Dichtewertes des Sterns (mitte). Die Raumzeitmetrik innerhalb und außerhalb des Sterns (z.B. g00-Komponente der Metrik, siehe rechte Abbildung (blaue und rote Kurve)) ändert sich als Funktion des radialen Abstandes r zum Sternzentrum. Wird die raumzeitliche Verzerrung im Sterninneren zu groß und überschreitet dieser die Maximalmasse Mmax, so wird der Stern instabil und kollabiert zwangsläufig zu einem schwarzen Loch (falls nicht der enorme Druck der Materie nach dem QCD-Phasenübergang zum Quark-Gluon Plasma diesen Kollaps aufhalten kann). Der Wert der maximalen Masse eines Neutronensterns ist durch die Zustandsgleichung der Materie bestimmt. Da im inneren Bereich des Stern die Dichte den mehrfachen Wert der normalen nuklearen Kerndichte erreichen kann, ist es sehr wahrscheinlich, dass ein Phasenübergang zu Quarkmaterie stattfindet - diese Sterne werden als sogenannte hybride, bzw. Quarksterne bezeichnet.
4) Das rotierende Schwarze Loch ( Version 1 , Version 2 , Das schwarze Loch in M87 (rotierend))
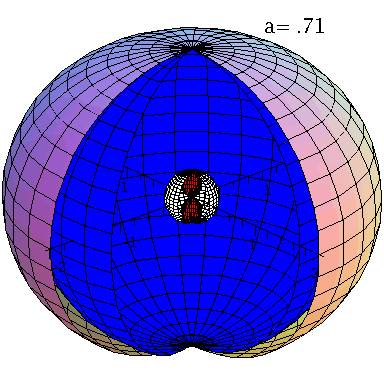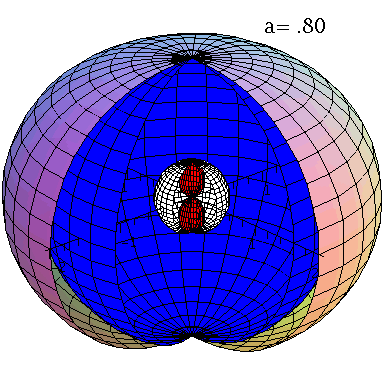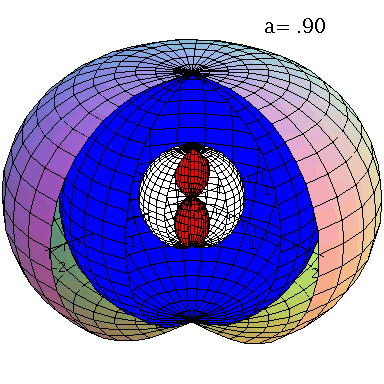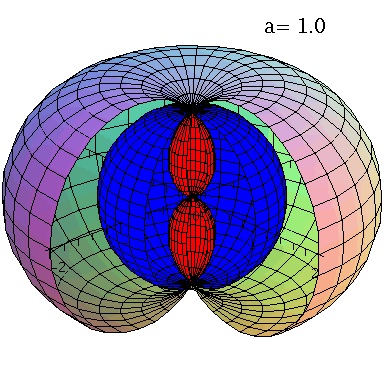
Ereignishorizonte (blaue und weiße Fläche) und Flächen unendlicher Rotverschiebung (äußere und rote Fläche) bei variierender Rotationsfreuenz des schwarzen Lochs.
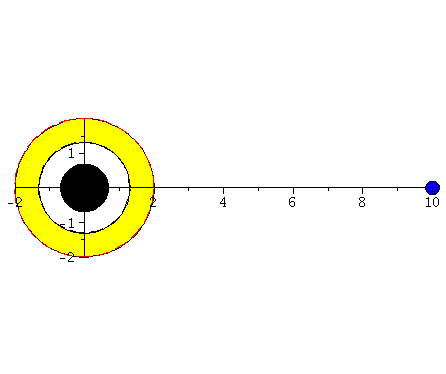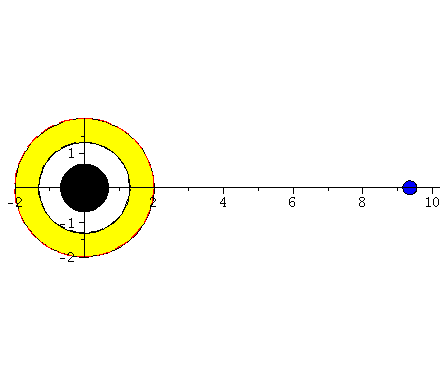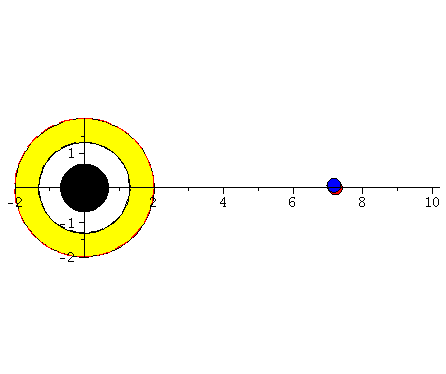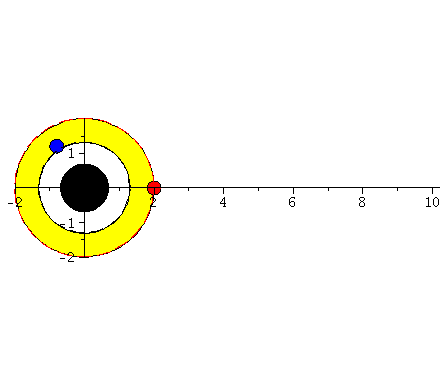
Probekörper der radial in ein rotierendes (blau), bwz. nichtrotierendes (rot) schwarzes Loch fällt.
Das im Teil I.2) behandelte Thema eines nichtrotierenden schwarzen Lochs ist nur eine erste Annäherung zum Verstäntniss des im Vorwort vorgestellten Bildes eines schwarzen Lochs im Zentrum unserer Nachbargalaxie M87 (siehe rechte Abbildung im Vorwort weiter oben). Die Geschwindigkeit mit der das SL im Zentrum von M87 rotiert (der Rotationsparameter a: keine Rotation a=0, maximale Rotation a=1) ist durch die bisherigen Beobachtungen noch nicht genau festgelegt, jedoch ist man sich einer schnellen Rotation des SLs sicher.
Im Teil I.4) dieser Vorlesung werden rotierende schwarze Löcher und die geodätische Bewegung von Probekörpern um diese näher betrachtet. Rotierende schwarze Löcher besitzen eine kompliziertere Struktur ihrer Ereignishorizonte und die Flächen unendlicher Rotverschiebung und die Grenzflächen stationärer Bewegungen sind im allgemeinen nicht identisch mit den Horizonten. Bei nichtverschwindender Rotation existieren zwei Ereignishorizonte (siehe Abbildung links, r+: blaue Fläche und r-: weiße Fläche) und ebenso existieren zwei Flächen unendlicher Rotverschiebung (rs+: äußere Fläche und rs-: rote Fläche). Der Bereich zwischen der äußeren Fläche unendlicher Rotverschiebung und dem äußeren Ereignishorizont bei r+ nennt man Ergosphäre; hier können Testteilchen nicht mehr entgegengesetzt der Rotationsrichtung des schwarzen Lochs rotieren, stationäre Bewegungen sind somit nicht mehr möglich.
Fällt ein Probekörper radial in ein rotierendes schwarzes Loch, so wird er aufgrund des Mitführungseffektes der rotierenden Raumzeit abgelenkt. Die rechte Abbildung veranschaulicht diesen Effekt und stellt die Bewegung eines radial in ein rotierendes schwarzes Loch (a=0.95) einfallenden Probekörpers im Vergleich mit einem nichtrotierenden schwarzen Loch (a=0) dar.
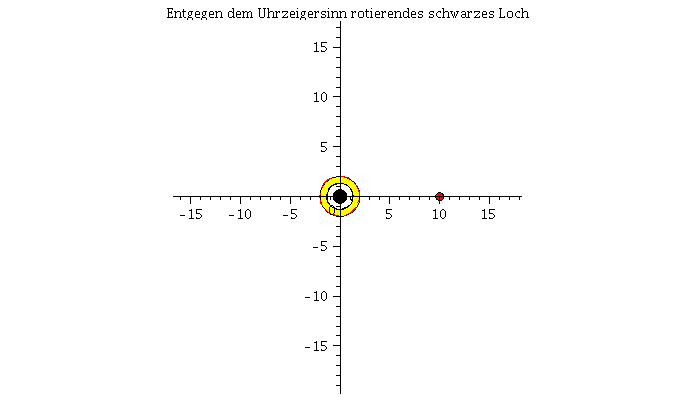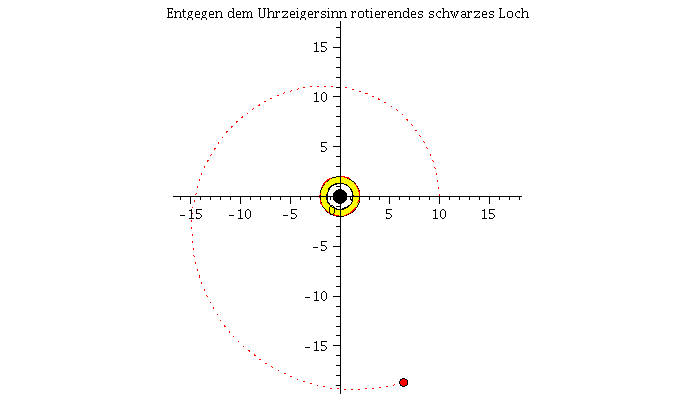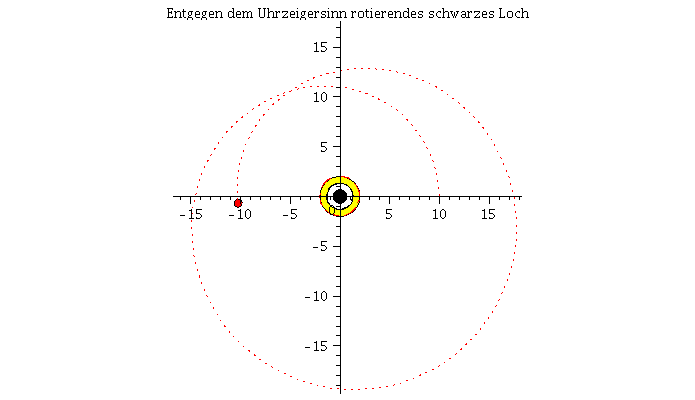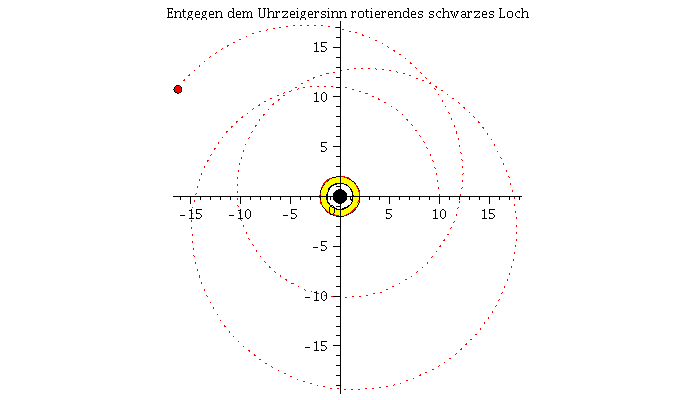
Die untere Abbildung vergleicht die Bewegung eines mit der Rotationrichtung des schwarzen Loches rotierenden Körpers (rechte untere Abbildung und rote Bahnbewegung) mit der Bewegung eines entgegen der Rotationrichtung des schwarzen Loches rotierenden Körpers (linke untere Abbildung und blaue Bahnbewegung). Der Rotationsparameter beträgt a=0.95 und die Winkelgeschwindigkeit am Anfang der Simulation ist bei beiden Körpern die gleiche. In der Version 2 des Teils I.4) wird das effektive Potential der Kerr Metrik definiert um die unterschiedlichen Bahnbewegungen zu klassifizieren, es werden dann kreisförmige Bewegungen und die innerste stabile Kreisbahn (der ISCO) betrachtet und schließlich der gravitomagnetische Effekt an einem Beispiel veranschaulicht.
Rotierende schwarze Löcher sind astrophysikalisch sehr relevante Objekte und im Zentrum von wohl jeder Galaxie existiert höchst warscheinlich ein solches superschweres rotierendes schwarzes Loch. Wissenschaftler (z.B. Prof. R.Genzel aus München) verfolgen schon seit Jahrzenten die Bewegung einzelner sogenannter S-Sterne um das rotierende schwarze Loch im Zentrum von unserer Galaxie. Leider sind die um das schwarze Loch kreisenden Sterne zu weit vom Lochzentrum entfernt, so dass sich die Mitführungseffektes der rotierenden Raumzeit nicht beobachten lassen. Neben diesen rotierenden, supermassiven schwarzen Löchern wurde mittels der bislang 11 gemessenen Gravitationswellen klar, dass es ebenfalls eine große Anzahl von mittelschweren SLern gibt (Massen im Bereich 10-100 Sonnenmassen) die sehr schnell rotieren (a>0.5) können. Es wird zudem vermutet, dass der nach der beobachteten Neutronensternkollission (GW170817) entstandenen hypermassive Neutronenstern extrem schnell rotierte und als Folge dessen, beim Kollaps ein schnell rotierendes Kerr schwarzes Loch erzeugt wurde.