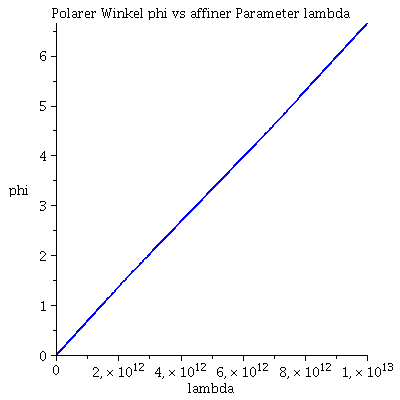Download Maple Worksheed
Allgemeine Relativitätstheorie mit dem Computer
General Theory of Relativity on the Computer
Vorlesung gehalten an der J.W.Goethe-Universität in Frankfurt am Main (Sommersemester 2016)
von Dr.phil.nat. Dr.rer.pol. Matthias Hanauske
Frankfurt am Main 11.04.2016
Erster Vorlesungsteil: Allgemeine Relativitätstheorie mit Maple
Zusatz-Worksheed: Der Merkur-Transit (allgemeinrelativistisch)
Der Merkurtransit in allgemeinrelativistischer Formulierung
Von einem Merkurtransit spricht man, wenn der Planet Merkur von der Erde aus gesehen vor die Sonne wandert. Merkur ist der sonnennächste Planet und ein Umlauf des Merkur um die Sonne dauert gerade einmal 88 Tage. Die Merkurbahn ist etwa um 7 Grad gegen die Erdbahnebene (Ekliptik) geneigt und nur wenn Merkur sich nahe seiner Bahn mit der Erdbahnebene befindet, kommt es zu einem Merkurtransit. Am 9.Mai 2016 wird sich um ca. 13.12 Uhr der Merkur vor die Sonne schieben (Merkurtransit). Merkur hat eine im Vergleich zu den anderen Planeten stark elliptische Umlaufbahn (Exzentrität 0.2056); sein Abstand zur Sonne schwankt zwischen 46 und 69.8 Millionen Kilometern. Bei dem Transit am 09.Mai befindet Merkur sich nahe des sonnenfernsten Bahnpunktes (Aphel). Näheres siehe www.merkurtransit.de . In der Vorlesung "Allgemeine Relativitätstheorie mit dem Computer" (SS 2016) nahmen wir das zum Anlass um uns die Planetenbahnen und speziell die Eigenschaften des Merkurtransits durch Computersimulationen zu verdeutlichen. Die Bewegung des Merkur und der Erde können gut (von der Periheldrehung mal abgesehen) mittels der Newtonschen Gravitationstheorie beschrieben werden. In diesem Maple-Worksheed betrachten wir dennoch die Bewegung der Erde und des Merkur allgemeinrelativistisch. Die Bewegung eines Probekörpers um ein nichtrotierendes schwarzes Loch wird mittels der Geodätengleichung in Schwarzschildkoordinaten beschrieben. Obwohl die Bewegung der Planenten unseres Sonnensystems um unser Zentralgestirn (die Sonne) ja sicherlich keine Bewegung um ein schwarzes Loch darstellt, können die Gleichungen der Planetenbewegungen in guter Approximation als solche beschrieben werden (siehe Birkov-Theorem).
| > | restart:
with( tensor ): with(plots): with(plottools): |
Definition der kovarianten Raumzeit-Metrik eines schwarzen Lochs der Masse M in Schwarzschildkoordinaten:
| > | coord := [t, r, theta, phi]:
g_compts := array(symmetric,sparse, 1..4, 1..4): g_compts[1,1] := 1-2*M/r: g_compts[2,2] := -1/g_compts[1,1]: g_compts[3,3] := -r^2: g_compts[4,4] := -r^2*sin(theta)^2: g := create( [-1,-1], eval(g_compts)); |
![table( [( index_char ) = [-1, -1], ( compts ) = array( 1 .. 4, 1 .. 4, [( 3, 3 ) = `+`(`-`(`*`(`^`(r, 2)))), ( 2, 2 ) = `+`(`-`(`/`(1, `*`(`+`(1, `-`(`/`(`*`(2, `*`(M)), `*`(r)))))))), ( 1, 1 ) = `+`(...](images/Der-Merkurtransit-ART_1.gif) |
(1.1) |
Berechnung der kontravarianten Metrik und der Christoffel Symbole:
| > | ginv := invert( g, 'detg' ):
D1g := d1metric( g, coord ): D2g := d2metric( D1g, coord ): Cf1 := Christoffel1( D1g ): Cf2:= Christoffel2( ginv, Cf1 ): |
Berechnung der Geodätengleichung als Funktion des affinen Parameters lambda. Die Geodätengleichung ist ein System gekoppelter Differentialgleichungen:
| > | eqns:=geodesic_eqns( coord, lambda, Cf2 ); |
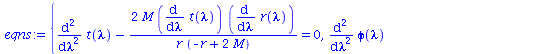 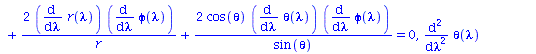 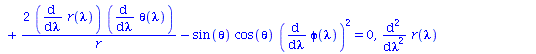 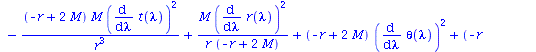  |
(1.2) |
Um den Merkurtransit zu berechnen benötigen wir alle vier Gleichungen:
| > | eq1:=subs({r=r(lambda),theta=theta(lambda)},eqns[1]):
eq2:=subs({r=r(lambda),theta=theta(lambda)},eqns[2]): eq3:=subs({r=r(lambda),theta=theta(lambda)},eqns[3]): eq4:=subs({r=r(lambda),theta=theta(lambda)},eqns[4]): eq1:=subs({r(lambda)(lambda)=r(lambda),theta(lambda)(lambda)=theta(lambda)},eq1); eq2:=subs({r(lambda)(lambda)=r(lambda),theta(lambda)(lambda)=theta(lambda)},eq2); eq3:=subs({r(lambda)(lambda)=r(lambda),theta(lambda)(lambda)=theta(lambda)},eq3); eq4:=subs({r(lambda)(lambda)=r(lambda),theta(lambda)(lambda)=theta(lambda)},eq4); |
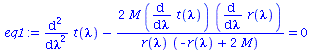 |
|
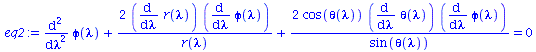 |
|
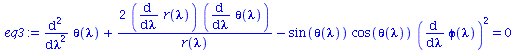 |
|
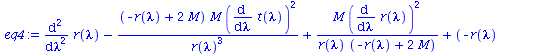 |
(1.3) |
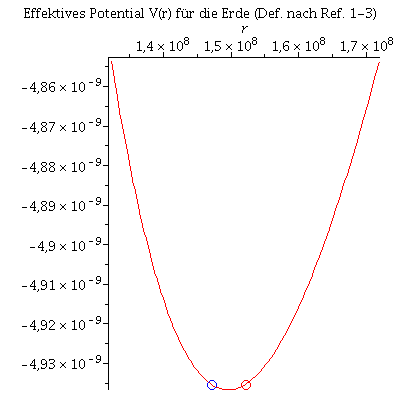
Wir setzen die Masse auf die Sonnenmasse (M=1.4766) und konstruieren das effektive Potential der Erdbewegung mittels bekannter Größen der Erde (siehe http://nssdc.gsfc.nasa.gov/planetary/factsheet/earthfact.html). Wir nehmen an, dass sich die Erde zur Zeit lambda=t=0 in ihrem Perihel (kleinster Abstand zur Sonne) befindet :
| > | setM:=1.4766;
E_rPerihel:=147090000; E_rAphel:=152100000; E_r0:=E_rPerihel; VeffFb:=(r,M,l)->-M/r+l^2/(2*r^2)-M*l^2/r^3; E_V1:=VeffFb(E_rPerihel,setM,l): E_V2:=VeffFb(E_rAphel,setM,l): E_setl:=rhs(solve({E_V1=E_V2},l)[1,1]); E_dphi0:=E_setl/(E_r0^2); E_Pot:=plot(VeffFb(r,setM,E_setl),r=0.9*E_rPerihel..1.13*E_rAphel,title="Effektives Potential V(r) für die Erde (Def. nach Ref. 1-3)"): E_PPerihel:=pointplot({[E_rPerihel, VeffFb(E_rPerihel,setM,E_setl)]}, symbol=circle,symbolsize=20,color=blue): E_PAphel:=pointplot({[E_rAphel, VeffFb(E_rAphel,setM,E_setl)]}, symbol=circle,symbolsize=20,color=red): display(E_Pot,E_PPerihel,E_PAphel); |
 |
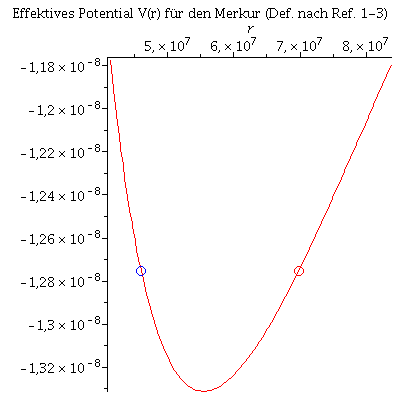
Das effektive Potential der Merkurbewegung wird ebenso mittels der bekannten Größen konstruiert (siehe http://nssdc.gsfc.nasa.gov/planetary/factsheet/mercuryfact.html). Bei dem Transit am 09.Mai befindet Merkur sich nahe des sonnenfernsten Bahnpunktes (Aphel); wir nehmen eine Inklination gegen die Ekliptik von 7 Grad an.
| > | inclination:=7:
M_rPerihel:=46000000; M_rAphel:=69820000; M_r0:=M_rAphel; VeffFb:=(r,M,l)->-M/r+l^2/(2*r^2)-M*l^2/r^3; M_V1:=VeffFb(M_rPerihel,setM,l); M_V2:=VeffFb(M_rAphel,setM,l); M_setl:=rhs(solve({M_V1=M_V2},l)[1,1]); M_dphi0:=evalf(M_setl/(M_r0^2)*sin((90-inclination)/360*2*Pi)); M_theta0:=evalf(M_setl/(M_r0^2)*sin(inclination/360*2*Pi)); M_Pot:=plot(VeffFb(r,setM,M_setl),r=0.9*M_rPerihel..1.2*M_rAphel,title="Effektives Potential V(r) für den Merkur (Def. nach Ref. 1-3)"): M_PPerihel:=pointplot({[M_rPerihel, VeffFb(M_rAphel,setM,M_setl)]}, symbol=circle,symbolsize=20,color=blue): M_PAphel:=pointplot({[M_rAphel, VeffFb(M_rAphel,setM,M_setl)]}, symbol=circle,symbolsize=20,color=red): display(M_Pot,M_PPerihel,M_PAphel); |
 |
Berechnung des infinitesimalen Weglängenelementes für die Berechnung von dt:
| > | dx:=create([1], array([dt,dr,dtheta,dphi])):
ds2:=get_compts(prod(dx,lower(g,dx,1),[1,1])): ds2:=collect( simplify(ds2), [dt,dr,dtheta,dphi]); Gl1:=subs(M=setM,dr=0,ds2=1); dt=solve(Gl1,dt)[1]; |
| (1.4) |
Numerische Lösung für die Erde:
| > | t0:=0:
phi0:=0: dphi0:=E_dphi0: r0:=E_r0: dr0:=0: theta0:=Pi/2: dtheta0:=0: dt0:=evalf(subs({r=r0,dphi=dphi0,theta=theta0,dtheta=dtheta0},50.*sqrt(-(1.*(2500.*r-7383.))*r*(cos(theta)^2*dphi^2*r^2-1.-1.*dtheta^2*r^2-1.*dphi^2*r^2))/(2500.*r-7383.))); |
| (1.5) |
| > | E_Loes:=dsolve({subs(M=setM,eq1),subs(M=setM,eq2),subs(M=setM,eq3),subs(M=setM,eq4),t(0)=t0,r(0)=r0,D(r)(0)=dr0,D(t)(0)=dt0,phi(0)=phi0,D(phi)(0)=dphi0,theta(0)=theta0,D(theta)(0)=dtheta0},{t(lambda),r(lambda),theta(lambda),phi(lambda)},type=numeric,output=listprocedure); |
| (1.6) |
Wir benutzen die weiteren Anfangswerte für den Merkur (nur Näherungswerte): wir setzen t=lambda=0 auf Montag 09.05.2016, 13.14 Uhr; dies entspricht ca. der Zeit, wenn das Zentrum des Merkurs auf dem Sonnenrand liegt. Obwohl dieser Punkt in Wirklichkeit leicht unter der Ekliptik liegt, nehmen wir in unserer Simulation an, dass Merkur bei t=0 genau auf der Ekliptik liegt (theta=0). Um diese Anfangswerte zu verdeutlichen betrachten wir im folgenden, wie der Merkur von der Erde aus gesehen sich darstellen würde. Um uns das Erscheinungsbild des Merkurtransiten am 9. Mai zu verdeutlichen, betrachten wir uns zunächst wie groß der Merkur im Vergleich zur Sonne, dem Mond und der Venus von der Erde aus gesehen erscheint. Wie groß die Planeten, die Sonne und der Mond einem Beobachter auf der Erde erscheinen, hängt von der Größe der Himmelskörper und von der ihrer Entfernung ab. Wir berechnen nun den jeweiligen Erscheinungswinkel der entsprechenden Himmelskörper (Gelb: Sonne, grau: Mond, schwarz:Venus und rot(der kleinste): Merkur):
| > | R_Sonne:=1392684/2:
R_Erde:=12756/2: R_Venus:=12104/2: R_Mond:=3475/2: R_Merkur:=4879/2: A_ESonne:=E_rPerihel: A_EVenus:=A_ESonne-108200000: A_EMond:=370300: A_EMerkur:=A_ESonne-M_rAphel: EW_Sonne:=evalf(arctan(R_Sonne/A_ESonne)): EW_Venus:=evalf(arctan(R_Venus/A_EVenus)): EW_Mond:=evalf(arctan(R_Mond/A_EMond)): EW_Merkur:=evalf(arctan(R_Merkur/A_EMerkur)): P_S:=display(disk([0,0],tan(EW_Sonne)),color=yellow): P_Mo:=display(disk([0.01,0],tan(EW_Mond)),color=grey): P_V:=display(disk([0.017,0],tan(EW_Venus)),color=black): P_Me:=display(disk([0.018,0],tan(EW_Merkur)),color=red): display(P_Me,P_V,P_Mo,P_S,scaling=constrained,axes=none); |
 |
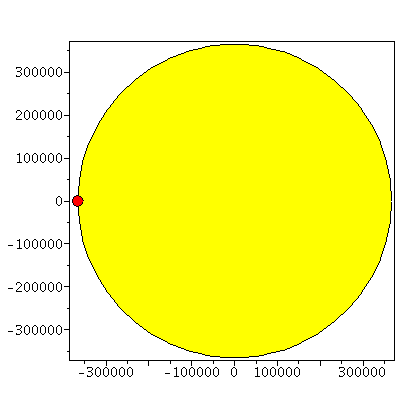
Die Anfangsbedingungen stellen sich somit wie folgt dar (Bem.: der Merkur ist hier 5mal größer veranschaulicht als in Wirklichkeit):
| > | P_S:=display(disk([0,0],A_EMerkur*tan(EW_Sonne)),color=yellow):
P_Me:=display(disk([A_EMerkur*tan(-EW_Sonne),0],5*R_Merkur),color=red): display(P_Me,P_S,scaling=constrained,axes=boxed); |
 |
Numerische Lösung für den Merkur:
| > | t0:=0:
phi0:=-EW_Sonne: dphi0:=M_dphi0: r0:=M_r0: dr0:=0: theta0:=Pi/2: dtheta0:=M_theta0: dt0:=evalf(subs({r=r0,dphi=dphi0,theta=theta0,dtheta=dtheta0},50.*sqrt(-(1.*(2500.*r-7383.))*r*(cos(theta)^2*dphi^2*r^2-1.-1.*dtheta^2*r^2-1.*dphi^2*r^2))/(2500.*r-7383.))); |
| (1.7) |
| > | M_Loes:=dsolve({subs(M=setM,eq1),subs(M=setM,eq2),subs(M=setM,eq3),subs(M=setM,eq4),t(0)=t0,r(0)=r0,D(r)(0)=dr0,D(t)(0)=dt0,phi(0)=phi0,D(phi)(0)=dphi0,theta(0)=theta0,D(theta)(0)=dtheta0},{t(lambda),r(lambda),theta(lambda),phi(lambda)},type=numeric,output=listprocedure): |
Veranschaulichung einiger Größen während der Bahnbewegung der Erde;
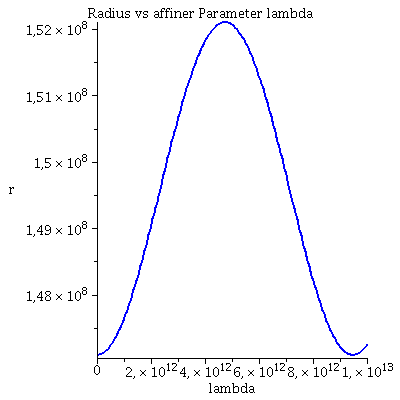
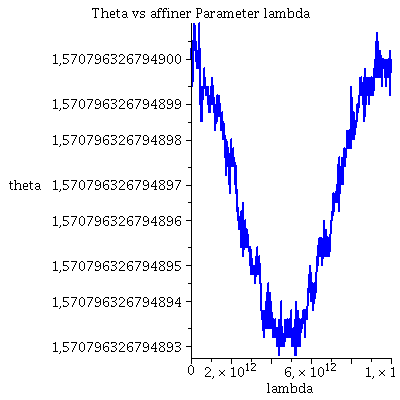
| > | lend:=10*10^12:
Plot1:=odeplot(E_Loes,[lambda,phi(lambda)],0..lend,numpoints=200,color=blue,thickness=2,title="Polarer Winkel phi vs affiner Parameter lambda"): Plot2:=odeplot(E_Loes,[lambda,r(lambda)],0..lend,numpoints=200,color=blue,thickness=2,title="Radius vs affiner Parameter lambda"): Plot3:=odeplot(E_Loes,[lambda,theta(lambda)],0..lend,numpoints=700,color=blue,thickness=2,title="Theta vs affiner Parameter lambda"): display(Matrix(1,3,[Plot1,Plot2,Plot3])); |
|
Veranschaulichung einiger Größen während der Bahnbewegung des Merkur:
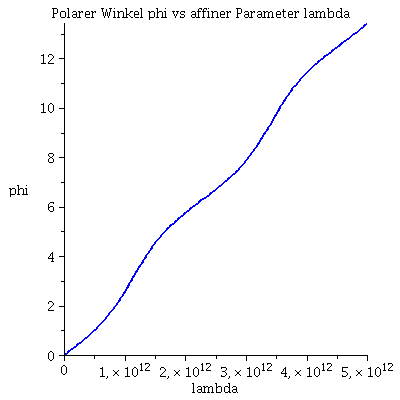
| > | lend:=5*10^12:
Plot1:=odeplot(M_Loes,[lambda,phi(lambda)],0..lend,numpoints=200,color=blue,thickness=2,title="Polarer Winkel phi vs affiner Parameter lambda"): Plot2:=odeplot(M_Loes,[lambda,r(lambda)],0..lend,numpoints=200,color=blue,thickness=2,title="Radius vs affiner Parameter lambda"): Plot3:=odeplot(M_Loes,[lambda,theta(lambda)],0..lend,numpoints=700,color=blue,thickness=2,title="Theta vs affiner Parameter lambda"): display(Matrix(1,3,[Plot1,Plot2,Plot3])); |
|
Berechnung der Umlaufzeiten:
| > | c:=2.99792458*10^5:
E_radius:=lambda->rhs(E_Loes(lambda)[4]): E_polarphi:=lambda->rhs(E_Loes(lambda)[2]): E_theta:=lambda->rhs(E_Loes(lambda)[8]): M_radius:=lambda->rhs(M_Loes(lambda)[4]): M_polarphi:=lambda->rhs(M_Loes(lambda)[2]): M_theta:=lambda->rhs(M_Loes(lambda)[8]): |
Berechnung der Umlaufzeiten der Erde:
| > | dum1:=0.1:
dum2:=0.00001: for i from 0 by dum1 to 1000 while E_polarphi(i*10^12) < evalf(2*Pi) do end do; for ii from i-dum1 by dum2 to 1000 while E_polarphi(ii*10^12) < evalf(2*Pi) do end do; E_umlaufzeit:=ii*10^12: print("Erde: Umlaufzeit in Tagen: ",E_umlaufzeit/(c*60*60*24),"[Tage]"); |
| (1.8) |
Berechnung der Umlaufzeit des Merkur:
| > | dum1:=0.1:
dum2:=0.00001: for i from 0 by dum1 to 1000 while M_polarphi(i*10^12) < evalf(2*Pi-EW_Sonne) do end do; for ii from i-dum1 by dum2 to 1000 while M_polarphi(ii*10^12) < evalf(2*Pi-EW_Sonne) do end do; M_umlaufzeit:=ii*10^12: print("Merkur: Umlaufzeit in Tagen: ",M_umlaufzeit/(c*60*60*24),"[Tage]"); |
| (1.9) |
Animation der Planetenbewegung projiziert auf die x-y-Achse:
| > | frames:=30:
lend:=M_umlaufzeit: BH:=display(disk([0,0],10^7,color=yellow)): for i from -2 by 1 to frames+2 do E_Koerper[i]:=display(disk([rhs(E_Loes(i*lend/frames)[4])*sin(rhs(E_Loes(i*lend/frames)[8]))*cos(rhs(E_Loes(i*lend/frames)[2])),rhs(E_Loes(i*lend/frames)[4])*sin(rhs(E_Loes(i*lend/frames)[8]))*sin(rhs(E_Loes(i*lend/frames)[2]))],5*10^6,color=blue)): E_Traj[i]:=listplot([seq([rhs(E_Loes(j*lend/frames)[4])*sin(rhs(E_Loes(i*lend/frames)[8]))*cos(rhs(E_Loes(j*lend/frames)[2])),rhs(E_Loes(j*lend/frames)[4])*sin(rhs(E_Loes(i*lend/frames)[8]))*sin(rhs(E_Loes(j*lend/frames)[2]))], j = -2 .. i)],color=blue,linestyle=dot): M_Koerper[i]:=display(disk([rhs(M_Loes(i*lend/frames)[4])*sin(rhs(M_Loes(i*lend/frames)[8]))*cos(rhs(M_Loes(i*lend/frames)[2])),rhs(M_Loes(i*lend/frames)[4])*sin(rhs(M_Loes(i*lend/frames)[8]))*sin(rhs(M_Loes(i*lend/frames)[2]))],2*10^6,color=red)): M_Traj[i]:=listplot([seq([rhs(M_Loes(j*lend/frames)[4])*sin(rhs(M_Loes(i*lend/frames)[8]))*cos(rhs(M_Loes(j*lend/frames)[2])),rhs(M_Loes(j*lend/frames)[4])*sin(rhs(M_Loes(i*lend/frames)[8]))*sin(rhs(M_Loes(j*lend/frames)[2]))], j = -2 .. i)],color=red,linestyle=dot): Ani[i]:=display({E_Koerper[i],E_Traj[i],M_Koerper[i],M_Traj[i],BH}); od: |
| > | display([seq(Ani[i],i=-2..frames+2)],insequence=true,scaling=constrained); |
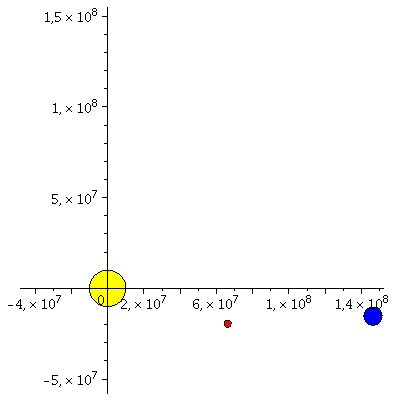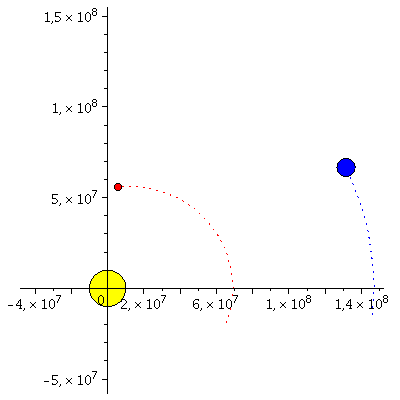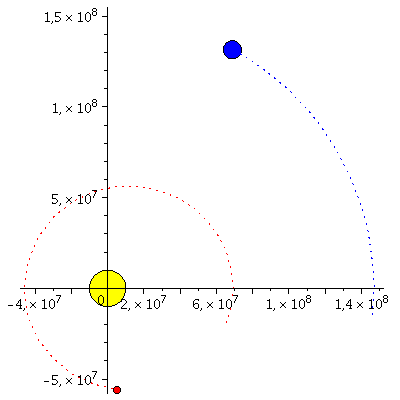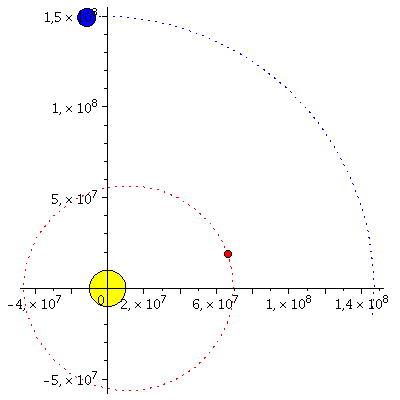 |
Veranschaulichung der beiden Bahnebenen.
| > | frames:=100:
lend:=E_umlaufzeit: P_erde:=pointplot3d([seq([rhs(E_Loes(i*lend/frames)[4])*sin(rhs(E_Loes(i*lend/frames)[8]))*cos(rhs(E_Loes(i*lend/frames)[2])),rhs(E_Loes(i*lend/frames)[4])*sin(rhs(E_Loes(i*lend/frames)[8]))*sin(rhs(E_Loes(i*lend/frames)[2])),rhs(E_Loes(i*lend/frames)[4])*cos(rhs(E_Loes(i*lend/frames)[8]))],i=0..frames)],color=blue): lend:=M_umlaufzeit: P_merkur:=pointplot3d([seq([rhs(M_Loes(i*lend/frames)[4])*sin(rhs(M_Loes(i*lend/frames)[8]))*cos(rhs(M_Loes(i*lend/frames)[2])),rhs(M_Loes(i*lend/frames)[4])*sin(rhs(M_Loes(i*lend/frames)[8]))*sin(rhs(M_Loes(i*lend/frames)[2])),rhs(M_Loes(i*lend/frames)[4])*cos(rhs(M_Loes(i*lend/frames)[8]))],i=0..frames)],color=red): display(P_erde,P_merkur,orientation=[0,84],scaling=constrained); |
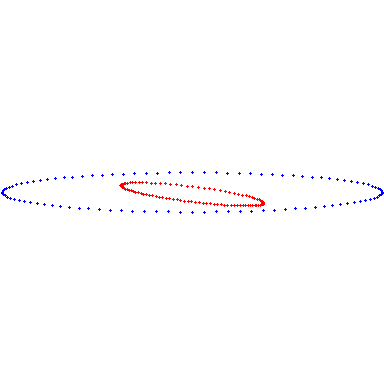 |
Dreidimensionale Animation der Planetenbewegung:
| > | frames:=2:
lend:=3*M_umlaufzeit: Sonne:=display(sphere([0,0,0],1.5*10^7,color=yellow)): for i from 0 by 1 to frames do Erde[i]:=display(sphere([rhs(E_Loes(i*lend/frames)[4])*sin(rhs(E_Loes(i*lend/frames)[8]))*cos(rhs(E_Loes(i*lend/frames)[2])),rhs(E_Loes(i*lend/frames)[4])*sin(rhs(E_Loes(i*lend/frames)[8]))*sin(rhs(E_Loes(i*lend/frames)[2])),rhs(E_Loes(i*lend/frames)[4])*cos(rhs(E_Loes(i*lend/frames)[8]))],0.6*10^7,color=blue,style=patchcontour)): Merkur[i]:=display(sphere([rhs(M_Loes(i*lend/frames)[4])*sin(rhs(M_Loes(i*lend/frames)[8]))*cos(rhs(M_Loes(i*lend/frames)[2])),rhs(M_Loes(i*lend/frames)[4])*sin(rhs(M_Loes(i*lend/frames)[8]))*sin(rhs(M_Loes(i*lend/frames)[2])),rhs(M_Loes(i*lend/frames)[4])*cos(rhs(M_Loes(i*lend/frames)[8]))],0.5*10^7,color=red,style=patchcontour)): Ani[i]:=display({Erde[i],Merkur[i],Sonne}); od: |
| > | display([seq(Ani[i],i=0..frames)],insequence=true,scaling=constrained,orientation=[45,75],axes=framed); |
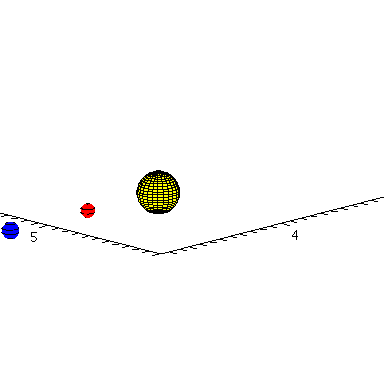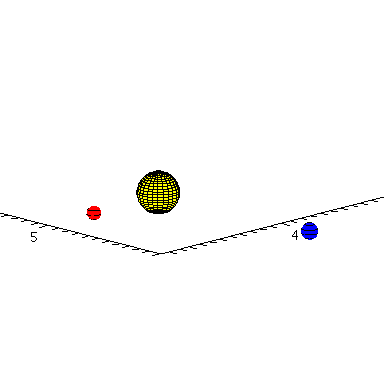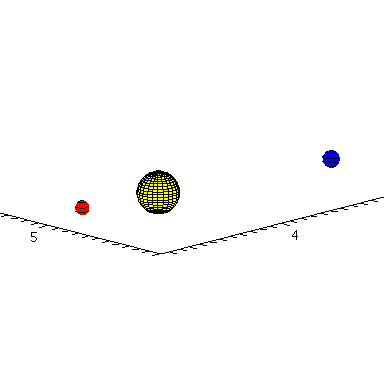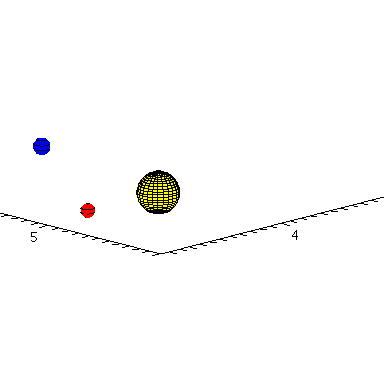 |
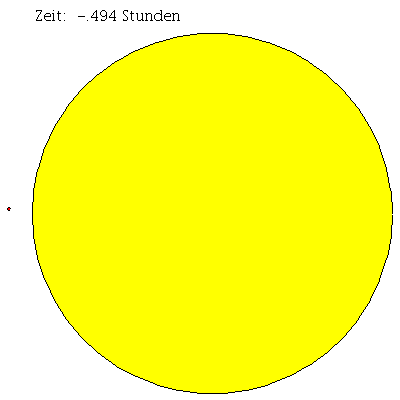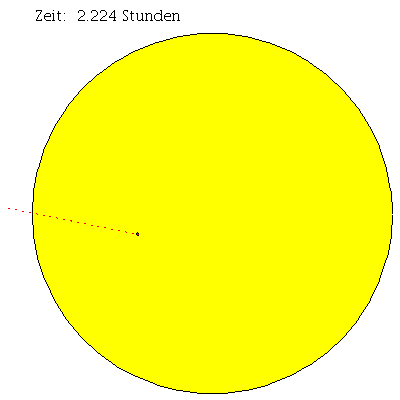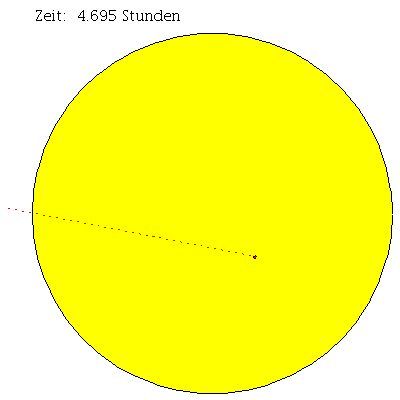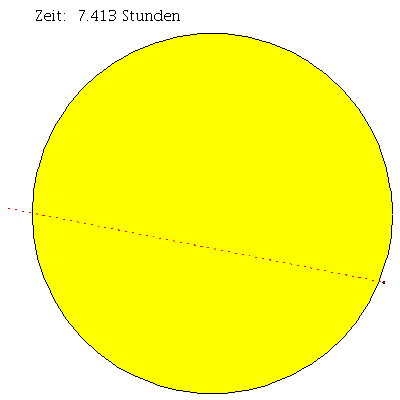
Animation des Merkurtransits:
| > | with(StringTools):
frames:=30: lend:=8*10^9: for i from -2 by 1 to frames do P_S[i]:=display(disk([0,0],rhs(M_Loes(i*lend/frames)[4])*tan(EW_Sonne)),color=yellow): M_Koerper[i]:=display(disk([rhs(M_Loes(i*lend/frames)[4])*sin(rhs(M_Loes(i*lend/frames)[8]))*sin(rhs(M_Loes(i*lend/frames)[2])-rhs(E_Loes(i*lend/frames)[2])),rhs(M_Loes(i*lend/frames)[4])*cos(rhs(M_Loes(i*lend/frames)[8]))],R_Merkur),color=red): Ptext1[i]:=textplot([-rhs(M_Loes(i*lend/frames)[4])*tan(EW_Sonne),1.1*rhs(M_Loes(i*lend/frames)[4])*tan(EW_Sonne), Join(["Zeit: ",convert(evalf(round((i*lend/frames/(c*60*60))*1000)*0.001),string),"Stunden"])], align =RIGHT,color=black,font = [TIMES, ROMAN, 12]): M_Traj[i]:=listplot([seq([rhs(M_Loes(j*lend/frames)[4])*sin(rhs(M_Loes(j*lend/frames)[8]))*sin(rhs(M_Loes(j*lend/frames)[2])-rhs(E_Loes(j*lend/frames)[2])),rhs(M_Loes(j*lend/frames)[4])*cos(rhs(M_Loes(j*lend/frames)[8]))], j = -2 .. i)],color=red,linestyle=dot): Ani[i]:=display({P_S[i],M_Koerper[i],M_Traj[i],Ptext1[i]}); od: |
| > | display([seq(Ani[i],i=-2..frames)],insequence=true,scaling=constrained,axes=none); |
 |
| > |