E-Learning
Zusatzmaterial auf der Online-Lernplatform Lon Capa
Zusäzlich zu den Informationen aus dieser Internetseite wurde ein separater Kurs auf der Online-Lernplatform Lon Capa eerstellt. Er beinhaltet neben den hier dargestellten Informationen zusäzliche Erläuterungen, diverse interaktive Übungsaufgaben, Feedbackmöglichkeiten und Probeklausuren. Falls Sie schon einen Lon Capa Account besitzen können Sie sich einfach mit diesem unter dem unten angegebenen Link einloggen. Falls Sie Student der Universiät Frankfurt sind, können Sie sich mit Ihrem HRZ-Account einloggen. Anderenfalls kontaktieren Sie bitte per E-Mail und ich werde für Sie einen Account für die Lernplatform erstellen.
Hier gehts zu Lon Capa
Projektarbeiten Teil I: Kosmologie und die Robertson-Walker Metrik in alternativen Gravitationstheorien
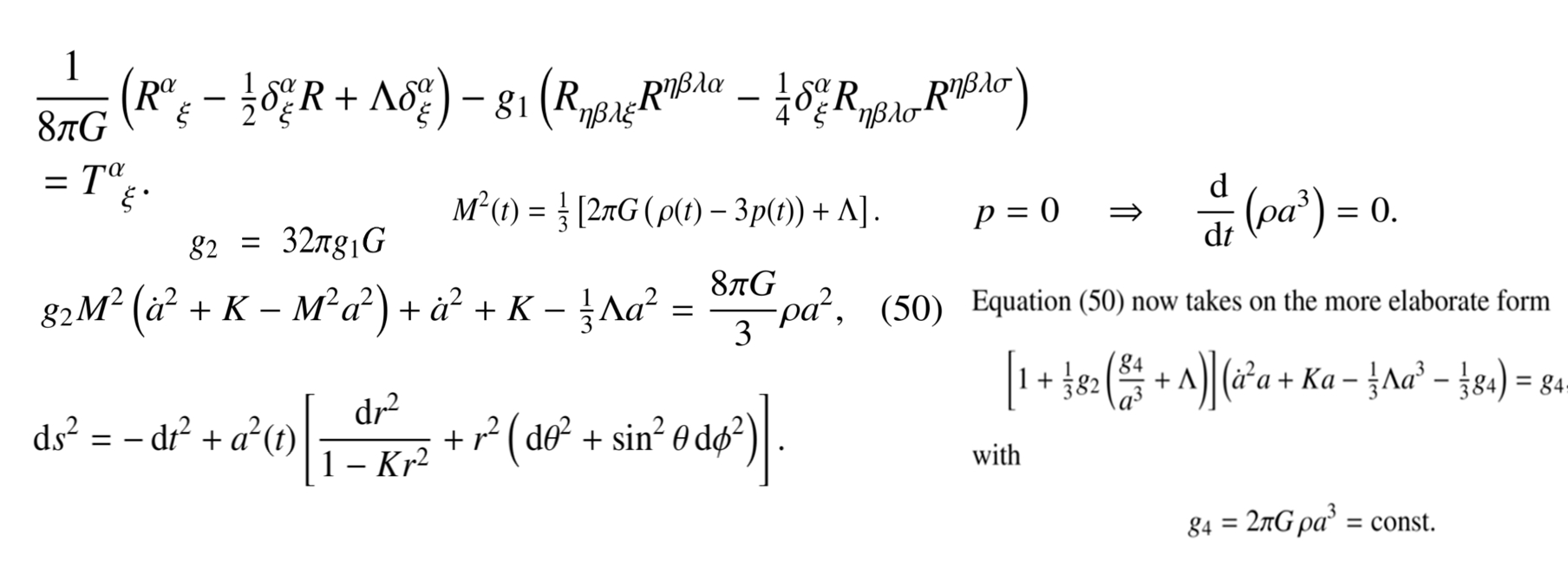
Dem humboldtschen Bildungsideal folgend, befasst sich diese Projektarbeit mit einem aktuellen Forschungsgebiet. Die nebenstehende modifizierte Einsteingleichung basiert auf einem eichtheoretischen Prinzip (näheres siehe arXiv:1704.07246). Es sollen nun die Auswirkungen der zusätzlichen quadratischen Riemanntensor-Terme am Beispiel der Robertson-Walker Metrik untersucht werden. Leiten Sie die entstehende, modifizierte Friedmanngleichung her. Die verallgemeinerte Einsteingleichung des "Struckmeier'schen", auf eichtheoretischen Prinzipien basierenden, alternativen Modells der Allgemeinen Relativitätstheorie besitzt das folgende Aussehen:
\[
\begin{equation}
g_{1}\underbrace{\left(R{_{\eta\beta\lambda\xi}}\,R{^{\eta\beta\lambda\alpha}}\!-
\frac{1}{4}\delta_{\xi}^{\alpha}\,R{_{\eta\beta\lambda\tau}}
R{^{\eta\beta\lambda\tau}}\right)}_{Q{_{\xi}^{\alpha}}}
+\frac{1}{8\pi G}\left(R{_{\xi}^{\alpha}}\!-
\frac{1}{2}\delta_{\xi}^{\alpha}\,R+\Lambda\,\delta_{\xi}^{\alpha}\right)
=-T{_{\xi}^{\alpha}}
\end{equation}
\]
Zeigen Sie mittels eines Maple (Mathematica) Worksheets, dass man unter Verwendung der Robertson-Walker Metrik
\[
\begin{equation}
g_{\mu\nu}=
\begin{pmatrix}
-1&0&0&0\\ 0&\frac{(R(t))^2}{1-k\,r^2}&0&0\\ 0&0&(R(t))^2r^{2}&0\\ 0&0&0&(R(t))^2r^{2}\sin^{2}\theta
\end{pmatrix}
\end{equation}
\]
die oben angegebene verallgemeinerte Friedmanngleichung im materiedominierten Fall erhält. Diskutieren Sie die numerischen Lösungen für den materiedominierten Fall und stellen Sie die kosmologische Entwicklung des Universums als Funktion der Zeit für geeignete Spezialfälle (z.B. mit und ohne kosmologische Konstante $\Lambda$) dar. Die folgenden Maple Dateien können Ihnen dabei helfen:
Datei 1
Datei 2
Projektarbeiten Teil I: Weiterführende Themen der Kerr-Metrik
Projektarbeiten Teil II: Die Masse-Radius Beziehung von Zwillingssternen
Die Möglichkeit von Zwillingsstern-Lösungen der TOV-Gleichung ist gegeben, falls die Zustandsgleichung der Materie einen starken Phasenübergang aufweisst. (siehe z.B. Catastrophic rearrangement of a compact star due to the quark core formation,Phase Transition to Hyperon Matter in Neutron Stars,Characteristics of hybrid compact stars with a sharp hadron-quark interface,,Stable hybrid stars within a SU(3) Quark-Meson-Model,, Eigenschaften von kompakten Sternen in QCD-motivierten Modellen). In diesem Projekt soll eine solche Zustandsgleichung mittels einer Maxwell-Konstruktion zwischen einem hadronischen Modell und einem Quarkmodell erzeugt werden und die Eigenschaften der enstehenden hybriden Neutronen-Quarksternen mittels des parallelen OpenMP-C++ Programms untersucht werden (Masse, Radius, Dichteprofile, ...). Zwillingsstern-Lösungen sind gewönlich nur in einem engen Parameterfenster möglich. Visualisieren Sie dieses Parameterfenster in einem $\Delta\epsilon/\epsilon_t$-$\epsilon_c$ Diagramm (siehe Abbildung Fig.20 in Stable hybrid stars within a SU(3) Quark-Meson-Model).
Projektarbeiten Teil III: Migration und Kollaps eines instabilen Neutronensterns
Projektarbeiten Teil III: Visualisieren der Ausgabedaten einer Neutronensternkollision mit Python
Näheres zu diesem Projekt finden Sie auf den folgenden Internetseiten:
Allgemeine Relativitätstheorie mit dem Computer (Teil III)
Die Peking Frühlingsschule 2017 (Teil II)
Probe Prüfung
Im folgenden wird ein Beispiel einer Prüfung vorgestellt.








