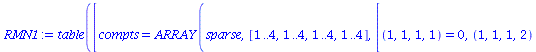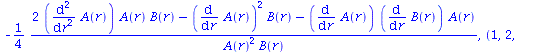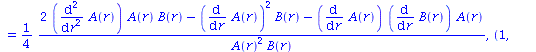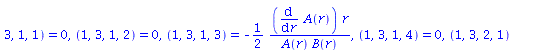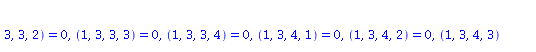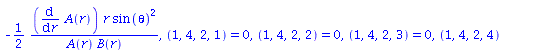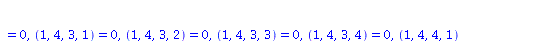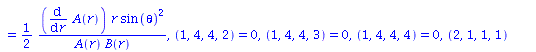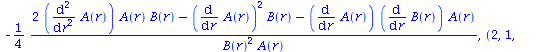Probeprüfung 

Aufgabe 1a. Maple Worksheet Vorlesung1.mw verwendet: 

Grundlegende Größen der Allgemeinen Relativitätstheorie 

Im folgenden werden einige grundlegende Größen der allgemeinen Relativitätstheorie am Beispiel der allgemeinen statischen, isotropen Metrik erläutert.Zunächst wird das "tensor"-Paket eingebunden: 

>	restart: with( tensor );

 

(2.1)

 

Definition der kovarianten Raumzeit-Metrik einer allgemeinen statischen, isotropen Metrik: 

>	coord := [t, r, theta, phi]: g_compts := array(symmetric,sparse, 1..4, 1..4): g_compts[1,1] := A(r): g_compts[2,2] := -B(r): g_compts[3,3] := -r^2:    g_compts[4,4] := -r^2*sin(theta)^2: g := create( [-1,-1], eval(g_compts));

 

(2.2)

 

Kontravariante Raumzeit-Metrik: 

>	ginv := invert( g, 'detg' );

 

(2.3)

 

Erste partielle Ableitung der Metrik: 

>	D1g := d1metric ( g, coord );

 

(2.4)

 

Chistoffel Symbole (kontravariante Form): 

>	Cf1 := Christoffel1 ( D1g );

 

(2.5)

 

Chistoffel Symbole (erster Index kontravariant, zweiter und dritter kontravariant): 

>	Cf2:= Christoffel2( ginv, Cf1 );

 

(2.6)

 

Angabe einzelner Komponenten eines Tensors: 

>	get_compts(Cf2)[2,3,3];

 

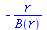(2.7)

 

Riemann Tensor: 

>	D2g := d2metric ( D1g, coord ): RMN := Riemann( ginv, D2g, Cf1 );

 

(2.8)

 

Hier wurde das Maple-File verändert: 

>	RMN1:=raise(ginv,RMN,1);

 

(2.9)

 

>	get_compts(RMN1)[1,3,1,3];

 

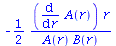(2.10)