Teil II: Paralleles Programmieren mit C++ und OpenMP/MPI
1) Einführung in die parallele Programmierung ( LibreOffice Datei , PDF Datei )
Dieser erste Unterpunkt des zweiten Teils der Vorlesung gibt eine Einführung in die parallele Programmierung mit C++ und OpenMP (Open Multi-Processing) / MPI (Message Passing Interface). Am Beispiel eines einfachen numerischen Problems (der Integration einer Funktion), wird das Programmierparadigma der parallelen Programmierung erläutert. Zunächst wird ein einfaches sequentielles C++-Programm erstellt, das die Integration der Funktion f(x)=1/(1 + a x2) in den Grenzen [0,1] und den Werten a=1..10 mit dem Gauss'schen Integrationsverfahren numerisch berechnet (siehe sequentielle Version 1 und sequentielle Version 2). In diesem Programm wird der Wert des Integrals ∫(1/(1 + a x2)) dx für die Parameterwerte a=1..10 ausgegeben und mit dem analytischen Ergebnis (arctan(√a)1/√a) verglichen. Die Parallelisierung dieses sequentiellen Programms wird zunächst mit OpenMP (siehe OpenMP Version 1 , OpenMP Version 2 , OpenMP Version 3 , OpenMP Version 4 und OpenMP Version 5 ) und danach mit MPI (siehe MPI Version 1 , MPI Version 2 ) durchgeführt.
2) C++ Programm zur Berechnung der Eigenschaften eines kompakten Sterns


Im Unterpunkt 3) des ersten Teils der Vorlesung wurden die Eigenschaften von Neutronensternen mit dem Computeralgebra-System Maple numerisch berechnet. In diesem Unterpunkt des zweiten Teils der Vorlesung wird das gleiche Problem betrachtet, die numerische Lösung wird jedoch auf unterer Ebene, fundamental mittels der Programmiersprache C++ generiert (siehe die links oben abgebildete iterative Vorgehensweise).
2.1) Sequentielle Version zur Berechnung eines Neutronensterns bei vorgegebener zentraler Energiedichte
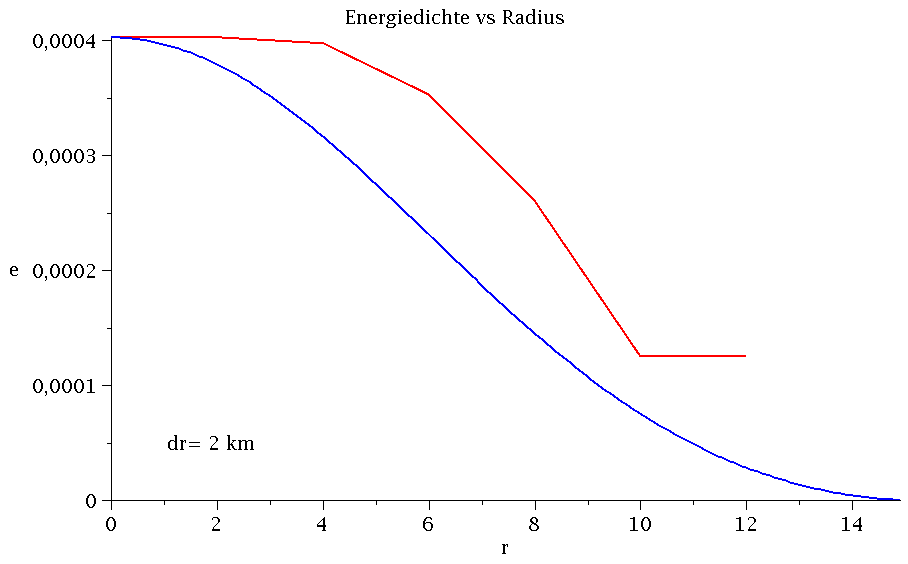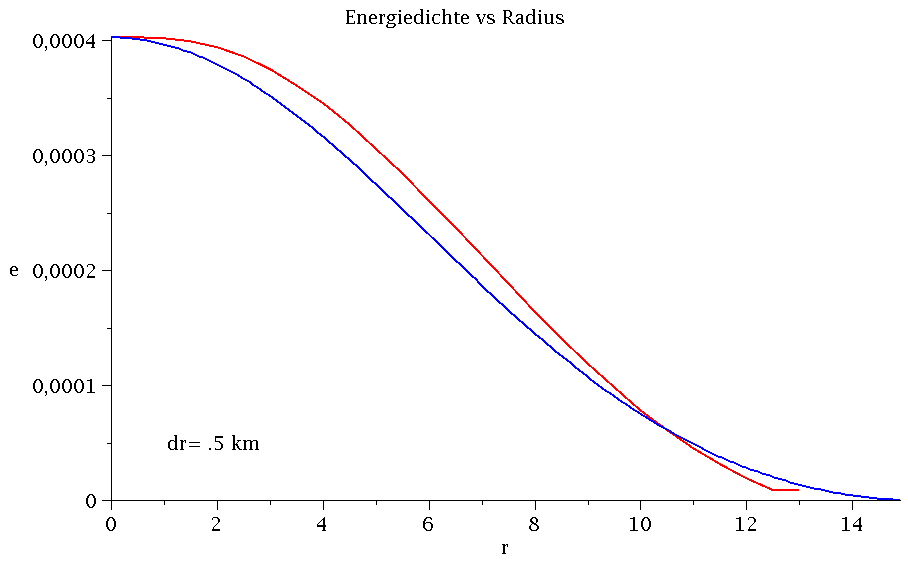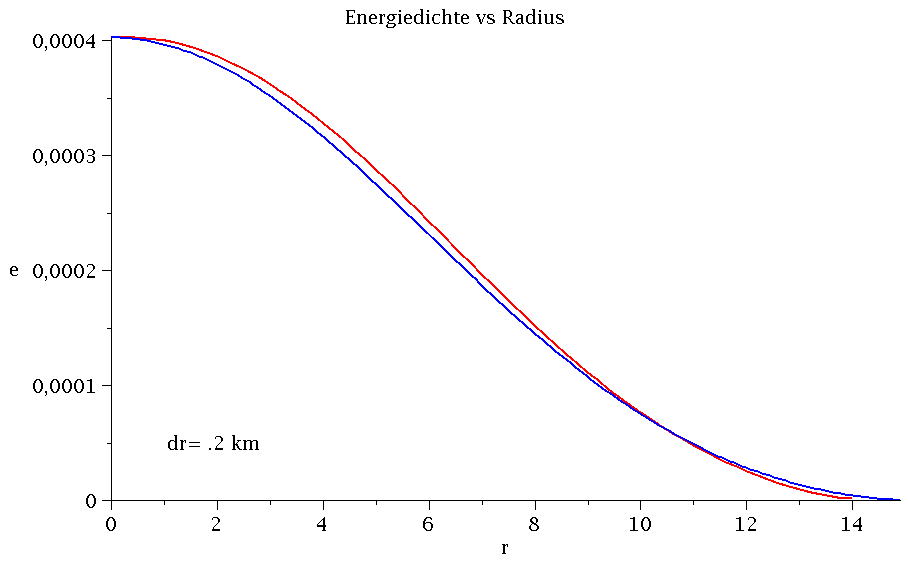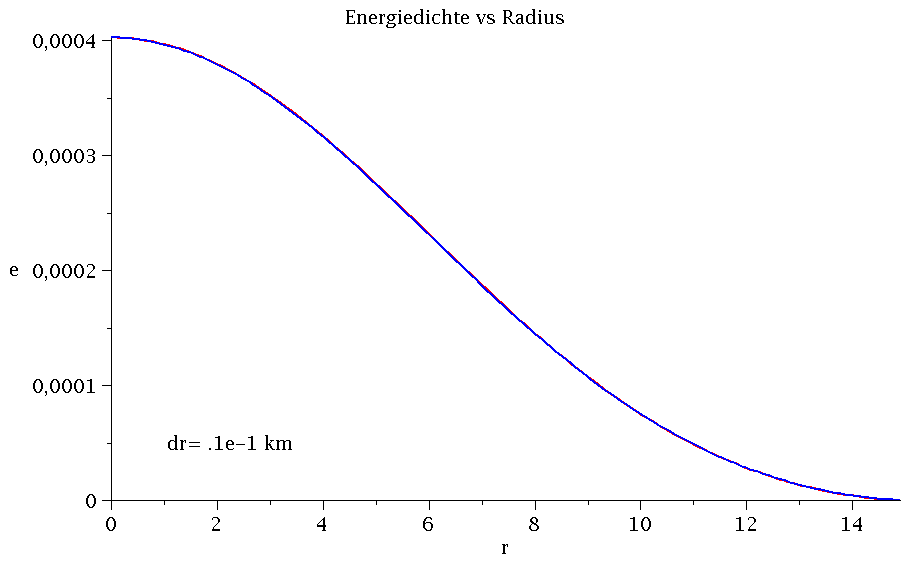
Vergleich Maple (blaue Kurve) und C++ (rote Kurve) bei Variation von dr.
Ausgehend von der, im ersten Teil hergeleiteten Tollmann-Openheimer-Volkov Gleichung, wird mittels des einfachen Euler-Verfahrens die Differentialgleichung in C++ implementiert (siehe TOV sequentielle Version 1). Die numerisch berechneten Werte des Neutronensternradius und seiner gravitativen Masse werden am Ende des Programs im Terminal ausgegeben.
Um die berechneten Resultate mit den Ergebnissen des ersten Teils der Vorlesung (TOV Gleichung mit Maple) zu vergleichen, werden die numerischen Werte des Energiedichtenprofiles in eine externe Datei ( tov.txt ) ausgegeben - die Ausgabedatei erfolgt im Unterordner 'output', welcher vor dem Ausführen des Programms angelegt werden muss (siehe TOV sequentielle Version 1 mit Maple Ausgabe). Das Ausgabeformat geschiet in einer Maple-Liste, so dass das Profil in Maple mittels der Funktion listplot(...) bzw. pointplot(...) einfach dargestellt werden kann. Die linke Abbildung veranschaulicht das mit Maple berechnete Energiedichtenprofil eines Neutronensterns (blaue Kurve) berechnet in einem einfachem nichtrelativistisches Fermigas Model ohne nukleare Wechselwirkungen (siehe z.B. I. Sagert, M. Hempel, C. Greiner, J. Schaffner-Bielich, "Compact Stars for Undergraduates", Eur.J.Phys.27:577-610,2006), indem eine polytrope Zustandsgleichung ( p = K eγ) mit K=7.3015389 und γ=5/3 angesetzt wurde. Die rote Kurve stellt hingegen das mit dem C++ Programm berechnete Profil dar, wobei die Radiusschrittweite von dr=2 km auf dr=0.01 km verändert wurde.
2.2) Sequentielle Version zur Berechnung einer Sequenz von Neutronensternen
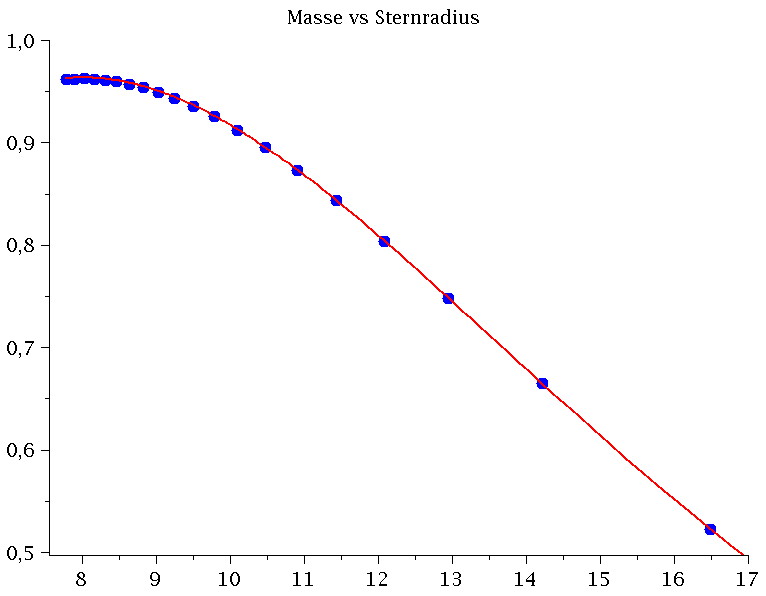
Vergleich Maple (blaue Kurve) und C++ (rote Kurve) bei Variation von dr.
In dieser Version werden, auf sequenzielle Weise, mehrere Neutronensterne bei festgelegter Zustandsgleichung berechnet. Dies wird einfach realisiert, indem man eine weitere for-Schleife über die zentrale Energiedichte einbaut. Zusätzlich zur Version 2.1) werden auch noch die zentralen Werte der Metrikkomponente g00 berechnet und im Terminal ausgegeben (siehe TOV sequentielle Version 2). Der Hauptunterschied zur vorigen sequentiellen Version ist, das nun eine ganze Sequenz von Neutronensternen berechnet wird.
Wieder werden die berechneten Resultate mit den Ergebnissen des ersten Teils der Vorlesung (TOV Gleichung mit Maple) verglichen (siehe TOV sequentielle Version 2 mit Maple Ausgabe). Das Ausgabeformat geschiet in einer Maple-Liste, so dass das Profil in Maple mittels der Funktion listplot(...) bzw. pointplot(...) einfach dargestellt werden kann. Die linke Abbildung vergleicht das mit Maple berechnete Masse-Radius Diagramm (blaue Punkte: p = K eγ) mit K=7.3015389 und γ=5/3) mit den Ergebnissen des C++ Programms (rote Kurve: dr=0.00001).
2.3) Parallele OpenMP-Version 1 von 2.2)
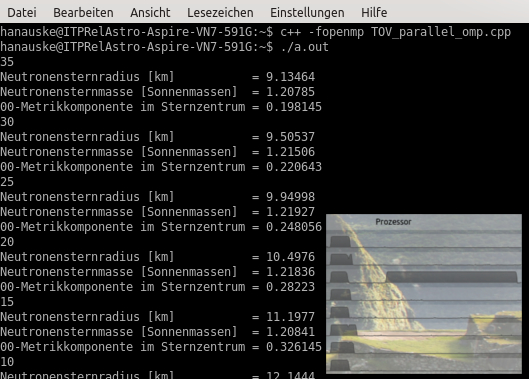
Das sequentielle Programm 2.2) wurde nun mittels OpenMP (siehe TOV OpenMP Version) parallelisiert. Hiebei wurde einfach das OpenMP-Pragma '#pragma omp parallel for private(i,M,p,e,r,nu,dM,dp,de,dnu)' vor die for-Schleife der unabhängigen Berechnung der einzelnen Neutronensterne geschrieben. Wichtig ist nun, dass man das Programm mit dem folgenden Befehl compiliert: 'c++ -fopenmp TOV_parallel_omp.cpp'. Führt man das Programm mit './a.out' aus, so erkennt man als erstes, dass es (in Abhängigkeit wieviele CPU-Kerne man in seinem Computer hat), viel schneller läuft. Die im Terminal ausgegebenen Werte sind jedoch nicht mehr geordnet, sondern die Berechnung der 40 Neutronensterne erfolgt parallel und ungeordnet. Die nebenstehende Abbildung zeigt die Terminalausgabe des parallelen Programms und die Auslastung der 8 CPU-Kerne meines Laptops, wobei zuerst das parallele Programm und dannach das sequentielle ausgeführt wurde.
2.4) Parallele OpenMP-Version 2 ( 2.3) mit geordneter Terminal-Ausgabe )
Diese Version entspricht Version 2.3) mit einer geordneten Ausgabe. Die geordnete Ausgabe wird hierbei realisiert, indem für die drei ausgegebenen, numerischen Werte (Radius, Masse, zentraler g00-Wert), drei Datenfelder (Arrays) der Länge 40 eingerichtet werden. Nachdem ein OpenMP-Thread mit seiner Berechnung fertig ist, speichert er sein individuelles Ergebnis in die spezifische Position innerhalb des Arrays und berechnet den nächsten Stern. Die geordnete Ausgabe aller Werte erfolgt dann sequentiell, außerhalb der parallelisierten Schleife.
2.5) Parallele OpenMP-Version 3 ( 2.4) mit Ausgabe in eine Datei )
Diese Version entspricht Version 2.4) wobei die geordnete Ausgabe nun nicht mehr in dem Terminal geschieht, sondern die berechneten Werte werden in eine externe Datei ( tov.txt ) ausgegeben - die Ausgabedatei erfolgt im Unterordner 'output', welcher vor dem Ausführen des Programms angelegt werden muss. Der Vorteil hierbei ist, dass nachdem das Programm ausgefürt wurde, die Ergebnisse einfacher verarbeitet und dargestellt werden können. So kann man z.B. mittels Gnuplot sich das Radius-Masse Diagramm darstellen. Noch einfacher, kann man sich die einzelnen Gnuplot-Befehle zum Darstellen diverser Diagramme in ein ausführbares Shell-Script schreiben, das dann automatisch die jeweiligen Plots erzeugt (siehe Gnuplot Shell-Script).
2.6) Parallele OpenMP-Version mit geordneter Ausgabe in eine Datei und variabler Zustandsgleichung
Diese Version entspricht Version 2.5), wobei die als Funktion definierte Zustandsgleichung variabler gestaltet wurde (EOS: ( e(P, K, γ)= (P/K)1/γ ) für Neutronensterne und Weiße Zwerge bzw. ( e(P,Bag)=3 p + 4 Bag ) für Quarksterne im MIT-Bag Model).
Struktur und Performance des parallelen OpenMP - C++ Programms
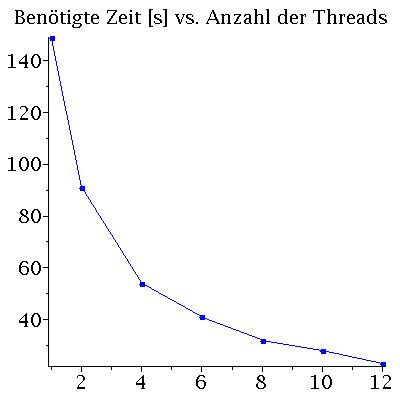
In dem oben angegebenen Link finden Sie eine Zusammenfassung der Beschreibung der Struktur des parallelen OpenMP - C++ Programms. Zusätzlich wird noch die Performance des Programms auf einem Laptop (Quadcore-i7 mit effektiv 8 Kernen) und auf einem Knoten des CPU-Cluster-Computers FUCHS ausgetestet. Die nebenstehende Abbildung zeigt die auf dem FUCHS-Rechner benötigte Zeit in Sekunden als Funktion der Thread-Anzahl, wobei hier speziell 500 Neutronensterne mit einer Schrittweite von dr=0.000005 berechnet wurden.
2.6a) Parallele OpenMP-Version: Version 2.6) mit zusätzlicher Terminal-Ausgabe der benötigten Zeit
2.7) Parallele MPI-Version mit geordneter Ausgabe in eine Datei und variabler Zustandsgleichung
Diese Version entspricht der OpenMP-Version Version 2.6), benutzt jedoch MPI und nicht OpenMP zur Parallelisierung und kann somit auch auf heutigen Großrechneranlagen, die über eine hohe Anzahl von Rechenknoten mit einer Vielzahl von CPU-Kernen verfügen, parallel ausgeführt werden. Wichtig ist nun, dass man das Programm mit dem folgenden Befehl compiliert: 'mpic++ TOV_parallel_omp2_eos_time.cpp' und das Programm mit 'mpirun -np 6 ./a.out' ausführt ('-np 6' ist hier nur ein Beispiel und die Zahl 6 gibt die Anzahl der Prozesse an).
Struktur und Performance des parallelen MPI - C++ Programms
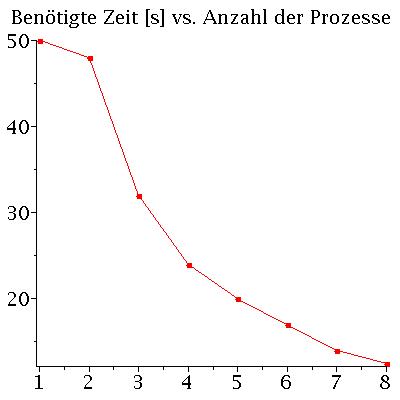
In dem oben angegebenen Link finden Sie eine Zusammenfassung der Beschreibung der Struktur des parallelen MPI - C++ Programms. Zusätzlich wird noch die Performance des Programms auf einem Laptop (Quadcore-i7 mit effektiv 8 Kernen) ausgetestet. Die nebenstehende Abbildung zeigt die auf dem Laptop benötigte Zeit in Sekunden als Funktion der Anzahl der MPI-Prozesse, wobei hier speziell 500 Neutronensterne mit einer Schrittweite von dr=0.000005 berechnet wurden.
2.8) Parallele MPI-Version: Version 2.7) mit zusätzlicher Terminal-Ausgabe der benötigten Zeit
2.9) Parallele OpenMP-Version mit zusätzlicher Schleife über mehrere Sequenzen von unterschiedlichen Zustandsgleichungen
Diese Version entspricht Version 2.6), wobei zusätzlich eine sequenzielle Schleife über mehrere Sequenzen von unterschiedlichen Zustandsgleichungen eingebaut wurde.
Berechnung einer Sequenz von Neutronensternen mittels eines Python Skripts (siehe TOV-Sequence-plot2.py).
Berechnung einer Sequenz von Neutronensternen mittels Python (ohne Parallelisierung)
Dieser Unterpunkt des zweiten Teils der Vorlesung gibt eine Einführung in die Programmierung mit Python. Ausgehend von der, im ersten Teil hergeleiteten Tollmann-Openheimer-Volkov Gleichung, wird mittels des einfachen Euler-Verfahrens die Differentialgleichung in Python implementiert (siehe TOV-Sequence-simple.py, entspricht der C++ Version 'TOV sequentielle Version 1' aus Teil 2.1). Die numerisch berechneten Werte des Neutronensternradius und seiner gravitativen Masse werden am Ende des Programs im Terminal ausgegeben.
Im nächsten Schritt wird eine Eigenschaft der berechneten Neutronensterne in einem Diagramm ausgegeben (siehe TOV-Sequence-plot.py) und danach mehrere Diagramme (siehe TOV-Sequence-plot1.py). Die nebenstehende Abbildung zeigt die Ergebnisse des Python Skripts TOV-Sequence-plot2.py in einer Animation. Hierbei wurden die einzelnen sequentiell berechneten Sterne als Bilder gespeichert und mittels 'ffmpeg -framerate 1 -i './img-%03d.jpg' -c:v libx264 -vf "scale=trunc(iw/2)*2:trunc(ih/2)*2" -s 2000x2000 tovpython.mp4' in einem Film zusammengefügt.
Fortran TOV-Solver mit Python-Skript zur Veranschaulichung der Ergebnisse
Diese Version ist im Rahmen der Vorlesung