Teil II: Parallele OpenMP - Version des TOV-Programms mit geordneter Ausgabe in eine Datei und variabler Zustandsgleichung
Diese Version entspricht Version 2.5), wobei die als Funktion definierte Zustandsgleichung variabler gestaltet wurde (EOS: ( e(P, K, γ)= (P/K)1/γ ) für Neutronensterne und Weiße Zwerge bzw. ( e(P,Bag)=3 p + 4 Bag ) für Quarksterne im MIT-Bag Model). Wichtig ist, dass man das Programm mit dem folgenden Befehl compiliert: 'c++ -fopenmp TOV_parallel_omp.cpp'. Führt man das Programm mit './a.out' aus, so erkennt man, dass es (in Abhängigkeit wieviele CPU-Kerne man in seinem Computer hat), viel schneller läuft.
Struktur des parallelen OpenMP-C++ Programms

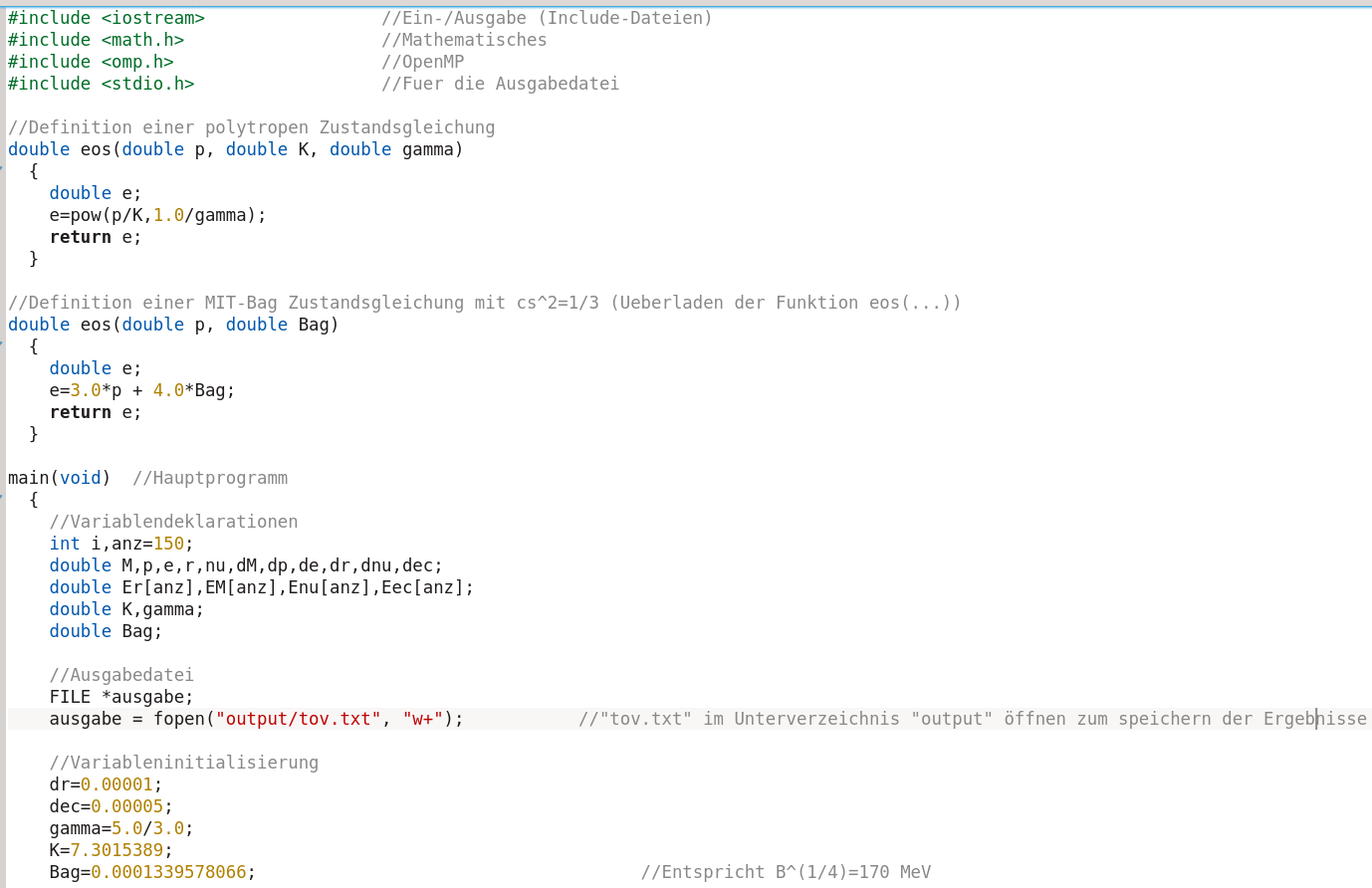
An dieser Stelle des Programms beginnt die parallelisierte Schleife. Es werden, abhängig von der Anzahl der verfügbaren Prozessoren im Computer, mehrere Threads erzeugt, die gleichzeitig die einzelnen Aufgaben der Schleife ausführen. Das OpenMP-Pragma '#pragma omp parallel for private(i,M,p,e,r,nu,dM,dp,de,dnu)' vor der for-Schleife realisiert die Parallelisierung, wobei der private(...) Zusatz sicherstellt, dass die während der Berechnung benötigten Hilfsvariablen (z.B. M, dM) nicht von anderen Threads überschrieben werden. Jeder Thread greift sich einen der 150 (anz=150) zu berechnenden Neutronensterne raus, löst die TOV-Gleichung und berechnet die Masse, den Radius und die für die zentrale g00-Komponente nötige Größe des Sterns. Wenn ein Thread fertig mit der Berechnung ist, nimmt er sich den nächsten noch nicht berechneten Stern vor.







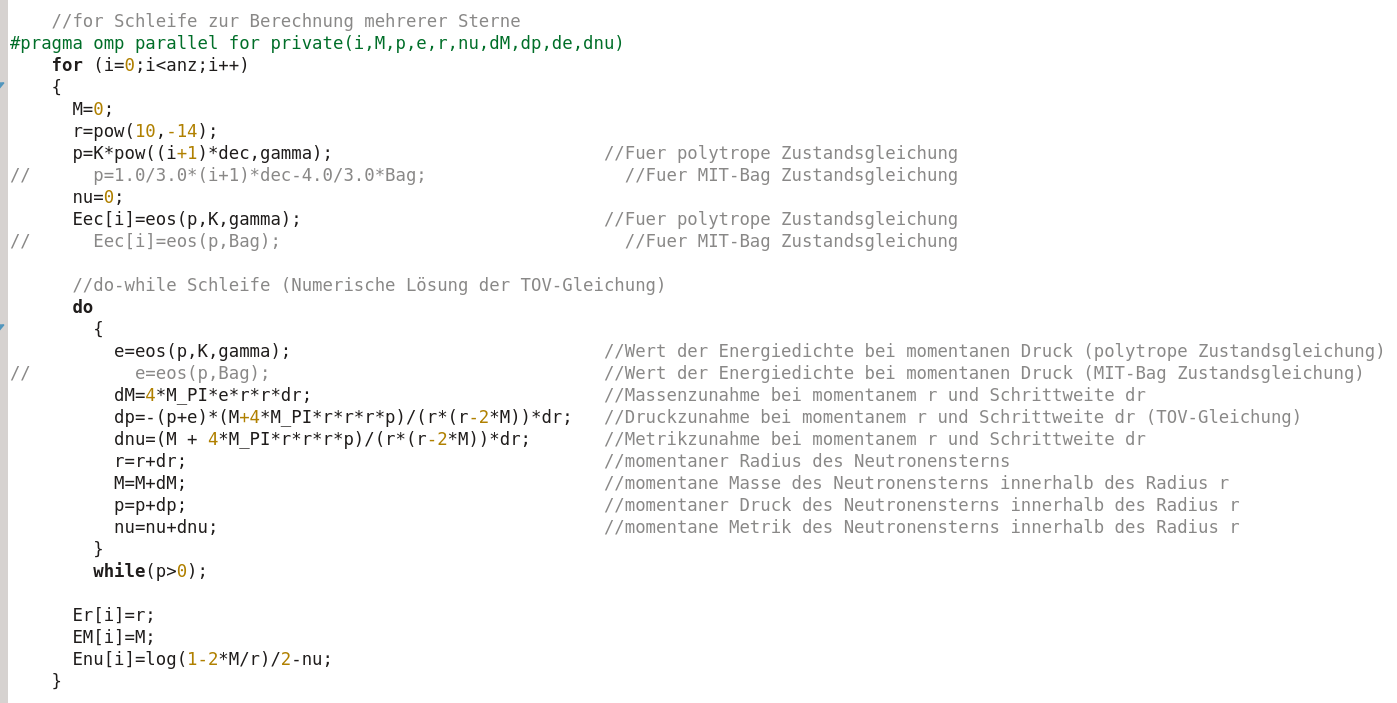
Nach der parallelen Ausführung der Schleife arbeitet wieder nur ein Prozessorkern, der das restliche Programm ausführt (Ausgabe der von den unterschiedlichen Threads berechneten Ergebnisse in eine externe Datei).



Performance des parallelen OpenMP-C++ Programms
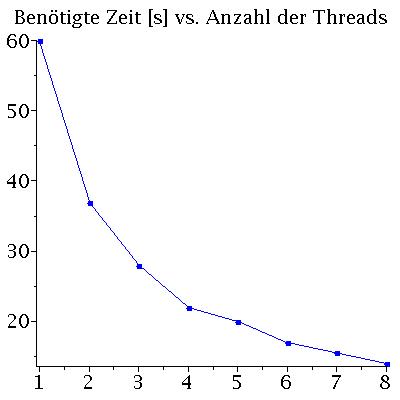
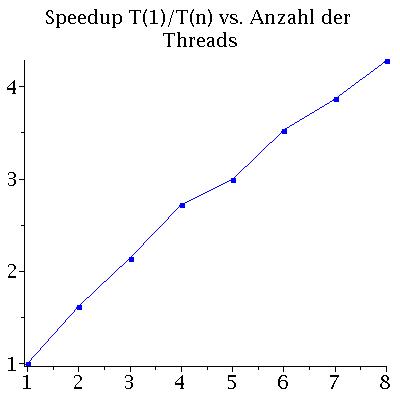
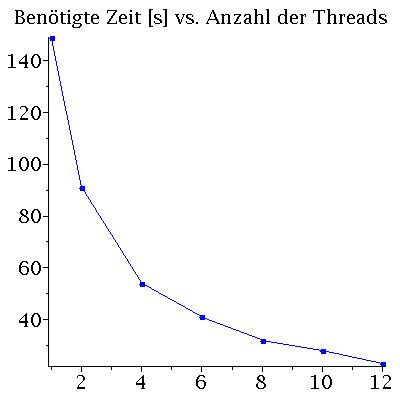
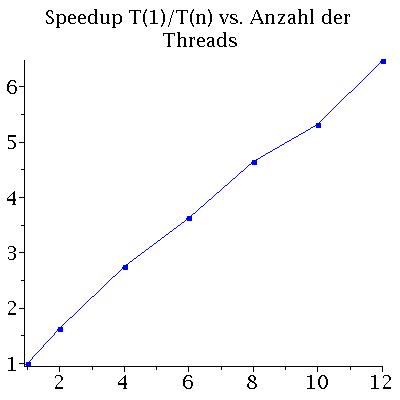
Die Performance eines parallelen Programms kann mit unterschiedlichen Größen quantisiert werden. Man definiert z.B. die beötigte Zeit T des Programms als Funktion der zu Verfügung stehenden CPU-Kerne n mit T(n), das sogenannte SpeedUp S mit S(n)=T(1)/T(n) und die Effizienz E des Programms mit E(n)=S(n)/n. Die folgenden Abbildungen zeigen die benötigte Zeit T(n) und den SpeedUp S(n) des Programms auf einem Laptop (Quadcore-i7: (Intel(R) Core(TM) i7-4710HQ CPU @ 2.50GHz) mit effektiv 8 Kernen: Links) und auf einem Knoten des CPU-Cluster-Computers FUCHS (Rechts). Die Abbildungen stellen die Ergebnisse einer Rechnung von 500 Neutronensternen mit einer Schrittweite von dr=0.000005 dar.