Teil III: Computersimulationen mit dem Einstein-Toolkit
In diesem dritten Teil der Vorlesung soll ein Einblick in die allgemeinrelativistische Simulation auf Supercomputern gegeben werden. Unter zuhilfenahme des sogenannten Einstein-Toolkit, einer frei zugänglichen Software zur Berechnung allgemeinrelativistischer Probleme, werden unterschiedliche, realistische Systeme betrachtet. Die folgende Animation wurde mit dem
Links: Amplitude der emittierte Gravitationswellen im Abstand 50 Mpc von der Kollision. Rechts: Logarithmus des Dichteprofils in der äquatorialen Ebene des Hypermassiven Neutronensterns; die rote Kontourlinie markiert den Anfang der Quarkphase im inneren Bereich des Sterns.
1) Die Einsteingleichung im (3+1)-Split
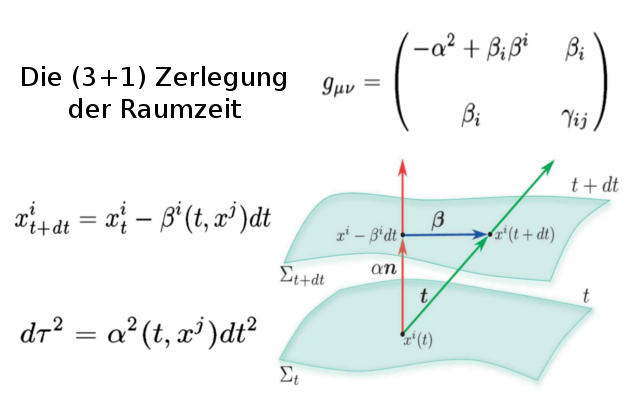
Credit: L. Rezzolla, O. Zanotti: Relativistic Hydrodynamics, Oxford Univ. Press (2013)
Um die zeitliche Entwicklung von komplizierten, allgemeinrelativistischen Systemen auf dem Computer zu simulieren muss die Einsteingleichung zunächst umformuliert werden. In der sogenannten (3+1)-Zerlegung der Raumzeit wird die vierdimensionale Mannigfaltigkeit der Raumzeit in dreidimensionale, raumartige Hyperflächen Σt zerlegt. Die Metrik der Raumzeit gμν (siehe nebenstehende Abbildung) besteht in dieser Zerlegung aus einer Lapse-Funktion α, aus einem Shift-Vektor βi und aus einer rein raumartigen Metrik γij (μν=0,..3 und i,j=1..3). Die Lapse-Funktion α beschreibt den Unterschied zwischen der Koordinatenzeit t und der Eigenzeit τ und der Shift-Vektor βi beschreibt wie stark ein Probekörper in der Raumrichtung "i" von der Struktur der Raumzeit mitgezogen wird, wenn er sich um einen infinitesimalen Zeitschritt dt bewegt. Setzt man diesen Ansatz in die Einsteingleichung ein, so gelangt man zu den sogenannten ADM-Gleichungen (nach Richard Arnowitt, Stanley Deser und Charles W. Misner), die ein System von Differentialgleichungen erster Ordnung darstellen. Um die Konvergenzeigenschaften numerischer Lösungen sicherzustellen wird im
2) Download und Kompilierung des Einstein-Toolkit
In diesem Unterpunkt werden die einzelnen Schritte beschrieben, wie man das frei erhältliche Simulationsprogramm
3) Ausführung einer Simulation
Bevor man eine Simulation mit dem
4) Kollaps eines Neutronensterns zum schwarzen Loch
In diesem Unterpunkt werden die Simulationsergebnisse eines Kollapses eines Neutronensterns zu einem schwarzen Loch vorgestellt (näheres siehe NS_collapse.pdf). Einige der Ausgabedateien der Simulation kann man sich unter dem folgenden Link herunterladen: output.zip
Visualisierung der Simulationsergebnisse mit Mathematica
Um die Simulationsergebnisse mit
Visualisierung der Simulationsergebnisse mit Python (matplotlib)
Oft wird auch die Programmiersprache
Kollaps eines Neutronensterns zum schwarzen Loch. Links die Lapse Funktion alpha und rechts der Logarithmus des Dichteprofils. Link zum Python -Script
5) Migration eines instabilen Neutronensterns
In diesem Unterpunkt werden die Simulationsergebnisse einer Migration eines instabilen Neutronensterns zum stabilen Zweig vorgestellt (näheres siehe Task 3). Einige der Ausgabedateien der Simulation kann man sich unter dem folgenden Link herunterladen: output.zip