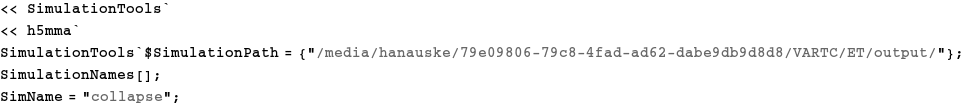
Allgemeine Relativitätstheorie mit dem Computer
General Theory of Relativity on the Computer
Vorlesung gehalten an der J.W.Goethe-Universität in Frankfurt am Main (Sommersemester 2016)
von Dr.phil.nat. Dr.rer.pol. Matthias Hanauske
Frankfurt am Main 11.04.2016
Dritter Vorlesungsteil: Computersimulationen mit dem Einstein-Toolkit
III.4) Kollaps eines Neutronensternszum schwarzen Loch
Download des
Einlesen des Zusatzpakets “SimulationTools” (siehe ) und Angabe des Pfade der Simulationsergebnisse des Einstein Toolkits
Auflistung der Ausgabedateien der Simulation
![]()
Welche Iterationszeitpunkte wurden ausgegeben und wie groß ist der Abstand zwischen ihnen:

Darstellung des Dichteprofils (rho(x) bzw. Log(rho(x)) am Anfang der Simulation (t=0).

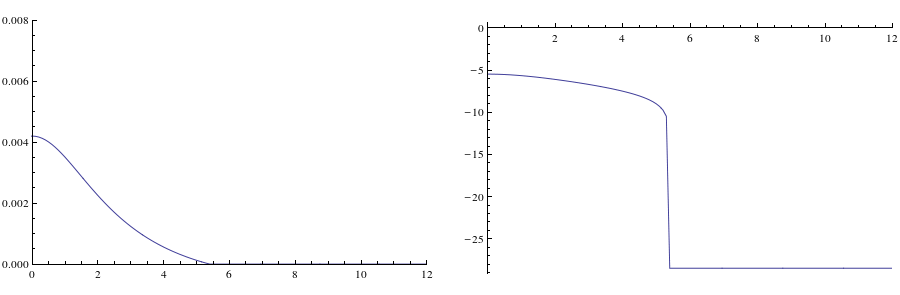
Zeitliche Animation des Dichteprofils (rho(x) bzw. Log(rho(x)). Bem.: Im Logarithmischen Plot erkennt man gut, dass die Abmessungen des Gitters (30 )viel zu klein sind (man hätte hier mehrere Refinement-Levels mit weit größeren Abmessung wählen sollen).

Darstellung der Lapse Funktion alpha(x) und der Flüssigkeits-Geschwindigkeitskomponente in x-Richtung vx(x)

Darstellung des Dichteprofils rho(x,y), der Lapse Funktion alpha(x,y) und der Flüssigkeits-Geschwindigkeitskomponente in x-Richtung vx(x,y) am Anfang der Simulation (t=0) und zur Iterationszeit 100*dt=1000 .

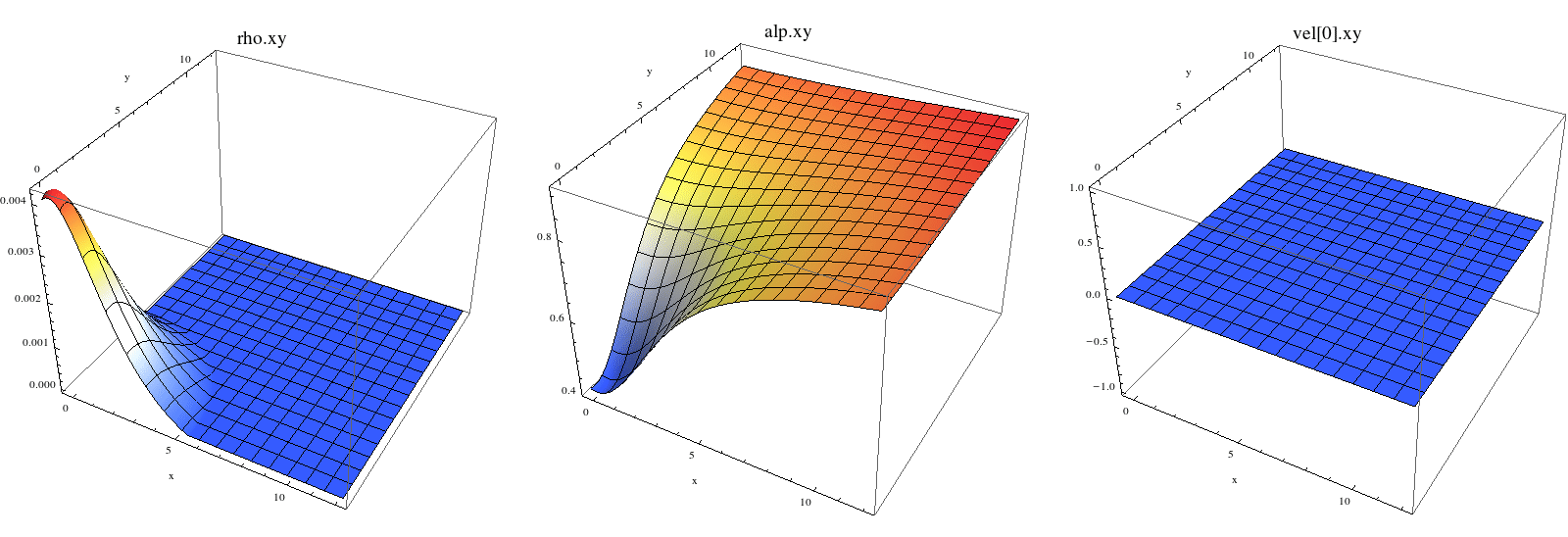
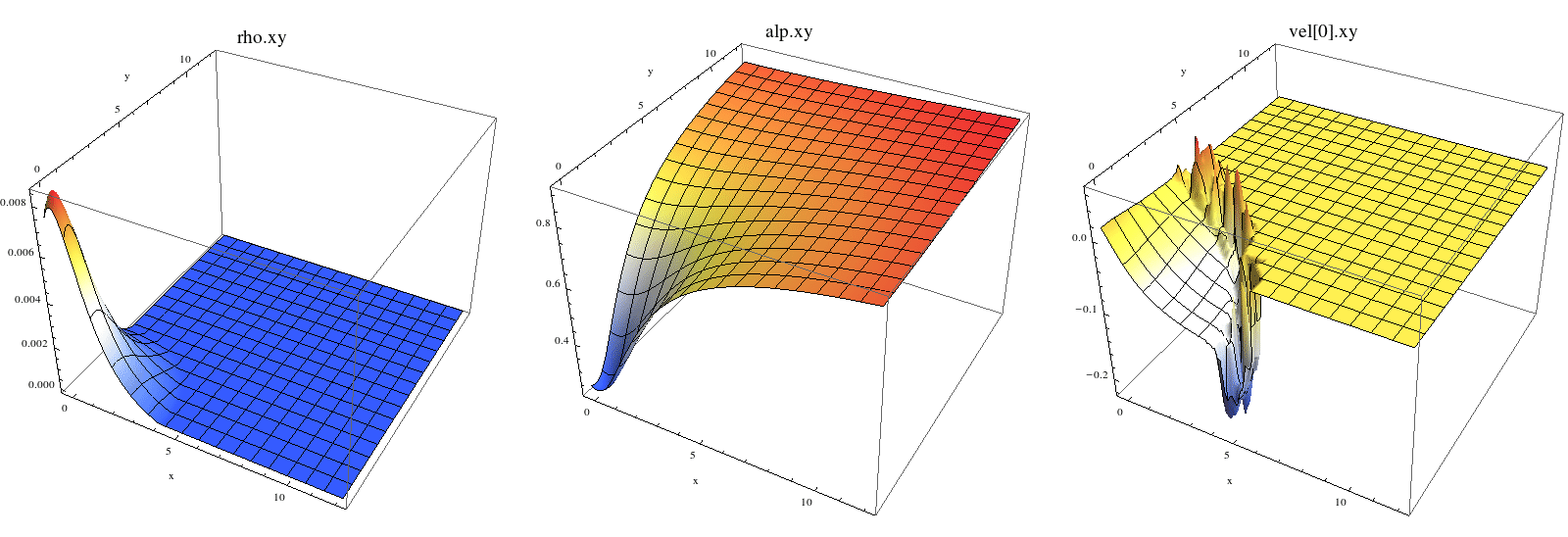
Animation des Dichteprofils rho(x,y) und Log(rho(x,y))

Darstellung des Aparent Horizon
Outermost Trapped Surface: Blaue Kurve
InnermostTrapped Surface: Rote Kurve

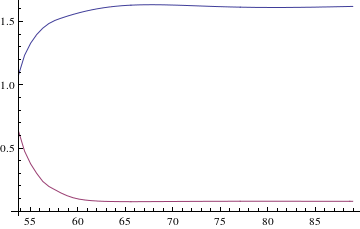
Darstellung der Oberfläche des Sterns und des Apparent Horizon in einem Raumzeitdiagramm