Probe Prüfung 

Aufgabe 7. Maple Worksheet Vorlesung4.mw verwendet. 

Die innere Schwarzschildlösung eines sphärisch symetrischen, statischen Objektes (z.B. Erde, Neutronenstern)   

Im folgenden wird die Einsteingleichung einer sphärisch symetrischen und statischen Matrieverteilung betrachtet. Die Matrie wird hierbei als ideale Flüssigkeit angesetzt.  

Von der Einstein Gleichung zur Tollman-Oppenheimer-Vollkov Gleichung (TOV) 

>	restart: with( tensor ):

 

Sphärisch symetrischer und statischer Ansatz der Metrik: 

>	coord := [t, r, theta, phi]: g_compts := array(symmetric,sparse, 1..4, 1..4): g_compts[1,1] := exp(2*phi(r)): #g_compts[2,2] := exp(2*lambda(r)): g_compts[2,2] := -1/(1-2*m(r)/r): g_compts[3,3] := -r^2:     g_compts[4,4] := -r^2*sin(theta)^2: g := create( [-1,-1], eval(g_compts));

 

(2.1.1)

 

>	ginv := invert( g, 'detg' ); D1g := d1metric ( g, coord ):   D2g := d2metric ( D1g, coord ): Cf1 := Christoffel1 ( D1g ): Cf2 := Christoffel2(ginv, Cf1):

 

(2.1.2)

 

>	RMN := Riemann( ginv, D2g, Cf1 ): RMNinv:= raise(ginv,RMN,1,2,3,4): RMNc:=get_compts(RMN): RICCI := Ricci( ginv, RMN ): RS := Ricciscalar( ginv, RICCI ):

 

Kovariante Form des Einsteintensors: 

>	G := Einstein( g, RICCI, RS );

 

(2.1.3)

 

 

Der Energie-Impuls Tensor (rechte Seite der Einsteingleichung) wird als ideale Flüssigkeit angesetzt: 

>	T:=create([1,-1], array([[e(r),0,0,0],[0,-p(r),0,0],[0,0,-p(r),0],[0,0,0,-p(r)]])); Tl:=lower(g,T,1); Tu:=raise(ginv,T,2): prod(ginv, Tl, [2, 1]): contract(T, [1, 2]):

 

 

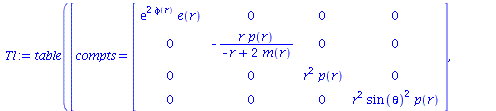	(2.1.4)

 

Nichtverschwindende Komponenten der Einsteingleichung: 

>	Einsteingl:=lin_com(G,8*Pi,Tl);

 

(2.1.5)

 

>	A:=get_compts(Einsteingl):

 

Erste Gleichung der Einsteingleichung (tt-Komponente) wird nach dm/dr aufgelößt. 

Zweite Gleichung der Einsteingleichung (rr-Komponente) wird nach dphi/dr aufgelößt. 

>	Einstein1:=diff(m(r), r)=solve(A[1,1],diff(m(r), r)); Einstein2:=diff(phi(r),r)=solve(A[2,2],diff(phi(r),r));

 

 

	(2.1.6)

 

Mittels der hydrodynamischen Gleichungen (kovariante Erhaltung des Energie-Impulses) erhalten wir 

>	DT:=cov_diff(T, coord, Cf2): DTa:=get_compts(contract(DT, [1, 3]))[2]=0;

 

(2.1.7)

 

.was nach dp/dr aufgelößt das folgende ergibt: 

>	diff(p(r), r)=collect(solve(DTa,diff(p(r), r)),diff(phi(r), r));

 

(2.1.8)

 

Die TOV-Gleichung erhalten wir, indem man diese Gleichung nach dphi/dr auflößt und das Ergebnis in die zweite Gleichung der Einsteingleichung einsetzt: 

>	solve(DTa,diff(phi(r), r))*(e(r)+p(r))*(-1)=rhs(Einstein2)*(e(r)+p(r))*(-1);

 

(2.1.9)

 

>	TOV1:=solve(DTa,diff(phi(r), r))*(e(r)+p(r))*(-1)=rhs(Einstein2)*(e(r)+p(r))*(-1); TOV2:=Einstein1; TOV3:=Einstein2;

 

 

 

	(2.1.10)

 

 

Numerische Lösung der TOV-Gleichungen 

Im folgenden werden die TOV-Gleichungen numerisch gelößt, indem wir einerseits eine Zustandsgleichung der Materie (eine Funktion p(e))  festlegen und von einem Startwert der zentralen Energiedichte im Inneren des sphärisch symetrischen Objektes nach Außen integrieren. Hier wurde das Maple-File verändert 

>	a:=7.3; b:=5/3: p(r):=a*(e(r))^b; W3:=plot(a*x^b,x=0..1,color=blue): TOV1:=solve(DTa,diff(phi(r), r))*(e(r)+p(r))*(-1)=rhs(Einstein2)*(e(r)+p(r))*(-1); TOV2:=Einstein1; TOV3:=Einstein2;

 

 

 

 

 

	(2.2.1)

 

Numerische Lösung der Gleichung mitfixierten Randbedingungen im Sternzentrum. Hier wurde das Maple-File verändert 

>	r0:=10^(-14): e0:=0.0015; Loes:=dsolve({TOV1,TOV2,m(r0)=0,e(r0)=e0},{m(r),e(r)},type=numeric,output=listprocedure);

 

 

	(2.2.2)

 

Numerische Lösung vom Sternzentrum aus integriert: 

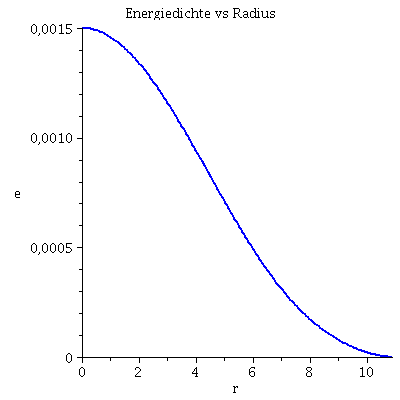
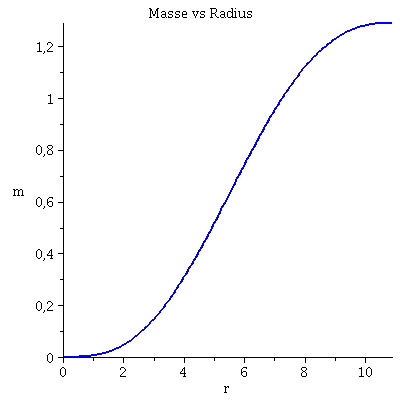
>	with(plots): rend:=10.8914829: Plot1:=odeplot(Loes,[r,e(r)],r0..rend,numpoints=200,color=blue,thickness=2,title="Energiedichte vs Radius"): Plot2:=odeplot(Loes,[r,m(r)],r0..rend,numpoints=200,color=blue,thickness=2,title="Masse vs Radius"): display(Matrix(1,2,[Plot1,Plot2]));

 

 

Aufgrund des Birkov Theorems muss die Innenlösung der Metrik in die äussere Schwarzschildmetrik am Sternrand übergehen. Da wir nun die Gesamtmasse des Sterns kennen, können wir auch die innere g00 und g11 Komponente der Metrik angeben: Integration nun von der Sternoberfläche nach Innen:Hier wurde das Maple-File verändert 

>	Mass := subs(Loes,m(r)): M:=Mass(rend): M/1.4766; Phi0:=(0.5*ln(1-2*Mass(rend)/rend)): Loes1:=dsolve({TOV1,TOV2,TOV3,m(rend)=Mass(rend),e(rend)=10^(-25),phi(rend)=Phi0},{m(r),e(r),phi(r)},type=numeric,output=listprocedure);

 

 

	(2.2.3)

 

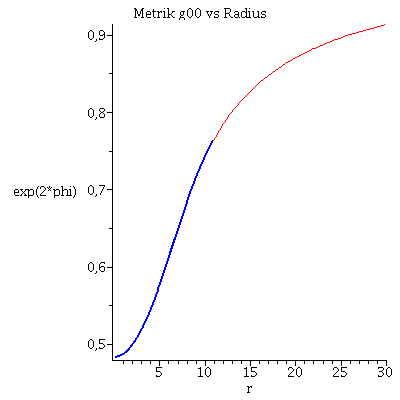
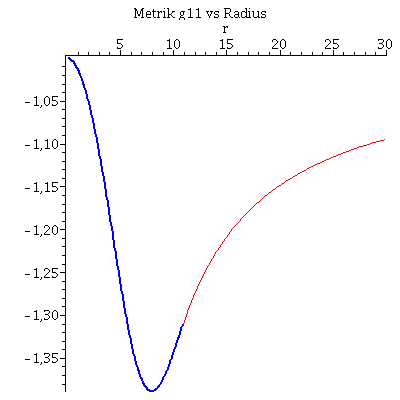
Veranschaulichung der g00-Komponente (linke Abbildung) und g11-Komponente (rechte Abbildung) der Innenraummetrik (blaue Kurven) und Außenraummetrik (rote Kurven). 

>

ranf:=10^(-1): Plot3:=odeplot(Loes1,[r,exp(2*phi(r))],ranf..rend,numpoints=200,color=blue,thickness=2,title="Metrik g00 vs Radius"): Plot4:=odeplot(Loes1,[r,-1/(1-2*m(r)/r)],ranf..rend,numpoints=200,color=blue,thickness=2,title="Metrik g11 vs Radius"): Plot5:=plot(1-2*M/r,r=rend..30,color=red): Plot6:=plot(-1/(1-2*M/r),r=rend..30,color=red): display(Matrix(1,2,[[display(Plot3,Plot5),display(Plot4,Plot6)]]));

 

 

>