Pruefung6.html

Pruefung6.mw

Allgemeine Relativitätstheorie mit dem Computer

General Theory of Relativity on the Computer

Vorlesung gehalten an der J.W.Goethe-Universität in Frankfurt am Main (Sommersemester 2016)

von Dr.phil.nat. Dr.rer.pol. Matthias Hanauske

Frankfurt am Main 11.04.2016

Erster Vorlesungsteil: Allgemeine Relativitätstheorie mit Maple

Probe Prüfung

Probe Prüfung

Aufgabe 6. Maple Worksheet Vorlesung4.mw verwendet.

Die innere Schwarzschildlösung eines sphärisch symetrischen, statischen Objektes (z.B. Erde, Neutronenstern)

Im folgenden wird die Einsteingleichung einer sphärisch symetrischen und statischen Matrieverteilung betrachtet. Die Matrie wird hierbei als ideale Flüssigkeit angesetzt.

Von der Einstein Gleichung zur Tolman–Oppenheimer–Volkoff Gleichung (TOV)

> restart:
with( tensor ):

Sphärisch symetrischer und statischer Ansatz der Metrik:Hier wurde das Maple-File verändert

> coord := [t, r, theta, phi]:
g_compts := array(symmetric,sparse, 1..4, 1..4):
g_compts[1,1] := a(r):
#g_compts[2,2] := exp(2*lambda(r)):
#g_compts[2,2] := -1/(1-2*m(r)/r):
g_compts[2,2] := -b(r):
g_compts[3,3] := -r^2:
g_compts[4,4] := -r^2*sin(theta)^2:
g := create( [-1,-1], eval(g_compts));

`:=`(g, table([compts = Matrix(%id = 16313168), index_char = [-1, -1]])) (2.1.1)

> ginv := invert( g, 'detg' );
D1g := d1metric ( g, coord ):
D2g := d2metric ( D1g, coord ):
Cf1 := Christoffel1 ( D1g ):
Cf2 := Christoffel2(ginv, Cf1):

`:=`(ginv, table([compts = Matrix(%id = 18612400), index_char = [1, 1]])) (2.1.2)

> RMN := Riemann( ginv, D2g, Cf1 ):
RMNinv:= raise(ginv,RMN,1,2,3,4):
RMNc:=get_compts(RMN):
RICCI := Ricci( ginv, RMN ):
RS := Ricciscalar( ginv, RICCI ):

Kovariante Form des Einsteintensors:

> G := Einstein( g, RICCI, RS );

`:=`(G, table([compts = Matrix(%id = 18176080), index_char = [-1, -1]]))

(2.1.3)

Der Energie-Impuls Tensor (rechte Seite der Einsteingleichung) wird als ideale Flüssigkeit angesetzt:

> T:=create([1,-1], array([[e(r),0,0,0],[0,-p(r),0,0],[0,0,-p(r),0],[0,0,0,-p(r)]]));
Tl:=lower(g,T,1);
Tu:=raise(ginv,T,2):
prod(ginv, Tl, [2, 1]):
contract(T, [1, 2]):

`:=`(T, table([compts = Matrix(%id = 20647656), index_char = [1, -1]]))

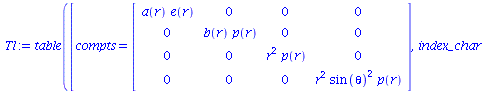table( [( compts ) = array( 1 .. 4, 1 .. 4, [( 4, 2 ) = 0, ( 1, 2 ) = 0, ( 2, 3 ) = 0, ( 3, 3 ) = `*`(`^`(r, 2), `*`(p(r))), ( 2, 1 ) = 0, ( 1, 4 ) = 0, ( 2, 4 ) = 0, ( 4, 4 ) = `*`(`^`(r, 2), `*`(`^`...
(2.1.4)

Nichtverschwindende Komponenten der Einsteingleichung:

> Einsteingl:=lin_com(G,8*Pi,Tl);

`:=`(Einsteingl, table([compts = Matrix(%id = 21725128), index_char = [-1, -1]]))

(2.1.5)

> A:=get_compts(Einsteingl):

Erste Gleichung der Einsteingleichung (tt-Komponente) wird nach dm/dr aufgelößt.

Zweite Gleichung der Einsteingleichung (rr-Komponente) wird nach dphi/dr aufgelößt.Hier wurde das Maple-File verändert

> Einstein1:=diff(b(r), r)=solve(A[1,1],diff(b(r), r));
Einstein2:=diff(a(r),r)=solve(A[2,2],diff(a(r),r));

(2.1.6)

Mittels der hydrodynamischen Gleichungen (kovariante Erhaltung des Energie-Impulses) erhalten wir

> DT:=cov_diff(T, coord, Cf2):
DTa:=get_compts(contract(DT, [1, 3]))[2]=0;

(2.1.7)

.was nach dp/dr aufgelößt das folgende ergibt:Hier wurde das Maple-File verändert

> diff(p(r), r)=collect(solve(DTa,diff(p(r), r)),diff(b(r), r));

(2.1.8)

Die TOV-Gleichung erhalten wir, indem man diese Gleichung nach dphi/dr auflößt und das Ergebnis in die zweite Gleichung der Einsteingleichung einsetzt:Hier wurde das Maple-File verändert

> solve(DTa,diff(a(r), r))*(e(r)+p(r))*(-1)/2/a(r)=rhs(Einstein2)*(e(r)+p(r))*(-1)/2/a(r);

(2.1.9)

> TOV1:=solve(DTa,diff(a(r), r))*(e(r)+p(r))*(-1)/2/a(r)=rhs(Einstein2)*(e(r)+p(r))*(-1)/2/a(r);
TOV2:=Einstein1;
TOV3:=Einstein2;

(2.1.10)