Probe Prüfung 

Aufgabe 2. Maple Worksheet Vorlesung2.mw verwendet. 

Die Geodätengleichung in vorgegebener Schwarzschild Raumzeit 

Im folgenden wird die Geodätengleichung in vorgegebener Schwarzschild Raumzeit betrachtet. Die Geodätengleichung beschreibt wie sich ein Probekörper (Masse = 0) im Raum bewegt und sagt voraus, dass diese Bewegung sich stehts entlang der kürzesten Kurve, in der durch die Metrik beschriebenen gekrümmten Raumzeit, vollzieht. 

Radial in ein schwarzes Loch einfallender Probekörper 

>	restart: with( tensor ): with(plots): with(plottools):

 

Definition der kovarianten Raumzeit-Metrik eines schwarzen Lochs der Masse M in Schwarzschildkoordinaten: 

>	coord := [t, r, theta, phi]: g_compts := array(symmetric,sparse, 1..4, 1..4): g_compts[1,1] := 1-2*M/r: g_compts[2,2] := -1/g_compts[1,1]: g_compts[3,3] := -r^2:    g_compts[4,4] := -r^2*sin(theta)^2: g := create( [-1,-1], eval(g_compts));

 

(2.1.1)

 

Berechnung der kontravarianten Metrik und der Christoffel Symbole: 

>	ginv := invert( g, 'detg' ): D1g := d1metric( g, coord ):   D2g := d2metric( D1g, coord ): Cf1 := Christoffel1( D1g ): Cf2:= Christoffel2( ginv, Cf1 ):

 

Berechnung der Geodätengleichung als Funktion des affinen Parameters lambda. Die Geodätengleichung ist ein System gekoppelter Differentialgleichungen:   

>	eqns:=geodesic_eqns( coord, lambda, Cf2 );

 

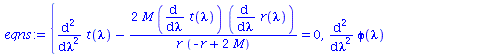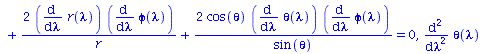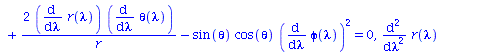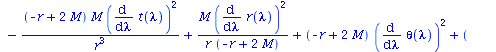(2.1.2)

 

Wir lassen nur radiale Bewegung zu und setzen die Masse des schwarzen Lochs auf M=0.5:Hier wurde das Maple-File verändert 

>

eq1:=subs({diff(phi(lambda),lambda)=0,diff(theta(lambda),lambda)=0,M=0.5},eqns[1]): eq2:=subs({diff(phi(lambda),lambda)=0,diff(theta(lambda),lambda)=0,M=0.5},eqns[2]): eq3:=subs({diff(phi(lambda),lambda)=0,diff(theta(lambda),lambda)=0,M=0.5},eqns[3]): eq4:=subs({diff(phi(lambda),lambda)=0,diff(theta(lambda),lambda)=0,M=0.5},eqns[4]): eq1:=simplify(subs({r=r(lambda)},eq1)): eq4:=simplify(subs({r=r(lambda)},eq4)): eq1:=simplify(subs({r(lambda)(lambda)=r(lambda)},eq1)); eq4:=simplify(subs({r(lambda)(lambda)=r(lambda)},eq4));

 

 

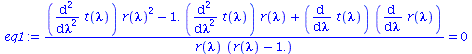	(2.1.3)

 

Anfangswerte: 

Zur Zeit t=0 sei der fallende Körper bei einem Radius von r=10=5*(Schwarzschildradius), die Anfangsgeschwindigkeit des Körpers sei 0. Wir beschreiben den Fall aus der Sichtweise eines im Unendlichen ruhenden Beobachters.Bemerkung: Der Anfangswert dt0 ergibt sich hierbei aus dem infinitesimalen Weglängenelements ds²=1 eines massiven Probekörpers: 

Hier wurde das Maple-File verändert 

>	r0:=50: t0:=0: dr0:=0: dt0:=evalf(1/sqrt(1-2/r0)):

 

Numerisches Lösen der Geodätengleichung: 

>	Loes:=dsolve({eq1,eq4,t(0)=t0,r(0)=r0,D(r)(0)=0,D(t)(0)=dt0},{r(lambda),t(lambda)},type=numeric,output=listprocedure):

 

Zum Vergleich lösen wir auch die Bewegungsgleichung nach Newton:Hier wurde das Maple-File verändert 

>	Loes_newton:=dsolve({diff(r(lambda),lambda,lambda)=-0.5/r(lambda)^2,r(0)=r0,D(r)(0)=0},{r(lambda)},type=numeric,output=listprocedure):

 

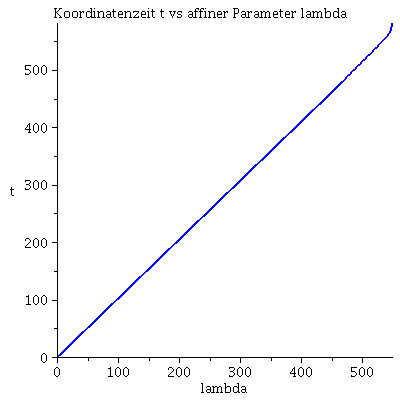
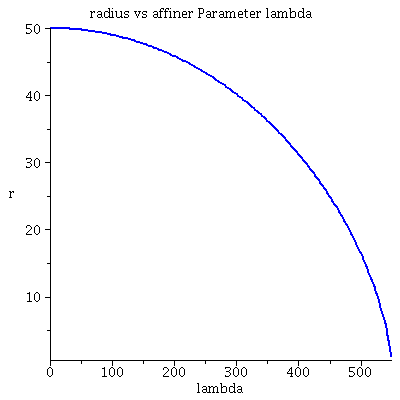
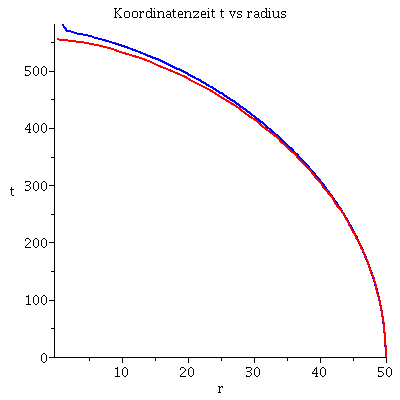
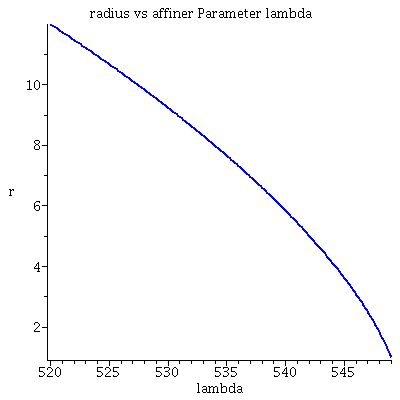
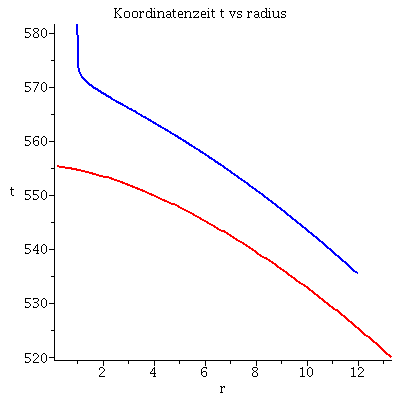
Grafische Veranschaulichung der Lösung (rote Kurve ist die nach Newton berechnete):Hier wurde das Maple-File verändert 

>

lend:=549.00042: lendn:=555.3: Plot1:=odeplot(Loes,[lambda,t(lambda)],0..lend,numpoints=200,color=blue,thickness=2,title="Koordinatenzeit t vs affiner Parameter lambda"): Plot2:=odeplot(Loes,[lambda,r(lambda)],0..lend,numpoints=200,color=blue,thickness=2,title="radius vs affiner Parameter lambda"): Plot3:=odeplot(Loes,[r(lambda),t(lambda)],0..lend,numpoints=700,color=blue,thickness=2,title="Koordinatenzeit t vs radius"): Plot_newton:=odeplot(Loes_newton,[r(lambda),lambda],0..lendn,numpoints=100,color=red,thickness=2): display(Matrix(1,3,[Plot1,Plot2,display(Plot3,Plot_newton)]));

 

 

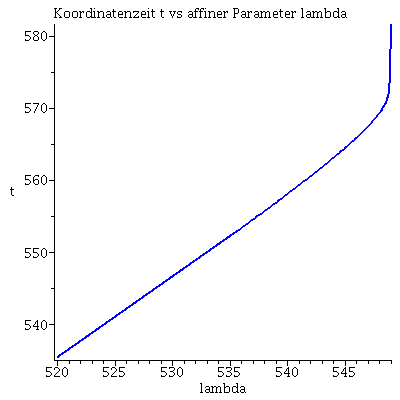
Hier wurde das Maple-File verändert 

>

lend:=549.00042: lendn:=555.3: lanf:=520: Plot1:=odeplot(Loes,[lambda,t(lambda)],lanf..lend,numpoints=200,color=blue,thickness=2,title="Koordinatenzeit t vs affiner Parameter lambda"): Plot2:=odeplot(Loes,[lambda,r(lambda)],lanf..lend,numpoints=200,color=blue,thickness=2,title="radius vs affiner Parameter lambda"): Plot3:=odeplot(Loes,[r(lambda),t(lambda)],lanf..lend,numpoints=700,color=blue,thickness=2,title="Koordinatenzeit t vs radius"): Plot_newton:=odeplot(Loes_newton,[r(lambda),lambda],lanf..lendn,numpoints=100,color=red,thickness=2): display(Matrix(1,3,[Plot1,Plot2,display(Plot3,Plot_newton)]));

 

 

Hier wurde das Maple-File verändert 

>	r=rhs(Loes(450)[2]);

 

(2.1.4)

 

>