Probe Prüfung 

Aufgabe 5. Maple Worksheet Vorlesung3.mw verwendet. 

Bewegung eines Probekörpers um ein schwarzes Loch in der Ebene 

Im folgenden wird die Geodätengleichung in vorgegebener Schwarzschild Raumzeit betrachtet. Die Geodätengleichung beschreibt wie sich ein Probekörper (Masse = 0) im Raum bewegt und sagt voraus, dass diese Bewegung sich stehts entlang der kürzesten Kurve, in der durch die Metrik beschriebenen gekrümmten Raumzeit, vollzieht. 

Die Geodätengleichung und das effektive Potential V(r) 

>	restart: with( tensor ): with(plots): with(plottools):

 

Definition der kovarianten Raumzeit-Metrik eines schwarzen Lochs der Masse M in Schwarzschildkoordinaten: 

>	coord := [t, r, theta, phi]: g_compts := array(symmetric,sparse, 1..4, 1..4): g_compts[1,1] := 1-2*M/r: g_compts[2,2] := -1/g_compts[1,1]: g_compts[3,3] := -r^2:    g_compts[4,4] := -r^2*sin(theta)^2: g := create( [-1,-1], eval(g_compts));

 

(2.1.1)

 

Berechnung der kontravarianten Metrik und der Christoffel Symbole: 

>	ginv := invert( g, 'detg' ): D1g := d1metric( g, coord ):   D2g := d2metric( D1g, coord ): Cf1 := Christoffel1( D1g ): Cf2:= Christoffel2( ginv, Cf1 ):

 

Berechnung der Geodätengleichung als Funktion des affinen Parameters lambda. Die Geodätengleichung ist ein System gekoppelter Differentialgleichungen:   

>	eqns:=geodesic_eqns( coord, lambda, Cf2 );

 

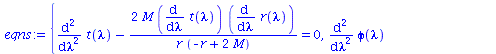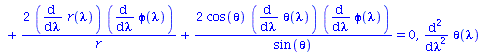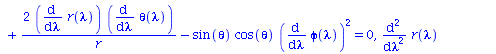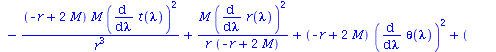(2.1.2)

 

Wir lassen nur ebene Bewegungen zu (theta=Pi/2, dtheta=0) und setzen M=1:Hier wurde das Maple-File verändert 

>

setM:=12: eq1:=subs({r=r(lambda),sin(theta)=1,cos(theta)=0,diff(theta(lambda),lambda)=0,theta=Pi/2,M=setM},eqns[1]): eq2:=subs({r=r(lambda),sin(theta)=1,cos(theta)=0,diff(theta(lambda),lambda)=0,theta=Pi/2,M=setM},eqns[2]): eq3:=subs({r=r(lambda),sin(theta)=1,cos(theta)=0,diff(theta(lambda),lambda)=0,theta=Pi/2,M=setM},eqns[3]): eq4:=subs({r=r(lambda),sin(theta)=1,cos(theta)=0,diff(theta(lambda),lambda)=0,theta=Pi/2,M=setM},eqns[4]): eq1:=subs({r(lambda)(lambda)=r(lambda)},eq1); eq2:=subs({r(lambda)(lambda)=r(lambda)},eq2); eq3:=subs({r(lambda)(lambda)=r(lambda)},eq3); eq4:=subs({r(lambda)(lambda)=r(lambda)},eq4);

 

 

 

 

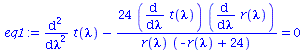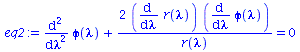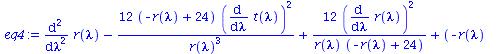	(2.1.3)

 

 

Bewegung von Licht (Photonen) um ein schwarzes Loch in der Ebene (Die Photonensphäre) 

In der Literatur wird die Bewegung von Licht um ein schwarzes Loch mittels eines definierten, effektiven Potentials illustriert: 

1. General relativity : An introduction for physicists by M. P. Hobson, G. P. Efstathiou and A. N. Lasenby  

2. Gravity : An introduction to Einstein's general relativity by James B. Hartle 

3. Allgemeine Relativitätstheorie by Torsten Fließbach  

4. Relativistic hydrodynamics by Luciano Rezzolla and Olindo Zanotti  

Dieses Potential hängt allein von der Masse des schwarzen Lochs ab. Die folgende Abbildung zeigt das effektive Potential (Definition nach Buch 1. bis 3.) als Funktion des Radius bei einer Masse von M=10:Hier wurde das Maple-File verändert 

>	setM:=12: VeffPhotonHobson:=(r,M)->1/r^2*(1-2*M/r); Pot:=plot(VeffPhotonHobson(r,setM),r=22..80): display(Pot,title="Effektives Potential V(r) (Def. nach Ref. 1-3) für Photonen");

 

 

 

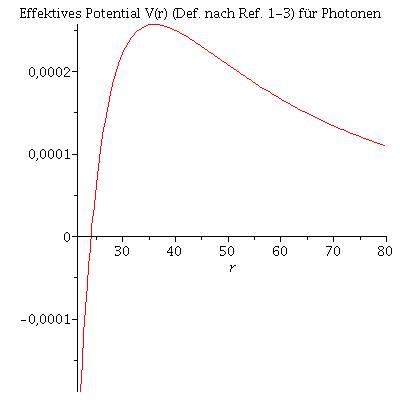Mittels ds²=0 (für Photonen) kann man die folgenden Anfangswerte für eine Photonenkreisbahn berechnen:Hier wurde das Maple-File verändert 

Der Anfangswert für dphi0 wurde hierbei mittels des infinitesimalen Weglängenelements ds²=0 berechnet: 

>	dx:=create([1], array([dt,dr,dtheta,dphi])): ds2:=get_compts(prod(dx,lower(g,dx,1),[1,1])): ds2:=collect( simplify(ds2), [dt,dr,dtheta,dphi]): subs({dr=0,dtheta=0,cos(theta)=0},ds2)=0; dphi=solve(subs({dr=0,dtheta=0,cos(theta)=0},ds2)=0,dphi);

 

 

	(2.2.1)

 

Hier wurde das Maple-File verändert 

>	setM=12: t0:=0: phi0:=0: theta0:=Pi/2: dtheta0:=0: dr0:=0: r0:=solve(diff(VeffPhotonHobson(r,setM),r)=0,r); dphi0:=evalf(sqrt(-r0*(-r0+2*setM))/r0^2); dt0:=1:

 

 

	(2.2.2)

 

 

>	Loes:=dsolve({eq1,eq2,eq4,t(0)=t0,r(0)=r0,D(r)(0)=dr0,D(t)(0)=dt0,phi(0)=phi0,D(phi)(0)=dphi0},{r(lambda),t(lambda),phi(lambda)},type=numeric,output=listprocedure):

 

Animation der Kreisbahn des Photons:Hier wurde das Maple-File verändert 

>

frames:=250: lend:=1000: BH:=display(disk([0,0],2*setM,color=black)): for i from 0 by 1 to frames do Photon[i]:=display(disk([rhs(Loes(i*lend/frames)[4])*cos(rhs(Loes(i*lend/frames)[2])),rhs(Loes(i*lend/frames)[4])*sin(rhs(Loes(i*lend/frames)[2]))],0.5,color=pink)): Ani[i]:=display({Photon[i],BH}); od:

 

>	display([seq(Ani[i],i=0..frames)],insequence=true,scaling=constrained,title="Kreisförmige Bewegung eines Photons bei r=3M");

 

 

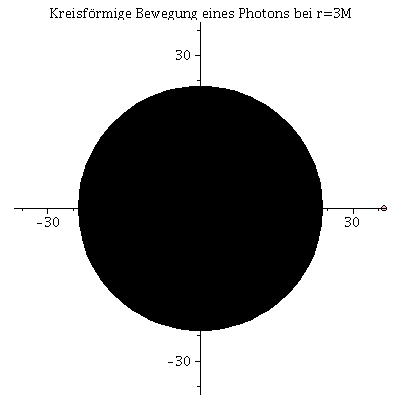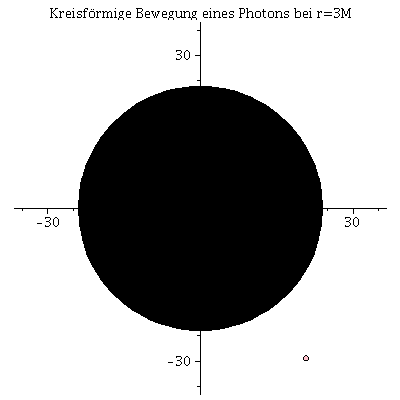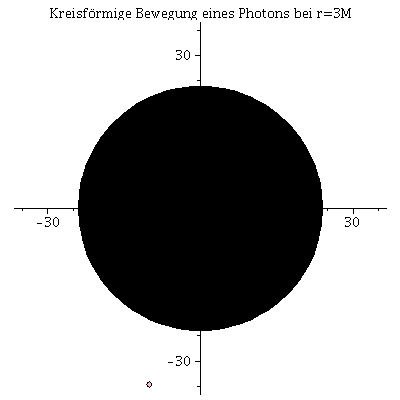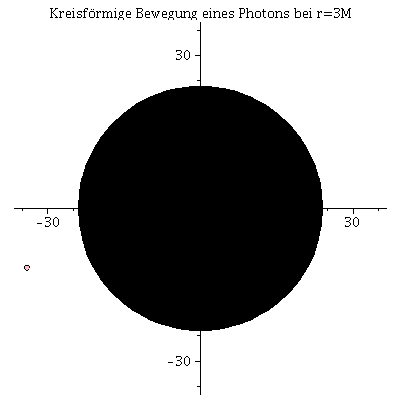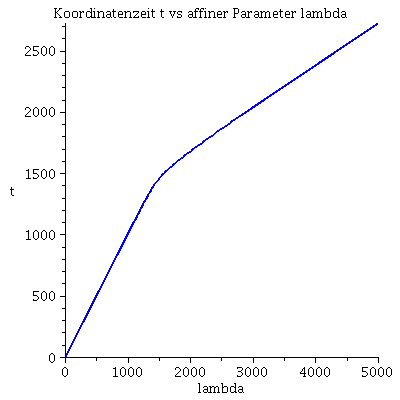
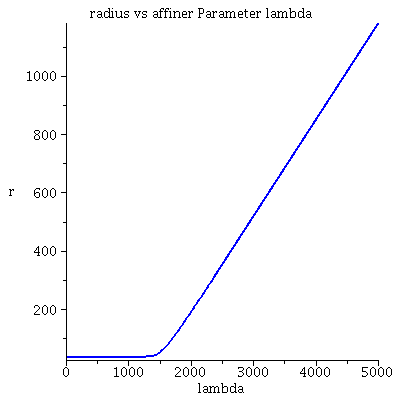
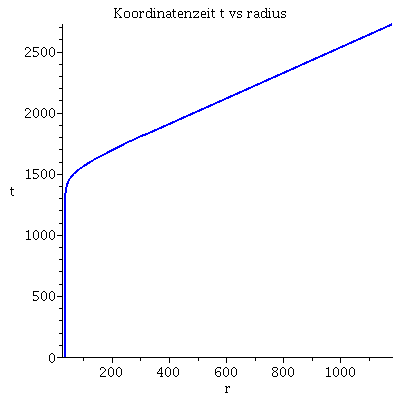
Numerischer Beweis der Instabilität der Lösung:Hier wurde das Maple-File verändert 

>

lend:=5000: Plot1:=odeplot(Loes,[lambda,t(lambda)],0..lend,numpoints=200,color=blue,thickness=2,title="Koordinatenzeit t vs affiner Parameter lambda"): Plot2:=odeplot(Loes,[lambda,r(lambda)],0..lend,numpoints=200,color=blue,thickness=2,title="radius vs affiner Parameter lambda"): Plot3:=odeplot(Loes,[r(lambda),t(lambda)],0..lend,numpoints=700,color=blue,thickness=2,title="Koordinatenzeit t vs radius"): display(Matrix(1,3,[Plot1,Plot2,Plot3]));

 

 

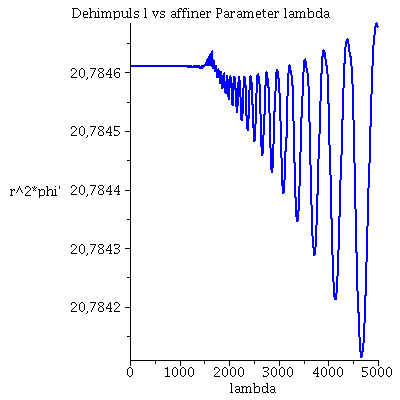
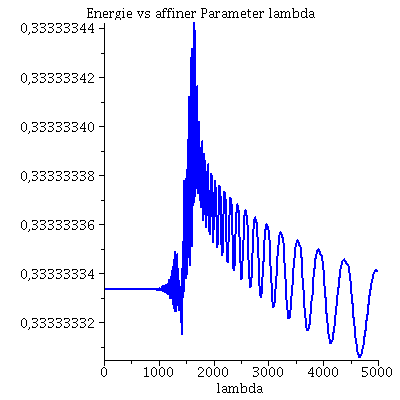
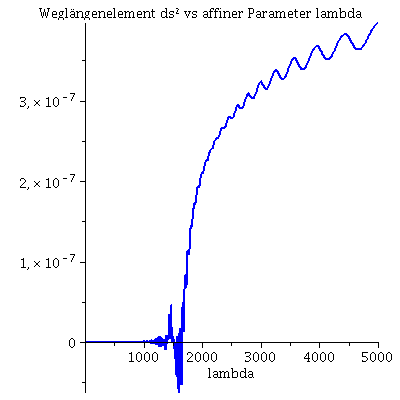
Während der Bewegung erhaltenen Größen (l: Drehimpuls pro Masse m, E: Energie pro Masse und Weglängenelement ds²): Hier wurde das Maple-File verändert 

>

Plot4:=odeplot(Loes,[lambda,r(lambda)^2*diff(phi(lambda), lambda)],0..lend,numpoints=700,color=blue,thickness=2,title="Dehimpuls l vs affiner Parameter lambda"): Plot5:=odeplot(Loes,[lambda,(1-2*setM/r(lambda))*diff(t(lambda), lambda)],0..lend,numpoints=700,color=blue,thickness=2,title="Energie vs affiner Parameter lambda"): Plot6:=odeplot(Loes,[lambda,(1-2*setM/r(lambda))*(diff(t(lambda), lambda))^2 - 1/(1-2*setM/r(lambda))*(diff(r(lambda), lambda))^2 - r(lambda)^2*(diff(phi(lambda), lambda))^2],0..lend,numpoints=700,color=blue,thickness=2,title="Weglängenelement ds² vs affiner Parameter lambda"): display(Matrix(1,3,[Plot4,Plot5,Plot6]));

 

 

 

>