Einführung 

Basierend auf den Ergebnissen der zweiten Vorlesung des ersten Teils wird im folgenden eine Klassifizierung der Umlaufbahnen eines Probekörpers um ein schwarzes Loch vorgestellt und mit den Newtonschen Umlaufbahnen verglichen. 

Bewegung eines Probekörpers um ein schwarzes Loch in der Ebene 

Im folgenden wird die Geodätengleichung in vorgegebener Schwarzschild Raumzeit betrachtet. Die Geodätengleichung beschreibt wie sich ein Probekörper (Masse = 0) im Raum bewegt und sagt voraus, dass diese Bewegung sich stehts entlang der kürzesten Kurve, in der durch die Metrik beschriebenen gekrümmten Raumzeit, vollzieht. 

Die Geodätengleichung und das effektive Potential V(r) 

>	restart: with( tensor ): with(plots): with(plottools):

 

Definition der kovarianten Raumzeit-Metrik eines schwarzen Lochs der Masse M in Schwarzschildkoordinaten: 

>	coord := [t, r, theta, phi]: g_compts := array(symmetric,sparse, 1..4, 1..4): g_compts[1,1] := 1-2*M/r: g_compts[2,2] := -1/g_compts[1,1]: g_compts[3,3] := -r^2:    g_compts[4,4] := -r^2*sin(theta)^2: g := create( [-1,-1], eval(g_compts));

 

(2.1.1)

 

Berechnung der kontravarianten Metrik und der Christoffel Symbole: 

>	ginv := invert( g, 'detg' ): D1g := d1metric( g, coord ):   D2g := d2metric( D1g, coord ): Cf1 := Christoffel1( D1g ): Cf2:= Christoffel2( ginv, Cf1 ):

 

Berechnung der Geodätengleichung als Funktion des affinen Parameters lambda. Die Geodätengleichung ist ein System gekoppelter Differentialgleichungen:   

>	eqns:=geodesic_eqns( coord, lambda, Cf2 );

 

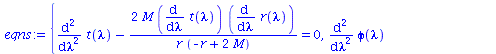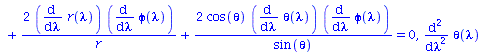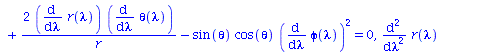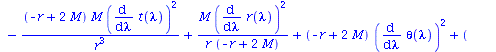(2.1.2)

 

Wir lassen nur ebene Bewegungen zu (theta=Pi/2, dtheta=0) und setzen M=1: 

>

setM:=1: eq1:=subs({r=r(lambda),sin(theta)=1,cos(theta)=0,diff(theta(lambda),lambda)=0,theta=Pi/2,M=setM},eqns[1]): eq2:=subs({r=r(lambda),sin(theta)=1,cos(theta)=0,diff(theta(lambda),lambda)=0,theta=Pi/2,M=setM},eqns[2]): eq3:=subs({r=r(lambda),sin(theta)=1,cos(theta)=0,diff(theta(lambda),lambda)=0,theta=Pi/2,M=setM},eqns[3]): eq4:=subs({r=r(lambda),sin(theta)=1,cos(theta)=0,diff(theta(lambda),lambda)=0,theta=Pi/2,M=setM},eqns[4]): eq1:=subs({r(lambda)(lambda)=r(lambda)},eq1); eq2:=subs({r(lambda)(lambda)=r(lambda)},eq2); eq3:=subs({r(lambda)(lambda)=r(lambda)},eq3); eq4:=subs({r(lambda)(lambda)=r(lambda)},eq4);

 

 

 

 

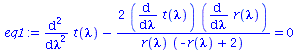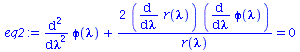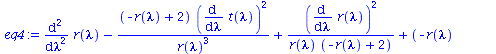	(2.1.3)

 

In Abhängigkeit von den Anfangswerten können unterschiedliche Bahnen der Bewegung entstehen. Wir wählen zunächst als Beispiel die Anfangswerte einer geschlossenen Bahn:  

Zur Zeit t=0 sei der fallende Körper bei einem Radius von r=10=5*(Schwarzschildradius), die Anfangsgeschwindigkeit des Körpers sei in radialer Richtung dr=0 und in phi-Richtung dphi=0.036. Wir beschreiben die Bewegung aus der Sichtweise eines im Unendlichen ruhenden Beobachters. 

>	r0:=10: t0:=0: phi0:=0: theta0:=Pi/2: dr0:=0: dphi0:=0.041: dt0:=evalf(1/sqrt(1-2/r0)*sqrt(1+r0^2*dphi0^2)): dtheta0:=0:

 

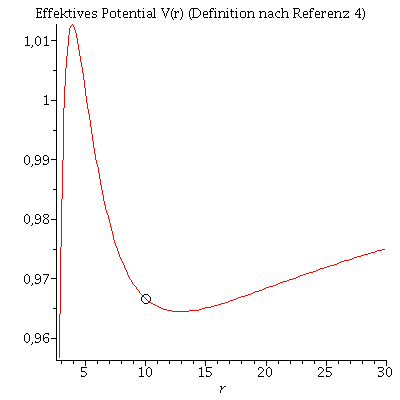
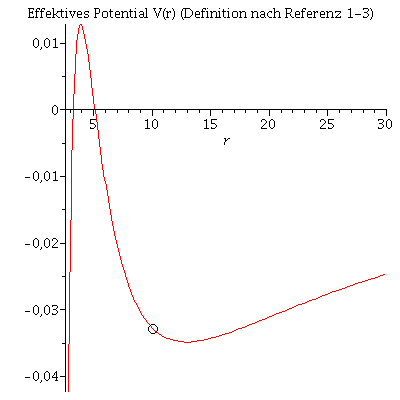
In der Literatur wird die Bewegung eines Probekörpers um ein schwarzes Loch mittels eines definierten, effektiven Potentials illustriert: 

1. General relativity : An introduction for physicists by M. P. Hobson, G. P. Efstathiou and A. N. Lasenby  

2. Gravity : An introduction to Einstein's general relativity by James B. Hartle 

3. Allgemeine Relativitätstheorie by Torsten Fließbach  

4. Relativistic hydrodynamics by Luciano Rezzolla and Olindo Zanotti  

Dieses Potential hängt von dem, bei der Bewegung erhaltenen Drehimpuls pro Masse m ab. Die im Zentralfeld möglichen Bewegungen werden mittels zweier erhaltener Größen (l: Drehimpuls pro Masse m und E: Energie pro Masse) charakteriesiert. Die folgende Abbildung zeigt (in der Nomenklatur des 4.Buches (Diagramm links) bzw. des 1. bis 3. Buches (Diagramm rechts) ) das effektive Potential als Funktion des Radius bei den obigen gewählten Anfangswerten: 

>

setl:=r0^2*dphi0; setE:=dt0*evalf((1-2/r0)); VeffFb:=(r,M,l)->-M/r+l^2/(2*r^2)-M*l^2/r^3; VeffRez:=(r,M,l)->sqrt(1-2*M/r)*sqrt(1+l^2/r^2); Pot:=plot(VeffRez(r,1,setl),r=2.85..30,title="Effektives Potential V(r) (Definition nach Referenz 4)"): Pot1:=plot(VeffFb(r,1,setl),r=2.85..30,title="Effektives Potential V(r) (Definition nach Referenz 1-3)"): B:=pointplot({[r0, VeffRez(r0,1,setl)]}, symbol=circle,symbolsize=20): B1:=pointplot({[r0, VeffFb(r0,1,setl)]}, symbol=circle,symbolsize=20): display(Matrix(1,2,[display(Pot,B),display(Pot1,B1)]));

 

 

 

 

 

 

Numerisches Lösen der Geodätengleichung: 

>	Loes:=dsolve({eq1,eq2,eq4,t(0)=t0,r(0)=r0,D(r)(0)=dr0,D(t)(0)=dt0,phi(0)=phi0,D(phi)(0)=dphi0},{r(lambda),t(lambda),phi(lambda)},type=numeric,output=listprocedure);

 

(2.1.4)

 

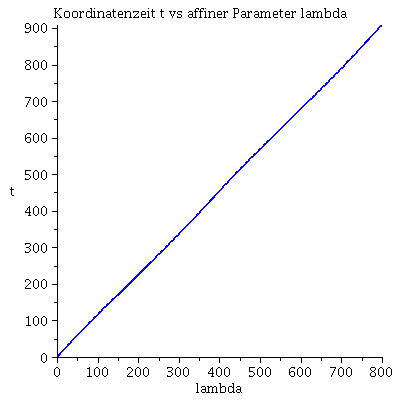
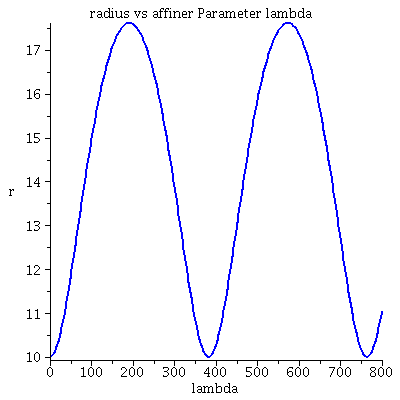
Grafische Veranschaulichung der Lösung: 

>

lend:=800: lendn:=35.12: Plot1:=odeplot(Loes,[lambda,t(lambda)],0..lend,numpoints=200,color=blue,thickness=2,title="Koordinatenzeit t vs affiner Parameter lambda"): Plot2:=odeplot(Loes,[lambda,r(lambda)],0..lend,numpoints=200,color=blue,thickness=2,title="radius vs affiner Parameter lambda"): Plot3:=odeplot(Loes,[r(lambda),t(lambda)],0..lend,numpoints=700,color=blue,thickness=2,title="Koordinatenzeit t vs radius"): display(Matrix(1,3,[Plot1,Plot2,Plot3]));

 

 

>	frames:=300: lend:=600: BH:=display(disk([0,0],2,color=black)): for i from 0 by 1 to frames do Koerper[i]:=display(disk([rhs(Loes(i*lend/frames)[4])*cos(rhs(Loes(i*lend/frames)[2])),rhs(Loes(i*lend/frames)[4])*sin(rhs(Loes(i*lend/frames)[2]))],0.4,color=blue)): Ani[i]:=display({Koerper[i],BH}); od:

 

>	display([seq(Ani[i],i=0..frames)],insequence=true,scaling=constrained);

 

 

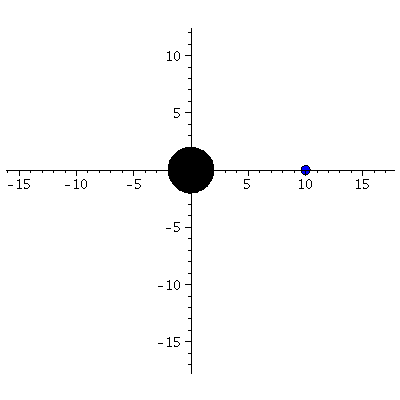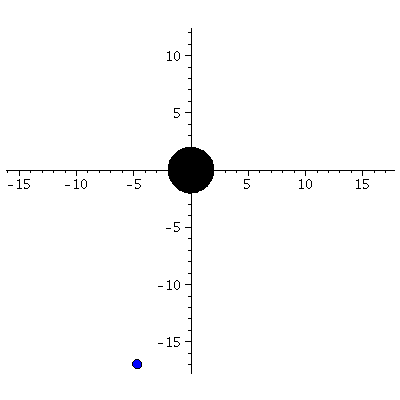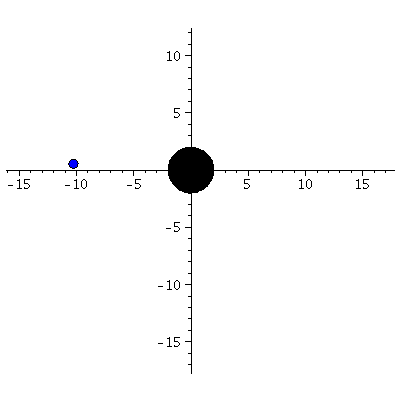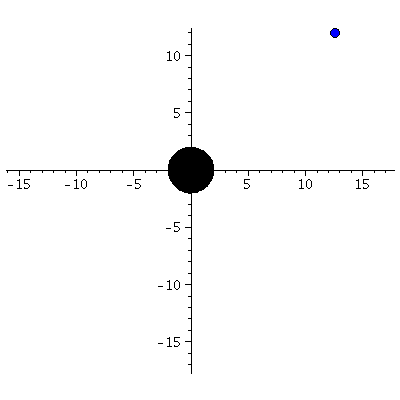Während der Bewegung erhaltenen Größen (l: Drehimpuls pro Masse m, E: Energie pro Masse und Weglängenelement ds²):  

>

Plot4:=odeplot(Loes,[lambda,r(lambda)^2*diff(phi(lambda), lambda)],0..lend,numpoints=700,color=blue,thickness=2,title="Dehimpuls l vs affiner Parameter lambda"): Plot5:=odeplot(Loes,[lambda,(1-2/r(lambda))*diff(t(lambda), lambda)],0..lend,numpoints=700,color=blue,thickness=2,title="Energie vs affiner Parameter lambda"): Plot6:=odeplot(Loes,[lambda,(1-2/r(lambda))*(diff(t(lambda), lambda))^2 - 1/(1-2/r(lambda))*(diff(r(lambda), lambda))^2 - r(lambda)^2*(diff(phi(lambda), lambda))^2],0..lend,numpoints=700,color=blue,thickness=2,title="Weglängenelement ds2 vs affiner Parameter lambda"): display(Matrix(1,3,[Plot4,Plot5,Plot6]));

 

 

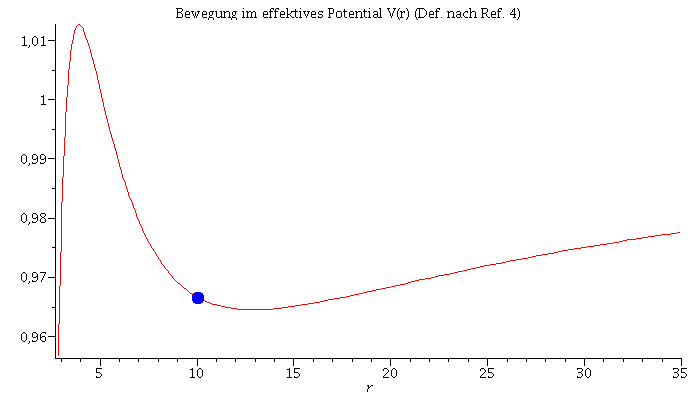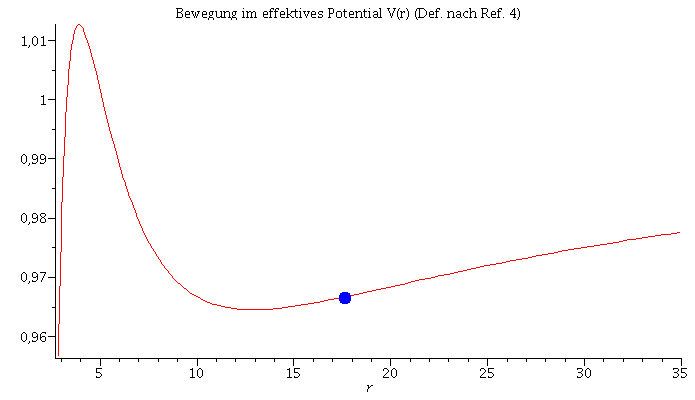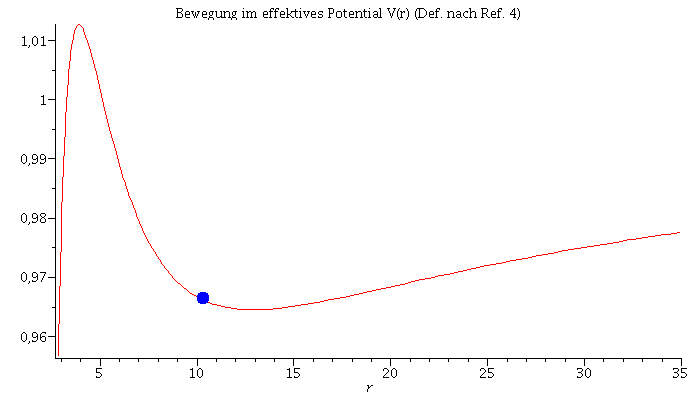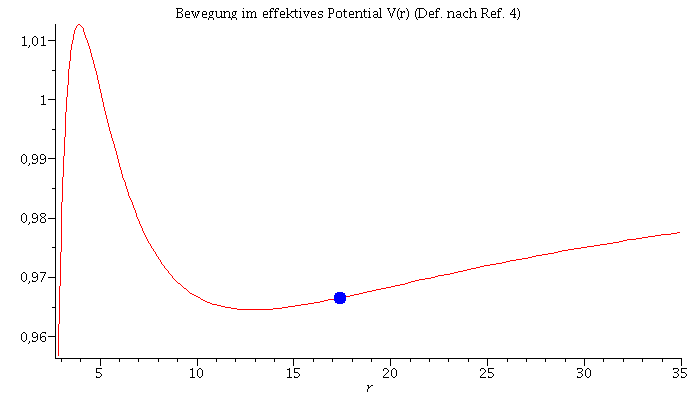
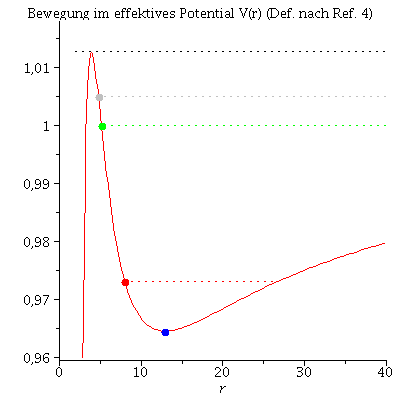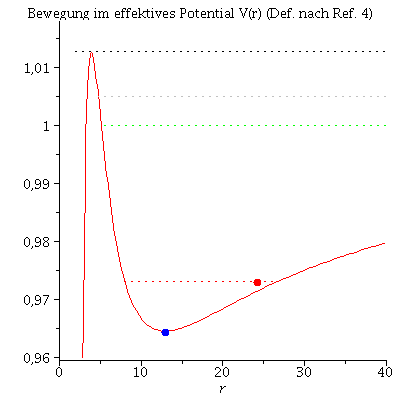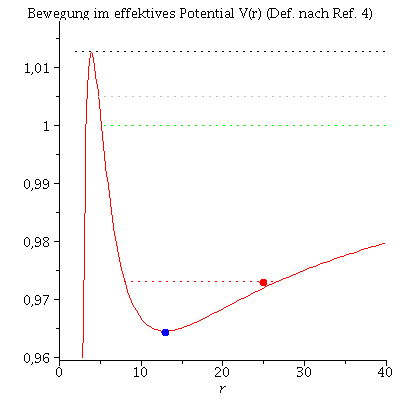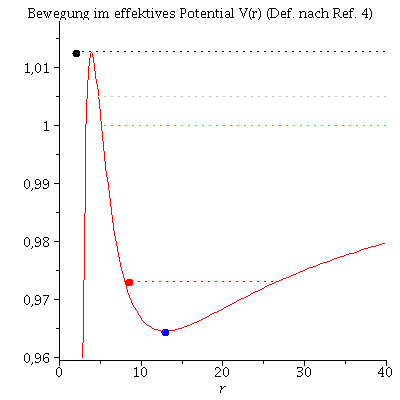
Animation der Bewegung im effektiven Potential: 

>	frames:=300: lend:=600: Pot:=plot(VeffRez(r,1,setl),r=2.85..35): for i from 0 by 1 to frames do Koerper[i]:=pointplot({[rhs(Loes(i*lend/frames)[4]), setE]}, symbol=solidcircle,symbolsize=20,color=blue): Ani1[i]:=display({Pot,Koerper[i]}); od:

 

>	display([seq(Ani1[i],i=0..frames)],insequence=true):

 

>	Animat1:=display([seq(Ani[i],i=0..frames)],insequence=true,scaling=constrained): Animat2:=display([seq(Ani1[i],i=0..frames)],insequence=true,title="Bewegung im effektives Potential V(r) (Def. nach Ref. 4)"): display(Array([Animat1,Animat2]));

 

 

>

 

Klassifizierung unterschiedlicher Bahnbewegungen 

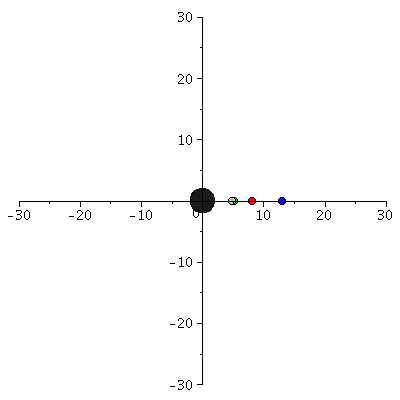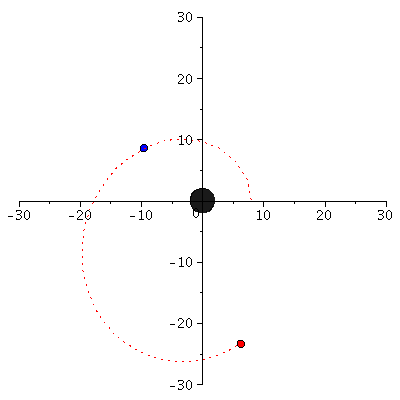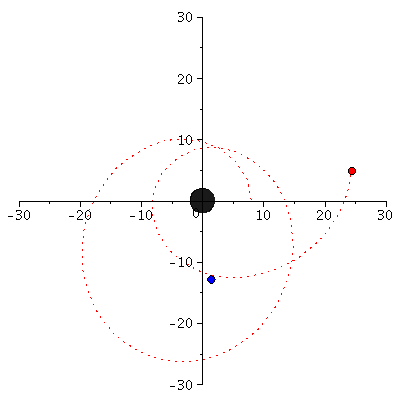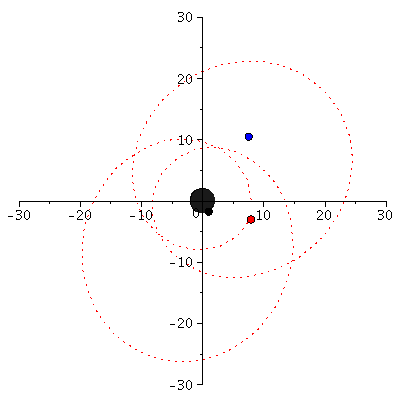
Im folgenden werden die unterschiedlichen Bahnbewegungen um ein schwarzes Loch klassifiziert. Neben den gebundenen kreisförmigen (A: blau) und eliptischen (B: rot) Bahnen, den parabolischen (C: grün) und hyperbolischen (D: grau) Bahnverläufen ist auch eine durch das schwarze Loch eingefangene Bahn (E: capture orbit, schwarz) möglich. Wir setzen M=1 und l=4.1. 

>

t0:=0: phi0:=0: theta0:=Pi/2: dtheta0:=0: dr0:=0: setl:=4.1: r0A:=subs({M=1,l=setl},solve(simplify(diff(VeffRez(r,M,l),r)=0),r)[1]): dphi0A:=setl/r0A^2: dt0A:=evalf(1/sqrt(1-2/r0A)*sqrt(1+r0A^2*dphi0A^2)): setEA:=dt0A*evalf((1-2/r0A)); r0B:=8: dphi0B:=setl/r0B^2: dt0B:=evalf(1/sqrt(1-2/r0B)*sqrt(1+r0B^2*dphi0B^2)): setEB:=dt0B*evalf((1-2/r0B)); setEC:=limit(VeffRez(r,1,setl),r=infinity); r0C:=solve(VeffRez(r,1,setl)=setEC,r)[1]: dphi0C:=setl/r0C^2: dt0C:=evalf(1/sqrt(1-2/r0C)*sqrt(1+r0C^2*dphi0C^2)): setED:=1.005; r0D:=solve(VeffRez(r,1,setl)=setED,r)[2]: dphi0D:=setl/r0D^2: dt0D:=evalf(1/sqrt(1-2/r0D)*sqrt(1+r0D^2*dphi0D^2)): setEE:=1.01273; r0E:=220: dphi0E:=setl/r0E^2: dr0E:=solve(subs({M=1,l=4.1,E=setEE,r=r0E},g_compts[1,1]*(E/g_compts[1,1])^2-1/g_compts[1,1]*x^2-r^2*(l/r^2)^2=1),x)[1]; dt0E:=1/(1-2/r0E)*setEE: Pot:=plot(VeffRez(r,1,setl),r=2.85..52,view=[2.85..52,0.955..1.02]): PlotEA:=pointplot({[r0A, VeffRez(r0A,1,setl)]}, symbol=solidcircle,symbolsize=20,color=blue): PlotEB:=pointplot({[r0B, VeffRez(r0B,1,setl)]}, symbol=solidcircle,symbolsize=20,color=red): PlotEC:=pointplot({[r0C, VeffRez(r0C,1,setl)]}, symbol=solidcircle,symbolsize=20,color=green): PlotED:=pointplot({[r0D, VeffRez(r0D,1,setl)]}, symbol=solidcircle,symbolsize=20,color=grey): PlotEE:=pointplot({[r0E, setEE]}, symbol=solidcircle,symbolsize=20,color=black): display(Pot,PlotEA,PlotEB,PlotEC,PlotED,PlotED,PlotEE):

 

 

 

 

 

 

	(2.2.1)

 

>

LoesA:=dsolve({eq1,eq2,eq4,t(0)=t0,r(0)=r0A,D(r)(0)=dr0,D(t)(0)=dt0A,phi(0)=phi0,D(phi)(0)=dphi0A},{r(lambda),t(lambda),phi(lambda)},type=numeric,output=listprocedure): LoesB:=dsolve({eq1,eq2,eq4,t(0)=t0,r(0)=r0B,D(r)(0)=dr0,D(t)(0)=dt0B,phi(0)=phi0,D(phi)(0)=dphi0B},{r(lambda),t(lambda),phi(lambda)},type=numeric,output=listprocedure): LoesC:=dsolve({eq1,eq2,eq4,t(0)=t0,r(0)=r0C,D(r)(0)=dr0,D(t)(0)=dt0C,phi(0)=phi0,D(phi)(0)=dphi0C},{r(lambda),t(lambda),phi(lambda)},type=numeric,output=listprocedure): LoesD:=dsolve({eq1,eq2,eq4,t(0)=t0,r(0)=r0D,D(r)(0)=dr0,D(t)(0)=dt0D,phi(0)=phi0,D(phi)(0)=dphi0D},{r(lambda),t(lambda),phi(lambda)},type=numeric,output=listprocedure): LoesE:=dsolve({eq1,eq2,eq4,t(0)=t0,r(0)=r0E,D(r)(0)=dr0E,D(t)(0)=dt0E,phi(0)=0,D(phi)(0)=dphi0E},{r(lambda),t(lambda),phi(lambda)},type=numeric,output=listprocedure):

 

Animation der Bewegungen im effektiven Potential: 

>

frames:=150: lend:=1058.812: BH:=display(disk([0,0],2,color=black,transparency=0.1)): Pot:=plot(VeffRez(r,1,setl),r=0..40,view=[0..40,0.96..1.018]): PotBline:=plot({[rhs(LoesB(0)[4]), setEB],[solve(VeffRez(r,1,setl)=setEB,r)[1], setEB]},color=red,linestyle=dot): PotCline:=plot({[rhs(LoesC(0)[4]), setEC],[40, setEC]},color=green,linestyle=dot): PotDline:=plot({[rhs(LoesD(0)[4]), setED],[40, setED]},color=grey,linestyle=dot): PotEline:=plot({[2, setEE],[40, setEE]},color=black,linestyle=dot): for i from 0 by 1 to frames do KoerperA[i]:=display(disk([rhs(LoesA(i*lend/frames)[4])*cos(rhs(LoesA(i*lend/frames)[2])),rhs(LoesA(i*lend/frames)[4])*sin(rhs(LoesA(i*lend/frames)[2]))],0.6,color=blue)): KoerperB[i]:=display(disk([rhs(LoesB(i*lend/frames)[4])*cos(rhs(LoesB(i*lend/frames)[2])),rhs(LoesB(i*lend/frames)[4])*sin(rhs(LoesB(i*lend/frames)[2]))],0.6,color=red)): KoerperC[i]:=display(disk([rhs(LoesC(i*lend/frames)[4])*cos(rhs(LoesC(i*lend/frames)[2])),rhs(LoesC(i*lend/frames)[4])*sin(rhs(LoesC(i*lend/frames)[2]))],0.6,color=green)): KoerperD[i]:=display(disk([rhs(LoesD(i*lend/frames)[4])*cos(rhs(LoesD(i*lend/frames)[2])),rhs(LoesD(i*lend/frames)[4])*sin(rhs(LoesD(i*lend/frames)[2]))],0.6,color=grey)): KoerperE[i]:=display(disk([rhs(LoesE(i*lend/frames)[4])*cos(rhs(LoesE(i*lend/frames)[2])),rhs(LoesE(i*lend/frames)[4])*sin(rhs(LoesE(i*lend/frames)[2]))],0.6,color=black)): TrajB[i]:=listplot([seq([rhs(LoesB(j*lend/frames)[4])*cos(rhs(LoesB(j*lend/frames)[2])),rhs(LoesB(j*lend/frames)[4])*sin(rhs(LoesB(j*lend/frames)[2]))], j = 0 .. i)],color=red,linestyle=dot): Ani[i]:=display({KoerperA[i],KoerperB[i],KoerperC[i],KoerperD[i],KoerperE[i],TrajB[i],BH}); PotA[i]:=pointplot({[rhs(LoesA(i*lend/frames)[4]), setEA]}, symbol=solidcircle,symbolsize=18,color=blue): PotB[i]:=pointplot({[rhs(LoesB(i*lend/frames)[4]), setEB]}, symbol=solidcircle,symbolsize=18,color=red): PotC[i]:=pointplot({[rhs(LoesC(i*lend/frames)[4]), setEC]}, symbol=solidcircle,symbolsize=18,color=green): PotD[i]:=pointplot({[rhs(LoesD(i*lend/frames)[4]), setED]}, symbol=solidcircle,symbolsize=18,color=grey): PotE[i]:=pointplot({[rhs(LoesE(i*lend/frames)[4]), setEE]}, symbol=solidcircle,symbolsize=18,color=black): Ani1[i]:=display({Pot,PotA[i],PotB[i],PotC[i],PotD[i],PotE[i],PotBline,PotCline,PotDline,PotEline}); od:

 

>	Animat:=display([seq(Ani[i],i=0..frames)],insequence=true,scaling=constrained,view=[-30..30,-30..30]): Animat1:=display([seq(Ani1[i],i=0..frames)],insequence=true,title="Bewegung im effektives Potential V(r) (Def. nach Ref. 4)"): display(Array([Animat,Animat1]));

 

 

>

 

>

 

Die innerste stabile kreisförmige Bahnbewegung (Innermost Stable Circular Orbit (ISCO)) eines Probekörpers 

In der vorigen Animation der unterschiedlichen Bahnbewegungen wurde der Drehimpuls l fest auf den Wert 4.1 und die Masse des schwarzen Lochs auf 1 festgelegt. Das effektive Potential V(r,M,l) war somit nur noch von r abhängig. Die folgende Animation zeigt wie sich die Form des effektiven Potentials bei Variation des Parameters l von l=6 bis l=1 verändert. 

>	animate(VeffFb(r,1,l),r=0..30,l=2..6,view=-0.6..0.5,title="Effektives Potential V(r) (Referenz 1-3), l=[2,6]",numpoints=500);

 

 

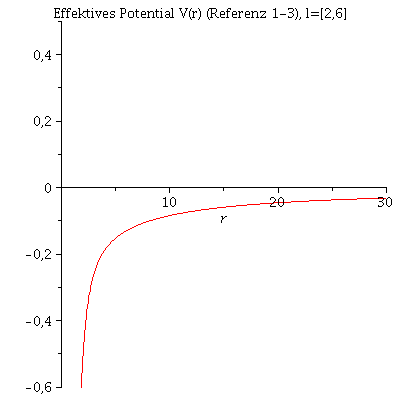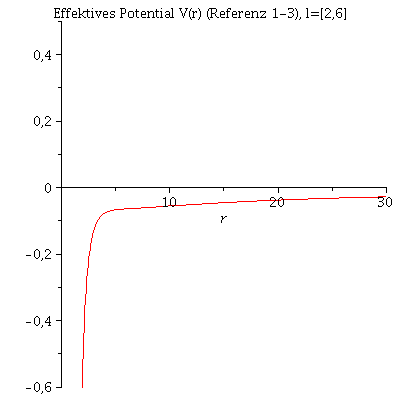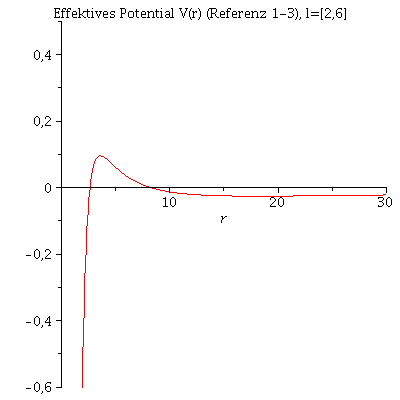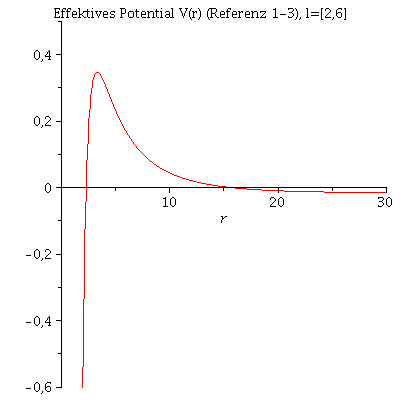>	animate(VeffRez(r,1,l),r=0..30,l=2..6,view=0.6..1.4,title="Effektives Potential V(r) (Referenz 4), l=[2,6]",numpoints=500);

 

 

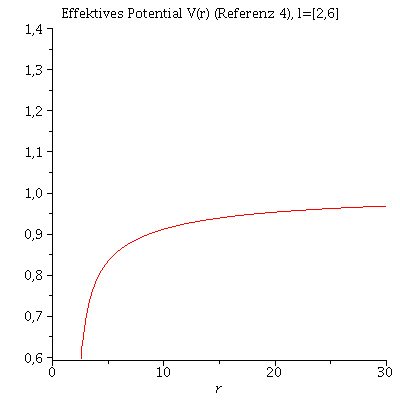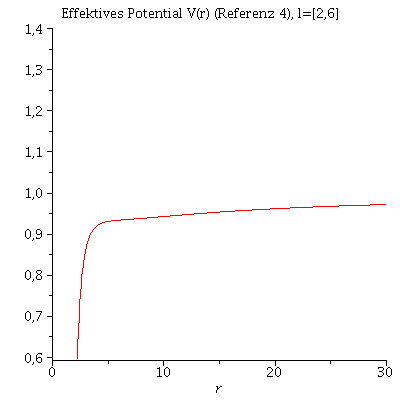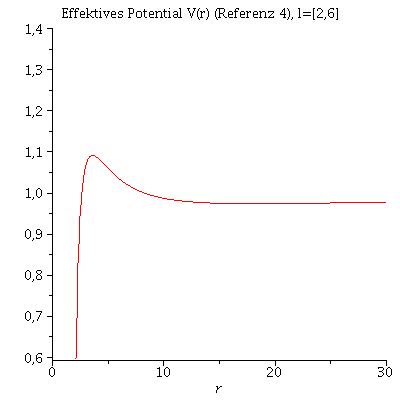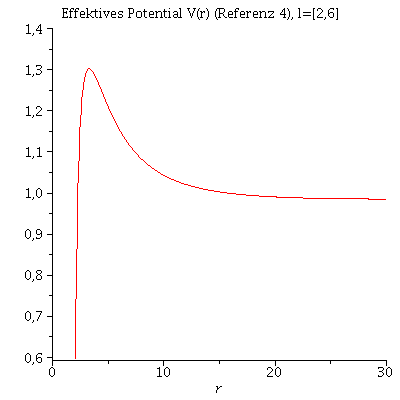Ist der Wert des Drehimpulses l oberhalb einer gewissen Grenze, so sind stabile Bahnen möglich, da ein Minimum im Potential vorhanden ist. Kreisförmige Bahnbewegungen sind dadurch charakterisiert, dass der Wert des Radiuses sich im laufe der Zeit nicht verändert und somit sich der radiale Abstand des Probekörpers vom schwarzen Loch gerade im Minimum des effektiven Potentials befindet. Es muss somit gelten: 

>	Diff(V(r,M,l),r)=0; ExtremaV:=diff(VeffFb(r,M,l),r)=0;

 

 

	(2.3.1)

 

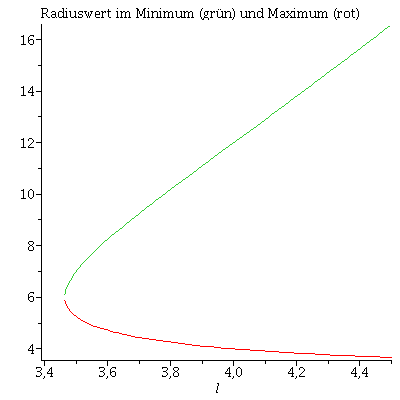
Lösen wir diese Gleichung nach r auf, so erhalten wir die folgenden Lösungen, wobei der erste Wert dem Minimum und der zweite dem Maximum entspricht: 

>	rextr:=solve(ExtremaV,r);

 

(2.3.2)

 

Darstellen des Radiuswertes im Minimum (grün) und Maximum (rot) des effektiven Potentials 

>	plot({subs(M=1,rextr[1]),subs(M=1,rextr[2])},l=3.4..4.5,title="Radiuswert im Minimum (grün) und Maximum (rot)");

 

 

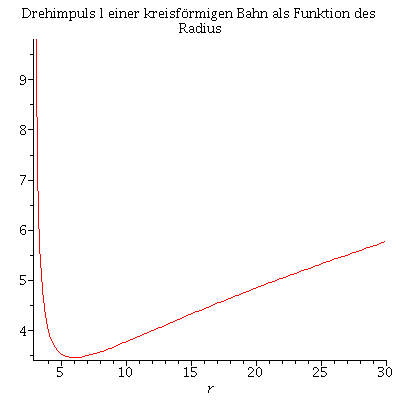
Der Drehimpuls l für eine kreisförmige Bahnbewegung ergibt sich duch Auflösen von V'=0 nach l: 

>	lextr:=solve(ExtremaV,l);

 

(2.3.3)

 

Die beiden Lösungen entsprechen rechts und links rotierenden Probekörpern; Darstellung einer Lösung: 

>	plot(subs(M=1,lextr[2]),r=3.1..30,title="Drehimpuls l einer kreisförmigen Bahn als Funktion des Radius");

 

 

Die innerste stabile Kreisbahn hat die Eigenschaft: V'=0 und V''=0. 

>	ExtremaV2:=diff(VeffFb(r,M,l),r,r)=0; lISCO:=solve(simplify(subs(r=rextr[1],ExtremaV2)),l); rISCO:=solve(simplify(subs(l=lextr[2],ExtremaV2)),r);

 

 

 

	(2.3.4)

 

 

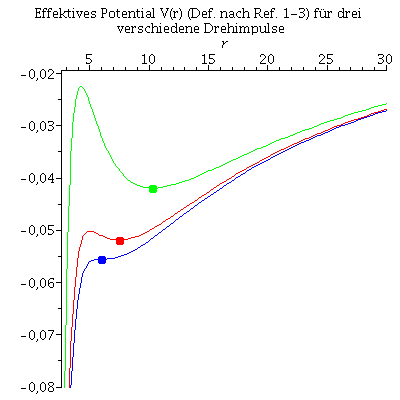
Definition der Anfangswerte der innersten stabilen Kreisbahn und zweier weiterer stabilen kreisförmigen Bahnbewegungen. 

>

setM=1: t0:=0: phi0:=0: theta0:=Pi/2: dtheta0:=0: dr0:=0: setlA:=2*sqrt(3)*setM; r0A:=subs({M=1,l=setlA},solve(simplify(diff(VeffFb(r,M,l),r)=0),r)[1]); dphi0A:=setlA/r0A^2: dt0A:=evalf(1/sqrt(1-2/r0A)*sqrt(1+r0A^2*dphi0A^2)): setEA:=dt0A*evalf((1-2/r0A)); print("------------------------------------------"); setlB:=1.02*setlA; r0B:=evalf(subs({M=1,l=setlB},solve(simplify(diff(VeffFb(r,M,l),r)=0),r)[1])); dphi0B:=setlB/r0B^2: dt0B:=evalf(1/sqrt(1-2/r0B)*sqrt(1+r0B^2*dphi0B^2)): setEB:=dt0B*evalf((1-2/r0B)); print("------------------------------------------"); setlC:=1.10*setlA; r0C:=evalf(subs({M=1,l=setlC},solve(simplify(diff(VeffFb(r,M,l),r)=0),r)[1])); dphi0C:=setlC/r0C^2: dt0C:=evalf(1/sqrt(1-2/r0C)*sqrt(1+r0C^2*dphi0C^2)): setEC:=dt0C*evalf((1-2/r0C));

 

 

 

 

 

 

 

 

 

 

 

	(2.3.5)

 

Struktur des effektiven Potentials der innersten stabilen Kreisbahn (blauer Kurve) und zweier weiterer stabilen kreisförmigen Bahnbewegungen. 

>

PotA:=plot(VeffFb(r,1,setlA),r=2.85..52,view=[2.85..30,-0.08..-0.02],color=blue): PotB:=plot(VeffFb(r,1,setlB),r=2.85..52,view=[2.85..30,-0.08..-0.02],color=red): PotC:=plot(VeffFb(r,1,setlC),r=2.85..52,view=[2.85..30,-0.08..-0.02],color=green): PlotEA:=pointplot({[r0A, VeffFb(r0A,1,setlA)]}, symbol=solidcircle,symbolsize=20,color=blue): PlotEB:=pointplot({[r0B, VeffFb(r0B,1,setlB)]}, symbol=solidcircle,symbolsize=20,color=red): PlotEC:=pointplot({[r0C, VeffFb(r0C,1,setlC)]}, symbol=solidcircle,symbolsize=20,color=green): display(PotA,PotB,PotC,PlotEA,PlotEB,PlotEC,title="Effektives Potential V(r) (Def. nach Ref. 1-3) für drei verschiedene Drehimpulse");

 

 

Numerische Lösung der drei Bahnbewegungen: 

>

LoesA:=dsolve({eq1,eq2,eq4,t(0)=t0,r(0)=r0A,D(r)(0)=dr0,D(t)(0)=dt0A,phi(0)=phi0,D(phi)(0)=dphi0A},{r(lambda),t(lambda),phi(lambda)},type=numeric,output=listprocedure): LoesB:=dsolve({eq1,eq2,eq4,t(0)=t0,r(0)=r0B,D(r)(0)=dr0,D(t)(0)=dt0B,phi(0)=phi0,D(phi)(0)=dphi0B},{r(lambda),t(lambda),phi(lambda)},type=numeric,output=listprocedure): LoesC:=dsolve({eq1,eq2,eq4,t(0)=t0,r(0)=r0C,D(r)(0)=dr0,D(t)(0)=dt0C,phi(0)=phi0,D(phi)(0)=dphi0C},{r(lambda),t(lambda),phi(lambda)},type=numeric,output=listprocedure):

 

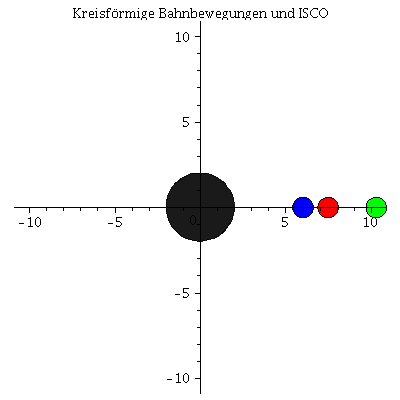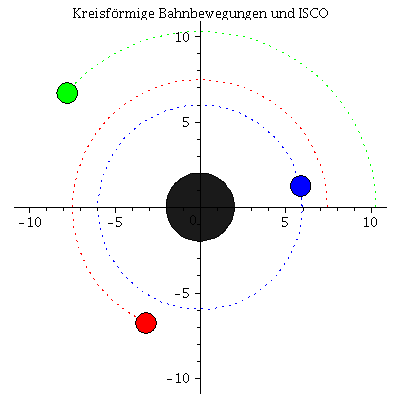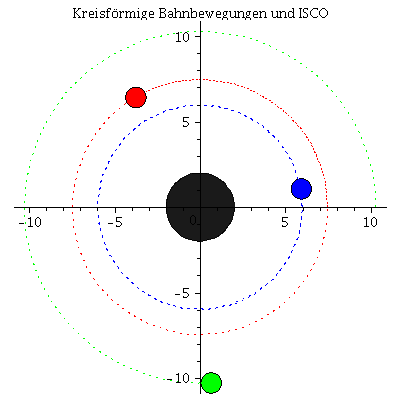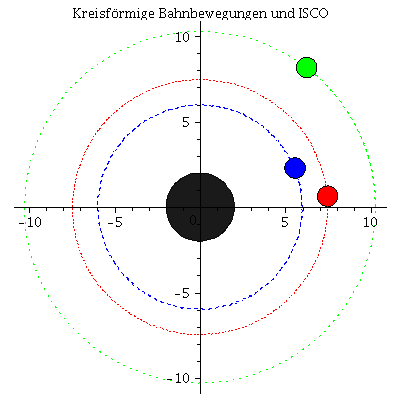
Animation der Bewegungen: Der ISCO ist die blaue Kurve 

>

frames:=80: lend:=200: BH:=display(disk([0,0],2,color=black,transparency=0.1)): for i from 0 by 1 to frames do KoerperA[i]:=display(disk([rhs(LoesA(i*lend/frames)[4])*cos(rhs(LoesA(i*lend/frames)[2])),rhs(LoesA(i*lend/frames)[4])*sin(rhs(LoesA(i*lend/frames)[2]))],0.6,color=blue)): KoerperB[i]:=display(disk([rhs(LoesB(i*lend/frames)[4])*cos(rhs(LoesB(i*lend/frames)[2])),rhs(LoesB(i*lend/frames)[4])*sin(rhs(LoesB(i*lend/frames)[2]))],0.6,color=red)): KoerperC[i]:=display(disk([rhs(LoesC(i*lend/frames)[4])*cos(rhs(LoesC(i*lend/frames)[2])),rhs(LoesC(i*lend/frames)[4])*sin(rhs(LoesC(i*lend/frames)[2]))],0.6,color=green)): TrajA[i]:=listplot([seq([rhs(LoesA(j*lend/frames)[4])*cos(rhs(LoesA(j*lend/frames)[2])),rhs(LoesA(j*lend/frames)[4])*sin(rhs(LoesA(j*lend/frames)[2]))], j = 0 .. i)],color=blue,linestyle=dot): TrajB[i]:=listplot([seq([rhs(LoesB(j*lend/frames)[4])*cos(rhs(LoesB(j*lend/frames)[2])),rhs(LoesB(j*lend/frames)[4])*sin(rhs(LoesB(j*lend/frames)[2]))], j = 0 .. i)],color=red,linestyle=dot): TrajC[i]:=listplot([seq([rhs(LoesC(j*lend/frames)[4])*cos(rhs(LoesC(j*lend/frames)[2])),rhs(LoesC(j*lend/frames)[4])*sin(rhs(LoesC(j*lend/frames)[2]))], j = 0 .. i)],color=green,linestyle=dot): Ani[i]:=display({KoerperA[i],KoerperB[i],KoerperC[i],TrajA[i],TrajB[i],TrajC[i],BH}); od:

 

>	display([seq(Ani[i],i=0..frames)],insequence=true,scaling=constrained,title="Kreisförmige Bahnbewegungen und ISCO");

 

 

 

>

 

Bewegung von Licht (Photonen) um ein schwarzes Loch in der Ebene (Die Photonensphäre) 

In der Literatur wird die Bewegung von Licht um ein schwarzes Loch mittels eines definierten, effektiven Potentials illustriert: 

1. General relativity : An introduction for physicists by M. P. Hobson, G. P. Efstathiou and A. N. Lasenby  

2. Gravity : An introduction to Einstein's general relativity by James B. Hartle 

3. Allgemeine Relativitätstheorie by Torsten Fließbach  

4. Relativistic hydrodynamics by Luciano Rezzolla and Olindo Zanotti  

Dieses Potential hängt allein von der Masse des schwarzen Lochs ab. Die folgende Abbildung zeigt das effektive Potential (Definition nach Buch 1. bis 3.) als Funktion des Radius bei einer Masse von M=1: 

>	setM=1: VeffPhotonHobson:=(r,M)->1/r^2*(1-2*M/r); Pot:=plot(VeffPhotonHobson(r,setM),r=1.8..10): display(Pot,title="Effektives Potential V(r) (Def. nach Ref. 1-3) für Photonen");

 

 

 

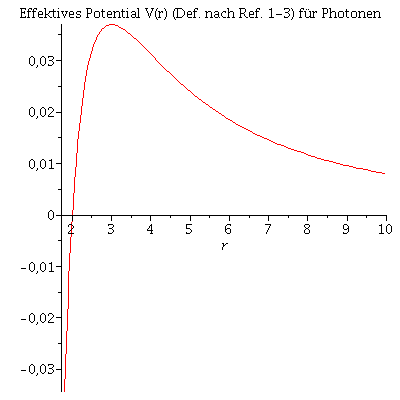Mittels ds²=0 (für Photonen) kann man die folgenden Anfangswerte für eine Photonenkreisbahn bei r=3 berechnen: 

>	setM=1: t0:=0: phi0:=0: theta0:=Pi/2: dtheta0:=0: dr0:=0: r0:=3: dphi0:=(1/9)*sqrt(3): dt0:=1:

 

Der Anfangswert für dphi0 wurde hierbei mittels des infinitesimalen Weglängenelements ds²=0 berechnet: 

>	dx:=create([1], array([dt,dr,dtheta,dphi])): ds2:=get_compts(prod(dx,lower(g,dx,1),[1,1])): ds2:=collect( simplify(ds2), [dt,dr,dtheta,dphi]): subs({dr=0,dtheta=0,cos(theta)=0},ds2)=0; dphi=solve(subs({dr=0,dtheta=0,cos(theta)=0,M=setM,r=r0},ds2)=0,dphi);

 

 

	(2.4.1)

 

>	Loes:=dsolve({eq1,eq2,eq4,t(0)=t0,r(0)=r0,D(r)(0)=dr0,D(t)(0)=dt0,phi(0)=phi0,D(phi)(0)=dphi0},{r(lambda),t(lambda),phi(lambda)},type=numeric,output=listprocedure):

 

Animation der Kreisbahn des Photons: 

>	frames:=250: lend:=200: BH:=display(disk([0,0],2,color=black)): for i from 0 by 1 to frames do Photon[i]:=display(disk([rhs(Loes(i*lend/frames)[4])*cos(rhs(Loes(i*lend/frames)[2])),rhs(Loes(i*lend/frames)[4])*sin(rhs(Loes(i*lend/frames)[2]))],0.1,color=pink)): Ani[i]:=display({Photon[i],BH}); od:

 

>	display([seq(Ani[i],i=0..frames)],insequence=true,scaling=constrained,title="Kreisförmige Bewegung eines Photons bei r=3M");

 

 

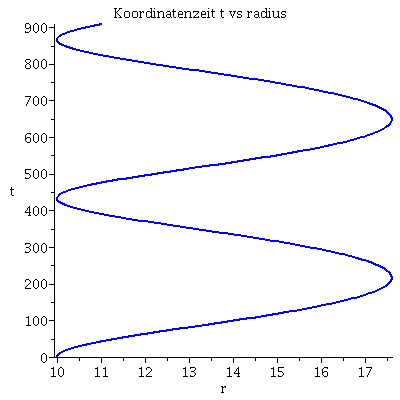
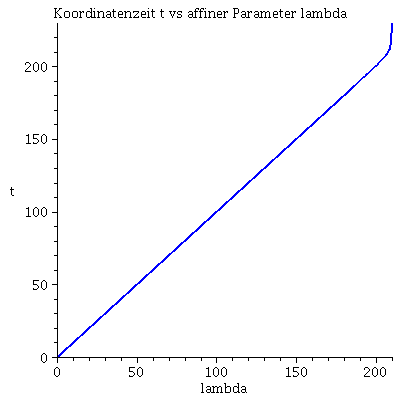
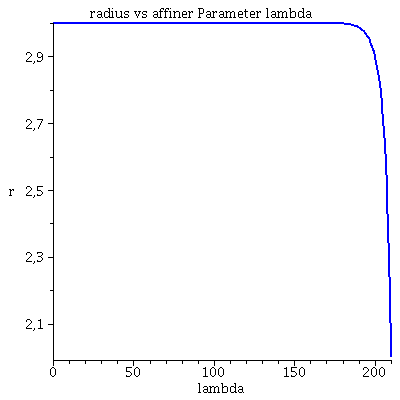
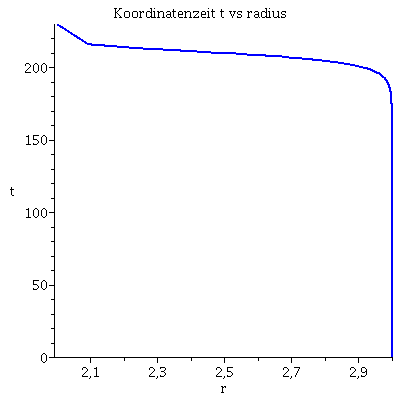
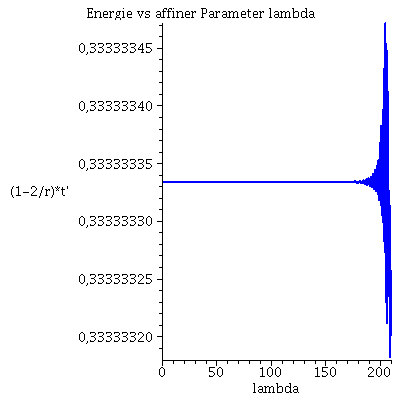
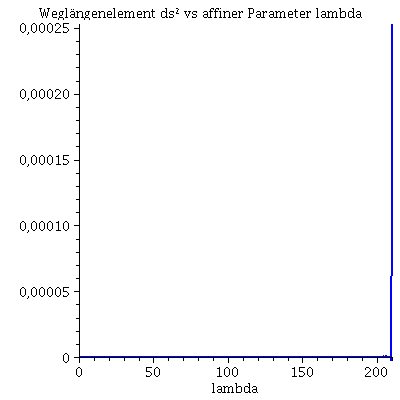
Numerischer Beweis der Instabilität der Lösung: 

>

lend:=210.098: Plot1:=odeplot(Loes,[lambda,t(lambda)],0..lend,numpoints=200,color=blue,thickness=2,title="Koordinatenzeit t vs affiner Parameter lambda"): Plot2:=odeplot(Loes,[lambda,r(lambda)],0..lend,numpoints=200,color=blue,thickness=2,title="radius vs affiner Parameter lambda"): Plot3:=odeplot(Loes,[r(lambda),t(lambda)],0..lend,numpoints=700,color=blue,thickness=2,title="Koordinatenzeit t vs radius"): display(Matrix(1,3,[Plot1,Plot2,Plot3]));

 

 

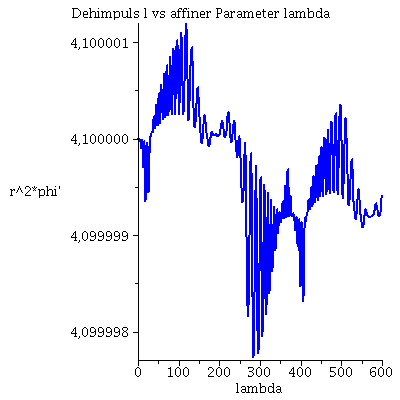
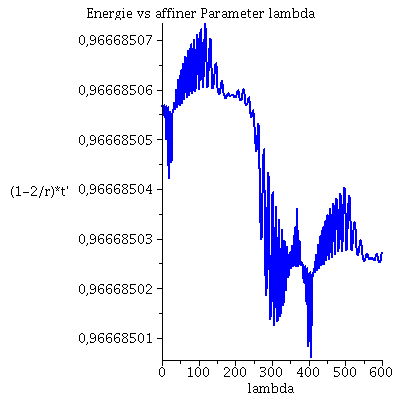
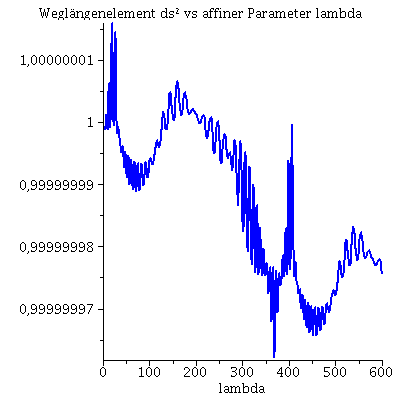
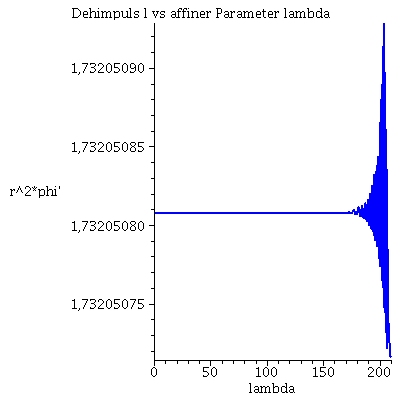
Während der Bewegung erhaltenen Größen (l: Drehimpuls pro Masse m, E: Energie pro Masse und Weglängenelement ds²):  

>

Plot4:=odeplot(Loes,[lambda,r(lambda)^2*diff(phi(lambda), lambda)],0..lend,numpoints=700,color=blue,thickness=2,title="Dehimpuls l vs affiner Parameter lambda"): Plot5:=odeplot(Loes,[lambda,(1-2/r(lambda))*diff(t(lambda), lambda)],0..lend,numpoints=700,color=blue,thickness=2,title="Energie vs affiner Parameter lambda"): Plot6:=odeplot(Loes,[lambda,(1-2/r(lambda))*(diff(t(lambda), lambda))^2 - 1/(1-2/r(lambda))*(diff(r(lambda), lambda))^2 - r(lambda)^2*(diff(phi(lambda), lambda))^2],0..lend,numpoints=700,color=blue,thickness=2,title="Weglängenelement ds2 vs affiner Parameter lambda"): display(Matrix(1,3,[Plot4,Plot5,Plot6]));

 

 

 

>