Download Maple Worksheed
Allgemeine Relativitätstheorie mit dem Computer
General Theory of Relativity on the Computer
Vorlesung gehalten an der J.W.Goethe-Universität in Frankfurt am Main (Sommersemester 2016)
von Dr.phil.nat. Dr.rer.pol. Matthias Hanauske
Frankfurt am Main 11.04.2016
Erster Vorlesungsteil: Allgemeine Relativitätstheorie mit Maple
1. Vorlesung
Einführung
In dieser Vorlesung werden die mathematisch anspruchsvollen Gleichungen der Allgemeinen Relativitätstheorie (ART) in diversen Programmierumgebungen analysiert. Im ersten Teil des Kurses erlernen die Studierenden die Verwendung von Computeralgebra-Systemen (Maple und Mathematica). Die oft komplizierten und zeitaufwendigen Berechnungen der tensoriellen Gleichungen der ART können mit Hilfe dieser Programme erleichtert werden. Diverse Anwendungen der Einstein- und Geodätengleichung werden in Maple implementiert, quasi analytische Berechnungen durchgeführt und entsprechende Lösungen berechnet und visualisiert. Der zweite Teil des Kurses befaßt sich mit der numerischen Berechnung von Neutronensternen und Weißen Zwergen mittels eines C/C++ Programms. Nach einer kurzen Auffrischung der grundlegenden Programmierkenntnisse, erstellen die Studierenden, gemeinsam mit dem Betreuer, ein Programm, das die Tolman-Oppenheimer-Volkov-Gleichung numerisch löst und visualisieren die Ergebnisse. Zusätzlich wird hierbei in die Grundkonzepte der parallelen Programmierung eingeführt und eine MPI- und OpenMP-Version des C/C++ Programms erstellt. Im dritten Teil des Kurses werden zeitabhängige numerische Simulationen der ART mittels des Einstein Toolkit durchgeführt und deren Ergebnisse mittels Python/Matplotlib visualisiert. Inhaltlich wird hierbei ebenfalls auf den, dem Programm zugrunde liegenden (3+1)-Split der ART eingegangen und, abhängig von den Vorkenntnissen der Studierenden, mehrere fortgeschrittene, astrophysikalisch relevante Probleme simuliert. Mögliche Themen dieses abschließenden Teils könnten die folgenden Systeme darstellen: Oszillationen eines Neutronensterns, Kollaps eines Neutronenstern zu einem Schwarzen Loch oder die Kollision zweier Neutronensterne unter Berücksichtigung der Aussendung von Gravitationswellen. Der Schwerpunkt der gesamten interaktiven Vorlesung liegt sowohl auf der Allgemeine Relativitätstheorie als auch auf der Vermittlung spezieller Programmierkenntnisse.
Grundlegende Größen der Allgemeinen Relativitätstheorie
Im folgenden werden einige grundlegende Größen der allgemeinen Relativitätstheorie am Beispiel der allgemeinen statischen, isotropen Metrik erläutert.Zunächst wird das "tensor"-Paket eingebunden:
| > | restart:
with( tensor ); |
| (2.1) |
Definition der kovarianten Raumzeit-Metrik einer allgemeinen statischen, isotropen Metrik:
| > | coord := [t, r, theta, phi]:
g_compts := array(symmetric,sparse, 1..4, 1..4): g_compts[1,1] := A(r): g_compts[2,2] := -B(r): g_compts[3,3] := -r^2: g_compts[4,4] := -r^2*sin(theta)^2: g := create( [-1,-1], eval(g_compts)); |
![`:=`(g, table([index_char = [-1, -1], compts = Matrix(%id = 22561976)]))](images/Vorlesung1_8.gif) |
(2.2) |
Kontravariante Raumzeit-Metrik:
| > | ginv := invert( g, 'detg' ); |
![`:=`(ginv, table([index_char = [1, 1], compts = Matrix(%id = 21688984)]))](images/Vorlesung1_9.gif) |
(2.3) |
Erste partielle Ableitung der Metrik:
| > | D1g := d1metric ( g, coord ); |
| (2.4) |
Chistoffel Symbole (kontravariante Form):
| > | Cf1 := Christoffel1 ( D1g ); |
| (2.5) |
Chistoffel Symbole (erster Index kontravariant, zweiter und dritter kontravariant):
| > | Cf2:= Christoffel2( ginv, Cf1 ); |
| (2.6) |
Angabe einzelner Komponenten eines Tensors:
| > | get_compts(Cf2)[2,3,3]; |
| (2.7) |
Riemann Tensor:
| > | D2g := d2metric ( D1g, coord ):
RMN := Riemann( ginv, D2g, Cf1 ); |
| (2.8) |
Ricci Tensor:
| > | RICCI := Ricci( ginv, RMN ); |
![`:=`(RICCI, table([index_char = [-1, -1], compts = Matrix(%id = 16977104)]))](images/Vorlesung1_114.gif) |
(2.9) |
Ricci Skalar:
| > | RS := Ricciscalar( ginv, RICCI ); |
| (2.10) |
Einsteintensor:
| > | Estn := Einstein(g, RICCI, RS); |
![`:=`(Estn, table([index_char = [-1, -1], compts = Matrix(%id = 26157592)]))](images/Vorlesung1_121.gif) ![`:=`(Estn, table([index_char = [-1, -1], compts = Matrix(%id = 26157592)]))](images/Vorlesung1_122.gif) ![`:=`(Estn, table([index_char = [-1, -1], compts = Matrix(%id = 26157592)]))](images/Vorlesung1_123.gif) |
(2.11) |
Berechnung des infinitesimalen Weglängenelements ds2:
| > | dx:=create([1], array([dt,dr,dtheta,dphi])):
ds2:=get_compts(prod(dx,lower(g,dx,1),[1,1])): ds2:=collect( simplify(ds2), [dt,dr,dtheta,dphi]); |
| (2.12) |
| > |
Die Schwarzschildmetrik
Im folgenden werden einige grundlegende Größen am Beispiel der Schwarzschildmetrik eines schwarzen Lochs definiert.
| > | restart:
with( tensor ): |
Definition der kovarianten Raumzeit-Metrik eines schwarzen Lochs der Masse M in Schwarzschildkoordinaten:
| > | coord := [t, r, theta, phi]:
g_compts := array(symmetric,sparse, 1..4, 1..4): g_compts[1,1] := 1-2*M/r: g_compts[2,2] := -1/g_compts[1,1]: g_compts[3,3] := -r^2: g_compts[4,4] := -r^2*sin(theta)^2: g := create( [-1,-1], eval(g_compts)); |
![`:=`(g, table([index_char = [-1, -1], compts = Matrix(%id = 21587064)]))](images/Vorlesung1_133.gif) |
(3.1) |
Einzelne Komponenten der Chistoffel Symbole (erster Index kontravariant, zweiter und dritter kontravariant)
| > | ginv := invert( g, 'detg' ):
D1g := d1metric ( g, coord ): Cf1 := Christoffel1 ( D1g ): Cf2:= Christoffel2( ginv, Cf1 ); |
| (3.2) |
Angabe des Wertes der (r,t,t)-Komponente des Chistoffel Symbols eines schwarzen Loches der Masse M=4 bei einem radialen Abstand von r=7:
| > | get_compts(Cf2)[2,1,1]=subs({M=4,r=7},get_compts(Cf2)[1,1,2]); |
| (3.3) |
Nichtverschwindende Komponenten des Riemann Tensors. Der Ricci Tensor und Ricci Skalar ist identisch Null.
| > | D2g := d2metric ( D1g, coord ):
RMN := Riemann( ginv, D2g, Cf1 ): RMNc:=get_compts(RMN): RiemannComponents=map(proc(x) if RMNc[op(x)]<>0 then x=RMNc[op(x)] else NULL end if end proc,[ indices(RMNc)] ); RICCI := Ricci( ginv, RMN ); RS := Ricciscalar( ginv, RICCI ); |
![table( [( compts ) = array( 1 .. 4, 1 .. 4, [( 3, 4 ) = 0, ( 1, 1 ) = 0, ( 1, 3 ) = 0, ( 1, 4 ) = 0, ( 2, 2 ) = 0, ( 2, 4 ) = 0, ( 2, 3 ) = 0, ( 3, 3 ) = 0, ( 4, 4 ) = 0, ( 1, 2 ) = 0 ] ), ( index_cha...](images/Vorlesung1_150.gif) |
|
| (3.4) |
Kontrahiert man das quadratische Produkt des Riemann Tensors, so erhält man folgenden Skalar:
| > | RMNinv:= raise(ginv,RMN,1,2,3,4):
prod(RMN,RMNinv,[1,1],[2,2],[3,3],[4,4]); |
| (3.5) |
| > |
Raumzeitdiagramme
Im folgenden werden zwei Darstellungsarten der Schwarzschildmetrik behandelt.
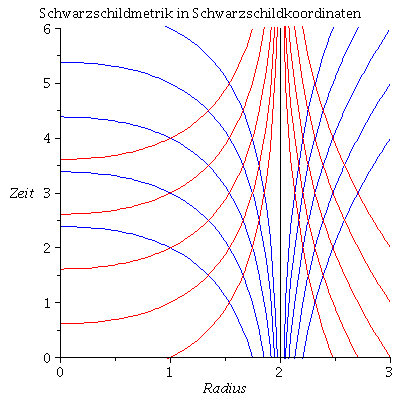
Schwarzschildmetrik in Schwarzschildkoordinaten
| > | restart:
with( tensor ): with(plots): |
Definition der kovarianten Raumzeit-Metrik eines schwarzen Lochs der Masse M in Schwarzschildkoordinaten:
| > | coord := [t, r, theta, phi];
g_compts := array(symmetric,sparse, 1..4, 1..4): g_compts[1,1] := 1-2*M/r: g_compts[2,2] := -1/g_compts[1,1]: g_compts[3,3] := -r^2: g_compts[4,4] := -r^2*sin(theta)^2: g := create( [-1,-1], eval(g_compts)); |
![table( [( index_char ) = [-1, -1], ( compts ) = array( 1 .. 4, 1 .. 4, [( 3, 3 ) = `+`(`-`(`*`(`^`(r, 2)))), ( 1, 1 ) = `+`(1, `-`(`/`(`*`(2, `*`(M)), `*`(r)))), ( 2, 2 ) = `+`(`-`(`/`(1, `*`(`+`(1, `...](images/Vorlesung1_154.gif) ![table( [( index_char ) = [-1, -1], ( compts ) = array( 1 .. 4, 1 .. 4, [( 3, 3 ) = `+`(`-`(`*`(`^`(r, 2)))), ( 1, 1 ) = `+`(1, `-`(`/`(`*`(2, `*`(M)), `*`(r)))), ( 2, 2 ) = `+`(`-`(`/`(1, `*`(`+`(1, `...](images/Vorlesung1_155.gif) |
(4.1.1) |
Berechnung des infinitesimalen Weglängenelements ds2:
| > | dx:=create([1], array([dt,dr,dtheta,dphi])):
ds2:=get_compts(prod(dx,lower(g,dx,1),[1,1])): ds2:=collect( simplify(ds2), [dt,dr,dtheta,dphi]); |
| (4.1.2) |
Gleichung eines radial einfallenden bzw. herausgehenden Lichtstahls ds2=0:
| > | Gl1:=subs(dtheta=0,dphi=0,ds2=0); |
| (4.1.3) |
Bestimmung der Lösungen der Gleichung:
| > | Loes1:=solve(Gl1,dt);
Loes2a:=evalf(int(Loes1[1]/dr,r))+c: Loes2b:=evalf(int(Loes1[2]/dr,r))+c: Loes2a := subs(ln(-1.*r+2.*M)=ln(abs(2*M-r)),Loes2a); Loes2b := subs(ln(-1.*r+2.*M)=ln(abs(2*M-r)),Loes2b); |
| (4.1.4) |
Festlegung der Masse des schwarzen Lochs auf M=1:
| > | Loes2a := subs(M=1,Loes2a);
Loes2b := subs(M=1,Loes2b); |
| (4.1.5) |
Visualisierung der Lösungen:
| > | rend:=3:
cend:=5: A:=plot({seq(Loes2a,c=1..cend)},r=0..rend,color=blue): B:=plot({seq(Loes2b,c=1..cend)},r=0..rend,color=red): C:=plot({seq(r+c,c=-cend..cend)},r=0..rend,color=black): EH:=PLOT(CURVES([[2,0],[2,6]])): display(A,B,EH,view=[0..rend,0..6],labels=[Radius, Zeit],title="Schwarzschildmetrik in Schwarzschildkoordinaten"); |
 |
| > |
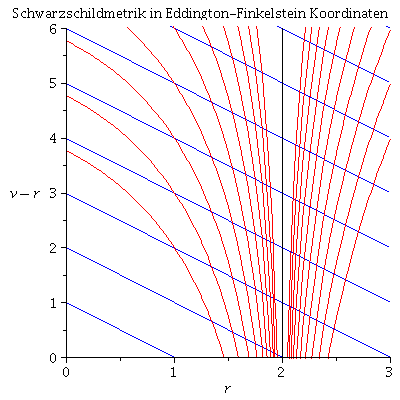
Schwarzschildmetrik in Eddington-Finkelstein Koordinaten
Die Koordinatensingularität der Schwarzschildmetrik kann man mittels spezieller Koordinatentransformationen beseitigen. Transformiert man z.B. in ein Koordinatensystem, welches sich mit einem in das schwarze Loch einfallenden Photons bewegt, so gelangt man zu den sogennanten avancierten (einlaufenden) Eddington-Finkelstein Koordinaten. In dieser Koordinatentransformation wird ein neuer Zeitparameter v definiert (v = t + r + 2M ln(|r/(2M) -1|) ), der die Bewegung der einlaufenden Photonen im Raumzeitdiagramm zu Geraden transformiert.
| > | restart:
with( tensor ): with(plots): |
Definition der kovarianten Raumzeit-Metrik eines schwarzen Lochs der Masse M in Eddington-Finkelstein Koordinaten:
| > | coord := [v, r, theta, phi];
g_compts := array(symmetric,sparse, 1..4, 1..4): g_compts[1,1] := 1-2*M/r: g_compts[2,2] := 0: g_compts[3,3] := -r^2: g_compts[4,4] := -r^2*sin(theta)^2: g_compts[1,2] := -1: g_compts[2,1] := -1: g := create( [-1,-1], eval(g_compts)); |
![table( [( index_char ) = [-1, -1], ( compts ) = array( 1 .. 4, 1 .. 4, [( 2, 2 ) = 0, ( 3, 3 ) = `+`(`-`(`*`(`^`(r, 2)))), ( 1, 2 ) = `+`(`-`(`/`(`*`(M), `*`(r)))), ( 4, 4 ) = `+`(`-`(`*`(`^`(r, 2), `...](images/Vorlesung1_166.gif) |
(4.2.1) |
Berechnung des infinitesimalen Weglängenelements ds2:
| > | dx:=create([1], array([dv,dr,dtheta,dphi])):
ds2:=get_compts(prod(dx,lower(g,dx,1),[1,1])): ds2:=collect( simplify(ds2), [dv,dr,dtheta,dphi]); |
| (4.2.2) |
Gleichung eines radial einfallenden bzw. herausgehenden Lichtstahls ds2=0:
| > | Gl1:=subs(dtheta=0,dphi=0,ds2=0); |
| (4.2.3) |
Bestimmung der Lösungen der Gleichung:
| > | Loes1:=solve(Gl1,dv);
Loes2a:=evalf(int(Loes1[1],r))+c: Loes2b:=evalf(int(Loes1[2]/dr,r))+c: Loes2a := subs(ln(-1.*r+2.*M)=ln(abs(2*M-r)),Loes2a); Loes2b := subs(ln(-1.*r+2.*M)=ln(abs(2*M-r)),Loes2b); |
| (4.2.4) |
Festlegung der Masse des schwarzen Lochs auf M=1:
| > | Loes2a := subs(M=1,Loes2a):
Loes2b := subs(M=1,Loes2b): |
Visualisierung der Lösungen in einem Raumzeitdiagramm, wobei y=v-r , x=r. Die blauen Geraden veranschaulichen die in das schwarze Loch einfallenden Photonen:
| > | rend:=3:
cend:=10: A:=plot({seq(Loes2a-r,c=1..cend)},r=0..rend,color=blue): B:=plot({seq(Loes2b-r,c=1..cend)},r=0..rend,color=red): C:=plot({seq(r+c,c=-cend..cend)},r=0..rend,color=black): EH:=PLOT(CURVES([[2,0],[2,6]])): display(A,B,EH,view=[0..rend,0..6],labels=[r, v-r],title="Schwarzschildmetrik in Eddington-Finkelstein Koordinaten"); |
 |
| > |
| > |