Die Kerr Metrik: Effektives Potential, kreisförmige Bewegungen, die innerste stabile Kreisbahn und der gravitomagnetische Effekt 

Basierend auf den Ergebnissen der geodätischen Bewegung eines Probekörpers um ein rotierendes Kerr schwarzes Loch (siehe Vorlesung 5), werden die möglichen Bewegungen mittels eines definierten effektiven Potential näher verstanden. Zusätzlich wird der durch den Mitführungseffekt der Raumzeit ("Frame-Dragging" bzw. Lense-Thiring Effekt) verursachte, gravitomagnetische Effekt an einem speziellen Beispiel veranschaulicht. 

Bahnbewegungen in der Ebene und das effektive Potential V(r) 

ähnlich wie im nichtrotierenden Fall (siehe Vorlesung 3) charakterisieren wir die unterschiedlichen Bahnbewegungen mittels eines effektiven Potentials: 

>	restart: with( tensor ): with(plots): with(plottools):

 

Definition der kovarianten Raumzeit-Metrik eines rotierenden schwarzen Lochs der Masse M und Rotation a in Kerrschildkoordinaten: 

>

coord := [t, r, theta, phi]: rho2:=r^2+(a*cos(theta))^2: Delta:=r^2-2*M*r+a^2: Sig2:=(r^2+a^2)^2-a^2*Delta*(sin(theta))^2: g_compts := array(symmetric,sparse, 1..4, 1..4): g_compts[1,1] := (1-2*M*r/rho2): g_compts[1,4] := +(2*a*M*r*(sin(theta))^2)/rho2: g_compts[2,2] :=-rho2/Delta: g_compts[3,3] := -rho2: g_compts[4,4] := -(r^2+a^2+2*M*r*a^2*(sin(theta))^2/rho2): g := create( [-1,-1], eval(g_compts));

 

(1.1.1)

 

Berechnung der kontravarianten Metrik, der Christoffel Symbole, des Riemanntensors...: 

>	ginv := invert( g, 'detg' ): D1g := d1metric( g, coord ):   D2g := d2metric( D1g, coord ): Cf1 := Christoffel1( D1g ): Cf2:= Christoffel2( ginv, Cf1 ): D2g := d2metric ( D1g, coord ): RMN := Riemann( ginv, D2g, Cf1 ): RICCI := Ricci( ginv, RMN ): RS := Ricciscalar( ginv, RICCI ):

 

Berechnung der Geodätengleichung als Funktion des affinen Parameters lambda. Die Geodätengleichung ist ein System gekoppelter Differentialgleichungen:   

>	eqns:=geodesic_eqns( coord, lambda, Cf2 );

 

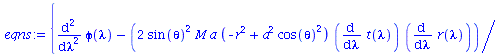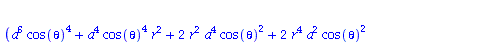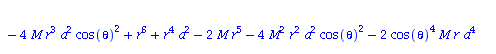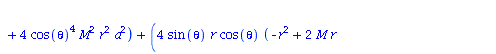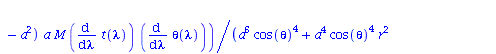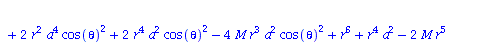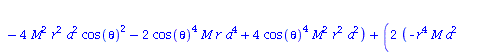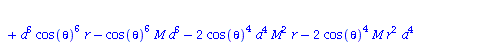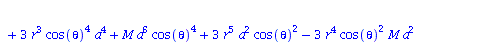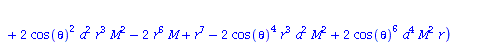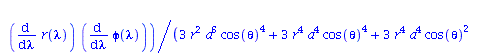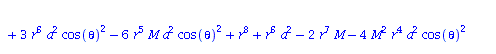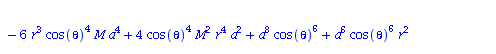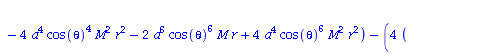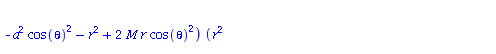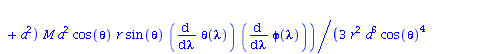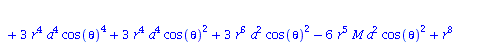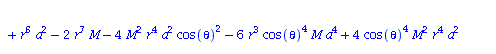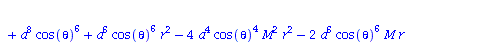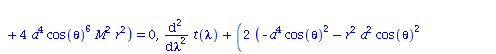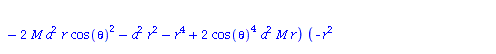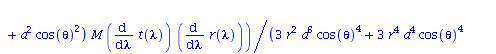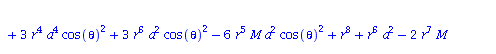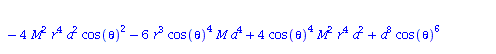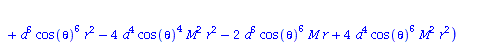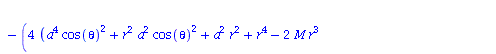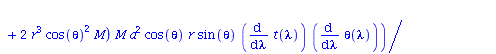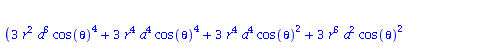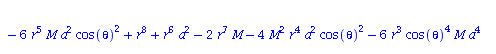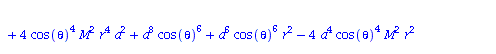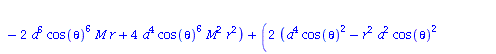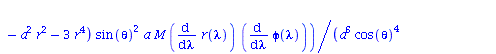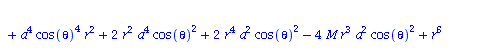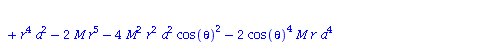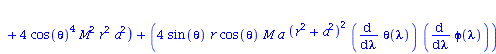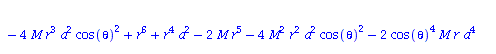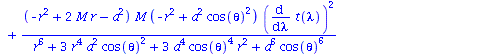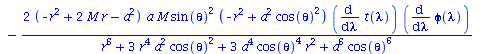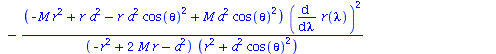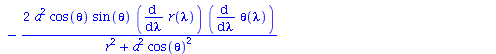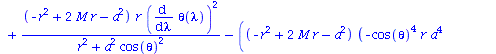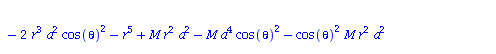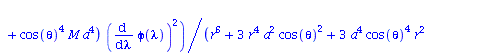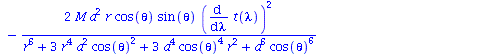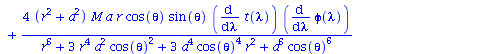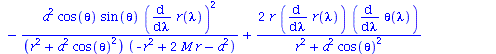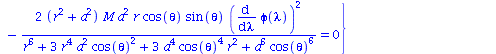(1.1.2)

 

Umschreiben der Variablen in den Bewegungsgleichungen (z.B. r->r(lambda)): 

>

eq1:=simplify(subs({r=r(lambda),theta=theta(lambda)},eqns[1])): eq2:=simplify(subs({r=r(lambda),theta=theta(lambda)},eqns[2])): eq3:=simplify(subs({r=r(lambda),theta=theta(lambda)},eqns[3])): eq4:=simplify(subs({r=r(lambda),theta=theta(lambda)},eqns[4])): eq1:=simplify(subs({r(lambda)(lambda)=r(lambda),theta(lambda)(lambda)=theta(lambda)},eq1)): eq2:=simplify(subs({r(lambda)(lambda)=r(lambda),theta(lambda)(lambda)=theta(lambda)},eq2)): eq3:=simplify(subs({r(lambda)(lambda)=r(lambda),theta(lambda)(lambda)=theta(lambda)},eq3)): eq4:=simplify(subs({r(lambda)(lambda)=r(lambda),theta(lambda)(lambda)=theta(lambda)},eq4)):

 

:Infinitesimales Weglängenelement ds²: 

>

dx:=create([1], array([dt,dr,dtheta,dphi])): ds2:=get_compts(prod(dx,lower(g,dx,1),[1,1])): ds2:=collect( simplify(ds2), [dt,dr,dtheta,dphi]): ds2a:=simplify(coeff(ds2, dt, 2)): ds2b:=simplify(coeff(ds2, dr, 2)): ds2c:=simplify(coeff(ds2, dtheta, 2)): ds2d:=simplify(coeff(ds2, dphi, 2)): ds2e:=simplify(coeff(ds2, dphi, 1)/dt): ds2:=ds2a*dt^2+ds2e*dt*dphi+ds2b*dr^2+ds2c*dtheta^2+ds2d*dphi^2;

 

(1.1.3)

 

Festlegung der Anfangswerte: 

>	setM:=1: seta:=0.95: r0:=10: t0:=0: theta0:=Pi/2: phi0:=0: dr0:=0: dtheta0:=0: dphi0:=0.041: dt0:=solve(subs({theta=theta0,dphi=dphi0,dr=dr0,dtheta=dtheta0,M=1,a=0.95,r=10},ds2)=1,dt)[1]:

 

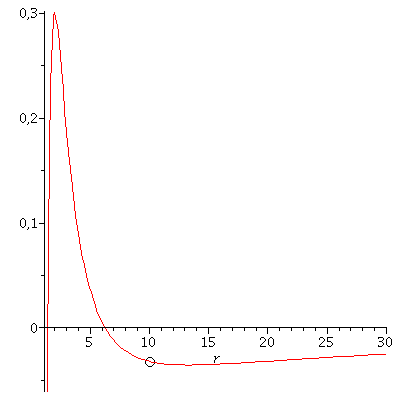
In der Literatur wird die Bewegung eines Probekörpers um ein rotierendes schwarzes Loch mittels eines definierten, effektiven Potentials illustriert (siehe z.B. Hartle- bzw. Hobson Buch). Dieses Potential hängt von dem, bei der Bewegung erhaltenem Drehimpuls pro Masse m und der Probekörper-Energie pro Masse ab. Die im Zentralfeld möglichen Bewegungen werden mittels zweier erhaltener Größen (l: Drehimpuls pro Masse m und E: Energie pro Masse) charakteriesiert. Die folgende Abbildung zeigt (in der Nomenklatur vom Hartle-Buch) das effektive Potential als Funktion des Radius bei den obigen gewählten Anfangswerten: 

>

Equ1:=solve({dt=1/Delta*((r^2+a^2+2*M*a^2/r)*energie-2*M*a/r*drehimpuls),dphi=1/Delta*((1-2*M/r)*drehimpuls+2*M*a/r*energie)},{energie,drehimpuls}): setE:=subs({dt=dt0,dphi=dphi0,M=setM,a=seta,r=r0},rhs(Equ1[1])): setl:=subs({dt=dt0,dphi=dphi0,M=setM,a=seta,r=r0},rhs(Equ1[2])): VeffHartleRot:=(r,M,l,a,en)->-M/r+(l^2-a^2*(en^2-1))/(2*r^2)-M*(l-a*en)^2/r^3; PotRot:=plot(VeffHartleRot(r,setM,setl,seta,setE),r=1.4..30): B:=pointplot({[r0, VeffHartleRot(r0,1,setl,seta,setE)]}, symbol=circle,symbolsize=20): display(B,PotRot);

 

 

 

Numerische Lösung bei vorgegebenen Anfangswerten: 

>

Loes:=dsolve({subs({a=seta,M=setM},eq1),subs({a=seta,M=setM},eq2),subs({a=seta,M=setM},eq3),subs({a=seta,M=setM},eq4),t(0)=t0,r(0)=r0,phi(0)=phi0,theta(0)=theta0,D(r)(0)=0,D(t)(0)=dt0,D(phi)(0)=dphi0,D(theta)(0)=dtheta0},{r(lambda),t(lambda),phi(lambda),theta(lambda)},type=numeric,output=listprocedure):

 

Grafische Veranschaulichung der Lösung: 

>

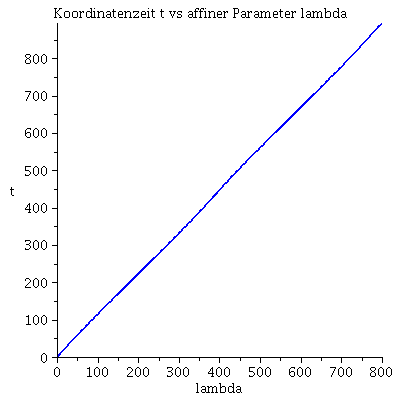
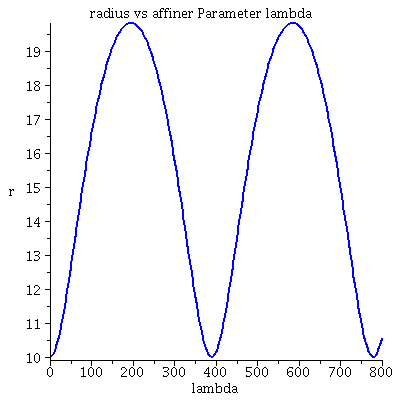
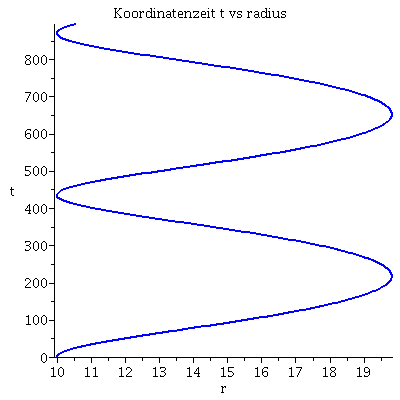
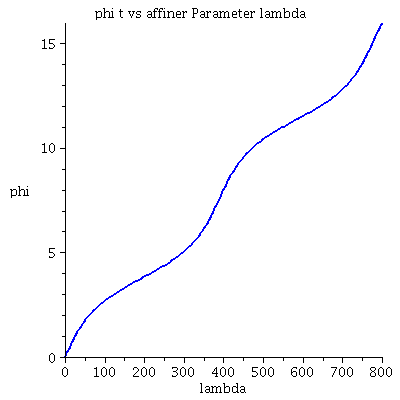
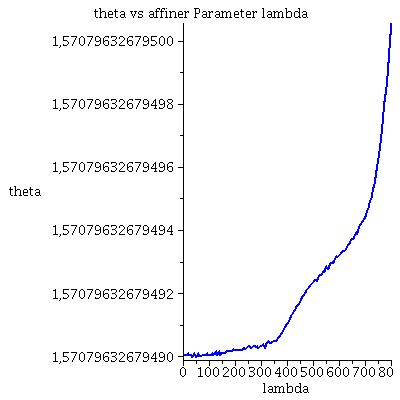
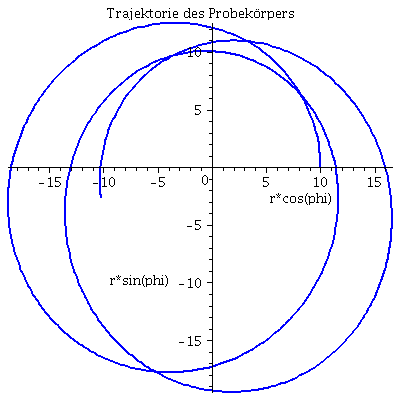
lend:=800: Plot1:=odeplot(Loes,[lambda,t(lambda)],0..lend,numpoints=200,color=blue,thickness=2,title="Koordinatenzeit t vs affiner Parameter lambda"): Plot2:=odeplot(Loes,[lambda,r(lambda)],0..lend,numpoints=200,color=blue,thickness=2,title="radius vs affiner Parameter lambda"): Plot3:=odeplot(Loes,[r(lambda),t(lambda)],0..lend,numpoints=700,color=blue,thickness=2,title="Koordinatenzeit t vs radius"): Plot4:=odeplot(Loes,[lambda,phi(lambda)],0..lend,numpoints=200,color=blue,thickness=2,title="phi t vs affiner Parameter lambda"): Plot5:=odeplot(Loes,[lambda,theta(lambda)],0..lend,numpoints=200,color=blue,thickness=2,title="theta vs affiner Parameter lambda"): Plot6:=odeplot(Loes,[r(lambda)*cos(phi(lambda)),r(lambda)*sin(phi(lambda))],0..lend,numpoints=700,color=blue,thickness=2,title="Trajektorie des Probekörpers"): display(Matrix(1,3,[Plot1,Plot2,Plot3])); display(Matrix(1,3,[Plot4,Plot5,Plot6]));

 

 

 

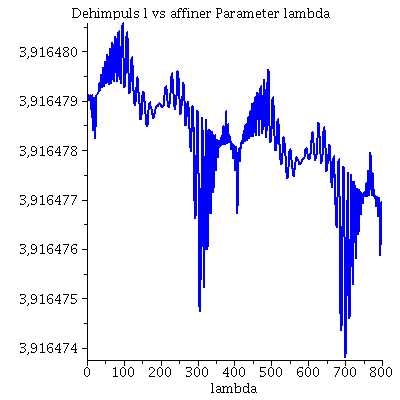
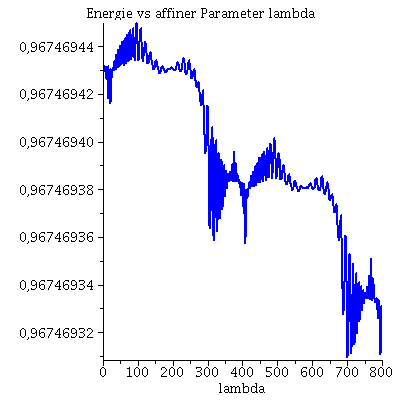
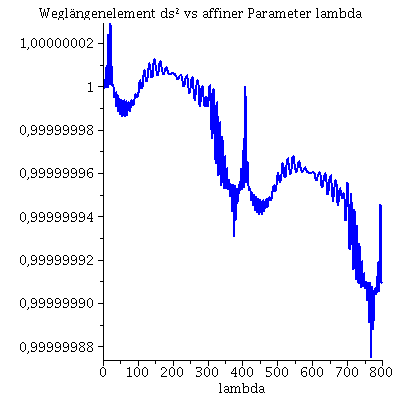
Während der Bewegung erhaltenen Größen (l: Drehimpuls pro Masse m, E: Energie pro Masse und Weglängenelement ds²):  

>

Plot4:=odeplot(Loes,[lambda,subs({dt=diff(t(lambda), lambda),dphi=diff(phi(lambda), lambda),M=1,a=0.95,r=r(lambda)},rhs(Equ1[2]))],0..lend,numpoints=700,color=blue,thickness=2,title="Dehimpuls l vs affiner Parameter lambda"): Plot5:=odeplot(Loes,[lambda,subs({dt=diff(t(lambda), lambda),dphi=diff(phi(lambda), lambda),M=1,a=0.95,r=r(lambda)},rhs(Equ1[1]))],0..lend,numpoints=700,color=blue,thickness=2,title="Energie vs affiner Parameter lambda"): Plot6:=odeplot(Loes,[lambda,subs({a=seta,M=1,r=r(lambda),phi=phi(lambda),theta=theta(lambda),dr=diff(r(lambda), lambda),dt=diff(t(lambda), lambda),dphi=diff(phi(lambda), lambda),dtheta=diff(theta(lambda), lambda)},ds2)],0..lend,numpoints=700,color=blue,thickness=2,title="Weglängenelement ds² vs affiner Parameter lambda"): display(Matrix(1,3,[Plot4,Plot5,Plot6]));

 

 

 

>

UnRot:=solve(get_compts(g)[1,1]=0,r): Horizon:=solve(get_compts(ginv)[2,2]=0,r): A:=implicitplot(r = subs({M=setM,a=seta,theta=Pi/2},UnRot[1]), r = 0 .. 3, phi = 0 .. 2*Pi, coords = polar,grid=[30,30],color=red,linestyle=dash,thickness=1): B:=implicitplot(r = subs({M=setM,a=seta,theta=Pi/2},UnRot[2]), r = 0 .. 3, phi = 0 .. 2*Pi, coords = polar,grid=[30,30],color=red,linestyle=solid): C:=implicitplot(r = subs({M=setM,a=seta,theta=Pi/2},Horizon[1]), r = 0 .. 3, phi = 0 .. 2*Pi, coords = polar,grid=[30,30],color=black,linestyle=dash,thickness=1): DD:=implicitplot(r = subs({M=setM,a=seta,theta=Pi/2},Horizon[2]), r = 0 .. 3, phi = 0 .. 2*Pi, coords = polar,grid=[30,30],color=black,linestyle=solid): BH1:=display(disk([0,0],subs({M=setM,a=seta,theta=Pi/2},Horizon[2]),color=black)): BH2:=display(disk([0,0],subs({M=setM,a=seta,theta=Pi/2},Horizon[1]),color=white)): BH3:=display(disk([0,0],subs({M=setM,a=seta,theta=Pi/2},UnRot[1]),color=yellow)): BH:=display({A,B,C,DD,BH1,BH2,BH3},scaling=constrained):

 

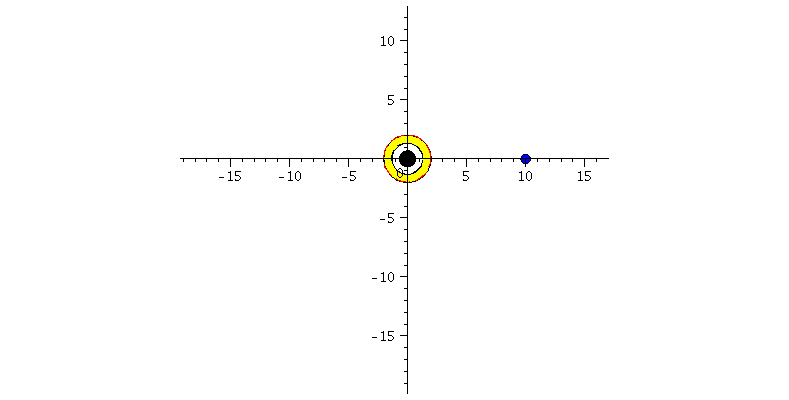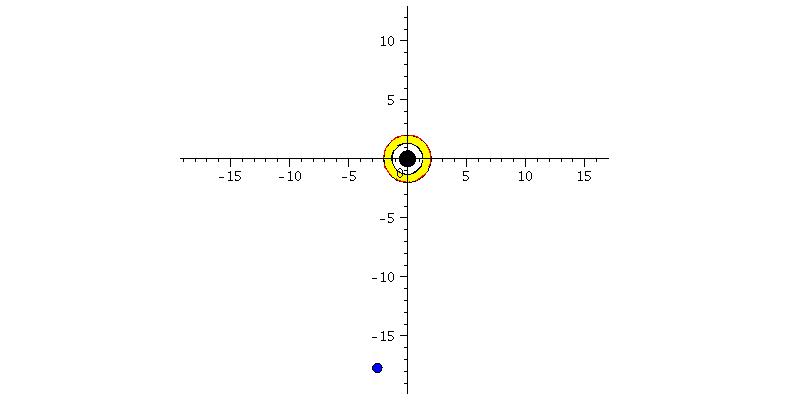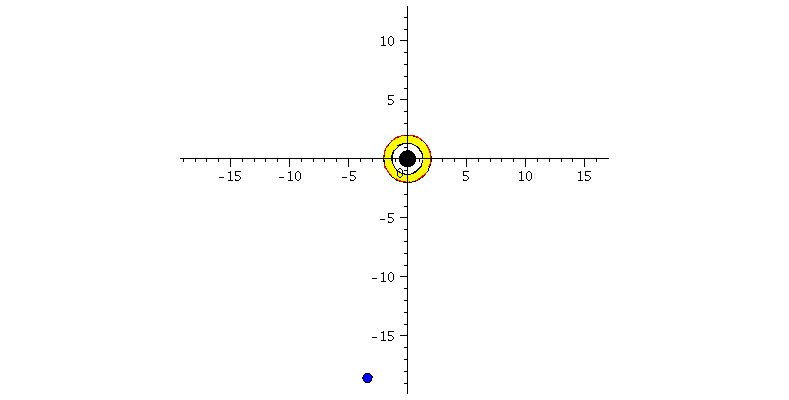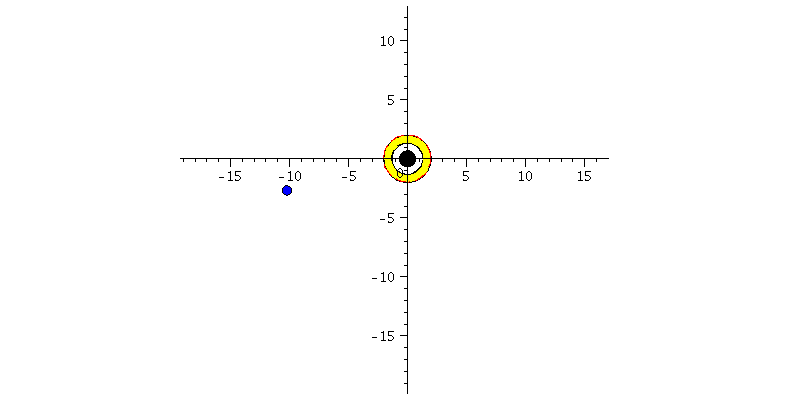
>	frames:=150: Lr := subs(Loes,r(lambda)): Lphi := subs(Loes,phi(lambda)): for i from 0 by 1 to frames do Koerper[i]:=display(disk([Lr(i*lend/frames)*cos(Lphi(i*lend/frames)),Lr(i*lend/frames)*sin(Lphi(i*lend/frames))],0.4,color=blue)): Ani[i]:=display({Koerper[i],BH}); od:

 

>	display([seq(Ani[i],i=0..frames)],insequence=true,scaling=constrained):

 

>	PotRot:=plot(VeffHartleRot(r,setM,setl,seta,setE),r=1.4..30): VE:=VeffHartleRot(r0,1,setl,seta,setE): for i from 0 by 1 to frames do Koerper[i]:=pointplot({[Lr(i*lend/frames), VE]}, symbol=solidcircle,symbolsize=20,color=blue): Ani1[i]:=display({PotRot,Koerper[i]}); od:

 

>	Animat1:=display([seq(Ani[i],i=0..frames)],insequence=true,scaling=constrained): Animat2:=display([seq(Ani1[i],i=0..frames)],insequence=true): display(Array([Animat1,Animat2]));

 

 

>

 

Kreisförmige Bewegung eines Probekörper und der ISCO 

Wir betrachten im folgenden die kreisförmige Bewegung eines Probekörpers. 

ähnlich wie im nichtrotierenden Fall (siehe Vorlesung 3) charakterisieren wir die unterschiedlichen Bahnbewegungen mittels eines effektiven Potentials: 

>	restart: with( tensor ): with(plots): with(plottools):

 

Definition der kovarianten Raumzeit-Metrik eines rotierenden schwarzen Lochs der Masse M und Rotation a in Kerrschildkoordinaten: 

>

coord := [t, r, theta, phi]: rho2:=r^2+(a*cos(theta))^2: Delta:=r^2-2*M*r+a^2: Sig2:=(r^2+a^2)^2-a^2*Delta*(sin(theta))^2: g_compts := array(symmetric,sparse, 1..4, 1..4): g_compts[1,1] := (1-2*M*r/rho2): g_compts[1,4] := +(2*a*M*r*(sin(theta))^2)/rho2: g_compts[2,2] :=-rho2/Delta: g_compts[3,3] := -rho2: g_compts[4,4] := -(r^2+a^2+2*M*r*a^2*(sin(theta))^2/rho2): g := create( [-1,-1], eval(g_compts));

 

(1.2.1)

 

Berechnung der kontravarianten Metrik, der Christoffel Symbole, des Riemanntensors...: 

>	ginv := invert( g, 'detg' ): D1g := d1metric( g, coord ):   D2g := d2metric( D1g, coord ): Cf1 := Christoffel1( D1g ): Cf2:= Christoffel2( ginv, Cf1 ): D2g := d2metric ( D1g, coord ): RMN := Riemann( ginv, D2g, Cf1 ): RICCI := Ricci( ginv, RMN ): RS := Ricciscalar( ginv, RICCI ):

 

Berechnung der Geodätengleichung als Funktion des affinen Parameters lambda. Die Geodätengleichung ist ein System gekoppelter Differentialgleichungen:   

>	eqns:=geodesic_eqns( coord, lambda, Cf2 ):

 

Umschreiben der Variablen in den Bewegungsgleichungen (z.B. r->r(lambda)): 

>

eq1:=simplify(subs({r=r(lambda),theta=theta(lambda)},eqns[1])): eq2:=simplify(subs({r=r(lambda),theta=theta(lambda)},eqns[2])): eq3:=simplify(subs({r=r(lambda),theta=theta(lambda)},eqns[3])): eq4:=simplify(subs({r=r(lambda),theta=theta(lambda)},eqns[4])): eq1:=simplify(subs({r(lambda)(lambda)=r(lambda),theta(lambda)(lambda)=theta(lambda)},eq1)): eq2:=simplify(subs({r(lambda)(lambda)=r(lambda),theta(lambda)(lambda)=theta(lambda)},eq2)): eq3:=simplify(subs({r(lambda)(lambda)=r(lambda),theta(lambda)(lambda)=theta(lambda)},eq3)): eq4:=simplify(subs({r(lambda)(lambda)=r(lambda),theta(lambda)(lambda)=theta(lambda)},eq4)):

 

:Infinitesimales Weglängenelement ds²: 

>

dx:=create([1], array([dt,dr,dtheta,dphi])): ds2:=get_compts(prod(dx,lower(g,dx,1),[1,1])): ds2:=collect( simplify(ds2), [dt,dr,dtheta,dphi]): ds2a:=simplify(coeff(ds2, dt, 2)): ds2b:=simplify(coeff(ds2, dr, 2)): ds2c:=simplify(coeff(ds2, dtheta, 2)): ds2d:=simplify(coeff(ds2, dphi, 2)): ds2e:=simplify(coeff(ds2, dphi, 1)/dt): ds2:=ds2a*dt^2+ds2e*dt*dphi+ds2b*dr^2+ds2c*dtheta^2+ds2d*dphi^2;

 

(1.2.2)

 

Aufgrund der Normalisierungseigenschaft der Vierergeschwindigkeit u*u=-1 sind die Zeit- und phi-Komponente der Viergeschwindigkeit wie folgt durch die Energie- und Drehimpulswerte bestimmt (siehe Hartle-Buch, S:318): 

>	Eqdt:=dt=1/Delta*((r^2+a^2+2*M*a^2/r)*en-2*M*a/r*l); Eqdphi:=dphi=1/Delta*((1-2*M/r)*l+2*M*a/r*en);

 

 

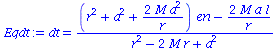	(1.2.3)

 

Wir beschränken uns im Folgenden auf äquatoriale, kreisförmige Bewegungen und nehmen die folgenden Anfangsbedingungen an: 

>	t0:=0: phi0:=0: theta0:=Pi/2: dr0:=0: dtheta0:=0:

 

Bei kreisförmige Bewegungen muss die Ableitung des effektiven Potentials nach r verschwinden: 

>	VeffHartleRot:=(r,M,l,a,en)->-M/r+(l^2-a^2*(en^2-1))/(2*r^2)-M*(l-a*en)^2/r^3; EqCirc:=diff(VeffHartleRot(r,M,l,a,en),r)=0;

 

 

	(1.2.4)

 

Das infinitesimales Weglängenelement eines massiven Probekörpers hat die Eigenschaft ds²=1: 

>	Eqds2:=subs({dtheta=dtheta0,dr=dr0,cos(theta)=0,sin(theta)=1},ds2)=1;

 

(1.2.5)

 

Einsetzen der obigen Gleichungen für dt und dphi ergibt: 

>	EqA:=simplify(subs({Eqdt,Eqdphi},Eqds2));

 

(1.2.6)

 

Wir nehmen nun einen Spezialfall an und setzen dphi0=0.066 für ein im Uhrzeigersinn rotierenden Probekörper und verarbeiten dies in die vorige Gleichung: 

>	dphi0:=0.066: EqB:=simplify(subs(l=solve(subs(dphi=dphi0,Eqdphi),l),EqA));

 

(1.2.7)

 

Verarbeiten der Bedingung, dass es sich um eine kreisförmige Bewegung handelt: 

>	EqCCorot:=simplify(subs(en=solve(EqB,en)[1],subs(l=solve(subs(dphi=dphi0,Eqdphi),l),EqCirc)));

 

(1.2.8)

 

Die folgende Abbildung zeigt wie sich der Wert des radialen Abstandes eines auf der letzten stabilen Kreisbahn rotierenden Probekörpers als Funktion des Parameters a (normierte Winkelgeschwindigkeit des Kerr schwarzen Loches) ändert (M=1 angenommen):   

>	setM:=1: implicitplot(subs(M=setM,EqCCorot), a = 0 .. 1,r=3..15,color=red);

 

 

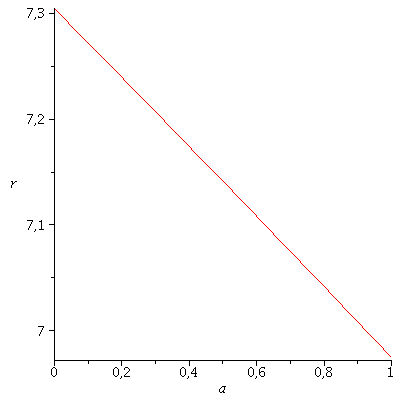Im folgenden setzen wir M=1 und a=0.95 

>

setM:=1: seta:=0.95: t0:=0: phi0:=0: theta0:=Pi/2: dr0:=0: dtheta0:=0: dphi0:=0.066: r0:=solve(subs({M=setM,a=seta},EqCCorot),r)[1]: dt0:=solve(subs({theta=theta0,dphi=dphi0,dr=dr0,dtheta=dtheta0,M=setM,a=seta,r=r0},Eqds2),dt)[1]: EquD:=solve(subs({theta=theta0,dphi=dphi0,dr=dr0,dtheta=dtheta0,dt=dt0,M=setM,a=seta,r=r0},{Eqdt,Eqdphi}),{en,l}): setE:=rhs(EquD[1]): setl:=rhs(EquD[2]):

 

Lösen der Geodätengleichung 

>

Loes:=dsolve({subs({a=seta,M=setM},eq1),subs({a=seta,M=setM},eq2),subs({a=seta,M=setM},eq3),subs({a=seta,M=setM},eq4),t(0)=t0,r(0)=r0,phi(0)=phi0,theta(0)=theta0,D(r)(0)=0,D(t)(0)=dt0,D(phi)(0)=dphi0,D(theta)(0)=dtheta0},{r(lambda),t(lambda),phi(lambda),theta(lambda)},type=numeric,output=listprocedure):

 

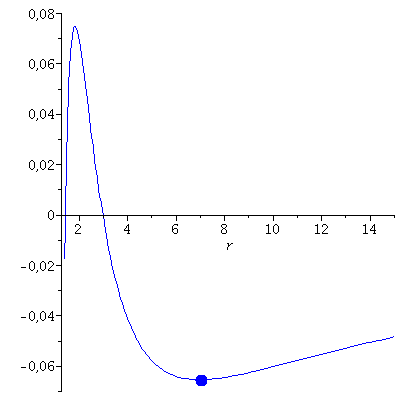
Veranschaulichung der Bewegung im effektiven Potential: 

>	PointB:=pointplot({[r0, VeffHartleRot(r0,setM,setl,seta,setE)]},symbol=solidcircle,symbolsize=25,color=blue): PlotB:=plot(VeffHartleRot(r,setM,setl,seta,setE),r=1.4..50,view=[1.4..15,-0.07..0.08],numpoints=300,color=blue): display(PointB,PlotB);

 

 

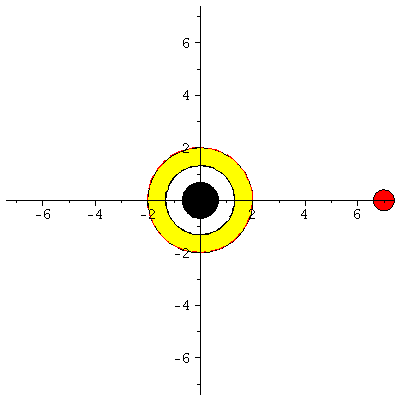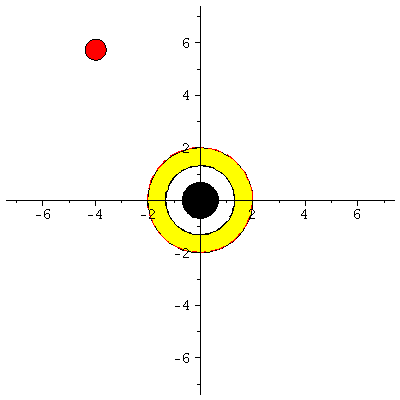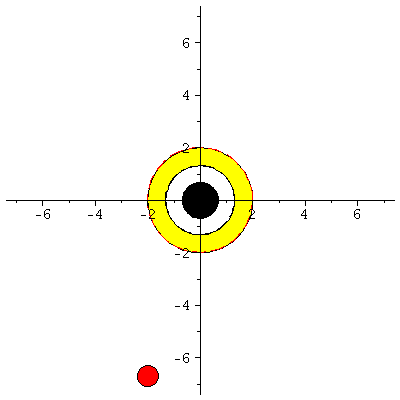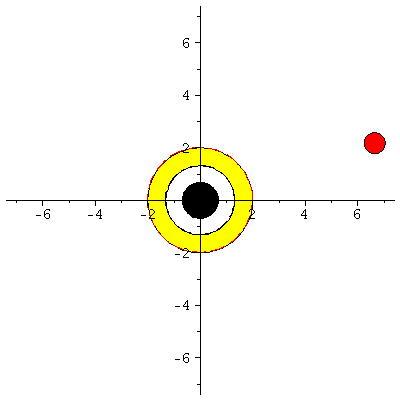
Animation der Bewegung: 

>

UnRot:=solve(get_compts(g)[1,1]=0,r): Horizon:=solve(get_compts(ginv)[2,2]=0,r): A:=implicitplot(r = subs({M=setM,a=seta,theta=Pi/2},UnRot[1]), r = 0 .. 3, phi = 0 .. 2*Pi, coords = polar,grid=[30,30],color=red,linestyle=dash,thickness=1): B:=implicitplot(r = subs({M=setM,a=seta,theta=Pi/2},UnRot[2]), r = 0 .. 3, phi = 0 .. 2*Pi, coords = polar,grid=[30,30],color=red,linestyle=solid): C:=implicitplot(r = subs({M=setM,a=seta,theta=Pi/2},Horizon[1]), r = 0 .. 3, phi = 0 .. 2*Pi, coords = polar,grid=[30,30],color=black,linestyle=dash,thickness=1): DD:=implicitplot(r = subs({M=setM,a=seta,theta=Pi/2},Horizon[2]), r = 0 .. 3, phi = 0 .. 2*Pi, coords = polar,grid=[30,30],color=black,linestyle=solid): BH1:=display(disk([0,0],subs({M=setM,a=seta,theta=Pi/2},Horizon[2]),color=black)): BH2:=display(disk([0,0],subs({M=setM,a=seta,theta=Pi/2},Horizon[1]),color=white)): BH3:=display(disk([0,0],subs({M=setM,a=seta,theta=Pi/2},UnRot[1]),color=yellow)): BH:=display({A,B,C,DD,BH1,BH2,BH3},scaling=constrained):

 

>	frames:=100: lend:=100: Lr := subs(Loes,r(lambda)): Lphi := subs(Loes,phi(lambda)): for i from 0 by 1 to frames do Koerper[i]:=display(disk([Lr(i*lend/frames)*cos(Lphi(i*lend/frames)),Lr(i*lend/frames)*sin(Lphi(i*lend/frames))],0.4,color=red)): Ani[i]:=display({Koerper[i],BH}); od:

 

>	display([seq(Ani[i],i=0..frames)],insequence=true,scaling=constrained);

 

 

 

Die innerste stabile kreisförmige Bahnbewegung (Innermost Stable Circular Orbit (ISCO)) eines Probekörpers 

>

 

Wir wollen nun, ähnlich wie beim nichtrotierenden Schwarzschild schwarzen Loch, die innerste stabile kreisformige Bahn (ISCO) berechnen. Das effektive Potential ist bei kreisförmigen Bahnbewegungen (dr/dlambda=0) wie folgt mit der Energie verknüpft : 

>	VeffHartleRot(r,M,l,a,e)=(e^2-1)/2;

 

(1.2.1.1)

 

Kreisförmige Bahnbewegungen sind dort, wo das effektive Potential sein Minimum hat: 

>	diff(VeffHartleRot(r,M,l,a,e),r)=0; CircOrbe:=solve(diff(VeffHartleRot(r,M,l,a,e),r)=0,e): CircOrbl:=solve(diff(VeffHartleRot(r,M,l,a,e),r)=0,l):

 

(1.2.1.2)

 

Die innerste stabile kreisformige Bahn hat dort zusätzlich noch einen Sattelpunkt: 

>	diff(VeffHartleRot(r,M,l,a,e),r,r)=0;

 

(1.2.1.3)

 

Setzt man die Eigenschaften des rotierenden schwarzen Loches (z.B. M=1 und a=0.95) fest, und löst drei Gleichungen, so erhält man die Werte für den ISCO. 

>	setM:=1; seta:=0.95; ISCO:=solve({diff(VeffHartleRot(r,setM,l,seta,e),r)=0,diff(VeffHartleRot(r,setM,l,seta,e),r,r)=0,VeffHartleRot(r,setM,l,seta,e)=(e^2-1)/2});

 

 

 

	(1.2.1.4)

 

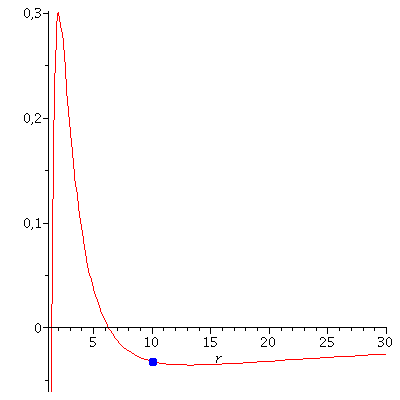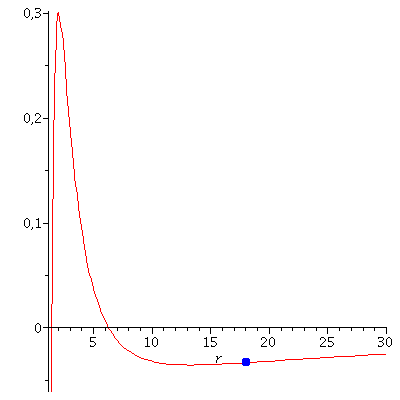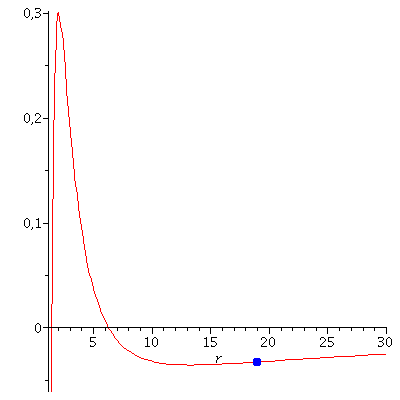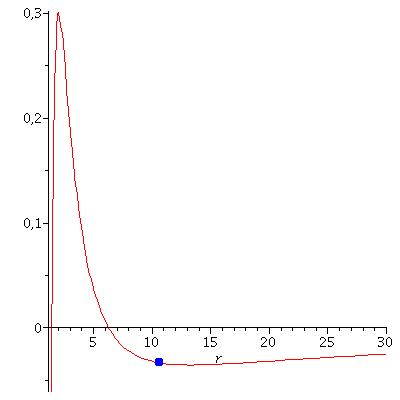
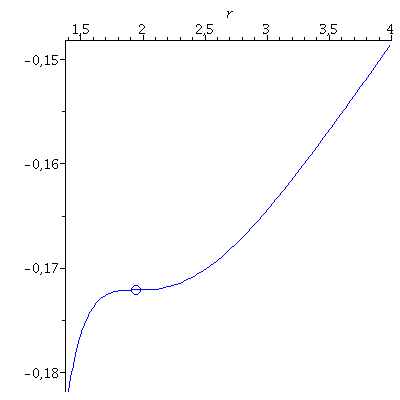
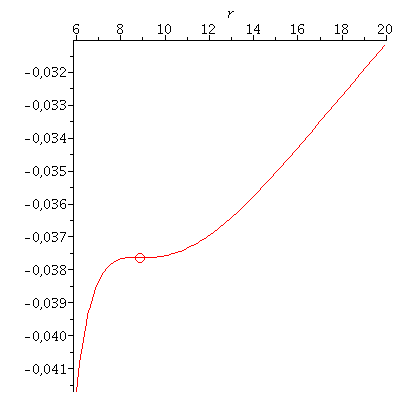
Die Lösungen des ISCO beinhalten eine eng um das schwarze Loch rotierende Lösung (r=1.94 km; Probekörper rotiert in gleicher Richtung wie die Rotationsrichtung des schwarzen Lochs) und eine weiter entfernte Lösung (r=8.86 km; Probekörper rotiert entgegen der Rotationsrichtung des schwarzen Lochs)  

>	setE1:=rhs(ISCO[1,1]); setl1:=rhs(ISCO[1,2]); r01:=rhs(ISCO[1,3]); setE2:=rhs(ISCO[3,1]); setl2:=rhs(ISCO[3,2]); r02:=rhs(ISCO[3,3]);

 

 

 

 

 

 

	(1.2.1.5)

 

Veranschaulichung der beiden Lösungen im effektiven Potential: 

>

PotRot1:=plot(VeffHartleRot(r,setM,setl1,seta,setE1),r=1.4..4,color=blue): B1:=pointplot({[r01, VeffHartleRot(r01,setM,setl1,seta,setE1)]}, symbol=circle,symbolsize=20,color=blue): PotRot2:=plot(VeffHartleRot(r,setM,setl2,seta,setE2),r=6..20,color=red): B2:=pointplot({[r02, VeffHartleRot(r02,setM,setl2,seta,setE2)]}, symbol=circle,symbolsize=20,color=red): display(Array([display(B1,PotRot1),display(B2,PotRot2)]));

 

 

Setzen der Anfangswerte beider Lösungen: 

>

t0:=0: phi0:=0: theta0:=Pi/2: dtheta0:=0: dr0:=0: dt01:=rhs(subs({M=setM,a=seta,r=r01,en=setE1,l=setl1},Eqdt)): dphi01:=rhs(subs({M=setM,a=seta,r=r01,en=setE1,l=setl1},Eqdphi)): dt02:=rhs(subs({M=setM,a=seta,r=r02,en=setE2,l=setl2},Eqdt)): dphi02:=rhs(subs({M=setM,a=seta,r=r02,en=setE2,l=setl2},Eqdphi)):

 

Lösung der Geodätengleichung: 

>

Loes1:=dsolve({subs({a=seta,M=setM},eq1),subs({a=seta,M=setM},eq2),subs({a=seta,M=setM},eq3),subs({a=seta,M=setM},eq4),t(0)=t0,r(0)=r01,phi(0)=phi0,theta(0)=theta0,D(r)(0)=dr0,D(t)(0)=dt01,D(phi)(0)=dphi01,D(theta)(0)=dtheta0},{r(lambda),t(lambda),phi(lambda),theta(lambda)},type=numeric,output=listprocedure): Loes2:=dsolve({subs({a=seta,M=setM},eq1),subs({a=seta,M=setM},eq2),subs({a=seta,M=setM},eq3),subs({a=seta,M=setM},eq4),t(0)=t0,r(0)=r02,phi(0)=phi0,theta(0)=theta0,D(r)(0)=dr0,D(t)(0)=dt02,D(phi)(0)=dphi02,D(theta)(0)=dtheta0},{r(lambda),t(lambda),phi(lambda),theta(lambda)},type=numeric,output=listprocedure):

 

Animation der Bewegung beider Fälle: 

>

UnRot:=solve(get_compts(g)[1,1]=0,r): Horizon:=solve(get_compts(ginv)[2,2]=0,r): A:=implicitplot(r = subs({M=setM,a=seta,theta=Pi/2},UnRot[1]), r = 0 .. 3, phi = 0 .. 2*Pi, coords = polar,grid=[30,30],color=red,linestyle=dash,thickness=1): B:=implicitplot(r = subs({M=setM,a=seta,theta=Pi/2},UnRot[2]), r = 0 .. 3, phi = 0 .. 2*Pi, coords = polar,grid=[30,30],color=red,linestyle=solid): C:=implicitplot(r = subs({M=setM,a=seta,theta=Pi/2},Horizon[1]), r = 0 .. 3, phi = 0 .. 2*Pi, coords = polar,grid=[30,30],color=black,linestyle=dash,thickness=1): DD:=implicitplot(r = subs({M=setM,a=seta,theta=Pi/2},Horizon[2]), r = 0 .. 3, phi = 0 .. 2*Pi, coords = polar,grid=[30,30],color=black,linestyle=solid): BH1:=display(disk([0,0],subs({M=setM,a=seta,theta=Pi/2},Horizon[2]),color=black)): BH2:=display(disk([0,0],subs({M=setM,a=seta,theta=Pi/2},Horizon[1]),color=white)): BH3:=display(disk([0,0],subs({M=setM,a=seta,theta=Pi/2},UnRot[1]),color=yellow)): BH:=display({A,B,C,DD,BH1,BH2,BH3},scaling=constrained):

 

>

frames:=100: lend:=36.73: Lr1 := subs(Loes1,r(lambda)): Lphi1 := subs(Loes1,phi(lambda)): Lr2 := subs(Loes2,r(lambda)): Lphi2 := subs(Loes2,phi(lambda)): for i from 0 by 1 to frames do Koerper1[i]:=display(disk([Lr1(i*lend/frames)*cos(Lphi1(i*lend/frames)),Lr1(i*lend/frames)*sin(Lphi1(i*lend/frames))],0.3,color=blue)): Koerper2[i]:=display(disk([Lr2(i*lend/frames)*cos(Lphi2(i*lend/frames)),Lr2(i*lend/frames)*sin(Lphi2(i*lend/frames))],0.3,color=red)): Ani[i]:=display({Koerper1[i],Koerper2[i],BH}); od:

 

>	display([seq(Ani[i],i=0..frames)],insequence=true,scaling=constrained);

 

 

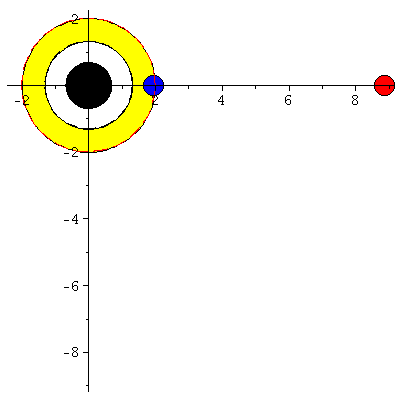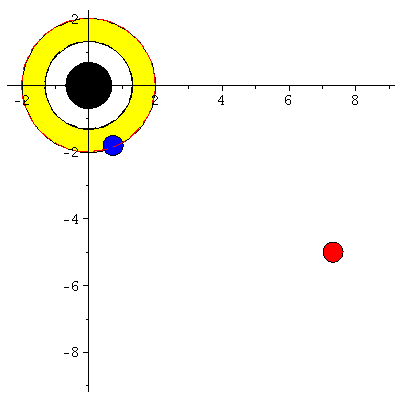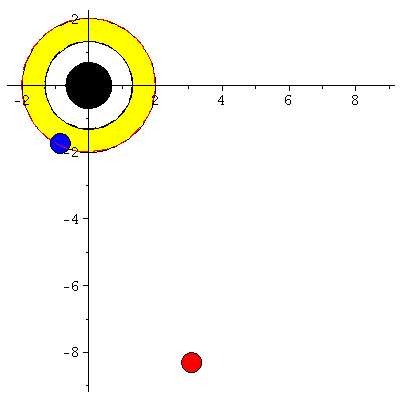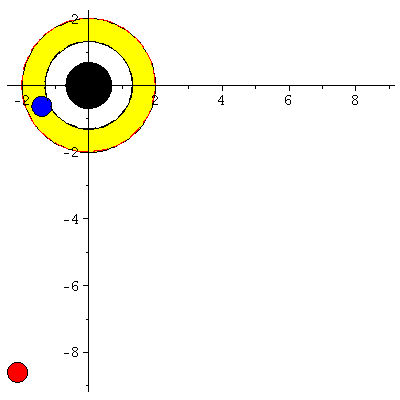Man erkennt, dass der ISCO nur eine metastabile Lösung ist, da es sich um einen Sattelpunkt des effektiven Potentials handelt (blauer Probekörper fällt nach ca. lambda=36.73 in das schwarze Loch). Die blaue Kurve (Probekörper rotiert in gleicher Richtung wie die Rotationsrichtung des schwarzen Loches) hällt sich zusätzlich noch innerhalb der Ergosphähre auf (r=1.94 km). 

>

 

 

Der gravitomagnetische Effekt 

Die durch die Rotation des schwarzen Lochs hervorgerufene Erscheinungen sind den magnetischen Eigenschaften in der Elektrodynamik sehr ähnlich. Der Mitführungseffekt der Raumzeit ("Frame-Dragging" bzw. Lense-Thiring Effekt) verursacht, gravitomagnetische Effekte die in ähnlicher Weise wie die Lorentzkraft in der Elektrodynamik wirken. Hier verdeutlichen wir dies an einem Beispiel: 

>	restart: with( tensor ): with(plots): with(plottools):

 

Definition der kovarianten Raumzeit-Metrik eines rotierenden schwarzen Lochs der Masse M und Rotation a in Kerrschildkoordinaten: 

>

coord := [t, r, theta, phi]: rho2:=r^2+(a*cos(theta))^2: Delta:=r^2-2*M*r+a^2: Sig2:=(r^2+a^2)^2-a^2*Delta*(sin(theta))^2: g_compts := array(symmetric,sparse, 1..4, 1..4): g_compts[1,1] := (1-2*M*r/rho2): g_compts[1,4] := +(2*a*M*r*(sin(theta))^2)/rho2: g_compts[2,2] :=-rho2/Delta: g_compts[3,3] := -rho2: g_compts[4,4] := -(r^2+a^2+2*M*r*a^2*(sin(theta))^2/rho2): g := create( [-1,-1], eval(g_compts));

 

(1.3.1)

 

Berechnung der kontravarianten Metrik, der Christoffel Symbole, des Riemanntensors...: 

>	ginv := invert( g, 'detg' ): D1g := d1metric( g, coord ):   D2g := d2metric( D1g, coord ): Cf1 := Christoffel1( D1g ): Cf2:= Christoffel2( ginv, Cf1 ): D2g := d2metric ( D1g, coord ): RMN := Riemann( ginv, D2g, Cf1 ): RICCI := Ricci( ginv, RMN ): RS := Ricciscalar( ginv, RICCI ):

 

Berechnung der Geodätengleichung als Funktion des affinen Parameters lambda. Die Geodätengleichung ist ein System gekoppelter Differentialgleichungen:   

>	eqns:=geodesic_eqns( coord, lambda, Cf2 ):

 

Umschreiben der Variablen in den Bewegungsgleichungen (z.B. r->r(lambda)): 

>

eq1:=simplify(subs({r=r(lambda),theta=theta(lambda)},eqns[1])): eq2:=simplify(subs({r=r(lambda),theta=theta(lambda)},eqns[2])): eq3:=simplify(subs({r=r(lambda),theta=theta(lambda)},eqns[3])): eq4:=simplify(subs({r=r(lambda),theta=theta(lambda)},eqns[4])): eq1:=simplify(subs({r(lambda)(lambda)=r(lambda),theta(lambda)(lambda)=theta(lambda)},eq1)): eq2:=simplify(subs({r(lambda)(lambda)=r(lambda),theta(lambda)(lambda)=theta(lambda)},eq2)): eq3:=simplify(subs({r(lambda)(lambda)=r(lambda),theta(lambda)(lambda)=theta(lambda)},eq3)): eq4:=simplify(subs({r(lambda)(lambda)=r(lambda),theta(lambda)(lambda)=theta(lambda)},eq4)):

 

Infinitesimales Weglängenelement ds²: 

>

dx:=create([1], array([dt,dr,dtheta,dphi])): ds2:=get_compts(prod(dx,lower(g,dx,1),[1,1])): ds2:=collect( simplify(ds2), [dt,dr,dtheta,dphi]): ds2a:=simplify(coeff(ds2, dt, 2)): ds2b:=simplify(coeff(ds2, dr, 2)): ds2c:=simplify(coeff(ds2, dtheta, 2)): ds2d:=simplify(coeff(ds2, dphi, 2)): ds2e:=simplify(coeff(ds2, dphi, 1)/dt): ds2:=ds2a*dt^2+ds2e*dt*dphi+ds2b*dr^2+ds2c*dtheta^2+ds2d*dphi^2;

 

(1.3.2)

 

Aufgrund der Normalisierungseigenschaft der Vierergeschwindigkeit u*u=-1 sind die Zeit- und phi-Komponente der Viergeschwindigkeit wie folgt durch die Energie- und Drehimpulswerte bestimmt (siehe Hartle-Buch, S:318): 

>	Eqdt:=dt=1/Delta*((r^2+a^2+2*M*a^2/r)*en-2*M*a/r*l); Eqdphi:=dphi=1/Delta*((1-2*M/r)*l+2*M*a/r*en);

 

 

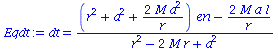	(1.3.3)

 

 

Das effektive Potential: 

>	VeffHartleRot:=(r,M,l,a,en)->-M/r+(l^2-a^2*(en^2-1))/(2*r^2)-M*(l-a*en)^2/r^3;

 

(1.3.4)

 

 

Im folgenden setzen wir M=1 und betrachten drei Fälle:
Fall 1: Schwarzes Loch rotiert nicht (a=0, grün) 

Fall 2: Schwarzes Loch rotiert nahe seines extremen Wertes im Uhrzeigersinn (a=0.99, blau)
Fall 3: Schwarzes Loch rotiert nahe seines extremen Wertes engegen dem Uhrzeigersinn (a=-0.99, rot) 

>

setM:=1: seta0:=0: setaP:=0.99: setaN:=-0.99: t0:=0: phi0:=Pi/10: theta0:=Pi/2: dtheta0:=0: #dphi0:=0.12: dphi0:=0.0685: dr0:=-0.6: r0:=10: Eqds2:=subs({dtheta=dtheta0,dr=dr0,cos(theta)=0,sin(theta)=1},ds2)=1: dt00:=solve(subs({theta=theta0,dphi=dphi0,dr=dr0,dtheta=dtheta0,M=setM,a=seta0,r=r0},Eqds2),dt)[1]: dt0P:=solve(subs({theta=theta0,dphi=dphi0,dr=dr0,dtheta=dtheta0,M=setM,a=setaP,r=r0},Eqds2),dt)[1]: dt0N:=solve(subs({theta=theta0,dphi=dphi0,dr=dr0,dtheta=dtheta0,M=setM,a=setaN,r=r0},Eqds2),dt)[1]: EquD0:=solve(subs({theta=theta0,dphi=dphi0,dr=dr0,dtheta=dtheta0,dt=dt00,M=setM,a=seta0,r=r0},{Eqdt,Eqdphi}),{en,l}): EquDP:=solve(subs({theta=theta0,dphi=dphi0,dr=dr0,dtheta=dtheta0,dt=dt0P,M=setM,a=setaP,r=r0},{Eqdt,Eqdphi}),{en,l}): EquDN:=solve(subs({theta=theta0,dphi=dphi0,dr=dr0,dtheta=dtheta0,dt=dt0N,M=setM,a=setaN,r=r0},{Eqdt,Eqdphi}),{en,l}): setE0:=rhs(EquD0[1]): setl0:=rhs(EquD0[2]): setEP:=rhs(EquDP[1]): setlP:=rhs(EquDP[2]): setEN:=rhs(EquDN[1]): setlN:=rhs(EquDN[2]):

 

Effektive Potentiale: 

>

Vmax:=1.4: Vmin:=-0.1: rmax:=20: PointB0:=pointplot({[r0, (setE0^2-1)/2]},symbol=solidcircle,symbolsize=25,color=green): PlotB0:=plot(VeffHartleRot(r,setM,setl0,seta0,setE0),r=1.4..50,view=[1.4..rmax,Vmin..Vmax],numpoints=700,color=green): PointBP:=pointplot({[r0, (setEP^2-1)/2]},symbol=solidcircle,symbolsize=25,color=blue): PlotBP:=plot(VeffHartleRot(r,setM,setlP,setaP,setEP),r=1.4..50,view=[1.4..rmax,Vmin..Vmax],numpoints=700,color=blue): PointBN:=pointplot({[r0, (setEN^2-1)/2]},symbol=solidcircle,symbolsize=25,color=red): PlotBN:=plot(VeffHartleRot(r,setM,setlN,setaN,setEN),r=1.4..50,view=[1.4..rmax,Vmin..Vmax],numpoints=700,color=red): display(PointB0,PlotB0,PointBN,PlotBN,PointBP,PlotBP);

 

 

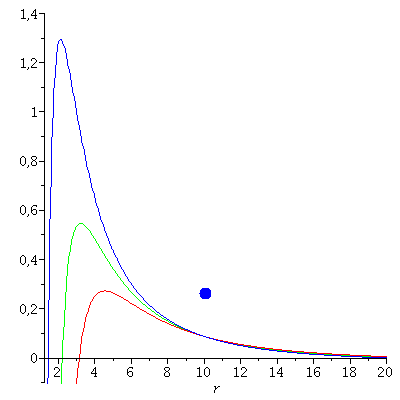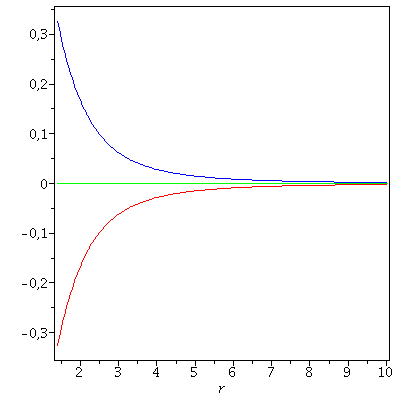
Die Rotationsfrequenz mit der die Raumzeit mitgeführt wird als "Frame dragging" Frequenz bezeichnet (siehe Vorlesung 5). Diese "Frame dragging" Frequenz (FD) wirkt in ähnlicher Weise auf die Geschwindigkeit von Probekörpern, wie das Magnetfeld in der Elektrodynamik die Lorentzkraft verursacht. Im Fall1 (grün) ist das gravitomagnetische Feld Null, im Fall 2 (blau) ist es aus der äquatoriellen Ebene nach oben gerichtet und im Fall 3 zeigt es nach unten. In erster Näherung (siehe Fließbach Buch, S:172) ist die gravitomagnetische Lorentzkraft gleich (2 FD x v), wobei x das Kreuzprodukt, FD der axiale Vektor der "Frame dragging" Frequenz und v der Geschwindigkeitsvektor des Probekörpers ist. 

>

FrameDrag:=get_compts(ginv)[1,4]/get_compts(ginv)[1,1]; FrameDrag0:=evalf(subs({M=setM,a=seta0,theta=theta0},FrameDrag)): FrameDragP:=evalf(subs({M=setM,a=setaP,theta=theta0},FrameDrag)): FrameDragN:=evalf(subs({M=setM,a=setaN,theta=theta0},FrameDrag)): FDmax:=0.35: FDmin:=-0.35: rmax:=10: PlotFD0:=plot(FrameDrag0,r=1.4..50,view=[1.4..rmax,FDmin..FDmax],numpoints=700,color=green): PlotFDP:=plot(FrameDragP,r=1.4..50,view=[1.4..rmax,FDmin..FDmax],numpoints=700,color=blue): PlotFDN:=plot(FrameDragN,r=1.4..50,view=[1.4..rmax,FDmin..FDmax],numpoints=700,color=red): display(PlotFD0,PlotFDP,PlotFDN,axes=boxed);

 

 

 

Lösen der Geodätengleichung für die drei Fälle: 

>

seta:=seta0: Loes0:=dsolve({subs({a=seta,M=setM},eq1),subs({a=seta,M=setM},eq2),subs({a=seta,M=setM},eq3),subs({a=seta,M=setM},eq4),t(0)=t0,r(0)=r0,phi(0)=phi0,theta(0)=theta0,D(r)(0)=dr0,D(t)(0)=dt00,D(phi)(0)=dphi0,D(theta)(0)=dtheta0},{r(lambda),t(lambda),phi(lambda),theta(lambda)},type=numeric,output=listprocedure): seta:=setaP: LoesP:=dsolve({subs({a=seta,M=setM},eq1),subs({a=seta,M=setM},eq2),subs({a=seta,M=setM},eq3),subs({a=seta,M=setM},eq4),t(0)=t0,r(0)=r0,phi(0)=phi0,theta(0)=theta0,D(r)(0)=dr0,D(t)(0)=dt0P,D(phi)(0)=dphi0,D(theta)(0)=dtheta0},{r(lambda),t(lambda),phi(lambda),theta(lambda)},type=numeric,output=listprocedure): seta:=setaN: LoesN:=dsolve({subs({a=seta,M=setM},eq1),subs({a=seta,M=setM},eq2),subs({a=seta,M=setM},eq3),subs({a=seta,M=setM},eq4),t(0)=t0,r(0)=r0,phi(0)=phi0,theta(0)=theta0,D(r)(0)=dr0,D(t)(0)=dt0N,D(phi)(0)=dphi0,D(theta)(0)=dtheta0},{r(lambda),t(lambda),phi(lambda),theta(lambda)},type=numeric,output=listprocedure):

 

Animation der Bewegung: 

>

seta:=setaP: UnRot:=solve(get_compts(g)[1,1]=0,r): Horizon:=solve(get_compts(ginv)[2,2]=0,r): A:=implicitplot(r = subs({M=setM,a=seta,theta=Pi/2},UnRot[1]), r = 0 .. 3, phi = 0 .. 2*Pi, coords = polar,grid=[30,30],color=red,linestyle=dash,thickness=1): B:=implicitplot(r = subs({M=setM,a=seta,theta=Pi/2},UnRot[2]), r = 0 .. 3, phi = 0 .. 2*Pi, coords = polar,grid=[30,30],color=red,linestyle=solid): C:=implicitplot(r = subs({M=setM,a=seta,theta=Pi/2},Horizon[1]), r = 0 .. 3, phi = 0 .. 2*Pi, coords = polar,grid=[30,30],color=black,linestyle=dash,thickness=1): DD:=implicitplot(r = subs({M=setM,a=seta,theta=Pi/2},Horizon[2]), r = 0 .. 3, phi = 0 .. 2*Pi, coords = polar,grid=[30,30],color=black,linestyle=solid): BH1:=display(disk([0,0],subs({M=setM,a=seta,theta=Pi/2},Horizon[2]),color=black)): BH2:=display(disk([0,0],subs({M=setM,a=seta,theta=Pi/2},Horizon[1]),color=white)): BH3:=display(disk([0,0],subs({M=setM,a=seta,theta=Pi/2},UnRot[1]),color=yellow)): BH:=display({A,B,C,DD,BH1,BH2,BH3},scaling=constrained):

 

>

frames:=100: lend:=33: Lr0 := subs(Loes0,r(lambda)): Lphi0 := subs(Loes0,phi(lambda)): LrP := subs(LoesP,r(lambda)): LphiP := subs(LoesP,phi(lambda)): LrN := subs(LoesN,r(lambda)): LphiN := subs(LoesN,phi(lambda)): for i from 0 by 1 to frames do Koerper0[i]:=display(disk([Lr0(i*lend/frames)*cos(Lphi0(i*lend/frames)),Lr0(i*lend/frames)*sin(Lphi0(i*lend/frames))],0.4,color=green)): KoerperP[i]:=display(disk([LrP(i*lend/frames)*cos(LphiP(i*lend/frames)),LrP(i*lend/frames)*sin(LphiP(i*lend/frames))],0.4,color=blue)): KoerperN[i]:=display(disk([LrN(i*lend/frames)*cos(LphiN(i*lend/frames)),LrN(i*lend/frames)*sin(LphiN(i*lend/frames))],0.4,color=red)): Traj0[i]:=listplot([seq([Lr0(j*lend/frames)*cos(Lphi0(j*lend/frames)),Lr0(j*lend/frames)*sin(Lphi0(j*lend/frames))], j = 0 .. i)],color=green,linestyle=dot): TrajP[i]:=listplot([seq([LrP(j*lend/frames)*cos(LphiP(j*lend/frames)),LrP(j*lend/frames)*sin(LphiP(j*lend/frames))], j = 0 .. i)],color=blue,linestyle=dot): TrajN[i]:=listplot([seq([LrN(j*lend/frames)*cos(LphiN(j*lend/frames)),LrN(j*lend/frames)*sin(LphiN(j*lend/frames))], j = 0 .. i)],color=red,linestyle=dot): Ani[i]:=display({Koerper0[i],KoerperP[i],KoerperN[i],BH,Traj0[i],TrajP[i],TrajN[i]}); od:

 

>	display([seq(Ani[i],i=0..frames)],insequence=true,scaling=constrained);

 

 

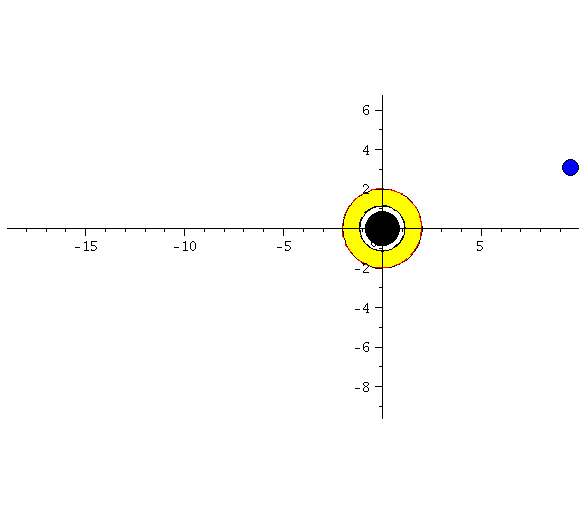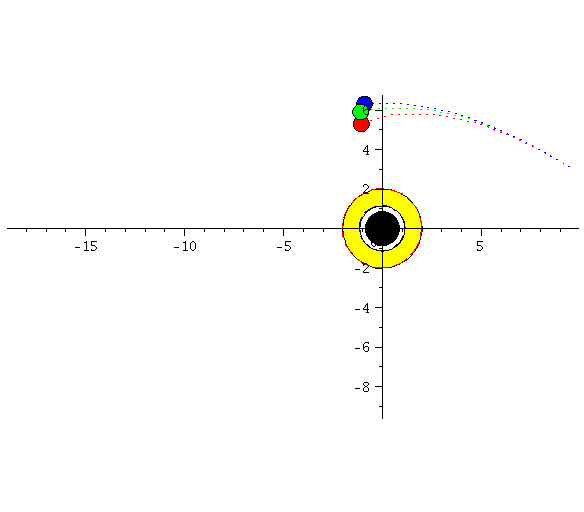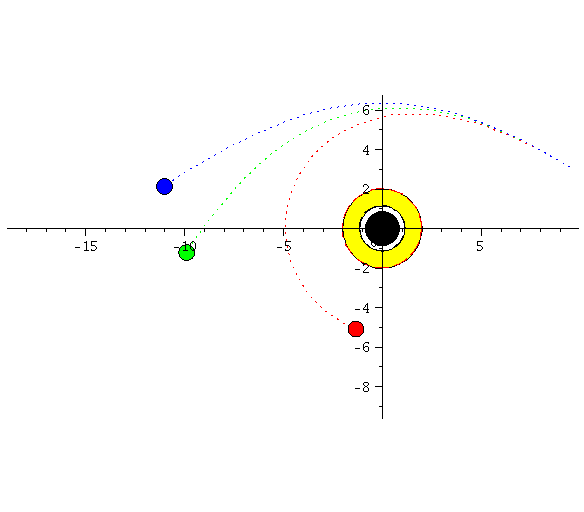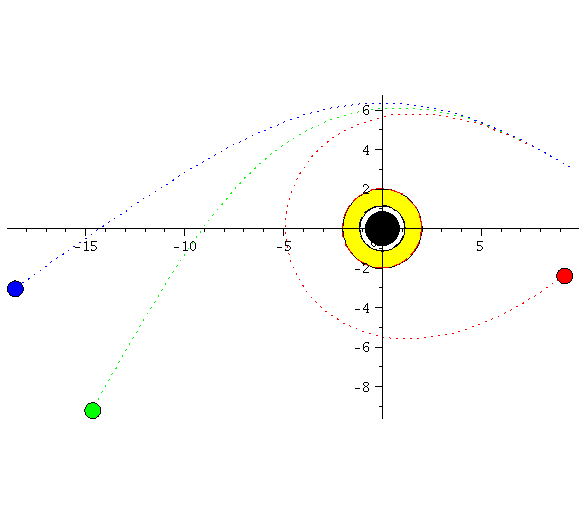Die Animation veranschaulicht den allgemeinrelativistischen gravitomagnetischen Effekt eines rotierenden schwarzen Loches. Die grüne Kurve entspricht einer Situation ohne Magnetfeld (nur Coulombkraft = keine Rotation), die blaue Kurve entspricht einer Situation wo das gravitomagnetische Feld in +z-Richtung (schwarzes Loch rotiert entgegen dem Uhrzeigersinn) zeigt und bei der roten Kurve zeigt das gravitomagnetische Feld in -z-Richtung (schwarzes Loch rotiert im Uhrzeigersinn). 

>

 

 

>