Download Maple Worksheed
Allgemeine Relativitätstheorie mit dem Computer
General Theory of Relativity on the Computer
Vorlesung gehalten an der J.W.Goethe-Universität in Frankfurt am Main (Sommersemester 2016)
von Dr.phil.nat. Dr.rer.pol. Matthias Hanauske
Frankfurt am Main 11.04.2016
Erster Vorlesungsteil: Allgemeine Relativitätstheorie mit Maple
2. Vorlesung
Einführung
Bewegung eines Probekörpers (Masse verschwindend klein gegenüber der Masse des schwarzen Lochs) um ein schwarzes Loch ist ein astrophysikalisch sehr relevantes Problem. Es gilt als so gut wie bestätigt, dass im Zentrum unserer Galaxie ein superschwehres schwarzes Loch existiert und man verfolgt seit Jahrzenten (siehe z.B. R.Genzel et,al.) die Bewegung einzelner sogenannter S-Sterne um dieses Zentrum.Neben diesen aktuellen Erkenntnissen, gilt die Perihel-Drehung des Merkur als ein, durch die allgemeine Relativitätstheorie verursachter, Effekt. Obwohl die Bewegung der Planenten unseres Sonnensystems um unser Zentralgestirn (die Sonne) ja sicherlich keine Bewegung um ein schwarzes Loch darstellt, können die Gleichungen der Planetenbewegungen in guter Approximation als solche beschrieben werden (siehe Birkov-Theorem).
Die Geodätengleichung in vorgegebener Schwarzschild Raumzeit
Im folgenden wird die Geodätengleichung in vorgegebener Schwarzschild Raumzeit betrachtet. Die Geodätengleichung beschreibt wie sich ein Probekörper (Masse = 0) im Raum bewegt und sagt voraus, dass diese Bewegung sich stehts entlang der kürzesten Kurve, in der durch die Metrik beschriebenen gekrümmten Raumzeit, vollzieht.
Radial in ein schwarzes Loch einfallender Probekörper
| > | restart:
with( tensor ): with(plots): with(plottools): |
Definition der kovarianten Raumzeit-Metrik eines schwarzen Lochs der Masse M in Schwarzschildkoordinaten:
| > | coord := [t, r, theta, phi]:
g_compts := array(symmetric,sparse, 1..4, 1..4): g_compts[1,1] := 1-2*M/r: g_compts[2,2] := -1/g_compts[1,1]: g_compts[3,3] := -r^2: g_compts[4,4] := -r^2*sin(theta)^2: g := create( [-1,-1], eval(g_compts)); |
![table( [( index_char ) = [-1, -1], ( compts ) = array( 1 .. 4, 1 .. 4, [( 3, 3 ) = `+`(`-`(`*`(`^`(r, 2)))), ( 2, 2 ) = `+`(`-`(`/`(1, `*`(`+`(1, `-`(`/`(`*`(2, `*`(M)), `*`(r)))))))), ( 4, 4 ) = `+`(...](images/Vorlesung2_1.gif) ![table( [( index_char ) = [-1, -1], ( compts ) = array( 1 .. 4, 1 .. 4, [( 3, 3 ) = `+`(`-`(`*`(`^`(r, 2)))), ( 2, 2 ) = `+`(`-`(`/`(1, `*`(`+`(1, `-`(`/`(`*`(2, `*`(M)), `*`(r)))))))), ( 4, 4 ) = `+`(...](images/Vorlesung2_2.gif) |
(2.1.1) |
Berechnung der kontravarianten Metrik und der Christoffel Symbole:
| > | ginv := invert( g, 'detg' ):
D1g := d1metric( g, coord ): D2g := d2metric( D1g, coord ): Cf1 := Christoffel1( D1g ): Cf2:= Christoffel2( ginv, Cf1 ): |
Berechnung der Geodätengleichung als Funktion des affinen Parameters lambda. Die Geodätengleichung ist ein System gekoppelter Differentialgleichungen:
| > | eqns:=geodesic_eqns( coord, lambda, Cf2 ); |
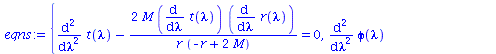 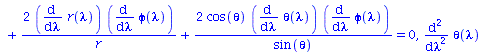 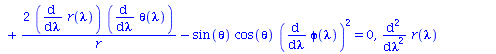 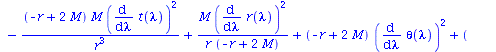  |
(2.1.2) |
Wir lassen nur radiale Bewegung zu und setzen die Masse des schwarzen Lochs auf M=1:
| > | eq1:=subs({diff(phi(lambda),lambda)=0,diff(theta(lambda),lambda)=0,M=1},eqns[1]):
eq2:=subs({diff(phi(lambda),lambda)=0,diff(theta(lambda),lambda)=0,M=1},eqns[2]): eq3:=subs({diff(phi(lambda),lambda)=0,diff(theta(lambda),lambda)=0,M=1},eqns[3]): eq4:=subs({diff(phi(lambda),lambda)=0,diff(theta(lambda),lambda)=0,M=1},eqns[4]): eq1:=simplify(subs({r=r(lambda)},eq1)): eq4:=simplify(subs({r=r(lambda)},eq4)): eq1:=simplify(subs({r(lambda)(lambda)=r(lambda)},eq1)); eq4:=simplify(subs({r(lambda)(lambda)=r(lambda)},eq4)); |
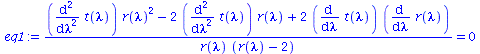 |
|
| (2.1.3) |
Anfangswerte:
Zur Zeit t=0 sei der fallende Körper bei einem Radius von r=10=5*(Schwarzschildradius), die Anfangsgeschwindigkeit des Körpers sei 0. Wir beschreiben den Fall aus der Sichtweise eines im Unendlichen ruhenden Beobachters.Bemerkung: Der Anfangswert dt0 ergibt sich hierbei aus dem infinitesimalen Weglängenelements ds2=1 eines massiven Probekörpers:
| > | r0:=10:
t0:=0: dr0:=0: dt0:=evalf(1/sqrt(1-2/r0)): |
Numerisches Lösen der Geodätengleichung:
| > | Loes:=dsolve({eq1,eq4,t(0)=t0,r(0)=r0,D(r)(0)=0,D(t)(0)=dt0},{r(lambda),t(lambda)},type=numeric,output=listprocedure): |
Zum Vergleich lösen wir auch die Bewegungsgleichung nach Newton:
| > | Loes_newton:=dsolve({diff(r(lambda),lambda,lambda)=-1/r(lambda)^2,r(0)=r0,D(r)(0)=0},{r(lambda)},type=numeric,output=listprocedure): |
Grafische Veranschaulichung der Lösung (rote Kurve ist die nach Newton berechnete):
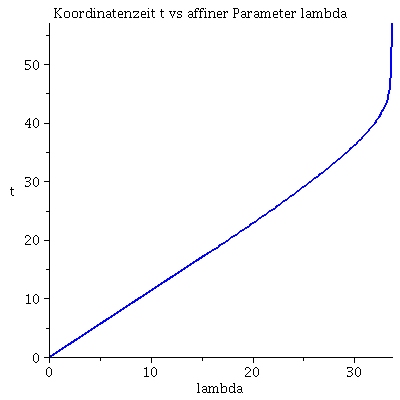
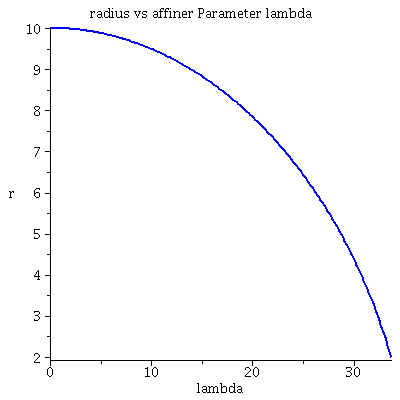
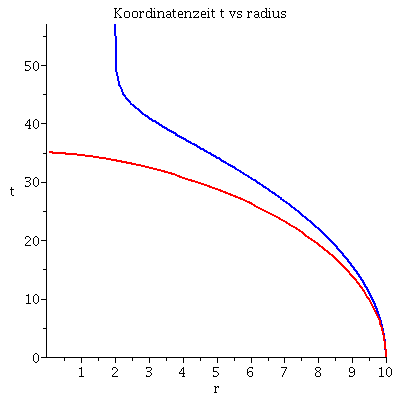
| > | lend:=33.7:
lendn:=35.12: Plot1:=odeplot(Loes,[lambda,t(lambda)],0..lend,numpoints=200,color=blue,thickness=2,title="Koordinatenzeit t vs affiner Parameter lambda"): Plot2:=odeplot(Loes,[lambda,r(lambda)],0..lend,numpoints=200,color=blue,thickness=2,title="radius vs affiner Parameter lambda"): Plot3:=odeplot(Loes,[r(lambda),t(lambda)],0..lend,numpoints=700,color=blue,thickness=2,title="Koordinatenzeit t vs radius"): Plot_newton:=odeplot(Loes_newton,[r(lambda),lambda],0..lendn,numpoints=100,color=red,thickness=2): display(Matrix(1,3,[Plot1,Plot2,display(Plot3,Plot_newton)])); |
|
Der in das schwarze Loch fallende Probekörpers bleibt somit, für einen äußeren Beobachter, anscheinend am Ereignishorizont bei r=2*M stehen (siehe das Raumzeitdiagramm oben links). Seine Bewegung in radialer Richtung wird nahe dem Ereignishorizont immer langsamer und das Bild, welches ein äußerer Beobachter wahrnimmt friert am Ereignishorizont ein. Man kann zeigen, dass das wahrgenommene Bild gleichzeitig unendlich rotverschoben wird, so dass es nahe dem Ereignishorizont, langsam den wahrnehmbaren, sichtbaren Bereich verläßt. Eine gute, pädagogische Verbildlichung dieser und weiterer seltsamen Eigenschaften von schwarzen Löchern spiegelt sich in der speziellen architektonischen Konstruktion des Berliner Reichstagsgebäudes wider (siehe Black Holes and the German Reichstag)
Bewegung eines Probekörpers um ein schwarzes Loch in der Ebene
| > | restart:
with( tensor ): with(plots): with(plottools): |
Definition der kovarianten Raumzeit-Metrik eines schwarzen Lochs der Masse M in Schwarzschildkoordinaten:
| > | coord := [t, r, theta, phi]:
g_compts := array(symmetric,sparse, 1..4, 1..4): g_compts[1,1] := 1-2*M/r: g_compts[2,2] := -1/g_compts[1,1]: g_compts[3,3] := -r^2: g_compts[4,4] := -r^2*sin(theta)^2: g := create( [-1,-1], eval(g_compts)); |
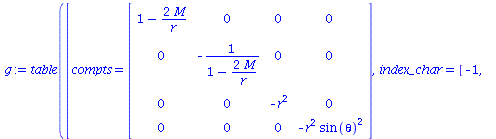  |
(2.2.1) |
Berechnung der kontravarianten Metrik und der Christoffel Symbole:
| > | ginv := invert( g, 'detg' ):
D1g := d1metric( g, coord ): D2g := d2metric( D1g, coord ): Cf1 := Christoffel1( D1g ): Cf2:= Christoffel2( ginv, Cf1 ): |
Berechnung der Geodätengleichung als Funktion des affinen Parameters lambda. Die Geodätengleichung ist ein System gekoppelter Differentialgleichungen:
| > | eqns:=geodesic_eqns( coord, lambda, Cf2 );
evalf(cos(Pi/2)); evalf(sin(Pi/2)); |
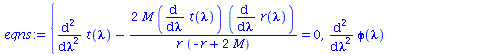 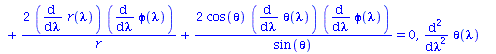 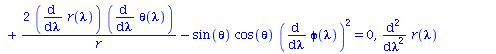 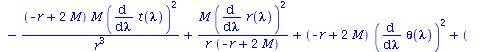  |
|
| (2.2.2) |
Wir lassen nur ebene Bewegungen zu (theta=Pi/2, dtheta=0) und setzen M=1:
| > | eq1:=subs({r=r(lambda),M=1,sin(theta)=1,cos(theta)=0,diff(theta(lambda),lambda)=0,theta=Pi/2},eqns[1]):
eq2:=subs({r=r(lambda),M=1,sin(theta)=1,cos(theta)=0,diff(theta(lambda),lambda)=0,theta=Pi/2},eqns[2]): eq3:=subs({r=r(lambda),M=1,sin(theta)=1,cos(theta)=0,diff(theta(lambda),lambda)=0,theta=Pi/2},eqns[3]): eq4:=subs({r=r(lambda),M=1,sin(theta)=1,cos(theta)=0,diff(theta(lambda),lambda)=0,theta=Pi/2},eqns[4]): eq1:=subs({r(lambda)(lambda)=r(lambda)},eq1); eq2:=subs({r(lambda)(lambda)=r(lambda)},eq2); eq3:=subs({r(lambda)(lambda)=r(lambda)},eq3); eq4:=subs({r(lambda)(lambda)=r(lambda)},eq4); |
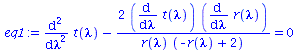 |
|
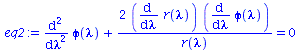 |
|
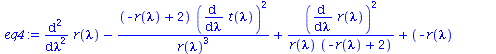 |
(2.2.3) |
In Abhängigkeit von den Anfangswerten können unterschiedliche Bahnen der Bewegung entstehen. Wir wählen zunächst als Beispiel die Anfangswerte einer geschlossenen Bahn:
Zur Zeit t=0 sei der fallende Körper bei einem Radius von r=10=5*(Schwarzschildradius), die Anfangsgeschwindigkeit des Körpers sei in radialer Richtung dr=0 und in phi-Richtung dphi=0.036. Wir beschreiben die Bewegung aus der Sichtweise eines im Unendlichen ruhenden Beobachters.
| > | r0:=10:
t0:=0: phi0:=0: theta0:=Pi/2: dr0:=0: dphi0:=0.036: dt0:=evalf(1/sqrt(1-2/r0)*sqrt(1+r0^2*dphi0^2)): dtheta0:=0: |
Bemerkung: Der Anfangswert dt0 ergibt sich hierbei aus dem infinitesimalen Weglängenelements ds2=1 eines massiven Probekörpers:
| > | dx:=create([1], array([dt,dr,dtheta,dphi])):
ds2:=get_compts(prod(dx,lower(g,dx,1),[1,1])): ds2:=collect( simplify(ds2), [dt,dr,dtheta,dphi]); Gl1:=subs(M=1,sin(theta)=1,cos(theta)=0,dtheta=0,dr=0,ds2=1); dt=solve(Gl1,dt); |
| (2.2.4) |
Numerisches Lösen der Geodätengleichung:
| > | Loes:=dsolve({eq1,eq2,eq4,t(0)=t0,r(0)=r0,D(r)(0)=dr0,D(t)(0)=dt0,phi(0)=phi0,D(phi)(0)=dphi0},{r(lambda),t(lambda),phi(lambda)},type=numeric,output=listprocedure); |
| (2.2.5) |
Grafische Veranschaulichung der Lösung:
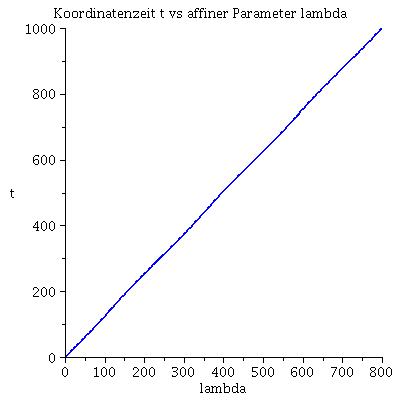
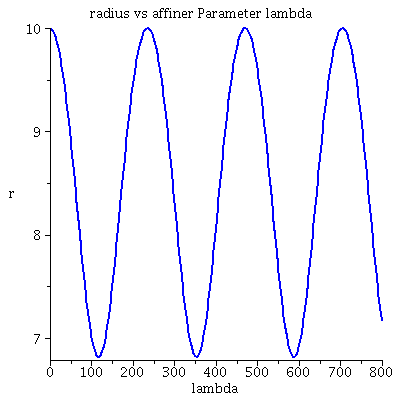
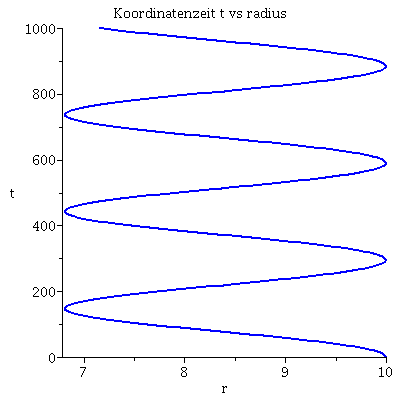
| > | lend:=800:
lendn:=35.12: Plot1:=odeplot(Loes,[lambda,t(lambda)],0..lend,numpoints=200,color=blue,thickness=2,title="Koordinatenzeit t vs affiner Parameter lambda"): Plot2:=odeplot(Loes,[lambda,r(lambda)],0..lend,numpoints=200,color=blue,thickness=2,title="radius vs affiner Parameter lambda"): Plot3:=odeplot(Loes,[r(lambda),t(lambda)],0..lend,numpoints=700,color=blue,thickness=2,title="Koordinatenzeit t vs radius"): display(Matrix(1,3,[Plot1,Plot2,Plot3])); |
|
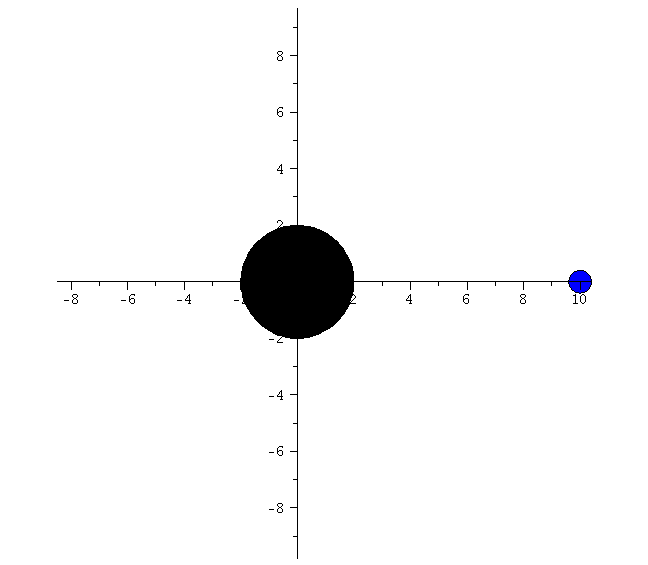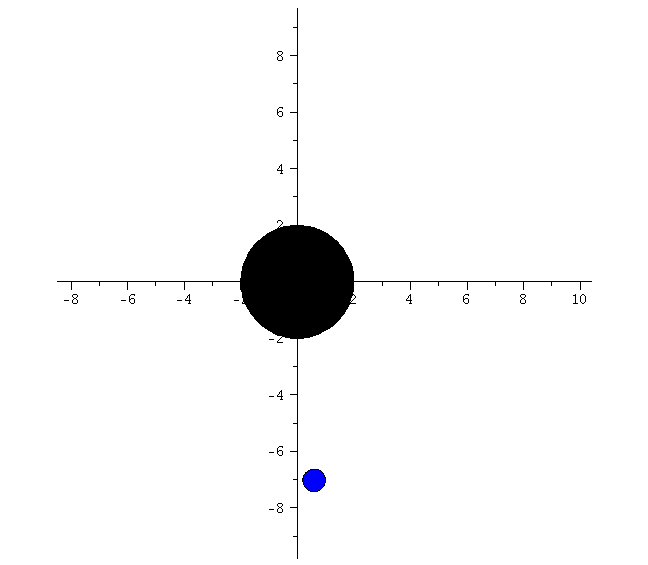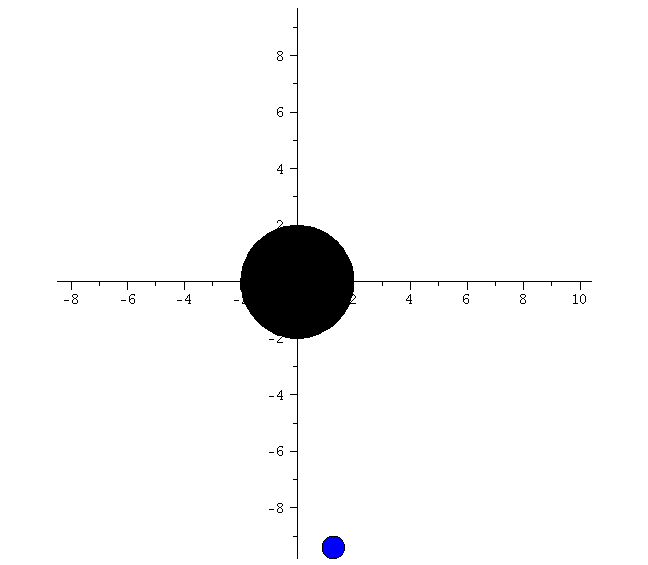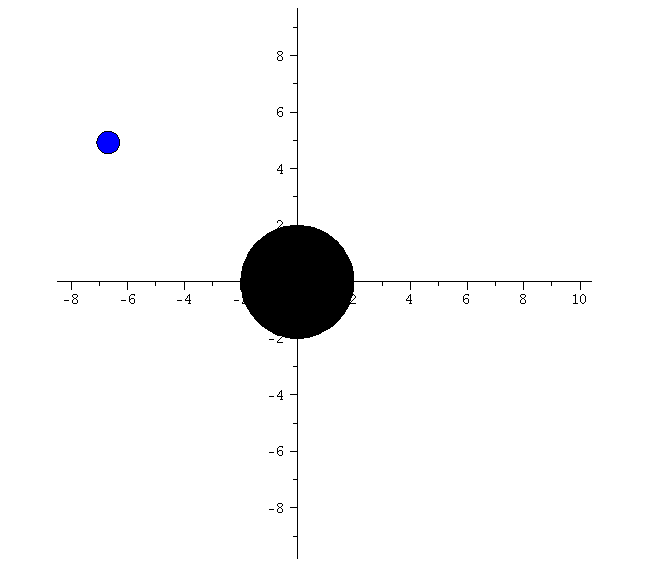
| > | frames:=100:
lend:=300: BH:=display(disk([0,0],2,color=black)): for i from 0 by 1 to frames do Koerper[i]:=display(disk([rhs(Loes(i*lend/frames)[4])*cos(rhs(Loes(i*lend/frames)[2])),rhs(Loes(i*lend/frames)[4])*sin(rhs(Loes(i*lend/frames)[2]))],0.4,color=blue)): Ani[i]:=display({Koerper[i],BH}); od: |
| > | display([seq(Ani[i],i=0..frames)],insequence=true,scaling=constrained); |
 |
| > |
| > |