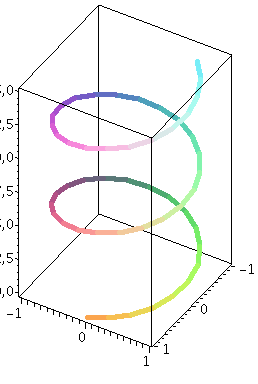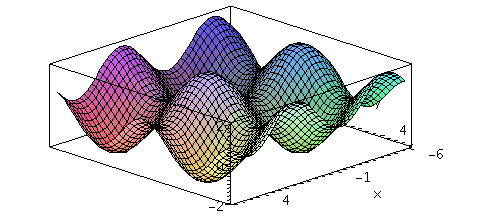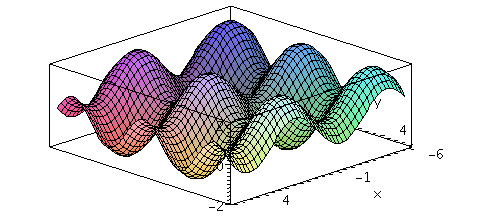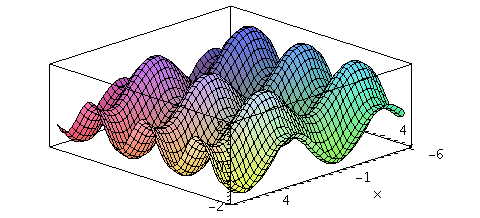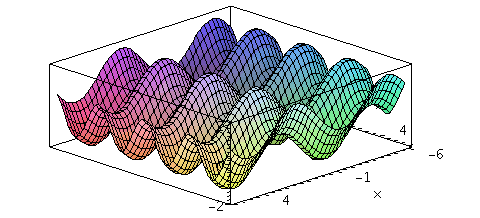Allgemeine Relativitätstheorie mit dem Computer
General Theory of Relativity on the Computer
Vorlesung gehalten an der J.W.Goethe-Universität in Frankfurt am Main (Sommersemester 2016)
von Dr.phil.nat. Dr.rer.pol. Matthias Hanauske
Frankfurt am Main 11.04.2016
Erster Vorlesungsteil: Allgemeine Relativitätstheorie mit Maple
Einführung in Maple
Getting started
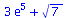 |
(1.1) |
| > |
evalf(3*exp(5)+sqrt(7)); |
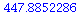 |
(1.2) |
| > |
Digits := 20:
evalf(3*exp(5)+sqrt(7)); |
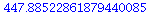 |
(1.3) |
Symbolic Calculations
Definition of Variables and Functions
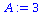 |
(2.1.1) |
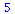 |
(2.1.2) |
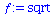 |
(2.1.3) |
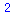 |
(2.1.4) |
| > |
g:=(x,y)->sin(x)+cos(y); |
 |
(2.1.5) |
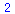 |
(2.1.6) |
Simplification of expressions
| > |
Exp1:=f(x)*(x^(5/2)+x^(3/2)); |
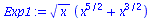 |
(2.2.1) |
 |
(2.2.2) |
| > |
Exp2:=sin(x)^2+cos(x)^2; |
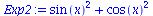 |
(2.2.3) |
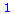 |
(2.2.4) |
Symbolic differentiation and integration
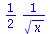 |
(2.3.1) |
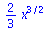 |
(2.3.2) |
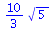 |
(2.3.3) |
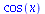 |
(2.3.4) |
| > |
int(int(g(x,y),x=0..Pi),y=0..Pi); |
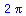 |
(2.3.5) |
| > |
Int(Int(g(x,y),x=0..Pi),y=0..Pi)=
int(int(g(x,y),x=0..Pi),y=0..Pi); |
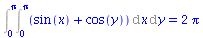 |
(2.3.6) |
Solving algebraic equations
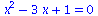 |
(2.4.1) |
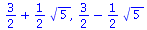 |
(2.4.2) |
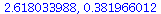 |
(2.4.3) |
Solving ordinary differential equations
| > |
DGL1:=diff(x(t),t)=3*x(t); |
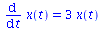 |
(2.5.1) |
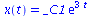 |
(2.5.2) |
| > |
dsolve({DGL1,x(0)=10},x(t)); |
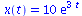 |
(2.5.3) |
Numerical Calculations
Limit finding
| > |
Limit(sin(x)/x,x=0)=limit(sin(x)/x,x=0); |
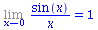 |
(3.1.1) |
Minimum (maximum) of lists
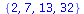 |
(3.2.1) |
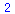 |
(3.2.2) |
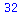 |
(3.2.3) |
Interpolation
![[0, 1, 2, 3, 4]](images/MapleTutorium_30.gif) |
(3.3.1) |
| > |
Yvalues:=[0.2,0.98,4.1,8.8,17]; |
![[.2, .98, 4.1, 8.8, 17]](images/MapleTutorium_31.gif) |
(3.3.2) |
| > |
Fit(a+b*x^2, Xvalues, Yvalues, x); |
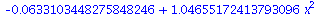 |
(3.3.3) |
Numerical integration
| > |
int(1/exp(x*ln(x)), x=1..infinity); |
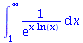 |
(3.4.1) |
| > |
evalf(int(1/exp(x*ln(x)), x=1..infinity)); |
 |
(3.4.2) |
Solving ordinary differential equations
| > |
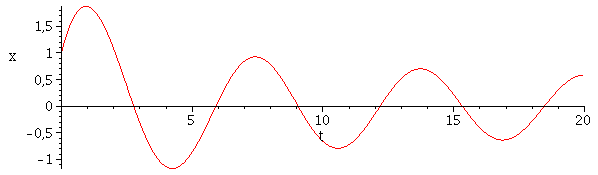
DGL2:=(t+1)^2*(diff(x(t),t,t))+(t+1)*(diff(x(t),t))+((t+1)^2-0.25)*x(t) = 0; |
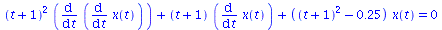 |
(3.5.1) |
| > |
Ergebnis:=dsolve({DGL2, x(0) = 1, (D(x))(0) = 2}, type=numeric,output=listprocedure); |
| > |
odeplot(Ergebnis,[t,x(t)],0..20,numpoints=1000); |
Visualisation of Data
2D plots
| > |
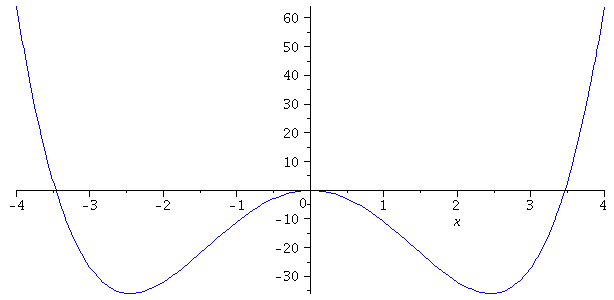
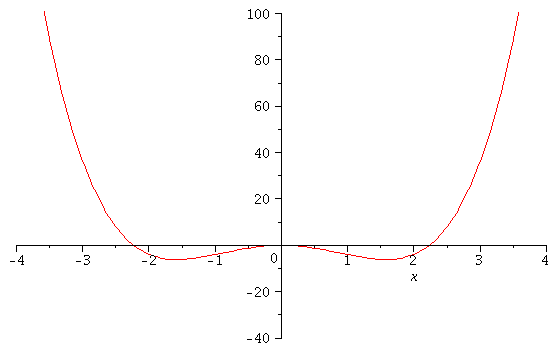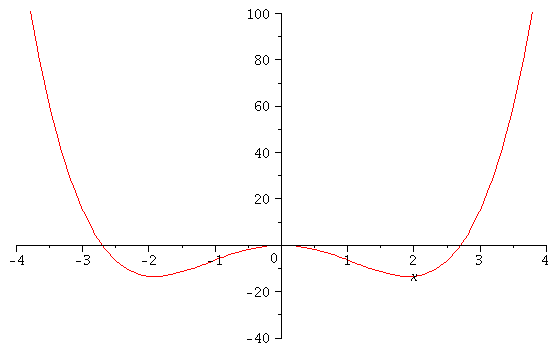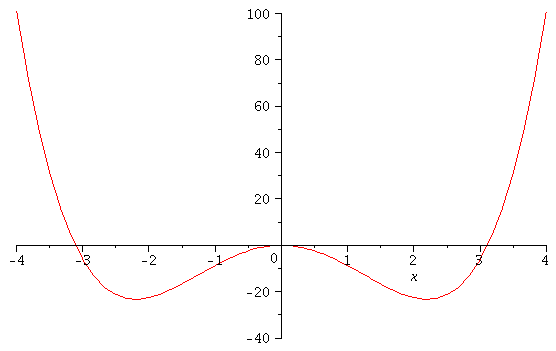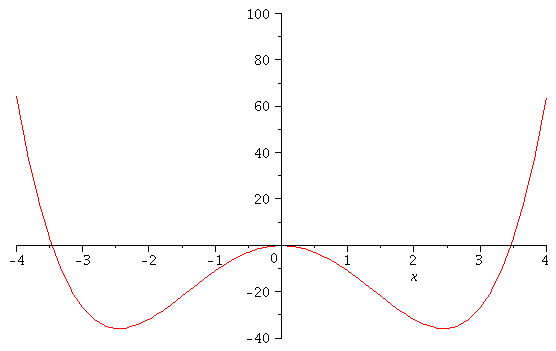
f:=(x)->x^4-12*x^2;
plot(f(x),x=-4..4,color=blue); |
Contour plots
| > |
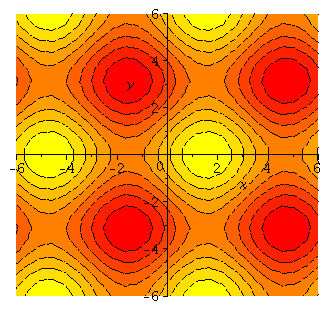
with(plots):
f:=(x,y)->sin(x)+cos(y);
contourplot(f(x,y),x=-6..6,y=-6..6,filledregions = true); |
3D surface plots
| > |
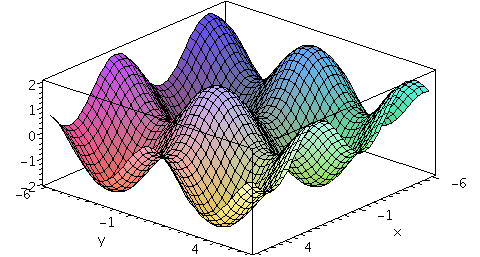
plot3d(f(x,y),x=-6..6,y=-6..6,axes=boxed,numpoints=1500); |
Spacecurves
| > |
spacecurve([cos(t), sin(t), t], t = 0 .. 15,axes=boxed,thickness=3); |
Animations
| > |
f:=(x,a)->x^4-a*x^2;
animate(f(x,a),x=-4..4,a=5..12,view=[-4..4,-40..100]); |
| > |
f:=(x,y,t)->sin(x)+cos(t*y);
animate3d(f(x,y,t),x=-6..6,y=-6..6,t=1..2,axes=boxed,numpoints=2000); |
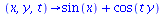 |
(4.5.1) |
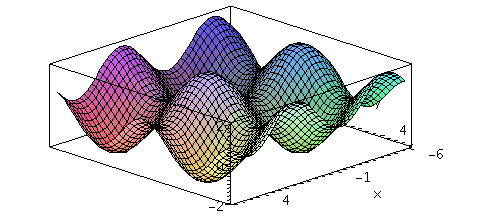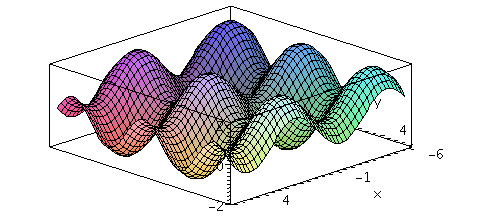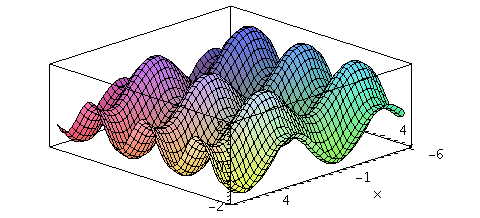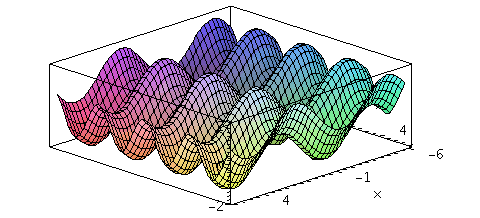 |
(4.5.1) |
Programming tools
Loops
| > |
a:=1:
for i from 1 by 1 to 10 do
a:=a*i:
od:
a; |
 |
(5.1.1) |
 |
(5.1.2) |
If procedures
| > |
a:=12:
b:=34:
if b < a then
print("a is greater than b") else print("a is not greater than b")
end if: |
 |
(5.2.1) |
Examples
| > |
Further Examples can be downloaded on the following internet page:
http://www.fias.uni-frankfurt.de/~hanauske/new/maple/ |