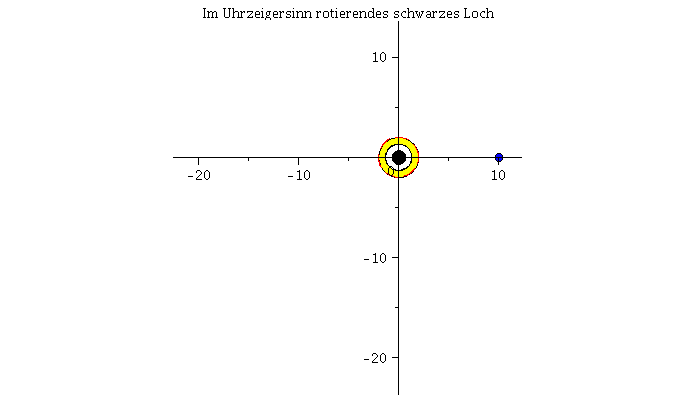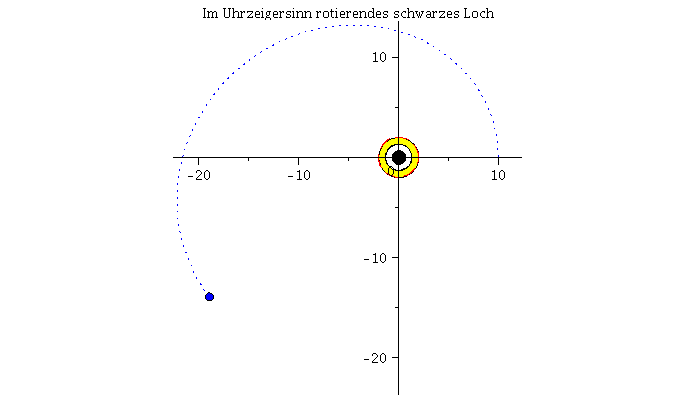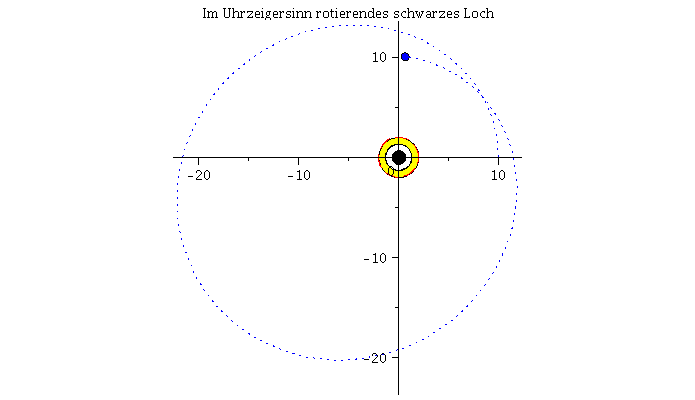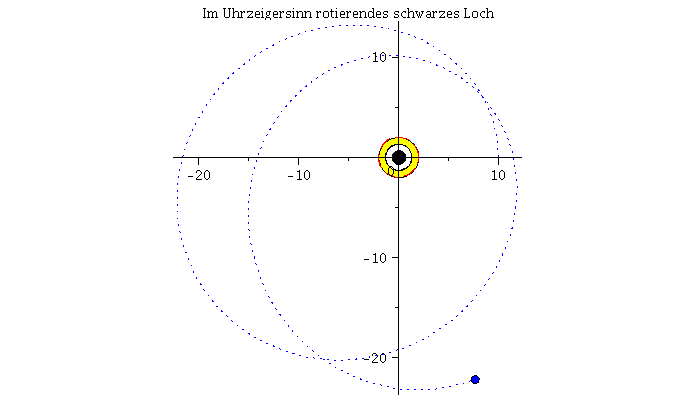Einführung 

Basierend auf den Ergebnissen der dritten Vorlesung des ersten Teils wird im folgenden die Bewegung eines Probekörpers um ein rotierendes schwarzes Loch vorgestellt.  

Bewegung eines Probekörpers um ein rotierendes schwarzes Loch 

Im folgenden wird die Geodätengleichung in vorgegebener Kerr-Raumzeit (in Boyer-Lindquist Koordinaten) betrachtet. Die Geodätengleichung beschreibt wie sich ein Probekörper (Masse = 0) im Raum bewegt und sagt voraus, dass diese Bewegung sich stehts entlang der kürzesten Kurve, in der durch die Metrik beschriebenen gekrümmten Raumzeit, vollzieht. 

Eigenschaften der Kerr-Metrik 

>	restart: with( tensor ): with(plots): with(plottools):

 

Definition der kovarianten Raumzeit-Metrik eines rotierenden schwarzen Lochs der Masse M und Rotation a in Boyer-Lindquist Koordinaten (a ist ein spezifischer Drehimpuls a=J/M und wird als der sogenannte Kerr-Rotationsparameter bezeichnet): 

>

coord := [t, r, theta, phi]: rho2:=r^2+(a*cos(theta))^2: Delta:=r^2-2*M*r+a^2:Sig2:=(r^2+a^2)^2-a^2*Delta*(sin(theta))^2: g_compts := array(symmetric,sparse, 1..4, 1..4): g_compts[1,1] := (1-2*M*r/rho2): g_compts[1,4] := +(2*a*M*r*(sin(theta))^2)/rho2: g_compts[2,2] :=-rho2/Delta: g_compts[3,3] := -rho2: g_compts[4,4] := -(r^2+a^2+2*M*r*a^2*(sin(theta))^2/rho2): g := create( [-1,-1], eval(g_compts));

 

(2.1.1)

 

Berechnung der kontravarianten Metrik, der Christoffel Symbole, des Riemanntensors...: 

>	ginv := invert( g, 'detg' ): D1g := d1metric( g, coord ):   D2g := d2metric( D1g, coord ): Cf1 := Christoffel1( D1g ): Cf2:= Christoffel2( ginv, Cf1 ): D2g := d2metric ( D1g, coord ): RMN := Riemann( ginv, D2g, Cf1 ): RICCI := Ricci( ginv, RMN ): RS := Ricciscalar( ginv, RICCI ):

 

Berechnung des infinitesimalen Weglängenelements ds²: 

>	dx:=create([1], array([dt,dr,dtheta,dphi])): ds2:=get_compts(prod(dx,lower(g,dx,1),[1,1])): ds2:=collect( simplify(ds2), [dt,dr,dtheta,dphi]);

 

(2.1.2)

 

>	ds2a:=simplify(coeff(ds2, dt, 2)): ds2b:=simplify(coeff(ds2, dr, 2)): ds2c:=simplify(coeff(ds2, dtheta, 2)): ds2d:=simplify(coeff(ds2, dphi, 2)): ds2e:=simplify(coeff(ds2, dphi, 1)/dt): ds2:=ds2a*dt^2+ds2e*dt*dphi+ds2b*dr^2+ds2c*dtheta^2+ds2d*dphi^2;

 

(2.1.3)

 

Struktur der Ereignishorizonte, Flächen der stationären Grenze und Flächen unendlicher Rotverschiebung 

Die Flächen der stationären Grenze (stationary limit surfaces) und die der unendlichen Rotverschiebung sind durch g_00=0 bestimmt: 

>	UnRot:=solve(get_compts(g)[1,1]=0,r);

 

(2.1.1.1)

 

Die Ereignishorizonte sind durch g^11=0 bestimmt: 

>	Horizon:=solve(get_compts(ginv)[2,2]=0,r);

 

(2.1.1.2)

 

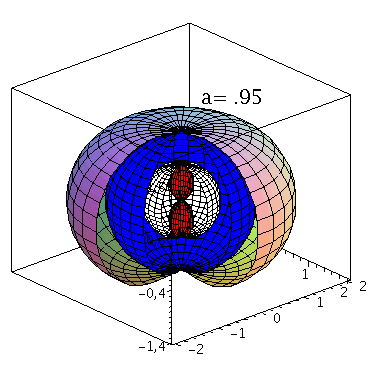
Grafische Veranschaulichung der Horizonte (a=0.95): 

>

with(StringTools): setM:=1: seta:=0.95: A:=plot3d({subs({M=setM,a=seta},UnRot[1])},phi=0..1.5*Pi,theta=0..Pi,coords=spherical,scaling=constrained): B:=plot3d({subs({M=setM,a=seta},UnRot[2])},phi=0..1.7*Pi,theta=0..Pi,coords=spherical,scaling=constrained,color=red): C:=plot3d({subs({M=setM,a=seta},Horizon[1])},phi=0..1.6*Pi,theta=0..Pi,coords=spherical,scaling=constrained,color=blue): DD:=plot3d({subs({M=setM,a=seta},Horizon[2])},phi=0..1.6*Pi,theta=0..Pi,coords=spherical,scaling=constrained,color=white): Ptext:=textplot3d([1, 1,2, Join(["a=",convert(seta,string)])], align =LEFT,color=black,font = [TIMES, ROMAN, 15]): display({A,B,C,DD,Ptext},axes=boxed,orientation=[-42,66], scaling=constrained);

 

 

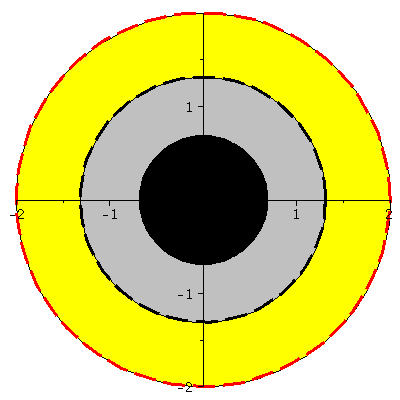
Horizontstruktur in der äquatorialen Ebene (Gelb: Ergosphäre, grau: Bereich zwischen äußerem und innerem Ereignishorizont, a=0.95): 

>

A:=implicitplot(r = subs({M=setM,a=seta,theta=Pi/2},UnRot[1]), r = 0 .. 3, phi = 0 .. 2*Pi, coords = polar,grid=[30,30],color=red,linestyle=dash,thickness=3): B:=implicitplot(r = subs({M=setM,a=seta,theta=Pi/2},UnRot[2]), r = 0 .. 3, phi = 0 .. 2*Pi, coords = polar,grid=[30,30],color=red,linestyle=solid): C:=implicitplot(r = subs({M=setM,a=seta,theta=Pi/2},Horizon[1]), r = 0 .. 3, phi = 0 .. 2*Pi, coords = polar,grid=[30,30],color=black,linestyle=dash,thickness=3): DD:=implicitplot(r = subs({M=setM,a=seta,theta=Pi/2},Horizon[2]), r = 0 .. 3, phi = 0 .. 2*Pi, coords = polar,grid=[30,30],color=black,linestyle=solid): BH1:=display(disk([0,0],subs({M=setM,a=seta,theta=Pi/2},Horizon[2]),color=black)): BH2:=display(disk([0,0],subs({M=setM,a=seta,theta=Pi/2},Horizon[1]),color=grey)): BH3:=display(disk([0,0],subs({M=setM,a=seta,theta=Pi/2},UnRot[1]),color=yellow)): display({A,B,C,DD,BH1,BH2,BH3},scaling=constrained);

 

 

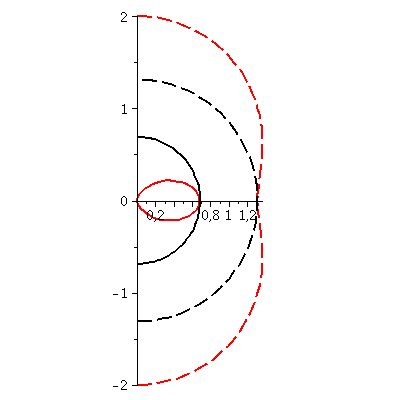
Horizontstruktur in der polaren Ebene (a=0.95): 

>

A:=implicitplot(r = subs({M=setM,a=seta},UnRot[1]), r = 0 .. 3, theta = -Pi/2 .. Pi/2, coords = polar,grid=[30,30],color=red,linestyle=dash,thickness=2): B:=implicitplot(r = subs({M=setM,a=seta},UnRot[2]), r = 0 .. 3, theta = -Pi/2 .. Pi/2, coords = polar,grid=[30,30],color=red,linestyle=solid,thickness=2): C:=implicitplot(r = subs({M=setM,a=seta},Horizon[1]), r = 0 .. 3, theta = -Pi/2 .. Pi/2, coords = polar,grid=[30,30],color=black,linestyle=dash,thickness=2): DD:=implicitplot(r = subs({M=setM,a=seta},Horizon[2]), r = 0 .. 3, theta = -Pi/2 .. Pi/2, coords = polar,grid=[30,30],color=black,linestyle=solid,thickness=2): BH1:=display(disk([0,0],subs({M=setM,a=seta},Horizon[2]),color=black)): BH2:=display(disk([0,0],subs({M=setM,a=seta},Horizon[1]),color=grey)): BH3:=display(disk([0,0],subs({M=setM,a=seta},UnRot[1]),color=yellow)): display({A,B,C,DD},scaling=constrained);

 

 

Animation der Horizontstruktur bei ansteigender Rotation des schwarzen Lochs: 

>

Digits:=2: setM:=1: frames:=30: for i from 1 by 1 to frames do seta:=0.7+0.3*i/frames: A:=plot3d({subs({M=setM,a=seta},UnRot[1])},phi=0..1.5*Pi,theta=0..Pi,coords=spherical,scaling=constrained): B:=plot3d({subs({M=setM,a=seta},UnRot[2])},phi=0..1.7*Pi,theta=0..Pi,coords=spherical,scaling=constrained,color=red): C:=plot3d({subs({M=setM,a=seta},Horizon[1])},phi=0..1.6*Pi,theta=0..Pi,coords=spherical,scaling=constrained,color=blue): DD:=plot3d({subs({M=setM,a=seta},Horizon[2])},phi=0..1.6*Pi,theta=0..Pi,coords=spherical,scaling=constrained,color=white): Ptext:=textplot3d([1, 1,2, Join(["a=",convert(seta,string)])], align =LEFT,color=black,font = [TIMES, ROMAN, 15]): Ani1[i]:=display({B,C,DD,Ptext,A},axes=normal,orientation=[-42,66], scaling=constrained); od:

 

>	display([seq(Ani1[i],i=1..frames)],insequence=true);

 

 

 

>

 

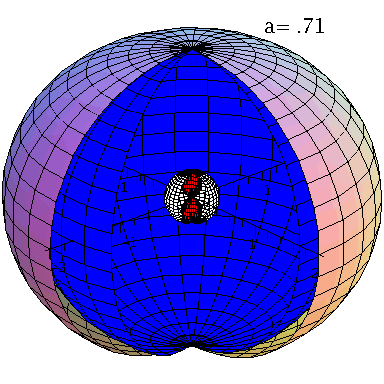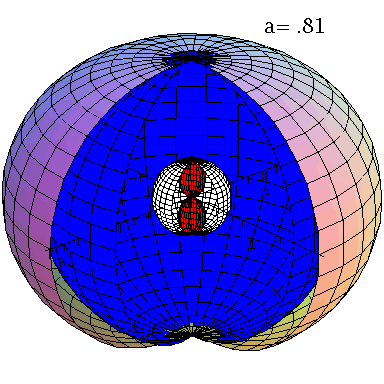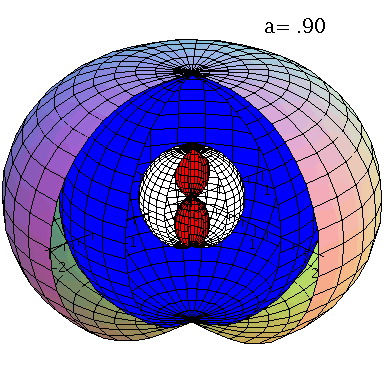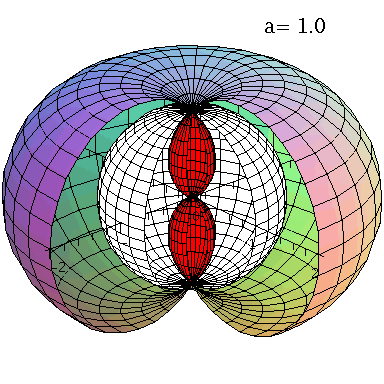Veranschaulichung der Metrikkomponenten 

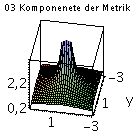
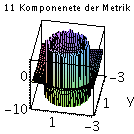
Die einzelnen Komponenten der Metrik in der äquatorialen Ebene (a=0.95): 

>

seta:=0.95: setz:=0: Plot1:=plot3d(subs(z=setz,subs({M=setM,a=seta,r=sqrt(x^2+y^2+z^2),cos(theta)=(z/sqrt(x^2+y^2+z^2))},get_compts(g)[1,1])),x=-3..3,y=-3..3,axes=boxed,view=-3..1,grid=[30,30],orientation=[100,50],title="00 Komponenete der Metrik"): Plot2:=plot3d(subs(z=setz,subs({M=setM,a=seta,r=sqrt(x^2+y^2+z^2),cos(theta)=(z/sqrt(x^2+y^2+z^2))},get_compts(g)[2,2])),x=-3..3,y=-3..3,axes=boxed,view=-10..5,grid=[30,30],orientation=[100,50],title="11 Komponenete der Metrik"): Plot3:=plot3d(subs(z=setz,subs({M=setM,a=seta,r=sqrt(x^2+y^2+z^2),theta=arccos(z/sqrt(x^2+y^2+z^2))},get_compts(g)[1,4])),x=-3..3,y=-3..3,axes=boxed,view=0.1..4,grid=[30,30],orientation=[100,50],title="03 Komponenete der Metrik"): display(Matrix(1,3,[Plot1,Plot2,Plot3]));

 

 

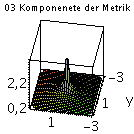
Die einzelnen Komponenten der Metrik in der äquatorialen Ebene (a=0.2): 

>

seta:=0.2: setz:=0: Plot1:=plot3d(subs(z=setz,subs({M=setM,a=seta,r=sqrt(x^2+y^2+z^2),cos(theta)=(z/sqrt(x^2+y^2+z^2))},get_compts(g)[1,1])),x=-3..3,y=-3..3,axes=boxed,view=-3..1,grid=[30,30],orientation=[100,50],title="00 Komponenete der Metrik"): Plot2:=plot3d(subs(z=setz,subs({M=setM,a=seta,r=sqrt(x^2+y^2+z^2),cos(theta)=(z/sqrt(x^2+y^2+z^2))},get_compts(g)[2,2])),x=-3..3,y=-3..3,axes=boxed,view=-10..5,grid=[30,30],orientation=[100,50],title="11 Komponenete der Metrik"): Plot3:=plot3d(subs(z=setz,subs({M=setM,a=seta,r=sqrt(x^2+y^2+z^2),theta=arccos(z/sqrt(x^2+y^2+z^2))},get_compts(g)[1,4])),x=-3..3,y=-3..3,axes=boxed,view=0.1..4,grid=[30,30],orientation=[100,50],title="03 Komponenete der Metrik"): display(Matrix(1,3,[Plot1,Plot2,Plot3]));

 

 

Die Rotation der raumzeitlichen Struktur um das schwarze Loch (das Frame dragging) 

Ein rotierendes schwarzes Loch zieht die Raumzeit mit sich mit. Die Rotationsfrequenz mit der die Raumzeit mitgeführt wird nennt man "Frame dragging" Frequenz; sie ist wie folgt definiert: 

>	FrameDrag:=get_compts(ginv)[1,4]/get_compts(ginv)[1,1]; #FrameDrag:=-get_compts(g)[1,4]/get_compts(g)[4,4];

 

(2.1.3.1)

 

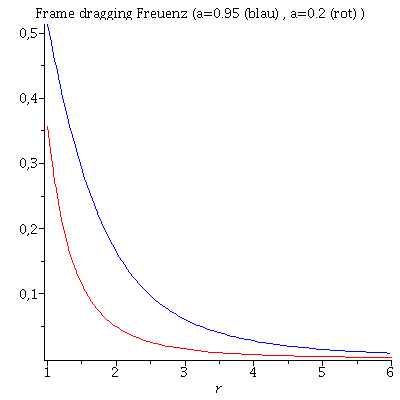
Die Frame Dragging Frequenz in der äquatorialen Ebene für a=0.95 (blau) und a=0.2 (rot). 

>	Plot1:=plot(subs({M=setM,a=0.95,theta=Pi/2},FrameDrag),r=1..6,color=blue): Plot2:=plot(subs({M=setM,a=0.2,theta=Pi/2},FrameDrag),r=1..6,color=red): display(Plot1,Plot2,title="Frame dragging Freuenz (a=0.95 (blau) , a=0.2 (rot) )");

 

 

 

 

Radial in ein rotierendes schwarzes Loch einfallender Probekörper 

Wir betrachten nun einen Probekörper der radial in ein rotierendes schwarzes Loch fällt. 

>	restart: with( tensor ): with(plots): with(plottools):

 

Definition der kovarianten Raumzeit-Metrik eines rotierenden schwarzen Lochs der Masse M und Rotation a in Kerrschildkoordinaten: 

>

coord := [t, r, theta, phi]: rho2:=r^2+(a*cos(theta))^2: Delta:=r^2-2*M*r+a^2:Sig2:=(r^2+a^2)^2-a^2*Delta*(sin(theta))^2: g_compts := array(symmetric,sparse, 1..4, 1..4): g_compts[1,1] := (1-2*M*r/rho2): g_compts[1,4] := +(2*a*M*r*(sin(theta))^2)/rho2: g_compts[2,2] :=-rho2/Delta: g_compts[3,3] := -rho2: g_compts[4,4] := -(r^2+a^2+2*M*r*a^2*(sin(theta))^2/rho2): g := create( [-1,-1], eval(g_compts));

 

(2.2.1)

 

Berechnung der kontravarianten Metrik, der Christoffel Symbole, des Riemanntensors...: 

>	ginv := invert( g, 'detg' ): D1g := d1metric( g, coord ):   D2g := d2metric( D1g, coord ): Cf1 := Christoffel1( D1g ): Cf2:= Christoffel2( ginv, Cf1 ): D2g := d2metric ( D1g, coord ): RMN := Riemann( ginv, D2g, Cf1 ): RICCI := Ricci( ginv, RMN ): RS := Ricciscalar( ginv, RICCI ):

 

Berechnung des infinitesimalen Weglängenelements ds²: 

>

dx:=create([1], array([dt,dr,dtheta,dphi])): ds2:=get_compts(prod(dx,lower(g,dx,1),[1,1])): ds2:=collect( simplify(ds2), [dt,dr,dtheta,dphi]): ds2a:=simplify(coeff(ds2, dt, 2)): ds2b:=simplify(coeff(ds2, dr, 2)): ds2c:=simplify(coeff(ds2, dtheta, 2)): ds2d:=simplify(coeff(ds2, dphi, 2)): ds2e:=simplify(coeff(ds2, dphi, 1)/dt): ds2:=ds2a*dt^2+ds2e*dt*dphi+ds2b*dr^2+ds2c*dtheta^2+ds2d*dphi^2;

 

(2.2.2)

 

Berechnung der Geodätengleichung als Funktion des affinen Parameters lambda. Die Geodätengleichung ist ein System gekoppelter Differentialgleichungen:   

>	eqns:=geodesic_eqns( coord, lambda, Cf2 );

 

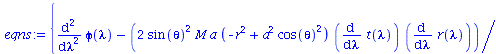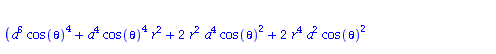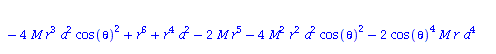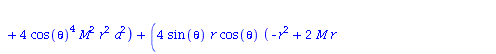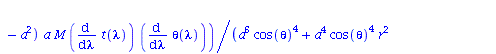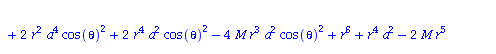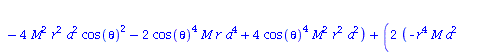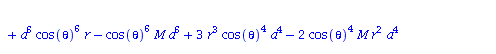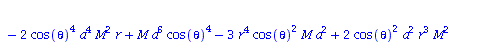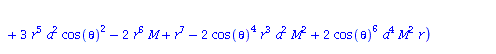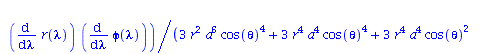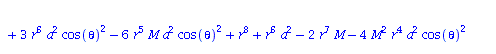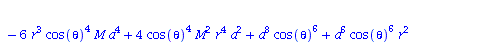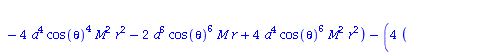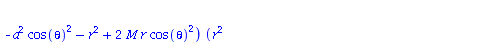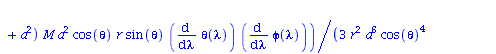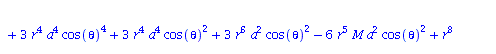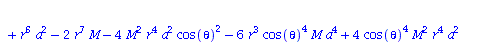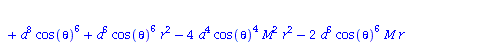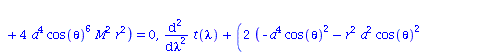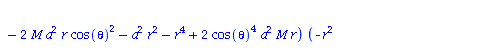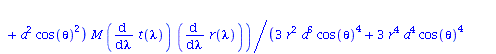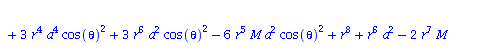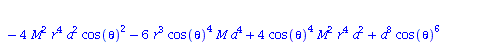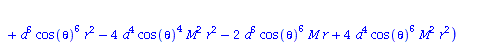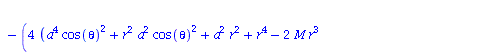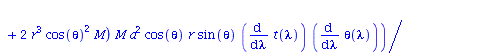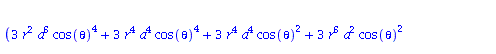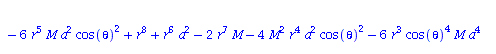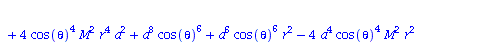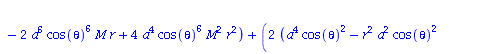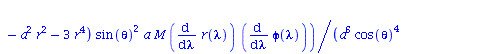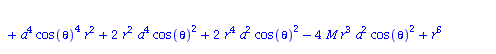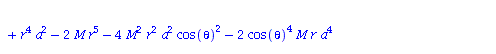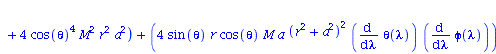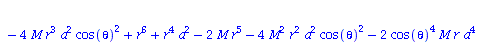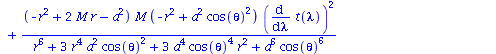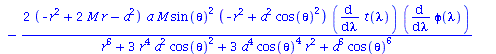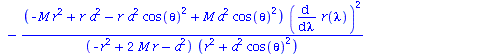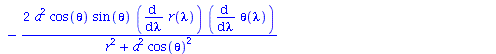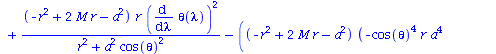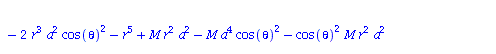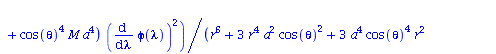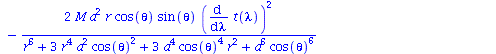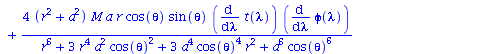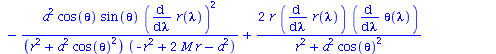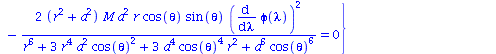(2.2.3)

 

Die Masse des schwarzen Lochs setzen wir auf M=1 und legen zusätzlich den Rotationsparameter a fest: 

>

seta:=0.95: setM:=1: eq1:=subs({M=setM,a=seta},eqns[1]): eq2:=subs({M=setM,a=seta},eqns[2]): eq3:=subs({M=setM,a=seta},eqns[3]): eq4:=subs({M=setM,a=seta},eqns[4]): eq1:=simplify(subs({r=r(lambda),theta=theta(lambda)},eq1)): eq2:=simplify(subs({r=r(lambda),theta=theta(lambda)},eq2)): eq3:=simplify(subs({r=r(lambda),theta=theta(lambda)},eq3)): eq4:=simplify(subs({r=r(lambda),theta=theta(lambda)},eq4)): eq1:=simplify(subs({r(lambda)(lambda)=r(lambda),theta(lambda)(lambda)=theta(lambda)},eq1)): eq2:=simplify(subs({r(lambda)(lambda)=r(lambda),theta(lambda)(lambda)=theta(lambda)},eq2)): eq3:=simplify(subs({r(lambda)(lambda)=r(lambda),theta(lambda)(lambda)=theta(lambda)},eq3)): eq4:=simplify(subs({r(lambda)(lambda)=r(lambda),theta(lambda)(lambda)=theta(lambda)},eq4)):

 

Anfangswerte: 

Zur Zeit t=0 sei der fallende Körper an der folgenden Position: (r=10,theta=Pi/2,phi=0), die Anfangsgeschwindigkeit des Körpers sei 0. Wir beschreiben den Fall aus der Sichtweise eines im Unendlichen ruhenden Beobachters.Bemerkung: Der Anfangswert dt0 ergibt sich hierbei aus dem infinitesimalen Weglängenelements ds²=1 eines massiven Probekörpers: 

>	dt=solve(evalf(subs({M=setM,a=seta,theta=Pi/2,dr=0,dtheta=0,dphi=0,r=10},ds2=1)),dt);

 

(2.2.4)

 

>	r0:=10: t0:=0: theta0:=Pi/2: phi0:=0: dr0:=0: dt0:=evalf(1/sqrt(1-2/r0)): dtheta0:=0: dphi0:=0:

 

Numerisches Lösen der Geodätengleichung: 

>	Loes:=dsolve({eq1,eq2,eq3,eq4,t(0)=t0,r(0)=r0,phi(0)=phi0,theta(0)=theta0,D(r)(0)=0,D(t)(0)=dt0,D(phi)(0)=dphi0,D(theta)(0)=dtheta0},{r(lambda),t(lambda),phi(lambda),theta(lambda)},type=numeric,output=listprocedure):

 

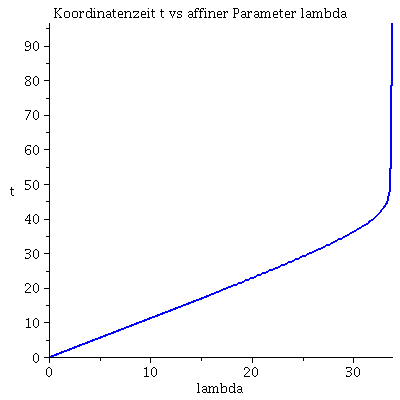
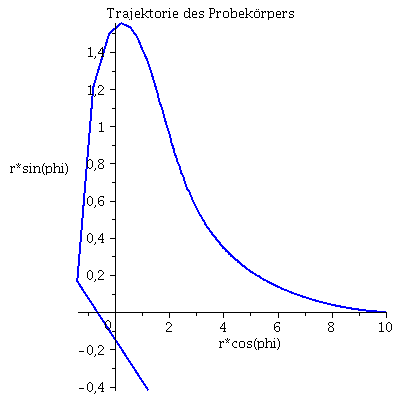
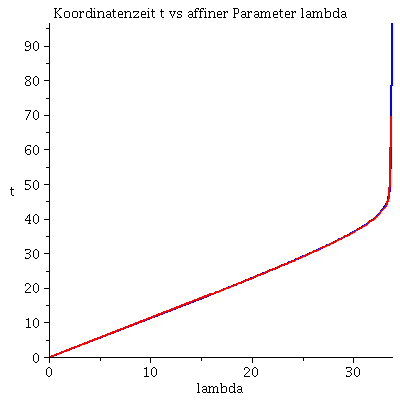
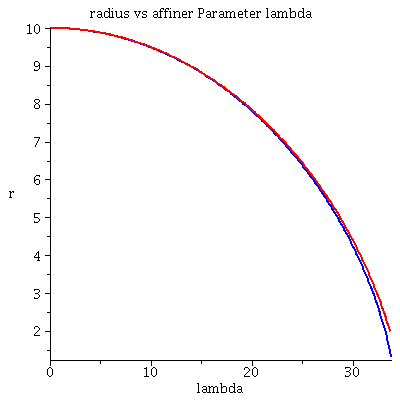
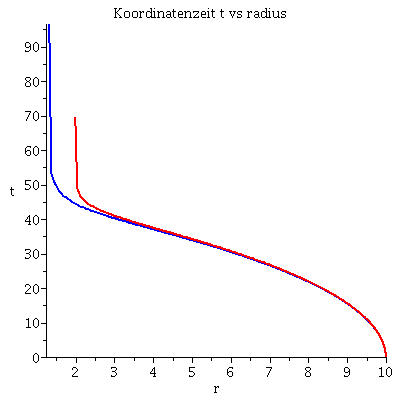
Grafische Veranschaulichung der Lösung: 

>

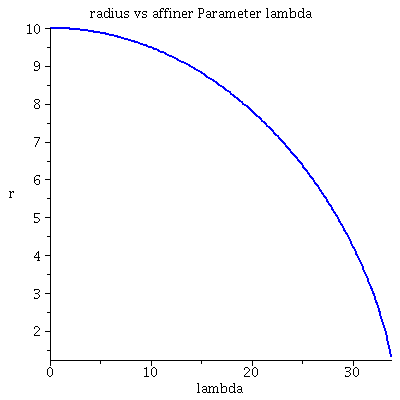
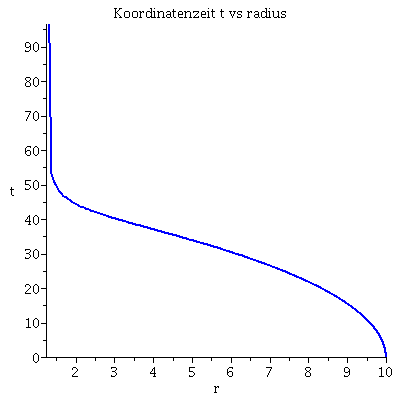
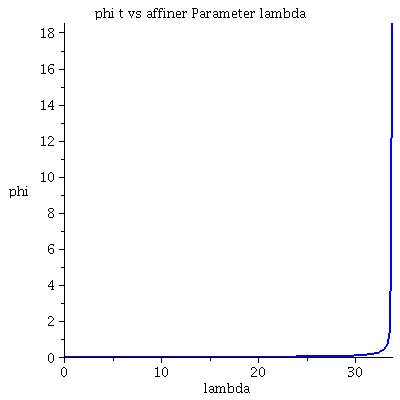
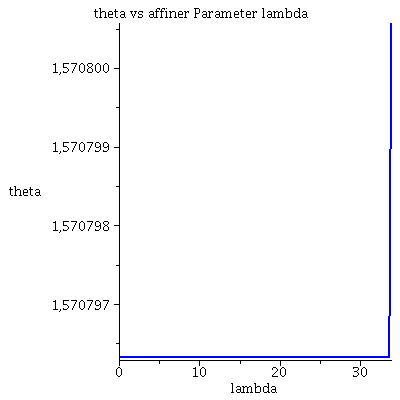
lend:=33.797644: Plot1:=odeplot(Loes,[lambda,t(lambda)],0..lend,numpoints=200,color=blue,thickness=2,title="Koordinatenzeit t vs affiner Parameter lambda"): Plot2:=odeplot(Loes,[lambda,r(lambda)],0..lend,numpoints=200,color=blue,thickness=2,title="radius vs affiner Parameter lambda"): Plot3:=odeplot(Loes,[r(lambda),t(lambda)],0..lend,numpoints=700,color=blue,thickness=2,title="Koordinatenzeit t vs radius"): Plot4:=odeplot(Loes,[lambda,phi(lambda)],0..lend,numpoints=200,color=blue,thickness=2,title="phi t vs affiner Parameter lambda"): Plot5:=odeplot(Loes,[lambda,theta(lambda)],0..lend,numpoints=200,color=blue,thickness=2,title="theta vs affiner Parameter lambda"): Plot6:=odeplot(Loes,[r(lambda)*cos(phi(lambda)),r(lambda)*sin(phi(lambda))],0..lend,numpoints=700,color=blue,thickness=2,title="Trajektorie des Probekörpers"): display(Matrix(1,3,[Plot1,Plot2,Plot3])); display(Matrix(1,3,[Plot4,Plot5,Plot6]));

 

 

 

Vergleich mit einem nichtrotierendem schwarzen Loch (a=0): 

>

seta:=0.0: eq1:=subs({M=1,a=seta},eqns[1]): eq2:=subs({M=1,a=seta},eqns[2]): eq3:=subs({M=1,a=seta},eqns[3]): eq4:=subs({M=1,a=seta},eqns[4]): eq1:=simplify(subs({r=r(lambda),theta=theta(lambda)},eq1)): eq2:=simplify(subs({r=r(lambda),theta=theta(lambda)},eq2)): eq3:=simplify(subs({r=r(lambda),theta=theta(lambda)},eq3)): eq4:=simplify(subs({r=r(lambda),theta=theta(lambda)},eq4)): eq1:=simplify(subs({r(lambda)(lambda)=r(lambda),theta(lambda)(lambda)=theta(lambda)},eq1)): eq2:=simplify(subs({r(lambda)(lambda)=r(lambda),theta(lambda)(lambda)=theta(lambda)},eq2)): eq3:=simplify(subs({r(lambda)(lambda)=r(lambda),theta(lambda)(lambda)=theta(lambda)},eq3)): eq4:=simplify(subs({r(lambda)(lambda)=r(lambda),theta(lambda)(lambda)=theta(lambda)},eq4)): LoesSS:=dsolve({eq1,eq2,eq3,eq4,t(0)=t0,r(0)=r0,phi(0)=phi0,theta(0)=theta0,D(r)(0)=0,D(t)(0)=dt0,D(phi)(0)=dphi0,D(theta)(0)=dtheta0},{r(lambda),t(lambda),phi(lambda),theta(lambda)},type=numeric,output=listprocedure):

 

Grafische Veranschaulichung beider Lösungen (Schwarzschildfall: rote Kurven): 

>

lend:=33.797644: Plot1:=odeplot(Loes,[lambda,t(lambda)],0..lend,numpoints=200,color=blue,thickness=2,title="Koordinatenzeit t vs affiner Parameter lambda"): Plot2:=odeplot(Loes,[lambda,r(lambda)],0..lend,numpoints=200,color=blue,thickness=2,title="radius vs affiner Parameter lambda"): Plot3:=odeplot(Loes,[r(lambda),t(lambda)],0..lend,numpoints=700,color=blue,thickness=2,title="Koordinatenzeit t vs radius"): Plot4:=odeplot(Loes,[lambda,phi(lambda)],0..lend,numpoints=200,color=blue,thickness=2,title="phi t vs affiner Parameter lambda"): Plot5:=odeplot(Loes,[lambda,theta(lambda)],0..lend,numpoints=200,color=blue,thickness=2,title="theta vs affiner Parameter lambda"): Plot6:=odeplot(Loes,[r(lambda)*cos(phi(lambda)),r(lambda)*sin(phi(lambda))],0..lend,numpoints=700,color=blue,thickness=2,title="Koordinatenzeit t vs radius"): lend:=33.700869: Plot1SS:=odeplot(LoesSS,[lambda,t(lambda)],0..lend,numpoints=200,color=red,thickness=2,title="Koordinatenzeit t vs affiner Parameter lambda"): Plot2SS:=odeplot(LoesSS,[lambda,r(lambda)],0..lend,numpoints=200,color=red,thickness=2,title="radius vs affiner Parameter lambda"): Plot3SS:=odeplot(LoesSS,[r(lambda),t(lambda)],0..lend,numpoints=700,color=red,thickness=2,title="Koordinatenzeit t vs radius"): Plot4SS:=odeplot(LoesSS,[lambda,phi(lambda)],0..lend,numpoints=200,color=red,thickness=2,title="phi t vs affiner Parameter lambda"): Plot5SS:=odeplot(LoesSS,[lambda,theta(lambda)],0..lend,numpoints=200,color=red,thickness=2,title="theta vs affiner Parameter lambda"): Plot6SS:=odeplot(LoesSS,[r(lambda)*cos(phi(lambda)),r(lambda)*sin(phi(lambda))],0..lend,numpoints=700,color=red,thickness=2,title="Trajektorie des Probekörpers"): display(Matrix(1,3,[display(Plot1,Plot1SS),display(Plot2,Plot2SS),display(Plot3,Plot3SS)])); display(Matrix(1,3,[display(Plot4,Plot4SS),display(Plot5,Plot5SS),display(Plot6,Plot6SS)]));

 

 

 

Animation beider Lösungen. Der blaue Körper fällt in ein rotierendes schwarzes Loch (a=0.95) und der rote Körper fällt in ein nichtrotierendes schwarzes Loch (a=0). Der gelbe Bereich stellt die Ergosphäre dar, die nur in dem rotierenden Fall existiert. 

>

seta:=0.95: UnRot:=solve(get_compts(g)[1,1]=0,r): Horizon:=solve(get_compts(ginv)[2,2]=0,r): A:=implicitplot(r = subs({M=setM,a=seta,theta=Pi/2},UnRot[1]), r = 0 .. 3, phi = 0 .. 2*Pi, coords = polar,grid=[30,30],color=red,linestyle=dash,thickness=1): B:=implicitplot(r = subs({M=setM,a=seta,theta=Pi/2},UnRot[2]), r = 0 .. 3, phi = 0 .. 2*Pi, coords = polar,grid=[30,30],color=red,linestyle=solid): C:=implicitplot(r = subs({M=setM,a=seta,theta=Pi/2},Horizon[1]), r = 0 .. 3, phi = 0 .. 2*Pi, coords = polar,grid=[30,30],color=black,linestyle=dash,thickness=1): DD:=implicitplot(r = subs({M=setM,a=seta,theta=Pi/2},Horizon[2]), r = 0 .. 3, phi = 0 .. 2*Pi, coords = polar,grid=[30,30],color=black,linestyle=solid): BH1:=display(disk([0,0],subs({M=setM,a=seta,theta=Pi/2},Horizon[2]),color=black)): BH2:=display(disk([0,0],subs({M=setM,a=seta,theta=Pi/2},Horizon[1]),color=white)): BH3:=display(disk([0,0],subs({M=setM,a=seta,theta=Pi/2},UnRot[1]),color=yellow)): BH:=display({A,B,C,DD,BH1,BH2,BH3},scaling=constrained):

 

>

frames:=150: Lr := subs(Loes,r(lambda)): Lphi := subs(Loes,phi(lambda)): Lr1 := subs(LoesSS,r(lambda)): Lphi1 := subs(LoesSS,phi(lambda)): for i from 0 by 1 to frames do Koerper[i]:=display(disk([Lr(i*lend/frames)*cos(Lphi(i*lend/frames)),Lr(i*lend/frames)*sin(Lphi(i*lend/frames))],0.2,color=blue)): KoerperSS[i]:=display(disk([Lr1(i*lend/frames)*cos(Lphi1(i*lend/frames)),Lr1(i*lend/frames)*sin(Lphi1(i*lend/frames))],0.2,color=red)): Ani[i]:=display({Koerper[i],KoerperSS[i],BH}); od:

 

>	display([seq(Ani[i],i=0..frames)],insequence=true);

 

 

 

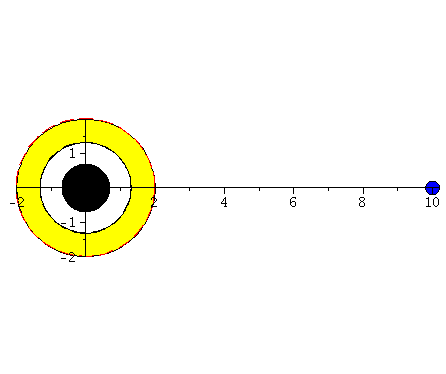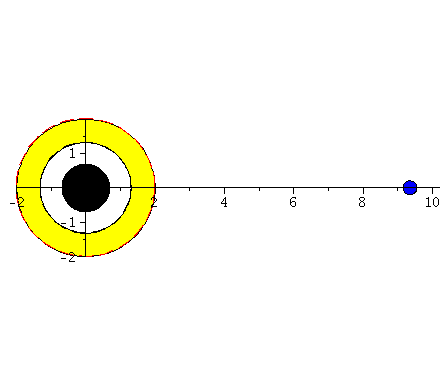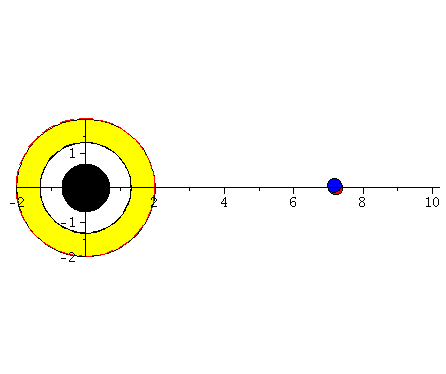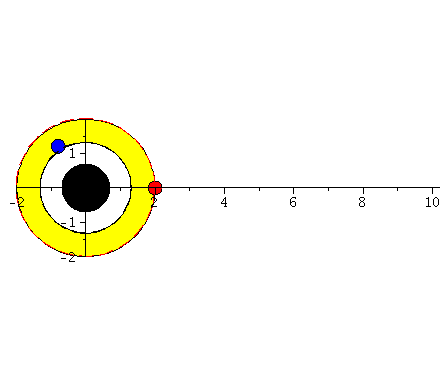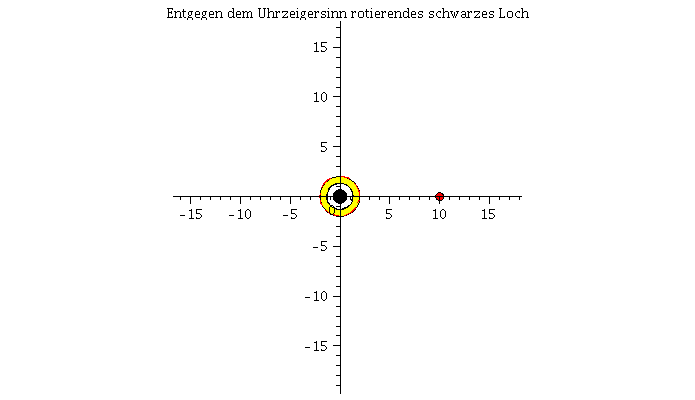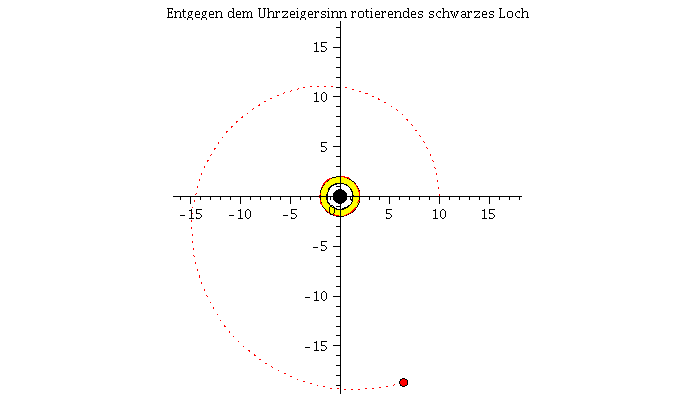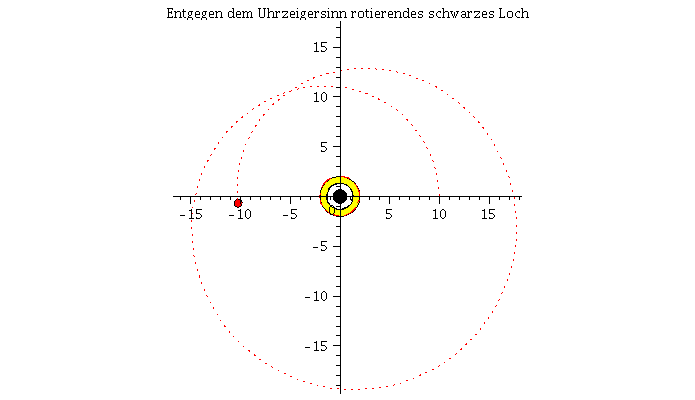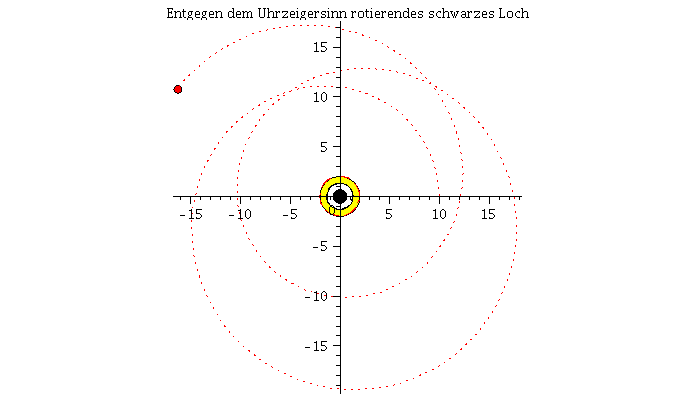
Bewegung eines Probekörpers um ein rotierendes schwarzes Loch in der Ebene
(Im Uhrzeigersinn und entgegen dem Uhrzeigersinn rotierendes schwarzes Loch) 

>	restart: with( tensor ): with(plots): with(plottools):

 

Definition der kovarianten Raumzeit-Metrik eines rotierenden schwarzen Lochs der Masse M und Rotation a in Kerrschildkoordinaten: 

>

coord := [t, r, theta, phi]: rho2:=r^2+(a*cos(theta))^2: Delta:=r^2-2*M*r+a^2: Sig2:=(r^2+a^2)^2-a^2*Delta*(sin(theta))^2: g_compts := array(symmetric,sparse, 1..4, 1..4): g_compts[1,1] := (1-2*M*r/rho2): g_compts[1,4] := +(2*a*M*r*(sin(theta))^2)/rho2: g_compts[2,2] :=-rho2/Delta: g_compts[3,3] := -rho2: g_compts[4,4] := -(r^2+a^2+2*M*r*a^2*(sin(theta))^2/rho2): g := create( [-1,-1], eval(g_compts));

 

(2.3.1)

 

Berechnung der kontravarianten Metrik, der Christoffel Symbole, des Riemanntensors...: 

>	ginv := invert( g, 'detg' ): D1g := d1metric( g, coord ):   D2g := d2metric( D1g, coord ): Cf1 := Christoffel1( D1g ): Cf2:= Christoffel2( ginv, Cf1 ): D2g := d2metric ( D1g, coord ): RMN := Riemann( ginv, D2g, Cf1 ): RICCI := Ricci( ginv, RMN ): RS := Ricciscalar( ginv, RICCI ):

 

Berechnung der Geodätengleichung als Funktion des affinen Parameters lambda. Die Geodätengleichung ist ein System gekoppelter Differentialgleichungen:   

>	eqns:=geodesic_eqns( coord, lambda, Cf2 ):

 

Die Masse des schwarzen Lochs setzen wir auf M=1: 

>

setM:=1: eq1:=subs({M=setM},eqns[1]): eq2:=subs({M=setM},eqns[2]): eq3:=subs({M=setM},eqns[3]): eq4:=subs({M=setM},eqns[4]): eq1:=simplify(subs({r=r(lambda),theta=theta(lambda)},eq1)): eq2:=simplify(subs({r=r(lambda),theta=theta(lambda)},eq2)): eq3:=simplify(subs({r=r(lambda),theta=theta(lambda)},eq3)): eq4:=simplify(subs({r=r(lambda),theta=theta(lambda)},eq4)): eq1:=simplify(subs({r(lambda)(lambda)=r(lambda),theta(lambda)(lambda)=theta(lambda)},eq1)): eq2:=simplify(subs({r(lambda)(lambda)=r(lambda),theta(lambda)(lambda)=theta(lambda)},eq2)): eq3:=simplify(subs({r(lambda)(lambda)=r(lambda),theta(lambda)(lambda)=theta(lambda)},eq3)): eq4:=simplify(subs({r(lambda)(lambda)=r(lambda),theta(lambda)(lambda)=theta(lambda)},eq4)):

 

:Mittels der Eigenschaft ds²=1 erhält man den Anfangswert für dt0: 

>

dx:=create([1], array([dt,dr,dtheta,dphi])): ds2:=get_compts(prod(dx,lower(g,dx,1),[1,1])): ds2:=collect( simplify(ds2), [dt,dr,dtheta,dphi]): ds2a:=simplify(coeff(ds2, dt, 2)): ds2b:=simplify(coeff(ds2, dr, 2)): ds2c:=simplify(coeff(ds2, dtheta, 2)): ds2d:=simplify(coeff(ds2, dphi, 2)): ds2e:=simplify(coeff(ds2, dphi, 1)/dt): ds2:=ds2a*dt^2+ds2e*dt*dphi+ds2b*dr^2+ds2c*dtheta^2+ds2d*dphi^2;

 

(2.3.2)

 

>	Eqdt:=dt=solve(subs({M=1,cos(theta)=0,sin(theta)=1,dr=0,dtheta=0},ds2=1),dt);

 

(2.3.3)

 

Anfangswerte: 

Zur Zeit t=0 sei der Probekörper an der folgenden Position: (r=10,theta=Pi/2,phi=0). Die Körper soll sich in der äquatorialen Ebene bewegen und die Anfangsgeschwindigkeit sei in radialer Richtung dr=0 und in phi-Richtung dphi=0.041. Wir beschreiben den Fall aus der Sichtweise eines im Unendlichen ruhenden Beobachters. Bemerkung: Der Anfangswert dt0 ergibt sich hierbei aus dem infinitesimalen Weglängenelements ds²=1 eines massiven Probekörpers. Wir lösen die Geodätengleichung einmal für den mitrotierenden Fall (a=0.95) und einmal für den gegenrotierenden Fall (a=-0.95): 

>

seta:=0.95; r0:=10: t0:=0: theta0:=Pi/2: phi0:=0: dr0:=0: dtheta0:=0: dphi0:=0.042: dt0:=evalf(subs({a=seta,dphi=dphi0,r=r0},rhs(Eqdt)[1])); Loes:=dsolve({subs({a=seta},eq1),subs({a=seta},eq2),subs({a=seta},eq3),subs({a=seta},eq4),t(0)=t0,r(0)=r0,phi(0)=phi0,theta(0)=theta0,D(r)(0)=0,D(t)(0)=dt0,D(phi)(0)=dphi0,D(theta)(0)=dtheta0},{r(lambda),t(lambda),phi(lambda),theta(lambda)},type=numeric,output=listprocedure):

 

 

	(2.3.4)

 

>

seta:=-0.95; r0:=10: t0:=0: theta0:=Pi/2: phi0:=0: dr0:=0: dt0:=evalf(1/sqrt(1-2/r0)): dtheta0:=0: dphi0:=0.042: dt0:=evalf(subs({a=seta,dphi=dphi0,r=r0},rhs(Eqdt)[1])); Loes1:=dsolve({subs({a=seta},eq1),subs({a=seta},eq2),subs({a=seta},eq3),subs({a=seta},eq4),t(0)=t0,r(0)=r0,phi(0)=phi0,theta(0)=theta0,D(r)(0)=0,D(t)(0)=dt0,D(phi)(0)=dphi0,D(theta)(0)=dtheta0},{r(lambda),t(lambda),phi(lambda),theta(lambda)},type=numeric,output=listprocedure):

 

 

	(2.3.5)

 

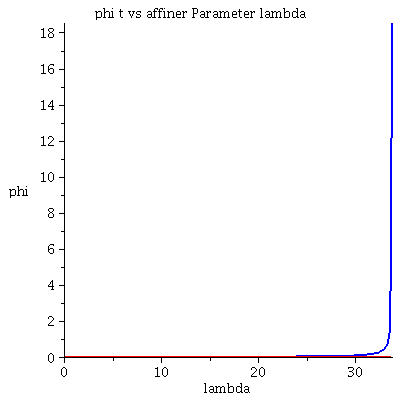
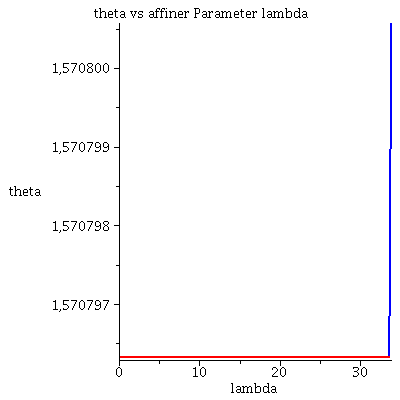
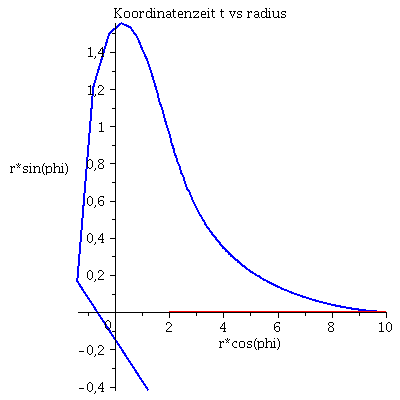
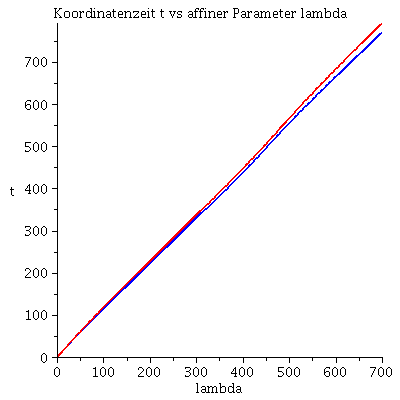
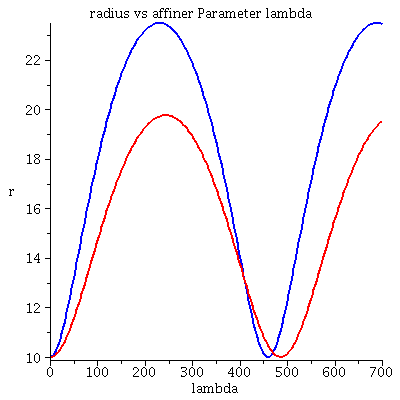
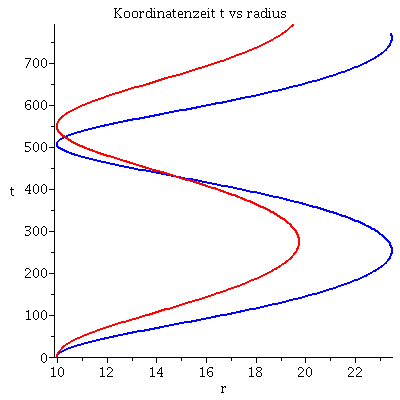
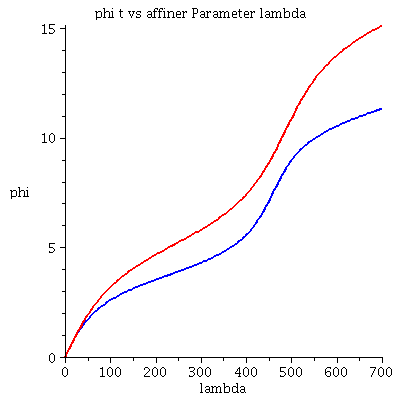
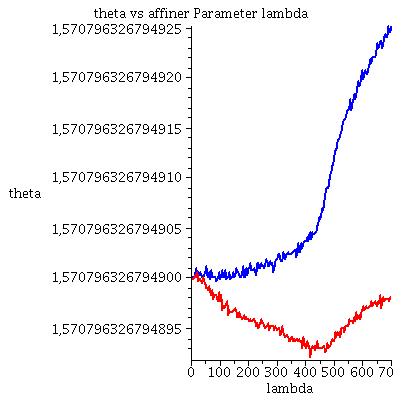
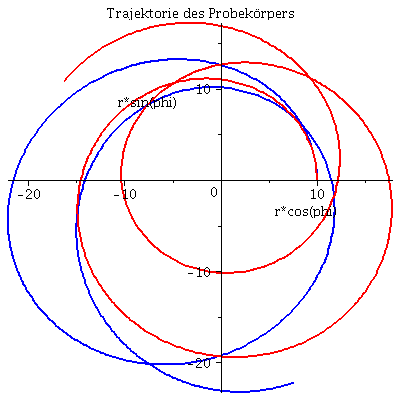
Grafische Veranschaulichung der Lösung (blau: Rotation des Probekörpers in Rotationsrichtung des schwarzen Loches,  rot: Rotation des Probekörpers entgegengesetzt der Rotationsrichtung des schwarzen Loches): 

>

lend:=700: Plot1:=odeplot(Loes,[lambda,t(lambda)],0..lend,numpoints=200,color=blue,thickness=2,title="Koordinatenzeit t vs affiner Parameter lambda"): Plot2:=odeplot(Loes,[lambda,r(lambda)],0..lend,numpoints=200,color=blue,thickness=2,title="radius vs affiner Parameter lambda"): Plot3:=odeplot(Loes,[r(lambda),t(lambda)],0..lend,numpoints=700,color=blue,thickness=2,title="Koordinatenzeit t vs radius"): Plot4:=odeplot(Loes,[lambda,phi(lambda)],0..lend,numpoints=200,color=blue,thickness=2,title="phi t vs affiner Parameter lambda"): Plot5:=odeplot(Loes,[lambda,theta(lambda)],0..lend,numpoints=200,color=blue,thickness=2,title="theta vs affiner Parameter lambda"): Plot6:=odeplot(Loes,[r(lambda)*cos(phi(lambda)),r(lambda)*sin(phi(lambda))],0..lend,numpoints=700,color=blue,thickness=2,title="Trajektorie des Probekörpers"): Plot1SS:=odeplot(Loes1,[lambda,t(lambda)],0..lend,numpoints=200,color=red,thickness=2,title="Koordinatenzeit t vs affiner Parameter lambda"): Plot2SS:=odeplot(Loes1,[lambda,r(lambda)],0..lend,numpoints=200,color=red,thickness=2,title="radius vs affiner Parameter lambda"): Plot3SS:=odeplot(Loes1,[r(lambda),t(lambda)],0..lend,numpoints=700,color=red,thickness=2,title="Koordinatenzeit t vs radius"): Plot4SS:=odeplot(Loes1,[lambda,phi(lambda)],0..lend,numpoints=200,color=red,thickness=2,title="phi t vs affiner Parameter lambda"): Plot5SS:=odeplot(Loes1,[lambda,theta(lambda)],0..lend,numpoints=200,color=red,thickness=2,title="theta vs affiner Parameter lambda"): Plot6SS:=odeplot(Loes1,[r(lambda)*cos(phi(lambda)),r(lambda)*sin(phi(lambda))],0..lend,numpoints=700,color=red,thickness=2,title="Trajektorie des Probekörpers"): display(Matrix(1,3,[display(Plot1,Plot1SS),display(Plot2,Plot2SS),display(Plot3,Plot3SS)])); display(Matrix(1,3,[display(Plot4,Plot4SS),display(Plot5,Plot5SS),display(Plot6,Plot6SS)]));

 

 

 

 

>

seta:=0.95: UnRot:=solve(get_compts(g)[1,1]=0,r): Horizon:=solve(get_compts(ginv)[2,2]=0,r): A:=implicitplot(r = subs({M=setM,a=seta,theta=Pi/2},UnRot[1]), r = 0 .. 3, phi = 0 .. 2*Pi, coords = polar,grid=[30,30],color=red,linestyle=dash,thickness=1): B:=implicitplot(r = subs({M=setM,a=seta,theta=Pi/2},UnRot[2]), r = 0 .. 3, phi = 0 .. 2*Pi, coords = polar,grid=[30,30],color=red,linestyle=solid): C:=implicitplot(r = subs({M=setM,a=seta,theta=Pi/2},Horizon[1]), r = 0 .. 3, phi = 0 .. 2*Pi, coords = polar,grid=[30,30],color=black,linestyle=dash,thickness=1): DD:=implicitplot(r = subs({M=setM,a=seta,theta=Pi/2},Horizon[2]), r = 0 .. 3, phi = 0 .. 2*Pi, coords = polar,grid=[30,30],color=black,linestyle=solid): BH1:=display(disk([0,0],subs({M=setM,a=seta,theta=Pi/2},Horizon[2]),color=black)): BH2:=display(disk([0,0],subs({M=setM,a=seta,theta=Pi/2},Horizon[1]),color=white)): BH3:=display(disk([0,0],subs({M=setM,a=seta,theta=Pi/2},UnRot[1]),color=yellow)): BH:=display({A,B,C,DD,BH1,BH2,BH3},scaling=constrained):

 

>

frames:=150: lend:=700: Lr := subs(Loes,r(lambda)): Lphi := subs(Loes,phi(lambda)): Lr1 := subs(Loes1,r(lambda)): Lphi1 := subs(Loes1,phi(lambda)): for i from 0 by 1 to frames do Koerper[i]:=display(disk([Lr(i*lend/frames)*cos(Lphi(i*lend/frames)),Lr(i*lend/frames)*sin(Lphi(i*lend/frames))],0.4,color=blue)): Koerper1[i]:=display(disk([Lr1(i*lend/frames)*cos(Lphi1(i*lend/frames)),Lr1(i*lend/frames)*sin(Lphi1(i*lend/frames))],0.4,color=red)): Traj[i]:=listplot([seq([Lr(j*lend/frames)*cos(Lphi(j*lend/frames)),Lr(j*lend/frames)*sin(Lphi(j*lend/frames))], j = 0 .. i)],color=blue,linestyle=dot): Traj1[i]:=listplot([seq([Lr1(j*lend/frames)*cos(Lphi1(j*lend/frames)),Lr1(j*lend/frames)*sin(Lphi1(j*lend/frames))], j = 0 .. i)],color=red,linestyle=dot): Ani[i]:=display({Koerper[i],BH,Traj[i]}); Ani1[i]:=display({Koerper1[i],BH,Traj1[i]}); od:

 

>	Animat1:=display([seq(Ani[i],i=0..frames)],insequence=true,scaling=constrained,title="Im Uhrzeigersinn rotierendes schwarzes Loch"): Animat2:=display([seq(Ani1[i],i=0..frames)],insequence=true,title="Entgegen dem Uhrzeigersinn rotierendes schwarzes Loch"): display(Array([Animat1,Animat2]));

 

 

>

 

>