Einführung 

In den folgenden drei Vorlesungen wurde die Geodätengleichung in vorgegebener Schwarzschild Raumzeit für unterschiedliche Anfangsbedingungen numerisch analysiert. Die raumzeitliche Struktur, die Metrik, wurde hierbei als gegeben vorausgesetzt. In der folgenden Vorlesung betrachteten wir nun wie man die Metrik bei vorgegebener Materieverteilung berechnet. Die zugrundeliegende Gleichung die es hier zu lösen gilt ist die Einstein Gleichung. 

Die innere Schwarzschildlösung eines sphärisch symetrischen, statischen Objektes (z.B. Erde, Neutronenstern)   

Im folgenden wird die Einsteingleichung einer sphärisch symetrischen und statischen Matrieverteilung betrachtet. Die Matrie wird hierbei als ideale Flüssigkeit angesetzt.  

Von der Einstein Gleichung zur Tolman-Oppenheimer-Volkoff Gleichung (TOV) 

>	restart: with( tensor ):

 

Sphärisch symetrischer und statischer Ansatz der Metrik: 

>	coord := [t, r, theta, phi]: g_compts := array(symmetric,sparse, 1..4, 1..4): g_compts[1,1] := exp(2*phi(r)): #g_compts[2,2] := exp(2*lambda(r)): g_compts[2,2] := -1/(1-2*m(r)/r): g_compts[3,3] := -r^2:     g_compts[4,4] := -r^2*sin(theta)^2: g := create( [-1,-1], eval(g_compts));

 

(2.1.1)

 

>	ginv := invert( g, 'detg' ); D1g := d1metric ( g, coord ):   D2g := d2metric ( D1g, coord ): Cf1 := Christoffel1 ( D1g ): Cf2 := Christoffel2(ginv, Cf1):

 

(2.1.2)

 

>	RMN := Riemann( ginv, D2g, Cf1 ): RMNinv:= raise(ginv,RMN,1,2,3,4): RMNc:=get_compts(RMN): RICCI := Ricci( ginv, RMN ): RS := Ricciscalar( ginv, RICCI ):

 

Kovariante Form des Einsteintensors: 

>	G := Einstein( g, RICCI, RS );

 

(2.1.3)

 

 

Der Energie-Impuls Tensor (rechte Seite der Einsteingleichung) wird als ideale Flüssigkeit angesetzt: 

>	T:=create([1,-1], array([[e(r),0,0,0],[0,-p(r),0,0],[0,0,-p(r),0],[0,0,0,-p(r)]])); Tl:=lower(g,T,1); Tu:=raise(ginv,T,2): prod(ginv, Tl, [2, 1]): contract(T, [1, 2]):

 

 

	(2.1.4)

 

Nichtverschwindende Komponenten der Einsteingleichung: 

>	Einsteingl:=lin_com(G,8*Pi,Tl);

 

(2.1.5)

 

>	A:=get_compts(Einsteingl):

 

Erste Gleichung der Einsteingleichung (tt-Komponente) wird nach dm/dr aufgelöst. 

Zweite Gleichung der Einsteingleichung (rr-Komponente) wird nach dphi/dr aufgelöst. 

>	Einstein1:=diff(m(r), r)=solve(A[1,1],diff(m(r), r)); Einstein2:=diff(phi(r),r)=solve(A[2,2],diff(phi(r),r));

 

 

	(2.1.6)

 

Mittels der hydrodynamischen Gleichungen (kovariante Erhaltung des Energie-Impulses) erhalten wir 

>	DT:=cov_diff(T, coord, Cf2): DTa:=get_compts(contract(DT, [1, 3]))[2]=0;

 

(2.1.7)

 

.was nach dp/dr aufgelöst das folgende ergibt: 

>	diff(p(r), r)=collect(solve(DTa,diff(p(r), r)),diff(phi(r), r));

 

(2.1.8)

 

Die TOV-Gleichung erhalten wir, indem man diese Gleichung nach dphi/dr auflöst und das Ergebnis in die zweite Gleichung der Einsteingleichung einsetzt: 

>	solve(DTa,diff(phi(r), r))*(e(r)+p(r))*(-1)=rhs(Einstein2)*(e(r)+p(r))*(-1);

 

(2.1.9)

 

>	TOV1:=solve(DTa,diff(phi(r), r))*(e(r)+p(r))*(-1)=rhs(Einstein2)*(e(r)+p(r))*(-1); TOV2:=Einstein1; TOV3:=Einstein2;

 

 

 

	(2.1.10)

 

 

Numerische Lösung der TOV-Gleichungen und Vergleich mit den C++ Resultaten aus Teil II 

Im folgenden werden die TOV-Gleichungen numerisch gelöst, indem wir einerseits eine Zustandsgleichung der Materie (eine Funktion p(e))  festlegen und von einem Startwert der zentralen Energiedichte im Inneren des sphärisch symetrischen Objektes nach Außen integrieren. Wir wählen im folgenden die Zustandsgleichung eines Models eines Neutronensterns bestehend aus einem nichtrelativistischen Fermigas ohne nukleare Wechselwirkungen (gamma=5/3 und K=7.3015: siehe z.B. I. Sagert, M. Hempel, C. Greiner, J. Schaffner-Bielich, "Compact Stars for Undergraduates", Eur.J.Phys.27:577-610,2006). 

>	print("Neutronenstern: Einfaches nichtrelativistisches Fermigas Model ohne nukleare Wechselwirkungen"); a:=7.3015389: b:=5/3: p(r):=a*(e(r))^b; W3:=plot(a*x^b,x=0..1,color=blue): TOV1:=solve(DTa,diff(phi(r), r))*(e(r)+p(r))*(-1)=rhs(Einstein2)*(e(r)+p(r))*(-1); TOV2:=Einstein1; TOV3:=Einstein2;

 

 

 

 

 

	(2.2.1)

 

Numerische Lösung der Gleichung mitfixierten Randbedingungen im Sternzentrum.Die zentrale Energiedichte sei der zweifache Wert der Kerndichte (normale nukleare Kerdichte: 2.705*10^14); Einheitenumrechnung siehe Glendenning "Compact Stars" (Seite 71).  

>	r0:=10^(-14): e0:=2*2.705*10^14*7.4327*10^(-19); Loes:=dsolve({TOV1,TOV2,TOV3,m(r0)=0,e(r0)=e0,phi(r0)=0},{m(r),e(r),phi(r)},type=numeric,output=listprocedure); energiedichte:=subs(Loes,e(r)); Mass:=subs(Loes,m(r)): PPhi:=subs(Loes,phi(r)): Mass(100000000);

 

 

 

 

Error, (in Mass) cannot evaluate the solution further right of 14.902170, probably a singularity

 

>	Radius:=14.902170: Masse:=Mass(Radius): Phi0:=(0.5*ln(1-2*Masse/Radius)): DPhi:=Phi0-PPhi(Radius): print("Sternradius in km R=",evalf(Radius)); print("Masse in Sonnenmassen: M=",evalf(Masse/1.4766)); print("Zentrale g00-Komponente g00=",evalf(exp(2*(DPhi))));

 

 

 

	(2.2.2)

 

Numerische Lösung vom Sternzentrum aus integriert: 

>

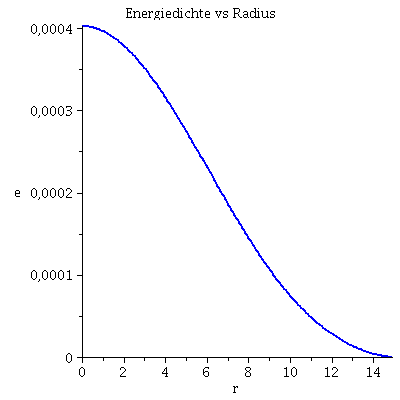
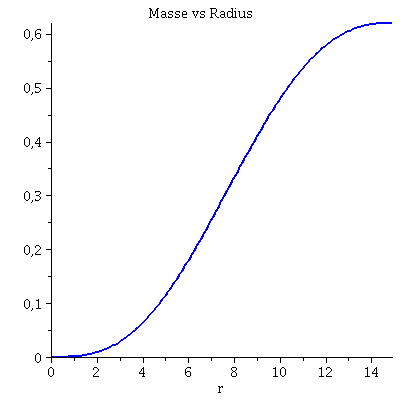
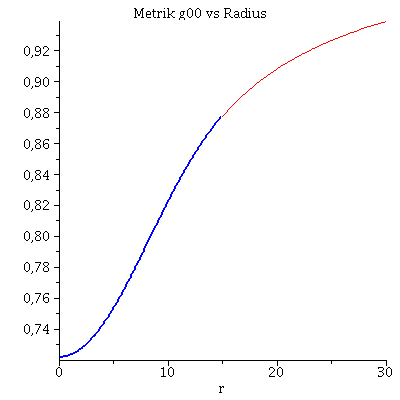
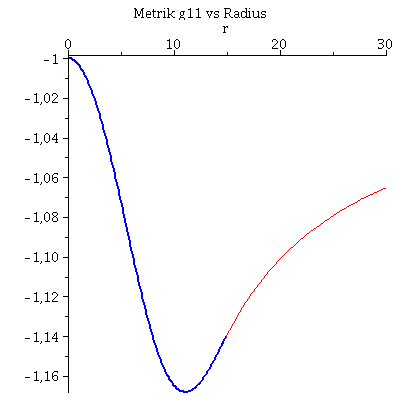
with(plots): rend:=Radius: Plot1:=odeplot(Loes,[r,e(r)],r0..rend,numpoints=200,color=blue,thickness=2,title="Energiedichte vs Radius"): Plot2:=odeplot(Loes,[r,m(r)/1.4766],r0..rend,numpoints=200,color=blue,thickness=2,title="Masse vs Radius"): display(Matrix(1,2,[Plot1,Plot2])); Plot3:=odeplot(Loes,[r,exp(2*(phi(r)+DPhi))],r0..rend,numpoints=200,color=blue,thickness=2,title="Metrik g00 vs Radius"): Plot4:=odeplot(Loes,[r,-1/(1-2*m(r)/r)],r0..rend,numpoints=200,color=blue,thickness=2,title="Metrik g11 vs Radius"): Plot5:=plot(1-2*Masse/r,r=rend..30,color=red): Plot6:=plot(-1/(1-2*Masse/r),r=rend..30,color=red): display(Matrix(1,2,[[display(Plot3,Plot5),display(Plot4,Plot6)]]));

 

 

 

Wir verwenden nun die Resultate aus dem Teil II der Vorlesung und vergleichen das Energiedichtenprofil des Neutronensterns der C++-Lösung (für unterschiedliche Schrittweiten dr) mit dem Maple Resulta; siehe Teil II, sequentielle Version 3.. 

>

CResultatdr001:=[[0.000000,4.021091e-04],[0.100000,4.020684e-04],[0.200000,4.019116e-04],[0.300000,4.016362e-04],[0.400000,4.012422e-04],[0.500000,4.007300e-04],[0.600000,4.001000e-04],[0.700000,3.993525e-04],[0.800000,3.984881e-04],[0.900000,3.975075e-04],[1.000000,3.964113e-04],[1.100000,3.952004e-04],[1.200000,3.938757e-04],[1.300000,3.924381e-04],[1.400000,3.908888e-04],[1.500000,3.892288e-04],[1.600000,3.874594e-04],[1.700000,3.855818e-04],[1.800000,3.835976e-04],[1.900000,3.815081e-04],[2.000000,3.793148e-04],[2.100000,3.770195e-04],[2.200000,3.746237e-04],[2.300000,3.721293e-04],[2.400000,3.695381e-04],[2.500000,3.668519e-04],[2.600000,3.640727e-04],[2.700000,3.612026e-04],[2.800000,3.582437e-04],[2.900000,3.551981e-04],[3.000000,3.520679e-04],[3.100000,3.488556e-04],[3.200000,3.455633e-04],[3.300000,3.421935e-04],[3.400000,3.387485e-04],[3.500000,3.352309e-04],[3.600000,3.316432e-04],[3.700000,3.279878e-04],[3.800000,3.242674e-04],[3.900000,3.204846e-04],[4.000000,3.166420e-04],[4.100000,3.127424e-04],[4.200000,3.087884e-04],[4.300000,3.047828e-04],[4.400000,3.007283e-04],[4.500000,2.966278e-04],[4.600000,2.924839e-04],[4.700000,2.882995e-04],[4.800000,2.840775e-04],[4.900000,2.798206e-04],[5.000000,2.755316e-04],[5.100000,2.712134e-04],[5.200000,2.668688e-04],[5.300000,2.625006e-04],[5.400000,2.581116e-04],[5.500000,2.537046e-04],[5.600000,2.492824e-04],[5.700000,2.448477e-04],[5.800000,2.404033e-04],[5.900000,2.359519e-04],[6.000000,2.314962e-04],[6.100000,2.270389e-04],[6.200000,2.225825e-04],[6.300000,2.181297e-04],[6.400000,2.136830e-04],[6.500000,2.092449e-04],[6.600000,2.048180e-04],[6.700000,2.004046e-04],[6.800000,1.960072e-04],[6.900000,1.916280e-04],[7.000000,1.872694e-04],[7.100000,1.829336e-04],[7.200000,1.786228e-04],[7.300000,1.743391e-04],[7.400000,1.700845e-04],[7.500000,1.658611e-04],[7.600000,1.616709e-04],[7.700000,1.575156e-04],[7.800000,1.533971e-04],[7.900000,1.493172e-04],[8.000000,1.452776e-04],[8.100000,1.412798e-04],[8.200000,1.373255e-04],[8.300000,1.334161e-04],[8.400000,1.295530e-04],[8.500000,1.257376e-04],[8.600000,1.219712e-04],[8.700000,1.182550e-04],[8.800000,1.145901e-04],[8.900000,1.109777e-04],[9.000000,1.074186e-04],[9.100000,1.039140e-04],[9.200000,1.004645e-04],[9.300000,9.707118e-05],[9.400000,9.373462e-05],[9.500000,9.045553e-05],[9.600000,8.723454e-05],[9.700000,8.407220e-05],[9.800000,8.096900e-05],[9.900000,7.792537e-05],[10.000000,7.494167e-05],[10.100000,7.201824e-05],[10.200000,6.915532e-05],[10.300000,6.635312e-05],[10.400000,6.361179e-05],[10.500000,6.093144e-05],[10.600000,5.831210e-05],[10.700000,5.575378e-05],[10.800000,5.325645e-05],[10.900000,5.082001e-05],[11.000000,4.844433e-05],[11.100000,4.612926e-05],[11.200000,4.387457e-05],[11.300000,4.168003e-05],[11.400000,3.954537e-05],[11.500000,3.747027e-05],[11.600000,3.545441e-05],[11.700000,3.349742e-05],[11.800000,3.159891e-05],[11.900000,2.975848e-05],[12.000000,2.797570e-05],[12.100000,2.625013e-05],[12.200000,2.458132e-05],[12.300000,2.296878e-05],[12.400000,2.141206e-05],[12.500000,1.991066e-05],[12.600000,1.846412e-05],[12.700000,1.707194e-05],[12.800000,1.573366e-05],[12.900000,1.444882e-05],[13.000000,1.321697e-05],[13.100000,1.203769e-05],[13.200000,1.091059e-05],[13.300000,9.835294e-06],[13.400000,8.811499e-06],[13.500000,7.838942e-06],[13.600000,6.917431e-06],[13.700000,6.046858e-06],[13.800000,5.227225e-06],[13.900000,4.458664e-06],[14.000000,3.741483e-06],[14.100000,3.076216e-06],[14.200000,2.463701e-06],[14.300000,1.905200e-06],[14.400000,1.402595e-06],[14.500000,9.587323e-07],[14.600000,5.781035e-07],[14.700000,2.684883e-07],[14.800000,4.650666e-08],[14.830000,1.570411e-08]]: CResultatdr01:=[[0.000000,4.021091e-04],[0.100000,4.021091e-04],[0.200000,4.020964e-04],[0.300000,4.019914e-04],[0.400000,4.017763e-04],[0.500000,4.014467e-04],[0.600000,4.010012e-04],[0.700000,4.004389e-04],[0.800000,3.997597e-04],[0.900000,3.989637e-04],[1.000000,3.980512e-04],[1.100000,3.970226e-04],[1.200000,3.958785e-04],[1.300000,3.946195e-04],[1.400000,3.932465e-04],[1.500000,3.917603e-04],[1.600000,3.901619e-04],[1.700000,3.884523e-04],[1.800000,3.866328e-04],[1.900000,3.847045e-04],[2.000000,3.826689e-04],[2.100000,3.805272e-04],[2.200000,3.782811e-04],[2.300000,3.759320e-04],[2.400000,3.734816e-04],[2.500000,3.709317e-04],[2.600000,3.682841e-04],[2.700000,3.655405e-04],[2.800000,3.627030e-04],[2.900000,3.597736e-04],[3.000000,3.567544e-04],[3.100000,3.536474e-04],[3.200000,3.504550e-04],[3.300000,3.471793e-04],[3.400000,3.438227e-04],[3.500000,3.403875e-04],[3.600000,3.368763e-04],[3.700000,3.332914e-04],[3.800000,3.296354e-04],[3.900000,3.259109e-04],[4.000000,3.221204e-04],[4.100000,3.182667e-04],[4.200000,3.143524e-04],[4.300000,3.103802e-04],[4.400000,3.063529e-04],[4.500000,3.022734e-04],[4.600000,2.981443e-04],[4.700000,2.939685e-04],[4.800000,2.897489e-04],[4.900000,2.854883e-04],[5.000000,2.811896e-04],[5.100000,2.768558e-04],[5.200000,2.724896e-04],[5.300000,2.680939e-04],[5.400000,2.636718e-04],[5.500000,2.592260e-04],[5.600000,2.547595e-04],[5.700000,2.502750e-04],[5.800000,2.457756e-04],[5.900000,2.412640e-04],[6.000000,2.367430e-04],[6.100000,2.322155e-04],[6.200000,2.276843e-04],[6.300000,2.231520e-04],[6.400000,2.186214e-04],[6.500000,2.140953e-04],[6.600000,2.095761e-04],[6.700000,2.050666e-04],[6.800000,2.005694e-04],[6.900000,1.960869e-04],[7.000000,1.916216e-04],[7.100000,1.871759e-04],[7.200000,1.827522e-04],[7.300000,1.783529e-04],[7.400000,1.739802e-04],[7.500000,1.696363e-04],[7.600000,1.653233e-04],[7.700000,1.610433e-04],[7.800000,1.567984e-04],[7.900000,1.525905e-04],[8.000000,1.484215e-04],[8.100000,1.442932e-04],[8.200000,1.402074e-04],[8.300000,1.361657e-04],[8.400000,1.321698e-04],[8.500000,1.282212e-04],[8.600000,1.243213e-04],[8.700000,1.204717e-04],[8.800000,1.166735e-04],[8.900000,1.129282e-04],[9.000000,1.092367e-04],[9.100000,1.056004e-04],[9.200000,1.020201e-04],[9.300000,9.849689e-05],[9.400000,9.503166e-05],[9.500000,9.162524e-05],[9.600000,8.827837e-05],[9.700000,8.499177e-05],[9.800000,8.176605e-05],[9.900000,7.860177e-05],[10.000000,7.549942e-05],[10.100000,7.245945e-05],[10.200000,6.948222e-05],[10.300000,6.656804e-05],[10.400000,6.371717e-05],[10.500000,6.092980e-05],[10.600000,5.820607e-05],[10.700000,5.554606e-05],[10.800000,5.294983e-05],[10.900000,5.041734e-05],[11.000000,4.794855e-05],[11.100000,4.554335e-05],[11.200000,4.320160e-05],[11.300000,4.092311e-05],[11.400000,3.870765e-05],[11.500000,3.655498e-05],[11.600000,3.446480e-05],[11.700000,3.243679e-05],[11.800000,3.047060e-05],[11.900000,2.856588e-05],[12.000000,2.672223e-05],[12.100000,2.493924e-05],[12.200000,2.321650e-05],[12.300000,2.155357e-05],[12.400000,1.995002e-05],[12.500000,1.840541e-05],[12.600000,1.691931e-05],[12.700000,1.549129e-05],[12.800000,1.412094e-05],[12.900000,1.280786e-05],[13.000000,1.155169e-05],[13.100000,1.035211e-05],[13.200000,9.208838e-06],[13.300000,8.121648e-06],[13.400000,7.090399e-06],[13.500000,6.115039e-06],[13.600000,5.195634e-06],[13.700000,4.332394e-06],[13.800000,3.525706e-06],[13.900000,2.776168e-06],[14.000000,2.084588e-06],[14.100000,1.451827e-06],[14.200000,8.777583e-07],[14.300000,3.517633e-07],[14.400000,3.517633e-07]]: CResultatdr02:=[[0.000000,4.021091e-04],[0.200000,4.021091e-04],[0.400000,4.020584e-04],[0.600000,4.016381e-04],[0.800000,4.007773e-04],[1.000000,3.994594e-04],[1.200000,3.976796e-04],[1.400000,3.954380e-04],[1.600000,3.927377e-04],[1.800000,3.895840e-04],[2.000000,3.859839e-04],[2.200000,3.819462e-04],[2.400000,3.774809e-04],[2.600000,3.725998e-04],[2.800000,3.673156e-04],[3.000000,3.616428e-04],[3.200000,3.555966e-04],[3.400000,3.491937e-04],[3.600000,3.424517e-04],[3.800000,3.353893e-04],[4.000000,3.280262e-04],[4.200000,3.203828e-04],[4.400000,3.124802e-04],[4.600000,3.043404e-04],[4.800000,2.959858e-04],[5.000000,2.874393e-04],[5.200000,2.787243e-04],[5.400000,2.698644e-04],[5.600000,2.608833e-04],[5.800000,2.518049e-04],[6.000000,2.426528e-04],[6.200000,2.334507e-04],[6.400000,2.242220e-04],[6.600000,2.149897e-04],[6.800000,2.057761e-04],[7.000000,1.966034e-04],[7.200000,1.874926e-04],[7.400000,1.784644e-04],[7.600000,1.695385e-04],[7.800000,1.607335e-04],[8.000000,1.520672e-04],[8.200000,1.435563e-04],[8.400000,1.352166e-04],[8.600000,1.270623e-04],[8.800000,1.191069e-04],[9.000000,1.113625e-04],[9.200000,1.038399e-04],[9.400000,9.654875e-05],[9.600000,8.949762e-05],[9.800000,8.269373e-05],[10.000000,7.614320e-05],[10.200000,6.985098e-05],[10.400000,6.382097e-05],[10.600000,5.805598e-05],[10.800000,5.255788e-05],[11.000000,4.732760e-05],[11.200000,4.236521e-05],[11.400000,3.767006e-05],[11.600000,3.324076e-05],[11.800000,2.907538e-05],[12.000000,2.517147e-05],[12.200000,2.152624e-05],[12.400000,1.813660e-05],[12.600000,1.499939e-05],[12.800000,1.211143e-05],[13.000000,9.469724e-06],[13.200000,7.071443e-06],[13.400000,4.913538e-06],[13.600000,2.989831e-06],[13.800000,1.266768e-06],[14.000000,1.266768e-06]]: CResultatdr05:=[[0.000000,4.021091e-04],[0.500000,4.021091e-04],[1.000000,4.017921e-04],[1.500000,3.991591e-04],[2.000000,3.937639e-04],[2.500000,3.855351e-04],[3.000000,3.745206e-04],[3.500000,3.608455e-04],[4.000000,3.446990e-04],[4.500000,3.263264e-04],[5.000000,3.060225e-04],[5.500000,2.841242e-04],[6.000000,2.610016e-04],[6.500000,2.370475e-04],[7.000000,2.126660e-04],[7.500000,1.882603e-04],[8.000000,1.642198e-04],[8.500000,1.409080e-04],[9.000000,1.186514e-04],[9.500000,9.773049e-05],[10.000000,7.837293e-05],[10.500000,6.075007e-05],[11.000000,4.497563e-05],[11.500000,3.110554e-05],[12.000000,1.913054e-05],[12.500000,8.901158e-06],[13.000000,8.901158e-06]]: CResultatdr1:=[[0.000000,4.021091e-04],[1.000000,4.021091e-04],[2.000000,4.008401e-04],[3.000000,3.902159e-04],[4.000000,3.683982e-04],[5.000000,3.355784e-04],[6.000000,2.931247e-04],[7.000000,2.434152e-04],[8.000000,1.896387e-04],[9.000000,1.354455e-04],[10.000000,8.440750e-05],[11.000000,3.910836e-05],[12.000000,3.910836e-05]]: CResultatdr2:=[[0.000000,4.021091e-04],[2.000000,4.021091e-04],[4.000000,3.970171e-04],[6.000000,3.528991e-04],[8.000000,2.603567e-04],[10.000000,1.246178e-04],[12.000000,1.246178e-04]]: CResultat:=[CResultatdr2,CResultatdr1,CResultatdr05,CResultatdr02,CResultatdr01,CResultatdr001]: dr:=[2,1,0.5,0.2,0.1,0.01]:

 

 

>

with(StringTools): frames:=6: Plot1:=odeplot(Loes,[r,e(r)],r0..rend,numpoints=200,color=blue,thickness=2,title="Energiedichte vs Radius",titlefont = [TIMES, ROMAN, 15]): for i from 1 by 1 to frames do PC[i]:=listplot(CResultat[i], thickness=2, color=red): Ptext[i]:=textplot([1,0.00005, Join(["dr=",convert(dr[i],string),"km"])], align =RIGHT,color=black,font = [TIMES, ROMAN, 15]): Ani[i]:=display({Plot1,PC[i],Ptext[i]}); od:

 

>	display([seq(Ani[i],i=1..frames)],insequence=true);

 

 

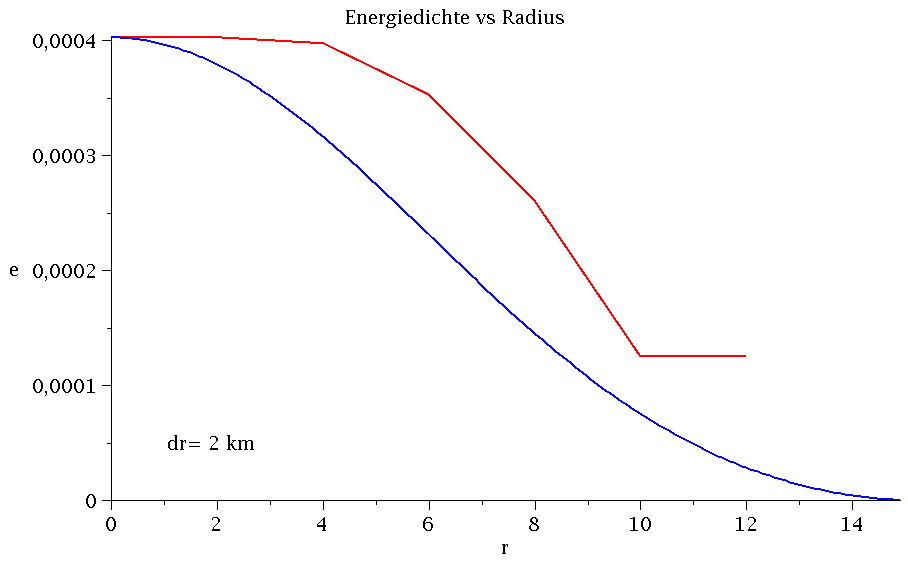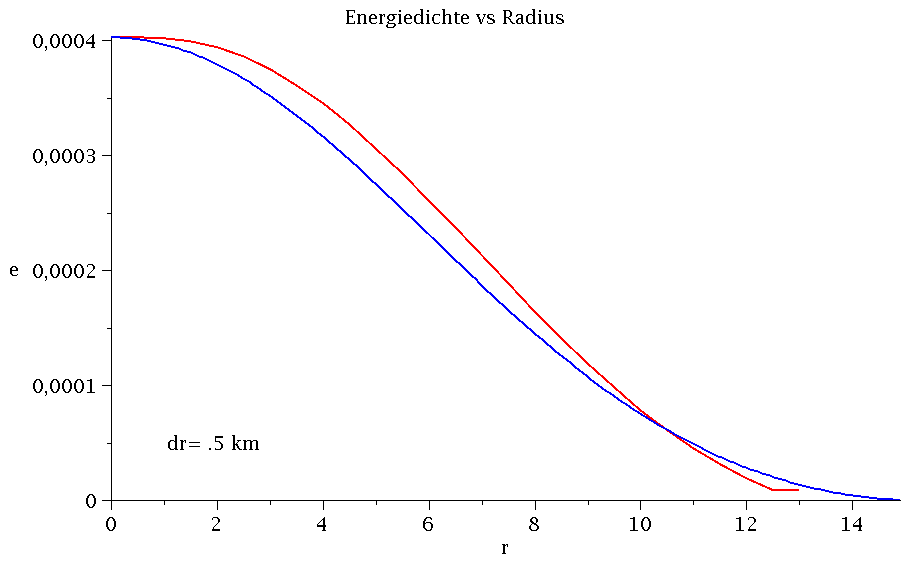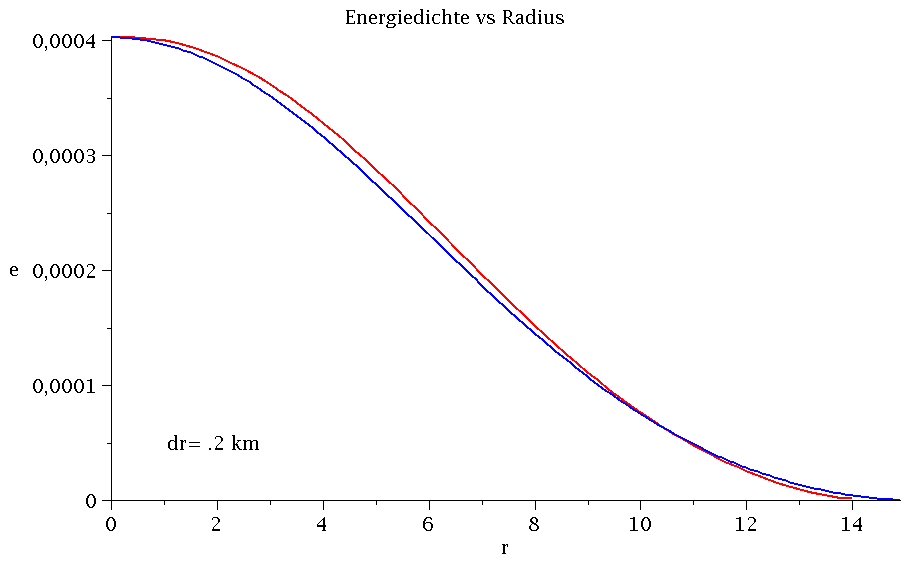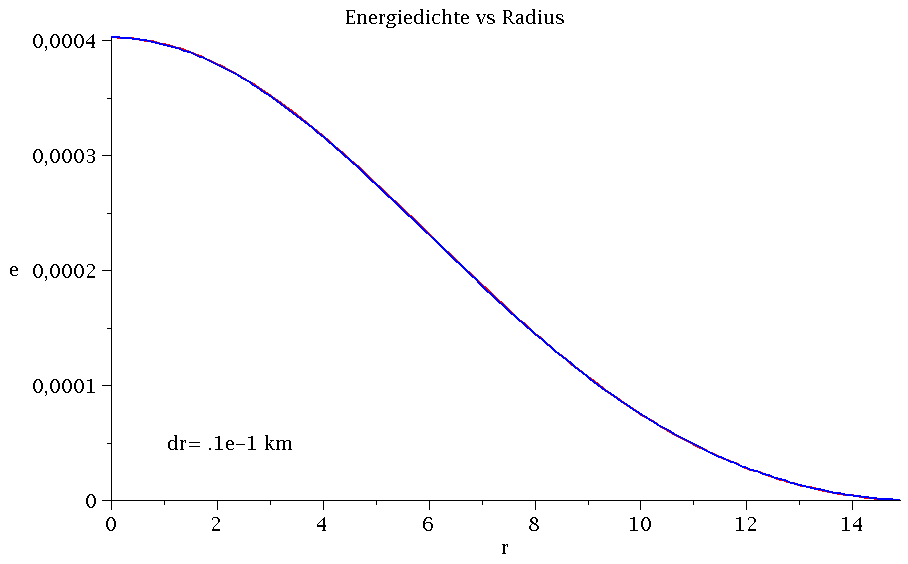Wie man anhand der obigen Animation sieht, unterscheiden sich die Energiedichtenprofile ab dr=0.01 km nur noch wenig voneinander; wobei die blaue Kurve das Maple-Profil und die rote Kurve die C++ Resultate darstellen. Vergleicht man den Sternradius, die Gesamtmasse und den zentralen Wert der g00-Komponente der Metrik miteinander, so erhält man z.B. für dr=0.0000001 km 

C++ Resultat: Neutronensternradius [km] = 14.90239587, Neutronensternmasse [Sonnenmassen]  = 0.6201093162, 00-Metrikkomponente im Sternzentrum = 0.7216928909 

Was gut mit den Resultaten von Maple übereinstimmt: 

Maple Resultate: Neutronensternradius [km] = 14.902170, Neutronensternmasse [Sonnenmassen]  = 0.6201090241, 00-Metrikkomponente im Sternzentrum = 0.7216929465 

Masse-Radius Beziehung und Vergleich mit den C++ Resultaten aus Teil II 

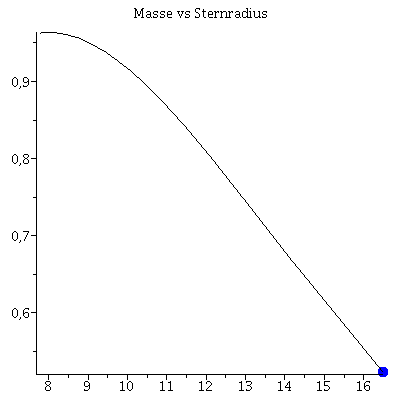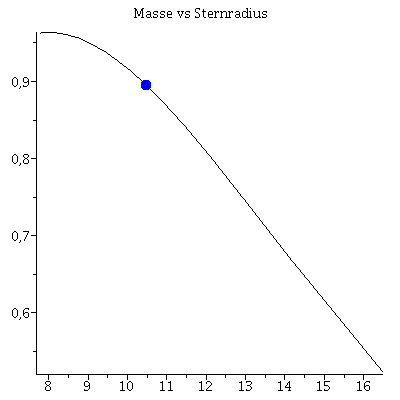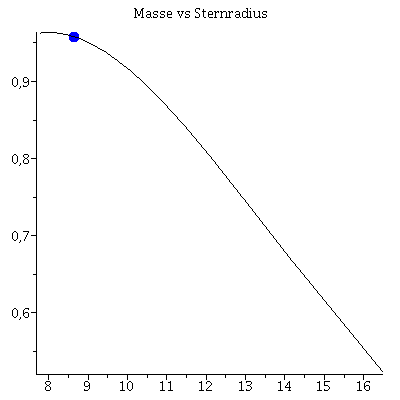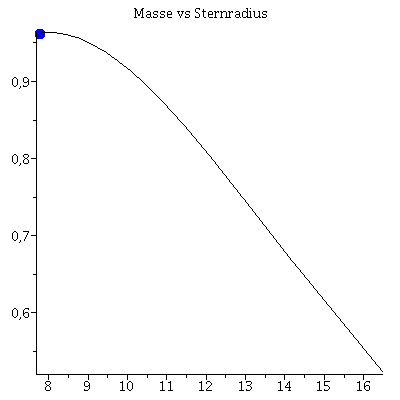
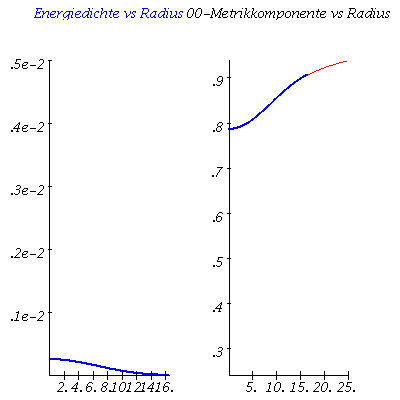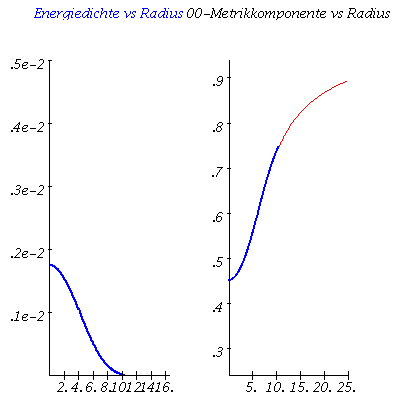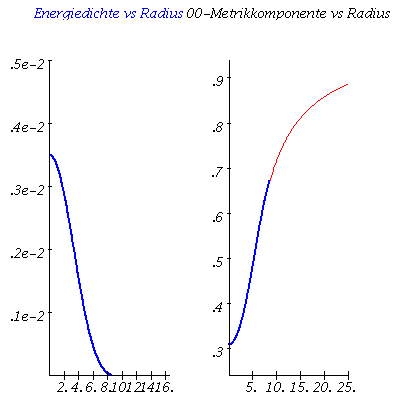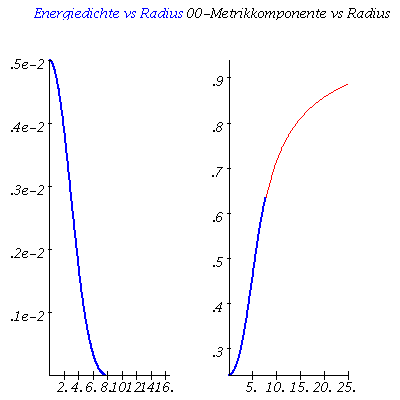
Im folgenden wird eine Sequenz von Sternen mit unterschiedlichen zentralen Energiedichten-Werten berechnet. Trägt man die Gesamtmasse der einzelnen Sterne gegen deren Radius auf, so erhält man die Masse-Radius Beziehung und erkennt die, der benutzten Zustandsgleichung eigenen, maximale Masse. Die Berechnung erfolgt durch eine for-Schleife über einen geeigneten zentralen Energiedichtebereich: 

>

r0:=10^(-14): ranf:=10^(-1): frames:=20: for i from 1 by 1 to frames do e0:=i*0.00025: Loes:=dsolve({TOV1,TOV2,TOV3,m(r0)=0,e(r0)=e0,phi(r0)=0},{m(r),e(r),phi(r)},type=numeric,output=listprocedure): energiedichte := subs(Loes,e(r)): Mass := subs(Loes,m(r)): PPhi := subs(Loes,phi(r)): for rr from 1 by 0.0001 while energiedichte(rr)>10^(-10) do Radius[i]:=rr: end do: Masse[i]:=Mass(Radius[i]); Plot1[i]:=odeplot(Loes,[r,e(r)],r0..Radius[i],numpoints=200,color=blue,thickness=2,title="Energiedichte vs Radius"): Phi0:=(0.5*ln(1-2*Masse[i]/Radius[i])): DPhi:=Phi0-PPhi(Radius[i]): Plot3[i]:=odeplot(Loes,[r,exp(2*(phi(r)+DPhi))],r0..Radius[i],numpoints=200,color=blue,thickness=2,labels=[Radius,"00-Metrikkomponente"],labeldirections=[horizontal, vertical],title="00-Metrikkomponente vs Radius"): Plot5[i]:=plot(1-2*Masse[i]/r,r=Radius[i]..25,color=red): Ani1[i]:=display(Matrix(1,2,[[Plot1[i],display(Plot3[i],Plot5[i])]])); PointA[i]:=pointplot({[Radius[i], Masse[i]/1.4766]}, symbol=solidcircle,symbolsize=23,color=blue): od:

 

>	MR:=listplot([seq([Radius[i], Masse[i]/1.4766], i = 1 .. frames)],title="Masse vs Sternradius"): for i from 1 by 1 to frames do Ani2[i]:=display(PointA[i],MR); od:

 

>	Animat:=display([seq(Ani1[i],i=1..frames)],insequence=true): Animat1:=display([seq(Ani2[i],i=1..frames)],insequence=true): display(Array([Animat1,Animat]));

 

 

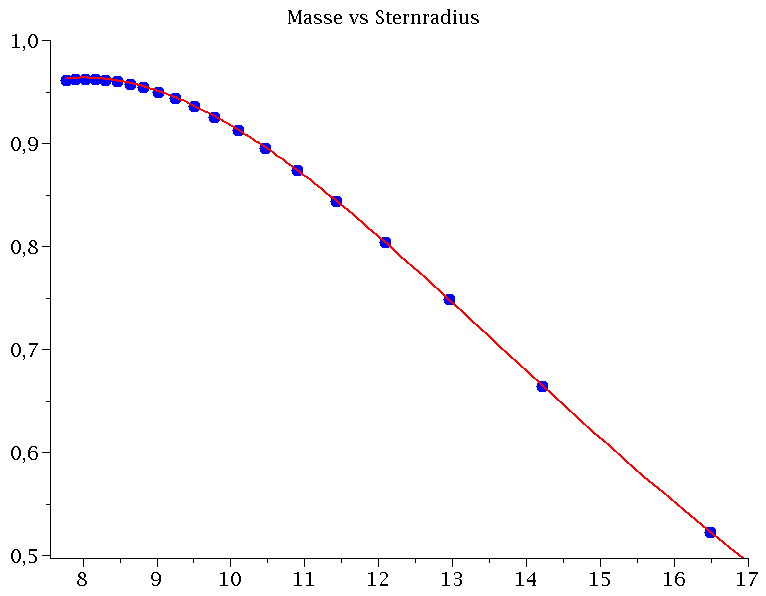
Wir vergleichen nun diese Lösung der Masse-Radius Beziehung mit den C++ Resultaten (dr=0.00001); siehe Teil II, sequentielle Version 4. 

>

CRes:=[[43.961420,0.040222],[25.211190,0.196875],[22.351070,0.268748],[20.773210,0.321155],[19.694540,0.363325],[18.880010,0.398917],[18.228150,0.429830],[17.686210,0.457202],[17.223310,0.481777],[16.819900,0.504075],[16.462810,0.524477],[16.142780,0.543269],[15.853060,0.560675],[15.588560,0.576872],[15.345370,0.592006],[15.120410,0.606194],[14.911220,0.619536],[14.715820,0.632116],[14.532550,0.644006],[14.360040,0.655268],[14.197150,0.665954],[14.042890,0.676113],[13.896440,0.685785],[13.757060,0.695008],[13.624140,0.703813],[13.497120,0.712230],[13.375530,0.720285],[13.258930,0.728002],[13.146960,0.735402],[13.039270,0.742505],[12.935570,0.749328],[12.835570,0.755888],[12.739050,0.762199],[12.645770,0.768275],[12.555550,0.774129],[12.468180,0.779772],[12.383510,0.785215],[12.301390,0.790469],[12.221660,0.795541],[12.144220,0.800442],[12.068930,0.805179],[11.995680,0.809760],[11.924380,0.814192],[11.854920,0.818480],[11.787230,0.822632],[11.721210,0.826654],[11.656800,0.830550],[11.593920,0.834327],[11.532510,0.837988],[11.472490,0.841538],[11.413830,0.844982],[11.356450,0.848325],[11.300310,0.851568],[11.245350,0.854718],[11.191540,0.857776],[11.138830,0.860746],[11.087180,0.863632],[11.036550,0.866436],[10.986900,0.869162],[10.938200,0.871811],[10.890420,0.874387],[10.843520,0.876892],[10.797470,0.879329],[10.752260,0.881699],[10.707840,0.884004],[10.664190,0.886248],[10.621300,0.888432],[10.579130,0.890557],[10.537670,0.892626],[10.496880,0.894640],[10.456770,0.896601],[10.417290,0.898510],[10.378440,0.900370],[10.340190,0.902181],[10.302540,0.903945],[10.265460,0.905664],[10.228930,0.907338],[10.192950,0.908969],[10.157500,0.910558],[10.122560,0.912106],[10.088120,0.913615],[10.054170,0.915085],[10.020700,0.916517],[9.987690,0.917914],[9.955130,0.919274],[9.923010,0.920600],[9.891320,0.921893],[9.860050,0.923153],[9.829190,0.924380],[9.798740,0.925577],[9.768670,0.926743],[9.738990,0.927880],[9.709680,0.928988],[9.680730,0.930068],[9.652150,0.931121],[9.623910,0.932147],[9.596010,0.933146],[9.568450,0.934121],[9.541210,0.935070],[9.514300,0.935995],[9.487700,0.936897],[9.461400,0.937776],[9.435410,0.938631],[9.409710,0.939465],[9.384300,0.940278],[9.359180,0.941069],[9.334330,0.941840],[9.309750,0.942591],[9.285440,0.943322],[9.261400,0.944034],[9.237610,0.944727],[9.214070,0.945402],[9.190780,0.946058],[9.167730,0.946698],[9.144920,0.947320],[9.122340,0.947925],[9.099990,0.948514],[9.077870,0.949087],[9.055970,0.949644],[9.034290,0.950186],[9.012820,0.950713],[8.991570,0.951224],[8.970510,0.951722],[8.949670,0.952205],[8.929020,0.952675],[8.908560,0.953131],[8.888310,0.953573],[8.868240,0.954003],[8.848350,0.954420],[8.828650,0.954824],[8.809140,0.955216],[8.789800,0.955596],[8.770630,0.955965],[8.751640,0.956322],[8.732810,0.956667],[8.714160,0.957002],[8.695670,0.957326],[8.677330,0.957639],[8.659160,0.957941],[8.641150,0.958234],[8.623290,0.958516],[8.605580,0.958789],[8.588030,0.959052],[8.570620,0.959305],[8.553350,0.959549],[8.536230,0.959784],[8.519250,0.960010],[8.502410,0.960228],[8.485710,0.960437],[8.469150,0.960637],[8.452710,0.960829],[8.436410,0.961013],[8.420240,0.961189],[8.404200,0.961357],[8.388280,0.961518],[8.372490,0.961670],[8.356820,0.961816],[8.341270,0.961954],[8.325850,0.962085],[8.310540,0.962210],[8.295340,0.962327],[8.280270,0.962437],[8.265300,0.962541],[8.250450,0.962639],[8.235710,0.962730],[8.221070,0.962814],[8.206550,0.962893],[8.192130,0.962965],[8.177820,0.963032],[8.163610,0.963093],[8.149500,0.963148],[8.135500,0.963197],[8.121590,0.963241],[8.107780,0.963279],[8.094070,0.963312],[8.080460,0.963340],[8.066940,0.963362],[8.053520,0.963380],[8.040190,0.963392],[8.026950,0.963400],[8.013800,0.963402],[8.000740,0.963400],[7.987770,0.963394],[7.974890,0.963383],[7.962100,0.963367],[7.949390,0.963347],[7.936760,0.963322],[7.924220,0.963294],[7.911760,0.963261],[7.899380,0.963224],[7.887090,0.963183],[7.874870,0.963137],[7.862730,0.963088],[7.850680,0.963036],[7.838690,0.962979],[7.826790,0.962919],[7.814960,0. 962855],[7.803210,0.962787],[7.791530,0.962716],[7.779920,0.962641]]:

 

>	PC:=listplot(CRes, thickness=2, color=red,view=[7.6..17,0.5..1]): MR:=pointplot([seq([Radius[i], Masse[i]/1.4766], i = 1 .. frames)],title="Masse vs Sternradius",symbol=solidcircle, symbolsize=15,color=blue,font = [TIMES, ROMAN, 15]): display(MR,PC);

 

 

Weiße Zwerge, Neutronensterne und Quarksterne  

Die zugrundeliegende Zustandsgleichung der Materie (die Funktion p(e))  zusammen mit dem Startwert der zentralen Energiedichte im Inneren des Sterns legen die Eigenschaften des Sterns fest. Weiße Zwerge haben eine viel geringere zentrale Energiedichte und ihre Zustandsgleichung wird durch den Elektronendruck verursacht. Bei Neutronen und Quarksternen ist die Zustandsgleichung maßgeblich durch den Druck der Neutronen bzw. der Quarks bestimmt. Im Teil 2 dieser Vorlesung werden wir die Eigenschaften dieser unterschiedlicher Sterne im Detail betrachten. 

Literatur: 

Sagert, Irina, Matthias Hempel, and Carsten Greiner. "Compact stars for undergraduates." European journal of physics 27.3 (2006): 577. 

Silbar, Richard R., and Sanjay Reddy. "Neutron stars for undergraduates." American journal of physics 72.7 (2004): 892-905. 

David Blaschke, "Structure of White Dwarfs and Neutron Stars"  (siehe www.ift.uni.wroc.pl-blaschke-vorles-CS_2.pdf) 

 

>