Allgemeine Relativitätstheorie mit dem Computer
General Theory of Relativity on the Computer
Dieses Mathematica Notebook ist im Rahmen der Vorlesung “Allgemeine Relativitätstheorie mit dem Computer” entstanden, die im Sommersemester 2016 von Matthias Hanauske an der J.W.Goethe-Universität in Frankfurt am Main gehalten wurde.
(siehe http://th.physik.uni-frankfurt.de/~hanauske/VARTC/ )
Mathematica Notebook erstellt von Marvin Kohls
Frankfurt am Main 25.05.2016
1) Grundlegende Größen der Allgemeinen Relativitätstheorie
Dieses Mathematica-Notebook soll am Ende seiner Entstehung eine äquivalente Alternative zu dem in der Vorlesung erarbeiteten Maple-Worksheet darstellen. Schritt für Schritt wird zuerst die Metrik definiert, woraufhin daraus die Christoffel-Symbole berechnet werden, welche uns mithilfe von Riemann- und Ricci-Tensor am Ende den Einstein-Tensor liefern. Diese Elemente evaluierend, soll am Ende der Betrachtung eine radialsymmetrische, statische, isotrope Raumzeit beschrieben werden. Das Konzept lässt sich auch auf beliebige andere Formen der Raumzeit übertragen.
Nun folgt erst einmal eine Definition des Koordinatensystems. In einem radialsymmetrischen Gebilde ist der naheliegendste Ansatz der von Kugelkoordinaten:
![]()
![]()
Hierzu gibt es eine wichtige Anmerkung im Buch “Gravity: An Introduction to Einstein’s General Relativity” von James B. Hartle. Sofern der Inhalt dieses notebooks in einen anderen Zusammenhang integriert wird und eine oder mehrere der Variablen bereits anderweitig vergeben ist, kann man diese vorige Deklaration entfernen, indem man vor der Neudeklaration beispielsweise “Clear[r, θ, φ, t]” eingibt und mit Shift+Enter bestätigt. Im Gegensatz zu Maple muss in Mathematica auch kein “;” an das Ende einer Zeile gesetzt werden, um eine Ausgabe zu erhalten. Setzt man in Mathematica ein “;”, so erhält man keine Ausgabe. Lässt man es jedoch weg, gibt das Programm das Ergebnis der Berechnung aus (siehe oben).
Nun definiert man die allgemeine statische, isotrope, kovariante Raumzeit-Metrik:
![]()
Dies lässt sich natürlich auch als Matrix ausdrücken:
![]()
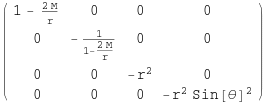
Für das weitere Vorgehen wird auch die kontravariante Form der Metrik benötigt, was einer Invertierung gleich kommt:
![]()
![]()
Oder ausgeschrieben als Matrix:
![]()
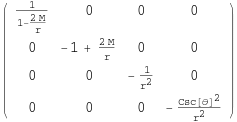
Nun ist man in der Lage, aus diesen Informationen die Christoffelsymbole zu bestimmen. Ein möglicher Ansatz hierzu wird in “Gravity: An Introduction to Einstein’s General Relativity” von James B. Hartle (das ich in der Folge mit [HARTLE] abkürze) beschrieben. Hierzu wird die rechte Seite der Formel
![]()
Eins zu Eins in Mathematica-Syntax umgesetzt. Es ist nichts weiter nötig, als unsere Metrik, ihre invertierte Form und die Mathematica-Funktion “D”, welche partiell differenziert. Die Funktion “Sum[]” wird für die Summation über sich wiederholende Indizes benötigt. Der Ausdruck “{x,1,4}” am Ende gibt die Summationsindizes für den Index “x” an. Man kann dies auch allgemeiner gestalten und statt einer “4” ein “n” verwenden, sodass man mit n-dimensionalen Objekten arbeiten und die Zahl der Dimensionen einfach variieren kann.

Für beliebige andere Indexstellungen muss lediglich die Form der genutzten Metrikdarstellungen variiert werden. Dem Ansatz in [HARTLE] weiter folgend, kann man sich die Ergebnisse dessen in einer sehr anschaulichen Form ausgeben lassen. Das Ganze ist sehr technisch und hat mit der eigentlichen Problemstellung wenig zu tun - deshalb wird nicht alles im Detail erläutert. Das Konzept ist jedoch einfach erklärt: Der Code lässt Mathematica nach Christoffelsymbolen suchen, die ungleich Null sind, und wandelt den Eintrag in einen String um - zusammen mit einem Gamma, das davor gesetzt wird und in Klammern die jeweilige Komponente angibt. Hat Mathematica alle Strings zusammen, werden sie als Tabelle mit zwei Spalten ausgegeben (links das Gamma und rechts die entsprechende Komponente). Wie auch in Maple läuft das Programm ebenfalls von 1 bis 4 - also Vorsicht bei der Identifikation der Komponenten!
![]()
![]()
| Γ[1, 2, 1] | |
| Γ[2, 1, 1] | |
| Γ[2, 2, 2] | |
| Γ[2, 3, 3] | 2 M-r |
| Γ[2, 4, 4] | |
| Γ[3, 3, 2] | |
| Γ[3, 4, 4] | -Cos[θ] Sin[θ] |
| Γ[4, 4, 2] | |
| Γ[4, 4, 3] | Cot[θ] |
Somit haben wir nun alle von Null verschiedenen Christoffelsymbole in einer Übersicht zusammengefasst. Nun erhalten wir analog den Riemann-Tensor in lokalen Koordinaten (nachzulesen etwa auf https://de.wikipedia.org/wiki/Riemannscher_Krümmungstensor) mit einem gehobenen und drei gesenkten Indizes. Die Unterteilung in zwei Schritte diente nur dem Zweck der Verkürzung der Terme (viele, viele Indizes...).
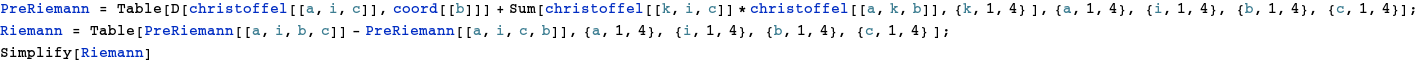
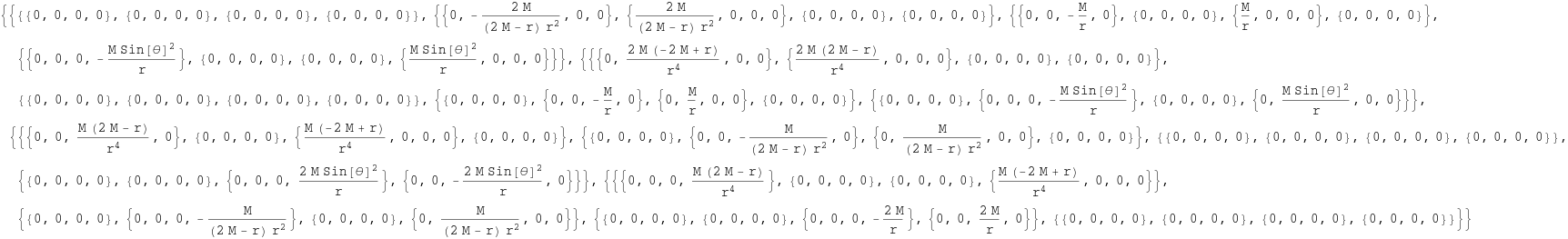
Nun kann man noch den Ricci-Tensor...
![]()
![]()
...und das Krümmungsskalar bestimmen:
![]()
![]()
Und nun, da wir alle Komponenten zusammen haben, kann der Einstein-Tensor aus den existierenden Größen bestimmt werden:
![]()
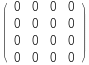
Abschließend möchten wir uns nun noch das Linienelement ausgeben lassen. Analog zu unserem Maple-Skript definieren wir:
![]()
![]()
Somit haben wir unser vollständig zusammengefasstes Linienelement erhalten.
All diese Konzepte lassen sich nun auf die Schwarzschildmetrik anwenden, indem man A[r] und B[r] die entsprechenden Werte zuweist und analog vorgeht. Um beispielsweise einen einfallenden Lichtstrahl zu betrachten, geht man dann wie folgt vor:
dθ = 0;
dφ = 0;
Gl1 = ds2/dtau^2;
Loes1 = Solve[Gl1==0,dt]
was einem die Lösungen für dt ausgibt, welche es in der Folge dann zu integrieren gilt. Gleiches gilt für dr und r.
Es soll nun in der Folge darum gehen, die Geodätengleichung der ART zu lösen. Sie gibt den Pfad an, entlang dessen sich ein Teilchen im Gravitationsfeld (gekrümmter Raum) bewegt. Geodäten entsprechen hierbei selten geraden Verbindungslinien (auf dem Globus beispielsweise sind Geodäten immer Teil eines eigenen Großkreises). Die Komponenten der Geodätengleichungen sind, gemäß [HARTLE]:
d![]() /dτ = -
/dτ = - ![]()
![]()
![]()
wobei auf der linken Seite die Ableitung der Vierergeschwindigkeit nach der Eigenzeit zu finden ist. Wer sich das Konzept der Geodäten noch einmal vor Augen führen möchte, kann dies beispielsweise mithilfe von [HARTLE] oder https://de.wikipedia.org/wiki/Geodäte tun.
Um die Lösung zu erhalten, definieren wir nun die Vierergeschwindigkeit (als Ableitung nach der Eigenzeit) und berechnen die Summe der rechten Seite der Gleichung:
![]()
In Analogie zu den Christoffelsymbolen, kann man nun alle Lösungen ungleich Null ausgeben lassen:
![]()
![]()
Nun wird die Geodätengleichung, ein System vier gekoppelter Differentialgleichungen, als Funktion der Eigenzeit tau berechnet. Die Masse wird gleich eins gesetzt, außerdem beschränkt man sich auf ebene Bewegungen (θ wird gleich π/2 gesetzt, dθ gleich Null).


![]()
![]()
![]()
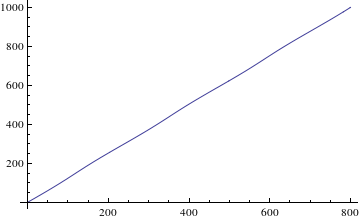
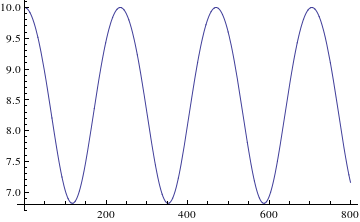
Je nach Anfangsbedingungen erhalten wir verschiedene Trajektorien der Testteilchen. In einem ersten Fall beschränken wir uns auf eine geschlossene Bahnkurve.
Der Testkörper befinde sich bei t=0 in einem Abstand von r=10, was dem fünffachen des Schwarzschildradius (bei r=2) entspricht. Das Teilchen sei zu Beginn radial in Ruhe (dr=0), in Phi-Richtung hingegen mit dphi=0.036 in Bewegung. Die gesamte Bewegung sei aus der Sicht eines äußeren, im Unendlichen sitzenden, Beobachters formuliert.
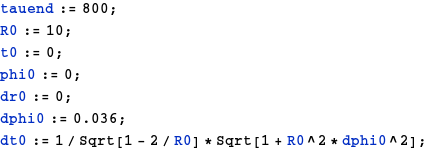
Der Anfangswert dt0 ergibt sich hierbei aus dem Linienelement ds²=1, wie es für einen massiven Probekörper gilt. Unter Angabe der Anfangsbedingungen, wird nun eine numerische Lösung berechnet und graphisch aufgetragen.
![]()
![]()
![]()
![]()
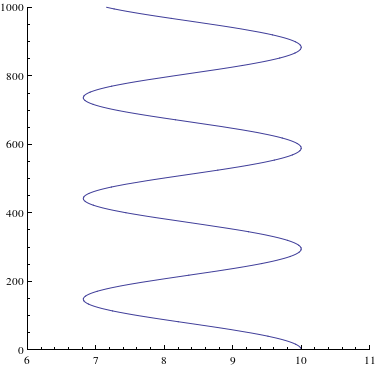
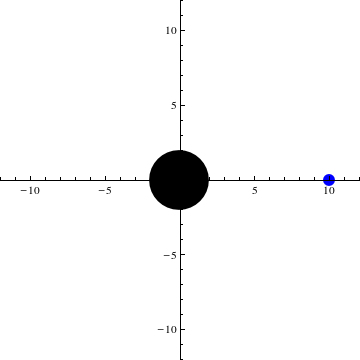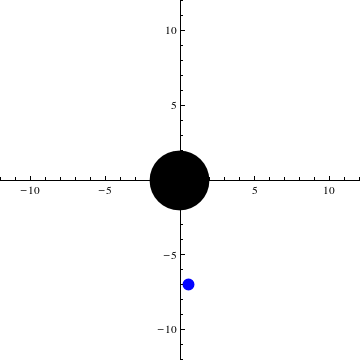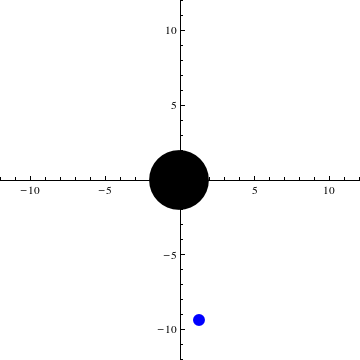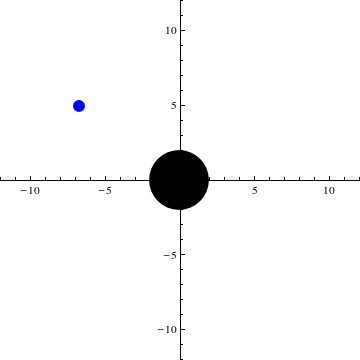
Die folgende Animation zeigt die Bewegung des Testteilchens im Gravitationsfeld des schwarzen Loches. Hier findet die Bewegung, wie oben beschrieben, in der Ebene statt. Das schwarze Loch wird als schwarze Scheibe symbolisiert, das Testteilchen als blaue. Über 100 Iterationen läuft nun eine Schleife, die jeweils in festen Schritten Lösungen der Differentialgleichung in das Koordinatensystem zeichnet und sie als Plot speichert. Diese Plots werden hintereinander gehängt und ergeben dann die unten sichtbare Animation.

![]()
![]()
![]()
Quellen:
1) “Gravity: An Introduction to Einstein’s General Relativity” von James B. Hartle
2) Hendrik van Hees, “Mathematica-Notebook zur Schwarzschild-Metrik”, http://th.physik.uni-frankfurt.de/~hees/cosmo-SS15/schwarzschild-eqs.nb
3) Tristian Hubsch, “GREAT.m” oder “General Relativity, Einstein & All That 4 Mathematica”, Paket für Mathematica (auf der Herstellerseite zum Download verfügbar)
Diese Quellen eignen sich ebenfalls sehr gut, um noch einmal das hier vorgebrachte Prinzip zu variieren. In der zweiten Quelle wird die Metrik noch etwas allgemeiner eingeführt und auf die Herleitung eingegangen.
Eine sehr gute Einführung in die ART liefert Eckhard Rebhan mit seinem Buch “Theoretische Physik: Relativitätstheorie und Kosmologie”, in dem er vielschichtig auf sehr viele verschiedene Aspekte der Theorie eingeht, die Entwicklung der gesamten Relativitätstheorie skizziert und dabei auch teilweise interdisziplinäre Ansätze erläutert.
![]()