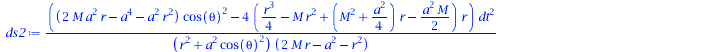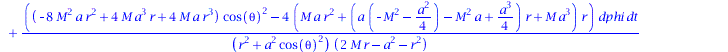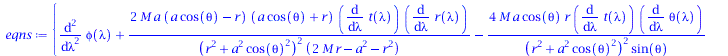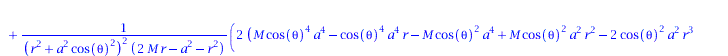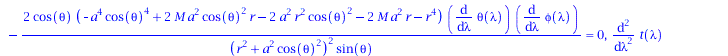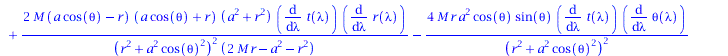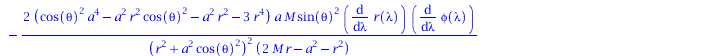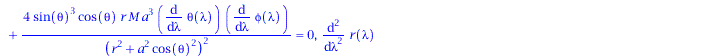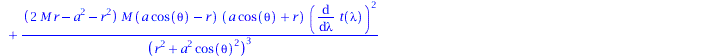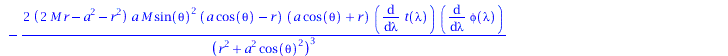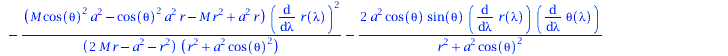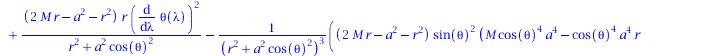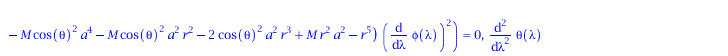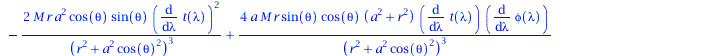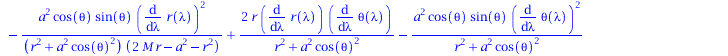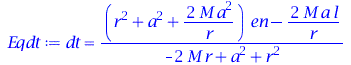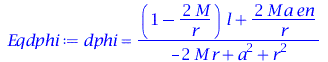Download SL-M87-Rot.mw
Allgemeine Relativitätstheorie mit dem Computer
General Theory of Relativity on the Computer
Vorlesung gehalten an der J.W.Goethe-Universität in Frankfurt am Main (Sommersemester 2016)
von Dr.phil.nat. Dr.rer.pol. Matthias Hanauske
Frankfurt am Main 01.05.2019
Erster Vorlesungsteil: Allgemeine Relativitätstheorie mit Maple
Das Schwarze Loch in M87
(mit Rotation)
Einführung
Ein wenig mehr als hundert Jahre nachdem Albert Einstein seine Feldgleichungen der Allgemeine Relativiätstheorie der Öffentlichkeit präsentierte, und er damit die Grundlage für Gravitationswellen und schwarzer Löcher formulierte, ist seit einigen Wochen ein Meilenstein in der Geschichte der Astronomie in aller Munde:

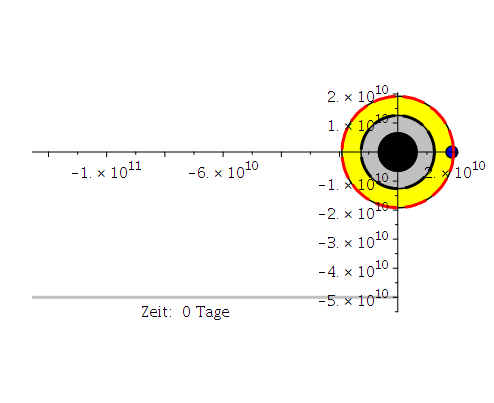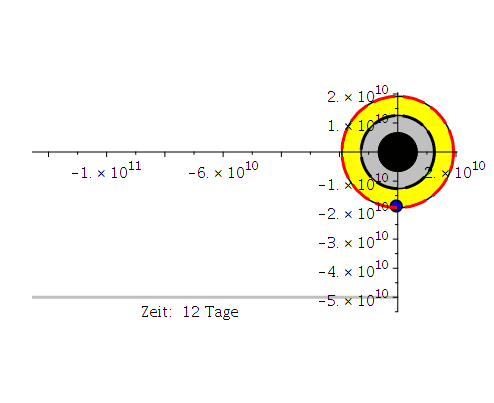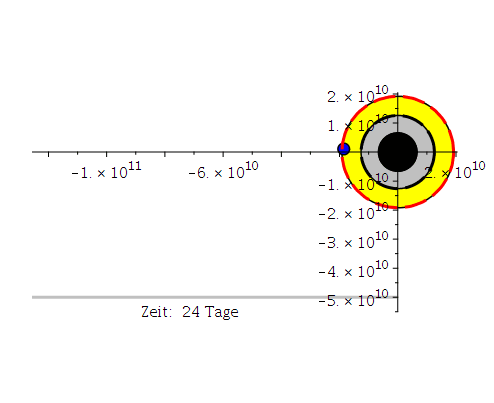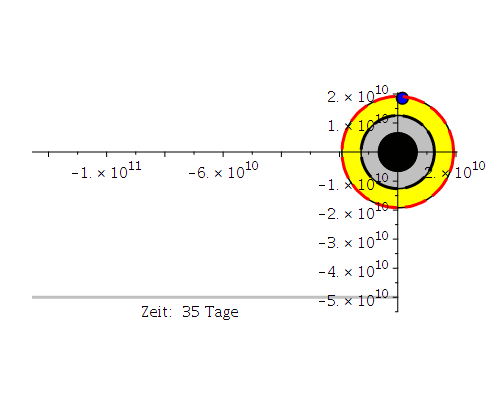
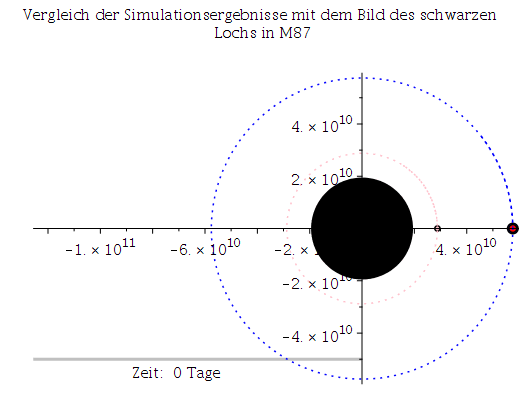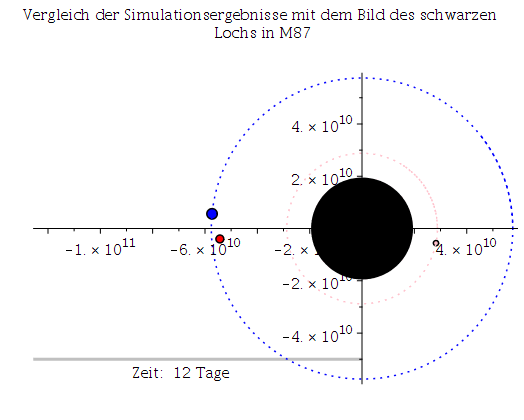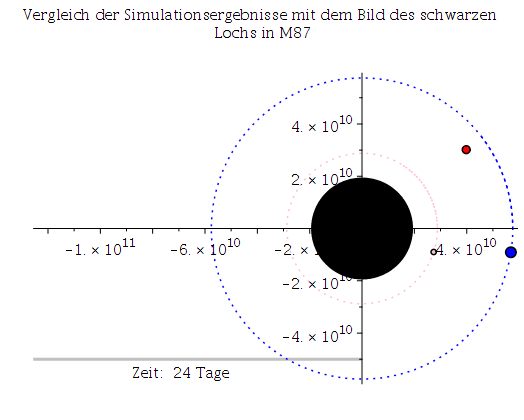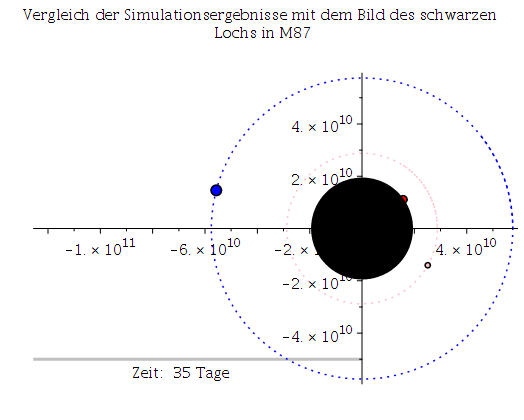
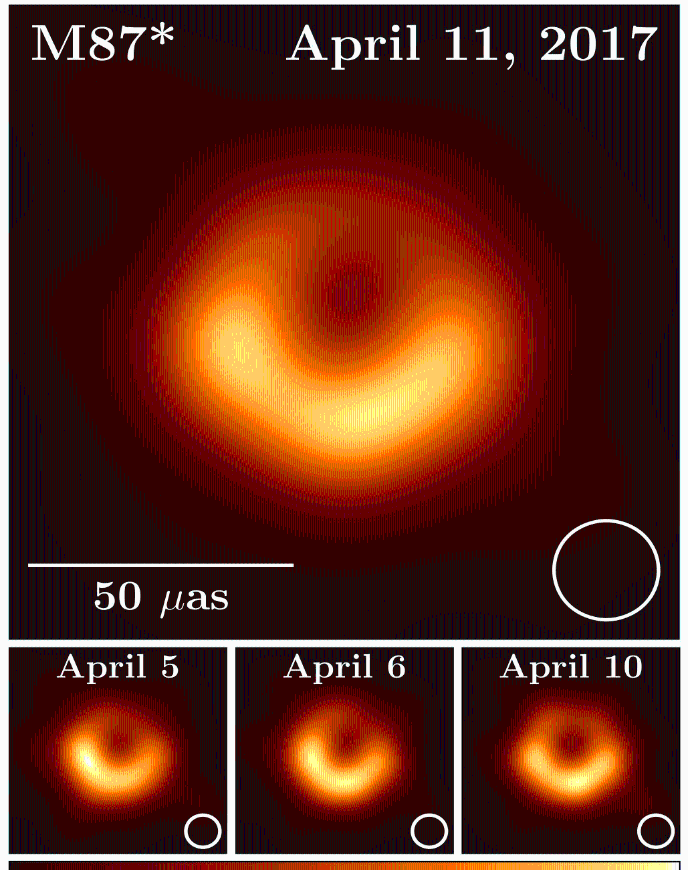
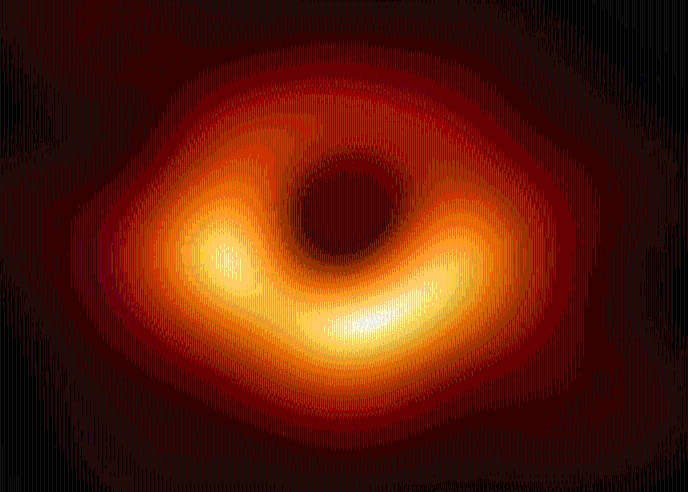
Abb. 1: Erstes Bild eines schwarzen Lochs im Vergleich mit den Simulationsergebnissen des Maple- Worksheets (links: mit Rotation a=0.95M, rechts: ohne Rotation a=0).
Das Bild zeigt das schwarze Loch im Zentrum unserer Nachbargalaxie M87; bzw. ein wenig genauer, die um ein schwarze Loch entstehende Radiostrahlung (das Bild wurde mittels eines weltweiten Verbunds von Radiowellenteleskopen (EHT: Event Horizon Teleskop) sichtbar gemacht). In Kürze (voraussichtlich im Sommer 2019) werden die aufgenommenen Bilder von Sagittarius A*, das schwarze Loch im Zentrum unserer Galaxie, ebenfalls ausgewertet sein, und weitere Bilder in verbesserter Auflösung werden wohl in einigen Jahren folgen. In beiden Systemen (SL in M87 und Sagittarius A*) kreist Materie in einer Akkretionsscheibe um ein supermassives SL und emittiert beim Einfallen Radiowellenstrahlung.Die Bewegung eines Probekörpers (Masse verschwindend klein gegenüber der Masse des schwarzen Lochs) um ein schwarzes Loch ist somit ein astrophysikalisch sehr relevantes Problem. Schon Jahre bevor die ersten Bilder eines SLs entstanden,
galt es als so gut wie bestätigt, dass im Zentrum unserer Galaxie ein superschweres schwarzes Loch existiert und man verfolgte schon seit Jahrzenten (siehe z.B. R.Genzel et,al.) die Bewegung einzelner sogenannter S-Sterne um dieses Zentrum.
In diesem Maple-Worksheet wird die Geodätengleichung in vorgegebener Kerr-Raumzeit betrachtet (die Kerr-Metrik der Raumzeit beschreibt ein rotierendes schwarzes Loch und stellt eine analytische Lösung der Vakuum-Einsteingleichungen dar) und die möglichen Bahnen von Probekörpern mittels eines definierten effektiven Potentials klassifiziert. Neben den gebundenen kreisförmigen und elliptischen Bahnen, den parabolischen und hyperbolischen Bahnverläufen ist auch eine durch das schwarze Loch eingefangene Bahn (capture orbit) möglich. Diese letzteren Bahnen beschreiben die in das schwarze Loch einfallenden Partikel, welche, aufgrund der extremem gravitativen Beschleinigungskräfte, sich aufheizen und elektromagnetische Strahlung emittieren. Ein Verständnis des Erscheinungsbildes des schwarzen Lochs ist möglich indem man sich die grundlegenden Begriffe, wie Ereignishorizonte, Photonensphären
und die letzten stabilen Kreisbahnen von rotierenden Probekörpern um ein SL veranschaulicht.
In diesem Maple-Worksheet werden die, mathematisch anspruchsvollen Gleichungen der Allgemeinen Relativitätstheorie (ART) am Beispiel des schwarzen Lochs in M87 behandelt. Dieses Maple-Worksheet entstand im Jahre 2019 im ersten Teil der Vorlesung "Allgemeine Relativitätstheorie mit dem Computer". Im ersten Teil (Grundlegende Größen der Allgemeinen Relativitätstheorie) erlernen die Studierenden die Verwendung von Computeralgebra-Systemen (Maple und Mathematica). Die oft komplizierten und zeitaufwendigen Berechnungen der tensoriellen Gleichungen der ART können mit Hilfe dieser Programme erleichtert werden. Diverse Anwendungen der Einstein- und Geodätengleichung werden in Maple implementiert, quasi analytische Berechnungen durchgeführt und entsprechende Lösungen berechnet und visualisiert. Der Schwerpunkt in diesem Worksheet liegt sowohl auf dem Verständnis des Bildes des schwarzen Lochs in M87 als auch in der Vermittlung der
seltsamen Eigenschaften rotierender Schwarzer Löcher.
Grundlegende Größen der Allgemeinen Relativitätstheorie
Im folgenden werden einige grundlegende Größen der allgemeinen Relativitätstheorie am Beispiel der Kerr-Metrik eines rotierenden schwarzen Lochs (SL) erläutert.
Zunächst wird das "tensor"-Paket und weitere Zusatzpakete eingebunden:
| > |
restart:
with( tensor ):
with ( plots ):
with( plottools ): |
Definition der kovarianten Raumzeit-Metrik eines rotierenden schwarzen Lochs der Masse M und Rotation a in Boyer-Lindquist Koordinaten (a ist der spezifische Drehimpuls (a=J/M , a=[0,M]) des rotierenden schwarzen Lochs und wird als der sogenannte Kerr-Rotationsparameter bezeichnet): Später werden wir die Masse des SLs auf 6.5*10^(9) Sonnenmassen setzen (der Wert der gravitativ wirkenden Masse des SLs in M87):
\[
\begin{eqnarray}
&g_{\mu\nu}=\left( \begin{array}{ccc} g_{tt}(r,\theta) & 0 & 0 & g_{t\phi}(r,\theta)\\ 0& g_{rr}(r,\theta)& 0&0 \\ 0& 0& g_{\theta\theta}(r,\theta)& 0\\ g_{\phi t}(r,\theta)& 0& 0& g_{\phi\phi}(r,\theta)\\ \end{array} \right) \quad , \hbox{wobei:}& \\
& g_{tt}(r,\theta)=\left( \frac{1-2\,M\,r}{\rho^2} \right)\,\,, \, g_{t\phi}(r,\theta)=\frac{2aMr\hbox{sin}^2(\theta)}{\rho^2} \,\,, \, g_{rr}(r,\theta)=-\frac{\rho^2}{\Delta}\,\,, & \\
& g_{\theta\theta}(r,\theta)=-\rho^2\,\,, \, g_{\phi\phi}(r,\theta)=-\left( \frac{r^2+a^2+2 M r a^2 \hbox{sin}^2(\theta)}{\rho^2} \right)\hbox{sin}^2(\theta)\,\,,\\
&\rho^2=r^2+a^2 \hbox{cos}^2(\theta) \,\,, \,\Delta=r^2-2Mr+a^2&
\end{eqnarray}
\]
| > |
coord := [t, r, theta, phi]:
rho2:=r^2+(a*cos(theta))^2:
Delta:=r^2-2*M*r+a^2:Sig2:=(r^2+a^2)^2-a^2*Delta*(sin(theta))^2:
g_compts := array(symmetric,sparse, 1..4, 1..4):
g_compts[1,1] := (1-2*M*r/rho2):
g_compts[1,4] := +(2*a*M*r*(sin(theta))^2)/rho2:
g_compts[2,2] :=-rho2/Delta:
g_compts[3,3] := -rho2:
g_compts[4,4] := -(r^2+a^2+(2*M*r*a^2*(sin(theta))^2)/rho2)*(sin(theta))^2:
g := create( [-1,-1], eval(g_compts)); |
![Typesetting:-mprintslash([g := TABLE([index_char = [-1, -1], compts = matrix([[`+`(1, `-`(`/`(`*`(2, `*`(M, `*`(r))), `*`(`+`(`*`(`^`(r, 2)), `*`(`^`(a, 2), `*`(`^`(cos(theta), 2)))))))), 0, 0, `+`(`/...](images/SL-M87-Rot_4.gif)
![Typesetting:-mprintslash([g := TABLE([index_char = [-1, -1], compts = matrix([[`+`(1, `-`(`/`(`*`(2, `*`(M, `*`(r))), `*`(`+`(`*`(`^`(r, 2)), `*`(`^`(a, 2), `*`(`^`(cos(theta), 2)))))))), 0, 0, `+`(`/...](images/SL-M87-Rot_5.gif) |
(2.1) |
Kontravariante Raumzeit-Metrik:
| > |
ginv := invert( g, 'detg' ): |
Erste partielle Ableitung der Metrik:
| > |
D1g := d1metric ( g, coord ): |
Chistoffel Symbole (kontravariante Form):
| > |
Cf1 := Christoffel1 ( D1g ): |
Chistoffel Symbole (erster Index kontravariant, zweiter und dritter kontravariant):
| > |
Cf2:= Christoffel2( ginv, Cf1 ): |
Angabe einzelner Komponenten eines Tensors (hier speziell die [t,r,phi] das Christoffelsymbol 2.Art, bei einem nichtrotierenden SL (a=0) wäre diese Komponente =0:
| > |
get_compts(Cf2)[1,2,4]; |
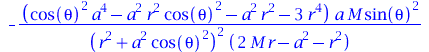 |
(2.2) |
Riemann Tensor:
| > |
D2g := d2metric ( D1g, coord ):
RMN := Riemann( ginv, D2g, Cf1 ): |
Ricci Tensor Da es sich bei der Kerr-Metrik um eine Lösung der Vakuum-Einsteingleichungen handelt, verschwindet der Ricci-Tensor identisch:
| > |
RICCI := Ricci( ginv, RMN ); |
![Typesetting:-mprintslash([RICCI := TABLE([index_char = [-1, -1], compts = matrix([[0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]])])], [table( [( index_char ) = [-1, -1], ( compts ) = array( 1...](images/SL-M87-Rot_7.gif) |
(2.3) |
Ricci Skalar:
| > |
RS := Ricciscalar( ginv, RICCI ): |
Einsteintensor:
| > |
Estn := Einstein(g, RICCI, RS): |
Berechnung des infinitesimalen Weglängenelements ds²:
| > |
dx:=create([1], array([dt,dr,dtheta,dphi])):
ds2:=get_compts(prod(dx,lower(g,dx,1),[1,1])):
ds2:=collect( simplify(ds2), [dt,dr,dtheta,dphi]); |
Hoch- und herunterheben der raumzeitlichen Indices:
| > |
raise(ginv,Cf1,1):
lower(g,Cf2,1): |
Beispiel: Riemann Tensor mit allen Indices oben:
| > |
RMNinv:=raise(ginv,RMN,1,2,3,4): |
Das Produkt zweier Tensoren:
Contraction zweier Indices:
| > |
contract(Cf1Cf2,[4,6]): |
Kontrahiert man das quadratische Produkt der Riemann Tensors vollständig, so erhält man den Kretschmann-Skalar:
| > |
Kret:=prod(RMN,RMNinv,[1,1],[2,2],[3,3],[4,4]); |
![Typesetting:-mprintslash([Kret := TABLE([index_char = [], compts = `+`(`-`(`/`(`*`(48, `*`(`^`(M, 2), `*`(`+`(`*`(a, `*`(cos(theta))), `-`(r)), `*`(`+`(`*`(a, `*`(cos(theta))), r), `*`(`+`(`*`(`^`(a, ...](images/SL-M87-Rot_14.gif)
![Typesetting:-mprintslash([Kret := TABLE([index_char = [], compts = `+`(`-`(`/`(`*`(48, `*`(`^`(M, 2), `*`(`+`(`*`(a, `*`(cos(theta))), `-`(r)), `*`(`+`(`*`(a, `*`(cos(theta))), r), `*`(`+`(`*`(`^`(a, ...](images/SL-M87-Rot_15.gif) |
(2.5) |
Struktur der Ereignishorizonte, Flächen der stationären Grenze und Flächen unendlicher Rotverschiebung
Die Flächen der stationären Grenze (stationary limit surfaces) und die der unendlichen Rotverschiebung sind durch g_00=0 bestimmt:
| > |
UnRot:=solve(get_compts(g)[1,1]=0,r); |
 |
(2.1.1) |
Die Ereignishorizonte sind durch g^11=0 bestimmt:
| > |
Horizon:=solve(get_compts(ginv)[2,2]=0,r); |
![Typesetting:-mprintslash([Horizon := `+`(M, `*`(`^`(`+`(`*`(`^`(M, 2)), `-`(`*`(`^`(a, 2)))), `/`(1, 2)))), `+`(M, `-`(`*`(`^`(`+`(`*`(`^`(M, 2)), `-`(`*`(`^`(a, 2)))), `/`(1, 2)))))], [`+`(M, `*`(`^`...](images/SL-M87-Rot_17.gif) |
(2.1.2) |
Wir setzen M auf den experimentell gefundenen Wert des SLs in M87 (6.5*10^9 Sonnenmassen; entspricht 6.5*10^(9)*1.4766 km) und betrachten uns die Struktur der stationären Grenzen und der Ereignishorizonte des rotierenden SLs in der äquatorialen Ebene mit a=0.95M.
| > |
setM:=6.5*10^9*1.4766:
seta:=0.95*setM:
theta0:=Pi/2:
print("Innerer Fläche unendlichen Rotverschiebung (a=0.95): r=", evalf(subs({M=setM,a=seta,theta=theta0},UnRot[2])));
print("Innerer Fläche unendlichen Rotverschiebung (a=0): r=", evalf(subs({M=setM,a=0,theta=theta0},UnRot[2])));
print("Äussere Fläche unendlichen Rotverschiebung (a=0.95): r=",evalf(subs({M=setM,a=seta,theta=theta0},UnRot[1])));
print("Äussere Fläche unendlichen Rotverschiebung (a=0): r=",evalf(subs({M=setM,a=0,theta=theta0},UnRot[1])));
print("Innerer Horizont (a=0.95): r=",evalf(subs({M=setM,a=seta},Horizon[2])));
print("Innerer Horizont (a=0): r=",evalf(subs({M=setM,a=0},Horizon[2])));
print("Ausserer Horizont (a=0.95): r=",evalf(subs({M=setM,a=seta},Horizon[1])));
print("Ausserer Horizont (a=0): r=",evalf(subs({M=setM,a=0},Horizon[1]))); |
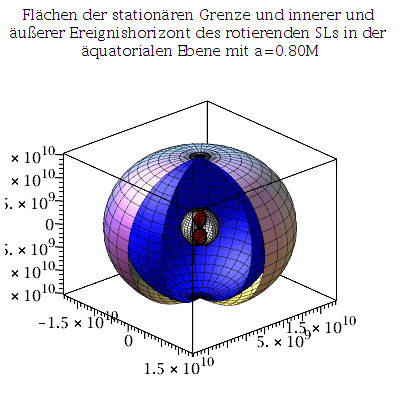
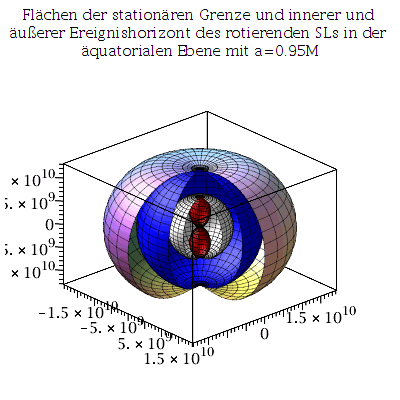
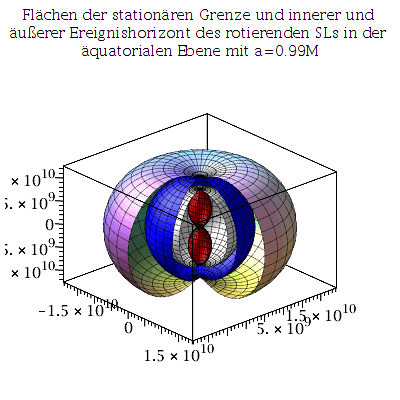
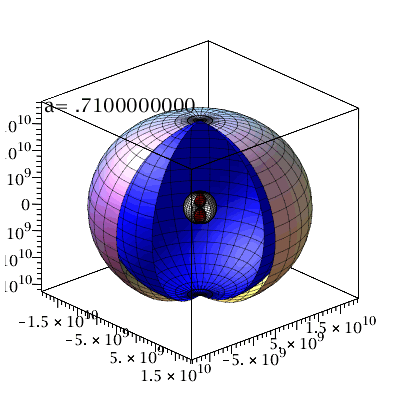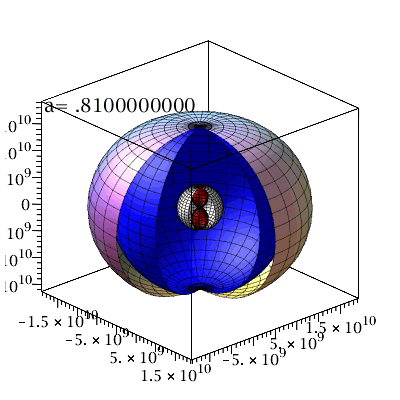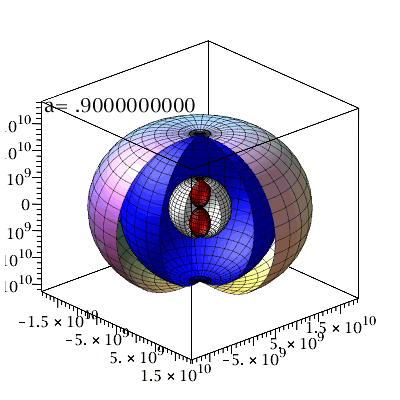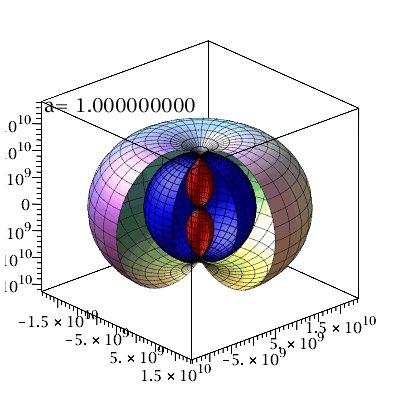
Bei einem nicht-rotierenden SLs gibt es nur einen Ereignishorizont (beim Schwarzschild Radius RS = 2M = 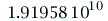 km) und die Fläche unendlicher Rotverschiebung liegt ebnfalls bei diesem Ereignishorizont. Bei einem rotierenden schwarzen Loch trennen sich diese Flächen voneinander und es entstehen vier markannte Fächen (siehe folgende grafische Veranschaulichung der Horizonte (Annahme: SL in M87 rotiert mit a=0.95):
km) und die Fläche unendlicher Rotverschiebung liegt ebnfalls bei diesem Ereignishorizont. Bei einem rotierenden schwarzen Loch trennen sich diese Flächen voneinander und es entstehen vier markannte Fächen (siehe folgende grafische Veranschaulichung der Horizonte (Annahme: SL in M87 rotiert mit a=0.95):
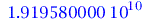 |
(2.1.4) |
| > |
with(StringTools):
A:=plot3d({subs({M=setM,a=seta},UnRot[1])},phi=0..1.5*Pi,theta=0..Pi,coords=spherical,scaling=constrained):
B:=plot3d({subs({M=setM,a=seta},UnRot[2])},phi=0..1.7*Pi,theta=0..Pi,coords=spherical,scaling=constrained,color=red):
C:=plot3d({subs({M=setM,a=seta},Horizon[1])},phi=0..1.6*Pi,theta=0..Pi,coords=spherical,scaling=constrained,color=blue):
DD:=plot3d({subs({M=setM,a=seta},Horizon[2])},phi=0..1.6*Pi,theta=0..Pi,coords=spherical,scaling=constrained,color=white):
seta1:=0.8*setM:
A1:=plot3d({subs({M=setM,a=seta1},UnRot[1])},phi=0..1.5*Pi,theta=0..Pi,coords=spherical,scaling=constrained):
B1:=plot3d({subs({M=setM,a=seta1},UnRot[2])},phi=0..1.7*Pi,theta=0..Pi,coords=spherical,scaling=constrained,color=red):
C1:=plot3d({subs({M=setM,a=seta1},Horizon[1])},phi=0..1.6*Pi,theta=0..Pi,coords=spherical,scaling=constrained,color=blue):
DD1:=plot3d({subs({M=setM,a=seta1},Horizon[2])},phi=0..1.6*Pi,theta=0..Pi,coords=spherical,scaling=constrained,color=white):
seta2:=0.99*setM:
A2:=plot3d({subs({M=setM,a=seta2},UnRot[1])},phi=0..1.5*Pi,theta=0..Pi,coords=spherical,scaling=constrained):
B2:=plot3d({subs({M=setM,a=seta2},UnRot[2])},phi=0..1.7*Pi,theta=0..Pi,coords=spherical,scaling=constrained,color=red):
C2:=plot3d({subs({M=setM,a=seta2},Horizon[1])},phi=0..1.6*Pi,theta=0..Pi,coords=spherical,scaling=constrained,color=blue):
DD2:=plot3d({subs({M=setM,a=seta2},Horizon[2])},phi=0..1.6*Pi,theta=0..Pi,coords=spherical,scaling=constrained,color=white):
Plot3:=display({A,B,C,DD},axes=boxed,orientation=[-42,66], scaling=constrained,title="Flächen der stationären Grenze und innerer und äußerer Ereignishorizont des rotierenden SLs in der äquatorialen Ebene mit a=0.95M"):
Plot2:=display({A2,B2,C2,DD2},axes=boxed,orientation=[-42,66], scaling=constrained,title="Flächen der stationären Grenze und innerer und äußerer Ereignishorizont des rotierenden SLs in der äquatorialen Ebene mit a=0.99M"):
Plot1:=display({A1,B1,C1,DD1},axes=boxed,orientation=[-42,66], scaling=constrained,title="Flächen der stationären Grenze und innerer und äußerer Ereignishorizont des rotierenden SLs in der äquatorialen Ebene mit a=0.80M"):
display(Matrix(1,3,[Plot1,Plot3,Plot2])); |
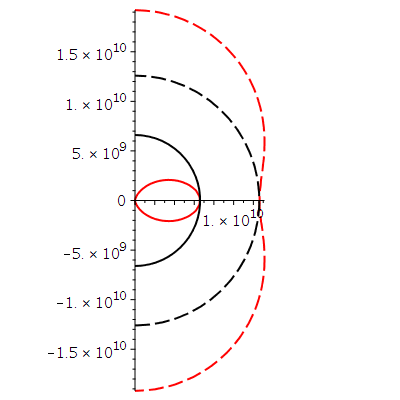
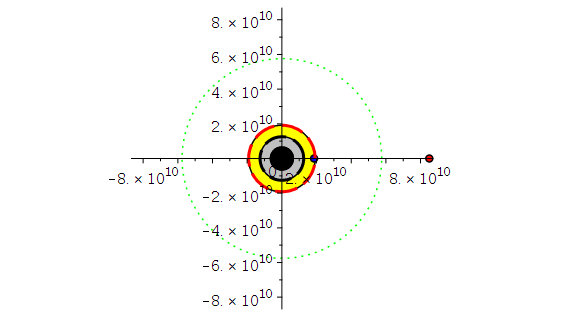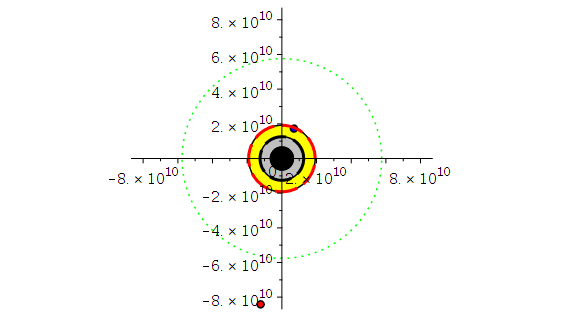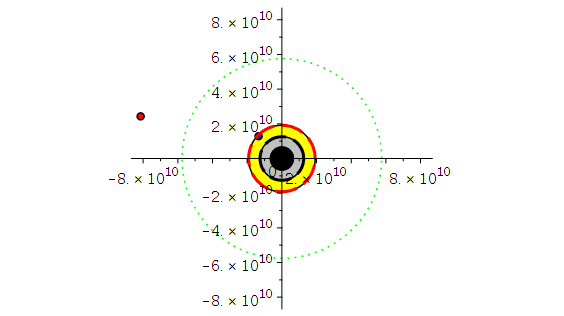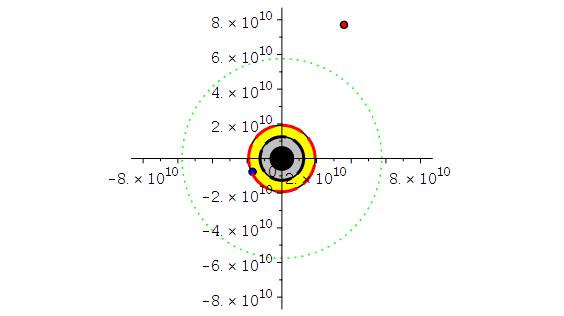
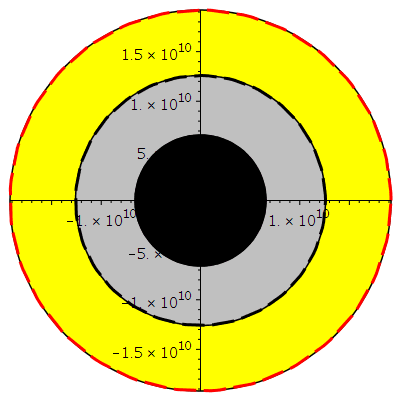
Horizontstruktur in der äquatorialen Ebene (Gelb: Ergosphäre, grau: Bereich zwischen äußerem und innerem Ereignishorizont, a=0.95):
| > |
plotrmin:=0.28*2*setM:
plotrmax:=5.0*2*setM:
A:=implicitplot(r = subs({M=setM,a=seta,theta=Pi/2},UnRot[1]), r = 0 .. plotrmax, phi = 0 .. 2*Pi, coords = polar,grid=[30,30],color=red,linestyle=dash,thickness=3):
B:=implicitplot(r = subs({M=setM,a=seta,theta=Pi/2},UnRot[2]), r = 0 .. plotrmax, phi = 0 .. 2*Pi, coords = polar,grid=[30,30],color=red,linestyle=solid):
C:=implicitplot(r = subs({M=setM,a=seta,theta=Pi/2},Horizon[1]), r = 0 .. plotrmax, phi = 0 .. 2*Pi, coords = polar,grid=[30,30],color=black,linestyle=dash,thickness=3):
DD:=implicitplot(r = subs({M=setM,a=seta,theta=Pi/2},Horizon[2]), r = 0 .. plotrmax, phi = 0 .. 2*Pi, coords = polar,grid=[30,30],color=black,linestyle=solid):
BH1:=display(disk([0,0],subs({M=setM,a=seta,theta=Pi/2},Horizon[2]),color=black)):
BH2:=display(disk([0,0],subs({M=setM,a=seta,theta=Pi/2},Horizon[1]),color=grey)):
BH3:=display(disk([0,0],subs({M=setM,a=seta,theta=Pi/2},UnRot[1]),color=yellow)):
display({A,B,C,DD,BH1,BH2,BH3},scaling=constrained);
|
 |
|
Horizontstruktur in der polaren Ebene (a=0.95):
| > |
A:=implicitplot(r = subs({M=setM,a=seta},UnRot[1]), r = 0 .. plotrmax, theta = -Pi/2 .. Pi/2, coords = polar,grid=[30,30],color=red,linestyle=dash,thickness=2):
B:=implicitplot(r=subs({M=setM,a=seta},UnRot[2]), r = 0 .. plotrmax, theta = -Pi/2 .. Pi/2, coords = polar,grid=[30,30],color=red,linestyle=solid,thickness=2):
C:=implicitplot(r = subs({M=setM,a=seta},Horizon[1]), r = 0 .. plotrmax, theta = -Pi/2 .. Pi/2, coords = polar,grid=[30,30],color=black,linestyle=dash,thickness=2):
DD:=implicitplot(r = subs({M=setM,a=seta},Horizon[2]), r = 0 .. plotrmax, theta = -Pi/2 .. Pi/2, coords = polar,grid=[30,30],color=black,linestyle=solid,thickness=2):
display({A,B,C,DD},scaling=constrained); |
Animation der Horizontstruktur bei ansteigender Rotation des schwarzen Lochs:
| > |
#Digits:=2:
frames:=30:
for i from 1 by 1 to frames do
seta:=(0.7+0.3*i/frames)*setM:
A:=plot3d({subs({M=setM,a=seta},UnRot[1])},phi=0..1.5*Pi,theta=0..Pi,coords=spherical,scaling=constrained):
B:=plot3d({subs({M=setM,a=seta},UnRot[2])},phi=0..1.7*Pi,theta=0..Pi,coords=spherical,scaling=constrained,color=red):
C:=plot3d({subs({M=setM,a=seta},Horizon[1])},phi=0..1.6*Pi,theta=0..Pi,coords=spherical,scaling=constrained,color=blue):
DD:=plot3d({subs({M=setM,a=seta},Horizon[2])},phi=0..1.6*Pi,theta=0..Pi,coords=spherical,scaling=constrained,color=white):
Ptext:=textplot3d([1, 1,2*setM, Join(["a=",convert(seta/setM,string)])], align =LEFT,color=black,font = [TIMES, ROMAN, 15]):
Ani1[i]:=display({B,C,DD,Ptext,A},axes=boxed,orientation=[-42,66], scaling=constrained);
od: |
| > |
display([seq(Ani1[i],i=1..frames)],insequence=true); |
Beispiel 1: Bewegung eines Probekörpers um ein rotierendes schwarzes Loch in der Ebene der Akkretionsscheibe
Basierend auf den im ersten Teil berechneten Größen wird im Folgenden die Geodätengleichung in vorgegebener Kerr Raumzeit betrachtet. Die Geodätengleichung beschreibt wie sich ein Probekörper (Masse m -> 0) im Raum bewegt und sagt voraus, dass diese Bewegung sich stehts entlang der kürzesten Kurve, in der durch die Metrik beschriebenen gekrümmten Raumzeit, vollzieht.Die Geodätengleichung ist ein System aus vier gekoppelten Differentialgleichungen, welche von einem affinen Parameter lambda (später die Eigenzeit tau des Probekörpers) funktional abhängt:
Berechnung der Geodätengleichung als Funktion des affinen Parameters $\lambda$: Die Geodätengleichung ist ein System gekoppelter Differentialgleichungen
\[
\begin{eqnarray}
&& \frac{d^2 t}{d\lambda^2} = - \Gamma^0_{\nu \rho} \frac{d x^\nu}{d\lambda} \frac{d x^\rho}{d\lambda} \\
&& \frac{d^2 r}{d\lambda^2} = - \Gamma^1_{\nu \rho} \frac{d x^\nu}{d\lambda} \frac{d x^\rho}{d\lambda}\\
&& \frac{d^2 \theta}{d\lambda^2} = - \Gamma^2_{\nu \rho} \frac{d x^\nu}{d\lambda} \frac{d x^\rho}{d\lambda}\\
&& \frac{d^2 \phi}{d\lambda^2} = - \Gamma^3_{\nu \rho} \frac{d x^\nu}{d\lambda} \frac{d x^\rho}{d\lambda} \quad ,
\end{eqnarray}
\]
wobei $\lambda$ ein affiner Parameter (z.B. die Eigenzeit), t, r, $\theta$ und $\phi$ die sphärischen Koordinaten und $\Gamma^\mu_{\nu \rho}$ die Christoffel Symbole zweiter Art darstellen.
| > |
eqns:=geodesic_eqns( coord, lambda, Cf2 ); |
Wir lassen zunächst nur ebene Bewegungen zu (theta=Pi/2, dtheta=0) und setzen M auf den experimentell gefundenen Wert (6.5*10^9 Sonnenmassen; entspricht 6.5*10^(9)*1.4766 km).
| > |
setM:=6.5*10^9*1.4766:
eq1:=simplify(subs({r=r(lambda),theta=theta(lambda)},eqns[1])):
eq2:=simplify(subs({r=r(lambda),theta=theta(lambda)},eqns[2])):
eq3:=simplify(subs({r=r(lambda),theta=theta(lambda)},eqns[3])):
eq4:=simplify(subs({r=r(lambda),theta=theta(lambda)},eqns[4])):
eq1:=simplify(subs({r(lambda)(lambda)=r(lambda),theta(lambda)(lambda)=theta(lambda)},eq1)):
eq2:=simplify(subs({r(lambda)(lambda)=r(lambda),theta(lambda)(lambda)=theta(lambda)},eq2)):
eq3:=simplify(subs({r(lambda)(lambda)=r(lambda),theta(lambda)(lambda)=theta(lambda)},eq3)):
eq4:=simplify(subs({r(lambda)(lambda)=r(lambda),theta(lambda)(lambda)=theta(lambda)},eq4)): |
In Abhängigkeit von den Anfangswerten und dem Kerr-Rotationsparameter a können unterschiedliche Bahnen der Bewegung entstehen. Wir wählen z.B. a=0.95 und betrachten zunächst als Beispiel die Anfangswerte einer elliptisch geschlossenen Bahn: Zur Zeit t=0 sei der Körper bei einem Radius von r=4.3*(Schwarzschildradius eines nichtrotierenden SLs), die Anfangsgeschwindigkeit des Körpers sei in radialer Richtung dr=0 und in phi-Richtung dphi=5.2*10^(-12). Den Anfangswert für dt erhalten wir wieder über die Bedingung ds^2=1. Wir beschreiben die Bewegung aus der Sichtweise eines im Unendlichen ruhenden Beobachters.
| > |
seta:=0.95*setM:
r0:=4.3*2*setM:
t0:=0:
phi0:=0:
theta0:=Pi/2:
dtheta0:=0:
dr0:=0:
dphi0:=5.2*10^(-12):
dtheta0:=0:
dt0:=solve(subs({theta=theta0,dphi=dphi0,dr=dr0,dtheta=dtheta0,M=setM,a=seta,r=r0},ds2)=1,dt)[1]: |
In der Literatur wird die Bewegung eines Probekörpers um ein rotierendes schwarzes Loch mittels eines definierten, effektiven Potentials illustriert und charakterisiert (siehe z.B. Hartle- bzw. Hobson Buch [1,2]).
1. General relativity : An introduction for physicists by M. P. Hobson, G. P. Efstathiou and A. N. Lasenby
2. Gravity : An introduction to Einstein's general relativity by James B. Hartle
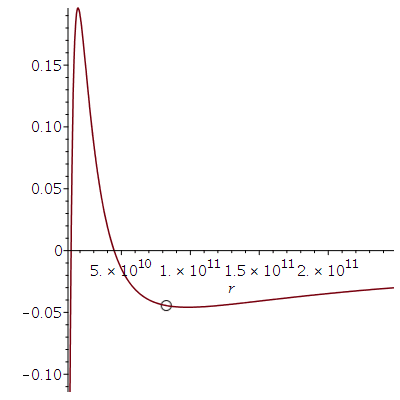
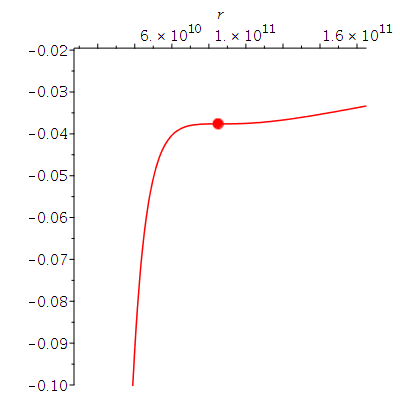
Dieses Potential hängt von dem, bei der Bewegung erhaltenem Drehimpuls pro Masse m, der Probekörper-Energie pro Masse und dem Kerr-Rotationsparameter ab. Die möglichen Bewegungen werden mittels dreier erhaltener Größen (l: Drehimpuls pro Masse m, E: Energie pro Masse und a: Rotationsparameter des SLs) charakterisiert. Die folgende Abbildung zeigt (in der Nomenklatur vom Hartle-Buch) das effektive Potential als Funktion des Radius bei den obigen gewählten Anfangswerten:
\[
V_{eff}(r,M,l,a,E) \,=\, -\frac{M}{r} + \frac{l^2 - a^2 \left( E^2 -1 \right)}{2\, r^2} - \frac{M \left( l - a\,E \right)^2}{r^3}
\]
| > |
plotrmin:=0.155*r0:
plotrmax:=3.0*r0:
Equ1:=solve({dt=1/Delta*((r^2+a^2+2*M*a^2/r)*energie-2*M*a/r*drehimpuls),dphi=1/Delta*((1-2*M/r)*drehimpuls+2*M*a/r*energie)},{energie,drehimpuls}):
setE:=subs({dt=dt0,dphi=dphi0,M=setM,a=seta,r=r0},rhs(Equ1[1]));
setl:=subs({dt=dt0,dphi=dphi0,M=setM,a=seta,r=r0},rhs(Equ1[2]));
VeffHartleRot:=(r,M,l,a,en)->-M/r+(l^2-a^2*(en^2-1))/(2*r^2)-M*(l-a*en)^2/r^3;
PotRot:=plot(VeffHartleRot(r,setM,setl,seta,setE),r=plotrmin..plotrmax):
B:=pointplot({[r0, VeffHartleRot(r0,setM,setl,seta,setE)]}, symbol=circle,symbolsize=20):
display(B,PotRot); |
Numerisches Lösen der Geodätengleichungfür a=0.95:
| > |
Loes:=dsolve({subs({a=seta,M=setM},eq1),subs({a=seta,M=setM},eq2),subs({a=seta,M=setM},eq3),subs({a=seta,M=setM},eq4),t(0)=t0,r(0)=r0,phi(0)=phi0,theta(0)=theta0,D(r)(0)=0,D(t)(0)=dt0,D(phi)(0)=dphi0,D(theta)(0)=dtheta0},{r(lambda),t(lambda),phi(lambda),theta(lambda)},type=numeric,output=listprocedure): |
Zum Vergleich berechnen wir auch die geodätische Bewegung des Probekörpers falls das SL nicht rotieren würde.
| > |
seta:=0:
r0:=4.3*2*setM:
t0:=0:
phi0:=0:
theta0:=Pi/2:
dtheta0:=0:
dr0:=0:
dphi0:=5.2*10^(-12):
dtheta0:=0:
dt0:=solve(subs({theta=theta0,dphi=dphi0,dr=dr0,dtheta=dtheta0,M=setM,a=seta,r=r0},ds2)=1,dt)[1]: |
Numerisches Lösen der Geodätengleichungfür a=0 (keine Rotation):
| > |
Loes0:=dsolve({subs({a=seta,M=setM},eq1),subs({a=seta,M=setM},eq2),subs({a=seta,M=setM},eq3),subs({a=seta,M=setM},eq4),t(0)=t0,r(0)=r0,phi(0)=phi0,theta(0)=theta0,D(r)(0)=0,D(t)(0)=dt0,D(phi)(0)=dphi0,D(theta)(0)=dtheta0},{r(lambda),t(lambda),phi(lambda),theta(lambda)},type=numeric,output=listprocedure): |
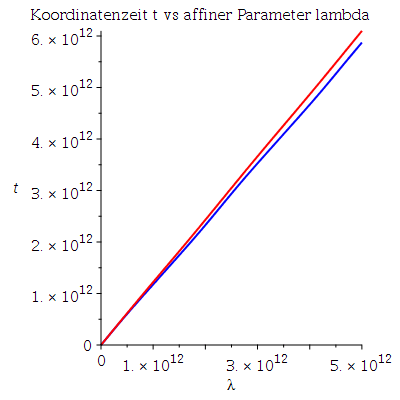
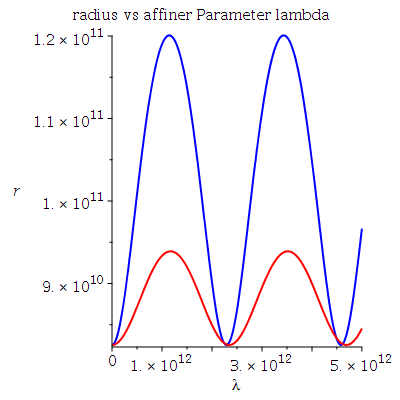
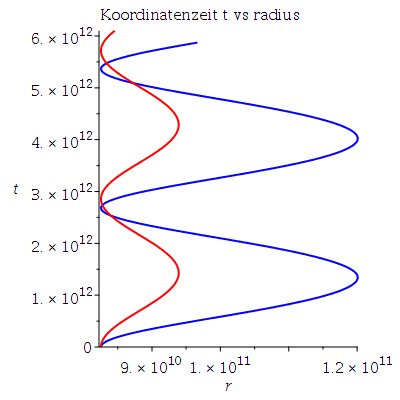
Grafische Veranschaulichung der Lösungen (Blau:a=0.95, Rot: a=0):
| > |
lend:=5*10^12:
Plot1:=odeplot(Loes,[lambda,t(lambda)],0..lend,numpoints=200,color=blue,thickness=2,title="Koordinatenzeit t vs affiner Parameter lambda"):
Plot2:=odeplot(Loes,[lambda,r(lambda)],0..lend,numpoints=200,color=blue,thickness=2,title="radius vs affiner Parameter lambda"):
Plot3:=odeplot(Loes,[r(lambda),t(lambda)],0..lend,numpoints=700,color=blue,thickness=2,title="Koordinatenzeit t vs radius"):
Plot10:=odeplot(Loes0,[lambda,t(lambda)],0..lend,numpoints=200,color=red,thickness=2,title="Koordinatenzeit t vs affiner Parameter lambda"):
Plot20:=odeplot(Loes0,[lambda,r(lambda)],0..lend,numpoints=200,color=red,thickness=2,title="radius vs affiner Parameter lambda"):
Plot30:=odeplot(Loes0,[r(lambda),t(lambda)],0..lend,numpoints=700,color=red,thickness=2,title="Koordinatenzeit t vs radius"):
display(Matrix(1,3,[display(Plot1,Plot10),display(Plot2,Plot20),display(Plot3,Plot30)])); |
| > |
seta:=0.95*setM:
UnRot:=solve(get_compts(g)[1,1]=0,r):
Horizon:=solve(get_compts(ginv)[2,2]=0,r):
A:=implicitplot(r = subs({M=setM,a=seta,theta=Pi/2},UnRot[1]), r = 0 .. plotrmax, phi = 0 .. 2*Pi, coords = polar,grid=[30,30],color=red,linestyle=dash,thickness=3):
B:=implicitplot(r = subs({M=setM,a=seta,theta=Pi/2},UnRot[2]), r = 0 .. plotrmax, phi = 0 .. 2*Pi, coords = polar,grid=[30,30],color=red,linestyle=solid):
C:=implicitplot(r = subs({M=setM,a=seta,theta=Pi/2},Horizon[1]), r = 0 .. plotrmax, phi = 0 .. 2*Pi, coords = polar,grid=[30,30],color=black,linestyle=dash,thickness=3):
DD:=implicitplot(r = subs({M=setM,a=seta,theta=Pi/2},Horizon[2]), r = 0 .. plotrmax, phi = 0 .. 2*Pi, coords = polar,grid=[30,30],color=black,linestyle=solid):
BH1:=display(disk([0,0],subs({M=setM,a=seta,theta=Pi/2},Horizon[2]),color=black)):
BH2:=display(disk([0,0],subs({M=setM,a=seta,theta=Pi/2},Horizon[1]),color=grey)):
BH3:=display(disk([0,0],subs({M=setM,a=seta,theta=Pi/2},UnRot[1]),color=yellow)):
BH:=display({A,B,C,DD,BH1,BH2,BH3},scaling=constrained):
display(BH): |
| > |
frames:=150:
Lr := subs(Loes,r(lambda)):
Lr0 := subs(Loes0,r(lambda)):
Lphi := subs(Loes,phi(lambda)):
Lphi0 := subs(Loes0,phi(lambda)):
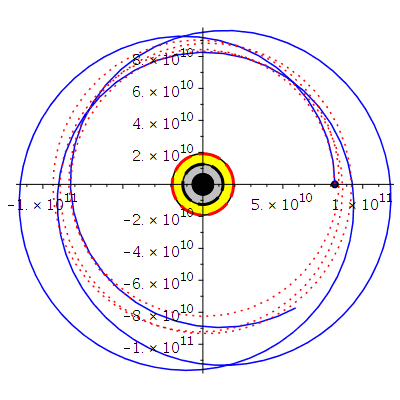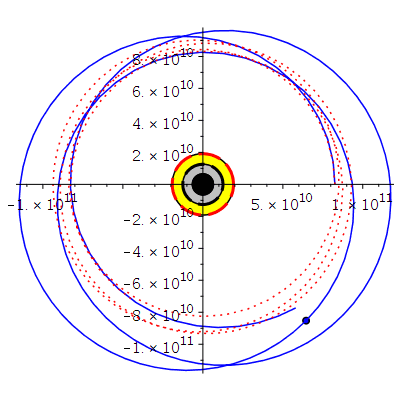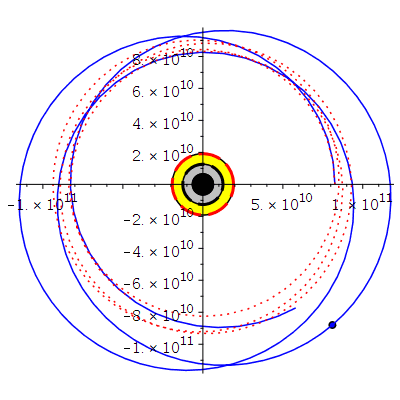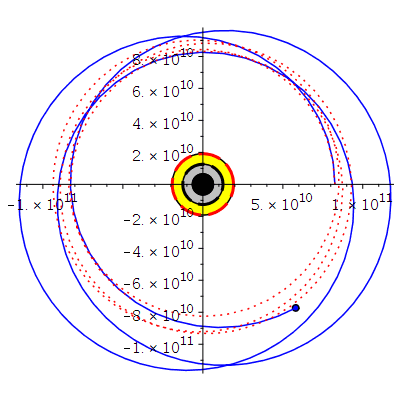
TrajA:=listplot([seq([Lr(j*lend/frames)*cos(Lphi(j*lend/frames)),Lr(j*lend/frames)*sin(Lphi(j*lend/frames))], j = 0 .. frames)],color=blue):
TrajB:=listplot([seq([Lr0(j*lend/frames)*cos(Lphi0(j*lend/frames)),Lr0(j*lend/frames)*sin(Lphi0(j*lend/frames))], j = 0 .. frames)],color=red,linestyle=dot):
for i from 0 by 1 to frames do
Koerper[i]:=display(disk([Lr(i*lend/frames)*cos(Lphi(i*lend/frames)),Lr(i*lend/frames)*sin(Lphi(i*lend/frames))],2*10^9,color=blue)):
Ani[i]:=display({Koerper[i],BH,TrajA,TrajB});
od: |
| > |
display([seq(Ani[i],i=0..frames)],insequence=true,scaling=constrained): |
| > |
PotRot:=plot(VeffHartleRot(r,setM,setl,seta,setE),r=plotrmin..plotrmax):
VE:=VeffHartleRot(r0,setM,setl,seta,setE):
for i from 0 by 1 to frames do
Koerper[i]:=pointplot({[Lr(i*lend/frames), VE]}, symbol=solidcircle,symbolsize=20,color=blue):
Ani1[i]:=display({PotRot,Koerper[i]});
od: |
| > |
Animat1:=display([seq(Ani[i],i=0..frames)],insequence=true,scaling=constrained):
Animat2:=display([seq(Ani1[i],i=0..frames)],insequence=true):
display(Array([Animat1,Animat2])); |
Die Animation zeigt die Bewegung eines Probekörpers um ein rotierendes SL (a=0.95M, blaue Trajektorie). Zu Vergleich zeigt die rote Trajektorie die Bewegung falls das SL nicht rotieren würde (a=0).
Die innerste stabile kreisförmige Bahnbewegung (Innermost Stable Circular Orbit (ISCO)) eines Probekörpers
Wir wollen nun, ähnlich wie beim nichtrotierenden Schwarzschild schwarzen Loch, die innerste stabile kreisformige Bahn (ISCO) berechnen. Das effektive Potential ist bei kreisförmigen Bahnbewegungen (dr/dlambda=0) wie folgt mit der Energie verknüpft (sieheHartle-Buch, S:318 bzw. Hobson-Buch, S:332) :
| > |
VeffHartleRot(r,M,l,a,e)=(e^2-1)/2; |
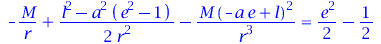 |
(4.1) |
Kreisförmige Bahnbewegungen sind dort, wo das effektive Potential sein Minimum hat:
| > |
diff(VeffHartleRot(r,M,l,a,e),r)=0;
CircOrbe:=solve(diff(VeffHartleRot(r,M,l,a,e),r)=0,e):
CircOrbl:=solve(diff(VeffHartleRot(r,M,l,a,e),r)=0,l): |
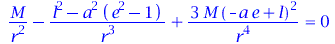 |
(4.2) |
Die innerste stabile kreisformige Bahn hat dort zusätzlich noch einen Sattelpunkt:
| > |
diff(VeffHartleRot(r,M,l,a,e),r,r)=0; |
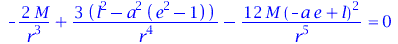 |
(4.3) |
Setzt man die Eigenschaften des rotierenden schwarzen Loches (SL in M87, M=6.5*10^9 Sonnenmassen und a=0.95) fest, und lößt die vorigen drei Gleichungen simultan, so erhält man die Werte für den ISCO.
| > |
seta:=0.95*setM:
ISCO:=solve({diff(VeffHartleRot(r,setM,l,seta,e),r)=0,diff(VeffHartleRot(r,setM,l,seta,e),r,r)=0,VeffHartleRot(r,setM,l,seta,e)=(e^2-1)/2}); |
Die Lösungen des ISCO beinhalten eine eng um das schwarze Loch rotierende Lösung (r=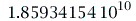 km; Probekörper rotiert in gleicher Richtung wie die Rotationsrichtung des schwarzen Lochs) und eine weiter entfernte Lösung (r=
km; Probekörper rotiert in gleicher Richtung wie die Rotationsrichtung des schwarzen Lochs) und eine weiter entfernte Lösung (r=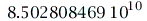 km; Probekörper rotiert entgegen der Rotationsrichtung des schwarzen Lochs)
km; Probekörper rotiert entgegen der Rotationsrichtung des schwarzen Lochs)
| > |
setE1:=rhs(ISCO[1,1]);
setl1:=rhs(ISCO[1,2]);
r01:=rhs(ISCO[1,3]);
setE2:=rhs(ISCO[3,1]);
setl2:=rhs(ISCO[3,2]);
r02:=rhs(ISCO[3,3]); |
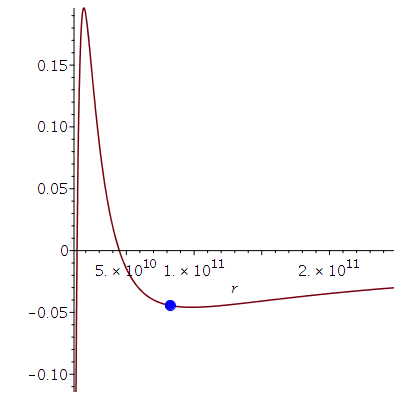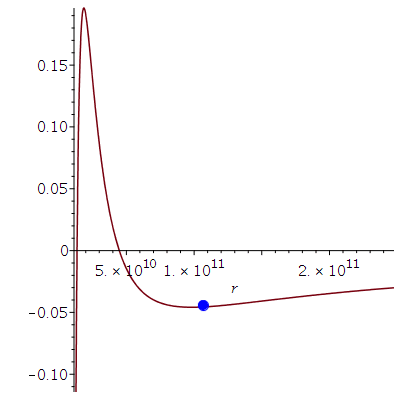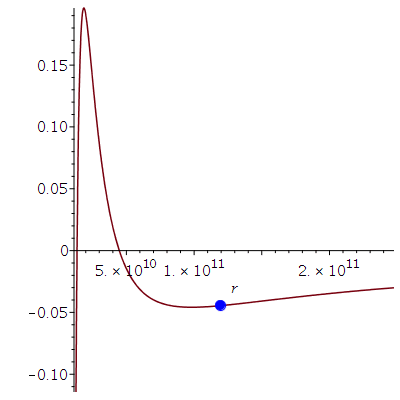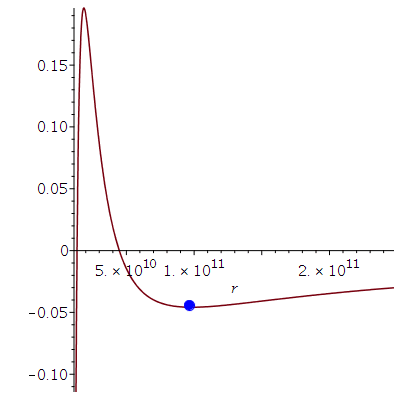
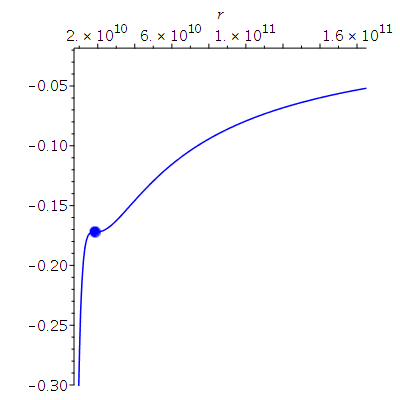
Veranschaulichung der beiden Lösungen im effektiven Potential:
| > |
plotrmin:=0.1*r0:
plotrmax:=2*r0:
PotRot1:=plot(VeffHartleRot(r,setM,setl1,seta,setE1),r=plotrmin..plotrmax,color=blue,view=[plotrmin..plotrmax,-0.3..-0.02]):
B1:=pointplot({[r01, VeffHartleRot(r01,setM,setl1,seta,setE1)]}, symbol=solidcircle,symbolsize=20,color=blue):
PotRot2:=plot(VeffHartleRot(r,setM,setl2,seta,setE2),r=plotrmin..plotrmax,color=red,view=[plotrmin..plotrmax,-0.1..-0.02]):
B2:=pointplot({[r02, VeffHartleRot(r02,setM,setl2,seta,setE2)]}, symbol=solidcircle,symbolsize=20,color=red):
display(Array([display(B1,PotRot1),display(B2,PotRot2)]));
|
Wir beschränken uns im folgenden auf äquatoriale Bewegungen. Aufgrund der Normalisierungseigenschaft der Vierergeschwindigkeit $u^\mu u_\mu =1 $ sind die Zeit- und phi-Komponente der Viergeschwindigkeit wie folgt durch die Energie- und Drehimpulswerte bestimmt (siehe Hartle-Buch, S:318):
\[
\begin{eqnarray}
\frac{dt}{d\tau} &=& \frac{1}{\Delta} \left[ \left( r^2 + a^2 +\frac{2Ma^2}{r} \right)\, E -\frac{2Ma}{r}\, l \right] \\
\frac{d\phi}{d\tau} &=& \frac{1}{\Delta} \left[ \left( 1 - \frac{2M}{r} \right)\, l +\frac{2Ma}{r}\, E \right]
\end{eqnarray}
\]
| > |
Eqdt:=dt=1/Delta*((r^2+a^2+2*M*a^2/r)*en-2*M*a/r*l);
Eqdphi:=dphi=1/Delta*((1-2*M/r)*l+2*M*a/r*en); |
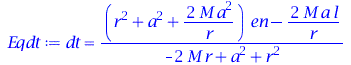 |
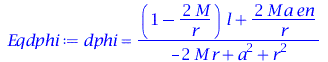 |
(4.6) |
Festsetzen der Anfangswerte der beiden Lösungen:
| > |
t0:=0:
phi0:=0:
theta0:=Pi/2:
dtheta0:=0:
dr0:=0:
dt01:=rhs(subs({M=setM,a=seta,r=r01,en=setE1,l=setl1},Eqdt)):
dphi01:=rhs(subs({M=setM,a=seta,r=r01,en=setE1,l=setl1},Eqdphi)):
dt02:=rhs(subs({M=setM,a=seta,r=r02,en=setE2,l=setl2},Eqdt)):
dphi02:=rhs(subs({M=setM,a=seta,r=r02,en=setE2,l=setl2},Eqdphi)): |
Lösung der Geodätengleichung für den inneren und äußeren ISCO:
| > |
Loes1:=dsolve({subs({a=seta,M=setM},eq1),subs({a=seta,M=setM},eq2),subs({a=seta,M=setM},eq3),subs({a=seta,M=setM},eq4),t(0)=t0,r(0)=r01,phi(0)=phi0,theta(0)=theta0,D(r)(0)=dr0,D(t)(0)=dt01,D(phi)(0)=dphi01,D(theta)(0)=dtheta0},{r(lambda),t(lambda),phi(lambda),theta(lambda)},type=numeric,output=listprocedure):
Loes2:=dsolve({subs({a=seta,M=setM},eq1),subs({a=seta,M=setM},eq2),subs({a=seta,M=setM},eq3),subs({a=seta,M=setM},eq4),t(0)=t0,r(0)=r02,phi(0)=phi0,theta(0)=theta0,D(r)(0)=dr0,D(t)(0)=dt02,D(phi)(0)=dphi02,D(theta)(0)=dtheta0},{r(lambda),t(lambda),phi(lambda),theta(lambda)},type=numeric,output=listprocedure): |
Animation der Bewegung beider Fälle:
| > |
frames:=150:
lend:=1*10^12:
Lr1 := subs(Loes1,r(lambda)):
Lphi1 := subs(Loes1,phi(lambda)):
Lr2 := subs(Loes2,r(lambda)):
Lphi2 := subs(Loes2,phi(lambda)):
TrajC:=listplot([seq([6*setM*cos(2*Pi*jj/frames),6*setM*sin(2*Pi*jj/frames)], jj = 0 .. frames)],color=green,linestyle=dot):
for i from 0 by 1 to frames do
Koerper1[i]:=display(disk([Lr1(i*lend/frames)*cos(Lphi1(i*lend/frames)),Lr1(i*lend/frames)*sin(Lphi1(i*lend/frames))],2*10^9,color=blue)):
Koerper2[i]:=display(disk([Lr2(i*lend/frames)*cos(Lphi2(i*lend/frames)),Lr2(i*lend/frames)*sin(Lphi2(i*lend/frames))],2*10^9,color=red)):
Ani[i]:=display({Koerper1[i],Koerper2[i],BH,TrajC});
od: |
| > |
display([seq(Ani[i],i=0..frames)],insequence=true,scaling=constrained); |
Die blaue Kurve (Probekörper rotiert in gleicher Richtung wie die Rotationsrichtung des schwarzen Loches) hält sich innerhalb der Ergosphäre auf. Der entgegen der Rotationsrichtung des SL rotierende ISCO befindet sich viel weiter ausserhalb des SLs. Zum Vergleich zeigt die gepunktete grüne Kurve den ISCO eine nicht-rotierenden SLs, der sich bei r=6M befindet.
Vergleich der Simulationsergebnisse mit dem beobachteten Bild
Um das wirkliche Bild des schwarzen Lochs mit unseren Simulationsergebnissen vergleichen zu können müssen wir die Längenskala des Bildes (50 micro arcsekunden = 2.42406841*10^(-10) rad) in km umrechnen:
| > |
with(StringTools):
EW_BH:=2.42406841*10^(-10):
A_EBH:=5.1839*10^20:
BHScala:=tan(EW_BH)*A_EBH:
c:=2.99792458*10^10:#Lichtgeschw. in cm/s
lambdazeit:=0.9145*10^12:
factorzeit:=lambdazeit*10^5/c/(60*60*24):#faktor in Tagen
factorzeit:=10^5/c/(60*60*24):#faktor in Tagen |
Wir nehmen im Folgenden an, dass die Emmission der Radiowellen von einfallender Materie in der Nähe des ISCOs (mitrotierend) erzeugt wird.
| > |
frames:=150:
lend:=0.9145*10^12:
Lr1 := subs(Loes1,r(lambda)):
Lphi1 := subs(Loes1,phi(lambda)):
Lr2 := subs(Loes2,r(lambda)):
Lphi2 := subs(Loes2,phi(lambda)):
BHsc:=line([-BHScala,-5*10^10], [0, -5*10^10], color = grey, linestyle = solid,thickness=3):
for i from 0 by 1 to frames do
Koerper1[i]:=display(disk([Lr1(i*lend/frames)*cos(Lphi1(i*lend/frames)),Lr1(i*lend/frames)*sin(Lphi1(i*lend/frames))],2*10^9,color=blue)):
Ptext1[i]:=textplot([-BHScala/1.4,-5.5*10^10, Join(["Zeit: ",convert(round(i*lend/frames*factorzeit),string),"Tage"])], align =RIGHT,color=black,font = [TIMES, ROMAN, 12]):
Ani[i]:=display({Koerper1[i],BH,BHsc,Ptext1[i]});
od: |
| > |
display([seq(Ani[i],i=0..frames)],insequence=true,scaling=constrained); |
Die obige Animation zeigt den inneren Bereich des rotierenden schwarzen Lochs (der gelbe Bereich stellt die Ergosphäre dar). Die blaue Bahn beschreibt die letzte stabile, kreisförmige Trajektorie eines massiven Probekörpers (ISCO mitrotierend mit dem SL) und liegt in der Ergosphäre. Die graue Linie zeigt die Längenskala von 50 micro Bogensekunden und zusätzlich wird die verstrichene Zeit in Tagen angegeben.



![Typesetting:-mprintslash([g := TABLE([index_char = [-1, -1], compts = matrix([[`+`(1, `-`(`/`(`*`(2, `*`(M, `*`(r))), `*`(`+`(`*`(`^`(r, 2)), `*`(`^`(a, 2), `*`(`^`(cos(theta), 2)))))))), 0, 0, `+`(`/...](images/SL-M87-Rot_4.gif)
![Typesetting:-mprintslash([g := TABLE([index_char = [-1, -1], compts = matrix([[`+`(1, `-`(`/`(`*`(2, `*`(M, `*`(r))), `*`(`+`(`*`(`^`(r, 2)), `*`(`^`(a, 2), `*`(`^`(cos(theta), 2)))))))), 0, 0, `+`(`/...](images/SL-M87-Rot_5.gif)
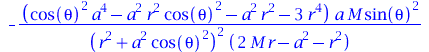
![Typesetting:-mprintslash([RICCI := TABLE([index_char = [-1, -1], compts = matrix([[0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]])])], [table( [( index_char ) = [-1, -1], ( compts ) = array( 1...](images/SL-M87-Rot_7.gif)