2.3.7 Der lineare harmonische Oszillator mit Dämfung 

Dieses Beispiel ist angelehnt an das Kapitel 23 "Der gedämpfte harmonische Oszillator" des Buches von Walter Greiner, Mechanik (Teil 1) [5. Auflage, 1989, siehe Seite 226- 237]. Siehe auch Vorlesungsskript Seite 117- 126, http://www.th.physik.uni-frankfurt.de/~drischke/Skript_MI_WiSe2016-2017.pdf ) 

>	restart: with(plottools): with(plots):

 

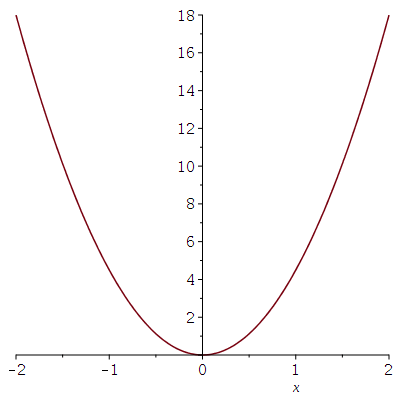
Wir betrachten den gedämpften harmonischen Oszillator am Beispiel eines reibungsfrei gelagerten Wagens (Masse=m) auf dem eine Rückstellkraft einwirkt (die proportional zu seiner Auslenkung x ist (Proportionalitätskonstante k; z.B. k=9).) , wobei zusätzlich eine geschwindigkeitsabhängige Reibungskraft auf den Wagen einwirkt (z.B. verursacht durch den auf den Wagen einwirkende Luftwiderstand, Stokesscher Ansatz: Proportionalitätskonstante alpha),  Aufgrund der Rückstellkraft, besitzt das zugrundeliegende Potential die Form einer Parabel: 

>	V:=k/2*x^2; plot(subs(k=9,V),x=-2..2);

 

Die entsprechende Bewegungsgleichung (Differentialgleichung) lautet wie folgt (wir setzen k/m=omega0^2) und beta = alpha/(2m): 

>	DGL:=diff(x(t),t,t)=-omega[0]^2*x(t) -2*beta*diff(x(t),t);

 

(1.1)

 

Da diese homogene Differentialgleichung (DGL) von zweiter Ordnung in der Zeit ist und die allgemeine Lösung somit zwei linear unabhängige Lösungen besitz, sind zwei freie Parameter (Neben- bzw. Anfangsbedingungen) noch festzulegen. Die allgemeine Lösung x(t) hat die folgende Struktur:  

>	dsolve(DGL);

 

(1.2)

 

Legen wir diese Anfangsbedingungen fest und schubsen z.B. den Wagen aus seiner Ruhelage an (im speziellen z.B.. x(0)=0 und x'(0)=40), dann lautet die spezielle Lösung der DGL: 

>	Loes:=dsolve({DGL,x(0)=0,D(x)(0)=40});

 

(1.3)

 

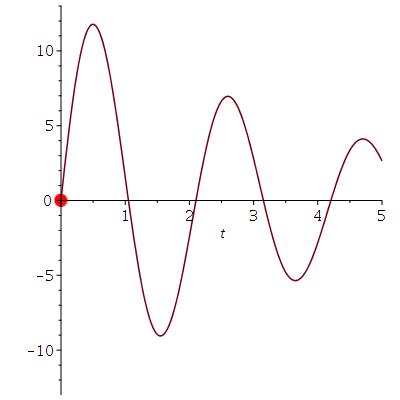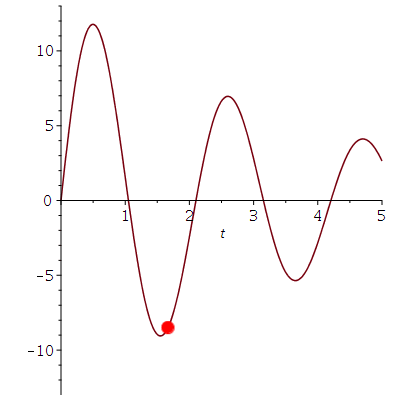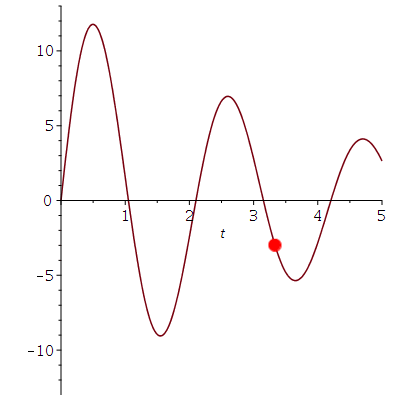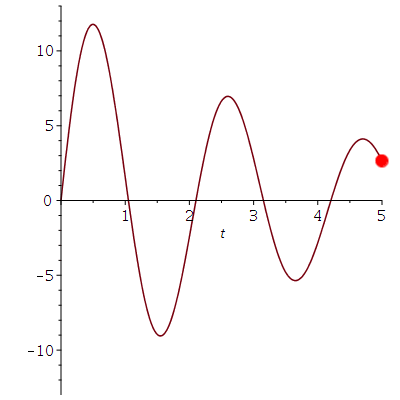
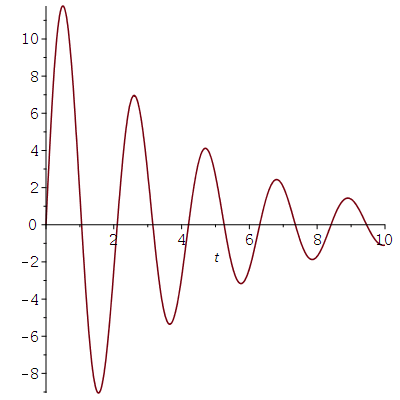
Die Lösung können wir uns wieder in einem Diagram darstellen wenn wir die noch freien Parameter der DGL festlegen (wir setzen z.B.  m=1, k=9 und alpha=0.5 -> omega0=3 und beta= 0.25). Durch diese spezielle Wahl entsteht im Argument der Exponentialfunktion eine imaginäre Zahl die man sich  mittels der Eulerschen Formel als eine periodische Schwingung vorstellen kann. Die enstehende Schwingung kann man entweder in der Exponentialdarstellung der komplexen Zahlen oder in der sinus- bzw. kosinus Schreibweise darstellen. x(t) 

>	simplify(subs({omega[0]=3,beta=1/4},Loes)); dsolve(subs({omega[0]=3,beta=1/4},{DGL,x(0)=0,D(x)(0)=40})); plot(subs({omega[0]=3,beta=1/4},rhs(Loes)),t=0..10);

 

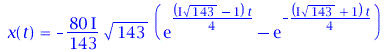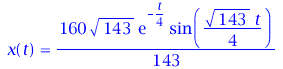Wir können uns die Bewegung in folgender Animation veranschaulichen: 

>

tend:=5: xend:=13: frames:=150: dt:=tend/frames: PLoes:=plot(subs({omega[0]=3,beta=1/4},rhs(Loes)),t=0..tend,view=[0..tend, -xend .. xend]): for i from 0 by 1 to frames do tt:=i*dt: rr:=Re(subs({omega[0]=3,beta=1/4,t=tt},rhs(Loes))); Ani1[i]:=display(rectangle([-1+rr, 1], [1+rr, 0], color = red),view=[-xend .. xend, 0 .. tend]): PointA[i]:=pointplot({[tt, rr]},symbol=solidcircle,symbolsize=23,color=red): Ani[i]:=display(Matrix(1,2,[[display(Ani1[i]),display(PLoes,PointA[i])]])): od:

 

>	display([seq(Ani[i],i=0..frames)],insequence=true);

 

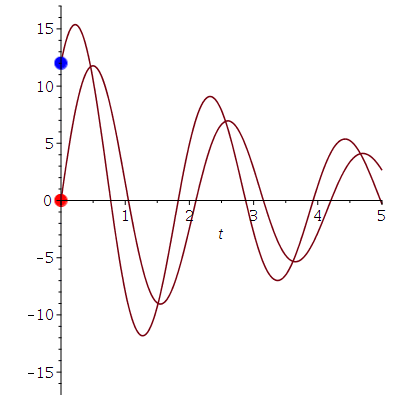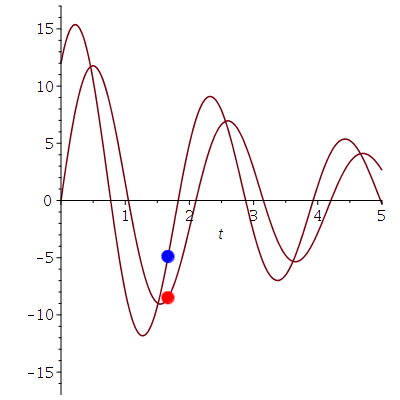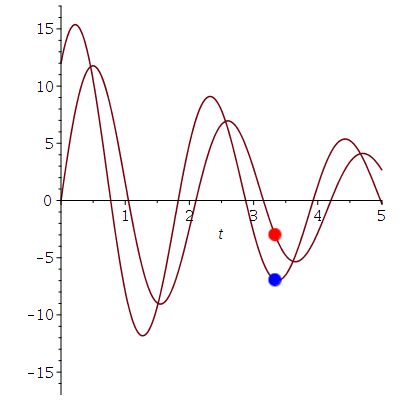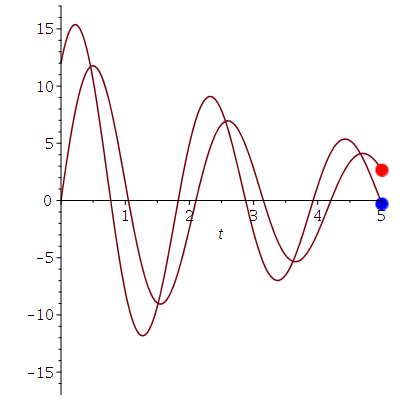
Verändern wir die Anfangsbedingungen, so ergeben sich unterschiedliche Bewegungen (roter Wagen: x(0)=0 und x'(0)=40, blauer Wagen: x(0)=12 und x'(0)=30). 

>

Loes:=dsolve({DGL,x(0)=0,D(x)(0)=40}); LoesB:=dsolve({DGL,x(0)=12,D(x)(0)=30}); tend:=5: xend:=17: frames:=150: dt:=tend/frames: PLoes:=plot(subs({omega[0]=3,beta=1/4},rhs(Loes)),t=0..tend,view=[0..tend, -xend .. xend]): PLoesB:=plot(subs({omega[0]=3,beta=1/4},rhs(LoesB)),t=0..tend,view=[0..tend, -xend .. xend]): for i from 0 by 1 to frames do tt:=i*dt: rr:=Re(subs({omega[0]=3,beta=1/4,t=tt},rhs(Loes))); Ani1[i]:=display(rectangle([-1+rr, 1], [1+rr, 0], color = red),view=[-xend .. xend, 0 .. tend]): PointA[i]:=pointplot({[tt, rr]},symbol=solidcircle,symbolsize=23,color=red): rrB:=Re(subs({omega[0]=3,beta=1/4,t=tt},rhs(LoesB))); Ani1B[i]:=display(rectangle([-1+rrB, 1], [1+rrB, 0], color = blue),view=[-xend .. xend, 0 .. tend]): PointB[i]:=pointplot({[tt, rrB]},symbol=solidcircle,symbolsize=23,color=blue): Ani[i]:=display(Matrix(1,2,[[display(Ani1[i],Ani1B[i]),display(PLoes,PointA[i],PLoesB,PointB[i])]])): od:

 

 

	(1.4)

 

>	display([seq(Ani[i],i=0..frames)],insequence=true);

 

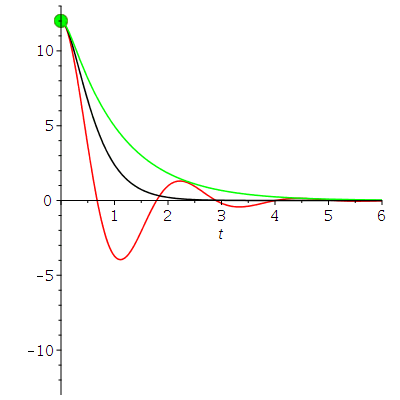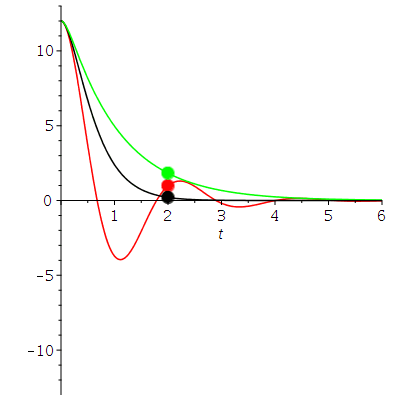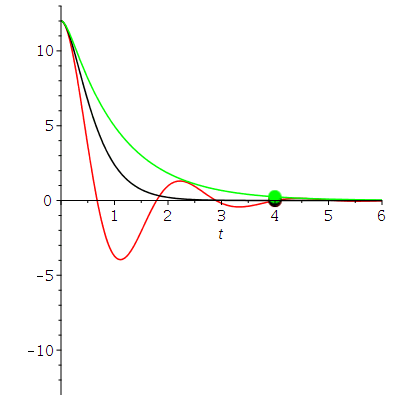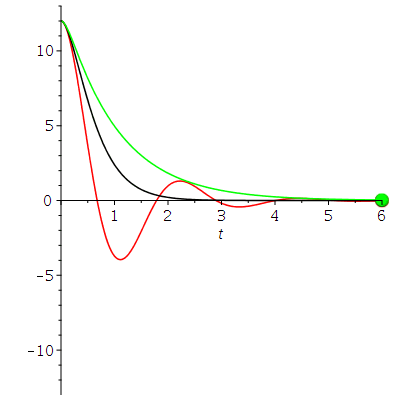
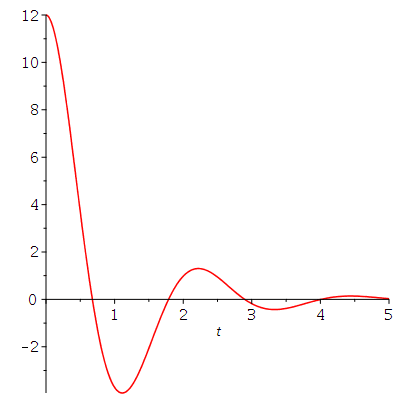
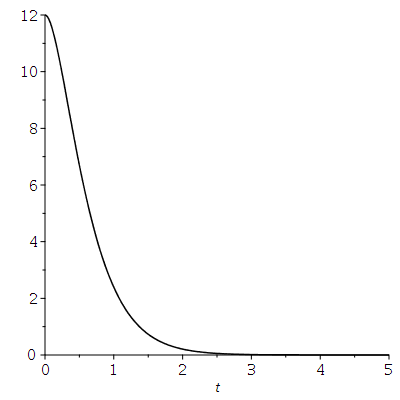
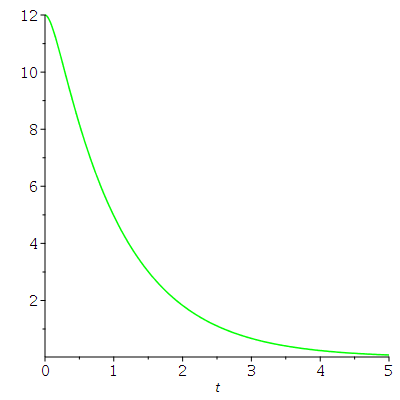
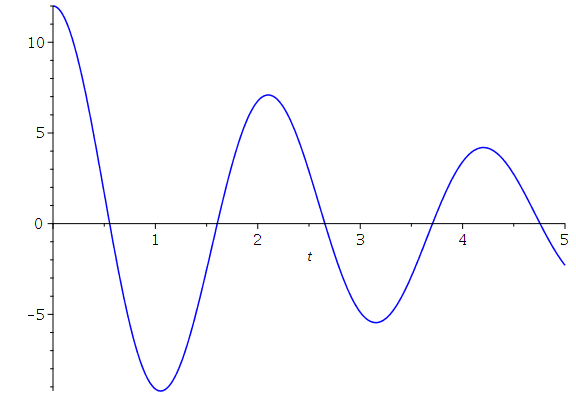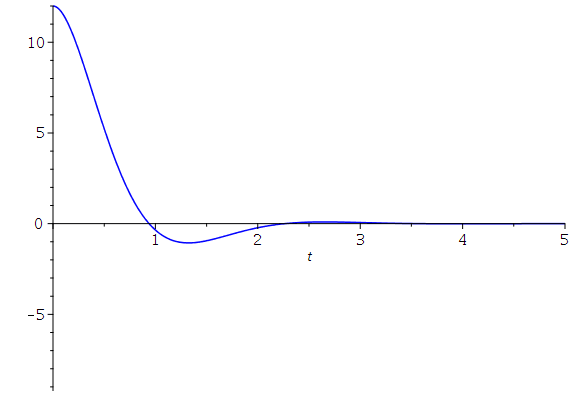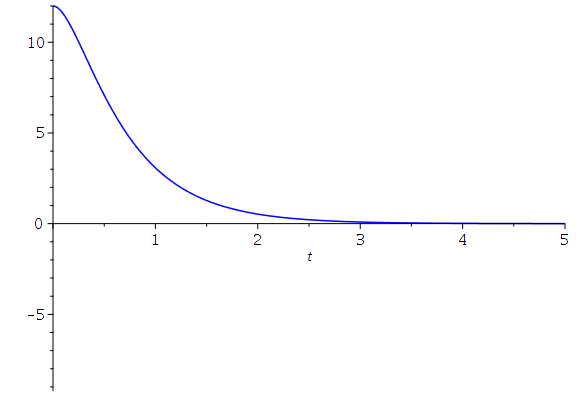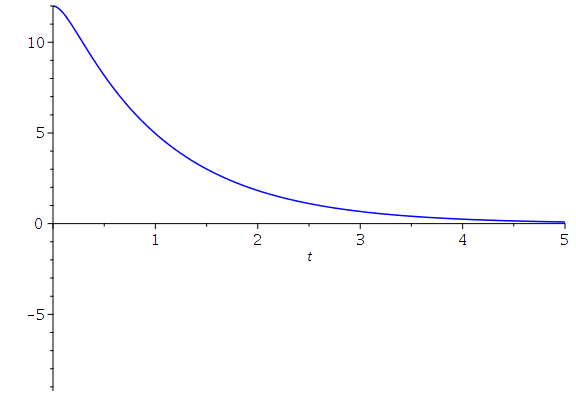
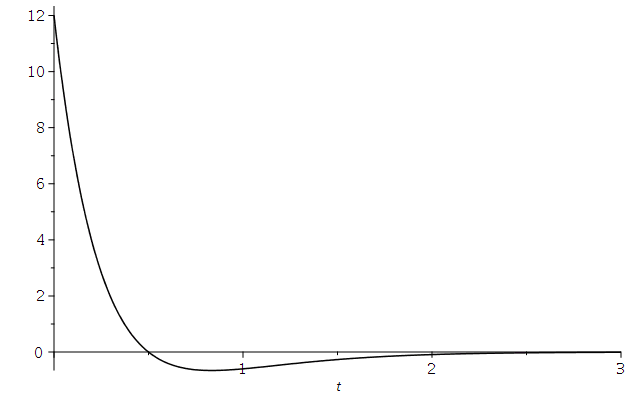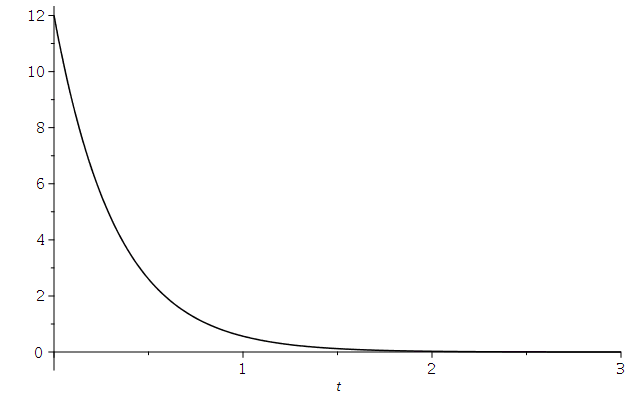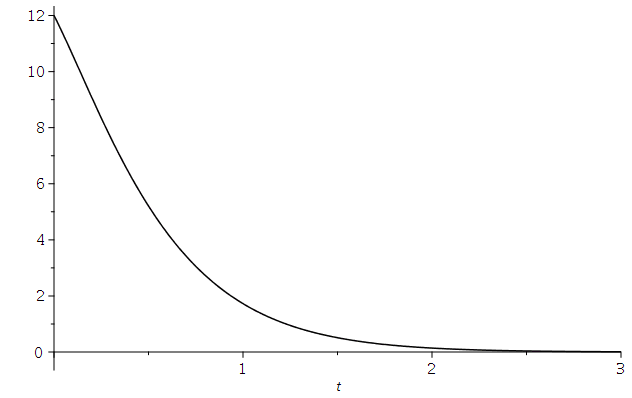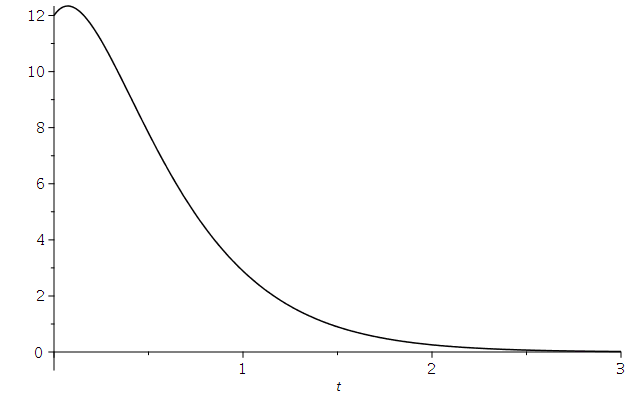
Die dargestellten speziellen Lösungen stellen den Fall einen schwachen Dämpfung dar, den sogennanten "Schwingfall". Man unterscheidet zusätzlich zwei weitere Fälle, deren allgemeine Lösungen sich qualitativ von dem "Schwingfall" unterscheiden: Den aperiodischen Grenzfall (kritischer Wert der Dämpfung, omega0=beta ) und das überdämpfte System (starke Dämpfung, Kriechfall). Im folgenden legen wir die Anfangsbedingungen fest und lenken den Wagen aus seiner Ruhelage aus, geben ihm jedoch keine Anfangsgeschwindigkeit (im speziellen z.B.. x(0)=12 und x'(0)=0). Die allgemeine Lösung der drei möglichen Fälle erhalten wir durch die Festlegung der freien Parameter der DLG; z.B.  

A) Schwingfall (rote Kurve):  m=1, k=9 und alpha=2 -> omega0=3 und beta= 1 

B) Aperiodischen Grenzfall  (schwarze Kurve): m=1, k=9 und alpha=6 -> omega0=3 und beta= 3 

C) Kriechfall (grüne Kurve): m=1, k=9 und alpha=10 -> omega0=3 und beta= 5 

>

tend:=5: LoesA:=simplify(dsolve(subs({omega[0]=3,beta=1},{DGL,x(0)=12,D(x)(0)=0}))); plot(rhs(LoesA),t=0..tend,color=red); LoesB:=simplify(dsolve(subs({omega[0]=3,beta=3},{DGL,x(0)=12,D(x)(0)=0}))); plot(rhs(LoesB),t=0..tend,color=black); LoesC:=dsolve(subs({omega[0]=3,beta=5},{DGL,x(0)=12,D(x)(0)=0})); plot(rhs(LoesC),t=0..tend,color=green);

 

Animation der drei Fälle: 

>

tend:=6: xend:=13: frames:=150: dt:=tend/frames: PLoesA:=plot(rhs(LoesA),t=0..tend,view=[0..tend, -xend .. xend], color = red): PLoesB:=plot(rhs(LoesB),t=0..tend,view=[0..tend, -xend .. xend], color = black): PLoesC:=plot(rhs(LoesC),t=0..tend,view=[0..tend, -xend .. xend], color = green): for i from 0 by 1 to frames do tt:=i*dt: rrA:=Re(subs({t=tt},rhs(LoesA))); rrB:=Re(subs({t=tt},rhs(LoesB))); rrC:=Re(subs({t=tt},rhs(LoesC))); Ani1A[i]:=display(rectangle([-1+rrA, 1], [1+rrA, 0], color = red),view=[-xend .. xend, 0 .. tend]): PointA[i]:=pointplot({[tt, rrA]},symbol=solidcircle,symbolsize=23,color=red): Ani1B[i]:=display(rectangle([-1+rrB, 1], [1+rrB, 0], color = black),view=[-xend .. xend, 0 .. tend]): PointB[i]:=pointplot({[tt, rrB]},symbol=solidcircle,symbolsize=23,color=black): Ani1C[i]:=display(rectangle([-1+rrC, 1], [1+rrC, 0], color = green),view=[-xend .. xend, 0 .. tend]): PointC[i]:=pointplot({[tt, rrC]},symbol=solidcircle,symbolsize=23,color=green): Ani[i]:=display(Matrix(1,2,[[display(Ani1A[i],Ani1B[i],Ani1C[i]),display(PLoesA,PointA[i],PLoesB,PointB[i],PLoesC,PointC[i])]])): od:

 

>	display([seq(Ani[i],i=0..frames)],insequence=true);

 

Die folgende Animation zeigt eine Variation des Dämpfungsparameters beta von 0.25 bis 5. 

>	tend:=5: Loes:=simplify(dsolve(subs({omega[0]=3},{DGL,x(0)=12,D(x)(0)=0}))); animate(rhs(Loes),t=0..tend, beta=0.25..5 ,color=blue,numpoints=500);

 

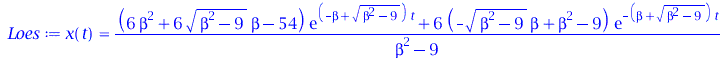Die folgende Animation zeigt eine Variation der Anfangsgeschwindigkeit v0 (von -60 bis 10) für den aperiodischen Grenzfall (schwarze Kurve). Ein Nulldurchgang von x(t) ist möglich, falls v0 < -beta x0 (hier speziell falls v0 < - 36): 

>	tend:=3: LoesB:=simplify(dsolve(subs({omega[0]=3,beta=3},{DGL,x(0)=12,D(x)(0)=v0}))); tN:=solve(rhs(LoesB)=0,t); animate(rhs(LoesB),t=0..tend, v0=-60..10 ,color=black,numpoints=500);

 

>