Bestantwort-Pfeile am Beispiel des Gefangenendilemma, Hirschjagd- und Angsthasen-Spiels
Das Gefangenendilemma
Das wohl bekannteste Beispiel eines (2 Personen)-(2 Strategien) Spiels ist das sogennante Gefangenendilemma:
"Bonnie und Clyde werden nach einem missglückten Banküberfall geschnappt und in verschiedenen Zellen untergebracht. Wenn beide schweigen kann der Staatsanwalt sie nur wegen verbotenen Waffenbesitzes für drei Jahre hinter Gitter bringen. Verrät jedoch einer den anderen, dann bekommt der Geständige als Zeuge der Anklage nur für ein Jahr hinter Gitter - der Nichtgeständige muss dann aber für neun Jahre ins Gefängnis. Gestehen beide, so müssen sie sieben Jahre absitzen."
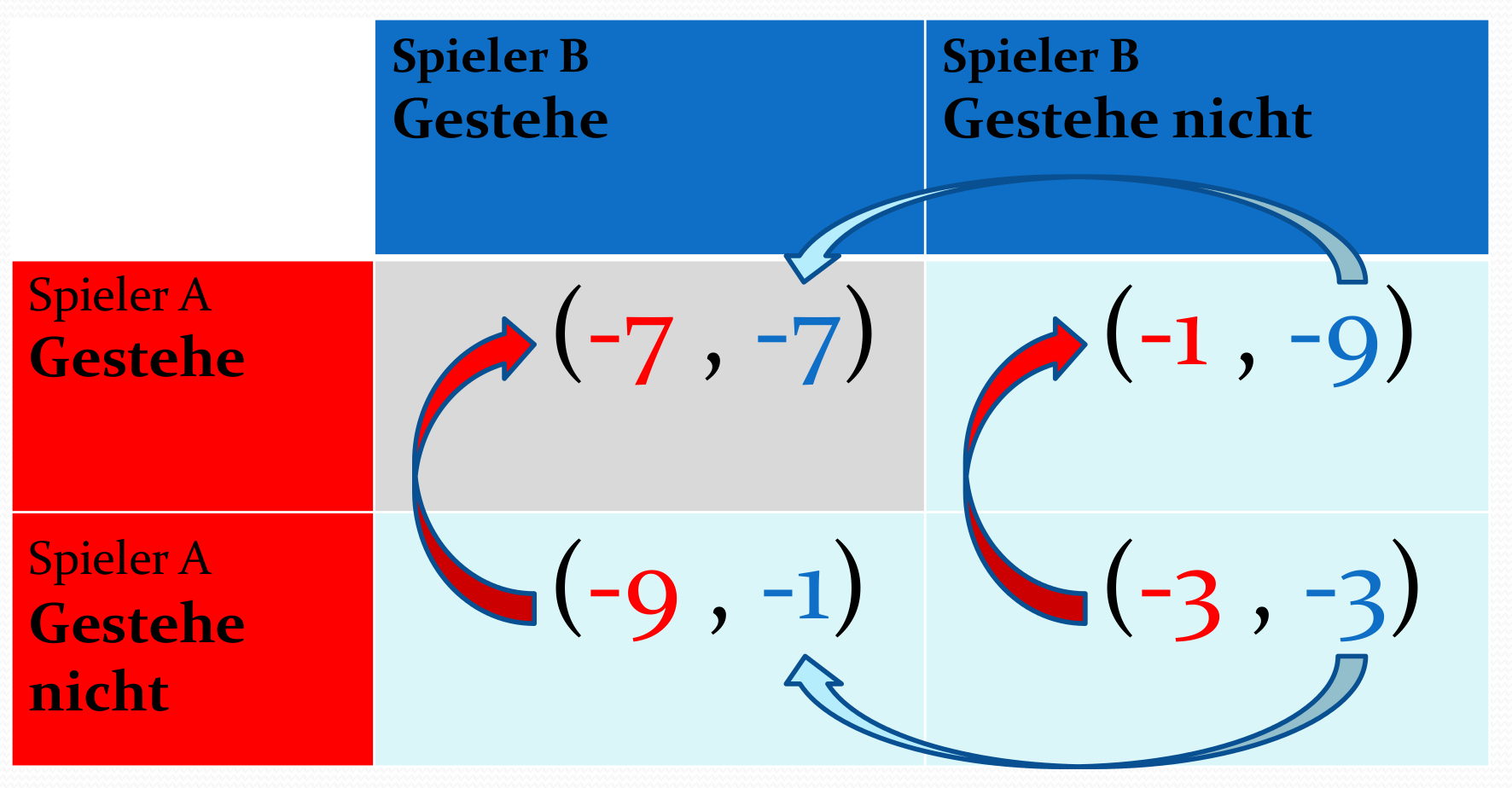
Veranschaulichung der dominanten Strategie "Gestehe" mittels der Abbildung der besten Antwort im Gefangenendilemma.
Es handelt sich bei dieser Entscheidungssituation um ein simultanes (2 Personen)-(2 Strategien) Spiel. Die Menge der Spieler besteht aus "Bonnie und Clyde" (${\bf \cal I} =\left\{ A, B \right\}=\left\{ \hbox{Bonnie}, \hbox{Clyde} \right\}$), die jeweils zwischen den Strategien "Gestehe" und "Gestehe nicht" auswählen können (${\cal S}^A = \left\{ s^A_1, s^A_2 \right\}=\left\{ \hbox{Gestehe}, \hbox{Gestehe nicht} \right\}= \left\{ s^B_1, s^B_2 \right\}={\cal S}^B$).
Die durch die Geschichte beschriebene Auszahlungsmatrix der Spieler stellt die Anzahl der Jahre der Gefängnisstrafe als negative Zahlen dar. Es ist üblich die Auszahlungen eines Spiels in Form einer Tabelle anzugeben (siehe nebenstehende Auszahlungstabelle). Die nebenstehende Abbildung zeigt die Tabelle der "Auszahlungen" (hier die Gefängnisstrafe in Jahren), wobei die roten und blauen Pfeile im Prinzip die Abbildung der besten Antwort der Spieler A (Bonnie) und B (Clyde) visuell darstellen (für eine exakte mathematische Definition der Abbildung der besten Antwort siehe z.B. S:20 in ''Schlee, Walter, Einführung in die Spieltheorie, Vieweg 2004''). Die Abbildung der besten Antwort des Spielers A ist hierbei wie folgt zu verstehen: Unter Annahme, dass Spieler B Gesteht, welche Strategie wäre für Spieler A die Vorteilhafteste? Da ${\bf {\cal \$}}^A \left( s^{A\dagger}=\hbox{Gestehe}, s^{B}=\hbox{Gestehe} \right)=-7 \,\, \geq \,\, {\bf {\cal \$}}^A \left( s^{A}=\hbox{Gestehe nicht}, s^{B}=\hbox{Gestehe} \right)=-9$ ist es für Spieler A das beste auch zu Gestehen (der linke rote Pfeil veranschaulicht dies). Dagegen, unter Annahme das Spieler B nicht Gesteht, wäre es das Beste für Spieler A zu Gestehen, da ${\bf {\cal \$}}^A \left( s^{A\dagger}=\hbox{Gestehe}, s^{B}=\hbox{Gestehe nicht} \right)=-1 \,\, \geq \,\, {\bf {\cal \$}}^A \left( s^{A}=\hbox{Gestehe nicht}, s^{B}=\hbox{Gestehe nicht} \right)=-3$ (der rechte rote Pfeil veranschaulicht diese Situation). In gleicher Weise kann man sich die besten Antworten aus der Sicht von Spieler B überlegen (blaue Pfeile). Zusammenfassend erkennt man das im Gefangenendilemma beide Spieler zur Strategie Gestehe gezogen werden und somit eine dominante Strategienkombination bei ${s}^{\dagger}=\left( {s}^{A\dagger}, {s}^{B\dagger} \right) = \left( \hbox{Gestehe}, \hbox{Gestehe} \right)$ auftritt welche auch das einzige Nash-Gleichgewicht des Spiels darstellt; ${s}^{\dagger}={s}^{*}$.
Das Hirschjagd-Spiel (Rousseau)
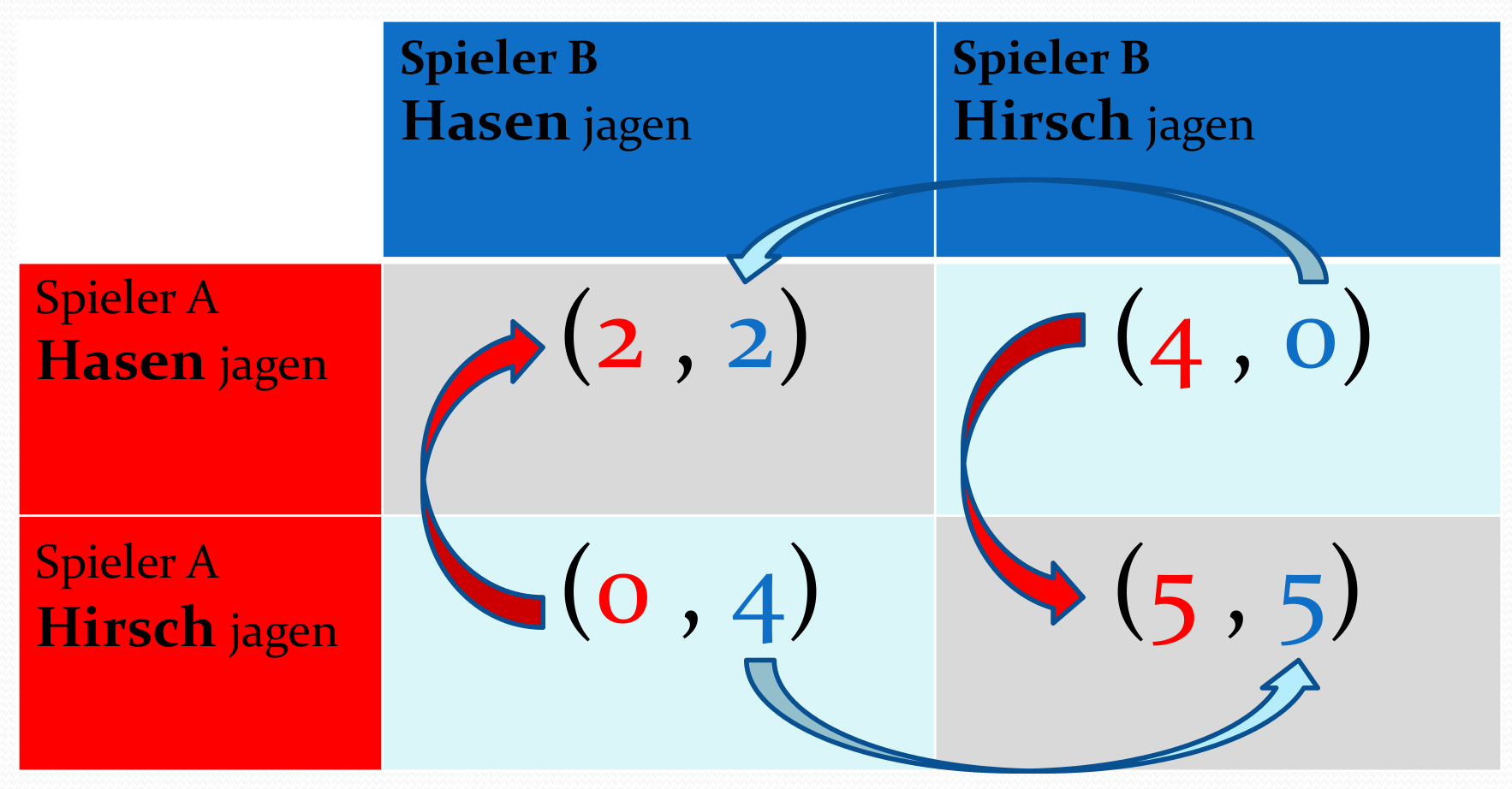
Veranschaulichung der beiden symmetrischen Nash-Gleichgewichte ${\bf {s}^{*} = \left( \hbox{Hasen jagen}, \hbox{Hasen jagen} \right)}$ und ${\bf {s}^{*} = \left( \hbox{Hirsch jagen}, \hbox{Hirsch jagen} \right)}$ mittels der Abbildung der besten Antwort im Hirschjagd-Spiel.
Ein weiteres bekanntes simultanes (2 Personen)-(2 Strategien) Spiel ist das sogennante Hirschjagd-Spiel von Rousseau:
"Zwei Jägern ist es im Laufe der Jagt gelungen einen Hirsch und vier Hasen einzukreisen. Die Jäger stehen nun vor der Entscheidung die Hasen entkommen zu lassen und gemeinsam den Hirsch zu erlegen oder sofort das Feuer auf die Hasen zu eröffnen. Leider können sich beide Jäger nicht miteinander verständigen oder Informationen austauschen - es handelt sich somit um eine simultane Entscheidung. Entscheiden sich beide dafür den Hirsch zu erlegen, dann hat der Hirsch keine Chance. Einen Hirsch kann man für 10 Goldmünzen verkaufen. Entscheiden sich beide für die Hasenjagd, dann erschiesst jeder Jäger zwei Hasen, für die man jeweils eine Goldmünze bekommt. Entscheidet sich jedoch nur einer für die Hirschjagd, so kann der Hirsch entkommen und derjenige der sich für die Hasenjagd entschieden hat kann alle vier Hasen erlegen."
Die nebenstehende Abbildung veranschaulicht die Auszahlungstabelle und zeigt mittels der Bestantwort-Pfeile, dass es in diesem Spiel keine dominante Strategie gibt, sondern zwei symmetrische Nash-Gleichgewicht bei den Strategienkombinationen ${s}^{*} = \left( \hbox{Hasen jagen}, \hbox{Hasen jagen} \right)$ und ${s}^{*} = \left( \hbox{Hirsch jagen}, \hbox{Hirsch jagen} \right)$. Z.B. ist ${s}^{*} = \left( \hbox{Hasen jagen}, \hbox{Hasen jagen} \right)$ ein Nash-Gleichgewicht, da ${\bf {\cal \$}}^A \left( s^{A*}=\hbox{Hasen jagen}, s^{B}=\hbox{Hasen jagen} \right)=2 \,\, \geq \,\, {\bf {\cal \$}}^A \left( s^{A}=\hbox{Hirsch jagen}, s^{B}=\hbox{Hasen jagen} \right)=0$ und ${\bf {\cal \$}}^B \left( s^{A}=\hbox{Hasen jagen}, s^{B*}=\hbox{Hasen jagen} \right)=2 \,\, \geq \,\, {\bf {\cal \$}}^B \left( s^{A}=\hbox{Hasen jagen}, s^{B}=\hbox{Hirsch jagen} \right)=0$.
Das Angsthasen-Spiel (Chicken Game)
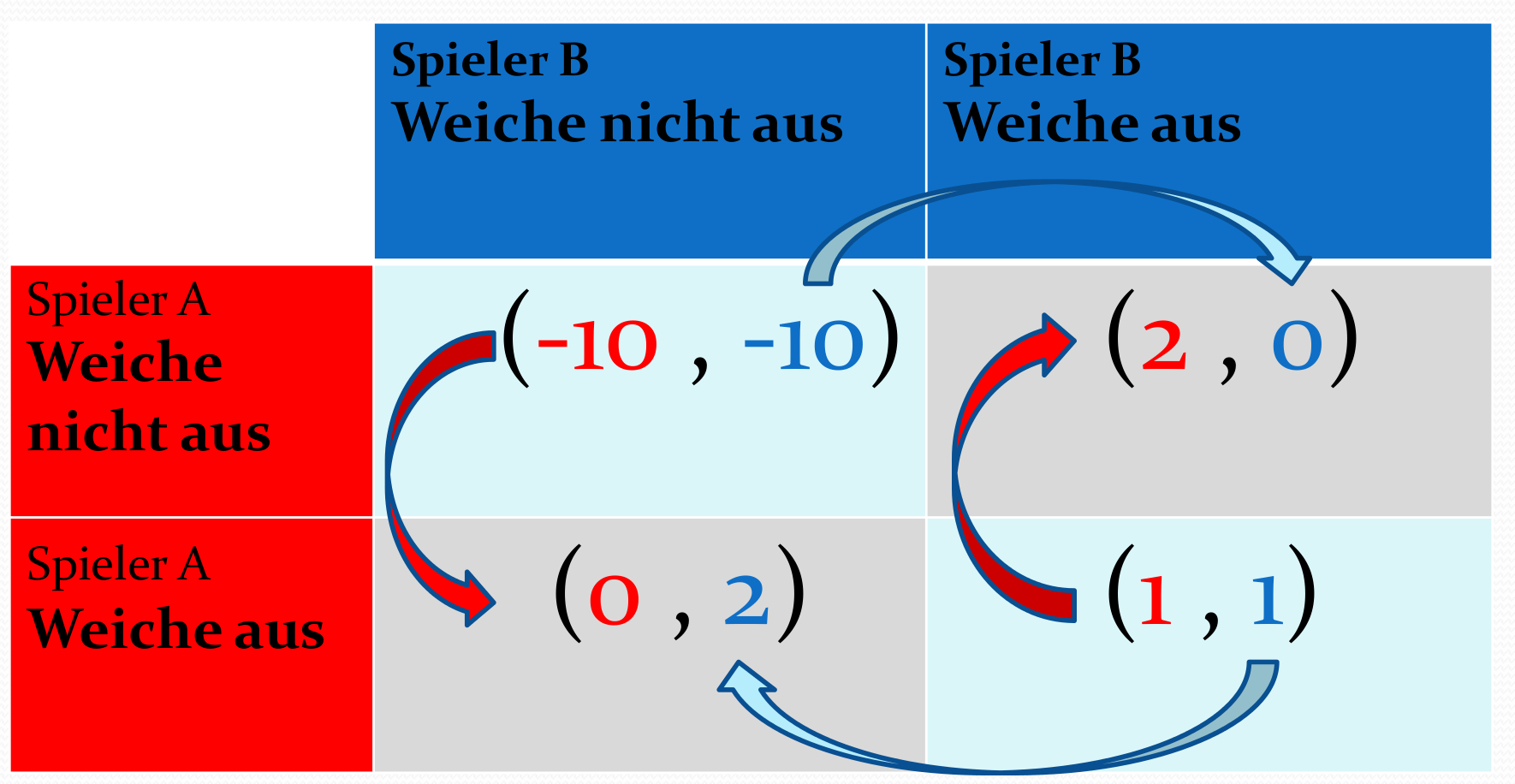
Veranschaulichung der dominanten Strategie "Gestehe" mittels der Abbildung der besten Antwort im Gefangenendilemma.
Das Angsthasen-Spiel ist ebenfalls ein simultanes (2 Personen)-(2 Strategien) Spiel und kann z.B. mittels der folgenden Geschichte illustriert werden (siehe z.B. S.16 in ''Schlee, Walter, Einführung in die Spieltheorie, Vieweg 2004'').
"Auf einer einsamen Landstraße in Indien, bei der es nur eine geteerte Fahrbahn gibt, kommen sich zwei Autos mit hoher Geschwindigkeit entgegen. Beide Fahrer stehen nun vor der Entscheidung ob sie dem Anderen die Fahrbahn überlassen und Ausweichen oder mit hoher Geschwindigkeit weiterfahren um zu hoffen, dass der Andere ausweicht." Eine weitere Deutung des Angsthasen-Spiel basiert auf dem Film von Nicholas Ray "Denn sie wissen nicht was sie tun" aus dem Jahre 1955 (mit James Dean): "Jimbo und sein Erzfeind Buzz machen eine Mutprobe und rasen in ihren Autos auf eine Klippe zu. Derjenige ist der Angsthase, der als erster aus seinem Auto herrausspringt."
Die nebenstehende Abbildung zeigt eine mögliche Tabelle der "Auszahlungen" für die Version der aufeinander zusteuernden Autos auf der Landstraße. In dem Fall das keiner der Fahrer ausweicht wurde angenommen, dass es zu einem Unfall mit hoch negativer Auszahlung kommt. Mittels der Bestantwort-Pfeile (siehe Unterkapitel I.1.2) kann man zeigen, dass es in diesem Spiel keine dominante Strategie gibt, sondern zwei anti-symmetrische Nash-Gleichgewicht bei den Strategienkombinationen ${s}^{*} = \left( \hbox{Weiche nicht aus}, \hbox{Weiche aus} \right)$ und ${s}^{*} = \left( \hbox{Weiche aus}, \hbox{Weiche nicht aus} \right)$.