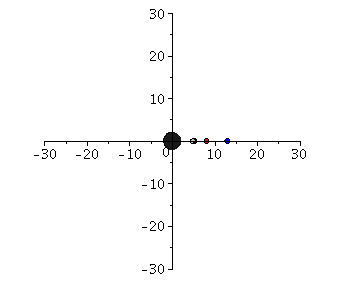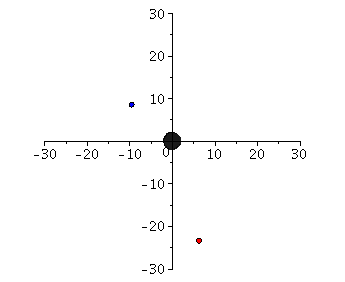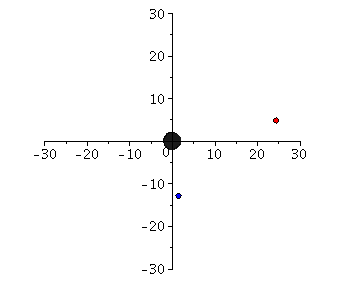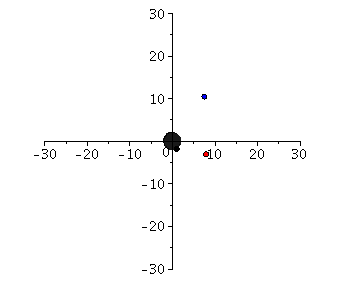ID: 794 847 5614, PWD: 785453
Vorwort

Die Vorlesung Allgemeine Relativitätstheorie mit dem Computer wurde im Sommersemester 2016 das erste Mal gehalten und viele der auf dieser Hauptseite erreichbaren Internetseiten basieren grundsätzlich auf dem damals erstellten Kurs. In der Vorlesung werden die mathematisch anspruchsvollen Gleichungen der Allgemeinen Relativitätstheorie (ART) in diversen Programmierumgebungen analysiert. Im ersten Teil des Kurses erlernen die Studierenden die Verwendung von Computeralgebra-Systemen (Python Jupyter Notebooks, Maple und Mathematica). Die oft komplizierten und zeitaufwendigen Berechnungen der tensoriellen Gleichungen der ART können mithilfe dieser Programme erleichtert werden. Diverse Anwendungen der Einstein- und Geodätengleichung werden in Jupyter Notebooks (eine Open-Source, web-basierte interaktive Programmierumgebung) und Maple Worksheets implementiert, quasi analytische Berechnungen durchgeführt und entsprechende Lösungen berechnet und visualisiert. Der zweite Teil des Kurses befasst sich mit der numerischen Berechnung von Neutronensternen und Weißen Zwergen mittels eines C/C++ Programms. Nach einer kurzen Auffrischung der grundlegenden Programmierkenntnisse, wird ein Programm besprochen, das die Tolman-Oppenheimer-Volkoff Gleichung numerisch löst und die Ergebnisse werden visualisiert. Zusätzlich wird hierbei in die Grundkonzepte der parallelen Programmierung eingeführt und eine MPI- und OpenMP-Version des C/C++ Programms erstellt. Im dritten Teil des Kurses werden zeitabhängige numerische Simulationen der ART mittels des Einstein Toolkit durchgeführt und deren Ergebnisse mittels Python/Matplotlib visualisiert. Inhaltlich wird hierbei ebenfalls auf den, dem Programm zugrunde liegenden (3+1)-Split der ART eingegangen und, mehrere fortgeschrittene, astrophysikalisch relevante Probleme behandelt. Mögliche Themen dieses abschließenden Teils könnten die folgenden Systeme darstellen: Oszillationen eines Neutronensterns, Kollaps eines Neutronenstern zu einem Schwarzen Loch oder die Kollision zweier Neutronensterne unter Berücksichtigung der Aussendung von Gravitationswellen.
Weiterführende Links

Allgemeine Relativitätstheorie mit dem Computer
(General Theory of Relativity on the Computer)
Vorlesung SS 2021
Aufgrund der andauernden Corona-Krise findet die Vorlesung und die Übungstermine auch in diesem Semester nur Online statt!
Diese Internetseite fasst die Online-Angebote der Vorlesung Allgemeine Relativitätstheorie mit dem Computer zusammen. Auf der linken Seite finden Sie die einzelnen Vorlesungsaufzeichnungen (Videos), Vorlesungspräsentationen (pdf-Dateien) und weiterführende Links. Die Vorlesungstermine (Zoom Meetings, synchrones Lehrangebot) finden jeweils freitags von 15.00-17.00 Uhr statt. An den Online-Übungen können Sie entweder freitags vor (13.30-15.00 Uhr) oder nach der Vorlesung (17:00-18:30 Uhr) teilnehmen. Alle Lehrangebote werden mittel der Zoom Meeting Software gemacht und die jeweiligen Zoom-Links sind in der rechten oberen Ecke dieser Internetseite angegeben.
Die Inhalte der Vorlesung gliedern sich in drei Teile (Teil I, Teil II, Teil III), die Sie in der zweiten oberen Spalte einsehen können. Weiteres Zusatzmaterial und diverse Online-Aufgaben sind über die Online-Lernplattformen OLAT und Lon Capa erhältlich (siehe E-Learning).
Der Schwerpunkt der gesamten interaktiven Vorlesung liegt sowohl auf der Allgemeine Relativitätstheorie als auch auf der Vermittlung spezieller Programmierkenntnisse. Bei regelmäßiger Teilnahme an der Online-Vorlesung und den zugehörigen Übungseinheiten kann man einen benoteten bzw. unbenoteten Schein mit fünf Creditpoints zu erhalten.
Weiterführende Literatur
- General relativity : An introduction for physicists von M. P. Hobson, G. P. Efstathiou und A. N. Lasenby
- Gravity : An introduction to Einstein's general relativity von James B. Hartle
- Allgemeine Relativitätstheorie von Torsten Fließbach
- Relativistic hydrodynamics von Luciano Rezzolla und Olindo Zanotti
- Einführung in die Relativitätstheorie von Ray D'Inverno
- Gravitation von Charles W. Misner, Kip S. Thorne und John Archibald Wheeler
- 100 Years of general Relativity - Vol.1: Numerical Relativity von Masaru Shibata
Vorlesung 1
Bevor wir uns mit den Inhalten der Vorlesung beschäftigen, werden in der Vorlesung 1 einige technische Dinge erläutert.
Während der Vorlesung und in den Übungsstunden werden diverse Anwendungsprogramme (z.B. Maple oder Mathematica) und Simulationsprogramme (Python und Jupyter Notebooks) von den Studenten selbst ausführt und bearbeitet. Die Teilnehmer der Vorlesung erhalten hierfür einen Account für die Rechner des Instituts für Theoretische Physik (ITP) der Goethe-Universität. Mittels dieses Accounts können Sie einen Remote Login auf den Server des ITP machen und die benötigten Programme nutzen. Im Folgenden wird der Remote Login beschrieben und gezeigt wie man das Programm Maple startet. Im Gegensatz zu den Vorlesungen der vergangenen Jahre werden die computerunterstützten Berechnungen im ersten Teil in diesem Sommersemester 2021 hauptsächlich mittels sogenannter Jupyter Notebooks durchführt.
Wie mache ich einen Remote Login auf den Server des ITP und starte ein der Maple-Worksheets?
Das nebenstehende Video beschreibt die einzelnen Schritte wie man einen Remote Login von einem Linux Betriebssystem zum Server des ITP aufbaut (weiteres siehe Graphical Remote Login with xrdp). Sie benötigen hierzu einen Account für die Rechner des ITP. Mittels des Remote Login können Sie sich durch einen Fernzugriff auf den Desktop des Servers des ITP verbinden und Anwendungsprogramme (z.B. Maple oder Mathematica) oder Simulationsprogramme (z.B. Python und Jupyter Notebooks) ausführen und auf Ihrem Computer darstellen. Zusätzlich wird am Ende des Videos gezeigt wie man das Passwort des eigenen ITP-Accounts ändert (empfohlen!). Im zweiten Video wird gezeigt, wie man das Computeralgebra-System Maple startet und das Maple-Worksheet Maple Tutorium ausführt.Einführung in Jupyter Notebooks
In den zugehörigen Übungsgruppen der Vorlesung werden wir die computerunterstützten Berechnungen hauptsächlich mittels sogenannter Jupyter Notebooks durchführen. In Jupyter Notebooks kann man die Programmiersprache Python in einer anwendungsfreundlichen Umgebung nutzen und die berechneten Ergebnisse auch gleich visualisieren. Auf den Computern des ITP kann man Jupyter Notebooks starten, indem man in einem Linux-Terminal den Befehl "jupyter-notebook" eingibt. Einige der in den Vorlesungen behandelten Jupyter Notebooks benutzen spezielle Python Module (z.B sympy), die man im Linux-Terminal für den Python3-Kernel mittels des Befehls "pip3 install sympy" installieren kann. Da es sich bei den Jupyter Notebooks um eine frei zugängliche Open-Source-Software handelt, kann man diese auch direkt auf dem eigenen Computer/Laptop installieren und benötigt nicht den Umweg mittels des Remote Logins auf den Server des ITP. In der ersten Vorlesung (siehe Folien der 1.Vorlesung) wird kurz besprochen, wie man eine solche Installation durchführt. In der ersten Übungsstunde werden Hilfestellungen zu dem Remote Login und der Installation von Python/Jupiter gegeben und eine einführendes Jupyter Notebook besprochen. Dieses Notebook finden Sie unter dem folgenden Link (IntroJupyter.ipynb) und zu dem html-Export gelangen Sie durch Klicken auf des nebenstehende obere Bild.
Allgemeine Relativitätstheorie mit Python
Die oft komplizierten und zeitaufwendigen Berechnungen der tensoriellen Gleichungen der allgemeinen Relativitätstheorie können mithilfe von Computeralgebra-Systemen erleichtert werden. Diverse Anwendungen der Einstein- und Geodätengleichung sind in schon vordefinierten Python Modulen implementiert, und analytische Berechnungen können durchgeführt und entsprechende Lösungen berechnet und visualisiert werden. Beim Klicken auf das nebenstehende Bild werden die grundlegenden Größen der allgemeinen Relativitätstheorie (z.B. die Metrik der Raumzeit, Christoffel Symbole, Ricci- und Einstein-Tensor) am Beispiel einer allgemeinen statischen und isotropen Raumzeit in Python berechnet. Im entsprechenden Python Jupyter Notebook Allgemeine Relativitätstheorie mit Python (GraviPy-EinsteinPy.ipynb) werden zwei unterschiedliche Python Module (GraviPy und EinsteinPy) vorgestellt, mit denen man die Berechnungen durchführen kann. Beide Module basieren auf dem Modul SymPy, welches symbolische Berechnungen mit Python vereinfacht.
Weiterführende Links

- Folien der 1.Vorlesung
- Vorlesungsaufzeichnung der 1.Vorlesung
- Graphical Remote Login with xrdp
- Einstein - Analen der Physik
- Black Hole Cam - Imaging the event horizon of black holes
- Event Horizon Telescope
- LIGO: Laser Interferometer Gravitational-Wave Observatory
- EinsteinPy - Making Einstein possible in Python
- GraviPy
- Das GraviPy-Tutorium GraviPy-Tutorium finden sie unter github.com/wojciechczaja/GraviPy
- View Jupyter Notebook: Einführung in Jupyter Notebooks
- Download Jupyter Notebook: Einführung in Jupyter Notebooks
- View Jupyter Notebook: Allgemeine Relativitätstheorie mit Python
- Download Jupyter Notebook: Allgemeine Relativitätstheorie mit Python
Vorlesung 1
In der ersten Vorlesung werden die Grundlagen der allgemeinen Relativitätstheorie wiederholt und es wird einen kurzen Überblick der Inhalte der gesamten Vorlesung geben.
A. Einstein stellte im Jahre 1915 seine revolutionäre allgemeinen Relativitätstheorie der wissenschaftlichen Öffentlichkeit vor. Seine Feldgleichungen leitete er mittels eines allgemeinen Kovarianzprinzips her und in Einstein, A. 1915, Preuss. Akad.Wiss. Berlin, Sitzungsber., 778-786 schrieb er über seine Theorie "Dem Zauber der Theorie wird sich kaum jemand entziehen können, der sie wirklich erfasst hat;...". Die Schönheit der Einstein Gleichung liegt neben ihrem zugrunde liegenden Kovarianzprinzip in der Einfachheit ihrer fundamentalen Aussage. Nach Einstein verbiegt jede Energieansammlung die Struktur der Raumzeit und diese gekrümmte Raumzeit ist der ursächliche Grund der Gravitation. Nach Einstein fällt der Apfel vom Baum zu Boden, da der große Energiegehalt der Erde die raumzeitliche Struktur so stark verbiegt, dass der Apfel sich in dieser gekrümmten Raumzeit nach geodätischen Gesetzen zu Boden bewegen muss.
Es werden im folgenden die Grundlagen der allgemeinen Relativitätstheorie und im Besonderen die Einsteingleichung
\[
R_{\mu\nu} - \frac{1}{2} g_{\mu\nu} R ~=~ -8 \pi \, T_{\mu\nu}
\]
und die Geodatengleichung
\[
\frac{d^2 x^\mu}{d\tau^2} + \Gamma^\mu_{\nu \rho} \frac{d x^\nu}{d\tau} \frac{d x^\rho}{d\tau} ~=~ 0
\]
als bekannt vorausgesetzt. Die griechischen, raumzeitlichen Indices $ \mu, \nu, \rho ... $ laufen von 0..3, wobei, falls nicht anders angegeben, diese den folgenden kartesischen Raumzeitkoordinaten entsprechen: $ x^\mu = \left( x^0, x^1, x^2, x^3 \right) = \left( t, x, y, z \right)$. Grundlegende Größen der allgemeinen Relativitätstheorie (z.B. die Metrik der Raumzeit, Christoffel Symbole, Ricci- und Einstein-Tensor) werden am Beispiel einer allgemeinen statischen und isotropen Raumzeit in Maple berechnet. Wir definieren z.B. die kovariante Metrik einer allgemeinen statischen, isotropen Raumzeit $ g_{\mu\nu} $, wobei wir ein sphärisches Koordinatensystem benutzen:
\[ g_{\mu\nu}=\left( \begin{array}{ccc} A(r) & 0 & 0 & 0\\ 0& -B(r)& 0&0 \\ 0& 0& -r^2& 0\\ 0& 0& 0& -r^2 \hbox{sin}^2(\theta)\\ \end{array} \right)
\]
, wobei $x^\mu=\left(t,r,\theta,\phi \right)$. Wie sehen die Christoffel Symbole (erste Art $\Gamma_{\mu \nu \rho}$, vollständig kontravariante Form)
\[
\Gamma_{\mu \nu \rho} = \frac{1}{2} \left( \partial_{\!\!\;\mu} g_{\nu \rho} + \partial_{\!\!\;\nu} g_{\mu \rho} - \partial_{\!\!\;\rho} g_{\mu \nu} \right) = \frac{1}{2} \left( g_{\nu \rho |\mu} + g_{\mu \rho |\nu} - g_{\mu \nu |\rho} \right)
\]
, (zweite Art $\Gamma^\mu_{\nu\rho}$)
\[
\Gamma^\mu_{\nu\rho} = g^{\mu\delta} \Gamma_{\nu \rho \delta} = \frac{1}{2} g^{\mu\delta} \left( g_{\delta \nu |\rho} + g_{\delta \rho |\nu} - g_{\nu \rho |\delta} \right)
\]
, der Riemann Tensor $R{^\mu}_{\nu\alpha\beta}$,
\[
R{^\mu}_{\nu\alpha\beta} = \Gamma^\mu_{\nu\beta|\alpha} - \Gamma^\mu_{\nu\alpha|\beta} + \Gamma^\mu_{\lambda\alpha} \Gamma^\lambda_{\nu\beta} - \Gamma^\mu_{\lambda\beta} \Gamma^\lambda_{\nu\alpha}
\]
, der Ricci Tensor $R_{\mu\nu}= g^{\alpha\beta} R_{\alpha\mu\beta\nu}$ und der Ricci Skalar $R=g^{\mu\nu} R_{\mu\nu}$ aus?
Mit den Computeralgebra-Systemen Maple und Mathematica und der Programmiersprache Python lassen sich auch komplizierte Berechnungen im Bereich der allgemeinen Relativitätstheorie einfach berechnen (siehe linkes Panel dieser Vorlesung).
Vorlesung 2
Die Schwarzschild-Metrik beschreibt das raumzeitliche Verhalten eines kugelsymmetrischen, nicht rotierenden und nicht geladenen schwarzen Loches der Masse M, wobei die gesamte Masse des schwarzen Loches in einem singulären Punkt im Zentrum vereint ist. Der Ricci Tensor verschwindet identisch ($R_{\mu \nu} \equiv 0$), da man eine leere Raumzeit betrachtet. Die skalare Invariante des vollständig kontrahierten Quadrates des Riemannschen Krümmungstensors $K = R_{\mu \nu \rho \sigma} R^{\mu \nu \rho \sigma}$, der sogenannte Kretschmann-Skalar $K$, wird im Ursprung singulär ($K=\frac{48\,M^2}{r^6}$) und die Schwarzschild-Metrik besitzt daher eine echte Singularität bei $r = 0$. Neben dieser echten Singularität besitzt die Schwarzschild-Metrik eine Koordinatensingularität bei dem sogenannten Schwarzschild-Radius $R_S=2M$. Im ersten Jupyter Notebook werden wir die wesentlichen Eigenschaften der Schwarzschild-Metrik mittels eingebetteter Diagramme und anhand von Raumzeit-Diagrammen visualisieren. Im zweiten Jupyter Notebook werden wir den radialen Fall eines Probekörpers in ein schwarzes Loch nummerisch berechnen.
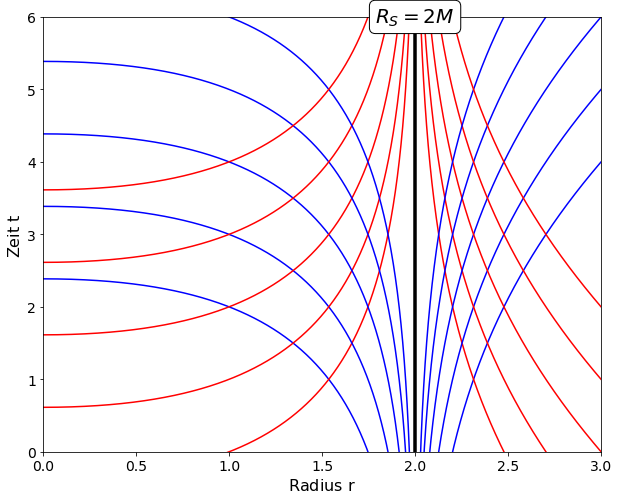
Eigenschaften der Schwarzschild-Metrik
Die Struktur der Raumzeit der Schwarzschild-Metrik kann man auf unterschiedliche Weisen visualisieren. Wir betrachten uns zunächst die sogenannten eingebetteten Diagramme der räumlichen Hypersphäre $\Sigma_t$ der Mannigfaltigkeit ${\cal M}$. Diese eingebetteten Diagramme besitzen eine Tricher-Form und zeigen eine Koordinatensingularität bei dem sogenannten Schwarzschild-Radius $R_S=2M$. Zusätzlich zu diesen Diagrammen werden in dem Jupyter Notebook (Eigenschaften der Schwarzschild-Metrik) die Raumzeit-Diagramme der Schwarzschild-Metrik in Schwarzschild-Koordinaten und Eddington-Finkelstein Koordinaten betrachtet. Die nebenstehende Abbildung zeigt das Raumzeit-Diagramm der Schwarzschild-Metrik ($M=1$) und beschreibt somit das raumzeitliche Verhalten eines kugelsymmetrischen schwarzen Loches aus dem Betrachtungsstandpunkt eines im Unendlichen ruhenden Beobachters (Schwarzschild Koordinaten). Die roten Kurven stellen in das schwarze Loch einlaufende Lichtstrahlen dar und die blauen Kurven auslaufende Lichtstrahlen. Für den äußeren Beobachter erscheint es, als ob die Raumzeit in zwei Bereiche geteilt ist (Bereich I: $r > R_S$ und Bereich II: $r < R_S$), die untereinander keinerlei Informationen austauschen können. Nähert man sich vom Bereich I dem Schwarzschildradius an ($r\rightarrow R_s$, $r > R_S$), so verengt sich der Lichtkegel so stark, dass man im Grenzfall unendlich lange Zeit benötigen würde um $R_S$ erreichen zu können. Im Bereich II dagegen hat die Raum- und Zeitkoordinate anscheinend ihren Sinn getauscht – die Zukunftslichtkegel zeigen unweigerlich in Richtung der echten Singularität im Ursprung. Ein Teilchen, das sich an einem Ort im Bereich II befindet muss sich zwangsläufig in Richtung der echten Singularität bewegen. Einem äußeren Beobachter erscheint die Kugelfläche des Schwarzschildradius demnach als eine Grenze eines Ereignishorizontes. Vom Bereich I kann keine Information in den Bereich II, und von dem Bereich II kann man nicht in den Bereich I vordringen. Die anscheinende Abgeschlossenheit beider Bereiche ist jedoch vom Standpunkt der Betrachtung d.h. von den zugrunde liegenden Koordinaten abhängig und die Koordinatensingularität der Schwarzschild-Metrik kann man mittels spezieller Koordinatentransformationen beseitigen (z.B Eddington-Finkelstein Koordinaten eines einfallenden Photons). Dieses Notebook finden Sie unter dem folgenden Link (Schwarzschild.ipynb).
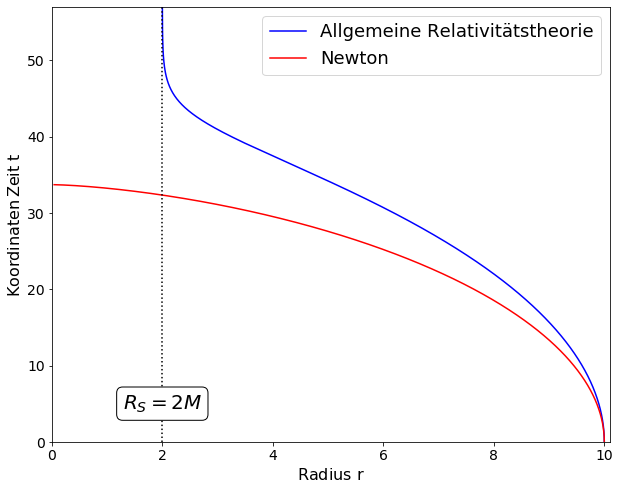
Radialer Fall eines Probekörpers in ein schwarzes Loch
In diesem Jupyter Notebook werden wir einen Probekörper radial in ein nicht-rotierendes schwarzes Loch fallen lassen (Masse Probekörper $m << M$ Masse schwarzes Loch). Wir betrachten somit eine spezielle nummerische Lösung der Geodätengleichung in vorgegebener Schwarzschild Raumzeit. Die Geodätengleichung beschreibt wie sich ein Körper im Raum bewegt und sagt voraus, dass diese Bewegung sich stets entlang der kürzesten Kurve, in der durch die Metrik beschriebenen gekrümmten Raumzeit, vollzieht. Einem im unendlichen ruhenden Beobachter erscheint es als ob ein in das schwarze Loch fallender Körper, kurz vor Erreichen des Ereignishorizontes, immer langsamer wird und diesen in endlicher Zeit nicht überschreiten wird. Die nebenstehende Abbildung zeigt die Raumzeit-Trajektorien des Probekörpers berechnet in allgemeiner Relativitätstheorie (blaue Kurve) im Vergleich mit der entsprechenden Lösung in Newtonscher Theorie (rote Kurve). Im Gegensatz zum Newtonschen Fall, bleibt der in das schwarze Loch fallende Probekörpers somit, für einen äußeren Beobachter, anscheinend am Ereignishorizont bei $R_S=2M$ stehen – der Körper selbst überschreitet jedoch den Ereignishorizont ohne Hindernisse, was man mittels einer Transformation in ein mitgeführtes Koordinatensystem sieht. Für einen äußeren Beobachter wird seine Bewegung in radialer Richtung, nahe dem Ereignishorizont, immer langsamer und das Bild des Körpers friert am Ereignishorizont ein. Man kann zeigen, dass das wahrgenommene Bild gleichzeitig unendlich rotverschoben wird, sodass es nahe dem Ereignishorizont, langsam den wahrnehmbaren, sichtbaren Bereich verlässt.
Weiterführende Links

- Folien der 2.Vorlesung
- Vorlesungsaufzeichnung der 2.Vorlesung
- View Jupyter Notebook: Eigenschaften der Schwarzschild-Metrik
- Download Jupyter Notebook: Eigenschaften der Schwarzschild-Metrik
- View Jupyter Notebook: Radialer Fall eines Probekörpers in ein schwarzes Loch
- Download Jupyter Notebook: Radialer Fall eines Probekörpers in ein schwarzes Loch
- Black Holes and the German Reichstag (Deutsche Version, Englische Version und Movies)
Vorlesung 2
In der zweiten Vorlesung werden wir die wohl bekannteste analytische Lösung der Einsteingleichung betrachten - die sogenannte Schwarzschild-Lösung. Bereits einige Monate nach der Publikation von Einsteins Artikel zur Allgemeinen Relativitätstheorie im Jahre 1915, erarbeitete Karl Schwarzschild in zwei Arbeiten mögliche analytische Lösungen der neuen Theorie der Raumzeitkrümmung. In der ersten dieser Arbeiten ("über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie", siehe Schwarzschild, K., Sitzungsberichte der Königlich-Preussischen Akademie der Wissenschaften. Reimer, Berlin 1916, S. 189-196) betrachtete Herr Schwarzschild die Einstein-Gleichung für den freien, leeren Raum ($T_{\mu\nu}=0 \quad \rightarrow \quad R_{\mu\nu}=0$), wobei er annahm, dass sich die gesamte Materie/Energie in einem singulären Punkt im Ursprung befindet (Massenpunkt der Masse $M$). Die so von ihm gefundene Lösung der resultierenden Feldgleichungen ist heutzutage unter dem Namen Schwarzschild-Metrik bekannt und lautet: \[ g_{\mu\nu}=\left( \begin{array}{ccc} 1-\frac{2\,M}{r} & 0 & 0 & 0\\ 0& -\frac{1}{1-\frac{2\,M}{r}}& 0&0 \\ 0& 0& -r^2& 0\\ 0& 0& 0& -r^2 \hbox{sin}^2(\theta)\\ \end{array} \right) \] , wobei wir ein sphärisch symmetrisches Koordinatensystem benutzt wurde ($x^\mu=\left(t,r,\theta,\phi \right)$). Diese Lösung ist von besonderer Bedeutung für astrophysikalische Betrachtungen, denn sie beschreibt einerseits die Metrik eines nicht-rotierenden schwarzen Lochs und andererseits, aufgrund des Birkhoff-Theorem, die Metrik außerhalb eines einzelnen isolierten, nichtrotierenden Sterns.
Im linken Panel dieser Vorlesung werden im ersten Jupyter Notebook die Eigenschaften der Schwarzschild-Metrik besprochen und in Raumzeit-Diagrammen visualisiert. Im zweiten Jupyter Notebook wird das Beispiel eines radial in das nicht-rotierende schwarzen Loch einfallenden Probekörpers als nummerische Lösung der Geodätengleichung in vorgegebener Schwarzschild Raumzeit berechnet.
Eine gute Verbildlichung der seltsamen Eigenschaften von schwarzen Löchern findet man in der speziellen architektonischen Konstruktion des Berliner Reichstagsgebäudes (siehe Black Holes and the German Reichstag).
Vorlesung 3
Bevor wir die Geodätengleichung und die Klassifikation möglicher Bahnen von Probekörpern in vorgegebener Schwarzschild-Raumzeit mittels eines definierten effektiven Potentials in einem Jupyter Notebook behandeln, wird eine kurze Einführung in das Computeralgebra-System Maple gegeben. Mithilfe der kommerziellen Computeralgebra-Systeme Maple und Mathematica kann man ebenfalls die komplizierten Berechnungen der tensoriellen Gleichungen der Allgemeinen Relativitätstheorie durchführen und numerische Simulationen der entstehenden Differentialgleichungen erstellen.
Das in dieser Vorlesung inhaltlich behandelte Thema (die Bewegung eines Probekörpers um ein schwarzes Loch) ist ein astrophysikalisch sehr relevantes Problem. Schon Jahre bevor die ersten Bilder eines schwarzes Lochs entstanden, galt es schon als so gut wie bestätigt, dass im Zentrum unserer Galaxie ein superschweres schwarzes Loch existiert und Reinhard Genzel (Physik Nobelpreisträger 2020) verfolgte schon seit Jahrzehnten die Bewegung einzelner, sogenannter S-Sterne um dieses schwarzes Loch. Neben diesen aktuellen Erkenntnissen, gilt die Perihel-Drehung des Merkur als ein, durch die allgemeine Relativitätstheorie verursachter Effekt. Obwohl die Bewegung der Planeten unseres Sonnensystems um unser Zentralgestirn (die Sonne) ja sicherlich keine Bewegung um ein schwarzes Loch darstellt, können die Gleichungen der Planetenbewegungen in guter Approximation als solche beschrieben werden (siehe Birkhoff-Theorem).
Allgemeine Relativitätstheorie mit Maple
Analytische Berechnungen und numerische Simulationen im Bereich der Allgemeine Relativitätstheorie können auch mittels des Computeralgebra-Systems Maple durchgeführt werden (siehe alter Teil I der Vorlesung). Die entsprechenden Maple Worksheets der bisher besprochenen Inhalte finden Sie unter den folgenden Links:- Einführung in Maple
Download Maple Worksheet - Grundlegende Größen der Allgemeinen Relativitätstheorie
Download Maple Worksheet - Die Geodätengleichung in vorgegebener Schwarzschild Raumzeit (Version 1)
Download Maple Worksheet - Die Geodätengleichung in vorgegebener Schwarzschild Raumzeit (Version 2)
Download Maple Worksheet
Weitere Maple Worksheets: Das Foucaultsche Pendel, Euler-Lagrange Theorie des Doppelpendels, Hamilton Theorie des Doppelpendels, Das begleitende Dreibein, Der harmonische Oszillator mit Dämpfung, Die Quantenmechanik mit Maple, Physik mit dem Computer, Physik der sozio-ökonomischen Systeme, Physik der sozio-ökonomischen Systeme (alt)
Bewegung eines Probekörpers um ein nicht-rotierendes schwarzes Loch und die Klassifikation möglicher Bahnen mittels eines definierten effektiven Potentials
Die Klassifikation möglicher Bahnen von Probekörpern in vorgegebener Schwarzschild-Raumzeit kann mittels eines definierten effektiven Potentials illustriert werden. Dieses Potential ($V(r,M,l)$) hängt von dem, bei der Bewegung erhaltenen Drehimpuls $l$ und der Masse des schwarzen Lochs $M$ ab. Die im Zentralfeld möglichen Bewegungen werden mittels zweier erhaltener Größen (l: Drehimpuls pro Masse m und e: Energie pro Masse) charakterisiert. Die Definition des effektiven Potential erfolgt mittels der radialen, 2. Geodätengleichung. So definieren z.B. die Literaturangaben 1-3 (siehe Literaturangaben im rechten obersten Panel) das effektive Potential wie folgt: \[ \begin{eqnarray} \hbox{2. Gleichung:}&\rightarrow&\frac{1}{2} \left( \frac{dr}{d\tau} \right)^2 + V(r,M,l) = \frac{1}{2} \left( e^2 -1 \right) \\ \hbox{wobei:} && V(r,M,l) = \frac{l^2}{2 r^2} \left( 1 - \frac{2 M}{r} \right) - \frac{M}{r} \quad . \end{eqnarray} \] In der Literaturangabe 4 (siehe Literaturangaben im rechten obersten Panel) wird das Potential $V(r,M,l)$ hingegen wie folgt definiert: \[ \begin{eqnarray} \hbox{2. Gleichung:}&\rightarrow& \left( \frac{dr}{d\tau} \right)^2 + \left( V(r,M,l) \right)^2 = e^2 \\ \hbox{wobei:} && V(r,M,l) = \sqrt{ \left( 1 - \frac{2 M}{r} \right) \left( 1 + \frac{l^2}{r^2} \right) } \quad . \end{eqnarray} \] Die unteren abgebildete Animation zeigt das effektive Potential als Funktion des Radius (in der Nomenklatur des 4. Buches) und die Trajektorien der Probekörper für unterschiedliche Anfangswerte in einem eingebetteten Raumzeit-Diagramm der Schwarzschild-Metrik.Weiterführende Links

- Folien der 3.Vorlesung
- Vorlesungsaufzeichnung der 3.Vorlesung
- View Jupyter Notebook: Klassifizierung unterschiedlicher Bahnbewegungen
- Download Jupyter Notebook: Klassifizierung unterschiedlicher Bahnbewegungen
- View Jupyter Notebook: Geodätengleichung mit GraviPy
- Download Jupyter Notebook: Geodätengleichung mit GraviPy
- View Mathematica Notebook: Die Geodätengleichung in vorgegebener Schwarzschild Raumzeit
- Download Mathematica Notebook: Die Geodätengleichung in vorgegebener Schwarzschild Raumzeit
Vorlesung 3
Die Geodätengleichung beschreibt wie sich ein Probekörper (Masse Probekörper $m << M$ Masse schwarzes Loch) im Raum bewegt und sagt voraus, dass diese Bewegung sich stets entlang der kürzesten Kurve, in der durch die Metrik beschriebenen gekrümmten Raumzeit, vollzieht. Sie lässt sich demnach durch folgendes Variationsprinzip herleiten:
\[
\delta \int_A^B ds= \delta \int_A^B \sqrt{g_{\mu\nu} dx^\mu dx^\nu}= \delta \int_A^B \sqrt{g_{\mu\nu} \frac{dx^\mu}{d\lambda} \frac{dx^\nu}{d\lambda}} d\lambda = 0
\]
, wobei sich dann die Geodätengleichung mittels der Euler-Lagrange Gleichungen
$L = \sqrt{g_{\mu\nu} \frac{dx^\mu}{d\lambda} \frac{dx^\nu}{d\lambda}}$, bzw.
alternativ $L = g_{\mu\nu} \frac{dx^\mu}{d\lambda} \frac{dx^\nu}{d\lambda}$ ergibt:
\[
\frac{d}{d\lambda} \left( \frac{\partial L}{\partial \frac{\partial x^\mu}{\partial \lambda}} \right) -
\frac{\partial L}{\partial x^\mu} = 0 \quad \rightarrow \quad \frac{d^2 x^\mu}{d\lambda^2} +
\Gamma^\mu_{\nu \rho} \frac{d x^\nu}{d\lambda} \frac{d x^\rho}{d\lambda} ~=~ 0
\]
$\Gamma^\mu_{\nu \rho}$ sind die Christoffel Symbole zweiter Art und $\lambda$ ein affiner Parameter (z.B. die Eigenzeit $\tau$ des Probekörpers).
In der dritten Vorlesung werden wir die Geodätengleichung in vorgegebener Schwarzschild-Raumzeit näher betrachten, wobei wir wieder ein sphärisches Koordinatensystem benutzen ($x^\mu=\left(t,r,\theta,\phi \right)$). Die Geodätengleichung stellt ein System gekoppelter nichtlinearer Differentialgleichungen dar
\[
\begin{eqnarray}
&& \frac{d^2 x^0}{d\lambda^2} = \frac{d^2 t}{d\lambda^2} = - \Gamma^0_{\nu \rho} \frac{d x^\nu}{d\lambda} \frac{d x^\rho}{d\lambda} \\
&& \frac{d^2 x^1}{d\lambda^2} = \frac{d^2 r}{d\lambda^2} = - \Gamma^1_{\nu \rho} \frac{d x^\nu}{d\lambda} \frac{d x^\rho}{d\lambda}\\
&& \frac{d^2 x^2}{d\lambda^2} = \frac{d^2 \theta}{d\lambda^2} = - \Gamma^2_{\nu \rho} \frac{d x^\nu}{d\lambda} \frac{d x^\rho}{d\lambda}\\
&& \frac{d^2 x^3}{d\lambda^2} = \frac{d^2 \phi}{d\lambda^2} = - \Gamma^3_{\nu \rho} \frac{d x^\nu}{d\lambda} \frac{d x^\rho}{d\lambda} \quad .
\end{eqnarray}
\]
Man kann zeigen (siehe z.B. Seite 206 in General relativity : An introduction for physicists by M. P. Hobson, G. P. Efstathiou and A. N. Lasenby), dass sich die erste und vierte Gleichung dieses Systems von Differentialgleichungen in die folgenden Gleichungen umschreiben lässt:
\[
\begin{eqnarray}
\hbox{1. Gleichung:}&& \frac{d}{d\lambda} \left[ \left( 1 - \frac{2 M}{r} \right) \frac{dt}{d\lambda} \right] = 0 \\
\rightarrow && \left( 1 - \frac{2 M}{r} \right) \frac{dt}{d\lambda} = e = \hbox{const} \\
\hbox{4. Gleichung:}&& \frac{d}{d\lambda} \left( r^2 \hbox{sin}^2(\theta) \frac{d\phi}{d\lambda} \right) = 0 \\
\rightarrow && r^2 \hbox{sin}^2(\theta) \frac{d\phi}{d\lambda} = l = \hbox{const}
\end{eqnarray}
\]
, wobei die während der Bewegungen erhaltenen Größen e (Teilchenenergie pro Masse) und l (Drehimpuls pro Masse m) sich aus der Definition des Viererimpulses $p_\mu = m u_\mu$ ergeben.
Die unterschiedlichen Bahnbewegungen um ein nicht-rotierendes schwarzes Loch lassen sich mittels eines effektiven Potentials klassifizieren (siehe linkes Panel dieser Vorlesung). Die im linken Panel veranschaulichte Abbildungen zeigen das effektive Potential als Funktion des Radius und die möglichen Trajektorien der Probekörper für unterschiedliche Anfangswerte in einem eingebetteten Raumzeit-Diagramm der Schwarzschild-Metrik. Bei der elliptische, roten Bahn erkennt man hierbei gut den allgemein-relativistischen Effekt der Apsidendrehung (Periheldrehung bei der Sonne); d.h. der näheste Punkt (der Perihel) und der am weitesten entfernte Punkt (der Aphel) vom Zentrum des schwarzen Lochs betrachtet, ändert seine Position und rotiert entgegen dem Uhrzeigersinn in $\phi$-Richtung.
Vorlesung 4
Im ersten Abschnitt dieser Vorlesung werden wir ein Jupyter Notebook behandeln, welches die Eigenschaften der innersten stabilen kreisförmigen Bahnbewegung eines massiven Probekörpers (ISCO, siehe rechtes Panel dieser Vorlesung) berechnet und diesen Grenzorbit verdeutlicht. Des Weiteren wird in diesem Notebook auch die Bewegung von masselosen Teilchen (z.B. Photonen) um ein nicht-rotierendes schwarzes Loch simuliert und die Photonensphäre eines schwarzen Loches berechnet. Die astrophysikalische Bedeutung des ISCOs und der Photonensphäre wird danach in einem Maple Worksheet diskutiert und mittels des vom Event Horizon Teleskop aufgenommenen Bildes des schwarzen Lochs in unserer Nachbargalaxie Messier 87 illustriert. Am Ende dieser Vorlesung werden die Planetenbewegungen unseres Sonnensystems allgemein-relativistisch berechnet und der Transit des Merkur am 9.Mai 2016 simuliert.
Die innerste stabile kreisförmige Bahnbewegung (der ISCO: Innermost Stable Circular Orbit) und die Photonensphäre
Die linke Seite der oberen Animation verdeutlicht die Trajektorien des ISCO und der Photonensphäre in einem eingebetteten Raumzeit-Diagramm der Schwarzschild-Metrik. Kreisförmige Bewegungen von massiven Probekörpern um ein nicht rotierendes schwarzes Loch können dem Loch nicht beliebig nahekommen. Die Grenze der Stabilität von kreisförmigen Trajektorien nennt man ISCO (siehe rechtes Panel dieser Vorlesung). Die linke obere Abbildung zeigt die simulierten Bahnen dreier kreisförmige Bewegungen, welche in unterschiedlichen Abstand um das schwarze Loch kreisen, wobei die Masse des schwarzen Loches auf $M=1$ gesetzt wurde. Der grüne Probekörper kreist mit einem Abstand von $r=12$ km, der rote Körper von $r=9.25$ km und der schwarze Körper von $r=6$ km um das schwarze Loch. Zusätzlich sind für diese kreisförmigen Orbits auf der rechten Seite der oberen Abbildung die zugehörigen effektiven Potentiale dargestellt. Da es sich um kreisförmige Bewegungen handelt befinden sich alle drei Probekörper im Minimum des zugehörigen Potentials bzw. der schwarze Orbit im Sattelpunkt des Potentials. Stabile kreisförmige Bewegungen um ein schwarzes Loch (nicht-rotierend) sind somit nur bis zu einem Abstand von $r=6 M$ möglich. Das gilt jedoch nicht für masselose Probekörper (z.B. Photonen). Die orange Kurve auf der linken Seite der oberen Abbildung zeigt die Bewegung eines masselosen Testteilchen im Abstand $r=3$ km. Bei diesem Abstand können Lichtteilchen kreisförmig um das schwarze Loch rotieren und man nennt die entsprechende Kugelschale bei $r=3 M$ auch deshalb die Photonensphäre eines schwarzen Loches.
Das Schwarze Loch in M87
Das nebenstehende Bild zeigt das schwarze Loch im Zentrum unserer Nachbargalaxie Messier 87 (M87); bzw. ein wenig genauer, die um ein schwarzes Loch entstehende Radiostrahlung. Das Bild wurde mittels eines weltweiten Verbunds von Radiowellenteleskopen (EHT: Event Horizon Teleskop, siehe auch Black Hole Cam) sichtbar gemacht. Das EHT beobachtete im Jahre 2017 zwei supermassive schwarze Löcher: das schwarze Loch in unserer Milchstraße (Sagittarius A*, Masse $M\approx 4.15 \cdot 10^6 M_\odot$, Abstand zur Erde $D \approx 26670$ Lichtjahre) und in unserer Nachbargalaxie Messier 87 (M87*, Masse $M\approx 6.5 \cdot 10^9 M_\odot$, Abstand zur Erde $D \approx 53$ Millionen Lichtjahre). In beiden Systemen kreist Materie in einer Akkretionsscheibe um ein supermassives schwarzes Loch und emittiert beim Einfallen elektromagnetische Strahlung. Die im vorigen Unterpunkt besprochenen Größen des ISCO und der Photonensphäre besitzen eine besondere Bedeutung beim Verständnis des Bildes. Kommen die in der magnetisierten Akkretionsscheibe befindlichen Probekörper (Gasteilchen des umgebenden Plasmas) dem schwarzen Loch näher als der Radiuswert des ISCOs, so fallen sie in das schwarze Loch, heizen sich auf und strahlen elektromagnetische Strahlung (Radiowellen) ab. Auf ihrem Weg zum Ereignishorizont des schwarzen Loches passieren sie auch die Photonensphäre und Licht, welches sie dort aussenden, wandert dort zunächst mehrmals um das schwarze Loch, bis es ihm entkommen kann. Zwischen der Photonensphäre und dem Ereignishorizont können zwar noch einige wenige Photonen entkommen, das gesehene Bild wird dort jedoch schon stark dunkler. Beim Klicken auf das nebenstehende Bild gelangen Sie zu dem Maple-Worksheet, in welchem diese Eigenschaften des schwarzen Loches in M87 simuliert werden.
Die Bewegung der Planeten in allgemeiner Relativitätstheorie
Obwohl die Bewegung der Planeten unseres Sonnensystems um unser Zentralgestirn (die Sonne) in sehr guter Näherung mittels der Newtonschen Gravitationstheorie beschrieben werden kann und unsere Sonne ja sicherlich kein schwarzes Loch darstellt, können die Bahnen der Planeten auch allgemein-relativistisch mittels der Geodätengleichung in vorgegebener Schwarzschild-Raumzeit berechnet werden. Dies ist aufgrund des Birkhoff-Theorems möglich, was besagt, dass eine sphärisch symmetrische Vakuumlösung der Einsteinschen Feldgleichungen außerhalb einer sphärisch symmetrischen Massenverteilung (Sonne) statisch sein muss und diese Lösung der Schwarzschild-Lösung entspricht. Die Periheldrehung des Merkur ist ein Beispiel eines nur in der allgemeinen Relativitätstheorie vorkommenden Effektes, der in der Newtonschen Gravitationstheorie nicht entsteht. Beim Klicken auf die nebenstehende Abbildung gelangt man zu einem Maple Worksheet, das die Bewegung der Erde und des Merkur um die Sonne allgemein-relativistisch berechnet und den Merkurtransit am 9.Mai 2016 simuliert.Weiterführende Links

- Folien der 4.Vorlesung
- Vorlesungsaufzeichnung der 4.Vorlesung
- View Jupyter Notebook: Der ISCO und die Photonensphäre
- Download Jupyter Notebook: Der ISCO und die Photonensphäre
- View Maple Worksheet: Das Schwarze Loch in M87 (nicht-rotierend)
- Download Maple Worksheet: Das Schwarze Loch in M87 (nicht-rotierend)
- View Maple Worksheet: Der Merkur-Transit (allgemein-relativistisch)
- Download Maple Worksheet: Der Merkur-Transit (allgemein-relativistisch)
- View Maple Worksheet: Der Transits der Venus am 8.Juni 2004 (Newtonsche Version)
- Download Maple Worksheet: Der Transits der Venus am 8.Juni 2004 (Newtonsche Version)
Vorlesung 4
In der vorigen Vorlesung hatten wir die Geodätengleichung in vorgegebener Schwarzschild-Raumzeit betrachtet und gezeigt, wie man eine Klassifizierung möglicher Bahnen von Probekörpern mittels eines definierten effektiven Potentials V(r,M,l) illustrieren kann ($M$ ist die Masse des schwarzen Lochs und l der Bahndrehimpuls pro Masse $m$ des Probekörpers). Eine dieser Bahnen ist von besonderer Bedeutung, die sogenannte innerste stabile kreisförmige Bahnbewegung (der ISCO: Innermost Stable Circular Orbit). Kreisförmige Bahnbewegungen sind dadurch charakterisiert, dass der Wert des Radiuses sich im laufe der Zeit nicht verändert und somit sich der radiale Abstand des Probekörpers vom schwarzen Loch gerade im Minimum des effektiven Potentials befindet. Es muss somit $\frac{dV}{dr}=0$ gelten. Löst man diese Gleichung nach r auf, so erhält man zwei Lösungen, wobei die erste (positives Vorzeichen) dem stabilen Minimum und die zweite (negatives Vorzeichen) dem instabilen Maximum entspricht:
$$
\begin{eqnarray}
\frac{d V}{dr}=0 \quad \Rightarrow \, r_\pm = \frac{l}{2 M} \left( l \pm \sqrt{l^2 -12 M^2} \right)
\end{eqnarray}
$$
Der ISCO hat gerade die Sattelpunkt-Eigenschaft, sodass zusätzlich $\frac{d^2V}{dr^2}=0$ gelten muss. Der Drehimpuls l des Probekörpers und sein radialer Abstand vom schwarzen Loch nehmen die folgenden Werte an:
$$
\begin{eqnarray}
\frac{d V}{dr}=0 \,\,,\,\,\, \frac{d^2 V}{dr^2}=0 \quad \underbrace{\Rightarrow}_{\hbox{ISCO}} r=6 M \,\,,\,\,\, l = 2 \sqrt{3} M
\end{eqnarray}
$$
Kreisförmige Bewegungen um ein nicht-rotierendes schwarzes Loch sind somit nur bis zu einem Abstand von $r_{\tiny ISCO}=6 M$ möglich. Kommt man dem schwarzen Loch näher, endet man zwangsläufig in der echten Singularität. Dies gilt jedoch nur für massive Probekörper und nicht für masselose Teilchen (z.B. Photonen). Photonenbahnen unterscheiden im Wert des infinitesimalen Weglängenelementes $ds^2 = g_{\mu\nu} \, dx^\mu dx^\nu$. Mittels der Eigenschaft für Photonen $\left( \frac{ds}{d\tau} \right)^2=0$ vereinfacht sich die radiale Gleichung der Geodätengleichung und man kann ein effektives Potential definieren, welches allein von der Masse des schwarzen Lochs abhängt:
$$
\begin{eqnarray}
&& \frac{1}{l^2} \left( \frac{dr}{d\lambda} \right)^2 + V_{\tiny Photon}(r) = \frac{1}{b^2}\\
&& V_{\tiny Photon}(r) = \frac{1}{r^2} \left( 1 - \frac{2 M}{r} \right) \quad,
\end{eqnarray}
$$
wobei der Parameter b der Impaktparameter der Photonenbahn darstellt. Dieses Potential besitzt ein Maximum bei $r=3 M$ welches die innerste kreisförmige Photonenbahn darstellt, die sogenannte Photonensphäre eines schwarzen Lochs. Mit $r=3 M$ ist diese nur ein wenig vom Ereignishorizont ($r=2 M$) entfernt.
Im linken Panel dieser Vorlesung werden die besprochenen Grenztrajektorien (ISCO und Photonensphäre) in einer Animation illustriert und die Bedeutung dieser Orbits beim Verständnis des vom Event Horizon Teleskop aufgenommenen Bildes des schwarzen Lochs in M87 erklärt.
Vorlesung 5
In dieser Vorlesung werden wir die Eigenschaften von rotierenden schwarzen Löchern und die Bewegung von Probekörper um diese mittels zweier Jupyter Notebook behandeln. Weiter unten in den ''Weiterführende Links'' werden auch die entsprechenden Maple Worksheets angegeben.
Rotierende schwarze Löcher und die Kerr-Metrik
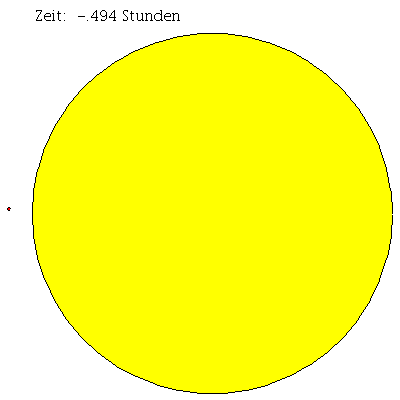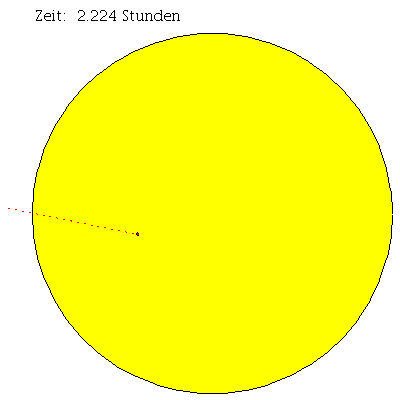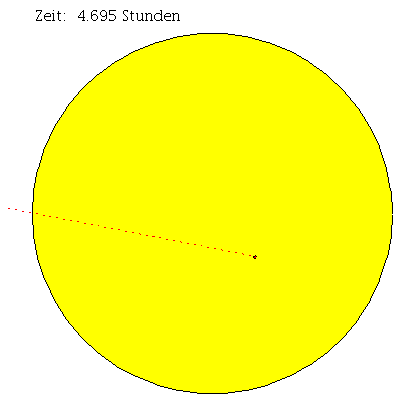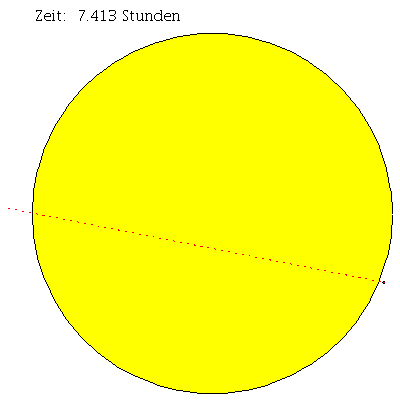
Rotierende schwarze Löcher besitzen eine kompliziertere Struktur der Ereignishorizonte und die Flächen unendlicher Rotverschiebung und die Grenzflächen stationärer Bewegungen sind im Allgemeinen nicht identisch mit den Horizonten. Die nebenstehende obere Abbildung zeigt die wichtigen Flächen der Kerr-Metrik in einer Animation, wobei der Kerr-Rotationsparameter im Bereich $a \in [0.2,1[$ variiert wurde. Rotiert das schwarze Loch, so existieren zwei Ereignishorizonte (r+: graue Fläche und r-: grüne Fläche) und zwei Flächen unendlicher Rotverschiebung (rs+: äußere rote Fläche und rs-: blaue Fläche). Der Bereich zwischen der äußeren roten Fläche unendlicher Rotverschiebung und dem äußeren Ereignishorizont bei r+ nennt man Ergosphäre; hier können Körper und sogar Lichtteilchen nicht mehr entgegengesetzt der Rotationsrichtung des schwarzen Lochs rotieren und stationäre Bewegungen sind somit nicht mehr möglich. Fällt ein Probekörper radial in ein rotierendes schwarzes Loch, so wird er aufgrund des Mitführungseffektes der rotierenden Raumzeit (Frame dragging, siehe rechtes Panel dieser Vorlesung) abgelenkt. Dieses Mitführen der Raumzeit erfolgt in Richtung der Rotation des schwarzen Lochs und nimmt bei Annäherung an das schwarze Loch zu. Das entsprechende Jupyter Notebook finden Sie unter dem folgenden Link: Das rotierende schwarzes Loch: Struktur der Horizonte und der radiale Fall eines Probekörpers.
Bewegung eines Probekörpers um ein rotierendes schwarzes Loch und die Klassifikation möglicher Bahnen mittels eines definierten effektiven Potentials
In dem Jupyter Notebook Das rotierende schwarzes Loch: Klassifikation möglicher Bahnen und der ISCO werden die möglichen Bewegungen eines Probekörpers um ein rotierendes schwarzes Loch (Kerr-Metrik) mittels eines definierten effektiven Potential illustriert. Wie bei einem nicht-rotierenden schwarzen Loch, können kreisförmige Bewegungen von massiven Probekörpern um ein rotierendes schwarzes Loch dem Loch nicht beliebig nahe kommen (siehe Vorlesung 4). Bei rotierenden schwarzen Löchern gibt es zwei solcher Grenzen der Stabilität von kreisförmigen Trajektorien (zwei ISCOs). Die obere nebenstehenden Abbildung zeigt die beiden effektiven Potentiale des co-rotierenden (Probekörper rotiert in gleicher Richtung wie die Rotationsrichtung des schwarzen Lochs) und contra-rotierenden (Körper rotiert entgegen der Rotationsrichtung des schwarzen Lochs) ISCOs bei Variation des Kerr-Rotationsparameter $a$, wobei in beiden Fällen die Sattelpunkteigenschaft gut zu erkennen ist. Im nicht-rotierenden Grenzfall ($a=0$) erhält man hingegen nur eine Lösung bei $r_{\tiny ISCO}=6 M$ (hier $M=1$).
Die nebenstehende untere Animation zeigt die innerste co-rotierende (blaue Trajektorie innerhalb der gelben Ergosphäre) und innerste contra-rotierende (roter Trajektorie) Bahn für ein rotierendes schwarzes Loch ($M=1$ und $a=0.95$). Zusätzlich ist die Trajektorie eines zunächst contra-rotierenden Probekörpers veranschaulicht, welcher in das schwarze Loch fällt (schwarze Kurve). Da der ''Frame dragging'' Effekt bei Annäherung an das schwarze Loch immer stärker wird dreht der Körper seine Rotationsrichtung kurz vor Erreichen der Ergosphäre um und fällt schließlich co-rotierend in das schwarze Loch.
Weiterführende Links

- Folien der 5.Vorlesung
- Vorlesungsaufzeichnung der 5.Vorlesung
- Experimentelle Bestätigung des Mitführungs-Effektes der Raumzeit (Frame-Dragging) durch die Satelliten-Mission Gravity Probe B (siehe auch Finaler Artikel, Clifford Will's Viewpoint, Gravity Probe B: Testing Einstein's Universe)
- View Jupyter Notebook: Das rotierende schwarzes Loch: Struktur der Horizonte und der radiale Fall eines Probekörpers
- Download Jupyter Notebook: Das rotierende schwarzes Loch: Struktur der Horizonte und der radiale Fall eines Probekörpers
- View Jupyter Notebook: Das rotierende schwarzes Loch: Klassifikation möglicher Bahnen und der ISCO
- Download Jupyter Notebook: Das rotierende schwarzes Loch: Klassifikation möglicher Bahnen und der ISCO
- View Maple Worksheet: Bewegung eines Probekörpers um ein rotierendes schwarzes Loch
- Download Maple Worksheet: Bewegung eines Probekörpers um ein rotierendes schwarzes Loch
- View Maple Worksheet: Die Kerr Metrik: Effektives Potential, kreisförmige Bewegungen, die innerste stabile Kreisbahn und der gravitomagnetische Effekt
- Download Maple Worksheet: Die Kerr Metrik: Effektives Potential, kreisförmige Bewegungen, die innerste stabile Kreisbahn und der gravitomagnetische Effekt
- View Maple Worksheet: Das Schwarze Loch in M87 (mit Rotation)
- Download Maple Worksheet: Das Schwarze Loch in M87 (mit Rotation)
Vorlesung 5
In den beiden vorigen Vorlesungen hatten wir die Geodätengleichung in vorgegebener Schwarzschild-Metrik (Raumzeit eines nicht-rotierenden schwarzen Loches) betrachtet und die möglichen Bahnen von Probekörpern und Licht studiert, die Grenz-Orbits des ISCO und der Photonensphäre definiert und die Bedeutung dieser Orbits beim Verständnis des Bildes des schwarzen Lochs in M87 diskutiert. Da dieses schwarze Loch und auch generell die allermeisten durch astrophysikalische Beobachtungen bekannten schwarzen Löcher nicht von statischer Natur sind, werden wir in dieser Vorlesung die Eigenschaften von rotierenden schwarzen Löchern besprechen.
Im Folgenden betrachten wir die Bewegung eines massiven Probekörpers um ein rotierendes schwarzes Loch und lösen die Geodätengleichung in vorgegebener Kerr-Raumzeit (in Boyer-Lindquist Koordinaten). Die kovariante Kerr-Metrik eines rotierenden schwarzen Lochs der Masse M und Rotation a ($ a \in [-1,1]$ ist ein spezifischer Drehimpuls $a=J/M$ und wird als der sogenannte Kerr-Rotationsparameter bezeichnet) besitzt in Boyer-Lindquist Koordinaten folgendes Aussehen:
$$
\begin{eqnarray}
&g_{\mu\nu}=\left( \begin{array}{ccc} g_{tt}(r,\theta) & 0 & 0 & g_{t\phi}(r,\theta)\\ 0& g_{rr}(r,\theta)& 0&0 \\ 0& 0& g_{\theta\theta}(r,\theta)& 0\\ g_{\phi t}(r,\theta)& 0& 0& g_{\phi\phi}(r,\theta)\\ \end{array} \right)& \\
& g_{tt}(r,\theta)=\left( \frac{1-2\,M\,r}{\rho^2} \right)\,\,, \, g_{t\phi}(r,\theta)=\frac{2aMr\hbox{sin}^2(\theta)}{\rho^2} &\\
&g_{rr}(r,\theta)=-\frac{\rho^2}{\Delta}\,\,, \quad g_{\theta\theta}(r,\theta)=-\rho^2\,\,, \, & \\
&g_{\phi\phi}(r,\theta)=-\left( \frac{r^2+a^2+2 M r a^2 \hbox{sin}^2(\theta)}{\rho^2} \right)\hbox{sin}^2(\theta)\,\,,&\\
&\rho^2=r^2+a^2 \hbox{cos}^2(\theta) \,\,, \quad \Delta=r^2-2Mr+a^2&
\end{eqnarray}
$$
Rotierende schwarze Löcher besitzen, im Gegensatz zu denen in den Vorlesung 3-4 besprochenen nicht-rotierenden schwarzen Löchern, eine Ringsingularität und eine kompliziertere Struktur der Ereignishorizonte. Ereignishorizonte ereignen sich formal an den Raumzeitpunkten, bei denen die radiale Komponente der zugrunde liegenden Metrik singulär wird ($g_{rr}\rightarrow\infty$ (bzw. $g^{rr}=0$). Für $a \neq 0$ erhält man zwei Lösungen, die man gewöhnlich mit den Symbolen $r_{+}$ und $r_{-}$ bezeichnet
$$
r_{+}= M + \sqrt{M^2 - a^2}\,, \quad r_{-}= M - \sqrt{M^2 - a^2}\quad,
$$
und die für $a = 0$ in den Schwarzschild-Limes des Ereignishorizontes eines nicht-rotierenden schwarzen Lochs übergehen ($a=0 \rightarrow r_{+}=r_{-}=2\,M$). Zusätzlich existieren die Flächen der stationären Grenze (stationary limit surfaces) und die der unendlichen Rotverschiebung; sie sind durch $g_{tt}=0$ bestimmt und werden gewöhnlich mit den Symbolen $r_{S^+}$ und $r_{S^-}$ bezeichnet:
$$
r_{S^+}= M + \sqrt{M^2 - a^2{{\rm cos}(\theta)}^2}\,, \,\, r_{S^-}= M - \sqrt{M^2 - a^2{{\rm cos}(\theta)}^2}
$$
In dem linken Panel dieser Internetseite ist die Horizontstruktur eines rotierenden schwarzen Lochs bei ansteigendem Kerr-Rotationparameter $a$ in einer Animation veranschaulicht.
Ein rotierendes schwarzes Loch zieht die Raumzeit mit sich mit. Die Rotationsfrequenz mit der die raumzeitlichen Struktur mitgeführt wird, nennt man ''Frame dragging'' Frequenz $\omega$; sie beschreibt wie viel sich die $\phi$-Koordinate pro Koordinatenzeit $t$ verändert:
$$
\begin{equation}
\omega(r,\theta)=\frac{d\phi}{dt} = \frac{\frac{d\phi}{d\tau}}{\frac{dt}{d\tau}} = \frac{u^\phi}{u^t} = \frac{g^{t\phi}}{g^{tt}}
\end{equation}
$$
Die möglichen Bewegungen von Probekörpern um ein rotierendes schwarzes Loch kann man sich wieder mithilfe eines effektiven Potentials illustrieren (siehe z.B. Hartle- bzw. Hobson Buch). In ähnlicher Weise wie in der Vorlesung 3 beschränken wir uns im Folgenden auf äquatoriale Bewegungen, schreiben das System der gekoppelten Differentialgleichungen der Geodätengleichung um und betrachten die zweite, radiale Gleichung. Das effektive Potential hängt von dem, bei der Bewegung erhaltenem Drehimpuls pro Masse $l$ und von der Probekörper-Energie pro Masse $e$ ab. Die im Zentralfeld möglichen Bewegungen werden mittels dieser zwei erhaltenen Größen charakterisiert:
\[
\begin{eqnarray}
&\frac{1}{2} \left( \frac{dr}{d\tau} \right)^2 + V(r,a,l,e) = \frac{1}{2} \left( e^2 -1 \right)& \\
& V(r,a,l,e) \,=\, -\frac{M}{r} + \frac{l^2 - a^2 \left( e^2 -1 \right)}{2\, r^2} - \frac{M \left( l - a\,e \right)^2}{r^3} &
\end{eqnarray}
\]
Die Bewegungen von Probekörpern ist aufgrund des ''Frame dragging'' Effekts unterschiedlich zu den Trajektorien um ein nicht-rotierendes schwarzes Loch und bei rotierenden schwarzen Löchern gibt es zwei unterschiedliche Grenzen der Stabilität von kreisförmigen Trajektorien (zwei ISCOs, siehe Animation im rechten Panel dieser Vorlesung). Die ''Frame dragging'' Frequenz wirkt in ähnlicher Weise auf die Geschwindigkeit von Probekörpern, wie das Magnetfeld in der Elektrodynamik die Lorentzkraft verursacht und die entstehende Kraft wird deshalb auch als Gravitomagnetische Kraft bezeichnet. In erster Näherung (siehe Fließbach Buch, S:172) ist die gravitomagnetische Kraft gleich $ \sim 2\,\left( {\bf \omega} \times {\bf v} \right) $, wobei $ \times $ das Kreuzprodukt, $ {\bf \omega} $ der axiale Vektor der "Frame dragging" Frequenz und $ {\bf v} $ der Geschwindigkeitsvektor des Probekörpers ist. Die Änderung des Geschwindigkeitsvektors nimmt in dieser Schwachfeldnäherung dann die folgende Gestalt an:
\[
\begin{eqnarray}
\frac{d{\bf v}}{d\tau} &=& \underbrace{-\hbox{grad}\, \Phi({\bf r})}_{\hbox{gewöhnlicher Teil der gravitativen Kraft}} +\\
&& \\
&& + \underbrace{2\, {\bf \omega}({\bf r}) \times {\bf v}}_{\hbox{gravitomagnetische Lorentzkraft}} \,\,+ {\cal O}(v^2/c^2)\,\,,
\end{eqnarray}
\]
wobei $\Phi({\bf r})$ das Newtonsche Gravitationspotential und ${\bf v}=(v^r,v^\theta,v^\phi)$ der Geschwindigkeitsvektor des Probekörpers ist.
Die gravitomagnetische Kraft und der Mitführungs-Effekt der Raumzeit (Frame-Dragging-Effekt, bzw. Lense-Thirring-Effekt) ist eine generelle Eigenschaft von rotierenden Körpern in der allgemeinen Relativitätstheorie, die in der Newtonschen Gravitationstheorie nicht auftritt und auch bei langsam rotierenden Körpern existent ist. Das Frame-Dragging konnte im Jahre 2004 mittels der NASA Satelliten-Mission Gravity Probe B am Beispiel des durch die Erdrotation verursachten Mitführungs-Effekt der Raumzeit experimentell nachgewiesen werden (siehe auch Gravity Probe B: Testing Einstein's Universe und linkes Panel dieser Vorlesung).
Vorlesung 6
Die im rechten Panel dieser Vorlesung dargestellten TOV-Gleichungen beschreiben das Druck- und Energiedichte-Verhalten innerhalb eines sphärisch symmetrischen Objektes und geben außerdem die Innenraum-Metrik des Objektes an. Außerhalb des Objektes ist die Raumzeit durch die Schwarzschildmetrik definiert, welche aufgrund des Birkhoff-Theorems die einzige sphärisch symmetrische Lösung der Einsteingleichung im Vakuum ($T^{\mu\nu}\equiv 0$) ist. Mittels der TOV-Gleichungen können die unterschiedlichsten Objekte in guter Näherung beschrieben werden. So kann man mit ihnen sowohl das Innere der Sonne, als auch die Eigenschaften von Weißen Zwergen und Neutronensternen gut beschreiben. Nach einer kurzen Einführung in die Astrophysik der Weißen Zwerge, Neutronensternen und Quarksterne werden in einem Python Jupyter Notebook, die TOV-Gleichungen analytisch hergeleitet und ihre nummerische Lösung, unter Verwendung einer polytropen Form der Zustandsgleichung der Neutronenstern-Materie behandelt.
Weiße Zwerge, Neutronensterne und Quarksterne
Neutronensterne sind neben weißen Zwergen und stellaren schwarzen Löchern die möglichen Endzustände des Evolutionsprozesses einer Sonne. Neutronensterne werden in gewaltigen Supernova-Explosionen geboren und sie stellen den letzten stabilen Zustand der Materie dar, bevor sie zu einem schwarzen Loch kollabiert. Diese faszinierenden stellaren Objekte besitzen lediglich einen Durchmesser von 20 Kilometern, vereinen dort jedoch auf engstem Raum eine Masse von 500 000 Erdmassen. Von den etwa 100 Millionen Neutronensternen die es in unserer Galaxie, der Milchstraße, vermutlich gibt, sind ca. 3000 als Pulsare bekannt. Pulsare sind schnell rotierende Neutronensterne mit einem starken Magnetfeld (bis zu 1011 Tesla), die bevorzugt entlang der Pole elektromagnetische Strahlung aussenden. Einige dieser Neutronensterne, die sogenannten Millisekunden-Pulsare rotieren so schnell, dass sie pro Sekunde mehrere hundert Umdrehungen schaffen. Für diese Millisekunden-Pulsare ist unser sphärisch symmetrische Ansatz der Metrik nicht mehr erfüllt. Unter den bekannten Neutronensternen gibt es auch einige, die sich in binären Systemen befinden, wobei ihr Begleiter entweder ein normaler Stern, ein Planet, ein weißer Zwerg oder auch wieder ein Neutronenstern sein kann. Diejenigen Neutronensterne, die in Zweiersystem umeinander kreisen, verringern ihren Abstand im Laufe der Zeit, da sie Energie durch Aussendung von Gravitationswellen abgeben. Das derzeit beeindruckendste Binärsystem ist der sogenannte Doppelpulsar: PSR J0737-3039A/B, welches im Jahre 2003 entdeckt wurde. Kollidieren zwei Neutronensterne miteinander wird eine enorme Energie in Form von Gravitationswellen frei gesetzt und eine solche Neutronenstern-Kollision konnte im Jahre 2017 mittels der Gravitationswellen-Detektoren beobachtet werden (siehe GW170817). Da die Dichte im inneren Bereich des Neutronensterns den mehrfachen Wert der normalen nuklearen Kerndichte erreichen kann, ist es wahrscheinlich, dass ein Phasenübergang zu Quarkmaterie stattfindet - diese Sterne werden als sogenannte hybride, bzw. Quarksterne bezeichnet (siehe GOETHE-UNI online: Gravitational waves could prove the existence of the quark-gluon plasma).
Die Tolman-Oppenheimer-Volkoff (TOV) Gleichung
Unter der Annahme einer sphärisch symmetrischen Materieverteilung einer idealen Flüssigkeit (z.B. Neutronenstern Materie) kann man die Einsteingleichung in die sogenannten TOV-Gleichungen umschreiben. In diesem Jupyter Notebook wird gezeigt, wie man von der Einsteingleichung zu den TOV-Gleichungen gelangt und ihre nummerische Lösung behandelt.
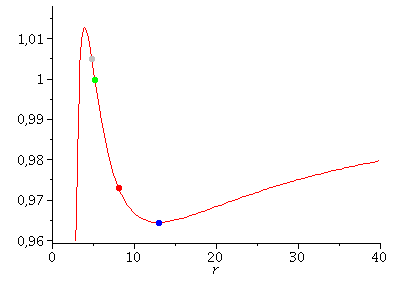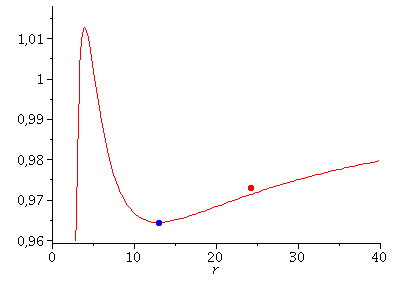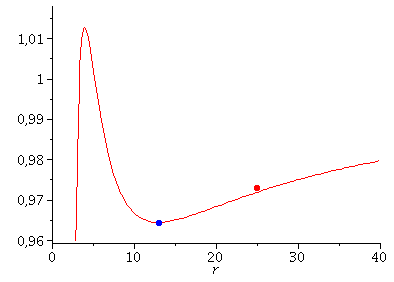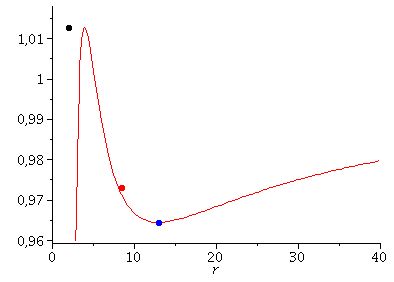
Die obere Animation zeigt die numerisch simulierten Resultate einer Sequenz von Neutronensternen mit unterschiedlichen zentralen Dichten unter Verwendung einer polytropen Zustandsgleichung ($p(e)=K\,e^{\gamma}$ mit $K\approx 20$ und $\gamma=\frac{5}{3}$). Die linke Abbildung zeigt die Gesamtmasse als Funktion des Sternradius (die Masse-Radius-Relation) und stellt zusätzlich einen der berechneten Sterne als blauen Punkt dar. Das radiale Energiedichten-Profil dieses blau markierten Sterns ist in der mittleren Abbildung in Einheiten der normalen nuklearen Kerndichte $e_{\rm nuc}$ darstellt. In der rechten Abbildung ist die $g_{00}=g_{tt}$ Komponente der Metrik visualisiert, wobei (aufgrund des Birkhoff-Theorems) die innere Lösung (durchgezogene Kurve) in die äußere Schwarzschildlösung (gepunktete Kurve) stetig ineinander übergeht. Die Gesamtmasse und der Radius der Neutronensterne ändert sich bei Variation der zentralen Dichte im Stern. Wird die Dichte und als Folge dessen, die raumzeitliche Verzerrung im Sterninneren zu groß und überschreitet dieser die Maximalmasse $M_{\rm max}$, so wird der Stern instabil und kollabiert zwangsläufig zu einem schwarzen Loch (falls nicht der enorme Druck der Materie nach dem QCD-Phasenübergang zum Quark-Gluon Plasma diesen Kollaps aufhalten kann). Der Wert der maximalen Masse und der Radius der Sterne sind durch die Zustandsgleichung der Neutronenstern-Materie bestimmt und diese ist oberhalb von ca. zweifacher nuklearer Kerndichte noch nicht bekannt. Durch astrophysikalische Beobachtungen der gemessenen Neutronenstern-Eigenschaften ist es jedoch möglich die Form der Zustandsgleichung einzuschränken. Einerseits muss eine adäquate Zustandsgleichung eine maximale Masse oberhalb von zwei Sonnenmassen ermöglichen, andererseits müssen auch die mittels des NICER-Telesops beobachteten Radiuswerte (siehe NASA's Neutron star Interior Composition Explorer (NICER)) im Einklang mit den simulierten Radien sein. Bei der in der oberen Animation benutzten polytropen Zustandsgleichung $p(e)=20\,e^{\frac{5}{3}}$ ist dies nicht der Fall, da die berechneten Sterne einen zu großen Radius haben. Die Modellierung von realistischen Zustandsgleichungen ist ein aktuelles Forschungsfeld. Die Internetseite CompOSE stellt eine Reihe von Zustandsgleichungen frei zur Verfügung, die man in realistischen astrophysikalischen Simulationen verwenden kann.
Weiterführende Links

- Folien der 6.Vorlesung
- Vorlesungsaufzeichnung der 6.Vorlesung
- View Jupyter Notebook: Die Tolman-Oppenheimer-Volkoff (TOV) Gleichung
- Download Jupyter Notebook: Die Tolman-Oppenheimer-Volkoff (TOV) Gleichung
- View Jupyter Notebook: Die Innenraum-Lösung eines sphärisch symmetrischen, statischen Objektes (mit GraviPy)
- Download Jupyter Notebook: Die Innenraum-Lösung eines sphärisch symmetrischen, statischen Objektes (mit GraviPy)
- View Maple Worksheet: Die Innenraum-Lösung eines sphärisch symmetrischen, statischen Objektes
- Download Maple Worksheet: Die Innenraum-Lösung eines sphärisch symmetrischen, statischen Objektes
- NASA's Neutron star Interior Composition Explorer (NICER)
- Realistische Zustandsgleichungen auf CompOSE
- GOETHE-UNI online: Gravitational waves could prove the existence of the quark-gluon plasma
Vorlesung 6
Bis zu dieser Vorlesung hatten wir die raumzeitliche Struktur der Metrik als gegeben vorausgesetzt (Schwarzschild-Metrik bzw. Kerr-Metrik) und die Bewegungen von Probekörpern, im sonst materiefreien Raum, mittels der Geodätengleichung studiert. In dieser Vorlesung betrachten wir den umgekehrten Fall: Wie kann man anhand einer speziellen Materie/Energieverteilung im Raum zu der zugehörigen raumzeitliche Struktur gelangen. Wir betrachten im Folgenden ein statisches, sphärisch symmetrisches Objekt (in Näherung z.B. die Erde, Sonne oder ein Neutronenstern) und setzen die Metrik im Inneren wie folgt an: $$g_{\mu\nu}=\left( \begin{array}{ccc} e^{2\Phi(r)} & 0 & 0 & 0\\ 0& - \left( 1 - \frac{2 m(r)}{r} \right)^{-1}& 0&0 \\ 0& 0& -r^2& 0\\ 0& 0& 0& -r^2 \hbox{sin}^2(\theta)\\ \end{array} \right) \quad , $$ wobei die Funktionen $\phi(r)$ und $m(r)$ an dieser Stelle noch unbekannt sind, später aber eine physikalische Bedeutung erhalten. Die Materie setzen wir als eine ideale Flüssigkeit mit folgendem Energie-Impuls Tensor an: $$ T^\mu{}\!_\nu=\left( \begin{array}{ccc} e(r) & 0 & 0 & 0\\ 0& -p(r)& 0&0 \\ 0& 0& -p(r)& 0\\ 0& 0& 0& -p(r)\\ \end{array} \right) \quad , $$ wobei die Funktionen $e(r)$ und $p(r)$ die Energiedichte und den Druck der Materie darstellen. Die raumzeitliche Struktur im Inneren der Materie erhält man mittels der Einstein Gleichung $$ G^\mu{}\!_\nu = R^\mu{}\!_\nu - \frac{1}{2}g^\mu{}\!_\nu R = 8\pi T^\mu{}\!_\nu \quad,$$ die im betrachteten Fall ein System von vier gekoppelten Differentialgleichungen darstellt. Zusätzlich folgt aus der Einsteingleichung die kovariante Erhaltung des Energie-Impulses. Diese sogenannten hydrodynamischen Gleichungen sind durch die folgenden vier Gleichungen definiert: $$ \nabla\!_\mu G^\mu{}\!_\nu = 0 \quad \rightarrow \quad \nabla\!_\mu T^\mu{}\!_\nu = 0 \quad , $$ wobei die kovariante Ableitung eines Tensors zweiter Stufe wie folgt definiert ist: $$ \nabla\!_\alpha T^\mu{}\!_\nu = \partial_\alpha T^\mu{}\!_\nu + \Gamma^\mu_{\alpha \rho} T^\rho{}\!_\nu - \Gamma^\rho_{\alpha \nu} T^\mu{}\!_\rho \quad . $$ Durch Umschreiben und Kombination der Gleichungen gelangt man zu einem System von drei gekoppelten Differentialgleichungen erster Ordnung, die sogenannten Tolman-Oppenheimer-Volkoff (TOV) Gleichungen: $$ \begin{eqnarray} \frac{dm}{dr} &=& 4\pi r^2~e(r) ~, \\ \frac{d\Phi}{dr} &=& \frac{m(r)+4 \pi r^3 p(r)}{r \left(r - 2m(r) \right)} ~, \\ \frac{dp}{dr} &=& -(e(r)+p(r)) \frac{d\Phi}{dr} \end{eqnarray} $$ Die Funktion $m(r)$, welche die $g_{rr}$-Komponente der Metrik bestimmt, erhält nun ihre physikalische Bedeutung. Integriert man vom Zentrum des betrachteten Objektes die erste der TOV-Gleichungen bis zu einem Radius $r$, so beschreibt $m(r)$ den, in dieser Kugel enthaltenen, Massen/Energiebetrag $\left( m(r)=\int_0^r 4\pi \tilde{r}^2~e(\tilde{r}) \, d\tilde{r} \right)$. Die gesamte gravitativ wirkende Masse des Objektes erhält man, indem man bis zum Rand des Objektes bei $r=R$ integriert $\left( M = m(R)=\int_0^R 4\pi \tilde{r}^2~e(\tilde{r}) \, d\tilde{r} \right)$. Um die TOV-Gleichungen numerisch lösen zu können benötigt man noch die Zustandsgleichung der Materie (eine Funktion $p(e)$). Auf der linken Seite dieser Internetseite wird in einem Jupyter Notebook die analytische Herleitung der TOV-Gleichungen und deren numerische Lösung für Neutronenstern-Materie behandelt.
Vorlesung 7
Im ersten Teil dieser Vorlesung werden wir in einem Jupyter Notebook drei zusätzliche Teilaspekte der TOV-Gleichungen behandelt. Zunächst wird der Spezialfall des Gravitationsfeldes einer Kugel konstante Dichte analytisch hergeleitet und die Ergebnisse numerisch überprüft. Dannach visualisieren wir uns die gekrümmte Raumzeit eines Neutronensterns in einem eingebetteten Diagramm. Als Drittes besprechen wir das numerische Euler-Verfahren zum iterativen Lösen der TOV-Differentialgleichungen. Der zweite Teil dieser Vorlesung gibt eine Einführung in die parallele Programmierung mit C++ und OpenMP (Open Multi-Processing) / MPI (Message Passing Interface).
Gravitationsfeld einer Kugel aus inkompressibler Flüssigkeit (konstante Dichte)
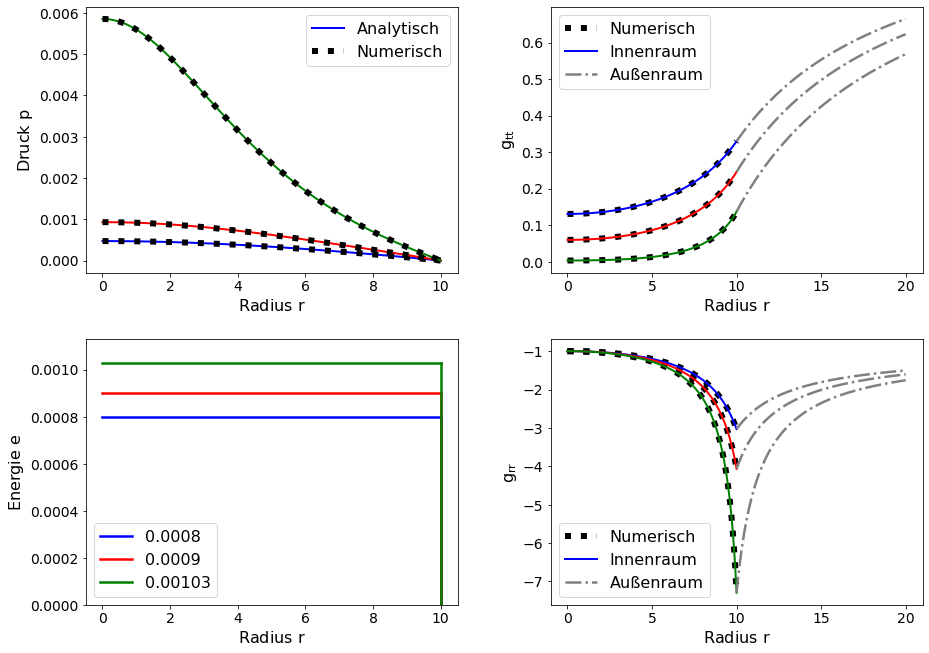
Die TOV-Gleichungen besitzen für den Spezialfall einer sphärisch symmetrischen Materieverteilung konstanter Dichte eine analytische Lösung ("Innere Schwarzschild Lösung", siehe rechtes Panel dieser Vorlesung). Die unteren Abbildungen zeigen die Eigenschaften von drei Körpern mit einem Radius $R$ von 10 km und unterschiedlicher konstanter Dichte $e_0$.
In der linken oberen Abbildung sind die drei analytischen Druckprofile und links unten die Energiedichten der "Sterne" dargestellt, wobei die schwarzen Punkte die numerisch berechneten Vergleichsrechnungen darstellen. Die rechten Abbildungen zeigen die Raumzeit-Eigenschaften im Innen- und Außenraum der Sterne (oben $g_{tt}$ und unten $g_{rr}$). Der Energiedichte Wert des grünen Sterns ist nahe dem kritischen Wert der "Buchdahl Grenze" (siehe rechtes Panel dieser Vorlesung: $R_{\rm crit}=\frac{9}{8} R_S = \frac{9}{8} \, 2 M$ $\rightarrow$ $e_{\rm crit}=\frac{1}{3 \, \pi \, R^2} \underbrace{\approx}_{R=10} 0.00106$). Der Druck im Zentrum des Sterns hat einen hohen Wert, die Metrik-Komponente $g_tt$ im Zentrum ist nahe null und die Metrik-Komponente $g_{rr}$ am Sternrand ist sehr klein. Durch Klicken auf die obere Abbildung gelangt man zu dem entsprechenden Jupyter Notebook.
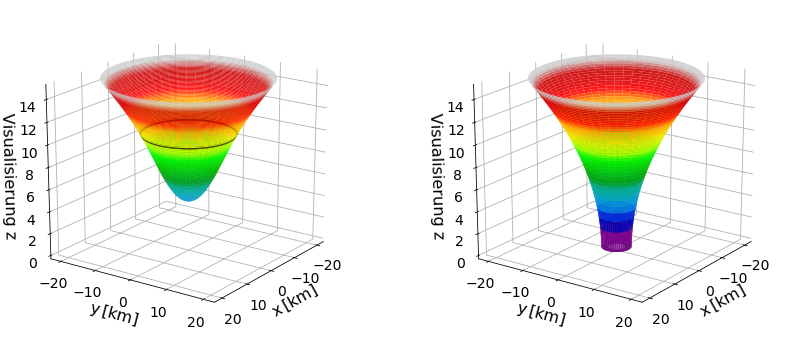
Eingebettetes Diagramm der räumlichen Hypersphäre der Mannigfaltigkeit eines Neutronensterns
Die untere rechte Abbildung zeigt das eingebettete Diagramm der räumlichen Hypersphäre $\Sigma_t$ der Mannigfaltigkeit ${\cal M}$, die durch ein massives kompaktes Objekt (beschrieben durch die TOV-Gleichungen mit polytropem Ansatz der Zustandsgleichung) gekrümmt ist. Die schwarze Linie markiert die Oberfläche des Körpers und somit die Grenze zwischen der Innenraum- und Außenraum-Metrik (Schwarzschild Metrik). In der rechten Abbildung wird zum Vergleich die räumliche Hypersphäre eines schwarzen Lochs mit gleicher Masse dargestellt. Durch Klicken auf die untere Abbildung gelangt man zu dem entsprechenden Jupyter Notebook.
Numerisches Lösen der TOV-Gleichungen mittels des Euler-Verfahrens
Die untere Animation zeigt die mittels des Python-Skripts (siehe TOV-Sequence-plot2021.py numerisch simulierten Resultate einer Sequenz von Neutronensternen mit unterschiedlichen zentralen Dichten. Das numerische Lösen der TOV-Gleichungen wurde mittels des Euler-Verfahrens gemacht (siehe rechtes Panel dieser Vorlesung).
Paralleles Programmieren mit C++ und OpenMP/MPI
Computersimulationen von realistischen, komplizierten Problemen in der Allgemeinen Relativitätstheorie (z.B. die Simulation einer Neutronenstern Kollision) erfordern, sogar auf "Supercomputern", eine enorme Rechenzeit. Bei der Konzeption der Simulationsprogramme ist es deshalb erforderlich, dass die Rechenleistung des Computers stets voll ausgelastet ist und separate, voneinander unabhängige Teilaufgaben innerhalb der Programme gleichzeitig (parallel) berechnet werden. Dieser Unterpunkt im Teil II der Vorlesung gibt eine Einführung in die parallele Programmierung mit C++ und OpenMP (Open Multi-Processing) / MPI (Message Passing Interface). Durch Klicken auf die neben stehende Abbildung gelangt man zu den entsprechenden Vortragsfolien. Am Beispiel eines einfachen numerischen Problems (der Integration einer Funktion), wird das Programmierparadigma der parallelen Programmierung erläutert. Zunächst wird ein einfaches sequentielles C++-Programm erstellt, das die Integration der Funktion $f(x)=\frac{1}{1 + a \, x^2}$ in den Grenzen [0,1] und den Werten $a \in [0,10]$ mit dem Gauß'schen Integrationsverfahren numerisch berechnet (siehe sequentielle Version 1 und sequentielle Version 2). In dem Programm wird der Wert $W(a)$ des Integrals $\int_0^1 \frac{1}{1 + a \, x^2} \, dx$ für die Parameterwerte $a \in [0,10]$ ausgegeben und mit dem analytischen Ergebnis $W(a)=\frac{{\rm arctan}(\sqrt{a})}{\sqrt{a}}$ verglichen. Die Parallelisierung dieses sequentiellen Programms wird zunächst mit OpenMP (siehe OpenMP Version 1 , OpenMP Version 2 , OpenMP Version 3 , OpenMP Version 4 und OpenMP Version 5 ) und danach mit MPI (siehe MPI Version 1 , MPI Version 2 ) durchgeführt.Weiterführende Links
Vorlesung 7
Die in der vorigen Vorlesung besprochenen TOV-Gleichungen wurden im Jahre 1939 in den folgenden zwei Arbeiten publiziert: Tolman, Richard C. "Static solutions of Einstein's field equations for spheres of fluid." Physical Review 55.4 (1939): 364. und Oppenheimer, J. Robert, and George M. Volkoff. "On massive neutron cores." Physical Review 55.4 (1939): 374.. Es ist beachtlich, dass Karl Schwarzschild bereits im Jahre 1916 einen wichtigen Spezialfall der TOV-Gleichungen analytisch berechnete. Herr Schwarzschild betrachtete einen sphärisch symmetrischen Körper mit konstanter Dichte (siehe Karl Schwarzschild, "Gravitationsfeld einer Kugel aus inkompressibler Flüssigkeit", Sitzungsberichte der Königlich-Preussischen Akademie der Wissenschaften. Reimer, Berlin 1916, S:424-434) und berechnete die Eigenschaften dieses Körpers in der Einsteins allgemeiner Relativitätstheorie. In seiner Arbeit zeigte er, dass eine solche Kugel nicht kleiner als $\frac{9}{8}$ seines Schwarzschildradius werden kann ($R > \frac{9}{8}R_S$), da sonst der Druck im Zentrum des Körpers unendlich wird. Hans Adolf Buchdahl gelang es dann im Jahre 1959 zu zeigen, das dieser Wert eine absolute Grenze der Stabilität von Körpern/Sternen darstellt, die sogenannte "Buchdahl Grenze" ( siehe Buchdahl, Hans A. "General relativistic fluid spheres." Physical Review 116.4 (1959): 1027. ). Die einzige Ausnahme sind die sogenannten "Gravastars", die auch kleiner als diese Grenze werden können. Diese besitzen jedoch einen Bereich im Stern, der eine negative Energiedichte aufweist. Im linken Panel dieser Vorlesung wird die von Schwarzschild gefundene Lösung analytisch hergeleitet und die Ergebnisse numerisch überprüft.
Die numerische Lösung der TOV-Gleichungen hatten wir bisher stets mittels der in Python vordefinierten Funktion "odeint()" berechnet. Man kann die numerische Lösung jedoch auch mittels eines einfachen iterativen Verfahrens berechnen, das sogenannte "Euler Verfahren". In diesem Verfahren schreibt man die TOV-Gleichungen wie folgt um $$ \begin{eqnarray} dm &=& 4\pi r^2 e \, dr \\ dp &=& -(e+p) \, \frac{m+4 \pi r^3 p}{r \left(r -2m \right)} \, dr \\ d\Phi &=& \frac{m+4 \pi r^3 p}{r \left(r -2m \right)} \, dr \quad , \end{eqnarray} $$ und geht nach folgendem Schema vor:
- Man definiert die Zustandsgleichung der Sternmaterie als eine Funktion e(p).
- Man startet im Sternzentrum und legt den Wert der zentralen Energiedichte und des zentralen Druckes fest. Da die TOV Gleichung bei $r=0$ singulär sind, wählt man hier einen sehr, sehr kleinen Wert (z.B. $r=10^{-14}$).
- Die TOV Gleichungen werden als Differenzengleichungen umgeschrieben und eine kleine Schrittweite $dr=\Delta r << 1$ wird festgelegt. In einer Schleife wird dann in jedem Radius-Schritt die Druck-, Massen- und $\Phi$-Änderungen berechnet ($\Delta p$, $\Delta m$ und $\Delta \Phi$) und die jeweiligen Größen beim nächsten Schritt um diesen Faktor erhöht bzw. verringert:
- Im Laufe der iterativen Lösung verringert sich der Druck ständig. Die Schleife wird so lange ausgeführt bis der Wert des Druckes gleich null bzw. negativ wird, da an der Sternoberfläche der Druck verschwindet.
Vorlesung 8
In der vorigen Vorlesung hatten wir in das parallele Programmieren mit C++ und OpenMP/MPI eingeführt und am Beispiel eines einfachen numerischen Problems (die Integration einer Funktion) die grundlegende Vorgehensweise eines OpenMP und MPI Programms kennengelernt. In dieser Vorlesung werden wir das numerische Lösen der Tolman-Oppenheimer-Volkoff (TOV Gleichungen, siehe Vorlesungen 6 und 7) mittels des Eulerverfahrens in einem C++ Programm durchführen und die besprochenen Parallelisierungsparadigmen (OpenMP und MPI) anwenden. Es wird sowohl ein sequentielles C++ Programm zur Berechnung der Eigenschaften von Neutronensternen, als auch eine mit OpenMP und MPI parallelisierte Version besprochen (siehe auch Teil II: Paralleles Programmieren mit C++ und OpenMP/MPI).
Sequentielles C++ Programm zur Berechnung der Eigenschaften von Neutronensternen durch numerisches Lösen der TOV Gleichungen mittels des Eulerverfahrens
Ausgehend von der, in der Vorlesung 6 hergeleiteten TOV Gleichung, wird mittels des einfachen Euler-Verfahrens die Differentialgleichung in C++ implementiert (siehe TOV sequentielle Version 2.1)). Die numerisch berechneten Werte des Neutronensternradius und seiner gravitativen Masse werden am Ende des Programms im Terminal ausgegeben. Die berechneten Resultate der Druck- und Energiedichtenprofile kann man mit den in der Vorlesung 6/7 mit Python (bzw. Maple) berechneten Ergebnissen vergleichen (siehe TOV sequentielle Version 2.1) mit Ausgabe der Ergebnisse in ein Textfile und Jupyter Notebook Die TOV-Gleichung: Zusätzliche Betrachtungen und Vergleich mit C++ Ergebnissen). Man kann zusätzlich, auf sequenzielle Weise, mehrere Neutronensterne bei festgelegter Zustandsgleichung berechnen. Dies wird einfach realisiert, indem man eine weitere for-Schleife über die zentrale Energiedichte einbaut. Der Hauptunterschied zur vorigen sequentiellen Version ist, das nun eine ganze Sequenz von Neutronensternen berechnet wird und man sich somit die Masse-Radius-Relation bei gegebener Zustandsgleichung vorstellen kann. Zusätzlich zur Version 2.1) werden auch noch die zentralen Werte der Metrikkomponente $g_{tt}$ berechnet und im Terminal ausgegeben (siehe TOV sequentielle Version 2.2)). Beachten Sie hier, dass im Gegensatz zu der in den Vorlesungen 6/7 benutzten Nomenklatur $g_{tt}(r)=e^{2 \, \Phi(r)}$ nun $g_{tt}(r)=e^{2 \, \nu(r)}$ benutzt wurde ($\Phi(r) \, \widehat{=} \, \nu(r)$)!
Parallele OpenMP-Version
Das sequentielle Programm 2.2) wurde nun mittels OpenMP parallelisiert (siehe TOV OpenMP Version). Hiebei wurde das OpenMP-Pragma '#pragma omp parallel for private(M,p,e,r,nu,dM,dp,de,dnu)' einfach vor die for-Schleife der unabhängigen Berechnung der einzelnen Neutronensterne geschrieben. Wichtig ist nun, dass man das Programm mit dem folgenden Befehl kompiliert: 'c++ -fopenmp TOV_parallel_omp.cpp'. Führt man das Programm mit './a.out' aus, so erkennt man als erstes, dass es, in Abhängigkeit wie viele Prozessoren (CPU-Kerne) man in seinem Computer hat, viel schneller läuft. Die im Terminal ausgegebenen Werte sind jedoch jetzt nicht mehr geordnet, sondern die Berechnung der 40 Neutronensterne erfolgt parallel und ungeordnet. Die nebenstehende Animation veranschaulicht die Vorgehensweise des OpenMP Programms. Durch Klicken auf die Bilder gelangen Sie zu der Version 2.6 : Parallele OpenMP-Version 2.6) mit geordneter Ausgabe in eine Datei und variabler Zustandsgleichung. Es werden, abhängig von der Anzahl der verfügbaren Prozessoren im Computer, mehrere Threads erzeugt, die gleichzeitig die einzelnen Aufgaben der Schleife ausführen. Das OpenMP-Pragma '#pragma omp parallel for private(M,p,e,r,nu,dM,dp,de,dnu)' vor der for-Schleife realisiert die Parallelisierung, wobei der private(...) Zusatz sicherstellt, dass die während der Berechnung benötigten Hilfsvariablen (z.B. M, dM) nicht von anderen Threads überschrieben werden. Jeder Thread greift sich einen der 150 (anz=150) zu berechnenden Neutronensterne raus, löst die TOV-Gleichung und berechnet die Masse, den Radius und die für die zentrale $g_{tt}$-Komponente nötige Größe $\nu$ des Sterns. Wenn ein Thread mit der Berechnung fertig ist, nimmt er sich den nächsten noch nicht berechneten Stern vor. Nach der parallelen Ausführung der Schleife arbeitet wieder nur ein Prozessorkern, der das restliche Programm ausführt (Ausgabe der von den unterschiedlichen Threads berechneten Ergebnisse in eine externe Datei).
Parallele MPI-Version
Die Version 2.7) Parallele MPI-Version mit geordneter Ausgabe in eine Datei und variabler Zustandsgleichung entspricht der OpenMP-Version Version 2.6), benutzt jedoch MPI und nicht OpenMP zur Parallelisierung und kann somit auch auf heutigen Großrechneranlagen, die über eine hohe Anzahl von Rechenknoten mit einer Vielzahl von CPU-Kernen verfügen, parallel ausgeführt werden. Wichtig ist nun, dass man das Programm mit dem folgenden Befehl kompiliert: 'mpic++ TOV_parallel_mpi2_eos.cpp' und es z.B. mit 'mpirun -np 6 ./a.out' ausführt ('-np 6' ist hier nur ein Beispiel und die Zahl 6 gibt die Anzahl der Prozesse an). Beim Ausführen des Programms spezifiziert somit der User mit wie vielen Prozessen er das Programm ausführen will (hier mit sechs Prozessen 'mpirun -np 6 ./a.out'). Ab diesem Zeitpunkt läuft das Programm mit sechs Prozessen, denen man im Laufe der weiteren Programmabfolge unterschiedliche Aufgaben zuweisen sollte, damit sie nicht alle das gleiche Ausführen. Die in der letzten Zeile angegebene Terminalausgabe erfolgt z.B. bei sechs Prozessen sechsmal; die Variable 'id' bezeichnet hier die fortlaufende Nummer des Prozesses (0,1,..,5). Eine sinnvolle Aufteilung der einzelnen Aufgaben des TOV-Programms auf die jeweiligen Prozesse kann man z.B. realisieren, indem die 150 (anz=150) zu berechnenden Neutronensterne auf die jeweiligen Prozesse aufteilt werden. Indem die for-Schleife von einem Prozess-abhängigen Startwert anfängt und in Schrittweiten 'psize' (Anzahl der Prozesse, hier z.B. 6) geht, rechnet jeder Prozess einen anderen Stern aus. Prozess 'id=0' rechnet z.B. die Sterne 'i=0,6,12,18,..' und Prozess 'id=4' rechnet z.B. die Sterne 'i=4,10,16,22,..' aus. Im Gegensatz zu den Threads in der OpenMP-Version, wissen die einzelnen Prozesse der MPI Version nichts über die Berechnungen und Ergebnisse der anderen Prozesse, sodass die Werte der berechneten Ergebnisse übermittelt werden müssen - dies geschieht mit einem 'MPI::COMM_WORLD.Send(...)'-Kommando. In dieser Version senden alle Prozesse ihre Ergebnisse an den Prozess mit 'id=0'. Die nebenstehende Animation veranschaulicht die Vorgehensweise des MPI Programms. Durch Klicken auf die Bilder gelangen Sie zu der Version ''2.7) Parallele MPI-Version mit geordneter Ausgabe in eine Datei und variabler Zustandsgleichung''.Weiterführende Links

Vorlesung 8
In dieser Vorlesung werden wir uns mit dem Programmierparadigma der parallelen Programmierung befassen. Wie schon am Ende der vorigen Vorlesung erwähnt, ist es bei der Konzeption von rechenintensiven Computerprogrammen wichtig, dass die Rechenleistung des Computers stets voll ausgelastet ist und separate, voneinander unabhängige Teilaufgaben innerhalb der Programme möglichst gleichzeitig (parallel) berechnet werden. Da die meisten der großen Computerprogramme im Bereich der Allgemeinen Relativitätstheorie in der Programmiersprache C/C++ geschrieben sind, werden wir die parallele Programmierung im Folgenden am Beispiel dieser Programmiersprache verdeutlichen. Die Parallelisierung eines Python-Programms ist aber natürlich auch möglich und kann z.B. mittels des Python-Moduls (threading oder multiprocessing) implementiert werden, bzw. unter Zuhilfenahme von MPI for Python realisiert werden.
Die Programmiersprachen C/C++ und Python unterscheiden sich voneinander und bei der Erstellung der Quelldateien (source codes) eines C++ Programms ist einiges zu beachten. Jede Variable, die im Programm benutzt wir muss zunächst mit einem Typ deklariert werden (z.B. "int" für eine ganze Zahl, oder "double" für eine Fließkommazahl), mit dem Präprozessorbefehl "#include" bindet man benötigte "Header-Dateien" in das Programm ein (ähnlich den Python Bibliotheken/Modulen), die Strukturierung eines C++ Programms benötigt nicht die in Python verwendete Block-Einrückung (z.B. bei for-Schleifen), sondern verwendet geschweifte Klammern und in C/C++ muss man den Quelltext mittels eines Kompilierers in ein ausführbares Programm umwandeln.
Die Art und Weise wie das parallele Programm zu konzipieren ist, hängt von der zugrundeliegenden Rechnerarchitektur des ausführenden Computers ab und man unterscheidet hier grob:
- "Shared Memory" Mehrprozessorsysteme: Mehrere Prozessoren eines Computers teilen sich einen gemeinsamen Arbeitsspeicher (RAM).
- "Distributed Memory" Mehrprozessorsysteme: Bei Hochleistungs-Großrechenanlagen sind mehrere Mehrprozessor-Computer zu Computer-Clustern verbunden, wobei jeder Computer seinen eigenen privaten Arbeitsspeicher hat.
Vorlesung 9
In dieser und der folgenden Vorlesung wird es einen Einblick in eine Softwareplattform Einstein Toolkit geben, mit der man viele komplizierte, zeitabhängige Probleme im Bereich der Allgemeinen Relativitätstheorie durch nummerische Berechnungen auf dem Computer simulieren kann. Die dem Programm zugrundeliegenden Gleichungen (Einsteingleichung und relativistische hydrodynamische Gleichungen) sind mittels des ($3+1$)-Split formuliert (siehe rechtes Panel dieser Vorlesung) und die allgemein-relativistische zeitliche Entwicklung eines Systems kann nach Angabe seiner Anfangskonfiguration in diskreten Zeitschritten simuliert werden. Diese Vorlesung gibt eine kurze Einführung in den ($3+1$)-Split und eine Vorstellung des Einstein Toolkit, wobei wir zunächst die aktuelle Bedeutung von allgemein-relativistischen Simulationen motivieren.
Eine neue Art und Weise unser Universum wahrzunehmen
Lange Zeit beschränkte sich die Erforschung astrophysikalischer Vorgänge auf mit den Augen sichtbare Ereignisse, und optische Teleskope wurden erst im 16. Jahrhundert entwickelt. Die Wahrnehmung des Universums in den anderen Frequenzbereichen der elektromagnetischen Strahlung wurde durch Radio-, Infrarot- und Röntgenteleskope ermöglicht, die erst im 20. Jahrhundert konstruiert wurden. Das gesamte wahrgenommene Bild, das wir von unserem Universum hatten, war daher auf astrophysikalische Phänomene beschränkt, die elektromagnetische Strahlung erzeugen. Dieser Umstand änderte sich im 21. Jahrhundert mit der Detektion von Gravitationswellen. Seit diesem Zeitpunkt ist es so, als hätte die Menschheit ein neues Sinnesorgan, wie eine neue wundersame Brille, mit der sie bisher nicht beobachtbare Ereignisse in unserem Universum wahrnehmen kann.Am 14. September 2015, fast genau hundert Jahre nachdem Albert Einstein die Feldgleichungen der Allgemeinen Relativitätstheorie entwickelt und die Existenz von Gravitationswellen vorhergesagt hatte, wurden diese merkwürdigen Raumzeit-Wellen von ein Paar verschmelzender Schwarzer Löcher durch die LIGO-Detektoren experimentell nachgewiesen. In den folgenden Jahren wurden drei wissenschaftliche Beobachtungsläufe durchgeführt, wobei die Ergebnisse der ersten beiden vollständig ausgewertet und veröffentlicht wurden (siehe GWTC-1). Mit den Gravitationswellendetektoren LIGO und Virgo wurden in den ersten beiden Beobachtungsläufen 11 Gravitationswellen nachgewiesen, wobei eine dieser Gravitationswellen (GW170817) durch die Kollision zweier Neutronensterne verursacht wurde, die sich vor ca. 130 Millionen Jahren ereignete. Bei diesem Ereignis wurde auch elektromagnetische Strahlung in allen anderen Frequenzbereichen emittiert und mittels unterschiedlicher Teleskope nachgewiesen. Die Gammastrahlen-Satellitenteleskope detektierten mit einer Verzögerung von 1,7 Sekunden einen hochenergetischen Gammablitz (GRB 170817A) und diese Koinzidenz des direkten Nachweises einer Gravitationswelle einer Neutronenstern-Kollision mit dem emittierten Gammastrahlenausbruch war der erste Beobachtungsbeweis, dass die Verschmelzung von binären Neutronensternen einen kurzen Gammablitz erzeugt. Die zuvor schon nummerisch simulierten Resultate einer solchen Kollision zeigen, dass nach der Verschmelzung der Sterne ein kurzzeitig metastabiler, hypermassiver Neutronenstern existiert, der dann zu einem rotierenden Kerr schwarzen Loch kollabiert, wobei die in das schwarze Loch fallende Materie einen Gammablitz erzeugt. Diese überragende übereinstimmung der simulierten Ergebnisse mit den beobachteten Daten des GW170817 und GRB 170817A Ereignisses waren ein großer Triumpf der numerischen Relativitätstheorie.
Die von LIGO und Virgo zwischen April 2019 und Oktober 2019 im dritten Beobachtungslauf beobachteten Gravitationswellen sind noch immer nur teilweise analysiert und während der ersten Hälfte dieses Beobachtungszeitraums wurden 39 Kandidaten für Gravitationswellenereignisse gefunden. GW190814 ist ein extrem asymmetrisches System, wobei ein $23$ Sonnenmassen schweres schwarzes Loch mit einem $\approx 2,6 M_\odot$ Objekt verschmilzt, das entweder das leichteste beobachtete schwarze Loch oder den schwerste Neutronenstern sein kann. GW190521 ist eine Verschmelzung zweier Schwarzer Löcher mit Massen von $85^{+21}_{-14} M_\odot$ und $66^{+17}_{-18} M_\odot$ ($m_{\rm tot}\approx 150 M_\odot$) und stellt das massivste bisher detektierte System dar. Zurzeit sind die großen Gravitationswellendetektoren abgeschaltet und werden noch empfindlicher gemacht, sodass im nächsten Beobachtungszeitraum, wahrscheinlich Anfang 2022, noch viel mehr Gravitationswellen detektiert werden können.
Einführung in das Einstein Toolkit
Das Einstein Toolkit (ET) ist eine Softwareplattform mit der man Probleme aus dem Bereich der relativistischen Astrophysik und Gravitationsphysik nummerisch am Computer simulieren kann. Das ET entwickelte sich im Jahre 1998 aus dem Cactus Code und im Laufe der letzten 20 Jahre wurde seine Performance (hocheffiziente OpenMP/MPI Parallelisierung) und Anwendungsbreite ständig verbessert. Mittlerweile kann man mit dem frei zugänglichen ET-Code Kollisionen von schwarzen Löchern und Neutronensternen simulieren und das ET besitzt sogar einen Youtube Kanal auf dem Simulationsergebnisse und Präsentationen zu diversen astrophysikalischen Themen gesammelt sind (klicken Sie dafür auf das obere nebenstehende Bild). Durch Klicken auf das mittlere Bild gelangen Sie zu einem Video, das die Entstehungsgeschichte der Programmstruktur des ET visualisiert und durch Klicken auf das untere Bild gelangen Sie zu einem Video, das eine binäre schwarze Loch Kollision simuliert (credits to SXS Collaboration). In der Vorlesung werden wir eine neuere, auch frei zugängliche Variante des ET benutzen, die von Dr. David Radice entwickelte wurde und die sich vom gewöhnlichen ET lediglich im nummerischen Verfahren der hydrodynamischen Gleichungen unterscheidet (siehe ET-WhiskyTHC: the General-Relativistic Templated Hydrodynamics Code).Weiterführende Links

- Folien der 9.Vorlesung
- Vorlesungsaufzeichnung der 9.Vorlesung
- Das Einstein Toolkit
- LIGO: Laser Interferometer Gravitational-Wave Observatory
- Gravitationswellendetektor GEO600
- Gravitationswellendetektor Virgo
- Gravitationswellendetektor KAGRA
- Under construction: Gravitationswellendetektor LIGO-India
- Under construction: Laser Interferometer Space Antenna (LISA)
- Geplant: Das Einstein-Teleskop
- Geplant: The Cosmic Explorer
Vorlesung 9
In den bisherigen Vorlesungen, sowohl bei der Analyse der Bewegungen um ein rotierendes/nicht-rotierendes schwarzes Loch als auch bei der Berechnung der Eigenschaften von Neutronensternen, hatten wir zeitunabhängige Raumzeiten betrachtet. Die zugrundeliegende Metrik $g_{\mu\nu}$ der betrachteten 4-dimensionale Mannigfaltigkeit ${\cal M}$ veränderte sich nicht mit der Zeit und hatte eine vorgegebene räumliche Symmetrie. In dieser und der folgenden Vorlesung wird es einen Einblick in eine Softwareplattform geben (das sogenannte Einstein Toolkit) mit der man zeitabhängige allgemein-relativistische Berechnungen, wie z.B. die Kollision zweier Neutronensterne durchführen kann. Realistische astrophysikalische Computersimulationen müssen die Einstein- und die zugehörigen hydrodynamischen Gleichungen ohne spezielle Symmetrie-Annahmen zeitabhängig lösen. Um dies auf dem Computer zu realisieren, ist es nötig die zugrundeliegenden Gleichungen umzuschreiben. Diese Neuformulierung der Einsteingleichung benutzt den sogenannten ($3+1$)-Split und teilt mit diesem die 4-dimensionale Mannigfaltigkeit ${\cal M}$ in 3-dimensionale raumartige Hyperflächen $\Sigma_t$ auf. Die Raumzeit Metrik $g_{\mu\nu}$ wird dadurch in eine rein räumliche Metrik $\gamma_{ij}$, eine Lapse-Funktion $\alpha$ und einen Verschiebungsvektor $\beta_i$ (Shift-Vektor) unterteilt ($i=1,2,3$): \[ \begin{equation} g_{\mu\nu} ~=~ \begin{pmatrix} -\alpha^2+\beta_i\beta^i & \beta_i \\ \beta_i & \gamma_{ij} \end{pmatrix} \end{equation} \] Die Lapse-Funktion $\alpha$ beschreibt die Differenz zwischen der Koordinatenzeit $t$ und der Eigenzeit $\tau$ eines Teilchens ($d\tau=\alpha ~ dt $). Der Verschiebungsvektor $\beta_i$ misst, wie die Koordinaten auf der raumartigen Hyperfläche $\Sigma_t$ verschoben werden, wenn sich das Teilchen einen infinitesimalen Zeitschritt weiter bewegt. Durch Einfügen dieses Ansatzes der Metrik in die Einstein Gleichung kann man die Gleichungen in ein System von Differentialgleichungen erster Ordnung umformulieren -- die sogenannten ADM-Gleichungen (benannt nach seinen Autoren Richard Arnowitt, Stanley Deser und Charles W. Misner). Da die ADM Gleichungen nicht ''well posed'' sind und sich kleine nummerische Störungen exponentiell aufschaukeln könnten, muss man diese noch weiter mittels einer konformen Transformation der Metrik umschreiben. Die Baumgarte-Shapiro-Shibata-Nakamura-Oohara-Kojima (BSSNOK) - Formulierung der allgemeinen Relativitätstheorie (oder alternativ die CCZ4-Formulierung) ist zusammen mit den relativistischen hydrodynamischen Gleichungen (unter Verwendung der Valencia-Formulierung) als Grundgleichungen in der Softwareplattform Einstein Toolkit implementiert. Das Programm benötigt die vom Benutzer spezifizierte Anfangshyperfläche $\Sigma_0$ und rechnet dann iterativ in Zeitabschnitten $dt$ die dynamische Evolution des betrachteten Systems. Die untere Abbildung visualisiert das besprochene Konzept der ($3+1$) Zerlegung der Raumzeit (Credits: L. Rezzolla, O. Zanotti: Relativistic Hydrodynamics, Oxford Univ. Press (2013)).
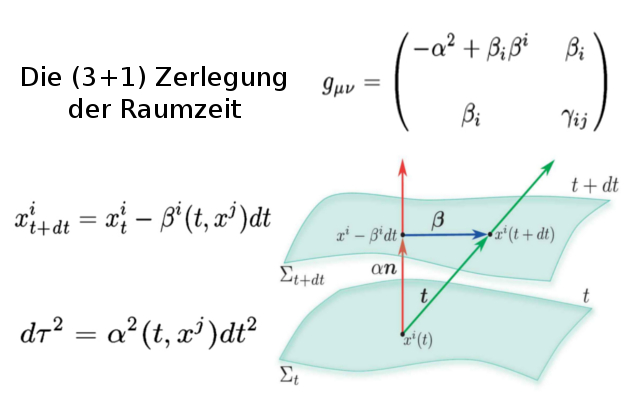
Vorlesung 10
In dieser Vorlesung werden wir das Einstein Toolkit näher betrachten und es wird gezeigt, wie man mit dem ET zeitabhängige allgemein-relativistische Simulationen einer Kollision zweier Neutronensterne durchführt und die Ergebnisse dann visualisiert. Am Ende dieser Vorlesung werden aktuelle Forschungsergebnisse besprochen und aufgezeigt, wie man mittels zukünftig detektierter Gravitationswellen von Neutronenstern Kollisionen den Hadron-Quark Phasenübergang studieren kann.
Computersimulationen mit dem Einstein Toolkit
Am Beispiel einer Neutronenstern Kollision Simulation werden die einzelnen nötigen Schritte erläutert, die man bei einer Computersimulation mit dem ET auszuführen hat. Zunächst muss man das ET (bzw. das ET-WhiskyTHC) herunterladen (siehe Download ET bzw. Download ET-WhiskyTHC) und installieren/kompilieren. Das so erzeugte ausführbare Programm benötigt nun die Anweisungen des Benutzers, was im Speziellen simuliert werden soll; dies geschieht in der sogenannten .par Datei (siehe z.B. .par file: Kollaps eines Neutronensterns zu einem schwarzen Loch). Neben der Spezifikation der Zustandsgleichung der Materie benötigt man bei einer binären Neutronenstern Kollision zusätzlich noch die Dichteverteilung auf der initialen Raumzeit-Hyperfläche ($\Sigma_0$) - diese wird meist mit dem separatem Programm LORENE erzeugt. Beim Starten einer Simulation muss die spezielle Architektur des zugrundeliegenden Computers/Computerclusters bei der Angabe der Parallelisierungsprozesse beachtet werden, wobei dies durch die Benutzung des im ET implementierten Teilprogrammes Simfactory erleichtert wird.
Visualisierung der Simulationsergebnisse
Die in der .par Datei definierten Output-Variablen können nach Beendigung der Simulation mittels unterschiedlicher Programme dargestellt werden. Um die Simulationsergebnisse mitOft wird auch die Programmiersprache
Neutronenstern Kollisionen und das Phasendiagramm der Quantenchromodynamik
Eine Neutronenstern Kollision kann grob in drei möglichen Szenarien ablaufen: Falls die Anfangsmasse der Sterne groß ist, kollabiert das System gleich nach der Kollision zu einem schwarzen Loch, falls die Anfangsmasse in einem mittleren Bereich liegt, bildet sich zunächst ein sogenannter hypermassiver Neutronenstern, der dann (nach einigen Millisekunden) zu einem schwarzen Loch kollabiert. Bei einer geringen Anfangsmasse bildet sich zunächst ein sogenannter supramassiver Neutronenstern, der sich dann zu einem gleichförmig, sehr schnell rotierenden Neutronenstern entwickelt.Die Dichte in einem hypermassiven Neutronenstern erreicht enorm große Werte und die im inneren Bereich befindlichen Neutronen werden eng aneinander gedrückt, sodas ihre Quark-Unterstruktur zum Vorschein tritt - einen solchen Stern nennt man dann einen hypermassiven hybriden Stern. Es ereignet sich somit ein Phasenübergang von hadronischen Teichen (in denen die Quarks noch eingesperrt sind) zu befreiter Quarkmaterie - der sogenannte Phasenübergang der Quantenchromodynamik (QCD). In aktuellen Computersimulationen von Kollisionen von Neutronensternen wird ein solcher Phasenübergang in der Zustandsgleichung der Materie berücksichtigt und anhand der emittierten Gravitationswelle wird es wohl in Zukunft möglich sein den Hadron-Quark Phasenübergang zu studieren.
Die Eigenschaften eines möglichen Hadron-Quark Phasenüberganges lassen sich z.B. gut analysieren, falls sich dieser erst in der Merengue Phase (siehe rechtes Panel dieser Vorlesung) ereignet und der dann entstehende hypermassive hybride Stern ein metastabiler Zustand ist (siehe "Delayed phase transition": Lukas R. Weih, Matthias Hanauske, and Luciano Rezzolla, ''Postmerger Gravitational-Wave Signatures of Phase Transitions in Binary Mergers'', Phys. Rev. Lett. 124, 171103 (2020)). Ein starker Phasenübergang in der Merengue Phase, würde die charakteristische $f_2$-Frequenz der emittierten Gravitationswelle in einer Art und Weise ansteigen lassen, anhand dessen man die Eigenschaften des Hadron-Quark Phasenüberganges bestimmen könnte.
Weiterführende Links
- Folien der 10.Vorlesung
- Vorlesungsaufzeichnung der 10.Vorlesung
- Teil III der Vorlesung
- View Jupyter Notebook: Neutronenstern Kollisionen mit dem Einstein Toolkit
- Download Jupyter Notebook: Neutronenstern Kollisionen mit dem Einstein Toolkit
- Tanz der Neutronensterne
- Tanz der Neutronensterne (Night of Science 2018, VR-Video)
- Matthias Hanauske, Kentaro Takami, Luke Bovard, Luciano Rezzolla, Jose A Font, Filippo Galeazzi, Horst Stöcker, "Rotational properties of hypermassive neutron stars from binary mergers", PRD 96.4 (2017): 043004.
- M. Hanauske, and L. Bovard, "Neutron star mergers in the context of the hadron-quark phase transition", Journal of Astrophysics and Astronomy 39.4 (2018): 1-11.
- Gloria Montana, Matthias Hanauske, and Luciano Rezzolla. "Constraining twin stars with GW170817." Physical Review D 99.10 (2019): 103009.
- Matthias Hanauske, Jan Steinheimer, Anton Motornenko, Volodymyr Vovchenko, Luke Bovard, Elias R Most, L Jens Papenfort, Stefan Schramm, Horst Stöcker, "Neutron star mergers: probing the EoS of hot, dense matter by gravitational waves." Particles 2.1 (2019): 44-56.
- Matthias Hanauske, Luke Bovard, Elias Most, Jens Papenfort, Jan Steinheimer, Anton Motornenko, Volodymyr Vovchenko, Veronica Dexheimer, Stefan Schramm, Horst Stöcker, "Detecting the hadron-quark phase transition with gravitational waves", Universe 5.6 (2019): 156.
- Elias R Most, L Jens Papenfort, Veronica Dexheimer, Matthias Hanauske, Stefan Schramm, Horst Stöcker, Luciano Rezzolla, "Signatures of quark-hadron phase transitions in general-relativistic neutron-star mergers", PRL 122(6) (2019), 061101.
- Elias R Most, L Jens Papenfort, Veronica Dexheimer, Matthias Hanauske, Horst Stoecker, Luciano Rezzolla, "On the deconfinement phase transition in neutron-star mergers." The European Physical Journal A 56.2 (2020): 1-11.
- M.Hanauske and H.Stöcker, ''Binary Compact Star Mergers and the Phase Diagram of Quantum Chromodynamics'', Discoveries at the Frontiers of Science, Springer (2020)
- Lukas R. Weih, Matthias Hanauske, and Luciano Rezzolla. "Postmerger gravitational-wave signatures of phase transitions in binary mergers." Physical review letters 124.17 (2020): 171103.
- Motornenko Anton, Hanauske Matthias, Weih Lukas, Steinheimer Jan, Stöcker Horst, "MAGIC: Matter in Astrophysics, Gravitational Waves, and Ion Collisions", Nuclear Physics Review, 37.3 (2020): 272-282.
- Hanauske, Matthias, Lukas R. Weih, Horst Stöcker, and Luciano Rezzolla. "Metastable hypermassive hybrid stars as neutron-star merger remnants." The European Physical Journal Special Topics (2021): 1-8.
Vorlesung 10
Am Ende der vorigen Vorlesung wurden die mittels der Gravitationswellen Detektoren beobachteten Gravitationswellen diskutiert. Zwei (vielleicht drei) der detektierten Gravitationswellen stammen von Neutronenstern Kollisionen (siehe GW170817, GW190425 und vielleicht GW190814). Mittels der in dieser und der vorigen Vorlesung dargestellten Softwareplattform Einstein Toolkit können z.B. auch binäre Neutronenstern Kollisionen auf dem Computer simuliert werden und man kann die berechneten Ergebnisse mit den astrophysikalisch observablen Größen der beobachteten Gravitationswellen der Neutronenstern Kollisionen vergleichen. Mittels einer solchen Analyse wird es in naher Zukunft möglich sein die Eigenschaften der elementaren Materie mittels der Gravitationswellen Detektoren zu studieren (z.B. die Eigenschaften, des von der Quantenchromodynamik vorhergesagten Hadron-Quark Phasenübergangs). Eine Kollision zweier Neutronensterne lässt sich in einzelne Phasen gliedern und das untere Video illustriert die unterschiedlichen Phasen einer binären Neutronenstern Kollision und die Dynamik des entstehenden hypermassiven Neutronensterns anhand eines Sammelsurium einzelner klassischer Tänze.
Die einzelnen Phasen werden z.B. in M.Hanauske and H.Stöcker, ''Binary Compact Star Mergers and the Phase Diagram of Quantum Chromodynamics'', Discoveries at the Frontiers of Science, Springer (2020) beschrieben. Die in dem Video verwendete Zustandsgleichung ermöglicht leider eine nur kurze Diskofox Phase, da die für diese Phase nötige ''double core'' Struktur des hypermassiven Neutronensterns nur kurz nach der Kollision auftritt. Unter Verwendung von anderen Zustandsgleichung kann die Diskofox Phase länger erhalten bleiben (siehe z.B. zweiter Tanz). Im linken Panel dieser Vorlesung werden die Simulationsergebnisse von Neutronenstern Kollisionen visualisiert und analysiert. Anhand der emittierten Gravitationswelle kann man die Eigenschaften der elementaren Materie bei hohen Dichten und Temperaturen studieren.
Vorlesung 11 - 14


Studentische Projekte
Mündliche Prüfung
Die mündlichen Prüfungen werden ebenfalls mittels der Zoom Meeting Software stattfinden, haben eine Dauer von ca. 30 Minuten und Sie dürfen alle auf der Homepage der Vorlesung befindlichen Hilfsmittel verwenden.Prüfungsrelevante Themen
Einstein Gleichung; Geodäten Gleichung; Berechnung von Christoffel Symbolen, Riemann Tensor, Ricci Tensor bei vorgegebener Metrik unter Verwendung von Maple/Python.
Eigenschaften eines nicht-rotierenden schwarzen Loches (Schwarzschild Raumzeit, Raumzeit Diagramme, eingebettetes Diagramm, Ereignishorizont, Photonensphäre). Bewegung eines massiven Probekörpers um ein nicht-rotierendes schwarzes Loch (Veranschaulichung der möglichen Bahnbewegungen mittels eines effektiven Potentials). Die innerste stabile kreisförmige Bahnbewegung eines Probekörpers (ISCO). Bewegung von masselosen Probekörpern (Licht) um ein nich-trotierendes schwarzes Loch, die Photonensphäre.
Rotierende schwarze Löcher (Kerr Metrik): Struktur der Ereignishorizonte und die Flächen der stationären Grenze. Was ist die Ergosphäre? Was bedeutet der Mitführungseffekt der Raumzeit (frame dragging)? Die innerste stabile kreisförmige Bahnbewegung eines massiven Probekörpers um ein rotierendes schwarzes Loch. Das erste Bild eines schwarzen Loches in M87*.
Neutronensterne: Wie gelangt man zur Tolman Oppenheimer Volkoff Gleichung (TOV) und was kann man mit dieser Gleichung berechnen? Wie löst man die TOV-Gleichungen nummerisch? Masse-Radius Relation einer Sequenz von Neutronensternen und die maximale Masse von Neutronensternen. Gravitationsfeld einer Kugel konstanter Dichte (innere Schwarzschild-Metrik).
Was ist parallele Programmierung und wie parallelisiert man ein Programm? Wie unterscheidet sich OpenMP von MPI?
Computersimulationen mit dem Einstein Toolkit. Phasen einer binären Neutronenstern Kollision und die in diesem Prozess ausgesandten Gravitationswellen. Beobachtete Gravitationswellen.
Vorlesung 11 - 14
Studentische Projekte



Die studentischen Projekte können alleine oder in Gruppen (bis zu vier Personen) durchgeführt werden. Under construction ...