ID: 794 847 5614 , PWD: 785453
Vorwort
Die Vorlesung Allgemeine Relativiätstheorie mit dem Computer wurde im Sommersemester 2016 das erste Mal gehalten und viele der auf dieser Hauptseite erreichbaren Internetseiten basieren grundsätzlich auf dem damals erstellten Kurs. Das nebenstehende, einührende Video (ist in Arbeit!) behandelt generelle Fragen zur Vorlesung. Es werden die Vorraussetzungen (technische und inhaltliche) dargestellt, die man benötigt um an der Online-Vorlesung und den zugehörigen Übungseinheiten teilzunehmen zu können um dadurch einen benoteten bzw. unbenotenden Schein mit drei Creditpoints zu erhalten.
Weiterführende Links

Allgemeine Relativitätstheorie mit dem Computer
(General Theory of Relativity on the Computer)
Vorlesung SS 2020
Augrund der Corona Krise findet die Vorlesung und die freiwilligen Übungstermine in diesem Semester nur Online statt!
Diese Internetseite fasst die Online-Angebote der Vorlesung Allgemeine Relativitätstheorie mit dem Computer zusammen. Auf der linken Seite finden Sie die einzelnen Vorlesungsaufzeichnungen (Videos), Vorlesungspräsentationen (pdf-Dateien) und weiterführende Links. Die Vorlesungstermine (Zoom Meetings, synchrones Lehrangebot) finden jeweils freitags von 15.15-16.45 Uhr statt und dienen zur Wissenvermittlung, gemeinsamen Nachbereitung der Vorlesungsinhalte und Bearbeitung der Übungsaufgaben. Zusätzlich werden freiwillige Online-Übungstermine eingerichtet, die als Diskussions und Frageforum genutzt werden können. Die gemeinsamen, syncronen Lehrangebote werden mittel der Zoom Meeting Software gemacht und die jeweiligen Zoom-Links werden in der rechten oberen Ecke dieser Internetseite angegeben.
Die Inhalte der Vorlesung gliedern sich in drei Teile (Teil I, Teil II, Teil III), die Sie in der zweiten oberen Spalte einsehen können. Weiteres Zusatzmaterial und diverse Online-Aufgaben sind über die Online-Lernplatform Lon Capa erhältlich (siehe E-Learning).
Vorlesung 1
In der ersten Vorlesung werden die Grundlagen der allgemeinen Relativitätstheorie wiederholt und es wird einen Überblick der Inhalte der gesamten Vorlesung geben. Die grundlegenden Gleichungen der allgemeinen Relativitätstheorie und im besonderen die Einsteingleichung und die Geodatengleichung werden kurz wiederholt. Die Eigenschaften von schwarzen Löchern werden anschaulich illustriert und das erste Bild des schwarzen Lochs im Zentrum unserer Nachbargalaxie M87 wird diskutiert. Gravitationswellen, verursacht durch Kollisionen von schwarzen Löchern und Neutronensternen werden seit ca. 5 Jahren mittels der Gravitationswellen Detektoren Ligo und Virgo beobachtet. Am Ende wird es eine kurze Einfürung in das Computeralgebra-System Maple geben mit welchem wir in Teil 1 einfache Probleme der allgemeinen Relativitätstheorie berechnen und simulieren werden.
Vorlesung 2
Bevor wir uns mit der allgemeinen Relativitätstheorie beschäftigen können werden in der Vorlesung 2 einige technische Dinge erläutert:
Wie mache ich von zuhause einen Remote Login auf den Server des ITP?
Das nebenstehende Video beschreibt die einzelnen Schritte wie man einen Remote Login von einem Linux Betriebssystem zum Server des Instituts für Theoretische Physik (ITP) der Goethe Universität aufbaut (weiteres siehe Graphical Remote Login with xrdp). Sie benötigen hierzu einen Account für die Rechner des ITP (wurde Ihnen per e-mail an Sie versendet; falls nicht, dann melden Sie sich bitte). Mittels des Remote Login können Sie sich durch einen Fernzugriff auf den Desktop des Servers des ITP verbinden und Anwendungsprogramme (z.B. Maple oder Mathematica) oder Simulationsprogramme (z.B. C++ oder Python) ausgeführen und auf Ihrem Computer dargestellen. Zusätzlich wird am Ende des Videos gezeigt wie man das Passwort des eigenen ITP-Account ändert (empfohlen!), das Computeralgebra-System Maple startet und wie man sich wieder vom Server des ITP abmeldet.
Wie führe ich eines der Maple-Worksheets aus Teil I auf dem Server des ITP aus?
Das nebenstehende Video beschreibt die einzelnen Schritte wie man ein Maple-Worksheets aus Teil I startet und Berechnungen ausführt und leicht abändert (Maple-Worksheet aus Teil I: Maple Tutorium).
Allgemeine Relativitätstheorie mit Maple und Mathematica
Zunächst werden die grundlegende Größen der allgemeinen Relativitätstheorie (z.B. die Metrik der Raumzeit, Christoffel Symbole, Ricci- und Einstein-Tensor) am Beispiel einer allgemeinen statischen und isotropen Raumzeit in Maple berechnet. Dannach werden diese Größen für den speziellen Fall der Schwarzschild Metrik betrachtet und das zugehörige Raumzeitdiagramm in Schwarzschild und Eddington-Finkelstein Koordinaten visualisiert (siehe Maple-Worksheet aus Teil I: Grundlegende Größen der Allgemeinen Relativitätstheorie, die Schwarzschildmetrik und Raumzeitdiagramme).Ist eine die raumzeitliche Struktur in Form einer Metrik vorgegeben, so beschreibt die Geodätengleichung wie sich ein Körper in dieser Raumzeit zu bewegen hat. Es wird die Geodätengleichung in vorgegebener Schwarzschild Raumzeit für den speziellen Fall eines radial in ein schwarzes Loch einfallender Probekörper in Maple berechnet und die Bewegung eines Probekörpers um ein schwarzes Loch in der Ebene betrachtet (siehe Maple-Worksheet aus Teil I: Die Geodätengleichung in vorgegebener Schwarzschild Raumzeit , Radial in ein schwarzes Loch einfallender Probekörper, Bewegung eines Probekörpers um ein schwarzes Loch in der Ebene, bzw. Mathematica Version aus Teil I).
Lon Capa Übungsaufgaben
Das nebenstehende Video beschreibt wie man die individualisierten Übungsaufgaben auf der Online-Lernplatform Lon Capa bearbeitet.
Vorlesung 2
Es werden im folgenden die Grundlagen der allgemeinen Relativitätstheorie und im besonderen die Einsteingleichung
\[
R_{\mu\nu} - \frac{1}{2} g_{\mu\nu} R ~=~ -8 \pi \, T_{\mu\nu}
\]
und die Geodatengleichung
\[
\frac{d^2 x^\mu}{d\tau^2} + \Gamma^\mu_{\nu \rho} \frac{d x^\nu}{d\tau} \frac{d x^\rho}{d\tau} ~=~ 0
\]
als bekannt vorausgesetzt. Die griechischen, raumzeitlichen Indices $ \mu, \nu, \rho ... $ laufen von 0..3, wobei, falls nicht anders angegeben, diese den folgenden kartesischen Raumzeitkoordinaten entsprechen: $ x^\mu = \left( x^0, x^1, x^2, x^3 \right) = \left( t, x, y, z \right)$. Grundlegende Größen der allgemeinen Relativitätstheorie (z.B. die Metrik der Raumzeit, Christoffel Symbole, Ricci- und Einstein-Tensor) werden am Beispiel einer allgemeinen statischen und isotropen Raumzeit in Maple berechnet. Wir definieren z.B. die kovariante Metrik einer allgemeinen statischen, isotropen Raumzeit $ g_{\mu\nu} $, wobei wir ein sphärisches Koordinatensystem benutzen:
\[ g_{\mu\nu}=\left( \begin{array}{ccc} A(r) & 0 & 0 & 0\\ 0& -B(r)& 0&0 \\ 0& 0& -r^2& 0\\ 0& 0& 0& -r^2 \hbox{sin}^2(\theta)\\ \end{array} \right)
\]
, wobei $x^\mu=\left(t,r,\theta,\phi \right)$. Wie sehen die Christoffel Symbole (erste Art $\Gamma_{\mu \nu \rho}$, vollständig kontravariante Form)
\[
\Gamma_{\mu \nu \rho} = \frac{1}{2} \left( \partial_{\!\!\;\mu} g_{\nu \rho} + \partial_{\!\!\;\nu} g_{\mu \rho} - \partial_{\!\!\;\rho} g_{\mu \nu} \right) = \frac{1}{2} \left( g_{\nu \rho |\mu} + g_{\mu \rho |\nu} - g_{\mu \nu |\rho} \right)
\]
, (zweite Art $\Gamma^\mu_{\nu\rho}$)
\[
\Gamma^\mu_{\nu\rho} = g^{\mu\delta} \Gamma_{\nu \rho \delta} = \frac{1}{2} g^{\mu\delta} \left( g_{\delta \nu |\rho} + g_{\delta \rho |\nu} - g_{\nu \rho |\delta} \right)
\]
, der Riemann Tensor $R{^\mu}_{\nu\alpha\beta}$,
\[
R{^\mu}_{\nu\alpha\beta} = \Gamma^\mu_{\nu\beta|\alpha} - \Gamma^\mu_{\nu\alpha|\beta} + \Gamma^\mu_{\lambda\alpha} \Gamma^\lambda_{\nu\beta} - \Gamma^\mu_{\lambda\beta} \Gamma^\lambda_{\nu\alpha}
\]
, der Ricci Tensor $R_{\mu\nu}= g^{\alpha\beta} R_{\alpha\mu\beta\nu}$ und der Ricci Skalar $R=g^{\mu\nu} R_{\mu\nu}$ aus?
Mit den Computeralgebra-Systemen Maple und Mathematica und der Programmiersprache Python lassen sich auch komplizierte Berechnungen im Bereich der allgemeinen Relativitätstheorie einfach berechnen.
Vorlesung 3
Bevor wir die Geodätengleichung und die Klassifikation möglicher Bahnen von Probekörpern mittels eines definierten effektiven Potentials in vorgegebener Schwarzschild-Raumzeit behandeln, wird gezeigt, wie man die grundlegenden Größen der allgemeinen Relativitätstheorie in Python berechnet.
Allgemeine Relativitätstheorie mit Python (grundlegenden Größen der ART)
Beim Klicken auf das nebenstehende Bild werden die grundlegenden Größen der allgemeinen Relativitätstheorie (z.B. die Metrik der Raumzeit, Christoffel Symbole, Ricci- und Einstein-Tensor) am Beispiel einer allgemeinen statischen und isotropen Raumzeit in Python berechnen (hier die .pdf Version). Das ensprechende Python Jupyter Notebook (Grundlegende Größen der ART in Python) basiert auf dem Python Tensor Paket GraviPy. GraviPy kann einfach mit pip install gravipy installiert werden und stellt zusammen mit dem Paket SymPy ein wichtiges Tool der Computer Algebra Systeme im Bereich der allgemeinen Relativitätstheorie dar. Die nebenstehenden und im folgenden dargestellten Jupyter Notebooks basieren auf dem GraviPy-Tutorium (GraviPy-tutorial.ipynb).
Allgemeine Relativitätstheorie mit Python (Schwarzschild Raumzeit, Geodätengleichung und Differentialgleichungen)
Beim Klicken auf das nebenstehende Bild wird die Bewegung eines Probekörpers um ein nicht-rotierendes schwarzes Loch in der Ebene (Schwarzschild Metrik) in Python berechnet (hier die .pdf Version). In diesem Python Jupyter Notebook (Bewegung eines Probekörpers um ein schwarzes Loch in der Ebene (Version 1)) werden zunächst die grundlegenden Größen der ART für die Schwarzschild Raumzeit und dannach die Geodätengleichung berechnet. Die Geodätengleichung stellt ein System gekoppelter Differentialgleichungen zweiter Ordnung, wobei dessen Lösung sich nicht in analytischer Form angeben lässt und deshalb numerisch mit dem Computer berechnet werden muss (näheres siehe nächste Vorlesung). Eine kurze Einführung in das Lösen von Differentialgleichungen in Python (analytisch und numerisch) findet sich am Ende des nebenstehenden Jupyter Notebooks.
Bewegung eines Probekörpers um ein nicht-rotierendes schwarzes Loch und die Klassifikation möglicher Bahnen mittels eines definierten effektiven Potentials (Maple)
Die unterschiedlichen Bahnbewegungen um ein nicht-rotierendes schwarzes Loch lassen sich mittels eines effektiven Potentials klassifizieren (siehe nebenstehende Animation und rechtes Panel dieser Vorlesung). Neben den gebundenen kreisförmigen (blau) und elliptischen Bahnen (rot), den parabolischen (grün) und hyperbolischen (grau) Bahnverläufen ist auch eine durch das schwarze Loch eingefangene Bahn (capture orbit, schwarz) möglich (siehe Maple-Worksheet aus Teil I: Bewegung eines Probekörpers um ein schwarzes Loch in der Ebene (Version 2).
Literatur

Vorlesung 3
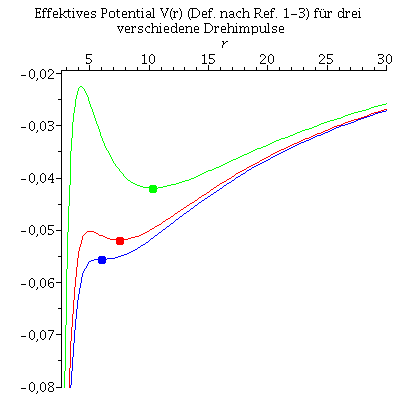
Wir betrachten im folgenden die Geodätengleichung \[ \frac{d^2 x^\mu}{d\tau^2} + \Gamma^\mu_{\nu \rho} \frac{d x^\nu}{d\tau} \frac{d x^\rho}{d\tau} ~=~ 0 \] in vorgegebener Schwarzschild-Raumzeit \[ g_{\mu\nu}=\left( \begin{array}{ccc} 1-\frac{2\,M}{r} & 0 & 0 & 0\\ 0& -\frac{1}{1-\frac{2\,M}{r}}& 0&0 \\ 0& 0& -r^2& 0\\ 0& 0& 0& -r^2 \hbox{sin}^2(\theta)\\ \end{array} \right) \] , wobei wir wieder ein sphärisches Koordinatensystem benutzen ($x^\mu=\left(t,r,\theta,\phi \right)$). Die Geodätengleichung stellt ein System gekoppelter nichtlinearer Differentialgleichungen dar \[ \begin{eqnarray} && \frac{d^2 t}{d\lambda^2} = - \Gamma^0_{\nu \rho} \frac{d x^\nu}{d\lambda} \frac{d x^\rho}{d\lambda} \\ && \frac{d^2 r}{d\lambda^2} = - \Gamma^1_{\nu \rho} \frac{d x^\nu}{d\lambda} \frac{d x^\rho}{d\lambda}\\ && \frac{d^2 \theta}{d\lambda^2} = - \Gamma^2_{\nu \rho} \frac{d x^\nu}{d\lambda} \frac{d x^\rho}{d\lambda}\\ && \frac{d^2 \phi}{d\lambda^2} = - \Gamma^3_{\nu \rho} \frac{d x^\nu}{d\lambda} \frac{d x^\rho}{d\lambda} \quad , \end{eqnarray} \] wobei $\lambda$ ein affiner Parameter (z.B. die Eigenzeit $\tau$), t, r, $\theta$ und $\phi$ die Koordinaten und $\Gamma^\mu_{\nu \rho}$ die Christoffel Symbole zweiter Art darstellen. Man kann zeigen (siehe z.B. Seite 206 in General relativity : An introduction for physicists by M. P. Hobson, G. P. Efstathiou and A. N. Lasenby), dass sich die erste und vierte Gleichung dieses Systems von Differentialgleichungen in die folgenden Gleichungen umschreiben läßt: \[ \begin{eqnarray} \hbox{1. Gleichung:}&& \frac{d}{d\lambda} \left[ \left( 1 - \frac{2 M}{r} \right) \frac{dt}{d\lambda} \right] = 0 \\ \rightarrow && \left( 1 - \frac{2 M}{r} \right) \frac{dt}{d\lambda} = E = \hbox{const} \\ \hbox{2. Gleichung:}&& \frac{d}{d\lambda} \left( r^2 \hbox{sin}^2(\theta) \frac{d\phi}{d\lambda} \right) = 0 \\ \rightarrow && r^2 \hbox{sin}^2(\theta) \frac{d\phi}{d\lambda} = l = \hbox{const} \quad , \end{eqnarray} \] wobei die während der Bewegungen erhaltenen Größen E (Teilchenenergie pro Masse) und l (Drehimpuls pro Masse m) sich aus der Definition des Viererimpulses $p_\mu = m u_\mu$ ergeben. Die Klassifikation möglicher Bahnen von Probekörpern in vorgegebener Schwarzschild-Raumzeit kann mittels eines definierten effektiven Potentials illustriert werden. Dieses Potential hängt von dem, bei der Bewegung erhaltenen Drehimpuls pro Masse m ab. Die im Zentralfeld möglichen Bewegungen werden mittels zweier erhaltener Größen (l: Drehimpuls pro Masse m und E: Energie pro Masse) charakterisiert. Die Definition des effektiven Potential erfolgt mittels der radialen, 2. Geodätengleichung. So definieren z.B. die Literaturangaben 1-3 (siehe Literatur im linken Panel) das effektive Potentail wie folgt: \[ \begin{eqnarray} \hbox{2. Gleichung:}&\rightarrow&\frac{1}{2} \left( \frac{dr}{d\tau} \right)^2 + V(r,M,l) = \frac{1}{2} \left( E^2 -1 \right) \\ \hbox{wobei:} && V(r,M,l) = \frac{l^2}{2 r^2} \left( 1 - \frac{2 M}{r} \right) - \frac{M}{r} \quad . \end{eqnarray} \] In der Literaturangabe 4 (siehe Literatur im linken Panel) wird das Potential V(r,M,l) hingegen wie folgt definiert: \[ \begin{eqnarray} \hbox{2. Gleichung:}&\rightarrow& \left( \frac{dr}{d\tau} \right)^2 + \left( V(r,M,l) \right)^2 = E^2 \\ \hbox{wobei:} && V(r,M,l) = \sqrt{ \left( 1 - \frac{2 M}{r} \right) \left( 1 + \frac{l^2}{r^2} \right) } \quad . \end{eqnarray} \] Die im linken Panel veranschaulichte Abbildungen zeigen das effektive Potential als Funktion des Radius (in der Nomenklatur des 1.-3. Buches) und die Trajektorien der Probekörper für unterschiedliche Anfangswerte. Bei der elliptische, roten Bahn erkennt man hierbei gut den allgemeinrelativistem Effekt der Apsidendrehung (Periheldrehung bei der Sonne); d.h. der näheste Punkt (der Perihel) und der am weitesten entfernte Punkt (der Aphel) vom Zentrum des schwarzen Lochs betrachtet, ändert seine Position und rotiert entgegen dem Uhrzeigersinn in $\phi$-Richtung.
Vorlesung 4
In der vorigen Vorlesung hatten wir gezeigt, wie man die grundlegenden Größen der allgemeinen Relativitätstheorie und die Geodätengleichung in Python berechnet. Am Anfang dieser Vorlesung werden wir zunächst mithilfe eines Maple-Worksheets (siehe Maple-Worksheet aus Teil I: Bewegung eines Probekörpers um ein schwarzes Loch in der Ebene (Version 2) die numerischen Lösungen berechnen und die Bahnbewegungen von massiven Probekörpern am ISCO und die Trajektorien von masselosen Teilchen in der Photonensphäre betrachten (siehe rechte Seite der Internetseite). Dannach werden wir die innere Schwarzschildlösung eines sphärisch symmetrischen Objektes betrachten und die Tollman-Openheimer-Volkov (TOV) Gleichungen in Python Programmen und Maple-Worksheets herleiten und deren numerische Lösung simulieren.
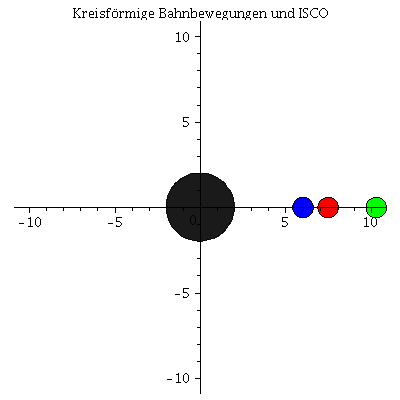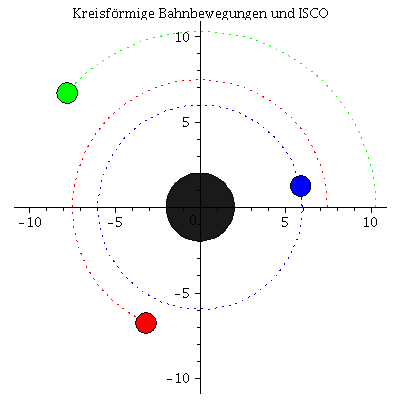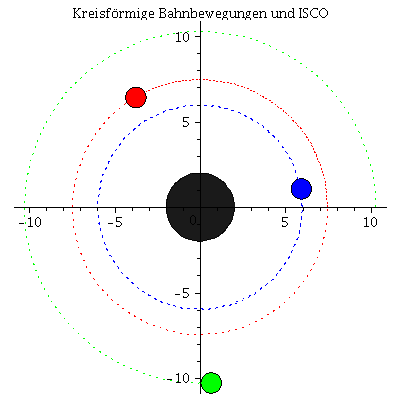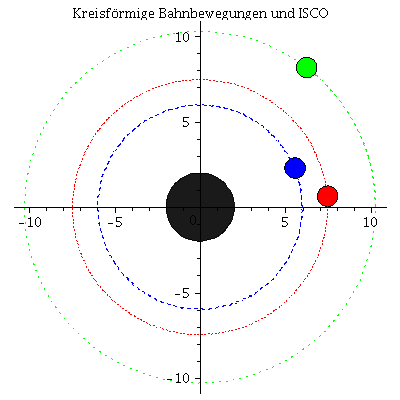
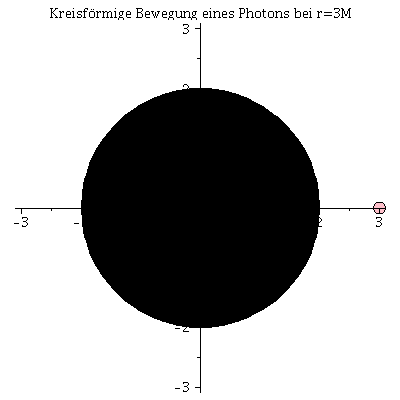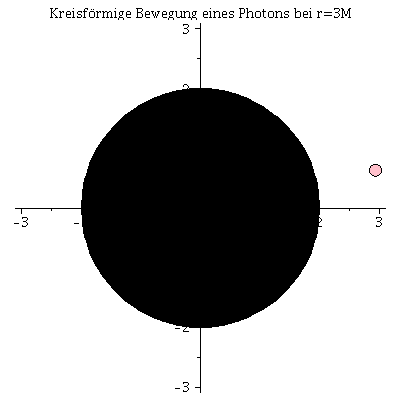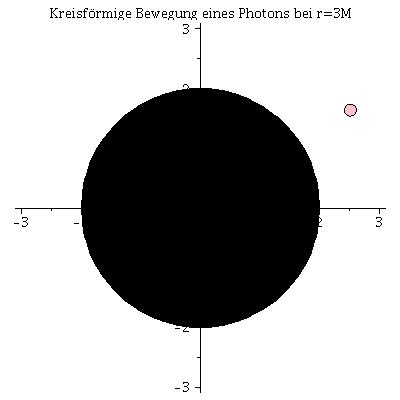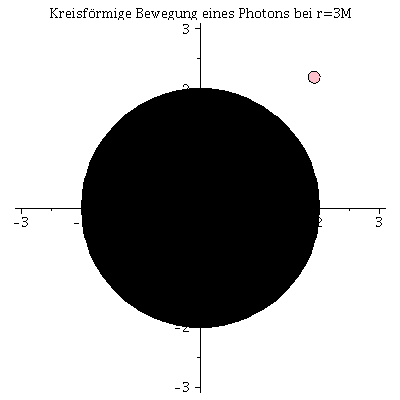
Die innerste stabile kreisförmige Bahngewegung (der ISCO: Innermost Stable Circular Orbit) und die Photonensphäre
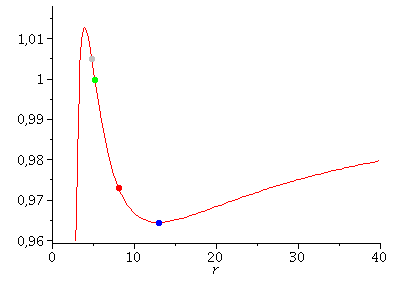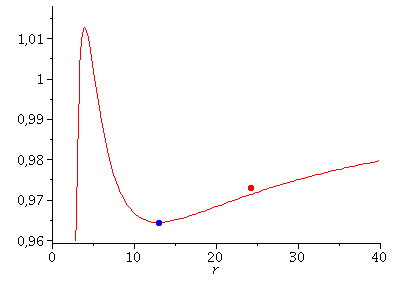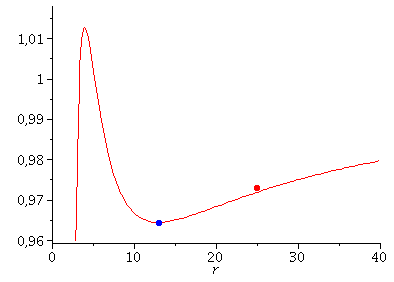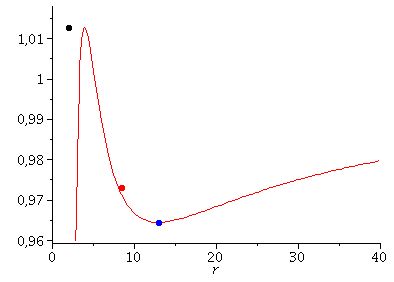
Beim Klicken auf die nebenstehenden Abbildungen gelangen Sie zu dem Maple-Worksheet in welchem die animierten Bilder erzeugt wurden. Kreisförmige Bewegungen von massiven Probekörpern um ein nicht rotierendes schwarzes Loch können dem Loch nicht beliebig nahe kommen. Die Grenze der Stabilität von kreisförmigen Trajektorien nennt man ISCO. Die oberen Abbildungen zeigen die simulierten Bahnen dreier kreisförmige Bewegungen, wobei die Masse des schwarzen Loches auf M=1 gesetzt wurde und die blaue Trajektorie die Bewegung am ISCO zeigt. In der linken oberen Abbildung sind die zugehörigen effektiven Potentiale dargestellt. Da es sich um kreisförmige Bewegungen handelt befinden sich alle drei Probekörper im Minimum des zugehörigen Potentials bzw. die blaue Trajektorie im Sattelpunkt des Potentials. Kreisförmige Bewegungen um ein schwarzes Loch (nicht-rotierend) sind somit nur bis zu einem Abstand von $r=6 M$ möglich. Das gilt jedoch nicht für masselose Probekörper (z.B. Photonen). Die nebenstehende untere Abbildung zeigt ein masseloses Testteilchen auf der Photonensphäre.
Die innere Schwarzschildlösung eines sphärisch symmetrischen Objektes und die Tollman-Openheimer-Volkov (TOV) Gleichungen
Unter der Annahme einer sphärisch symmetrischen Materieverteilung einer idealen Flüssigkeit (z.B. Neutronenstern Materie) kann man die Einsteingleichung in die so genannten TOV Gleichungen umschreiben. In diesem Teil der Vorlesung 4 wird anhand von Python Programmen und Maple-Worksheets gezeigt, wie man von der Einsteingleichung zu den TOV Gleichungen gelangt (siehe Maple-Worksheet aus Teil I: Die innere Schwarzschildlösung eines sphärisch symetrischen, statischen Objektes bzw. Python Jupyter Notebook: Die innere Schwarzschildlösung eines sphärisch symmetrischen, statischen Objektes Jupyter Notebook .ipynb). Die nebenstehende Animation zeigt die mittels des Python Skripts (siehe TOV-Sequence-plot2.py numerisch simulierten Resultate einer Sequenz von Neutronensternen mit unterschiedlichen zentralen Dichten. In den mittleren Abbildungen ist die $g_{00}=g_{tt}$ (oben) und $g_{11}=g_{rr}$ Komponente der Metrik visualisiert, wobei (aufgrund des Birkhoff Theorems) die innere Schwarzschildlösung (blue Kurven) in die (äussere) Schwarzschildlösung (rote Kurve) stetig ineinander übergehen müssen.
Vorlesung 4
In der vorigen Vorlesung hatten wir die Geodätengleichung in vorgegebener Schwarzschild-Raumzeit betrachtet und gezeigt, wie man eine Klassifizierung möglicher Bahnen von Probekörpern mittels eines definierten effektiven Potentials V(r,M,l) illustrieren kann ($M$ ist die Masse des schwarzen Lochs und l der Bahndrehimpuls des Probekörperns). Eine dieser Bahnen ist von besonderer Bedeutung, die so genannte innerste stabile kreisförmige Bahngewegung (der ISCO: Innermost Stable Circular Orbit). Kreisförmige Bahnbewegungen sind dadurch charakterisiert, dass der Wert des Radiuses sich im laufe der Zeit nicht verändert und somit sich der radiale Abstand des Probekörpers vom schwarzen Loch gerade im Minimum des effektiven Potentials befindet. Es muss somit $\frac{dV}{dr}=0$ gelten. Lösst man diese Gleichung nach r auf, so erhält man zwei Lösungen, wobei die erste (positives Vorzeichen) dem stabilen Minimum und die zweite (negatives Vorzeichen) dem instabilen Maximum entspricht: $$ \begin{eqnarray} \frac{d V}{dr}=0 \quad \Rightarrow \, r_\pm = \frac{l}{2 M} \left( l \pm \sqrt{l^2 -12 M^2} \right) \end{eqnarray} $$ Der ISCO hat gerade die Sattelpunkt Eigenschaft, so dass zusätzlich $\frac{d^2V}{dr^2}=0$ gelten muss. Der Drehimpuls l des Probekörperns und sein radiale Abstand vom schwarzen Loch nehmen die folgenden Werte an: $$ \begin{eqnarray} \frac{d V}{dr}=0 \,\,,\,\,\, \frac{d^2 V}{dr^2}=0 \quad \underbrace{\Rightarrow}_{\hbox{ISCO}} r=6 M \,\,,\,\,\, l = 2 \sqrt{3} M \end{eqnarray} $$ Kreisförmige Bewegungen um ein schwarzes Loch (nicht-rotierend) sind somit nur bis zu einem Abstand von $r=6 M$ möglich. Kommt man dem schwarzen Loch näher, endet man zwangsläufig in der echte Singularität. Dies gilt jedoch nur für massive Probekörper und nicht für masselose Teilchen (z.B. Photonen). Photonenbahnen unterscheiden im Wert des infinitesimalen Weglängenelementes $ds^2 = g_{\mu\nu} dx^\mu dx^\nu$. Mittels der Eigenschaft für Photonen ($ds^2=0$) vereinfacht sich die radiale Gleichung der Geodätengleichung und man kann ein effektives Potential definieren, welches allein von der Masse des schwarzen Lochs abhängt.: $$ \begin{eqnarray} && \frac{1}{l^2} \left( \frac{dr}{d\lambda} \right)^2 + V_{\hbox{eff}}(r) = \frac{1}{b^2}\\ && V_{\hbox{eff}}(r) = \frac{1}{r^2} \left( 1 - \frac{2 M}{r} \right) \quad, \end{eqnarray} $$ wobei der Parameter b der Impaktparameter der Photonenbahn darstellt. Dieses Potential besitzt ein Maximum bei $r=3 M$ und stellt somit die innerste stabile kreisförmige Photonenbahn dar, die sogenannte Photonensphäre eines schwarzen Lochs. Mit $r=3 M$ ist diese nur ein wenig vom Ereignishorizont ($r=2 M$) entferent. Bis jetzt wurde die Geodätengleichung in vorgegebener Schwarzschild Raumzeit betrachtet, wobei die raumzeitliche Struktur der Metrik als gegeben vorausgesetzt wurde. Bevor wir zu rotierenden schwarzen Löchern übergehen, wollen wir den umgekehrten Fall betrachten: Wie man anhand einer speziellen Materie/Energieverteilung im Raum zu der zugehörigen raumzeitliche Struktur gelangen kann. Wir betrachten nun eine spezielle Lösung der Einsteingleichung, die so genannte innere Schwarzschildlösung eines sphärisch symmetrischen, statischen Objektes (z.B. Erde, Neutronenstern). Im folgenden wird die Einsteingleichung einer sphärisch symmetrischen und statischen Matrieverteilung betrachtet. Die Matrie wird hierbei als ideale Flüssigkeit angesetzt. Setzt man einen sphärisch symmetrischen und statischen Ansatz der Metrik an, z.B: $$g_{\mu\nu}=\left( \begin{array}{ccc} e^{2\Phi(r)} & 0 & 0 & 0\\ 0& - \left( 1 - \frac{2 m(r)}{r} \right)^{-1}& 0&0 \\ 0& 0& -r^2& 0\\ 0& 0& 0& -r^2 \hbox{sin}^2(\theta)\\ \end{array} \right) \quad , $$ wobei die Funktionen $\phi(r)$ und $m(r)$ an dieser Stelle noch unbekannt sind, später aber eine physikalische Bedeutung besitzen. Der Energie-Impuls Tensor (rechte Seite der Einsteingleichung) wird als ideale Flüssigkeit angesetzt: $$ T^\mu{}\!_\nu=\left( \begin{array}{ccc} e(r) & 0 & 0 & 0\\ 0& -p(r)& 0&0 \\ 0& 0& -p(r)& 0\\ 0& 0& 0& -p(r)\\ \end{array} \right) \quad , $$ wobei die Funktionen $e(r)$ und $p(r)$ die Energiedichte und den Druck der Neutronensternmaterie darstellen, die ihrerseits über die Zustandsgleichung $p(e)$ miteinander verknüpft sind. Die Einstein Gleichung $$ G^\mu{}\!_\nu = R^\mu{}\!_\nu - \frac{1}{2}g^\mu{}\!_\nu R = 8\pi T^\mu{}\!_\nu$$ stellt demnach (in dem betrachteten Fall) ein System von vier gekoppelten Differentialgleichungen zweiter Ordnung dar. Zusätzlich folgt aus der Einsteingleichung die kovariante Erhaltung des Energie-Impulses. Diese sogenannten hydrodynamischen Gleichungen sind durch die folgenden vier Gleichungen definiert: $$ \nabla\!_\mu G^\mu{}\!_\nu = D\!_\mu G^\mu{}\!_\nu = G^\mu{}_{\nu \, ||\mu} = 0 \quad \rightarrow \quad \nabla\!_\mu T^\mu{}\!_\nu = 0 \quad , $$ wobei die kovariante Ableitung eines Tensors zweiter Stufe wie folgt definiert ist: $$ \nabla\!_\alpha T^\mu{}\!_\nu = \partial_\alpha T^\mu{}\!_\nu + \Gamma^\mu_{\alpha \rho} T^\rho{}\!_\nu - \Gamma^\rho_{\alpha \nu} T^\mu{}\!_\rho \quad . $$ Durch Umschreiben und Kombination der Gleichungen gelangt man zu einem System von drei gekoppelten Differentialgleichungen erster Ordnung, die so genannten Tollman-Openheimer-Volkov (TOV) Gleichungen: $$ \begin{eqnarray} \frac{dm}{dr} &=& 4\pi r^2~e(r) ~, \\ \frac{d\Phi}{dr} &=& \frac{m(r)+4 \pi r^3 p(r)}{r \left(2m(r) -r \right)} ~, \\ \frac{dp}{dr} &=& -(e(r)+p(r)) \frac{d\Phi}{dr} \end{eqnarray} $$ Die auf der linken Seite dieser Internetseite der Vorlesung 4 bahandelten Maple bzw. Python Programme behandeln die numerische Lösung der TOV Gleichungen. Im Teil II dieses Kurses werden wir ebenfalls das TOV System behandeln und auf die parallele Programierung eingegangen.
Vorlesung 5
In der vorigen Vorlesung hatten wir die innere Schwarzschildlösung eines sphärisch symmetrischen Objektes betrachten und die Tollman-Openheimer-Volkov (TOV) Gleichungen in Python Programmen und Maple-Worksheets herleitet. Am Beispiel von Neutronensternen wird in dieser Vorlesung gezeigt wie man die TOV Gleichungen numerisch in Python lösst, wobei es zunächst eine kurze Einführung in ''Weiße Zwerge, Neutronensterne und Quarksterne'' gibt. Am Ende dieser Vorlesung werden dann ''Rotierende schwarze Löcher und die Kerr Metrik'' behandelt.
Weiße Zwerge, Neutronensterne und Quarksterne
Beim Klicken auf die nebenstehenden obere Abbildung gelangen Sie zu einer einführenden Präsentation der Eigenschaften von weißen Zwergen, Neutronensternen und Quarksternen. Neutronensterne sind neben weißen Zwergen und schwarzen Löchern die möglichen Endzustände der Evolution eines Sterns. Diese extrem dichten astrophysikalischen Objekte, die im Zentrum einer Supernova Explosion entstehen, stellen den letzten stabilen Zustand der Materie dar, bevor die Materie zu einem schwarzes Loch kollabiert. Aufgrund ihrer großen Magnetfelder und schnellen Rotation emittieren Neutronensterne periodische Radiowellen. In unserer Galaxie sind derzeit etwa 2500 dieser exotischen Objekte bekannt, die hauptsächlich als Pulsare mittels großer Radioteleskope beobachtet werden. Unter den bekannten Neutronensternen gibt es einige, die sich in binären Systemen befinden, wobei ihr Begleiter entweder ein normaler Stern, ein Planet, ein weißer Zwerg oder auch wieder ein Neutronenstern sein kann. Das derzeit beeindruckendste Binärsystem ist der sogenannte Doppelpulsar: PSR J0737-3039A/B, welches im Jahre 2003 entdeckt wurde.Die makroskopischen Eigenschaften von weißen Zwergen, Neutronensternen und Quarksternen können in guter Näherung mittels der TOV Gleichungen beschrieben werden. Durch Klicken auf die nebenstehenden untere Abbildung gelangen Sie zu einem Python Jupyter Notebook (Jupyter Notebook .ipynb), das dem in der vorigen Vorlesung behandeltem ähnlich ist, jedoch auch die nummerische Lösung der TOV Gleichungen in Python mittels der Funktion odeint(), unter Verwendung einer polytropen Form der Zustandsgleichung von Neutronensternmaterie, behandelt.
Rotierende schwarze Löcher und die Kerr Metrik
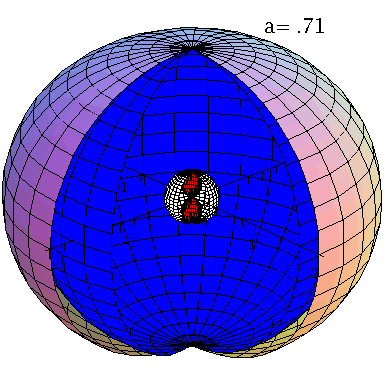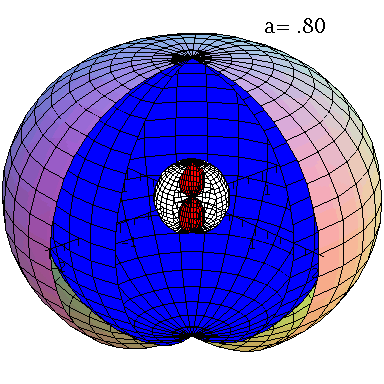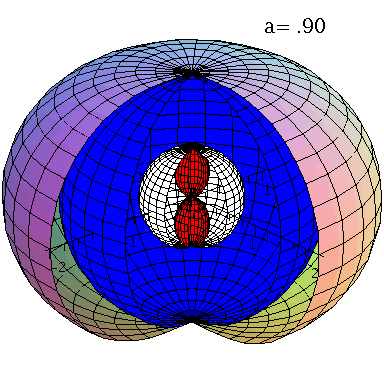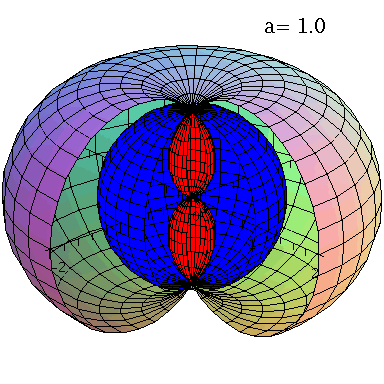
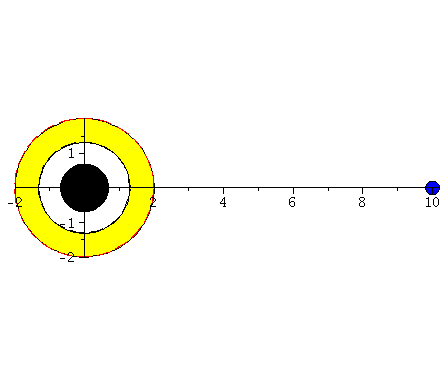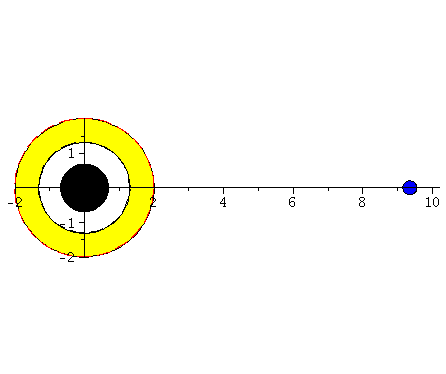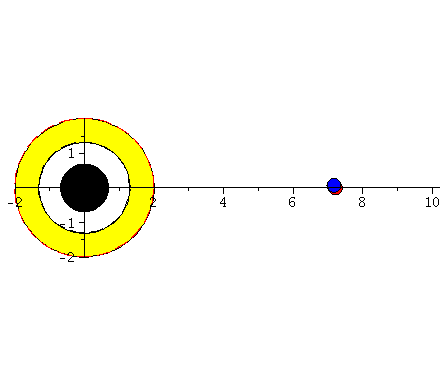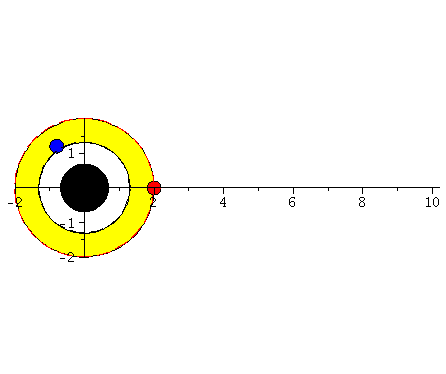
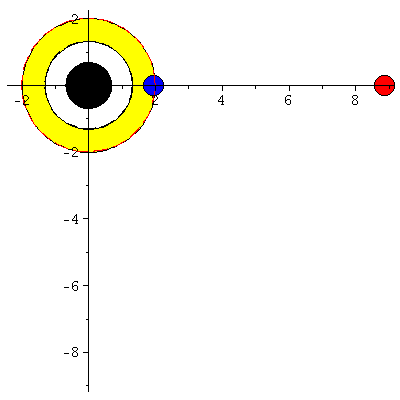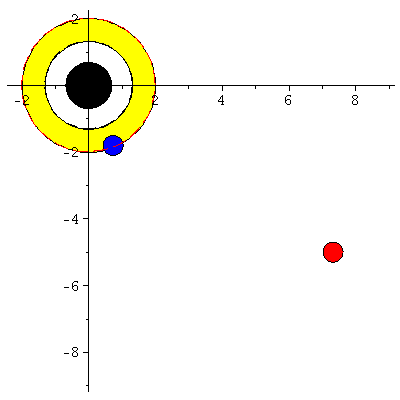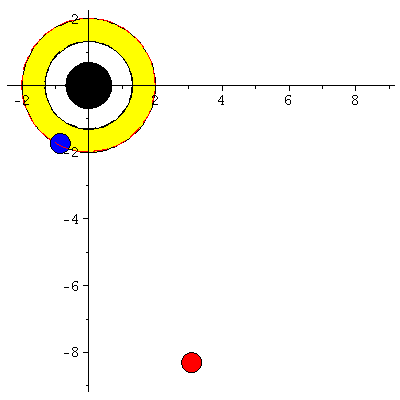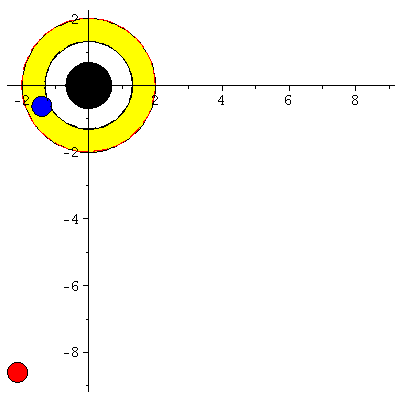
Rotierende schwarze Löcher besitzen eine kompliziertere Struktur der Ereignishorizonte und die Flächen unendlicher Rotverschiebung und die Grenzflächen stationärer Bewegungen sind im allgemeinen nicht identisch mit den Horizonten. Die nebenstehende obere Abbildung zeigt diese Flächen in einer Animation, wobei der Kerr Rotationsparameter im Bereich $a \in [0.7,1]$ variiert wurde. Rotiert das schwarze Loch, so existieren zwei Ereignishorizonte (r+: blaue Fläche und r-: weiße Fläche) und zwei Flächen unendlicher Rotverschiebung (rs+: äußere Fläche und rs-: rote Fläche ganz Innen). Der Bereich zwischen der äußeren Fläche unendlicher Rotverschiebung und dem äußeren Ereignishorizont bei r+ nennt man Ergosphäre; hier können Körper nicht mehr entgegengesetzt der Rotationsrichtung des schwarzen Lochs rotieren und stationäre Bewegungen sind somit nicht mehr möglich.Fällt ein Probekörper radial in ein rotierendes schwarzes Loch, so wird er aufgrund des Mitführungseffektes der rotierenden Raumzeit (Frame dragging) abgelenkt. Dieses Mitführen der Raumzeit erfolgt in Richtung der Rotation des schwarzen Lochs und nimmt bei Annäherung an das schwarze Loch zu. Die untere Abbildung veranschaulicht diesen Effekt und stellt die Bewegung eines radial in ein rotierendes schwarzes Loch ($a=0.95$) einfallenden Probekörpers (blauer Körper) im Vergleich mit einem nichtrotierenden schwarzen Loch ($a=0$) dar (roter Körper). Die Bewegung erfolgt hier auf der äquatorialen Ebene und die Ergosphäre des rotierenden schwarzen Loches ist durch einen gelben Ring gekennzeichnet. Bewegungen von Probekörpern innerhalb der Ergosphäre sind ohne weiteres möglich, da sich der äussere Ereignishorizont (r+) erst bei kleineren Abständen ereignet. Durch Klicken auf die nebenstehenden Abbildungen gelangen Sie zu dem Maple-Worksheet aus Teil I: Bewegung eines Probekörpers um ein rotierendes schwarzes Loch (Version 1) mittels dessen diese Animationen erzeugt wurden.
Aktuelles
- GOETHE-UNI online -- Aktuelle Nachrichten aus Wissenschaft, Lehre und Gesellschaft:
Gravitational waves could prove the existence of the quark-gluon plasma - Vortrag am 03.06.2020 von 16:30 bis 18:30 Uhr im CERN ''TH Cosmo Coffee'' Seminar:
Postmerger Gravitational-Wave Signatures of Phase Transitions in Binary Compact Star Mergers by Matthias Hanauske
Zoom connection: https://cern.zoom.us/j/99377496227 , Meeting ID: 993 7749 6227 , Password: 636648
Vorlesung 5
Die Tollman-Openheimer-Volkov (TOV) Gleichungen (siehe vorige Vorlesung) beschreibt das Druck/Dichte Verhalten und die raumzeitliche Struktur innerhalb eines sphärisch symmetrischen Objektes: $$ \begin{eqnarray} \frac{dm(r)}{dr} &=& 4\pi r^2~e(r) ~, \\ \frac{d\Phi(r)}{dr} &=& \frac{m(r)+4 \pi r^3 \, p(r)}{r \left(2\,m(r) -r \right)} ~, \\ \frac{dp(r)}{dr} &=& -(e(r)+p(r)) \frac{d\Phi}{dr} \end{eqnarray} $$ Ausserhalb des Objektes ist die Raumzeit durch die Schwarzschildmetrik definiert, welche aufgrund des Birkhoff-Theorems die einzige sphärisch symmetrische Lösung der Einsteingleichung im Vakuum ($T^{\mu\nu}\equiv 0$) ist. Mittels der TOV Gleichungen können die unterschiedlichsten Objekte in guter Näherung beschrieben werden. So kann man mit ihnen sowohl das Innere der Sonne und die durch sie verursachte Gravitationswirkung auf Planeten beschreiben, als auch die Eigenschaften von Weissen Zwergen, Neutronen und sogar Quarksterne beschreiben. Quarksterne stellen den letzten stabilen Zustand der elementaren Materie dar, bevor sie unaufhaltsam zu einer echten Singularität (dem schwarzen Loch) kollabiert - sie stehen wohlmöglich kurz vor ihrer experimentellen Entdeckung. Eine kurze Einführung in diese seltsamen astrophysikalischen Objekte findet sich in dem linken Panel dieser Internetseite. Die meissten durch Radioteleskope bekannten Neutronensterne rotieren sehr schnell (bis zu 760 mal in einer Sekunde) um die eigene Achse, so dass unser sphärisch symmetrischer Ansatz der Metrik nicht mehr erfüllt ist. Bevor wir jedoch zu rotierenden Neutronensternen übergehen, wollen wir am Ende dieser Vorlesung zunächst die Eigenschaften von rotierenden schwarzen Löchern besprechen. Im folgenden betrachten wir die Bewegung eines massiven Probekörpers um ein rotierendes schwarzes Loch und lösen die Geodätengleichung in vorgegebener Kerr-Raumzeit (in Boyer-Lindquist Koordinaten). Die kovarianten Kerr Raumzeit-Metrik eines rotierenden schwarzen Lochs der Masse M und Rotation a ($ a \in [-1,1]$ ist ein spezifischer Drehimpuls $a=J/M$ und wird als der sogenannte Kerr-Rotationsparameter bezeichnet) besitz in Boyer-Lindquist Koordinaten folgendes Aussehen: $$ \begin{eqnarray} &g_{\mu\nu}=\left( \begin{array}{ccc} g_{tt}(r,\theta) & 0 & 0 & g_{t\phi}(r,\theta)\\ 0& g_{rr}(r,\theta)& 0&0 \\ 0& 0& g_{\theta\theta}(r,\theta)& 0\\ g_{\phi t}(r,\theta)& 0& 0& g_{\phi\phi}(r,\theta)\\ \end{array} \right)& \\ & g_{tt}(r,\theta)=\left( \frac{1-2\,M\,r}{\rho^2} \right)\,\,, \, g_{t\phi}(r,\theta)=\frac{2aMr\hbox{sin}^2(\theta)}{\rho^2} &\\ &g_{rr}(r,\theta)=-\frac{\rho^2}{\Delta}\,\,, \quad g_{\theta\theta}(r,\theta)=-\rho^2\,\,, \, & \\ &g_{\phi\phi}(r,\theta)=-\left( \frac{r^2+a^2+2 M r a^2 \hbox{sin}^2(\theta)}{\rho^2} \right)\hbox{sin}^2(\theta)\,\,,&\\ &\rho^2=r^2+a^2 \hbox{cos}^2(\theta) \,\,, \quad \Delta=r^2-2Mr+a^2& \end{eqnarray} $$ Rotierende schwarze Löcher besitzen, im Gegensatz zu denen in den Vorlesung 3-4 besprochenen nicht-rotierenden schwarzen Löchern, eine Ringsingularität und eine kompliziertere Struktur der Ereignishorizonte. Ereignishorizonte ereignen sich formal an den Raumzeitpunkten bei denen die radiale Komponente der zugrunde liegenden Metrik singulär wird ($g_{rr}\rightarrow\infty$ (bzw. $g^{rr}=0$). Für $a \neq 0$ erhält man zwei Lösungen, die man gewöhnlich mit den Symbolen $r_{+}$ und $r_{-}$ bezeichnet $$ r_{+}= M + \sqrt{M^2 - a^2}\,, \quad r_{-}= M - \sqrt{M^2 - a^2}\quad, $$ und die für $a = 0$ in den Schwarzschild-Limes des Ereignishorizontes eines nicht-rotierenden schwarzen Lochs übergehen ($a=0 \rightarrow r_{+}=r_{-}=2\,M$). Zusätzlich existieren die Flächen der stationären Grenze (stationary limit surfaces) und die der unendlichen Rotverschiebung; sie sind durch $g_{tt}=0$ bestimmt und werden gewöhnlich mit den Symbolen $r_{S^+}$ und $r_{S^-}$ bezeichnet: $$ r_{S^+}= M + \sqrt{M^2 - a^2{{\rm cos}(\theta)}^2}\,, \,\, r_{S^-}= M - \sqrt{M^2 - a^2{{\rm cos}(\theta)}^2} $$ In dem linken Panel dieser Internetseite ist die Horizontstruktur eines rotierenden schwarzen Lochs bei ansteigendem Kerr-Rotationparameter $a$ in einer Animation veranschaulicht. Ein rotierendes schwarzes Loch zieht die Raumzeit mit sich mit. Die Rotationsfrequenz mit der die raumzeitlichen Struktur mitgeführt wird, nennt man ''Frame dragging'' Frequenz $\omega$; sie beschreibt wieviel sich die $\phi$-Koordinate pro Koordinatenzeit $t$ verändert: $$ \begin{equation} \omega(r,\theta)=\frac{d\phi}{dt} = \frac{\frac{d\phi}{d\tau}}{\frac{dt}{d\tau}} = \frac{u^\phi}{u^t} = \frac{g^{t\phi}}{g^{tt}} \end{equation} $$ Die Bewegung eines Probekörpers um ein rotierendes schwarzes Loch und das der Bewegung zugrundeliegende effektive Potential wird in der nächsten Vorlesung im Detail besprochen.
Vorlesung 6
In dieser Vorlesung werden wir die Bewegung eines Probekörpers um ein rotierendes schwarzes Loch und die Klassifikation möglicher Bahnen mittels eines definierten effektiven Potentials betrachten. Die Anwendung auf das rotierende schwarze Loch in M87 wird ebenfalls besprochen und der erste Vorlesungsteil somit beendet. In den Teil II dieser Veranstaltung (Paralleles Programmieren mit C++ und OpenMP/MPI) wird am Ende dieser Vorlesung eingeführt.
Bewegung eines Probekörpers um ein rotierendes schwarzes Loch und die Klassifikation möglicher Bahnen mittels eines definierten effektiven Potentials (Maple)
In diesem Maple-Worksheet werden die möglichen Bewegungen eines Probekörpers um ein rotierendes schwarzes Loch (Kerr Metrik) mittels eines definierten effektiven Potential illustriert. Zusätzlich wird der, durch den Mitführungseffekt der Raumzeit ("Frame-Dragging" bzw. Lense-Thiring Effekt) verursachte, gravitomagnetische Effekt an einem speziellen Beispiel veranschaulicht. Beim Klicken auf die nebenstehenden Abbildungen gelangen Sie zu dem Maple-Worksheet in welchem das nebenstehende animierte Bild erzeugt wurde. Wie bei einem nicht-rotierenden schwarzen Loch, können kreisförmige Bewegungen von massiven Probekörpern um ein rotierendes schwarzes Loch dem Loch nicht beliebig nahe kommen (siehe Vorlesung 4). Bei rotierenden schwarzen Löchern gibt es zwei solcher Grenzen der Stabilität von kreisförmigen Trajektorien (zwei ISCOs). In der nebenstehenden Abbildung wurden die Eigenschaften des rotierenden schwarzen Loches festgelegt (Masse $M=1$ und Kerr-Rotationsparameter $a=0.95$), und die Bedingung der Sattelpunktseigenschaft des effektiven Potentials (siehe rechtes Panel dieser Vorlesung) am ISCO verwendet. Die Lösungen des ISCO beinhalten eine eng um das schwarze Loch rotierende Lösung (blauer Körper bei $r=1.94$ km: Probekörper rotiert in gleicher Richtung wie die Rotationsrichtung des schwarzen Lochs) und eine weiter entfernte Lösung (roter Körper bei $r=8.86$ km: Probekörper rotiert entgegen der Rotationsrichtung des schwarzen Lochs). Man erkennt, dass sich die innere, blaue Kurve innerhalb der Ergosphähre (gelber Bereich, der bei $r=2$ km beginnt) aufhält.
Das Schwarze Loch in M87
Das nebenstehende Bild zeigt das schwarze Loch im Zentrum unserer Nachbargalaxie M87; bzw. ein wenig genauer, die um ein schwarze Loch entstehende Radiostrahlung (das Bild wurde mittels eines weltweiten Verbunds von Radiowellenteleskopen (EHT: Event Horizon Teleskop) sichtbar gemacht). In Kürze werden die aufgenommenen Bilder von Sagittarius A*, das schwarze Loch im Zentrum unserer Galaxie, ebenfalls ausgewertet sein, und weitere Bilder in verbesserter Auflösung werden wohl in einigen Jahren folgen. In beiden Systemen (schwarzes Loch in M87 und Sagittarius A*) kreist Materie in einer Akkretionsscheibe um ein supermassives schwarzes Loch und emittiert beim Einfallen Radiowellenstrahlung. Die Bewegung eines Probekörpers um ein rotierendes schwarzes Loch ist somit ein astrophysikalisch sehr relevantes Problem. Schon Jahre bevor die ersten Bilder eines schwarzes Loches entstanden, galt es als so gut wie bestätigt, dass im Zentrum unserer Galaxie ein superschweres schwarzes Loch existiert und man verfolgte schon seit Jahrzenten (siehe z.B. R.Genzel et,al.) die Bewegung einzelner sogenannter S-Sterne um dieses Zentrum. Beim Klicken auf das nebenstehende Bild gelangen Sie zu dem Maple-Worksheet in welchem die Eigenschaften des schwarzen Loches in M87 simuliert werden.
Teil II: Paralleles Programmieren mit C++ und OpenMP/MPI
Dieser erste Unterpunkt des zweiten Teils der Vorlesung gibt eine Einführung in die parallele Programmierung mit C++ und OpenMP (Open Multi-Processing) / MPI (Message Passing Interface). Die Folien der Präsentation sind unter den folgenden Links einsebar: Einführung in die parallele Programmierung ( LibreOffice Datei , PDF Datei. Am Beispiel eines einfachen numerischen Problems (der Integration einer Funktion), wird das Programmierparadigma der parallelen Programmierung erläutert. Zunächst wird ein einfaches sequentielles C++-Programm erstellt, das die Integration der Funktion f(x)=1/(1 + a x2) in den Grenzen [0,1] und den Werten a=1..10 mit dem Gauss'schen Integrationsverfahren numerisch berechnet (siehe sequentielle Version 1 und sequentielle Version 2). In diesem Programm wird der Wert des Integrals ∫(1/(1 + a x2)) dx für die Parameterwerte a=1..10 ausgegeben und mit dem analytischen Ergebnis (arctan(√a)1/√a) verglichen. Die Parallelisierung dieses sequentiellen Programms wird zunächst mit OpenMP (siehe OpenMP Version 1 , OpenMP Version 2 , OpenMP Version 3 , OpenMP Version 4 und OpenMP Version 5 ) und danach mit MPI (siehe MPI Version 1 , MPI Version 2 ) durchgeführt.
Vorlesung 6
In der vorigen Vorlesung hatten wir die Bewegung eines massiven Probekörpers um ein rotierendes schwarzes Loch in vorgegebener Kerr-Raumzeit (in Boyer-Lindquist Koordinaten) betrachtet, wobei der spezifischer Drehimpuls $a=J/M$ des schwarzen Lochs mittels des Kerr-Rotationsparameters a ($ a \in [-1,1]$ quantifiziert wurde. Die Struktur der Ereignishorizonte, die Flächen der stationären Grenze (stationary limit surfaces) und die ''Frame dragging'' Frequenz $\omega$ der Mitführung der raumzeitlichen Struktur des rotierenden schwarzen Lochs wurden ebenfalls behandelt.
In dieser Vorlesung werden wir das Lösen der Geodätengleichung in vorgegebener Kerr-Raumzeit behandeln und die möglichen Trajektorien von massiven Probekörpern analysieren. In der Literatur wird die Bewegung eines Probekörpers um ein rotierendes schwarzes Loch mittels eines definierten, effektiven Potentials illustriert (siehe z.B. Hartle- bzw. Hobson Buch). In ähnlicher Weise wie in Vorlesung 3 beschränken wir uns im folgenden auf äquatoriale Bewegungen, schreiben das System der gekoppelten Differentialgleichungen der Geodätengleichung um und betrachten die zweite, radiale Gleichung. Das effektive Potential hängt von dem, bei der Bewegung erhaltenem Drehimpuls pro Masse m (m ist hierbei die Masse die Probekörpers) und von der der Probekörper-Energie pro Masse ab. Die im Zentralfeld möglichen Bewegungen werden mittels zweier erhaltener Größen (l: Drehimpuls pro Masse m und E: Energie pro Masse) charakteriesiert:
\[
\begin{eqnarray}
&\frac{1}{2} \left( \frac{dr}{d\tau} \right)^2 + V(r,M,l,a,E) = \frac{1}{2} \left( E^2 -1 \right)& \\
& V(r,M,l,a,E) \,=\, -\frac{M}{r} + \frac{l^2 - a^2 \left( E^2 -1 \right)}{2\, r^2} - \frac{M \left( l - a\,E \right)^2}{r^3} &
\end{eqnarray}
\]
Aufgrund der Normalisierungseigenschaft der Vierergeschwindigkeit $ds^2=u^\mu u_\mu =1 $ sind die t- und $\phi$-Komponente der Viergeschwindigkeit wie folgt durch die Energie- und Drehimpulswerte bestimmt (siehe Hartle-Buch, S:318):
\[
\begin{eqnarray}
\frac{dt}{d\tau} &=& \frac{1}{\Delta} \left[ \left( r^2 + a^2 +\frac{2Ma^2}{r} \right)\, E -\frac{2Ma}{r}\, l \right] \\
\frac{d\phi}{d\tau} &=& \frac{1}{\Delta} \left[ \left( 1 - \frac{2M}{r} \right)\, l +\frac{2Ma}{r}\, E \right]
\end{eqnarray}
\]
Die Bewegung von Probekörpern ist aufgrund des ''Frame dragging'' Effekts unterschiedlich zum Verhalten um ein nicht-rotierendes schwarzes Loch und bei rotierenden schwarzen Löchern gibt es zwei unterschiedliche Grenzen der Stabilität von kreisförmigen Trajektorien (zwei ISCOs, siehe Animation im rechten Panel dieser Vorlesung).
Die ''Frame dragging'' Frequenz wirkt in ähnlicher Weise auf die Geschwindigkeit von Probekörpern, wie das Magnetfeld in der Elektrodynamik die Lorentzkraft verursacht. Im Fall1 (grün) ist das gravitomagnetische Feld Null, im Fall 2 (blau) ist es aus der äquatoriellen Ebene nach oben gerichtet und im Fall 3 zeigt es nach unten. In erster Näherung (siehe Fließbach Buch, S:172) ist die gravitomagnetische Lorentzkraft gleich $ \sim 2\,\left( {\bf \omega} \times {\bf v} \right) $, wobei $ \times $ das Kreuzprodukt, $ {\bf \omega} $ der axiale Vektor der "Frame dragging" Frequenz und $ {\bf v} $ der Geschwindigkeitsvektor des Probekörpers ist. Die Änderung des Geschwindigkeitsvektors nimmt in Schwachfeldnäherung dann die folgende Gestalt an:
\[
\begin{eqnarray}
\frac{d{\bf v}}{d\tau} &=& \underbrace{-\hbox{grad}\, \Phi({\bf r})}_{\hbox{gewoehnlicher Teil der gravitativen Kraft}} +\\
&& \\
&& + \underbrace{2\, {\bf \omega}({\bf r}) \times {\bf v}}_{\hbox{gravitomagnetische Lorentzkraft}} \,\,+ {\cal O}(v^2/c^2)\,\,,
\end{eqnarray}
\]
wobei $\Phi({\bf r})$ das Newtonsche Gravitationspotential und ${\bf v}=(v^r,v^\theta,v^\phi)$ der Geschwindigkeitsvektor des Probekörpers ist. Die unten abgebildete Grafik zeigt die "Frame dragging" Frequenz $ {\bf \omega} = \omega_z(r)$ für die Kerr Metrik, wobei bei der schwarzen Kurve a=0, bei der blauen Kurve a=0.99 und bei der roten Kurve a=-0.99 ist.
Vorlesung 7
In der vorigen Vorlesung hatten wir in den Teil II dieser Veranstaltung (Paralleles Programmieren mit C++ und OpenMP/MPI) eingeführt und am Beispiel von einem einfachen numerischen Problem (die Integration einer Funktion) die grundlegende Vorgehensweise eines OpenMP und MPI Programms kennengelernt. In dieser Vorlesung werden wir das numerische Lösen der Tolman-Oppenheimer-Volkoff (TOV Gleichungen, siehe Vorlesungen 4 und 5) mittels des Eulerverfahrens in einem C++ Programm durchführen und die besprochenen Parallelisierungsparadigmen (OpenMP und MPI) anwenden. Es wird sowohl ein sequentielles C++ Programm zur Berechnung der Eigenschaften von Neutronensternen, als auch eine mit OpenMP und MPI parallelisierte Version besprochen.
Sequentielles C++ Programm zur Berechnung der Eigenschaften von Neutronensternen durch numerisches Lösen der TOV Gleichungen mittels des Eulerverfahrens
Ausgehend von der, in der Vorlesung 4 hergeleiteten Tollmann-Openheimer-Volkov Gleichung, wird mittels des einfachen Euler-Verfahrens die Differentialgleichung in C++ implementiert (siehe TOV sequentielle Version 1). Die numerisch berechneten Werte des Neutronensternradius und seiner gravitativen Masse werden am Ende des Programs im Terminal ausgegeben. Man kann zusätzlich, auf sequenzielle Weise, mehrere Neutronensterne bei festgelegter Zustandsgleichung berechnen. Dies wird einfach realisiert, indem man eine weitere for-Schleife über die zentrale Energiedichte einbaut. Zusätzlich zur Version 2.1) werden auch noch die zentralen Werte der Metrikkomponente g00 berechnet und im Terminal ausgegeben (siehe TOV sequentielle Version 2). Der Hauptunterschied zur vorigen sequentiellen Version ist, das nun eine ganze Sequenz von Neutronensternen berechnet wird. Die berechneten Resultate kann man mit den Ergebnissen des in der Vorlesung 4 mit Maple berechneten verglichen werden (siehe TOV sequentielle Version 2 mit Maple Ausgabe). Das Ausgabeformat geschiet in einer Maple-Liste, so dass das Profil in Maple mittels der Funktion listplot(...) bzw. pointplot(...) einfach dargestellt werden kann.
Parallele OpenMP-Version
Das sequentielle Programm 2.2) wurde nun mittels OpenMP (siehe TOV OpenMP Version) parallelisiert. Hiebei wurde einfach das OpenMP-Pragma '#pragma omp parallel for private(i,M,p,e,r,nu,dM,dp,de,dnu)' vor die for-Schleife der unabhängigen Berechnung der einzelnen Neutronensterne geschrieben. Wichtig ist nun, dass man das Programm mit dem folgenden Befehl compiliert: 'c++ -fopenmp TOV_parallel_omp.cpp'. Führt man das Programm mit './a.out' aus, so erkennt man als erstes, dass es (in Abhängigkeit wieviele CPU-Kerne man in seinem Computer hat), viel schneller läuft. Die im Terminal ausgegebenen Werte sind jedoch nicht mehr geordnet, sondern die Berechnung der 40 Neutronensterne erfolgt parallel und ungeordnet. Die nebenstehende Animation veranschaulicht die Vorgehensweise des OpenMP Programms. Durch Klicken auf die Bilder gelangen Sie zu der Version ''2.6) Parallele OpenMP-Version mit geordneter Ausgabe in eine Datei und variabler Zustandsgleichung''. Es werden, abhängig von der Anzahl der verfügbaren Prozessoren im Computer, mehrere Threads erzeugt, die gleichzeitig die einzelnen Aufgaben der Schleife ausführen. Das OpenMP-Pragma '#pragma omp parallel for private(i,M,p,e,r,nu,dM,dp,de,dnu)' vor der for-Schleife realisiert die Parallelisierung, wobei der private(...) Zusatz sicherstellt, dass die während der Berechnung benötigten Hilfsvariablen (z.B. M, dM) nicht von anderen Threads überschrieben werden. Jeder Thread greift sich einen der 150 (anz=150) zu berechnenden Neutronensterne raus, löst die TOV-Gleichung und berechnet die Masse, den Radius und die für die zentrale g00-Komponente nötige Größe des Sterns. Wenn ein Thread fertig mit der Berechnung ist, nimmt er sich den nächsten noch nicht berechneten Stern vor. Nach der parallelen Ausführung der Schleife arbeitet wieder nur ein Prozessorkern, der das restliche Programm ausführt (Ausgabe der von den unterschiedlichen Threads berechneten Ergebnisse in eine externe Datei).
Parallele MPI-Version
Diese Version entspricht der OpenMP-Version Version 2.6), benutzt jedoch MPI und nicht OpenMP zur Parallelisierung und kann somit auch auf heutigen Großrechneranlagen, die über eine hohe Anzahl von Rechenknoten mit einer Vielzahl von CPU-Kernen verfügen, parallel ausgeführt werden. Wichtig ist nun, dass man das Programm mit dem folgenden Befehl compiliert: 'mpic++ TOV_parallel_omp2_eos_time.cpp' und das Programm mit 'mpirun -np 6 ./a.out' ausführt ('-np 6' ist hier nur ein Beispiel und die Zahl 6 gibt die Anzahl der Prozesse an). Beim Ausführen des Programms spezifiziert somit der User mit wie vielen Prozessen er das Programm ausführen will (hier mit sechs Prozessen 'mpirun -np 6 ./a.out'). Ab diesem Zeitpunkt läuft das Programm mit sechs Prozessen, denen man im Laufe der weiteren Programmabfolge unterschiedliche Aufgaben zuweisen sollte, damit sie nicht alle das gleiche Ausführen. Die in der letzten Zeile angegebene Terminalausgabe erfolgt z.B. bei sechs Prozessen sechs mal; die Variable 'id' bezeichnet hier die fortlaufende Nummer des Prozesses (0,1,..,5). Eine sinnvolle Aufteilung der einzelnen Aufgaben des TOV-Programms auf die jeweiligen Prozesse kann man z.B. realisieren, indem die 150 (anz=150) zu berechnenden Neutronensterne auf die jeweiligen Prozesse aufteilt werden. In dem die for-Schleife von einem prozessabhängigen Startwert anfängt und in Schrittweiten 'psize' (Anzahl der Prozesse, hier z.B. 6) geht, rechnet jeder Prozess einen anderen Stern aus. Prozess 'id=0' rechnet z.B. die Sterne 'i=0,6,12,18,..' und Prozess 'id=4' rechnet z.B. die Sterne 'i=4,10,16,22,..' aus. Im Gegensatz zu den Threads in der OpenMP-Version wissen die einzelnen Prozesse der MPI Version nichts über die Berechnungen und Ergebnisse der anderen Prozesse, so dass die Werte der berechneten Ergebnisse übermittelt werden müssen - dies geschiet mit einem 'MPI::COMM_WORLD.Send(...)'-Kommando. In dieser Version senden alle Prozesse ihre Ergebnisse an Prozess mit 'id=0'. Die nebenstehende Animation veranschaulicht die Vorgehensweise des MPI Programms. Durch Klicken auf die Bilder gelangen Sie zu der Version ''2.7) Parallele MPI-Version mit geordneter Ausgabe in eine Datei und variabler Zustandsgleichung''.
Vorlesung 7
In dieser Vorlesung wird das numerische Lösen des Tolman-Oppenheimer-Volkoff Differentialgleichungssystem (TOV Gleichungen, siehe Vorlesungen 4 und 5) im Detail beschrieben. In einem C++ Programm wird das TOV-System mittels des Eulerverfahrens numerisch gelöst und die besprochenen Parallelisierungsparadigmen (OpenMP und MPI) angewendet. Wie wir in Vorlesungen 4 zeigten, besitzt das Differentialgleichungssystem der TOV Gleichung das folgende Aussehen $$ \begin{eqnarray} \frac{dp}{dr} &=& -\frac{\left( p + e \right) \left( m + 4\pi r^3 p \right)}{r \left( r - 2 m \right)} \\ \frac{dm}{dr} &=& 4\pi r^2 e\\ \frac{d\Phi}{dr} &=& \frac{ m + 4\pi r^3 p }{r \left( r - 2 m \right)} \qquad, \end{eqnarray} $$ wobei $p=p(r)$ und $e=e(r)$ der Druck und die Energiedichte der Materie darstellen, $m=m(r)$ die radiusabhängige gravitative Masse ist und die Funktion $\Phi=\Phi(r)$ die 00- bzw. $tt$-Komponente der Metrik bestimmt ($g_{00}=e^{2\Phi}$; hier bezeichnet e die Eulersche Zahl!). Eine numerische Lösung der Sterneigenschaften benötigt lediglich die erste und zweite Differentialgleichung und geht im einfachsten Fall (einfaches Euler Verfahren) nach folgendem Schema vor:
- Man definiert die Zustandsgleichung (EOS) der Sternmaterie als eine Funktion e(p).
- Man startet im Sternzentrum $r=r_0$ und legt den Wert des zentralen Druckes $p=p_0:=p(r_0)$, der zentralen Energiedichte $e=e_0:=e(r_0)$ und der Masse $m=m_0:=m(r_0)=0$ fest. Da die este TOV Gleichung bei $r_0=0$ singulär wird, wählt man hier einen sehr, sehr kleinen Wert für $r_0$ (z.B. $r_0=10^{-14}$). Die Randbedingungen sind somit wie folgt definiert: \begin{equation} r=10^{-14}\,, \quad p=p_0\,, \quad e=e_0\,, \quad m=0 \nonumber \end{equation}
- Die TOV Gleichungen werden als Differenzengleichungen umgeschrieben und eine kleine Schrittweite $dr=\Delta r << 1$ wird festgelegt. In einer Schleife wird dann in jedem Radiusschritt die Druck- und Massenänderung berechnet und die jeweiligen Grössen beim nächsten Schritt um diesen Faktor erhöht bzw. verringert: \begin{eqnarray} dp &=& -\frac{\left( p + e \right) \left( m + 4\pi r^3 p \right)}{r \left( r - 2 m \right)} \, dr \nonumber \\ dm &=& 4\pi r^2 e \, dr \nonumber \\ p &=& p + dp \nonumber \\ m &=& m + dm \nonumber \\ r &=& r + dr \nonumber \end{eqnarray}
- Im Laufe der iterativen Lösung verringert sich der Druck ständig. Die Schleife wird solange ausgeführt bis der Wert des Druckes gleich Null bzw. negativ wird (Abruchbedingung: $p\leq0$), da an der Sternoberfläche der Druck verschwindet.
Vorlesung 8
In dieser Vorlesung wird es einen Einblick in eine Softwareplattform geben (das so genannte Einstein Toolkit) mit der man zeitabhängige allgemeinrelativistische Berechnungen, wie z.B. die Kollission zweier Neutronensterne durchführen kann.
Einführung in das Einstein Toolkit
Das Einstein Toolkit (ET) ist eine Softwareplattform mit der man Probleme aus dem Bereich der relativistischen Astrophysik und Gravitationsphysik nummerisch am Computer simulieren kann. Das ET entwickelte sich im Jahre 1998 aus dem Cactus Code und im Laufe der letzten 20 Jahre wurde seine Performance (hoch effiziente OpenMP/MPI Parallelisierung) und Anwendungsbreite ständig verbessert. Mittlerweile kann man mit dem frei zugänglichen ET-Code Kollissionen von schwarzen Löchern und Neutronensternen simulieren und das ET besitzt sogar einen Youtube Kanal auf dem Simulationsergebnisse und Präsentationen zu diversen astrophysikalischen Themen gesammelt sind (klicken Sie dafür auf das obere nebenstehende Bild). Durch Klicken auf des mittlere Bild gelangen Sie zu einem Video das die Entstehungsgeschichte der Programstruktur des ET visualisiert und durch Klicken auf das das untere Bild gelangen Sie zu einem Video das eine binäre schwarze Loch Kollission simuliert (credits to SXS Collaboration). In der Vorlesung werden wir eine neuere, auch frei zugängliche Variante des ET (ET) benutzen, die von Dr. David Radice entwickelte wurde und die sich vom gewöhnlichen ET lediglich im nummerischen Verfahren der hydrodynamischen Gleichungen unterscheidet (siehe ET-WhiskyTHC: the General-Relativistic Templated Hydrodynamics Code).
Computersimulationen mit dem Einstein Toolkit
Am Beispiel einer Neutronenstern Kollission Simulation werden die einzelnen nötigen Schritte erläutert, die man bei einer Computersimulation mit dem ET auszuführen hat. Zunächst muss man das ET (bzw. das ET-WhiskyTHC) herunterladen (siehe Download ET bzw. Download ET-WhiskyTHC) und installieren/kompilieren. Das so erzeugte ausführbare Programm benötigt nun die Anweisungen des Benutzers was im speziellen simuliert werden soll; dies geschiet in der sogennanten .par Datei (siehe z.B. .par file: Kollaps eines Neutronensterns zu einem schwarzen Loch). Bei einer binären Neutronenstern Kollission benötigt man zusätzlich noch die Spezifikation der Zustandsgleichung der Materie und die Energiedichtenverteilung auf der initialen Raumzeit-Hyperfläche ($\Sigma_0$) - diese wird meisst mit dem separatem Progamm LORENE erzeugt. Ein Beispiel einer solchen .par Datei und den zugehörigen LORENE output finden Sie hier. Beim Starten einer Simulation muss die spezielle Architektur des zugrundeliegenden Computers/Computerclusters bei der Angabe der Parallelisierungsprozesse beachtet werden, wobei dies durch die Benutzung des im ET implementierten Teilprogrammes Simfactory erleichtert wird.
Visualisierung der Simulationsergebnisse
Die in der .par Datei definierten Output-Variablen können nach Beendigung der Simulation mittels unterschiedlicher Programme dargestellt werden. Um die Simulationsergebnisse mitOft wird auch die Programmiersprache
Vorlesung 8
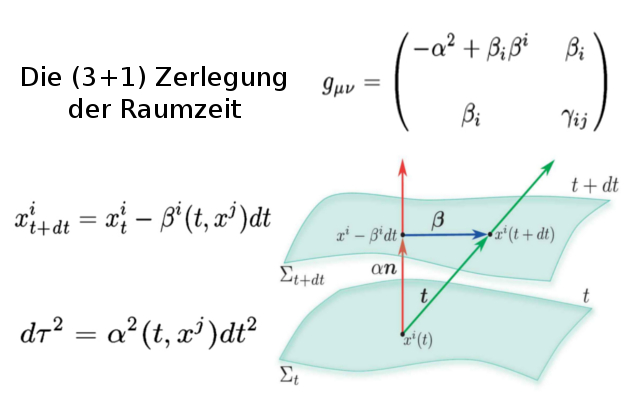
In den vorigen Vorlesungen (sowohl bei der Analyse der Bewegungen um ein rotierendes/nicht-rotierendes schwarzes Loch als auch bei der Berechnung der Eigenschaften von Neutronensternen) hatten wir zeitunabhängige Raumzeiten betrachtet. Die zugrundeliegende Metric $g_{\mu\nu}$ der betrachteten 4-dimensionale Mannigfaltigkeit ${\cal M}$ veränderte sich nicht mit der Zeit und hatte eine vorgegebene räumliche Symmetrie. In dieser Vorlesung wird es einen Einblick in eine Softwareplattform geben (das so genannte Einstein Toolkit) mit der man zeitabhängige allgemeinrelativistische Berechnungen, wie z.B. die Kollission zweier Neutronensterne durchführen kann. Realistische astrophysikalische Computersimulationen müssen die Einstein- und die zugehörigen hydrodynamische Gleichungen ohne spezielle Symmetrieannahmen zeitabhängig lösen. Um dies auf dem Computer zu realisieren muss man die Gleichungen umschreiben. Diese Neuformulierung der Einsteingleichung benutzt den sogenannten ($3+1$)-Split und teilt damit die 4-dimensionale Mannigfaltigkeit ${\cal M}$ in 3-dimensionale raumähnliche Hyperflächen $\Sigma_t$ auf. Die Raumzeit Metrik $g_{\mu\nu}$ wird dadurch in eine rein räumliche Metrik $\gamma_{ij}$, eine Lapse-Funktion $\alpha$ und einen Verschiebungsvektor $\beta_i$ unterteilt: \[ \begin{equation} g_{\mu\nu} ~=~ \begin{pmatrix} -\alpha^2+\beta_i\beta^i & \beta_i \\ \beta_i & \gamma_{ij} \end{pmatrix} \end{equation} \] Die Lapse-Funktion $\alpha$ beschreibt die Differenz zwischen der Koordinatenzeit $t$ und der Eigenzeit eines Fluidteilchens $\tau$ ($d\tau=\alpha ~ dt $). Der Verschiebungsvektor $\beta_i$ misst, wie die Koordinaten auf der räumlichen Hyperfläche $\Sigma_t$ verschoben werden, wenn sich das Fluidteilchen einen infinitesimalen Zeitschritt weiter bewegt. Durch Einfügen dieses Ansatzes der Metrik in die Einstein Gleichung kann man die Gleichungen in ein System von Differentialgleichungen erster Ordnung umformulieren -- die sogenannten ADM-Gleichungen (benannt nach seinen Autoren Richard Arnowitt, Stanley Deser und Charles W. Misner). Da die ADM Gleichungen nicht ''well posed'' sind und sich kleine nummerische Störungen exponentiell aufschaukeln könnten muss man diese noch umschreiben. Die Baumgarte-Shapiro-Shibata-Nakamura-Oohara-Kojima (BSSNOK) - Formulierung der allgemeinen Relativitätstheorie (oder alternativ die CCZ4-Formulierung) ist zusammen mit den relativistischen hydrodynamischen Gleichungen (unter Verwendung der Valencia-Formulierung) als Grundgleichungen in der Softwareplattform Einstein Toolkit implementiert, welches im linken Panel dieser Vorlesung beschrieben wird. Das Programm benötigt die vom Benutzer spezifizierte Anfangs-Hyperfläche $\Sigma_0$ und rechnet dann iterativ in Zeitabschnitten $dt$ die dynamische evolution des betrachteten Systems. Die untere Abbildung visualisiert das besprochene Konzept der ($3+1$) Zerlegung der Raumzeit (Credits: L. Rezzolla, O. Zanotti: Relativistic Hydrodynamics, Oxford Univ. Press (2013)).
Vorlesung 9
Diese Vorlesung stellt den letzten Abschnitt der Vorlesungsreihe dar und die im Semester angegebenen drei folgenden Vorlesungen werden dazu benutzt die gesamten Inhalte des Kurses zu wiederholen und an selbst gewählten Projekten zu arbeiten (siehe rechtes Panel dieser Vorlesung). Am Anfang der Vorlesung wird es jedoch zunächst um Neutronenstern Kollission und deren astrophysikalisch observablen Größen gehen ...
Die Phasen einer binären Neutronenstern Kollission
Mittels der in der vorigen Vorlesung dargestellten Softwareplattform Einstein Toolkit können z.B. eigene Simulationen angefertigt werden oder die Simulationsergebnisse aktueller Simulationen visualisiert und analysiert werden. Die Kollission zweier Neutronensterne und die von dem System ausgesandten Gravitationswellen können mittels aufwendiger Simulationen auf Großrechnern berechnet und mit den gemessenen Gravitationswellen (z.B. GW..) verglichen werden. Mittels einer solchen Analyse wird es in naher Zukunft möglich sein die Eigenschaften der elementaren Materie mittels Gravitationswellen Detektoren zu studieren (z.B. die Eigenschaften des von der QCD vorhergesagten Hadron-Quark Phasenübergang zu studieren). Eine Kollission zweier Neutronensterne läßt sich in einzelne Phasen gliedern und das Video auf der linken Seite illustriert die unterschiedlichen Phasen und die Dynamik des enstehenden hypermassiven hybriden Sterns anhand eines Samelsuriums einzelner klassischer Tänze. Die einzelnen Phasen werden z.B. in M.Hanauske and H.Stöcker, ''Binary Compact Star Mergers and the Phase Diagram of Quantum Chromodynamics'', Discoveries at the Frontiers of Science, Springer (2020) beschrieben. Die in dem Video verwendete Zustandsgleichung ermöglicht leider eine nur kurze Diskofox Phase da die für diese Phase nötige ''double core'' Struktur des hypermassiven Neutronensterns nur kurz nach der Kollission auftritt. Unter Verwendung einer anderen Zustandsgleichung hält sich die Diskofox Phase länger (siehe zweiter Tanz). Die Eigenschaften eines möglichen Hadron-Quark Phasenüberganges lassen sich wohl am besten analysieren, falls sich dieser erst in der Merengue Phase ereignet (siehe Lukas R. Weih, Matthias Hanauske, and Luciano Rezzolla, ''Postmerger Gravitational-Wave Signatures of Phase Transitions in Binary Mergers'', Phys. Rev. Lett. 124, 171103 (2020) und Videos der Simulationsergebnisse in Vorlesung 8). Das letzte Bild des Videos zeigt das emittierte Profil der Gravitationswelle (oben) und das zugehörige Frequenzspektrum (unten) in der Diskofox und Merengue Phase für eine Simulation mit rein hadronischer Zustandsgleichung. Würde sich ein starker Phasenübergang in der Merengue Phase ereignen, so würde die charakteristische $f_2$ Frequenz in einer Art und weise ansteigen, anhand dessen man die Eigenschaften des Hadron-Quark Phasenüberganges bestimmen könnte. Die Tango Phase ereignet sich nur, falls der erzeugte Stern instabil wird und zu einem Kerr schwarzen Loch kollabiert. Der äußere Beobachter nimmt ein Einfrieren des Kollabierenden hypermassiven hybriden Sterns war (siehe Vorlesung 1). Am Ende der Vorlesung werden die astrophysikalisch observablen Größen der zwei (vielleicht drei) detektierten Gravitationswellen von Neutronenstern Kollissionen (siehe GW170817, GW190425 und vielleicht GW190814) präsentiert.
Vorlesung 9
Studentische Projekte



Die studentischen Projekte können alleine oder in Gruppen (bis zu drei Personen) durchgeführt werden. Under construction ...




Vorlesung 10 (Projektarbeit)
Vorlesung 11 (Projektarbeit)
Vorlesung 12
Mögliche Inhalte der mündlichen Prüfung: Einstein Gleichung; Geodäten Gleichung; Berechnung von Chistoffel Symbolen, Riemann Tensor, Ricci Tensor bei vorgegebener Metrik unter Verwendung von Maple/Python; Eigenschaften eines nichtrotierenden schwarzen Loches (Schwarzschild Raumzeit, Ereignishorizont, Photonensphäre), Bewegung eines massiven Probekörpers um ein nichtrotierendes schwarzes Loch (Veranschaulichung der möglichen Bahnbewegungen mittels eines effektiven Potentials), die innerste stabile kreisförmige Bahnbewegung eines Probekörpers (ISCO), Bewegung von masselosen Probekörpern (Licht) um ein nichtrotierendes schwarzes Loch, die Photonensphäre; Neutronensterne: Wie gelangt man zur Tolman Oppenheimer Volkoff Gleichung (TOV) und was kann man mit dieser Gleichung berechnen? Innere Schwarzschild-Metrik, Die Masse-Radius Relation einer Sequenz von Neutronensternen, wie löst man die TOV-Gleichungen nummerisch? Was ist parallele Programmierung und wie parallelisiert man ein Programm? Wie unterscheidet sich OpenMP von MPI; Rotierende schwarze Löcher (Kerr Metrik): Struktur der Ereignishorizonte und der Flächen der stationären Grenze, was ist die Ergosphäre? Was bedeutet der Mitführungseffekt der Raumzeit (frame dragging)?, die innerste stabile kreisförmige Bahnbewegung eines massiven Probekörpers um ein rotierendes schwarzes Loch, das erste Bild eines schwarzen Loches in M87*; Computersimulationen mit dem Einstein Toolkit, Phasen einer binären Neutronenstern Kollission und die in diesem Prozess ausgesandten Gravitationswellen.