Die Quantenmechanik mit Maple
Einführung in die Quantenmechanik
Die Quantenmechanik ist von ihrer Entstehungsgeschichte her als eine experimentell getriebene Theorie anzusehen, d.h. das zunächst Experimente durchgeführt wurden, dessen Ergebnisse nicht im Einklang mit dem damaligen Verständnis der theoretischen Beschreibung standen. Da viele der Aussagen dieser Experimente der Erfahrung und Intuition widersprachen, dauerte es mehrere Jahrzehnte bis eine angemessene theoretische und mathematische Beschreibung gefunden wurde. In dem folgenden Unterpunkt werden die wichtigsten Experimente im Bereich der Quantentheorie vorgestellt, wohingegen der darauf folgende Teil (Von der klassischen Physik zur Quantentheorie) einen ersten Einblick in die theoretische Formulierung der als revolutionär anzusehenden Quantentheorie gibt.
Experimentelle Befunde im Bereich der Quantenmechanik
Der erste Zugang zur Quantenmechanik erfolgt meist über die grundlegenden quantenmechanischen Experimente. In den folgenden Links können Sie sich über die wichtigsten Experimente (Photoeffekt, Doppelspalt-Experiment, Frank-Herz-Versuch, Compton Effekt, Stern-Gerlach-Experiment, Experimente zum Einstein-Podolsky-Rosen-Paradoxon) informieren: Grundlegenden quantenmechanischen Experimente (pdf-Datei, odp-Datei, pptx-Datei), speziell Franck-Herz Versuch (pdf-Datei, odp-Datei) und Compton-Effekt (pdf-Datei, odp-Datei).
Von der klassischen Physik zur Quantentheorie
Um die, in den zuvor beschriebenen Experimenten gewonnenen Resultate theoretisch beschreiben zu können, musste eine gänzlich neue Formulierung der Physik entstehen. Bei der mathematischen Konstruktion dieser neuen Theorie stand man vor dem Dilemma, dass man einerseits daran gebunden ist, jedes physikalische Experiment in den Begriffen der klassischen Physik zu beschreiben, andererseits benötigte man neue, nicht klassische Elemente innerhalb der Theorie, um z.B. den Welle-Teilchen-Dualismus oder nichtlokale Eigenschaften von Teilchen adäquat zu beschreiben. Am Ende dieser Entwicklung stand ein vollkommen neues Gerüst einer mathematischen Beschreibung, welches z.B. mittels der ''Kopenhagener Deutung der Quantentheorie'' interpretiert und verstanden wurde. In diesem Unterkapitel soll der Übergang von der klassischen Physik zur Quantentheorie und die zugrundeliegende ''Kopenhagener Deutung'' am Beispiel des harmonischen Oszillators illustriert werden - bitte klicken Sie dafür auf den unterliegenden Link der Überschrift.
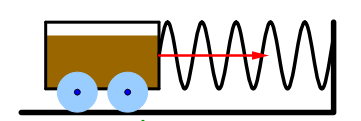
Der harmonische Oszillator am Beispiel eines schwingenden Wagens (siehe Beispiel auf schulphysikwiki.de
In diesem Unterpunkt wird der Übergang von der klassischen Physik zur Quantentheorie und die zugrundeliegende ''Kopenhagener Deutung'' am Beispiel des harmonischen Oszillators illustriert. Da die experimentell überprüfbaren Größen letztendlich mittels der klassischen Begriffe der Physik beschrieben werden müssen steht die Quantenphysik vor einem Dilemma. Einerseits soll die Quantentheorie den Welle-Teilchen-Dualismus und die nichtlokale Eigenschaften von Teilchen adäquat beschreiben, andererseits muss sie auch den Prozess der Zustandsänderung miteinbeziehen, der die Verbindung zu den klassischen Größen ermöglicht.
Betrachten wir z.B. den harmonischen Oszillator in der klassischen Physik. Ein reibungsfreier Wagen sei mittels einer Kraftfeder an einer Wand befestigt. Schubst man den Wagen an, so führt dieser periodische Schwingungen aus, da die Feder eine rücktreibende Kraft ausübt. In der klassischen Physik lassen sich die Größen, die die Bewegung des Wagens charakterisieren zu jeder Zeit experimentell bestimmen und mittels der Bewegungsgleichung theoretisch vorhersagen. Hat man z.B. den Ort und die Geschwindigkeit des Wagens zur Zeit t=0 experimentell bestimmt bzw. festgelegt, so kann man mittels der entsprechenden Lösung der Bewegungsgleichung den Ort und die Geschwindigkeit zu einem späteren Zeitpunkt angeben.
$$
\begin{eqnarray}
\hbox{Bewegungsgleichung} \quad +& \hbox{Anfangsbedingungen} \quad \Rightarrow & \quad \hbox{Trajektorie der Bewegung} \\
\frac{d^2 r(t)}{dt^2} = -\frac{k}{m} r(t) \qquad & r(0)=0, v(0)=40 \quad & r(t)= \frac{40}{\sqrt(\frac{k}{m})} \hbox{sin}\left( \frac{k}{m} t \right)
\end{eqnarray}
$$
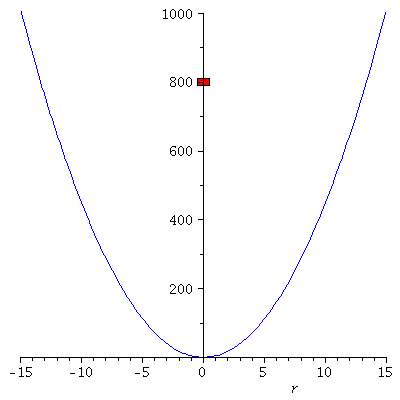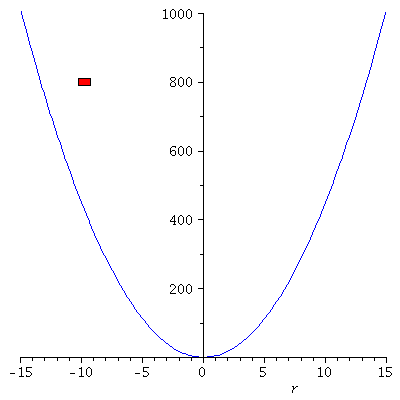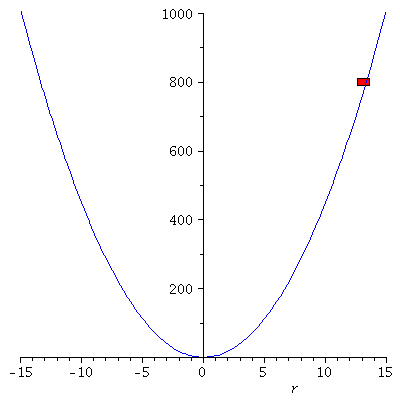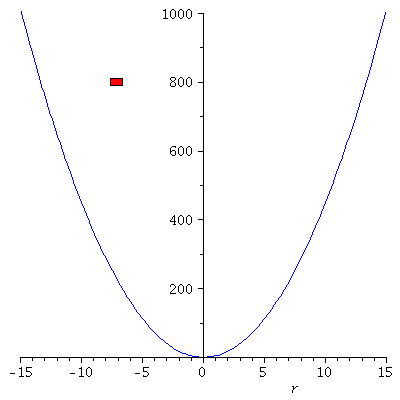
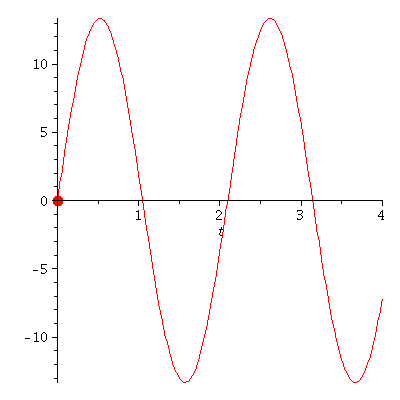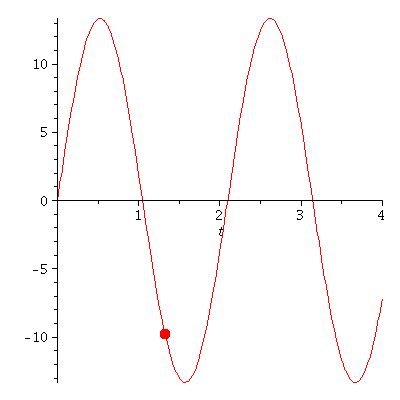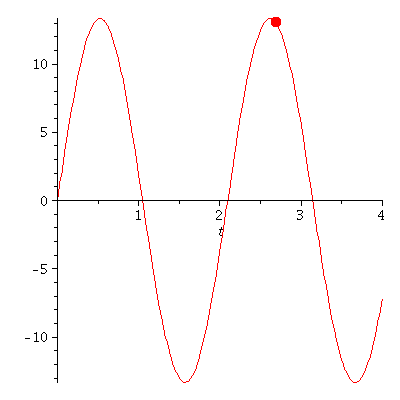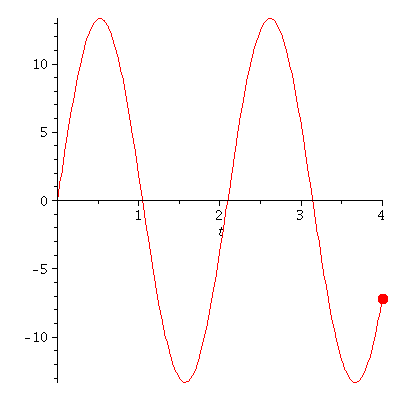
Veranschaulichung der Bewegung eines klassischen harmonischen Oszillators.
Die zugrundeliegenden mathematischen Schritte, die den Weg von der Bewegungsgleichung hin zu der Angabe der Lösung beschreiben, werden in dem folgenden Link mittels Maple berechnet (siehe Maple Worksheet: Der Harmonische Oszillator aus klassischen Sichtweise). Eine kurze Einfürung in das Computeralgebra-System Maple finden Sie unter den folgenden Link: Maple Worksheet: Einfürung in Maple. Zusätzlich können in Maple Animationen erstellt werden, die die Dynamik der Bewegung veranschaulichen. Die neben stehende Abbildung zeigt eine solche Animation und veranschaulicht die Bewegung des Wagens, wobei die linke Abbildung die Bewegung im parabolischen Potential veranschaulicht und die rechte Abbildung die Lösung der Bewegungsgleichung r(t) als Funktion der Zeit darstellt (es wurde k=9, m=1, r(0)=0 und v(0)=40 gesetzt).
Die den Körper beschreibenden Größen, der Ort r an dem sich der Wagen befindet und die Geschwindigkeit v (bzw. der Impuls $p = m v $) können in der klassischen Physik zu jeder Zeit exakt theoretisch vorhergesagt und innerhalb der Grenzen der experimentellen Genauigkeit bestimmt werden. In der Quantenmechanik ist dies nicht mehr der Fall. Aufgrund der Heisenbergsche Unschärferelation können die komplementären Größen Ort und Impuls nicht gleichzeitig exakt angegeben werden. Bestimmt man z.B. den Ort des Wagens zur Zeit t=0 sehr genau, dann ist die Angabe seines Impulses (seiner Geschwindigkeit) nur noch mit großer Ungenauigkeit möglich. Hätte man eine solche fundamentale Unschärfe in den Anfangsbedingungen auch in der klassischen Physik, dann wären die durch die Bewegungsgleichung festgelegten Trajektorien des Wagens ebenfalls unterschiedlich und man könnte seinen zukünftigen Ort nicht genau vorhersagen. Der Übergang zur quantenmechanischen Beschreibung manifestiert sich nun in mehreren neuen Begriffen: Zunächst definiert man die Zustandsfunktion $\psi(r,t)$ bzw. die Wellenfunktion des Quantenobjektes (hier speziell des Quanten-Wagens). Diese Größe beschreibt den Zustand des Quantenobjektes vollständig und ihre Interpretation und Deutung ist in einer klassischen Denkweise nicht möglich. Nach der ''Kopenhagener Deutung'' beschreibt die Zustandsfunktion $\psi(r,t)$ die Wahrscheinlichkeit von messbaren Ereignissen die man an dem Quantenobjekt durchführen kann (z.B. die Orts- oder Impulsmessung). Sie stellt jedoch nicht den Ablauf von wirklichen Ereignissen dar, sondern beschreibt mehr eine Tendenz einer zeitlichen Entwicklung.

Veranschaulichung der quantentheoretischen Konzepte der Quantenmechanik.
Mathematisch wird dies dadurch realisiert, dass die Zustandsfunktion $\psi(r,t)$ ein Element aus einem ganz speziellem, der klassischen Physik nicht zugänglichem Raum (dem sog. Hilbertraum $ \psi(r,t) \in {\cal H}$) ist, welcher auf dem Konzept der komplexen Zahlen (reelle und imaginäre Zahlen) aufgebaut ist. Um die Vorhersagen der Quantentheorie experimentell überprüfen zu können, musste man ein weiteres Konzept innerhalb der Theorie implementieren - den sog. quantenmechanischen Messprozess. Möchte man durch ein Experiment eine gewisse Eigenschaft des Quantenzustandes messen (z.B. den Ort oder den Impuls des Quantenobjektes), so zwingt der Experimentator mittels des Messprozesses den Zustand in den reellen Raum der Messgrößen überzugehen. Mathematisch wird die Vorgehensweise des Experimentators durch die Anwendung eines Operators $\hat{M}$ auf den Zustand $\psi(r,t)$ formuliert. Der Erwartungswert der Messgröße bestimmt sich mittels der folgenden Gleichung: $\left< \hat{M} \right> \,=\, \int_{-\infty}^\infty \psi(r,t)^*\, \hat{M}\, \psi(r,t)\,\, dr$. Die nebenstehende Abbildung veranschaulicht die besprochenen quantentheoretischen Konzepte. Im Laufe dieser Vorlesung werden die Konzepte der Quantenmechanik näher erläutert und die Bewegungsgleichung, die die zeitliche Entwicklung der Zustandsfunktion bestimmt (die sog. Schrödingergleichung) wird angegeben und an mehreren Beispielen illustriert werden.
Die Schrödinger-Gleichung
Wie in der Einleitung erläutert, wird in der quantenmechanischen Beschreibung ein apriorischer Zustand $\Psi$ des Teilchens definiert. Wie beschreibt man nun diesen Zustand eines Quantenobjektes mathematisch? Einerseits soll die zeitliche Entwicklung dieses Zustandes keine wirkliche, reale Abfolge von Ereignissen darstellen - eher eine Tendenz der Entwicklung. Der Zustand soll einer Wahrscheinlichkeitsbeschreibung von meßbaren Ereignissen dienen aber paradoxerweise selbst nicht real und empirisch fassbar sein. Die mathematische Beschreibung einer solchen Zustandsfunktion benutzt neben der realen Zahlenwelt auch die imaginären Zahlen und beschreibt den Zustand des Teilchens in einem komplexwertigen sog. Hilbertraum $\Psi \in {\cal H}$. Im Moment der Messung kollabiert dieser Zustand zu einer beobachtbaren Eigenschaft des Teilchens und diese observable Größe des Zustandes wird real.
In diesem Unterpunkt wird die wichtigste Gleichung der nichtrelativistischen Quantenmechanik (die sog. Schrödinger-Gleichung) vorgestellt und diversen Beispielen erläutert. Die Schrödinger-Gleichung beschreibt wie sich die Zustandsfunktion eines Quantenobjektes $\Psi(\vec{r},t)$ zeitlich verändert und bestimmt zusätzlich ihr räumliches Verhalten unter Einwirkung einer Kraft, die durch ein Potential $V(\vec{r},t)$ hervorgerufen wird. Sie besitzt das folgende Aussehen:
$$
\begin{equation}
i \hbar \frac{\partial\, \Psi(\vec{r},t)}{\partial t} = \hat{H} \, \Psi(\vec{r},t) \quad \hbox{wobei:} \quad \hat{H} = -\frac{\hbar^2}{2 m} \Delta + V(\vec{r},t)
\end{equation}
$$
$\hat{H}$ ist der sog. Hamiltonoperator und $\Delta=\vec{\nabla}^2=\frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2}$ der Laplace-Operator.
Unter der Annahme, dass das Potential nicht von der Zeit abhängt ($V(\vec{r},t)=V(\vec{r})$), lässt sich die Schrödinger-Gleichung mittels des Produktansatzes $\Psi(\vec{r},t)=\psi(\vec{r}) \cdot f(t)$ in die sog. stationäre (zeitunabhängige) Schrödinger-Gleichung umschreiben:
$$
\begin{equation}
\hat{H} \, \psi(\vec{r}) = E \, \psi(\vec{r}) \quad \hbox{mit:}\qquad \Psi(\vec{r},t)=\psi(\vec{r})\,\underbrace{e^{-\frac{i\,E}{\hbar}\,t}}_{f(t)} \quad,
\end{equation}
$$
wobei E die Energie des Zustandes darstellt.
Der quantenmechanische Zustand und die ''de Broglieschen Materiewelle''
Die einfachste Lösung der Schrödinger-Gleichung ist die eines freien, ungebundenen Quantenteilchens; man bezeichnet sie als die sog. "de Broglieschen Materiewellen". Um die Beschreibung dieser Materiewellen auf räumlich begrenzte Teichen anwenden zu können, muss man zu endlichen Wellenpaketen übergehen. Das entsprechende Maple Worksheet finden Sie unter folgendem Link: Maple Worksheet: Der quantenmechanische Zustand und die ''de Broglieschen Materiewelle''. Zusätzlich gibt es die zwei folgenden Worksheets: Maple Worksheet: Das zeitliche Verhalten von Materiewellen (Wellenpaketen) und Maple Worksheet: Zusatz: Die Fourier-Reihe und das Fourier-Integral
Ein Quantenteilchen im Potentialtopf
In diesem Unterpunkt betrachten wir die stationäre Lösung der Schrödinger-Gleichung eines Quantenteilchen in einem Potentialtopf. Zunächst nehmen wir an, dass der Potentialtopf unendlich hohe Wände hat und beschränken uns auf den eindimensionalen bzw. zweidimensionalen Fall. Das entsprechende Maple Worksheet finden Sie unter folgendem Link: Maple Worksheet: Ein Quantenteilchen im Potentialtopf mit unendlich hohen Wänden. Danach betrachten wir einen endlich hohen Potentialtopf in einer Dimension. Das entsprechende Maple Worksheet finden Sie unter folgendem Link: Maple Worksheet: Ein Quantenteilchen im eindimensionalen Potentialtopf mit endlicher Tiefe. Wir werden sehen, dass in allen betrachteten Fällen eine Quantisierung der Energie in natürlicher Weise entsteht und die möglichen Zustände des Quantenteilchens in diskrete Eigenzustände untergliedert werden können.
Der harmonische Oszillator in der Quantenmechanik
Wir betrachten im Folgenden den quantenmechanischen Zustand eines Teilchens, welcher in einem Potentialtopf mit parabolischer Gestalt gebunden ist und beschränken uns auf eine räumliche Dimension. Ein Vergleich mit dem klassischen harmonische Oszillator zeigt, dass ein Quantenteilchen sich vollkommen anders verhält. Aufgrund der Eigenschaften der Quantentheorie entsteht wiederum eine Quantisierung der Energie und die möglichen Zustände des Quantenteilchens treten nur in diskrete Eigenzuständen auf. Das entsprechende Maple Worksheet finden Sie unter folgendem Link: Maple Worksheet: Der harmonische Oszillator in der Quantenmechanik.
Superposition von Zuständen und deren zeitliche Entwicklung
Die letzten beiden Teilkapitel stellten Beispiele von stationären Eigenzustände dar. Ein allgemeiner Zustand eines Quantenteilchens setzt sich aus einer überlagerung (Superposition) dieser Eigenzustände zusammen - dies wird hier am Beispiel des harmonische Oszillator gezeigt. Die zeitliche Entwicklung eines Zustandes wird ebenfalls in diesem Unterkapitel besprochen. Das entsprechende Maple Worksheet finden Sie unter folgendem Link: Maple Worksheet: Superposition von Zuständen und deren zeitliche Entwicklung.
Der Tunneleffekt
Der Tunneleffekt ist eine wichtige Eigenschaft von Quantenteilchen. Dieser Effekt wird in diesem Unterkapitel am Beispiel des eindimensionalen, rechteckigen Potentialwalls illustriert. Das entsprechende Maple Worksheet finden Sie unter folgendem Link: Maple Worksheet: Der Tunneleffekt.
Streuzustände eines Quantenteilchens an einem eindimensionalen Potentialtopf mit endlicher Tiefe
In diesem Unterkapitel werden ungebundene Zustände (Streuzustände) eines Quantenteilchens am Beispiel des eindimensionalen Potentialtopfes endlicher Tiefe diskutiert. Das entsprechende Maple Worksheet finden Sie unter folgendem Link: Maple Worksheet: Streuzustände eines Quantenteilchens an einem eindimensionalen Potentialtopf mit endlicher Tiefe.
Das Wasserstoffatom
Die Herleitung des Elektronen-Zustandes im Wasserstoffatoms erfolgt in unterschiedlichen Schritten. Maple Worksheet: Das Wasserstoffatom.