Download Maple Worksheet
Theoretische Physik 3 für Lehramt L3
Quantenmechanik, Spezielle Relativitätstheorie und weitere Gebiete der Theoretischen Physik
Vorlesung gehalten an der J.W.Goethe-Universität in Frankfurt am Main (Wintersemester 2016/17)
von Prof. Dr. Dr.h.c. Horst Stöcker und Dr.phil.nat. Dr.rer.pol. Matthias Hanauske
Frankfurt am Main 17.10.2016
Erster Vorlesungsteil: Quantenmechanik
Kapitel I: 1) Einführung in die Quantenmechanik (Von der klassischen Physik zur Quantentheorie)
Der Harmonische Oszillator aus klassischen Sichtweise
Einführung
In diesem Maple Worksheet wird zunächst eine kurze Einführung in das Computeralgebra-System Maple gegeben. Im zweiten Unterpunkt wird der harmonische Ozillator aus klassischer Sichtweise betrachtet.
Eine kleine Einführung in Maple
Definition einer Variable m und einer Funktion V
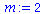 |
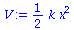 |
(2.1) |
Beide Größen haben jetzt die festgelegten Werte:
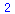 |
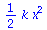 |
(2.2) |
Man kann die Funktion V wie folgt differenzieren und integrieren:
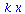 |
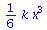 |
(2.3) |
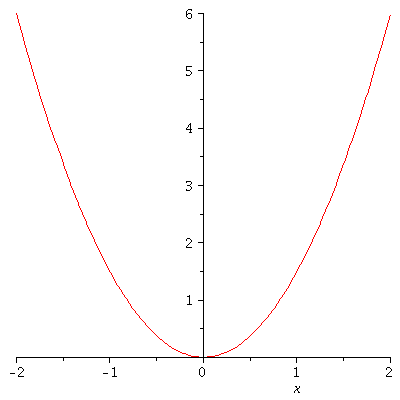
Legt man den Parameter k fest (z.B. k=3), so kann man die Funktion darstellen (hier z.B. von x=-2 bis x=2):
| > |
plot(subs(k=3,V),x=-2..2); |
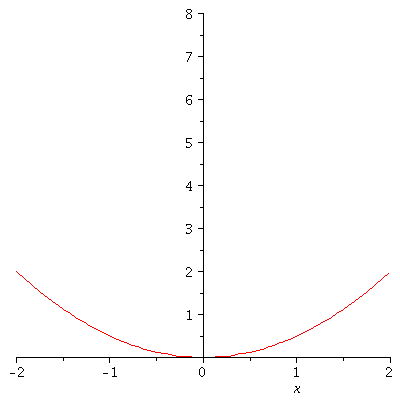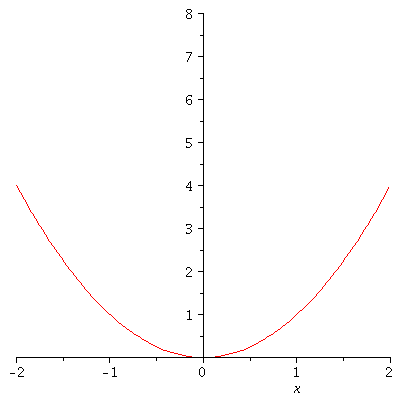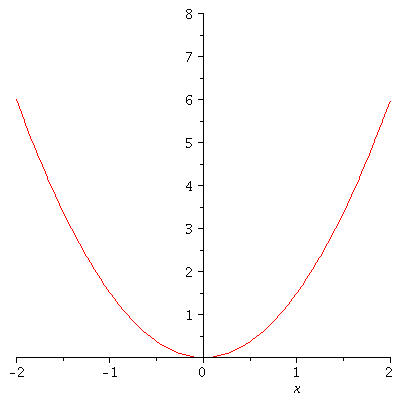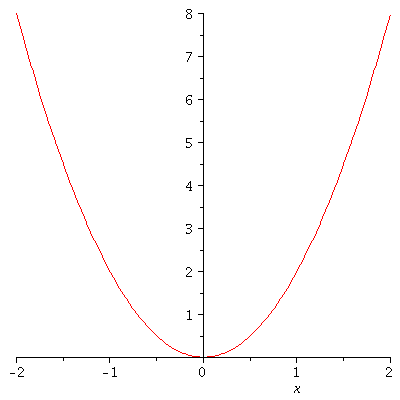
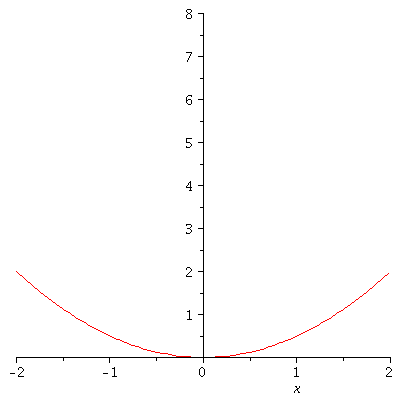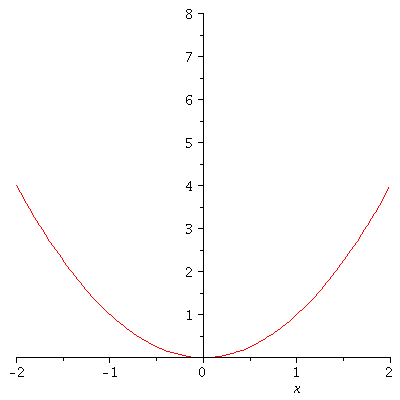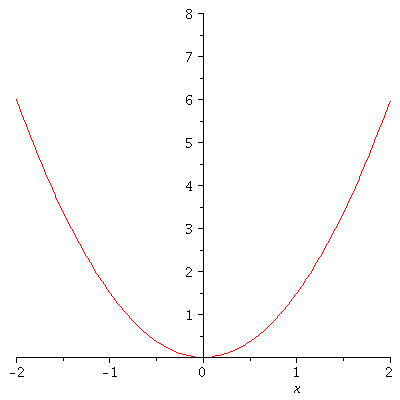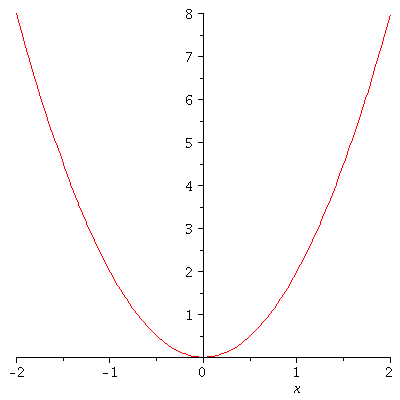
Legt man k nicht fest, so kann man die Funktion in einer Sequenz von k-Werten in einer animierten Grafik darstellen (Zusatzpacket plots erforderlich):
| > |
with(plots):
animate(V,x=-2..2,k=1..4); |
Die selbe Animation kann man auch mittels einer itterativen Aneinanderreihung der einzelnen Bilder erzeugen:
| > |
for i from 1 by 1 to 4 do
Ani[i]:=plot(subs(k=i,V),x=-2..2);
od: |
| > |
display([seq(Ani[i],i=1..4)],insequence=true); |
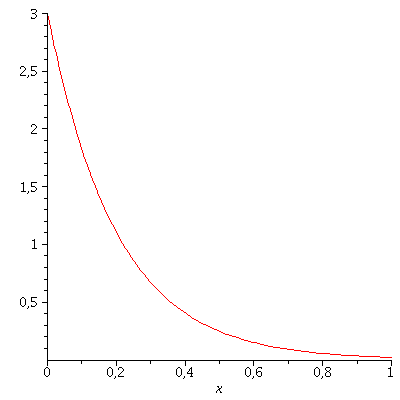
Die Lösung von Differentialgleichungen erfolgt wie folgt: Hier behandeln wir eine einfache Differentialgleichung erster Ordnung und legen den Anfangswert der Funktion f auf f(0)=3 fest
| > |
DGL:=diff(f(x),x)=-5*f(x);
Loes:=dsolve({DGL,f(0)=3});
plot(rhs(Loes),x=0..1); |
Der Harmonische Oszillator aus klassischer Sichtweise
| > |
restart:
with(plottools):
with(plots): |
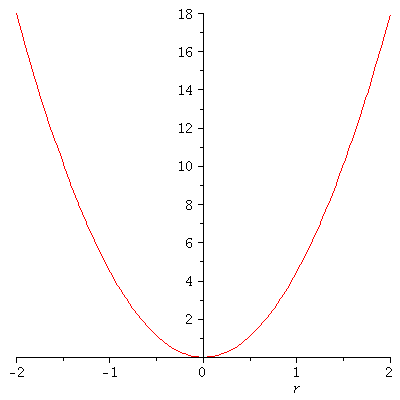
Wir betrachten den Harmonischen Oszillator am Beispiel eines reibungsfrei gelagerten Wagens (Masse=m) auf dem eine Rückstellkraft einwirkt die proportional zu seiner Auslenkung r ist (Proportionalitätskonstante k). Aufgrund dieser Form der Krafteinwirkung besitzt das zugrundeliegende Potential die Form einer Parabel:
| > |
V:=k/2*r^2;
plot(subs(k=9,V),r=-2..2); |
Die entsprechende Differentialgleichung lautet wie folgt (wir setzen k/m=omega^2):
| > |
DGL:=diff(r(t),t,t)=-k/m*r(t);
DGL:=diff(r(t),t,t)=-omega^2*r(t); |
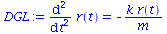 |
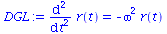 |
(3.1) |
Da die Differentialgleichung von zweiter Ordnung in der Zeit ist, sind zwei freie Parameter (Neben- bzw. Anfangsbedingungen) noch festzulegen. Wir wählen z.B. r(0)=0 und r'(0)=40.
| > |
Loes:=dsolve({DGL,r(0)=0,D(r)(0)=40}); |
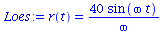 |
(3.2) |
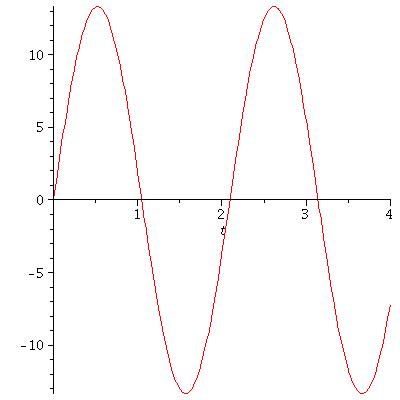
Die Lösung können wir uns wieder in einem Diagram darstellen (wir setzen z.B. k=9 und m=1):
| > |
plot(subs(omega=3,rhs(Loes)),t=0..4); |
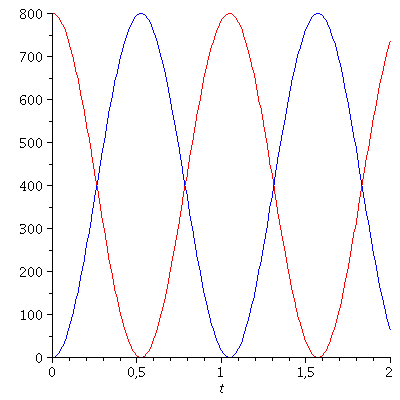
Die kinetische und potentielle Energie variieren ebenfalls zyklisch, wobei die Gesamtenergie erhalten ist:
| > |
KinE:=m/2*(diff(subs(omega=3,rhs(Loes)),t))^2;
PotE:=subs(omega=3,subs({k=9,r=rhs(Loes)},V));
PlotKinE:=plot(subs(m=1,KinE),t=0..2):
PlotPotE:=plot(PotE,t=0..2,color=blue):
display(PlotKinE,PlotPotE); |
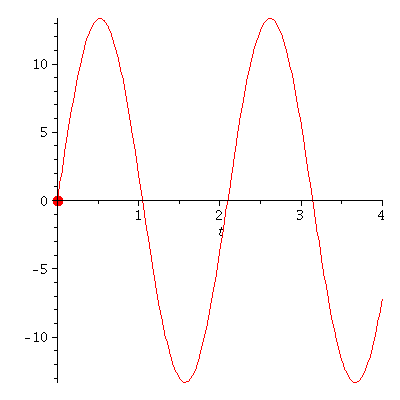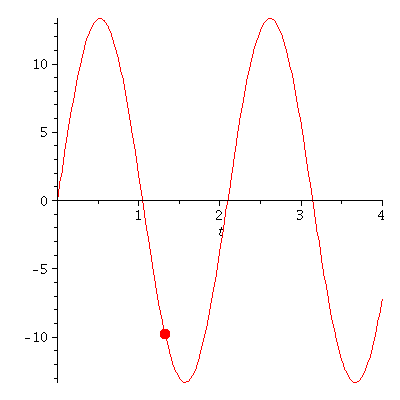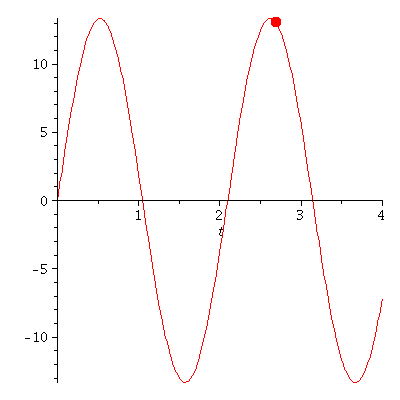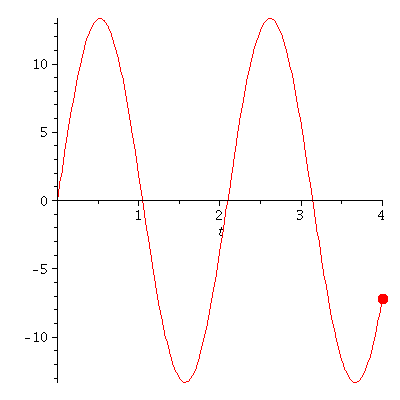
Wir können uns die Bewegung in folgender Animation veranschaulichen:
| > |
tend:=4:
frames:=100:
dt:=tend/frames:
PLoes:=plot(subs(omega=3,rhs(Loes)),t=0..tend):
PPot:=plot(subs(k=9,V),r=-15..15,color=blue,view=[-15..15, 0..1000]):
for i from 0 by 1 to frames do
tt:=i*dt:
rr:=subs({omega=3,t=tt},rhs(Loes)):
Ani1[i]:=display(rectangle([-0.5+rr, 810], [0.5+rr, 790], color = red)):
PointA[i]:=pointplot({[tt, rr]},symbol=solidcircle,symbolsize=23,color=red):
Ani[i]:=display(Matrix(1,2,[[display(PPot,Ani1[i]),display(PLoes,PointA[i])]]));
od: |
| > |
display([seq(Ani[i],i=0..frames)],insequence=true); |
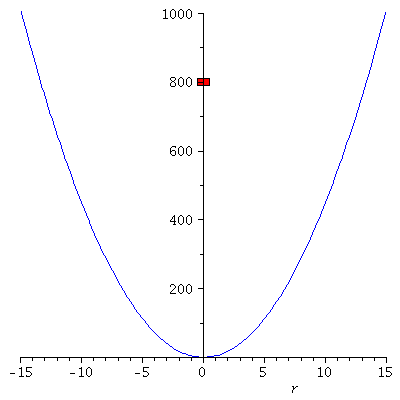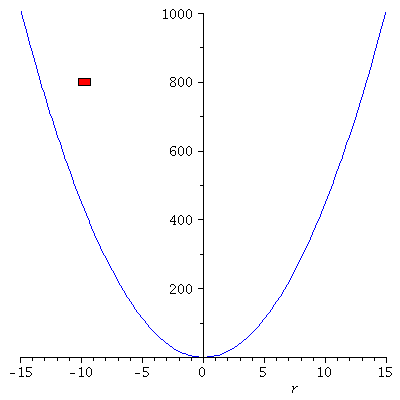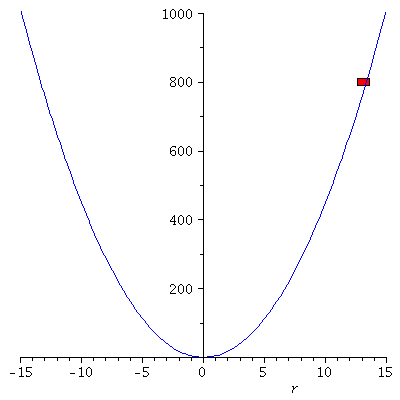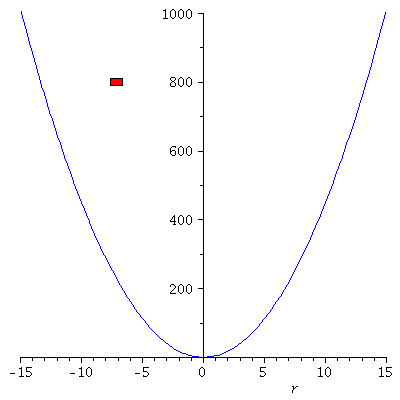
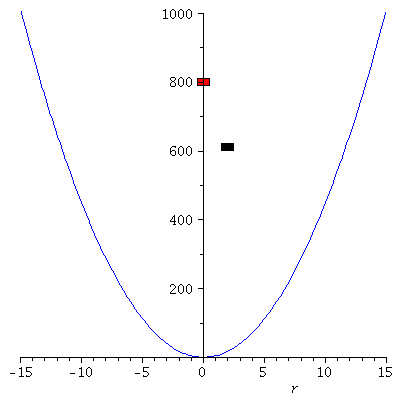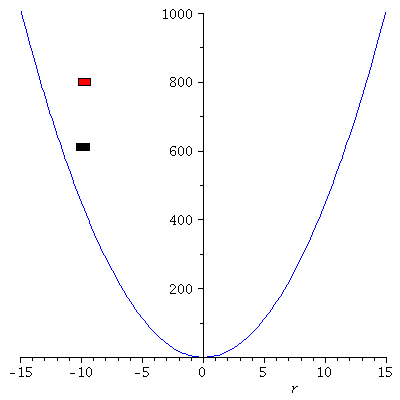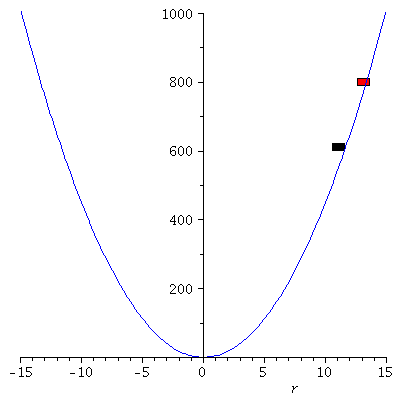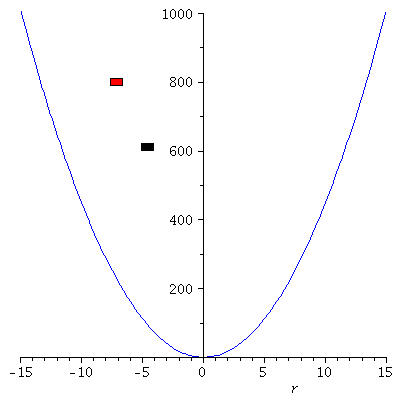
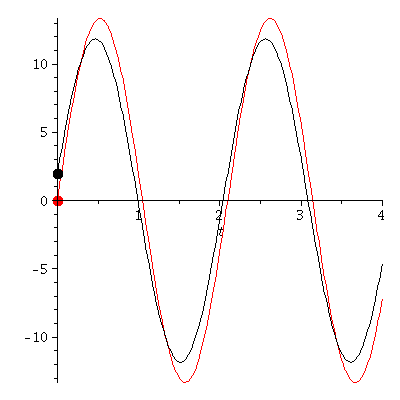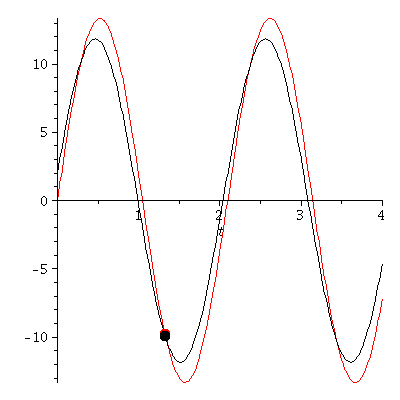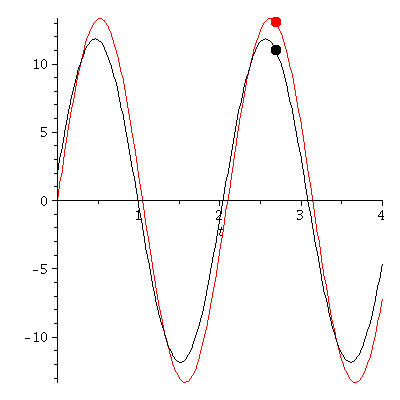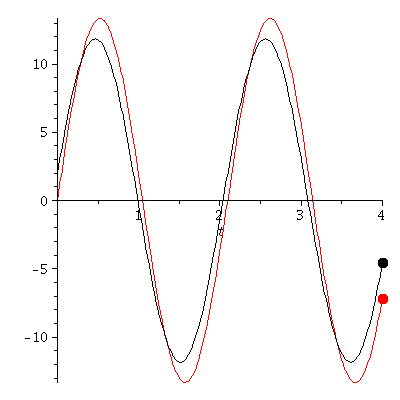
Verändern wir die Anfangsbedingungen, so ergeben sich unterschiedliche Bewegungen (Roter Wagen: r(0)=0 und r'(0)=40, Schwarzer Wagen: r(0)=2 und r'(0)=35)
| > |
Loes1:=dsolve({DGL,r(0)=2,D(r)(0)=35}):
tend:=4:
frames:=100:
dt:=tend/frames:
PLoes1:=plot(subs(omega=3,rhs(Loes1)),t=0..tend,color=black):
PLoes:=plot(subs(omega=3,rhs(Loes)),t=0..tend,color=red):
PPot:=plot(subs(k=9,V),r=-15..15,color=blue,view=[-15..15, 0..1000]):
for i from 0 by 1 to frames do
tt:=i*dt:
rr:=subs({omega=3,t=tt},rhs(Loes)):
Ani1[i]:=display(rectangle([-0.5+rr, 810], [0.5+rr, 790], color = red)):
PointA[i]:=pointplot({[tt, rr]},symbol=solidcircle,symbolsize=23,color=red):
rr1:=subs({omega=3,t=tt},rhs(Loes1)):
Ani11[i]:=display(rectangle([-0.5+rr1, 602.5], [0.5+rr1, 622.5], color = black)):
PointA1[i]:=pointplot({[tt, rr1]},symbol=solidcircle,symbolsize=23,color=black):
Ani[i]:=display(Matrix(1,2,[[display(PPot,Ani1[i],Ani11[i]),display(PLoes,PLoes1,PointA[i],PointA1[i])]]));
od: |
| > |
display([seq(Ani[i],i=0..frames)],insequence=true); |