Der harmonische Oszillator in der Quantenmechanik  

>	restart: with(plots): with(StringTools):

 

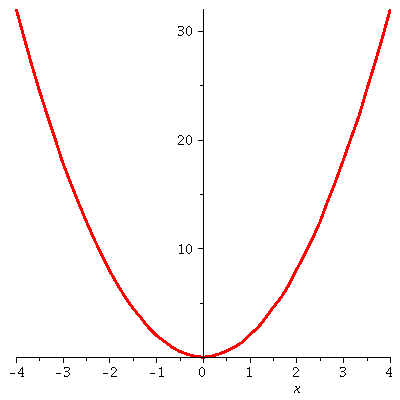
Wir betrachten im folgenden einen quantenmechanischen Zustand eines Teilchens, welcher in einem Potentialtopf gebunden ist der eine parabolische Gestalt hat. Wir beschränken uns zunächst auf eine räumliche Dimension. Der Potentialtopf besitz z.B. das folgende Aussehen: 

>	V:=k/2*x^2; setk:=4; plot(subs({k=setk},V),x=-4..4,thickness=3);

 

Da der Hamiltonoperator dieses Systems nicht von der Zeit abhängt, vereinfacht sich die Schrödingergleichung. Der stationäre Teil der Schrödingergleichung lautet: 

>	SGL:=hq^2/(2*m)*diff(psi(x),x,x) +V*psi(x) = E*psi(x);

 

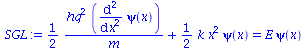(1.1)

 

Mit den folgenden Abkürzungen (omega^2=k/m, a=sqrt(omega*m/hq) und b=2*E/(hq*omega)) schreibt sich die Schrödingergleichung wie folgt: 

>	SGL:=diff(psi(x),x,x) + (a^4*x^2-b*a^2)*psi(x)=0;

 

(1.2)

 

Wir führen zusätzlich noch eine Skalierung der Ortskoordinate x durch (u=a*x) ein: 

>	SGL:=diff(psi(u),u,u) + (b-u^2)*psi(u)=0;

 

(1.3)

 

und machen den folgenden Lösungsansatz psi(u)=H(u)*exp(-u^2/2) und setzen diesen in die vorige Differentialgleichung ein: 

>	psi(u)=H(u)*exp(-u^2/2); SGLa:=eval(subs({psi(u)=H(u)*exp(-u^2/2)},SGL));

 

 

	(1.4)

 

Dur Division von exp(-u^2/2) kann man die Gleichung wie folgt vereinfachen: 

>	SGLb:=simplify(SGLa/exp(-(1/2)*u^2));

 

(1.5)

 

Wir nehmen nun an, dass sich die gesuchte Funktion H(u) durch einen Potenzreihenansatz darstellen lässt und setzen diesen in die obige Differentialgleichung ein. Zur Veranschaulichung der Vorgehensweise haben wir hier die Potenzreihe nur bis n=6 dargestellt. Im Allgemeinen (zumindest an dieser Stelle noch), hat die Potenzreihe im Prinzip unendlich viele Glieder: 

>	H(u)=sum(c[i]*u^i,i=0..6); Eq1:=sort(expand(subs(H(u)=sum(c[i]*u^i,i=0..6),SGLb)),u);

 

 

	(1.6)

 

Da diese Gleichung für alle u erfüllt sein sollte, muss sie für jeden Potenzgrad in u separat erfüllt sein. Aufgrund dieser Eigenschaft gelangt man zu den folgenden Bedingungen an die Koeffizienten c[l] der Potenzreihe.  

>	Beda:=coeffs(lhs(Eq1), u): for ii from 1 by 1 to 5 do Beda[ii]=0; od;

 

 

 

 

 

	(1.7)

 

Diese Bedingungen an die Koeffizienten c[l] lassen sich durch die folgende Rekursionsformel darstellen: c[l+2]:=-(b-1-2*l)/((l+1)*(l+2))*c[l] . Da die ursprüngliche Differentialgleichung von zweiter Ordnung ist, sind zwei der Koeffizienten frei wählbar (z.B. c[0] und c[1]). Die weiteren Koeffizienten sind dann durch die Rekursionsformel festgelegt: 

>	for l from 0 by 1 to 5 do c[l+2]:=-(b-1-2*l)/((l+1)*(l+2))*c[l]: od;

 

 

 

 

 

 

	(1.8)

 

Man kann zeigen, dass aufgrund der Forderung der Normierbarkeit der Funktion psi(u), die Potenzreihe nicht unendlich sein darf und somit die Koeffizienten c[l] nach einem gewissen Wert identisch verschwinden müssen. Die Potenzreihe bricht genau dann ab, wenn der Parameter b gleich einer ungeraden Zahl ist. Setzen wir z.B. b=15, c[0]=0, so folgt 

>	c[0]:=0; for l from 0 by 1 to 10 do c[l+2]:=-(15-1-2*l)/((l+1)*(l+2))*c[l]: od;

 

 

 

 

 

 

 

 

 

 

 

 

	(1.9)

 

Die Potenzreihe hätte dann das folgende Aussehen: 

>	H(u)=sum(c[i]*u^i,i=0..12);

 

(1.10)

 

Eine solche Funktion nennt man hermitesches Polynom, sie ist in Maple schon vordefiniert. Bei geeigneter Wahl von c[1] entspricht die Funktion H(u) dieser Funktion (hier speziell c[1]=): 

>	simplify(HermiteH(7, u)/(-1680));

 

(1.11)

 

Die gesamte Lösung der Zustandes des Quantenteilchens im parabolischen Potential setzt sich somit aus dem hermitesches Polynom des Grades n und dem Faktor exp(-u^2/2) zusammen, wobei eine Normierungskonstante A noch festzulegen ist. Wir setzen im folgenden  hq=m=1, so dass a=sqrt(omega) und b=2*E/omega. Zusätzlich führen wir eine Rücksubstitution der Variablen u durch (u=a*x) 

>	PSI:=A*HermiteH(n, u)*exp(-u^2/2): PSI:=subs({u=sqrt(omega)*x},PSI);

 

(1.12)

 

Betrachten wir nun z.B. den Grundzustand n=0 und setzen omega=2 (m=1,k=4), so können wir die noch unbekannte Amplitude durch die Normierungsbedingung festlegen: 

>	setn:=0: setomega:=2: psi[0]:=subs({omega=setomega,n=setn,u=sqrt(omega)*x},PSI); GLNorm:=int(psi[0]*psi[0],x=-infinity..infinity)=1:

 

(1.13)

 

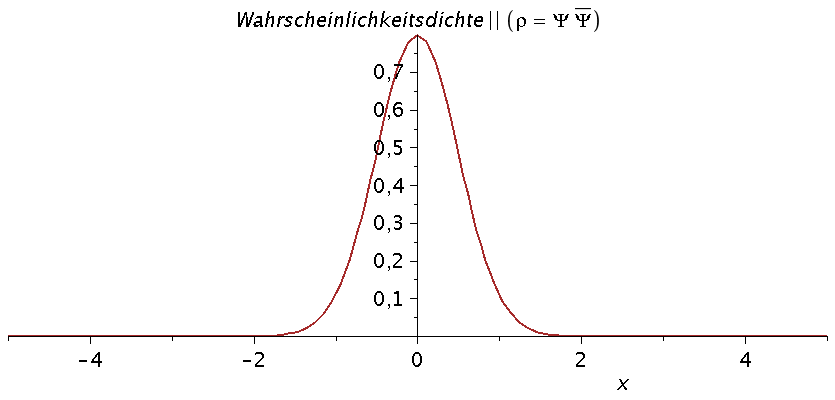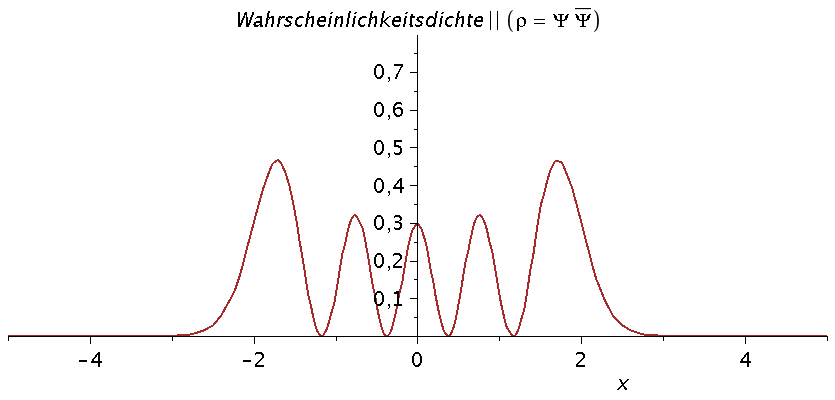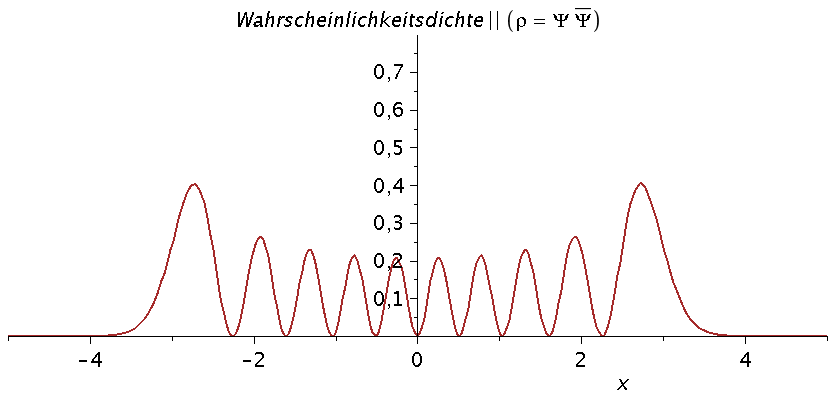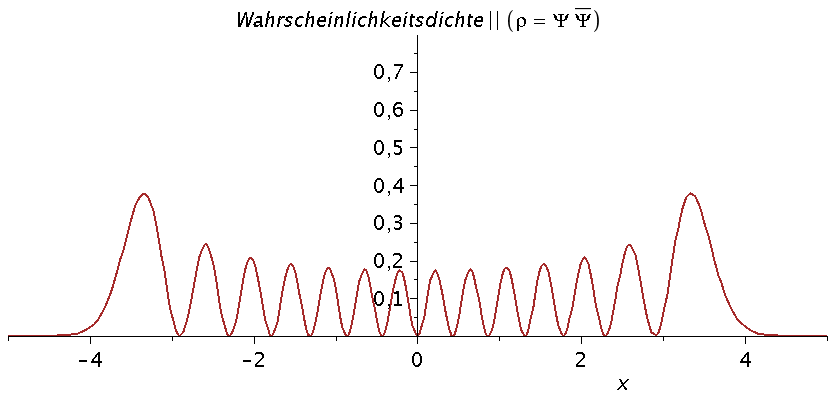
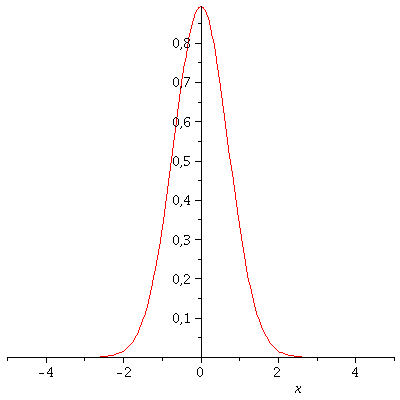
Der Grundzustandzustand des Quantenteilchens besitzt somit das folgende Aussehen, wobei sich die Energie des Zustandes durch den folgenden Ausdruck festgelegt ist E= b*omega/2 mit (b=2*n+1) 

>	psi[0]:=subs(A=simplify(solve(GLNorm,A)[1]),psi[0]); E[0]=subs({omega=setomega,n=setn},(2*n+1)*omega/2); plot(psi[0],x=-5..5);

 

Betrachten wir nun z.B. den Zustand n=5, setzen omega=2 und legen die unbekannte Amplitude durch die Normierungsbedingung fest: 

>	setn:=5: psi[setn]:=subs({omega=setomega,n=setn,u=sqrt(omega)*x},PSI); GLNorm:=int(psi[setn]*psi[setn],x=-infinity..infinity)=1;

 

 

	(1.14)

 

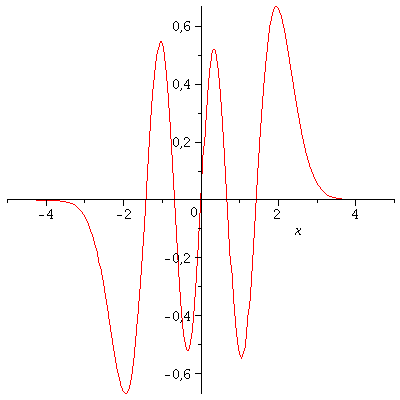
Der n=5 Zustand des Quantenteilchens besitzt somit das folgende Aussehen, wobei sich die Energie des Zustandes durch den folgenden Ausdruck festgelegt ist E= b*omega/2 mit (b=2*n+1) 

>	psi[setn]:=subs(A=simplify(solve(GLNorm,A)[1]),psi[setn]); E[setn]=subs({omega=setomega,n=setn},(2*n+1)*omega/2); plot(psi[setn],x=-5..5);

 

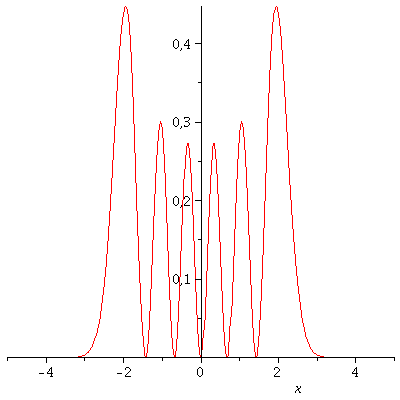
Die Wahrscheinlichkeit das Teilchen am Ort x zu finden ist nun durch die sog. Wahrscheinlichkeitsdichte rho=psi*psi gegeben. Für den n=5 Zustand erhält man: 

>	rho[setn]:=conjugate(psi[setn])*psi[setn]: plot(rho[setn],x=-5..5);

 

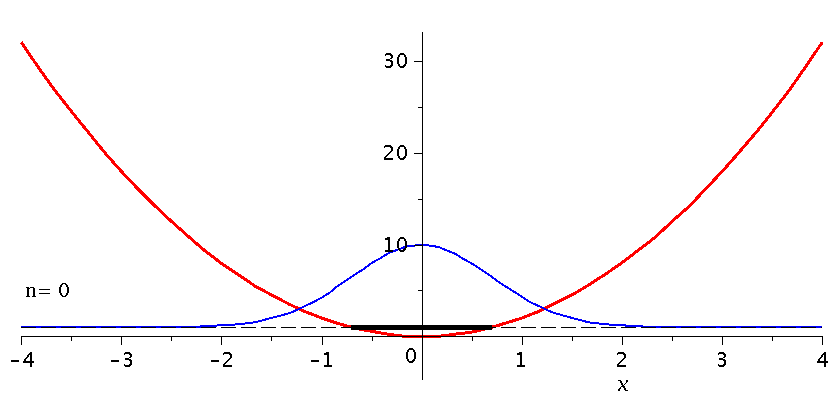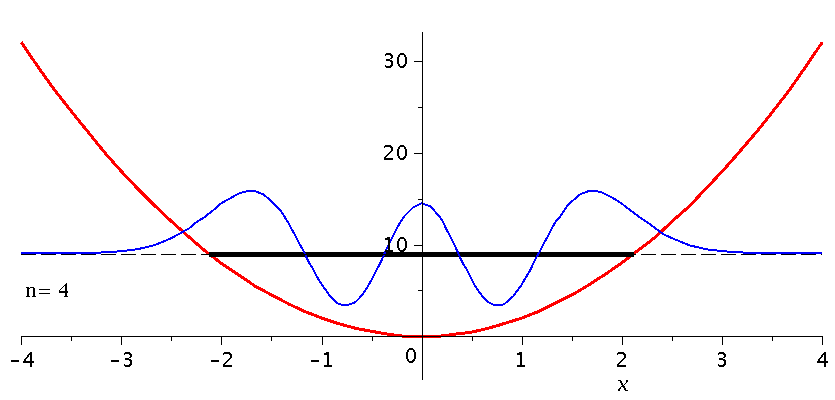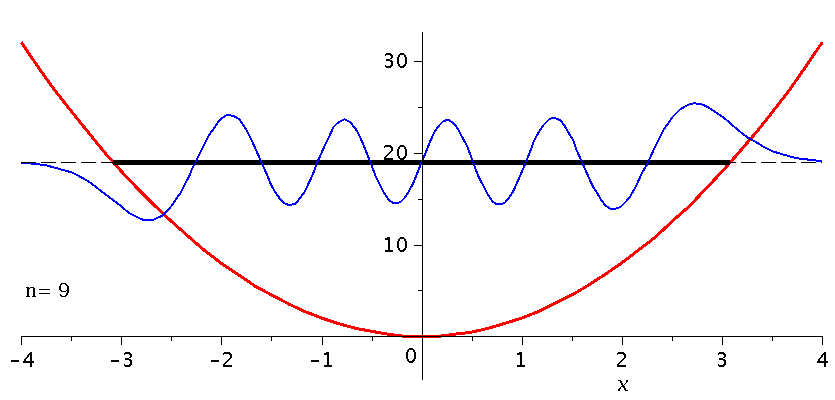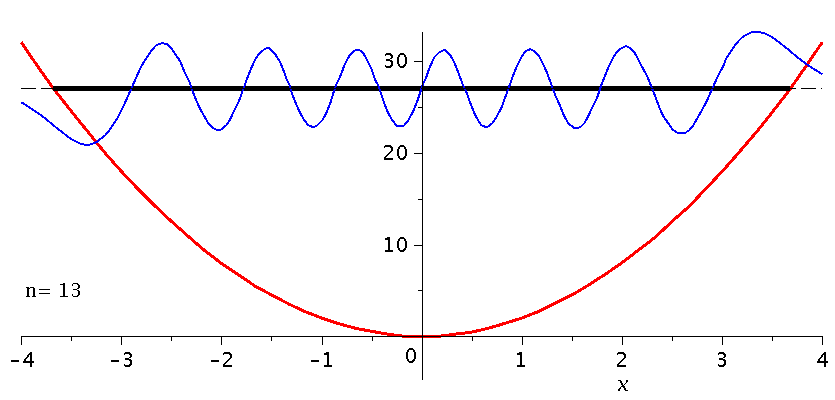
Die folgende Animation stellt die unterschiedlichen Quantenzustände (n=0 bis n=13) im parabolischen Potential dar (siehe untere Abbildung). Die normierten Zustände wurden deshalb aus Visualisierungsgründen mit dem Faktor 10 multipliziert und um den Betrag der entsprechenden Energie nach oben verschoben. Zusätzlich ist die zugehörige Wahrscheinlichkeitsdichte des Quantenteilchens in der oberen Abbildung veranschaulicht. 

>

setomega:=2: setk:=4: nend:=13: PlotPot:=plot(subs({k=setk},V),x=-4..4,thickness=3,titlefont = [HELVETICA, 16]): for nn from 0 by 1 to nend do setn:=nn: psi[setn]:=subs({omega=setomega,n=setn,u=sqrt(omega)*x},PSI); GLNorm:=int(psi[setn]*psi[setn],x=-infinity..infinity)=1; psi[setn]:=subs(A=simplify(solve(GLNorm,A)[1]),psi[setn]); PlotPSI[setn]:=plot(psi[setn],x=-4..4,thickness=2,color=blue); Energie[setn]:=subs({omega=setomega,n=setn},(2*n+1)*omega/2); PlotPSI1[setn]:=plot(10*psi[setn]+Energie[setn],x=-4..4,thickness=2,color=blue); PlotEnergie[setn]:=plot(Energie[setn],x=-solve(subs({k=setk},V)=Energie[setn])[2]..solve(subs({k=setk},V)=Energie[setn])[2],thickness=5,color=black): PlotEnergie1[setn]:=plot(Energie[setn],x=-4..4,thickness=1,color=black,linestyle=3): rho[setn]:=conjugate(psi[setn])*psi[setn]: Prho[setn]:=plot(rho[setn],x=-5..5,thickness=2,color=brown,title=cat(Wahrscheinlichkeitsdichte,rho=Psi*conjugate(Psi)),titlefont = [HELVETICA, 16]); Ptext:=textplot([-4,5, Join(["n=",convert(setn,string)])], align =RIGHT,color=black,font = [TIMES, ROMAN, 15]): Ani[setn]:=display(Matrix(2,1,[display(Prho[setn]),display(PlotPot,PlotEnergie[setn],PlotPSI1[setn],PlotEnergie1[setn],Ptext)])); od:

 

>	display([seq(Ani[i],i=0..nend)],insequence=true);

 

>