Das Wasserstoffatom  

>	restart: with(plots): with(StringTools):

 

Wir betrachten im Folgenden den quantenmechanischen Zustand des Elektrons im Wasserstoffatom. Die stationäre Schrödinger-Gleichung in sphärischen Koordinaten für das H-Atom lautet : 

>	V:=e^2/(4*Pi*eps0*r); SGL:=-hq^2/(2*me)*(1/r^2*diff((r^2*diff(psi(r,theta,phi),r)),r)+ 1/(r^2*sin(theta))*diff(sin(theta)*diff(psi(r,theta,phi),theta),theta)+1/(r^2*(sin(theta))^2)*diff(psi(r,theta,phi),phi,phi))+V*psi(r,theta,phi)=E*psi(r,theta,phi);

 

 

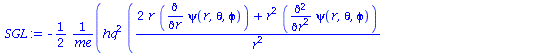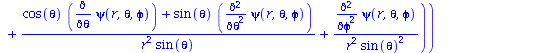	(1.1)

 

Wir machen für die Zustandsfunktion den folgenden Separationsansatz und setzen diesen in die Schrödinger-Gleichung ein: 

>	psi(r,theta,phi):=R(r)*Y(theta,phi); SGL;

 

 

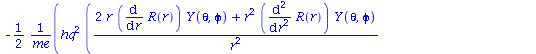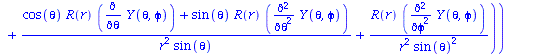	(1.2)

 

Division der Gleichung durch -hq^2/(2*me*r^2)*R(r)*Y(theta,phi) 

>	SGL1:=expand(SGL/(-hq^2/(2*me*r^2)*R(r)*Y(theta,phi)));

 

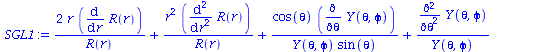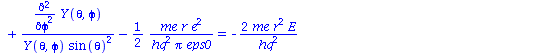(1.3)

 

und Trennung der Gleichung in einen rein radialen und einen rein winkelabhängigen Teil: 

>	SGL2:=SGL1 + (1/2)*me*r*e^2/(hq^2*Pi*eps0) - (2*r*(diff(R(r), r))/R(r)+r^2*(diff(R(r), r, r))/R(r)); RSGL:=rhs(SGL2):

 

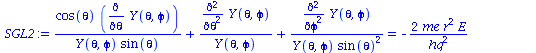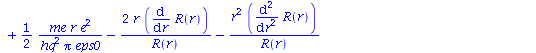(1.4)

 

Da die Gleichung für beliebige Werte der Variablen r, theta und phi erfüllt sein muss, müssen beide Seiten gleich einer Konstanten sein. Diese Konstante schreiben wir als const=-l(l+1) ; den Sinn hierfür versteht man erst später. 

Der winkelabhängige Teil der Schrödinger Gleichung 

Multipliziert man den winkelabhängigen Teil der Gleichung mit Y(theta,phi)*sin(theta)^2, so erhält man 

>	WSGL:=expand(lhs(SGL2)*Y(theta, phi)*sin(theta)^2)=-l*(l+1)*Y(theta, phi)*sin(theta)^2;

 

(1.1.1)

 

Für Y(theta,phi) wählen wir den folgenden Separationsansatz: 

>	Y(theta, phi):=f(theta)*g(phi); WSGL1:=expand(WSGL/(f(theta)*g(phi)));

 

 

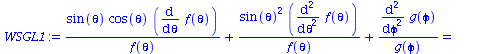	(1.1.2)

 

Trennung der Gleichung in einen Teil der nur von theta und nur von phi abhängt: 

>	WSGL2:=WSGL1 +l^2*sin(theta)^2+l*sin(theta)^2 -(diff(g(phi), phi, phi))/g(phi);

 

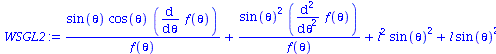(1.1.3)

 

Da diese Gleichung für beliebige Werte der Variablen theta und phi erfüllt sein muss, müssen beide Seiten gleich einer Konstanten sein. Diese Konstante schreiben wir als const=m^2 ; den Sinn hierfür versteht man erst später. Für den phi-abhängigen Teil erhalten wir: 

>	WSGL3:=rhs(WSGL2)=m^2;

 

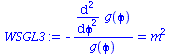(1.1.4)

 

Die Lösung dieser Differentialgleichung ist einfach: 

>	dsolve(WSGL3);

 

(1.1.5)

 

bzw: 

>	g(phi)=exp(I*m*phi);

 

(1.1.6)

 

Für den theta-abhängigen Teil erhalten wir: 

>	WSGL4:=lhs(WSGL2)=m^2;

 

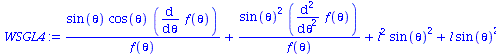(1.1.7)

 

Die Herleitung der Lösung dieser Differentialgleichung ist nicht so einfach. Es ergibt sich (siehe z.B. Greiner) 

>	PP:=(l,m,x)->(1-x^2)^(abs(m)/2)*diff(1/(2^l*l!)*diff((x^2-1)^l,x$l),x$abs(m)); P0:=(l,m,x)->1/(2^l*l!)*diff((x^2-1)^l,x$l): P:=(l,m,x)->piecewise(l>0 and m>0, PP(l,m,x), l=0, 1,l>0 and m=0,P0(l,m,x),l>0 and m<0,PP(l,m,x)): P(0,0,x); P(1,-1,x); P(1,0,x); P(1,1,x); P(2,0,x);

 

 

 

 

 

 

	(1.1.8)

 

Wir erhalten somit als Lösung des winkelabhängigen Teils der Schrödingergleichung die folgenden sogenannten Kugelflächenfunktionen, wobei sich der komplizierte Vorfaktor durch die Normierungseigenschaft bestimmen läßt.: 

>	eps:=m->piecewise(m>0, (-1)^m, m<=0,1); A:=(l,m)->eps(m)*sqrt(((2*l+1)*((l-abs(m))!))/(4*Pi*((l+abs(m))!))); g:=(m,phi)->exp(I*m*phi); f:=(l,m,theta)->A(l,m)*subs(x=cos(theta),P(l,m,x)); Y:=(l,m,theta,phi)->f(l,m,theta)*g(m,phi);

 

 

 

 

 

	(1.1.9)

 

Im folgenden sind die einzelnen Teile der Kugelflächenfunktion für l=2 und m=1 berechnet. Zusätzlich ist noch gezeigt, dass die Funktionen auf 1 normiert sind. 

>	setl:=2; setm:=1; A=A(setl,setm); g=g(setm,phi); f=f(setl,setm,theta); Y=Y(setl,setm,theta,phi); int(int(conjugate(Y(setl,setm,theta,phi))*Y(setl,setm,theta,phi)*sin(theta),theta=0..Pi),phi=0..2*Pi);

 

 

 

 

 

 

 

	(1.1.10)

 

Man erhält somit für die ersten Kugelflächenfunktionen: 

>

setl:=0: setm:=0: print("l=0 , m=0"); Y=Y(setl,setm,theta,phi); setl:=1: setm:=0: print("l=1 , m=0"); Y=Y(setl,setm,theta,phi); setl:=1: setm:=1: print("l=1 , m=1"); Y=Y(setl,setm,theta,phi); setl:=1: setm:=-1: print("l=1 , m=-1"); Y=Y(setl,setm,theta,phi); setl:=2: setm:=1: print("l=2 , m=1"); Y=Y(setl,setm,theta,phi);

 

 

 

 

 

 

 

 

 

 

	(1.1.11)

 

Die Kugelflächenfunktion für l=0 und m=0 ist im Folgenden dargestellt: 

>

setl:=0; setm:=0; Y=Y(setl,setm,theta,phi); minmax:=3*10^(-1): plot3d(Re(Y(setl,setm,theta,phi)), phi=0..2*Pi, theta=0..Pi, coords = spherical, axes = boxed,grid=[50,50],orientation=[24,55], scaling=CONSTRAINED,view=[-minmax..minmax,-minmax..minmax,-minmax..minmax],labels=[x, y,z]); plot(Re(subs(theta=Pi/2,Y(setl,setm,theta,phi))), phi=0..2*Pi, coords = polar,color=black,thickness=2);

 

 

 

 

 

 

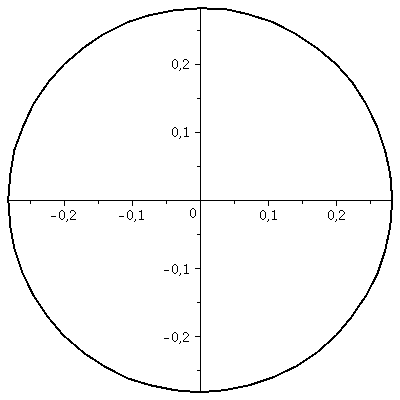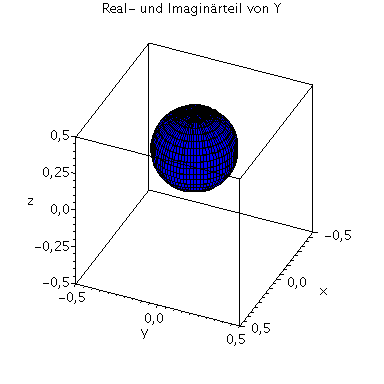
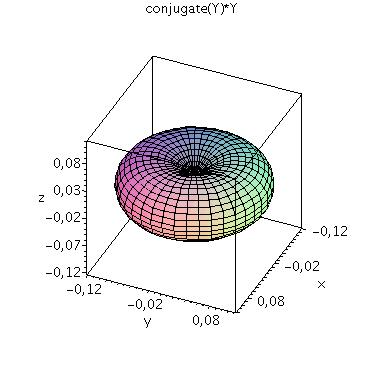
Die Kugelflächenfunktion für l=1 und m=0 und weitere Kugelflächenfunktionen sind im Folgenden dargestellt (Erstes Bild: Y (Realteil blau, Imaginärteil rot), zweites Bild: conjugate(Y)*Y): 

>

setl:=1; setm:=0; Y=Y(setl,setm,theta,phi); minmax:=0.5: P1:=plot3d(Re(Y(setl,setm,theta,phi)), phi=0..2*Pi, theta=0..Pi, coords = spherical, axes = boxed,grid=[40,40],orientation=[24,55],view=[-minmax..minmax,-minmax..minmax,-minmax..minmax],labels=[x, y,z],color=blue): P2:=plot3d(Im(Y(setl,setm,theta,phi)), phi=0..2*Pi, theta=0..Pi, coords = spherical, axes = boxed,grid=[40,40],orientation=[24,55],view=[-minmax..minmax,-minmax..minmax,-minmax..minmax],labels=[x, y,z],color=red): minmax:=0.5^2: display(P1,P2,title="Real- und Imaginärteil von Y"); plot3d(conjugate(Y(setl,setm,theta,phi))*Y(setl,setm,theta,phi), phi=0..2*Pi, theta=0..Pi, coords = spherical, axes = boxed,grid=[40,40],orientation=[24,55], scaling=CONSTRAINED,view=[-minmax..minmax,-minmax..minmax,-minmax..minmax],labels=[x, y,z],title="conjugate(Y)*Y");

 

 

 

 

 

 

>

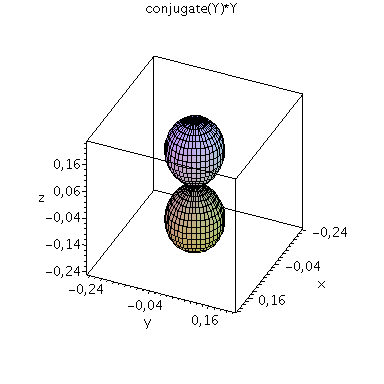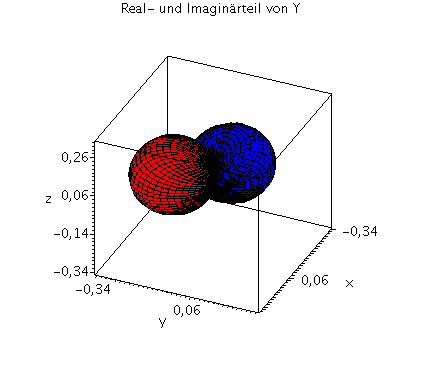
setl:=1; setm:=1; Y=Y(setl,setm,theta,phi); minmax:=0.35: P1:=plot3d(Re(Y(setl,setm,theta,phi)), phi=0..2*Pi, theta=0..Pi, coords = spherical, axes = boxed,grid=[40,40],orientation=[24,55],view=[-minmax..minmax,-minmax..minmax,-minmax..minmax],labels=[x, y,z],color=blue): P2:=plot3d(Im(Y(setl,setm,theta,phi)), phi=0..2*Pi, theta=0..Pi, coords = spherical, axes = boxed,grid=[40,40],orientation=[24,55],view=[-minmax..minmax,-minmax..minmax,-minmax..minmax],labels=[x, y,z],color=red): display(P1,P2,title="Real- und Imaginärteil von Y"); minmax:=0.35^2: plot3d(conjugate(Y(setl,setm,theta,phi))*Y(setl,setm,theta,phi), phi=0..2*Pi, theta=0..Pi, coords = spherical, axes = boxed,grid=[40,40],orientation=[24,55], scaling=CONSTRAINED,view=[-minmax..minmax,-minmax..minmax,-minmax..minmax],labels=[x, y,z],title="conjugate(Y)*Y");

 

 

 

 

 

 

>

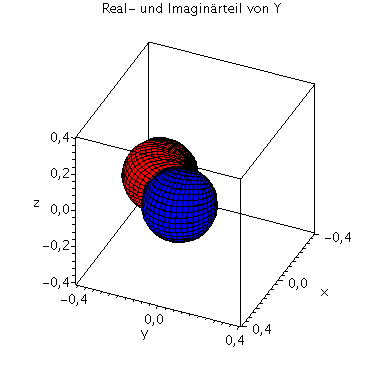
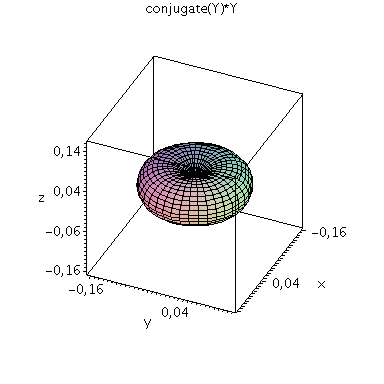
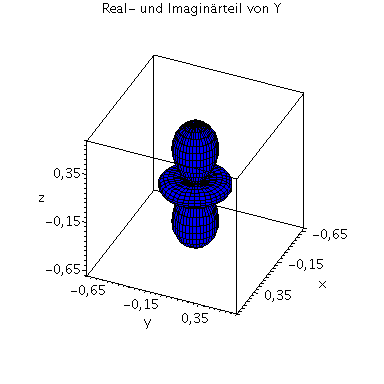
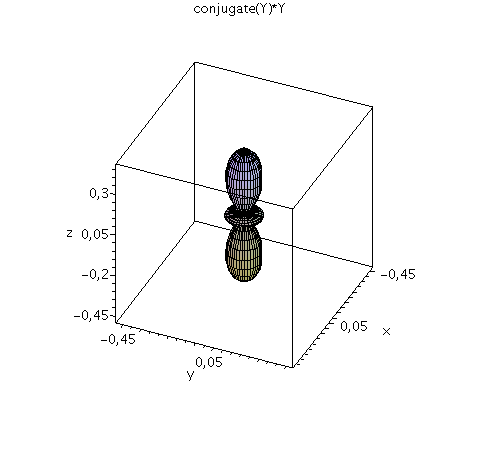
setl:=1; setm:=-1; Y=Y(setl,setm,theta,phi); minmax:=0.41: P1:=plot3d(Re(Y(setl,setm,theta,phi)), phi=0..2*Pi, theta=0..Pi, coords = spherical, axes = boxed,grid=[40,40],orientation=[24,55],view=[-minmax..minmax,-minmax..minmax,-minmax..minmax],labels=[x, y,z],color=blue): P2:=plot3d(Im(Y(setl,setm,theta,phi)), phi=0..2*Pi, theta=0..Pi, coords = spherical, axes = boxed,grid=[40,40],orientation=[24,55],view=[-minmax..minmax,-minmax..minmax,-minmax..minmax],labels=[x, y,z],color=red): display(P1,P2,title="Real- und Imaginärteil von Y"); minmax:=0.41^2: plot3d(conjugate(Y(setl,setm,theta,phi))*Y(setl,setm,theta,phi), phi=0..2*Pi, theta=0..Pi, coords = spherical, axes = boxed,grid=[40,40],orientation=[24,55], scaling=CONSTRAINED,view=[-minmax..minmax,-minmax..minmax,-minmax..minmax],labels=[x, y,z],title="conjugate(Y)*Y");

 

 

 

 

 

 

>

setl:=2; setm:=0; Y=Y(setl,setm,theta,phi); minmax:=0.7: P1:=plot3d(Re(Y(setl,setm,theta,phi)), phi=0..2*Pi, theta=0..Pi, coords = spherical, axes = boxed,grid=[40,40],orientation=[24,55],view=[-minmax..minmax,-minmax..minmax,-minmax..minmax],labels=[x, y,z],color=blue): P2:=plot3d(Im(Y(setl,setm,theta,phi)), phi=0..2*Pi, theta=0..Pi, coords = spherical, axes = boxed,grid=[40,40],orientation=[24,55],view=[-minmax..minmax,-minmax..minmax,-minmax..minmax],labels=[x, y,z],color=red): display(P1,P2,title="Real- und Imaginärteil von Y"); minmax:=0.7^2: plot3d(conjugate(Y(setl,setm,theta,phi))*Y(setl,setm,theta,phi), phi=0..2*Pi, theta=0..Pi, coords = spherical, axes = boxed,grid=[40,40],orientation=[24,55], scaling=CONSTRAINED,view=[-minmax..minmax,-minmax..minmax,-minmax..minmax],labels=[x, y,z],title="conjugate(Y)*Y");

 

 

 

 

 

 

>

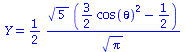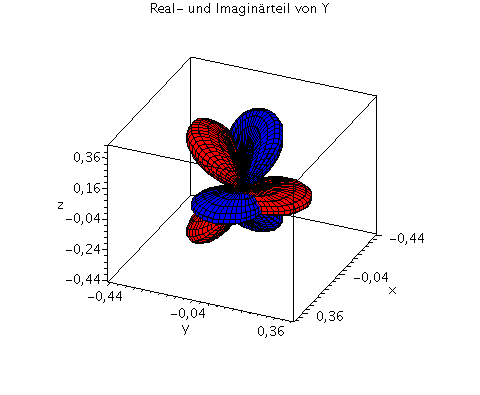
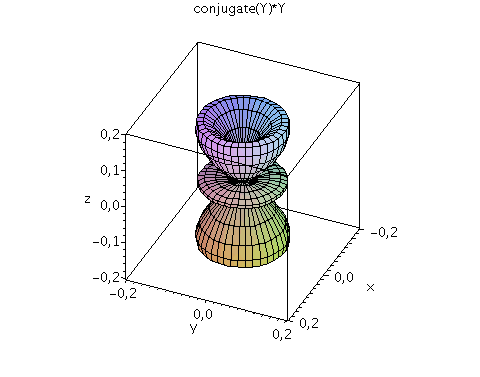
setl:=3; setm:=1; Y=Y(setl,setm,theta,phi); minmax:=0.45: P1:=plot3d(Re(Y(setl,setm,theta,phi)), phi=0..2*Pi, theta=0..Pi, coords = spherical, axes = boxed,grid=[40,40],orientation=[24,55],view=[-minmax..minmax,-minmax..minmax,-minmax..minmax],labels=[x, y,z],color=blue): P2:=plot3d(Im(Y(setl,setm,theta,phi)), phi=0..2*Pi, theta=0..Pi, coords = spherical, axes = boxed,grid=[40,40],orientation=[24,55],view=[-minmax..minmax,-minmax..minmax,-minmax..minmax],labels=[x, y,z],color=red): display(P1,P2,title="Real- und Imaginärteil von Y"); minmax:=0.45^2: plot3d(conjugate(Y(setl,setm,theta,phi))*Y(setl,setm,theta,phi), phi=0..2*Pi, theta=0..Pi, coords = spherical, axes = boxed,grid=[40,40],orientation=[24,55], scaling=CONSTRAINED,view=[-minmax..minmax,-minmax..minmax,-minmax..minmax],labels=[x, y,z],title="conjugate(Y)*Y");

 

 

 

 

 

 

>

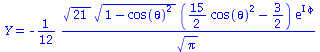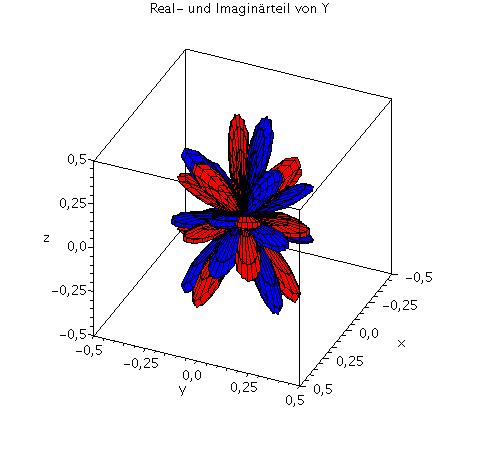
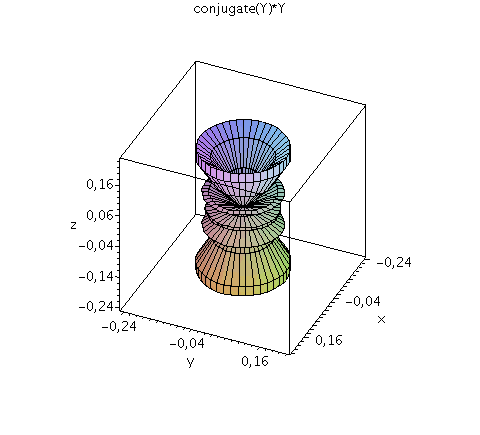
setl:=7; setm:=3; Y=Y(setl,setm,theta,phi); minmax:=0.5: P1:=plot3d(Re(Y(setl,setm,theta,phi)), phi=0..2*Pi, theta=0..Pi, coords = spherical, axes = boxed,grid=[40,40],orientation=[24,55],view=[-minmax..minmax,-minmax..minmax,-minmax..minmax],labels=[x, y,z],color=blue): P2:=plot3d(Im(Y(setl,setm,theta,phi)), phi=0..2*Pi, theta=0..Pi, coords = spherical, axes = boxed,grid=[40,40],orientation=[24,55],view=[-minmax..minmax,-minmax..minmax,-minmax..minmax],labels=[x, y,z],color=red): display(P1,P2,title="Real- und Imaginärteil von Y"); minmax:=0.5^2: plot3d(conjugate(Y(setl,setm,theta,phi))*Y(setl,setm,theta,phi), phi=0..2*Pi, theta=0..Pi, coords = spherical, axes = boxed,grid=[40,40],orientation=[24,55], scaling=CONSTRAINED,view=[-minmax..minmax,-minmax..minmax,-minmax..minmax],labels=[x, y,z],title="conjugate(Y)*Y");

 

 

 

 

 

 

>

 

Der radiale Teil der Schrödinger Gleichung 

Der radiale Teil der Schrödingergleichung lautet: 

>	RSGL:=expand(RSGL*R(r))=-l*(l+1)*R(r);

 

(1.2.1)

 

Wir definieren eine neue Funktion u(r)=r*R(r) und setzen diesen in RSGL ein: 

>	subs(R(r)=u(r)/r,RSGL);

 

(1.2.2)

 

Die Lösung dieser Differentialgleichung ähnelt der Vorgehensweise beim harmonischen Oszillator. Aufgrund der Normierungsbedingung muss wiederum eine zunächst als unendich definierte Reihe ab einer natürlichen Zahl (die Hauptquantenzahl n=[1,2,3,...]) abbrechen. Als Endresultat erhält man den folgenden Ausdruck für den normierten radialen Teil der Schrödingergleichung, wobei der Parameter a den Bohr'schen Radius darstellt (a=(2*Pi*eps0*hq^2)/(me*e^2)): 

>	AA:=(n,l,a)->sqrt((2/(n*a))^3*((n-l-1)!)/(2*n*((n+l)!)^3)); LL1:=(q,x)->exp(x)*diff(exp(-x)*x^q,x$q); LL:=(p,q,x)->(-1)^p*diff(LL1(q,x),x$p); RR1:=(n,l,a,r)->exp(-r/(n*a))*(2*r/(n*a))^l*subs({p=2*l+1,q=n-l-1+(2*l+1),x=2*r/(n*a)},LL(p,q,x)); RR:=(n,l,a,r)->AA(n,l,a)*RR1(n,l,a,r);

 

 

 

 

 

	(1.2.3)

 

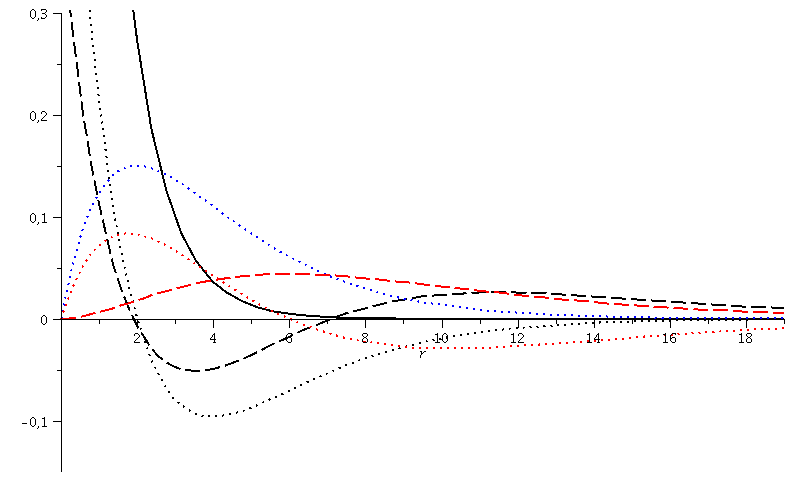
Stellt man sich die einzelnen Lösungen dar, so erhält man das folgende Bild: 

Schwarze Kurven: Durchgehend(n=1,l=0), gepunktet(n=2,l=0), gestrichen(n=3,l=0) 

Blaue Kurve: (n=2,l=1) 

Rote Kurven: Gepunktet(n=3,l=1), gestrichen(n=3,l=2) 

>

P10:=plot(RR(1,0,1,r),r=0.001..19,color=black,thickness=2,view=-0.15..0.3): P20:=plot(RR(2,0,1,r),r=0.001..19,color=black,thickness=2,view=0..0.3,linestyle=2): P30:=plot(RR(3,0,1,r),r=0.001..19,color=black,thickness=2,view=0..0.3,linestyle=3): P21:=plot(RR(2,1,1,r),r=0.001..19,color=blue,thickness=2,view=0..0.3,linestyle=2): P31:=plot(RR(3,1,1,r),r=0.001..19,color=red,thickness=2,view=0..0.3,linestyle=2): P32:=plot(RR(3,2,1,r),r=0.001..19,color=red,thickness=2,view=0..0.3,linestyle=3): display(P10,P20,P30,P21,P31,P32);

 

 

 

Die Zustandsfunktion des Wasserstoffatoms 

Die gesamte Zustandsfunktion des Wasserstoffatoms lautet demnach: 

>	psi:=(n,l,m,a,r,theta,phi)->RR(n,l,a,r)*Y(l,m,theta,phi);

 

(1.3.1)

 

Wir setzen im Folgenden a=1. Der auf Eins normierte (n=4,l=2,m=2)-Zustand lautet somit  

>	setn:=4; setl:=2; setm:=2; seta:=1; psi=evalf(psi(setn,setl,setm,seta,r,theta,phi)); int(int(int(conjugate(evalf(psi(setn,setl,setm,seta,r,theta,phi)))*evalf(psi(setn,setl,setm,seta,r,theta,phi))*r^2*sin(theta),r=0..infinity),theta=0..Pi),phi=0..2*Pi);

 

 

 

 

 

 

	(1.3.2)

 

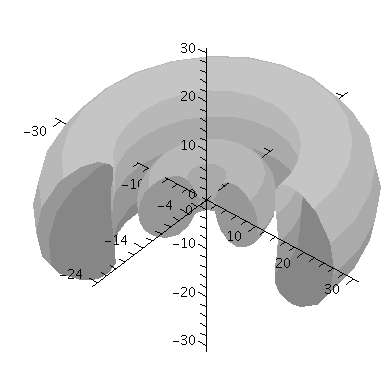
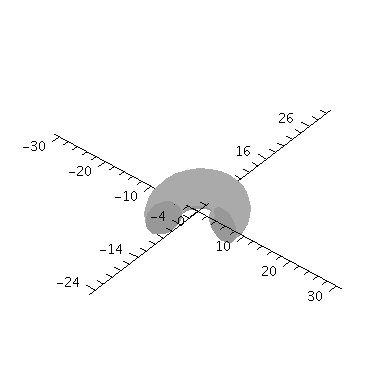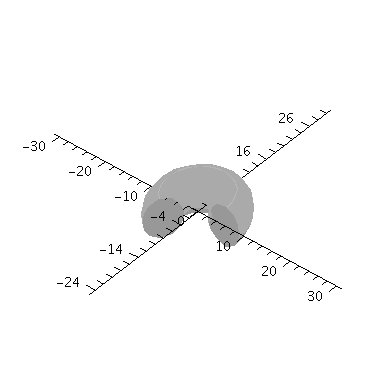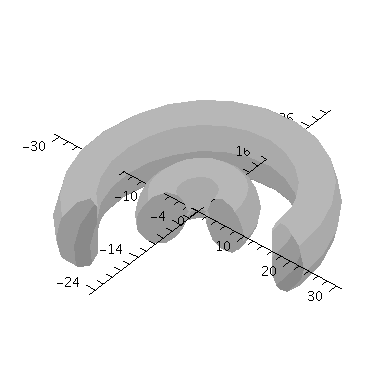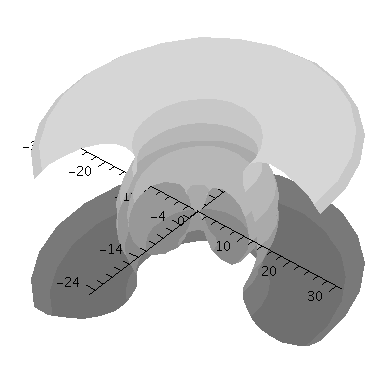
Die folgende Abbildung stellt eine Möglichkeit der Veranschaulichung der Wahrscheinlichkeitsdichte des Zustandes dar. Die Fläche repräsentiert Punkte mit gleicher Wahrscheinlichkeit (hier speziell rho=0.00001) 

>	implicitplot3d(0.00001 = evalf(conjugate(evalf(psi(setn,setl,setm,seta,r,theta,phi)))*evalf(psi(setn,setl,setm,seta,r,theta,phi))), r = 0..30, phi=0..1.3*Pi, theta=0..Pi, coords = spherical,axes=normal,numpoints=3000,orientation=[-50,50],style=surface,shading=zgrayscale);

 

 

In dieser Animation wird der Wahrscheinlichkeitswert von 0.00005 zu 0.0000025 verändert: 

>

frames:=20: dr:=0.0000025: for i from 0 by 1 to frames-1 do rr:=frames*dr - i*dr: Ani[i]:=implicitplot3d(rr = evalf(conjugate(evalf(psi(setn,setl,setm,seta,r,theta,phi)))*evalf(psi(setn,setl,setm,seta,r,theta,phi))), r = 0..30, phi=0..1.3*Pi, theta=0..Pi, coords = spherical,axes=normal,numpoints=3000,orientation=[-50,50],style=surface,shading=zgrayscale): od:

 

>	display([seq(Ani[i],i=0..frames-1)],insequence=true);

 

 

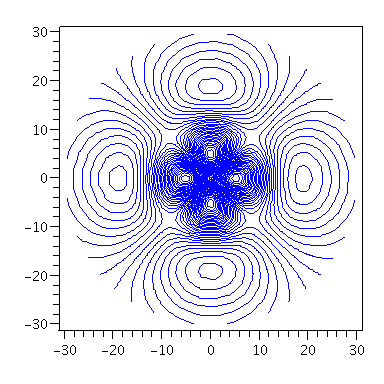
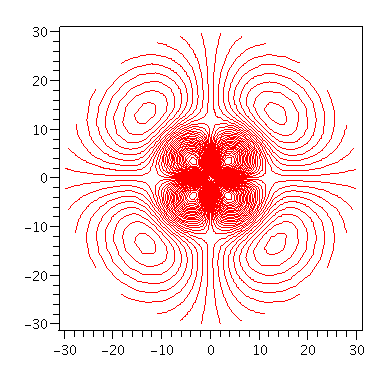
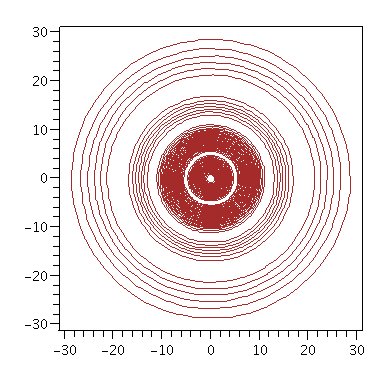
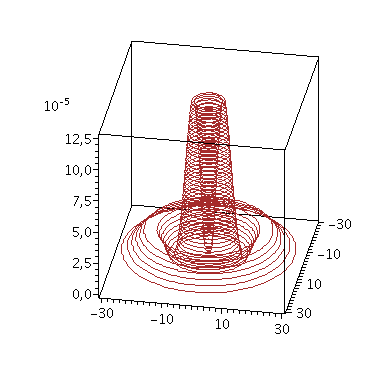
In der Äquatorialen Ebene ergibt sich das folgenden Bilder (Realteil blau, Imaginärteil rot, Warscheinlichkeitsdichte braun)  

>

evalf(subs(theta=Pi/2,conjugate(evalf(psi(setn,setl,setm,seta,r,theta,phi)))*evalf(psi(setn,setl,setm,seta,r,theta,phi)))); plot3d([r*cos(phi), r*sin(phi), Re(evalf(subs(theta=Pi/2,evalf(psi(setn,setl,setm,seta,r,theta,phi)))))],r = 0..30,phi = 0..2*Pi,style=contour,grid=[50,50],contours=40,color=blue,orientation=[-90,0],axes=boxed); plot3d([r*cos(phi), r*sin(phi), Im(evalf(subs(theta=Pi/2,evalf(psi(setn,setl,setm,seta,r,theta,phi)))))],r = 0..30,phi = 0..2*Pi,style=contour,grid=[50,50],contours=40,color=red,orientation=[-90,0],axes=boxed); plot3d([r*cos(phi), r*sin(phi), evalf(subs(theta=Pi/2,conjugate(evalf(psi(setn,setl,setm,seta,r,theta,phi)))*evalf(psi(setn,setl,setm,seta,r,theta,phi))))],r = 0..30,phi = 0..2*Pi,style=contour,grid=[50,50],contours=40,color=brown,orientation=[-90,0],axes=boxed); plot3d([r*cos(phi), r*sin(phi), evalf(subs(theta=Pi/2,conjugate(evalf(psi(setn,setl,setm,seta,r,theta,phi)))*evalf(psi(setn,setl,setm,seta,r,theta,phi))))],r = 0..30,phi = 0..2*Pi,style=contour,grid=[50,50],contours=40,color=brown,orientation=[10,60],axes=boxed);

 

 

 

 

 

 

>