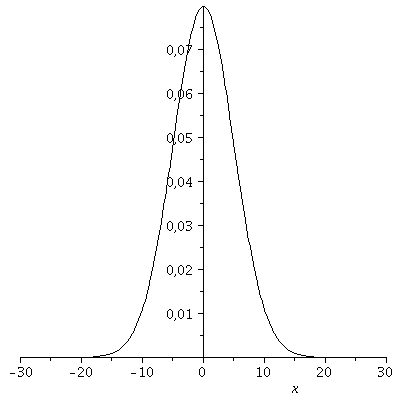Das zeitliche Verhalten von Wellenpakete mit kastenförmiger Impulsverteilung
Um die Beschreibung der de Broglieschen Materiewellen auf räumlich begrenzte Teichen anwenden zu können, müssen wir zu endlichen Wellenpaketen übergehen. Wellenpakete werden als eine Überlagerung harmonischer, monocromatischer Wellen dargestellt, die sich hinsichtlich ihrer Wellenlänge und Fortpflanzungsgeschwindigkeit unterscheiden. Wir betrachten im Folgenden eine spezielle Art von Wellenpaketes (Wellenpakete mit kastenförmiger Impulsverteilung in einer Dimension (x-Richtung)).
| > | restart:
with(plots): |
Ein allgemeines Wellenpaket besitz in einer Dimension die folgende raum-zeit-abhängige Zustandsfunktion:
| > | psi:=int(c(k)*exp(-I*(omega(k)*t-k*x)),k=-infinity..infinity); |
| (2.1) |
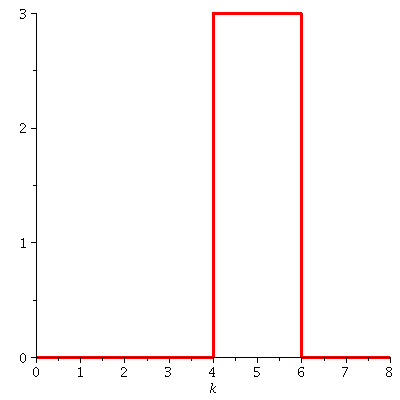
Wir nehmen im Folgenden ein Wellenpaket mit kastenförmiger Impulsverteilung an. Die Funktion c(k), welche die Impulsverteilung charakterisiert hat in diesem Fall z.B. das folgende Aussehen (hier c0=3, Dk=1 und k0=5):
| > | c:=piecewise( abs(k-k0)<=Dk, c0);
setk0:=5: setDk:=1: setc0:=3: plot(subs({k0=setk0,Dk=setDk,c0=setc0},c),k=0..8,thickness=3); |
 |
Wir betrachten nun zunächst eine solche Materiewelle zum Zeitpunkt t=0 und legen den Parameter c0 (Höhe des Kastens der Impulsverteilung) durch die Normierungsbedingung der Aufenthalts-Wahrscheinlichkeit des Quantenteilchens fest:
| > | psi0:=eval(subs({c(k)=subs({k0=setk0,Dk=setDk},c),t=0},psi)); |
| (2.2) |
| > | rho0:=conjugate(psi0)*psi0:
GLNorm:=int(rho0,x=-infinity..infinity)=1; Hoehek:=solve(subs(conjugate(c0)=c0,GLNorm),c0)[1]; |
| (2.3) |
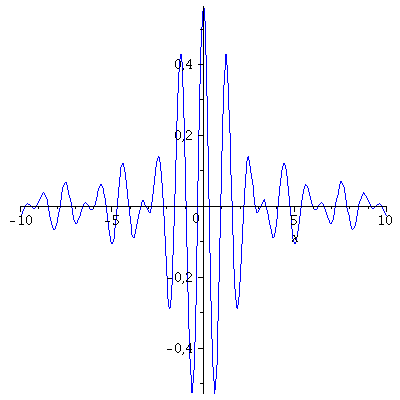
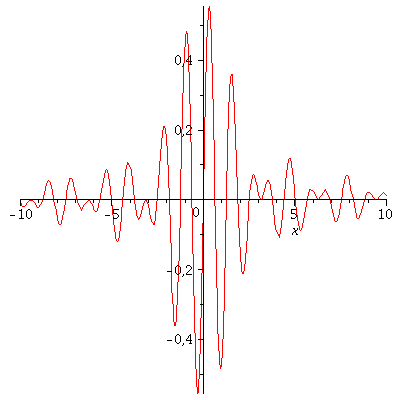
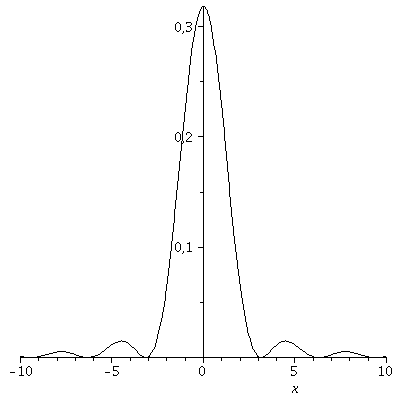
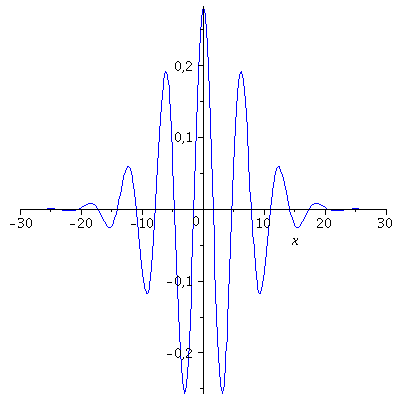
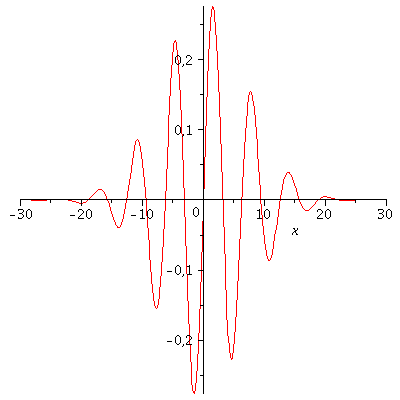
Die Zustandsfunktion (Realteil: blau, Imaginärteil: rot) und die Aufenthalts-Wahrscheinlichkeit des Quantenteilchens sind für t=0 in den folgenden Abbildungen dargestellt:
| > | psi0:=subs(c0=Hoehek,psi0);
P1:=plot(Re(psi0),x=-10..10,color=blue): P2:=plot(Im(psi0),x=-10..10,color=red): P3:=plot(eval(subs(c0=Hoehek,conjugate(psi0)*psi0)),x=-10..10,color=black): display(Matrix(1,3,[[P1,P2,P3]])); |
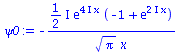 |
||||
|
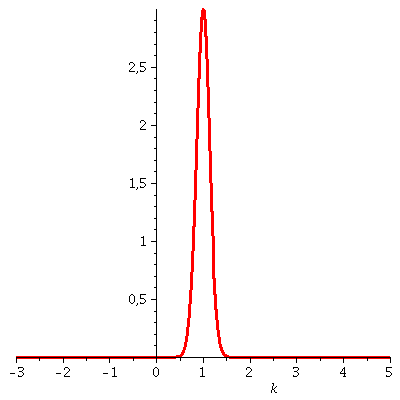
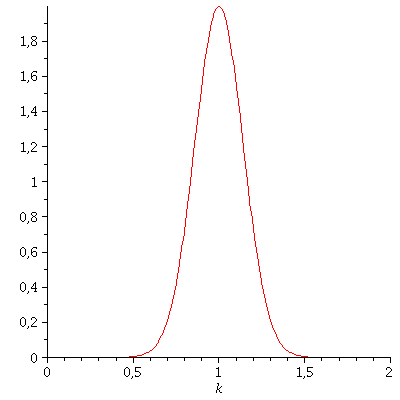
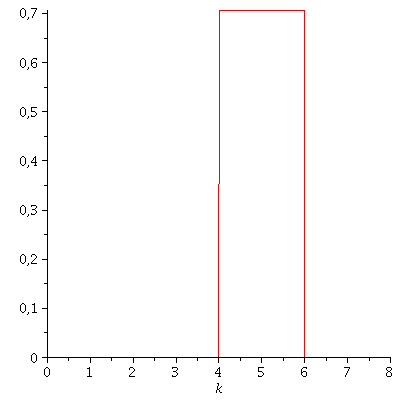
Durch Fouriertransformation der Zustandsfunktion kann man nochmals überprüfen, dass das Impulsspektrum wirklich ein kastenförmiges Aussehen hat:
| > | with(inttrans):
FourPsi0:=1/sqrt(2*Pi)*fourier(psi0,x,k); plot(FourPsi0,k=0..8); |
 |
Das Quadrat dieser Fouriertransformierten ist wieder auf 1 normiert:
| > | int(FourPsi0^2,k=-infinity..infinity); |
| (2.4) |
Wir wollen nun das zeitliche Verhalten dieses Zustandes untersuchen.
| > | psi0t:=eval(subs({c(k)=subs({k0=setk0,Dk=setDk,c0=Hoehek},c)},psi)); |
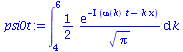 |
(2.5) |
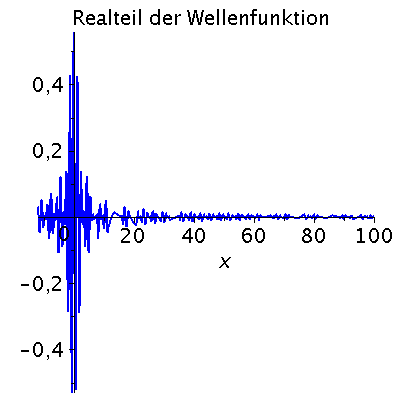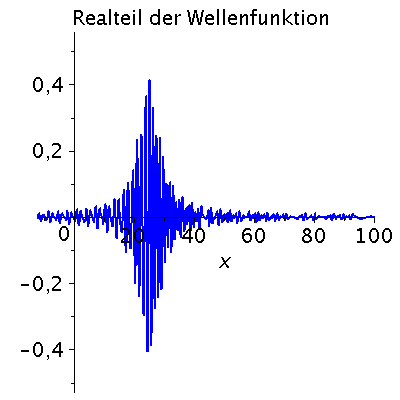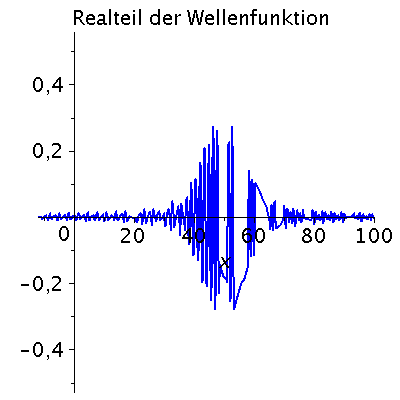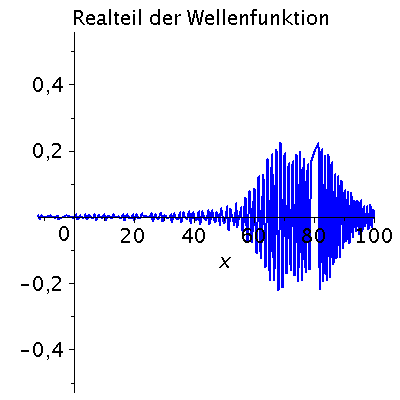
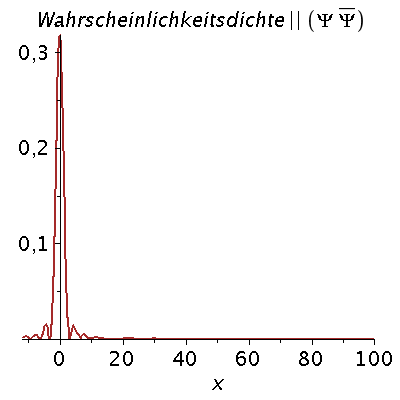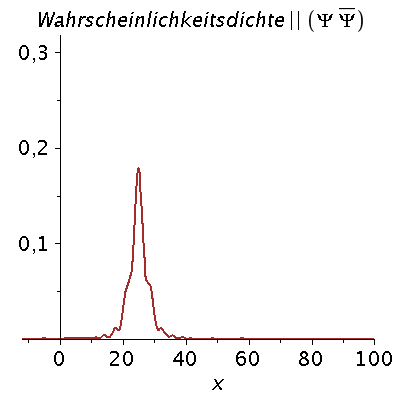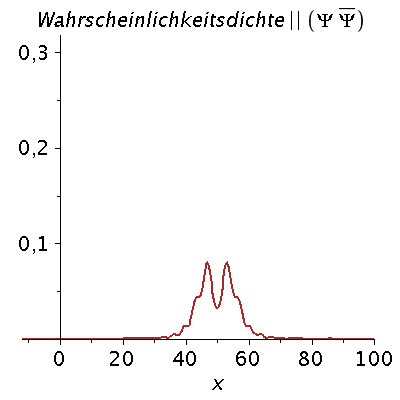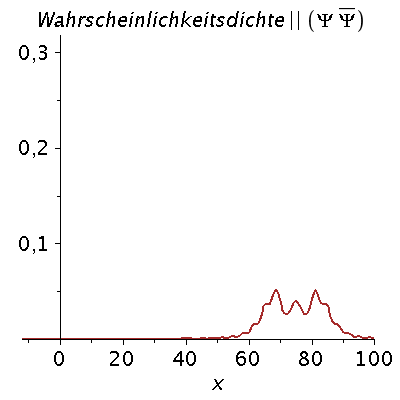
Das Frequenzspektrum ist für de Brogliesche Materiewelle wie folgt definiert omega(k)=hq*k^2/(2*m). Im Folgenden setzen wir hq=1=m. Die folgende Abbildung zeigt die zeitliche Entwicklung des Zustandes in einer Animation (t=[0,15]):
| > | Pend:=100:
iend:=15: for i from 0 by 1 to iend do tt:=i; psi0tt:=eval(subs({omega(k)=k^2/2,t=tt},psi0t)); PReal:=plot(Re(psi0tt),x=-12..Pend,color=blue,thickness=2): #PIm:=plot(Im(psi0tt),x=-12..Pend,color=red,thickness=2): POrt:=display(PReal,title="Realteil der Wellenfunktion",titlefont = [HELVETICA, 16]): rho:=conjugate(psi0tt)*psi0tt: Prho:=plot(rho,x=-12..Pend,color=brown,title=cat(Wahrscheinlichkeitsdichte,Psi*conjugate(Psi)),titlefont = [HELVETICA, 16],thickness=2): Ani[i]:=display(Matrix(1,2,[[POrt,Prho]])); od: |
| > | display([seq(Ani[i],i=0..iend)],insequence=true); |
|
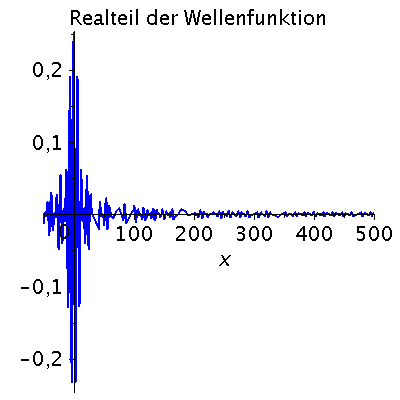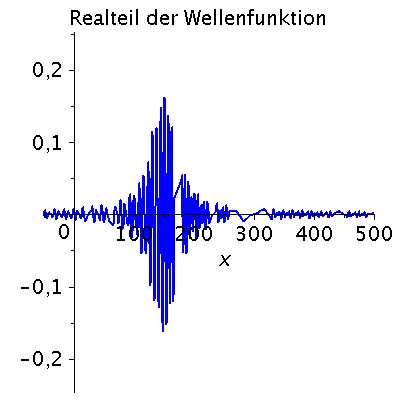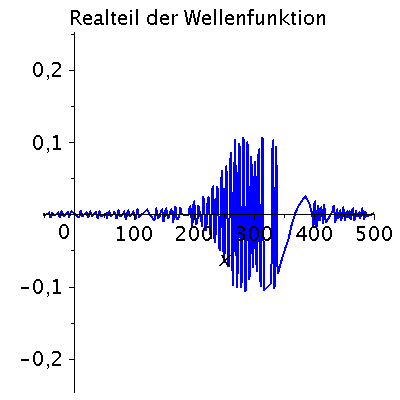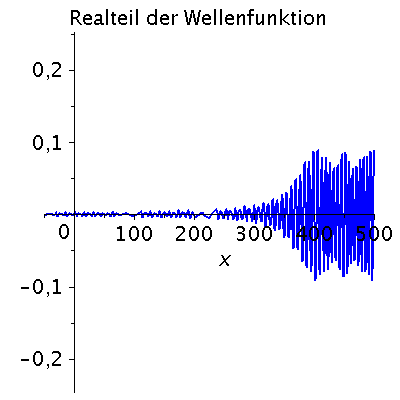
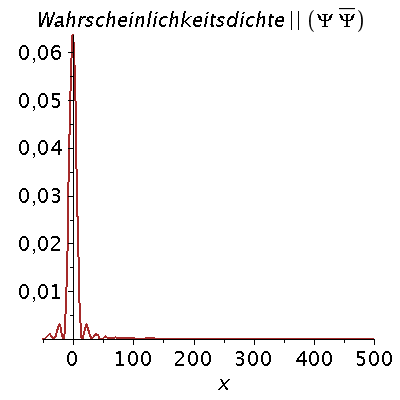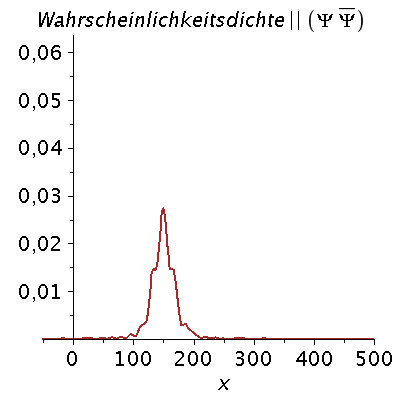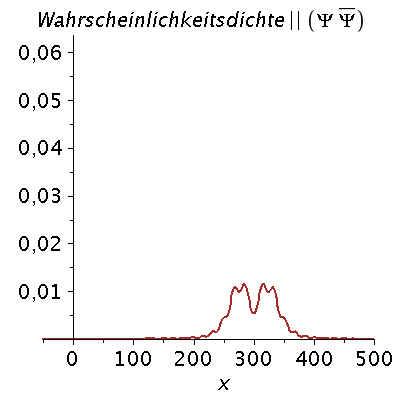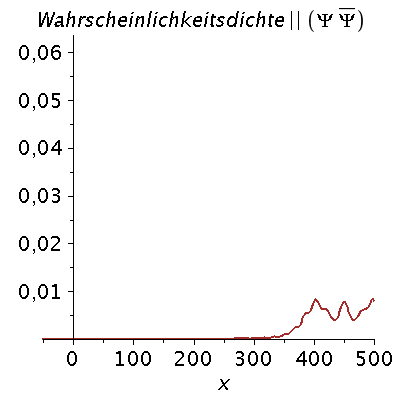
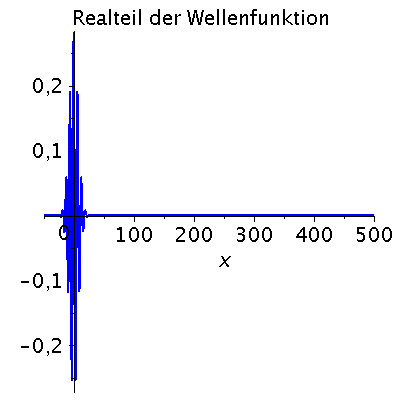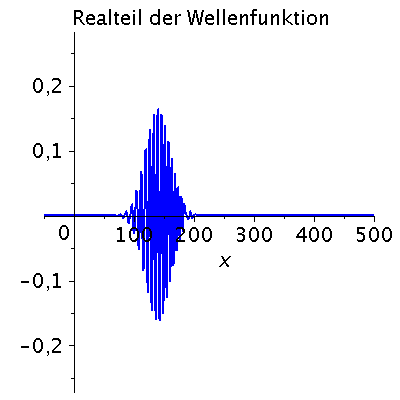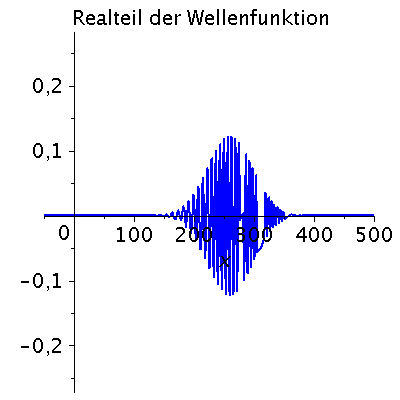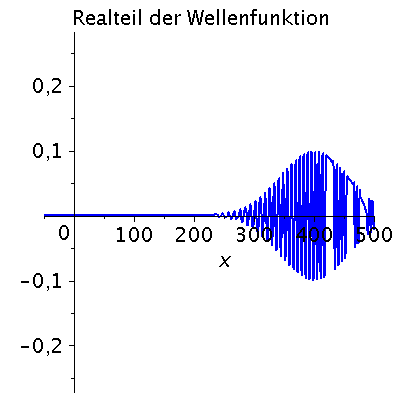
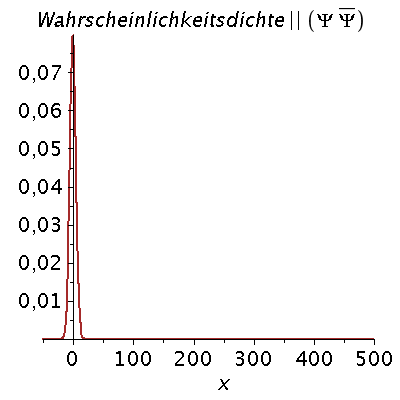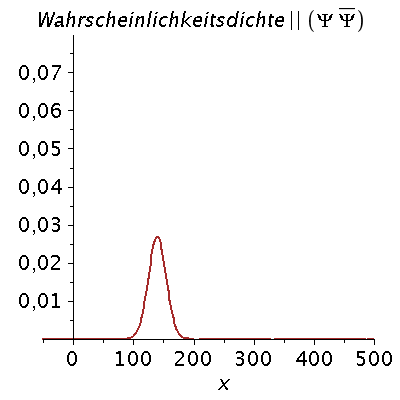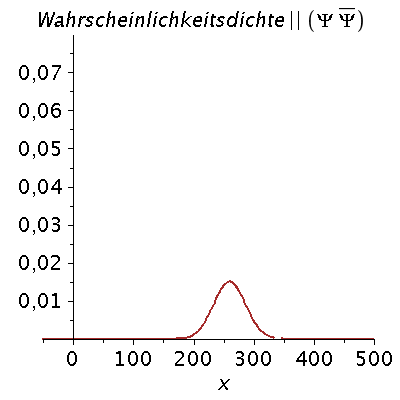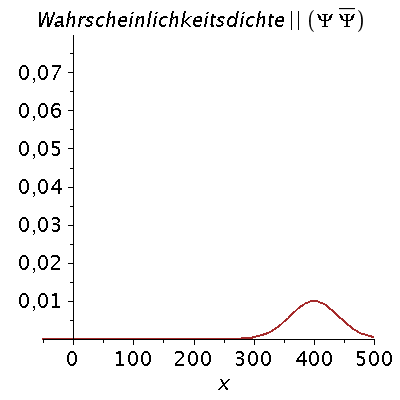
Ein weiteres Beispiel einer zeitlichen Ausbreitung eines Wellenpaketes mit kastenförmiger Impulsverteilung zeigt das folgende Beispiel (siehe Skript von Dr. J.Reinhardt S:22). hq=m=k0=1, Dk=0.2 und t=[0,450].
| > | setk0:=1:
setDk:=0.2: Pend:=500: iend:=15: psi0:=eval(subs({c(k)=subs({k0=setk0,Dk=setDk},c),t=0},psi)): rho0:=conjugate(psi0)*psi0: GLNorm:=int(rho0,x=-infinity..infinity)=1: Hoehek:=solve(subs(conjugate(c0)=c0,GLNorm),c0)[1]: psi0:=subs(c0=Hoehek,psi0): psi0t:=eval(subs({c(k)=subs({k0=setk0,Dk=setDk,c0=Hoehek},c)},psi)): for i from 0 by 1 to iend do tt:=30*i; psi0tt:=eval(subs({omega(k)=k^2/2,t=tt},psi0t)); PReal:=plot(Re(psi0tt),x=-50..Pend,color=blue,thickness=2): #PIm:=plot(Im(psi0tt),x=-50..Pend,color=red,thickness=2): POrt:=display(PReal,title="Realteil der Wellenfunktion ",titlefont = [HELVETICA, 16]): rho:=conjugate(psi0tt)*psi0tt: Prho:=plot(rho,x=-50..Pend,color=brown,title=cat(Wahrscheinlichkeitsdichte,Psi*conjugate(Psi)),titlefont = [HELVETICA, 16],thickness=2): Ani[i]:=display(Matrix(1,2,[[POrt,Prho]])); od: |
| > | display([seq(Ani[i],i=0..iend)],insequence=true); |
|
| > |