V4.html

Download Maple Worksheet

Theoretische Physik 3 für Lehramt L3

Quantenmechanik, Spezielle Relativitätstheorie und weitere Gebiete der Theoretischen Physik

Vorlesung gehalten an der J.W.Goethe-Universität in Frankfurt am Main (Wintersemester 2016/17)

von Prof. Dr.Dr.h.c. Horst Stöcker und Dr.phil.nat. Dr.rer.pol. Matthias Hanauske

Frankfurt am Main 17.10.2016

Erster Vorlesungsteil: Quantenmechanik

Kapitel I: 2.2) Ein Quantenteilchen im eindimensionalen Potentialtopf mit endlicher Tiefe

Ein Quantenteilchen im eindimensionalen Potentialtopf mit endlicher Tiefe

> restart:

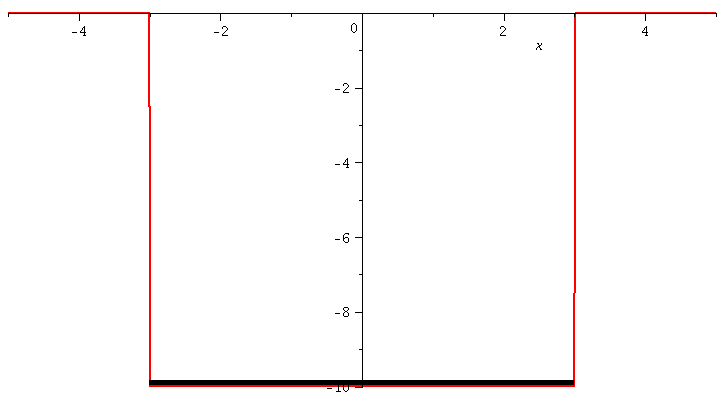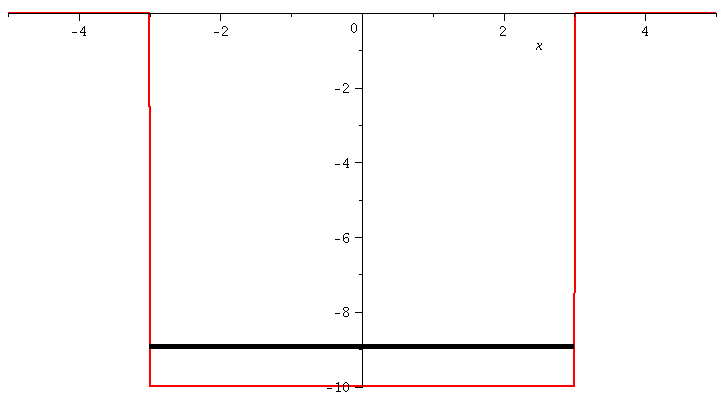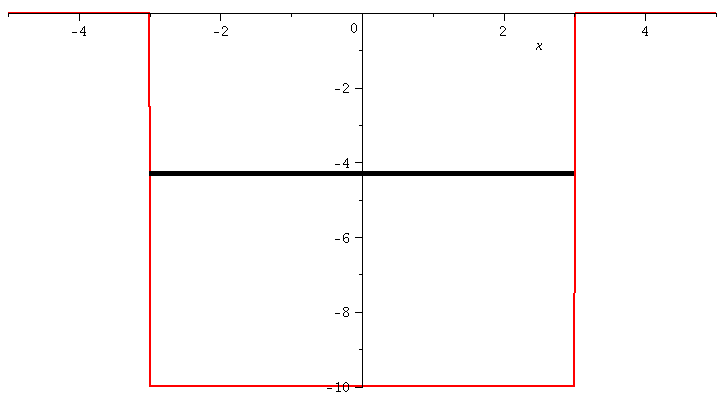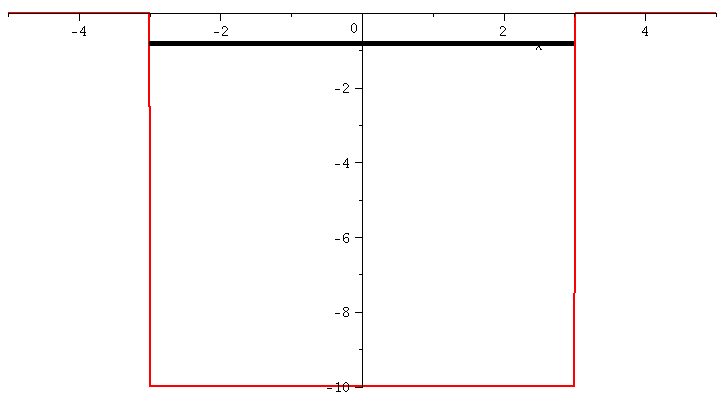
Wir betrachten im folgenden einen quantenmechanischen Zustand eines Teilchens, welcher in einem Potentialtopf gebunden ist und wir beschränken uns zunächst auf eine räumliche Dimension. Der Potentialtopf besitz das folgende Aussehen:

> V:=piecewise(abs(x) <=a, -V0);
seta:=3;
setV0:=10;
plot(subs({a=seta,V0=setV0},V),x=-5..5,thickness=3);

Plot_2d

Da der Hamiltonoperator dieses Systems nicht von der Zeit abhängt, vereinfacht sich die Schrödingergleichung. Wir betrachten nun einen gebundenen Zustand des Teichens (-V0<=E<=0) an drei unterschiedlichen Orten. Die Schrödingergleichung links vom Potentialtopf (x < -3 ) lautet:

> SGLLinks:=diff(psi[L](x),x,x)=-2*m*E/hq^2*psi[L](x);
SGLLinks:=diff(psi[L](x),x,x)=kappa^2*psi[L](x):

(1.1)

Im inneren Bereich lautet sie:

> SGLInnen:=diff(psi[M](x),x,x)=-2*m*(E+V0)/hq^2*psi[M](x);
SGLInnen:=diff(psi[M](x),x,x)=-k^2*psi[M](x):

(1.2)

Im äußeren Bereich lautet sie hingegen:

> SGLRechts:=diff(psi[R](x),x,x)=-2*m*E/hq^2*psi[R](x);
SGLRechts:=diff(psi[R](x),x,x)=kappa^2*psi[R](x):

(1.3)

Die allgemeinen Lösungen für den inneren und äußeren Bereich ergeben sich somit zu:

(wobei kappa^2=-2*m*E/hq^2 und k^2=2*m*(E+V0)/hq^2)

> Loes1:=subs({_C1=A[L],_C2=B[L]},dsolve(SGLLinks));
Loes2:=subs({_C1=A[M],_C2=B[M]},dsolve(SGLInnen));
Loes3:=subs({_C1=A[R],_C2=B[R]},dsolve(SGLRechts));

(1.4)

Aufgrund der Forderung der Normierbarkeit der gesamten Zustandsfunktion des Teilchens muß die Konstante BL der linksseitigen Zustandsfunktion (Amplitude vor exp(- kappa x)) und die Konstante AR der rechtsseitigen Zustandsfunktion (Amplitude vor exp( kappa x)) Null sein (Beachte: Bei mehrfachem Ausführen des Maple-Worksheets kann es auch vorkommen das AL bzw. BR Null sein müssen) Aufgabe: Begründen Sie warum BL und AR Null sein müssen.

> A[L]:=0;
B[R]:=0;
Loes1;
Loes2;
Loes3;

(1.5)

Lösungen bei positiver Parität der Zustandsfunktion

Wir beschränken uns zunächst auf symmetrische Zustandsfunktion mit positive Parität (psi(x)=psi(-x)) und erhalten die folgenden Gleichungen:

> EqPosPari1:=rhs(Loes2)=subs(x=-x,rhs(Loes2));
EqPosPari2:=subs(x=-x,rhs(Loes1))=rhs(Loes3);

(1.1.1)

Daraus folgen Bedingungen an die jeweiligen Amplituden:

> solve({EqPosPari1,EqPosPari2});

(1.1.2)

Die drei stückweise definierten Zustandsfunktionen ergeben sich somit zu:

(Beachte: Bei mehrfachem Ausführen des Maple-Worksheets kann es auch vorkommen das z.B. AL = AR ist)

> A[M]:=0;
B[L]:=A[R];
Loes1;
Loes2;
Loes3;

(1.1.3)

Zusätzlich muss noch ein stetiger und glatter Übergang der Funktionen an den Grenzen des Potentialtopfes gefordert werden:

> EqStetig1:=subs(x=-a,rhs(Loes1))=subs(x=-a,rhs(Loes2));
EqStetig2:=subs(x=a,rhs(Loes2))=subs(x=a,rhs(Loes3));
EqGlatt1:=subs(x=-a,diff(rhs(Loes1),x))=subs(x=-a,diff(rhs(Loes2),x));
EqGlatt2:=subs(x=a,diff(rhs(Loes2),x))=subs(x=a,diff(rhs(Loes3),x));

(1.1.4)

Dividiert man z.B. Gleichung 3 durch Gleichung 1, so erhält man

> EqComb1:=lhs(EqGlatt1)/lhs(EqStetig1)=rhs(EqGlatt1)/rhs(EqStetig1);

(1.1.5)

Andererseits gilt für k und kappa auch die folgende Gleichung:

> EqComb2:=kappa^2 + k^2=simplify(-2*m*E/hq^2 + 2*m*(E+V0)/hq^2);

(1.1.6)

Setzen wir im folgenden z.B. hq=m=1, a=3 und V0=10, so können wir beide Kurven in einem kappa-k Diagramm darstellen:

> with(plots):
K1:=subs({hq=1,m=1,V0=10,a=3},EqComb1);
K2:=subs({hq=1,m=1,V0=10},EqComb2);
Plot1:=implicitplot(K1,k=0..5,kappa=0..5,numpoints=5000,color=red):
Plot2:=implicitplot(K2,k=0..5,kappa=0..5,numpoints=5000,numpoints=5000,color=blue):
display(Plot1,Plot2);

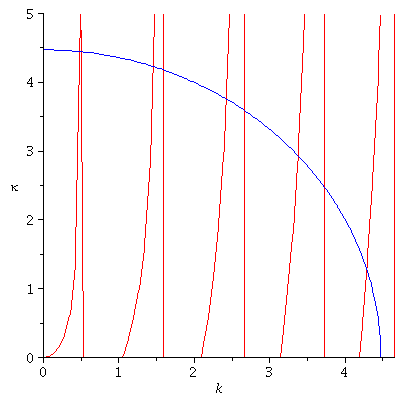Plot_2d

Laut Diagramm ergeben sich fünf Schnittpunkte. Diese berechnen sich numerisch zu:

> S[1]:=fsolve({K1,K2},{k=0..1,kappa=0..5});
S[2]:=fsolve({K1,K2},{k=1..2,kappa=0..5});
S[3]:=fsolve({K1,K2},{k=2..3,kappa=0..5});
S[4]:=fsolve({K1,K2},{k=3..4,kappa=0..5});
S[5]:=fsolve({K1,K2},{k=4..5,kappa=0..5});

(1.1.7)

An dieser Stelle tritt gerade die Quantisierung der möglichen observablen Eigenzustände auf. Die diskreten Werte für k bzw. kappa entsprechen den diskreten Werten des Energiespektrums. Im folgenden berechnen wir die zugehörigen Eigenzustände des Teilchen (unter Voraussetzung positiver Parität). Aufgrund der Stetigkeit an den Potentialgrenzen gelten für die fünf diskreten Zustände die folgenden Bedingungen an die Amplituden:

> for n from 1 by 1 to 5 do
GL[n]:=A[R]=solve(evalf(subs({k=rhs(S[n][1]),kappa=rhs(S[n][2]),a=3},EqStetig1)),A[R]);
od;

(1.1.8)

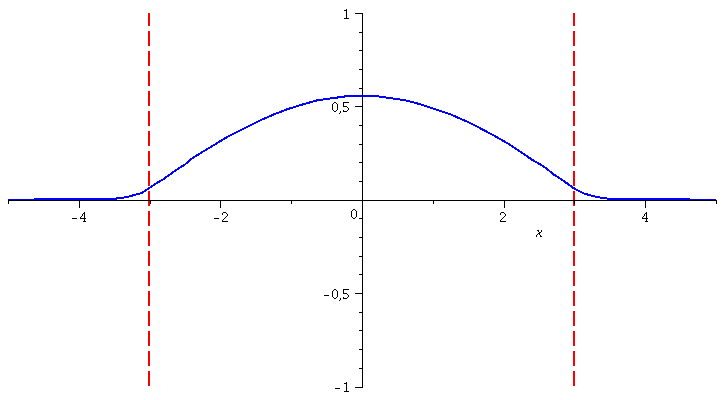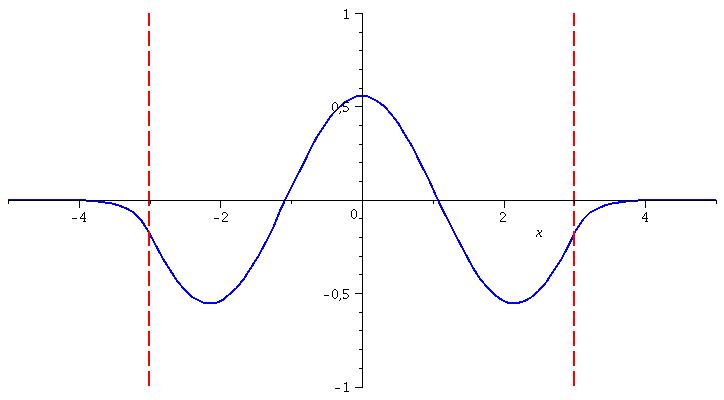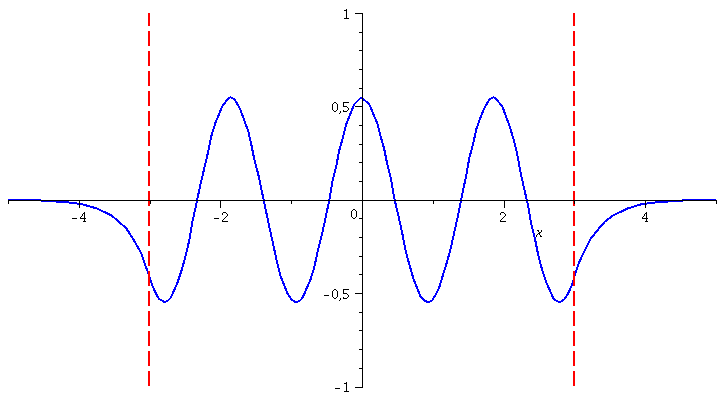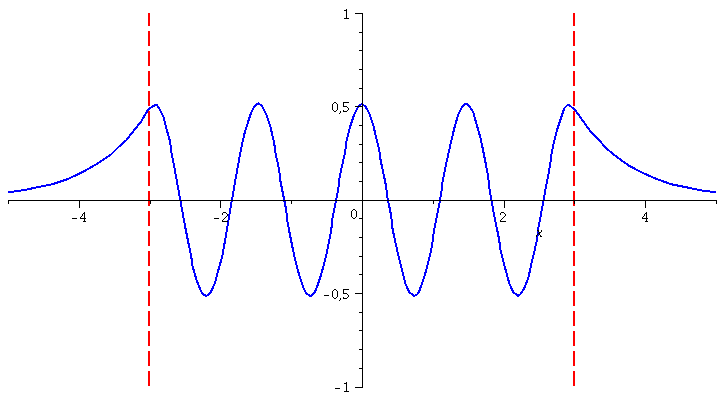
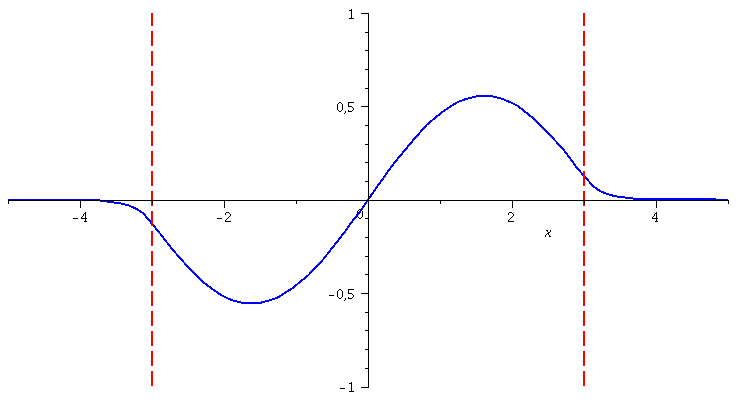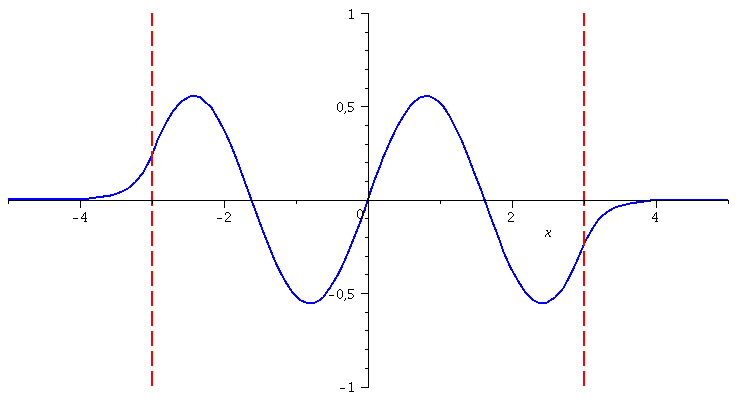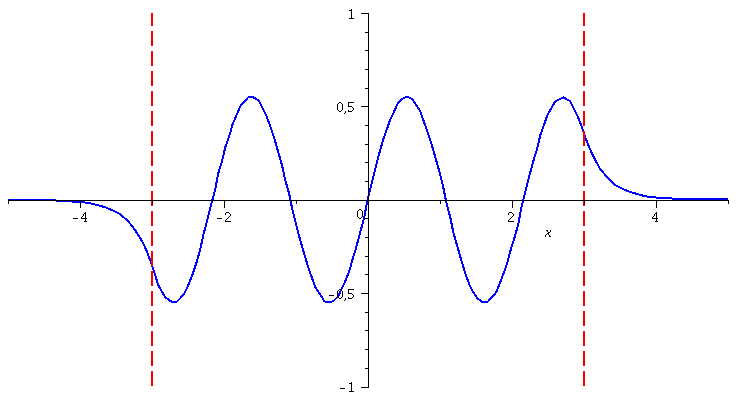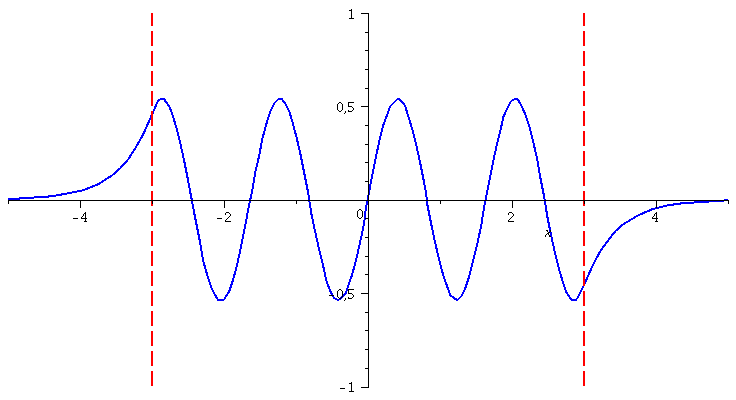
Betrachten wir uns z.B. den Grundzustand (n=5), so setzt sich dieser aus den folgenden Komponenten zusammen:

> nn:=1:
LoesL:=subs({A[R]=rhs(GL[nn]),k=rhs(S[nn][1]),kappa=rhs(S[nn][2])},Loes1);
LoesM:=subs({A[R]=rhs(GL[nn]),k=rhs(S[nn][1]),kappa=rhs(S[nn][2])},Loes2);
LoesR:=subs({A[R]=rhs(GL[nn]),k=rhs(S[nn][1]),kappa=rhs(S[nn][2])},Loes3);

(1.1.9)

Die noch unbekannte Amplitude lässt sich durch die Normierungsbedingung festlegen:

> GLNorm:=int(conjugate(rhs(LoesL))*rhs(LoesL),x=-infinity..-3)+int(conjugate(rhs(LoesM))*rhs(LoesM),x=-3..3)+int(conjugate(rhs(LoesR))*rhs(LoesR),x=3..infinity)=1;
GLNorm:=subs(conjugate(B[M])=B[M],GLNorm):

(1.1.10)

Somit setzt sich die gesamte Zustandsfunktion des Teichens im Grundzustang wie folgt zusammen

> LoesL:=subs({B[M]=solve(GLNorm)[1]},LoesL):
LoesM:=subs({B[M]=solve(GLNorm)[1]},LoesM):
LoesR:=subs({B[M]=solve(GLNorm)[1]},LoesR):
PSI:=piecewise(x < -seta, rhs(LoesL), abs(x) <= seta, rhs(LoesM), x > seta, rhs(LoesR));
Energie:=solve(rhs(S[nn][1])^2=2*(E+setV0)/1);

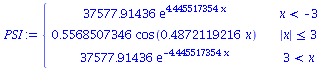`:=`(PSI, piecewise(`<`(x, -3), `+`(`*`(37577.91436, `*`(exp(`+`(`*`(4.445517354, `*`(x))))))), `<=`(abs(x), 3), `+`(`*`(.5568507346, `*`(cos(`+`(`*`(.4872119216, `*`(x))))))), `<`(3, x), `+`(`*`(3757...

(1.1.11)

und besitz das folgende grafische Aussehen:

> plot(PSI,x=-5..5);

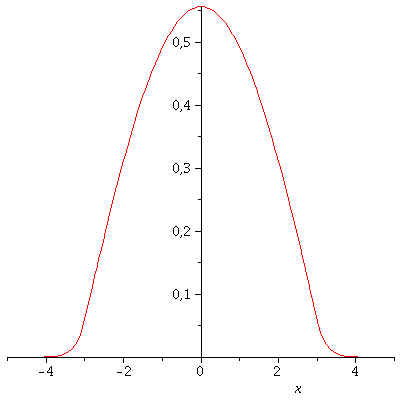Plot_2d

Die Zustandsfunktionen positiver Parität der höherenergetischen Zustände berechnet man in gleicher Weise:

> for n from 1 by 1 to 5 do
LoesL:=subs({A[R]=rhs(GL[n]),k=rhs(S[n][1]),kappa=rhs(S[n][2])},Loes1):
LoesM:=subs({A[R]=rhs(GL[n]),k=rhs(S[n][1]),kappa=rhs(S[n][2])},Loes2):
LoesR:=subs({A[R]=rhs(GL[n]),k=rhs(S[n][1]),kappa=rhs(S[n][2])},Loes3):
GLNorm:=int(conjugate(rhs(LoesL))*rhs(LoesL),x=-infinity..-3)+int(conjugate(rhs(LoesM))*rhs(LoesM),x=-3..3)+int(conjugate(rhs(LoesR))*rhs(LoesR),x=3..infinity)=1;
GLNorm:=subs(conjugate(B[M])=B[M],GLNorm):
LoesL:=subs({B[M]=solve(GLNorm)[1]},LoesL):
LoesM:=subs({B[M]=solve(GLNorm)[1]},LoesM):
LoesR:=subs({B[M]=solve(GLNorm)[1]},LoesR):
PSI[n]:=piecewise(x < -seta, rhs(LoesL), abs(x) <= seta, rhs(LoesM), x > seta, rhs(LoesR)):
Energie[n]:=solve(rhs(S[n][1])^2=2*(E+setV0)/1);
PlotTopf[n]:=plot(subs({a=seta,V0=setV0},V),x=-5..5,thickness=2,color=red):
PlotEnergie[n]:=plot(Energie[n],x=-seta..seta,thickness=5,color=black):
PlotPSI[n]:=plot(PSI[n],x=-5..5,thickness=2,color=blue):
GrenzeLinks:=implicitplot(x=-3, x=-5..5, y=-1..1, colour=red,linestyle=3, thickness=2):
GrenzeRechts:=implicitplot(x=3, x=-5..5, y=-1..1, colour=red,linestyle=3, thickness=2);
Ani[n]:=display(Matrix(2,1,[display(PlotPSI[n],GrenzeLinks,GrenzeRechts),display(PlotTopf[n],PlotEnergie[n])]));
od:

> display([seq(Ani[i],i=1..5)],insequence=true);

Plot_2d

Plot_2d

Lösungen bei negativer Parität der Zustandsfunktion

Wir beschränken uns nun auf antisymmetrische Zustandsfunktion mit negativer Parität (psi(x)=-psi(-x)) und erhalten die folgenden Gleichungen:

> EqNegPari1:=rhs(Loes2)=-subs(x=-x,rhs(Loes2));
EqNegPari2:=subs(x=-x,rhs(Loes1))=-rhs(Loes3);

(1.2.1)

Daraus folgen Bedingungen an die jeweiligen Amplituden:

> solve({EqNegPari1,EqNegPari2});

(1.2.2)

Die drei stückweise definierten Zustandsfunktionen ergeben sich somit zu:

(Beachte: Bei mehrfachem Ausführen des Maple-Worksheets kann es auch vorkommen das z.B. AL = AR ist)

> B[M]:=0;
A[R]:=-B[L];
Loes1;
Loes2;
Loes3;

(1.2.3)

Zusätzlich muss noch ein stetiger und glatter Übergang der Funktionen an den Grenzen des Potentialtopfes gefordert werden:

(1.2.4)

Dividiert man z.B. Gleichung 3 durch Gleichung 1, so erhält man

> EqComb1:=lhs(EqGlatt1)/lhs(EqStetig1)=rhs(EqGlatt1)/rhs(EqStetig1);

(1.2.5)

Andererseits gilt für k und kappa auch die folgende Gleichung:

> EqComb2:=kappa^2 + k^2=simplify(-2*m*E/hq^2 + 2*m*(E+V0)/hq^2);

(1.2.6)

Setzen wir im folgenden z.B. hq=m=1, a=3 und V0=10, so können wir beide Kurven in einem kappa-k Diagramm darstellen:

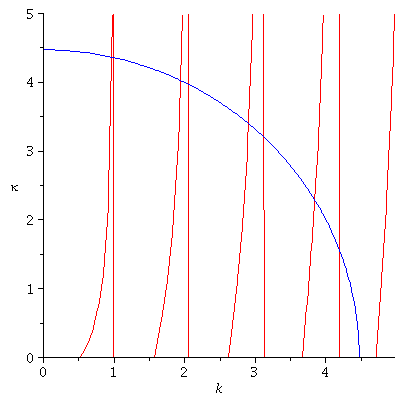Plot_2d

Laut Diagramm ergeben sich vier Schnittpunkte. Diese berechnen sich numerisch zu:

> SN[1]:=fsolve({K1,K2},{k=0..1.5,kappa=0..5});
SN[2]:=fsolve({K1,K2},{k=1.5..2.5,kappa=0..5});
SN[3]:=fsolve({K1,K2},{k=2.5..3.5,kappa=0..5});
SN[4]:=fsolve({K1,K2},{k=3.5..5,kappa=0..5});

(1.2.7)

An dieser Stelle tritt gerade die Quantisierung der möglichen observablen Eigenzustände auf. Die diskreten Werte für k bzw. kappa entsprechen den diskreten Werten des Energiespektrums. Im folgenden berechnen wir die zugehörigen Eigenzustände des Teilchen (unter Voraussetzung negativer Parität). Aufgrund der Stetigkeit an den Potentialgrenzen gelten für die fünf diskreten Zustände die folgenden Bedingungen an die Amplituden:

> for n from 1 by 1 to 4 do
GL[n]:=B[L]=solve(evalf(subs({k=rhs(SN[n][1]),kappa=rhs(SN[n][2]),a=3},EqStetig1)),B[L]);
od;

(1.2.8)

Betrachten wir uns z.B. den Grundzustand (n=1), so setzt sich dieser aus den folgenden Komponenten zusammen:

> nn:=1:
LoesL:=subs({B[L]=rhs(GL[nn]),k=rhs(SN[nn][1]),kappa=rhs(SN[nn][2])},Loes1);
LoesM:=subs({B[L]=rhs(GL[nn]),k=rhs(SN[nn][1]),kappa=rhs(SN[nn][2])},Loes2);
LoesR:=subs({B[L]=rhs(GL[nn]),k=rhs(SN[nn][1]),kappa=rhs(SN[nn][2])},Loes3);

(1.2.9)

Die noch unbekannte Amplitude lässt sich durch die Normierungsbedingung festlegen:

(1.2.10)

Somit setzt sich die gesamte Zustandsfunktion des Teichens im Grundzustang wie folgt zusammen

> LoesL:=subs({A[M]=solve(GLNorm)[1]},LoesL):
LoesM:=subs({A[M]=solve(GLNorm)[1]},LoesM):
LoesR:=subs({A[M]=solve(GLNorm)[1]},LoesR):
PSI:=piecewise(x < -seta, rhs(LoesL), abs(x) <= seta, rhs(LoesM), x > seta, rhs(LoesR));
Energie:=solve(rhs(SN[nn][1])^2=2*(E+setV0)/1);

`:=`(PSI, piecewise(`<`(x, -3), `+`(`-`(`*`(58926.03379, `*`(exp(`+`(`*`(4.364779474, `*`(x)))))))), `<=`(abs(x), 3), `+`(`*`(.5564918464, `*`(sin(`+`(`*`(.9740123924, `*`(x))))))), `<`(3, x), `+`(`*`...

(1.2.11)

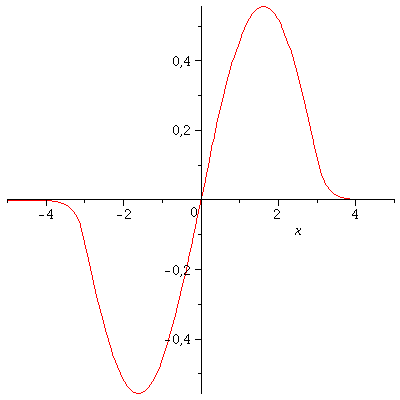
und besitz das folgende grafische Aussehen:

> plot(PSI,x=-5..5);

Plot_2d

Die Zustandsfunktionen negativer Parität der höherenergetischen Zustände berechnet man in gleicher Weise:

> for n from 1 by 1 to 4 do
LoesL:=subs({B[L]=rhs(GL[n]),k=rhs(SN[n][1]),kappa=rhs(SN[n][2])},Loes1):
LoesM:=subs({B[L]=rhs(GL[n]),k=rhs(SN[n][1]),kappa=rhs(SN[n][2])},Loes2):
LoesR:=subs({B[L]=rhs(GL[n]),k=rhs(SN[n][1]),kappa=rhs(SN[n][2])},Loes3):
GLNorm:=int(conjugate(rhs(LoesL))*rhs(LoesL),x=-infinity..-3)+int(conjugate(rhs(LoesM))*rhs(LoesM),x=-3..3)+int(conjugate(rhs(LoesR))*rhs(LoesR),x=3..infinity)=1;
GLNorm:=subs(conjugate(A[M])=A[M],GLNorm):
LoesL:=subs({A[M]=solve(GLNorm)[1]},LoesL):
LoesM:=subs({A[M]=solve(GLNorm)[1]},LoesM):
LoesR:=subs({A[M]=solve(GLNorm)[1]},LoesR):
PSI[n]:=piecewise(x < -seta, rhs(LoesL), abs(x) <= seta, rhs(LoesM), x > seta, rhs(LoesR)):
Energie[n]:=solve(rhs(SN[n][1])^2=2*(E+setV0)/1);
PlotTopf[n]:=plot(subs({a=seta,V0=setV0},V),x=-5..5,thickness=2,color=red):
PlotEnergie[n]:=plot(Energie[n],x=-seta..seta,thickness=5,color=black):
PlotPSI[n]:=plot(PSI[n],x=-5..5,thickness=2,color=blue):
GrenzeLinks:=implicitplot(x=-3, x=-5..5, y=-1..1, colour=red,linestyle=3, thickness=2):
GrenzeRechts:=implicitplot(x=3, x=-5..5, y=-1..1, colour=red,linestyle=3, thickness=2);
Ani[n]:=display(Matrix(2,1,[display(PlotPSI[n],GrenzeLinks,GrenzeRechts),display(PlotTopf[n],PlotEnergie[n])]));
od:

> display([seq(Ani[i],i=1..4)],insequence=true);

Plot_2d

Plot_2d