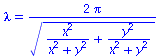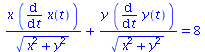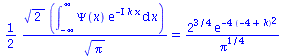Einführung 

In diesem Unterpunkt werden wir die einfachste Lösung der Schrödingergleichung, die ebene Materiewelle (de Brogliesche Materiewelle) betrachten. Zusätzlich werden wir am Ende noch den Begriff des Wellenpaketes diskutieren und veranschaulichen. 

Die Schrödinger-Gleichung eines ungebundenen, freien Teilchens 

>	restart: with(plots):

 

Die einfachste Form der Schrödinger-Gleichung ist die eines ungebundenen, freien Quantenteilchens (Potential V=0). Wir betrachten die Schrödinger-Gleichung zunächst nur in einer Dimension (x-Richtung) : 

>	SGL:=I*hq*diff(psi(x,t),t)=-hq^2/(2*m)*diff(psi(x,t),x,x);

 

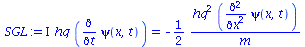(2.1)

 

Man kann zeigen, das eine Lösung dieser partiellen Differentialgleichung durch die folgende Funktion gegeben ist, die man als eine de Brogliesche Materiewelle bezeichnet: 

>	psi=A*exp(I*(k*x-omega*t));

 

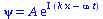(2.2)

 

Wir überprufen dies indem wir diese Funktion in die linke und rechte Seite der Schrödinger-Gleichung einsetzen: 

>	LinkeGL:=lhs(SGL)=eval(subs({psi(x,t)=A*exp(I*(k*x-omega*t))},lhs(SGL))); RechteGL:=rhs(SGL)=eval(subs({psi(x,t)=A*exp(I*(k*x-omega*t))},rhs(SGL)));

 

 

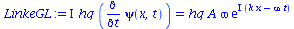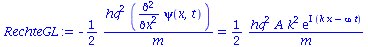	(2.3)

 

Durch einfache elementare Umformungen kann man zeigen, dass die Lösung wirklich die Schrödinger-Gleichung erfüllt, falls omega=hq*k^2/(2*m) ist: 

>	rhs(LinkeGL)=rhs(RechteGL); (rhs(LinkeGL)=rhs(RechteGL))/(hq*A*exp(I*(k*x-omega*t)));

 

 

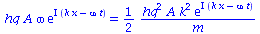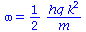	(2.4)

 

De Broglieschen Materiewellen  

>	restart: with(plots):

 

Wir betrachten im folgenden einen quantenmechanischen Zustand eines Teilchens in einer Dimesion (x-Richtung) und beschreiben diesen als eine de Brogliesche Materiewelle (k=kx): 

>	psi:=A*exp(I*(k*x-omega*t));

 

(3.1)

 

Der Impuls des Teilchens p ist mit dem Wellenvektor k durch p=hq*k und die Energie E ist mit der Frequenz omega wie folgt verknüpft E=hq*omega.Für die Wellenlänge des Teilchens gilt: 

>	lambda=2*Pi/k;

 

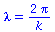(3.2)

 

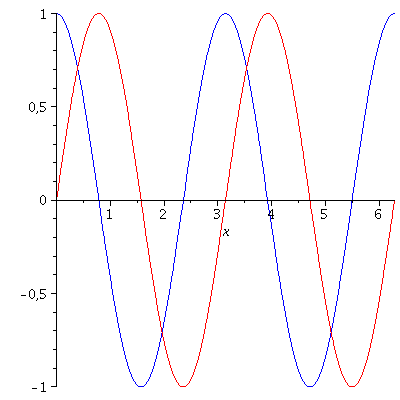
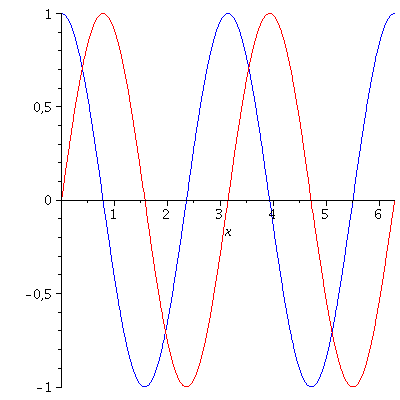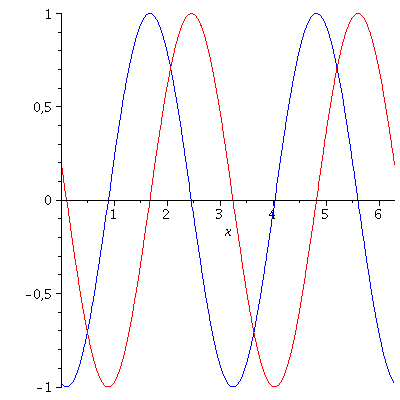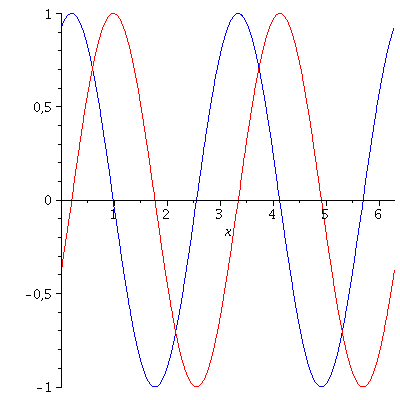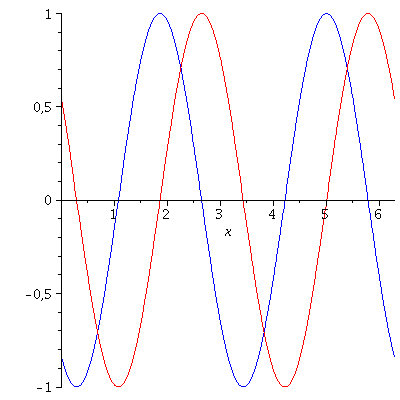
Wie nehmen im folgenden z.B. an, dass die Energie und der Impuls des Teilchens festgelegt sind und setzen die Amplitude auf eins (z.B. A=1, k=2 und omega=10). Der Real- und Imaginärteil der Wellenfunktion hat zur Zeit t=0 dann das folgende Aussehen ( Realteil=blau und Imaginärteil=rot): 

>	setA:=1: setk:=2: setomega:=10: sett:=0: subs({k=setk},lambda=2*Pi/k); PReal:=plot(Re(subs({A=setA,k=setk,omega=setomega,t=sett},psi)),x=0..2*Pi,color=blue,numpoints=700): PIm:=plot(Im(subs({A=setA,k=setk,omega=setomega,t=sett},psi)),x=0..2*Pi,color=red,numpoints=700): display(PReal,PIm);

 

Betrachten wir die zeitliche Entwicklung der Materiewelle von t=0 bis t=1, so ergibt sich die folgende Animation: 

>	AnReal:=animate(Re(subs({A=setA,k=setk,omega=setomega},psi)),x=0..2*Pi,t=0..1,color=blue,numpoints=700): AnIm:=animate(Im(subs({A=setA,k=setk,omega=setomega},psi)),x=0..2*Pi,t=0..1,color=red,numpoints=700): display(AnReal,AnIm);

 

Die Phasengeschwindigkeit der Welle berechnet sich wie folgt 

>	Phase:=k*x(t)-omega*t; Eq1:=diff(Phase,t)=0; Eq2:=(Eq1+omega)/k; subs({k=setk,omega=setomega},Eq2);

 

 

 

 

	(3.3)

 

Wir betrachten im folgenden den gleichen Fall aber in zwei Dimesion (x-Richtung und y-Richtung) und beschreiben den Zustand des Teilchens wieder  als eine de Brogliesche Materiewelle: 

>	restart: with(plots): psi:=A*exp(I*(k[x]*x+k[y]*y-omega*t));

 

(3.4)

 

Der Impuls des Teilchens p ist mit dem Wellenvektor k durch p=hq*k und die Energie E ist mit der Frequenz omega wie folgt verknüpft E=hq*omega.Für die Wellenlänge des Teilchens gilt: 

>	lambda=2*Pi/sqrt(k[x]^2+k[y]^2);

 

(3.5)

 

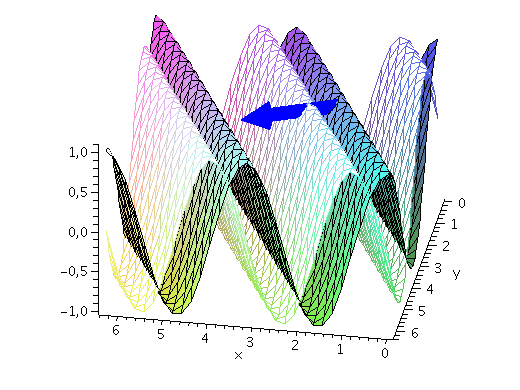
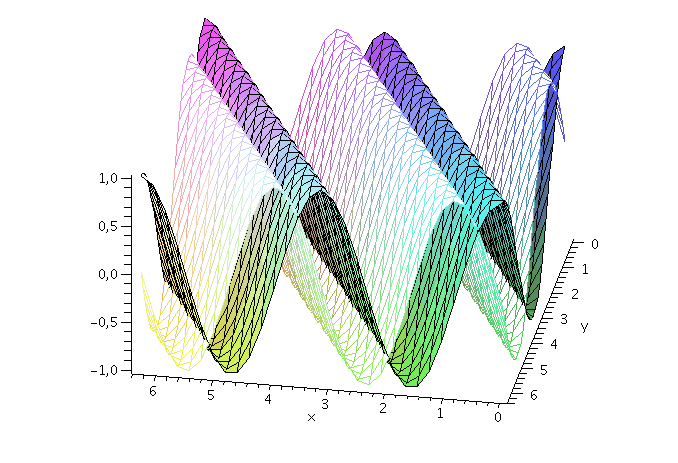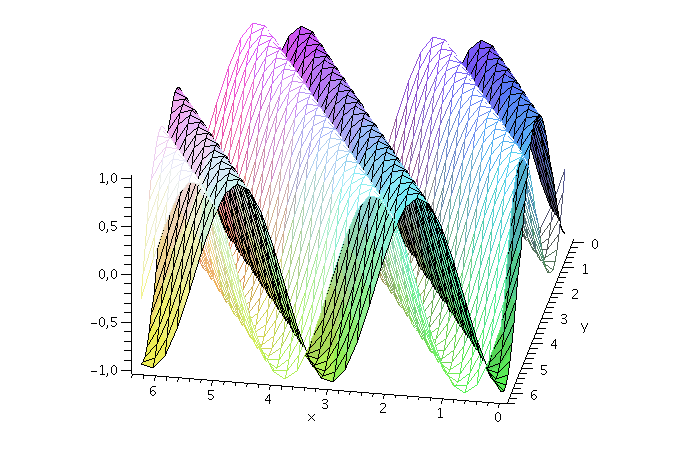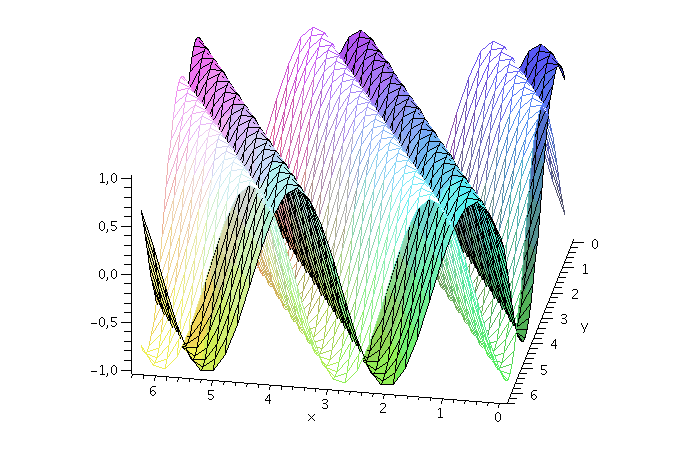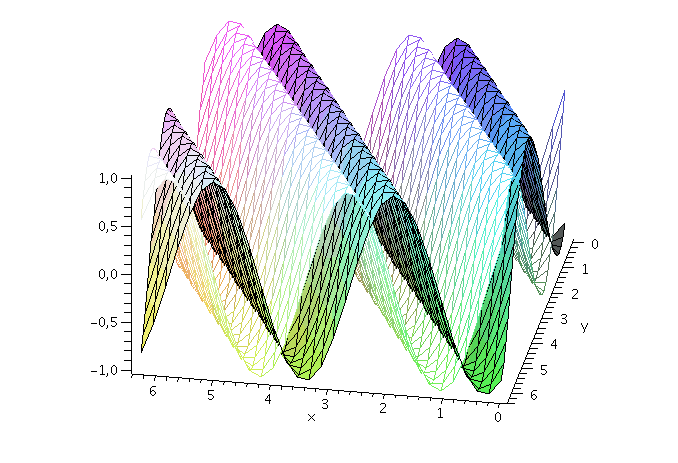
Wie nehmen im folgenden z.B. an, dass die Energie und der Impuls des Teilchens festgelegt sind und setzen die Amplitude auf eins (z.B. A=1, kx=2, ky=1 und omega=10). Der Real- und Imaginärteil der Wellenfunktion hat zur Zeit t=0 dann das folgende Aussehen ( Realteil: farbige Fläche und Imaginärteil: weiße Fläche, der blaue Pfeil kennzeichnet den k-Vektor und somit die Ausbreitungsrichtung der Wellenfront): 

>

setA:=1: setk[x]:=2: setk[y]:=1: setomega:=10: sett:=0: subs({k[x]=setk[x],k[y]=setk[y]},lambda=2*Pi/sqrt(k[x]^2+k[y]^2)); PReal:=plot3d(Re(subs({A=setA,k[x]=setk[x],k[y]=setk[y],omega=setomega,t=sett},psi)),x=0..2*Pi,y=0..2*Pi,numpoints=900): PIm:=plot3d(Im(subs({A=setA,k[x]=setk[x],k[y]=setk[y],omega=setomega,t=sett},psi)),x=0..2*Pi,y=0..2*Pi,numpoints=900,style=wireframeopaque): kVec:=arrow(<1.7,3,0.9>,<setk[x],setk[y],0>,width = [.08, relative], head_length = [.3, relative],color=blue): display(PReal,PIm,kVec,axes=framed,orientation=[100, 50]);

 

Betrachten wir die zeitliche Entwicklung der Materiewelle von t=0 bis t=1, so ergibt sich die folgende Animation: 

>

AnReal:=animate3d(Re(subs({A=setA,k[x]=setk[x],k[y]=setk[y],omega=setomega},psi)),x=0..2*Pi,y=0..2*Pi,t=0..1,numpoints=900): AnIm:=animate3d(Im(subs({A=setA,k[x]=setk[x],k[y]=setk[y],omega=setomega},psi)),x=0..2*Pi,y=0..2*Pi,t=0..1,numpoints=900,style=wireframeopaque): display(AnReal,AnIm,axes=framed,orientation=[100, 50]);

 

Die Phasengeschwindigkeit der Welle berechnet sich wie folgt 

>	Phase:=k[x]*x(t)+k[y]*y(t)-omega*t; Eq1:=diff(Phase,t)=0; Eq2:=(Eq1+omega); subs({k[x]=setk[x],k[y]=setk[y],omega=setomega},Eq2);

 

 

 

 

	(3.6)

 

Da die Ausbreitungsrichtung der Welle und die zeitliche Ableitung des Vektors (x(t),y(t)) die selbe Richtung haben, gilt für die Phasengeschwindigkeit: v=omega/k (siehe Greiner S:34). 

>	omega/sqrt(k[x]^2+k[y]^2)=evalf(subs({k[x]=setk[x],k[y]=setk[y],omega=setomega},omega/sqrt(k[x]^2+k[y]^2)));

 

(3.7)

 

Der Einheitsvektor der Ausbreitungsgeschwindigkeit der Welle ist: 

>	Betragk:=evalf(subs({k[x]=setk[x],k[y]=setk[y],omega=setomega},sqrt(k[x]^2+k[y]^2))); n[x]:=setk[x]/Betragk; n[y]:=setk[y]/Betragk; sqrt(n[x]^2+n[y]^2);

 

 

 

 

	(3.8)

 

Kugelwellen in zwei Dimensionen. 

>	restart: with(plots): psi:=A*exp(I*(k[x]*x+k[y]*y-omega*t));

 

(3.9)

 

Der Impuls des Teilchens p ist mit dem Wellenvektor k durch p=hq*k und die Energie E ist mit der Frequenz omega wie folgt verknüpft E=hq*omega.Für die Wellenlänge des Teilchens gilt: 

>	lambda=2*Pi/sqrt(k[x]^2+k[y]^2);

 

(3.10)

 

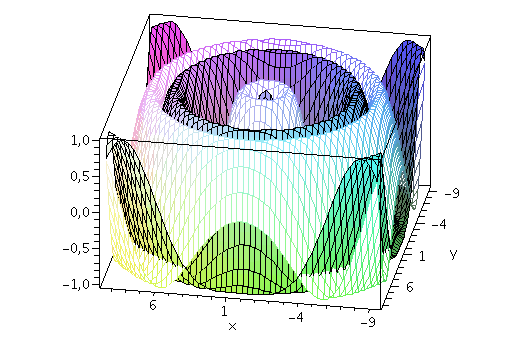
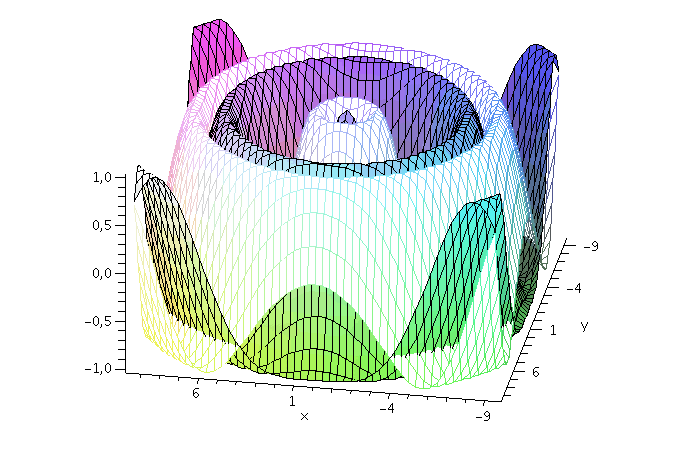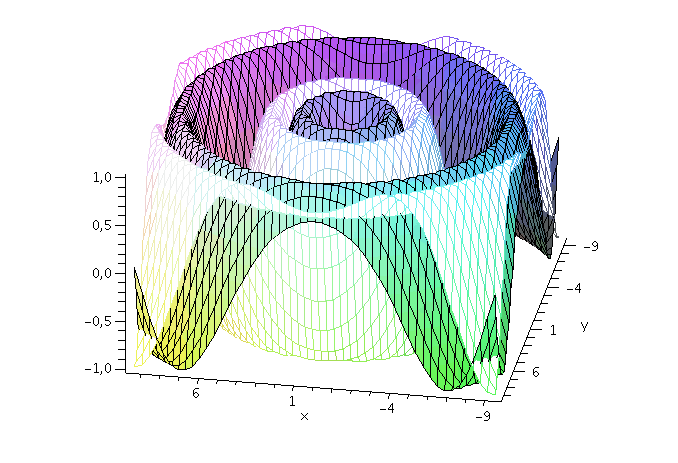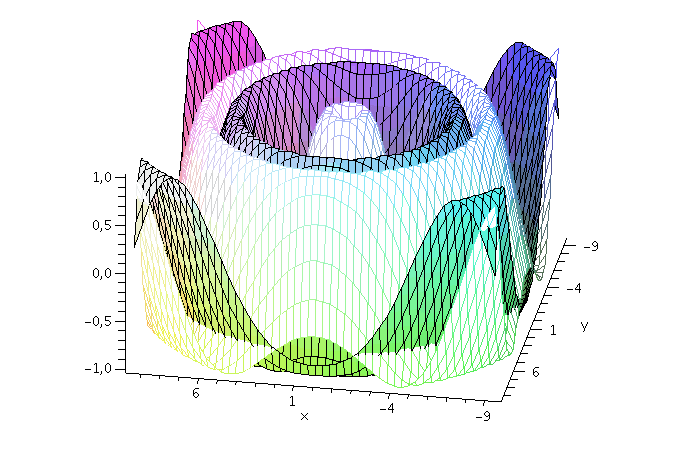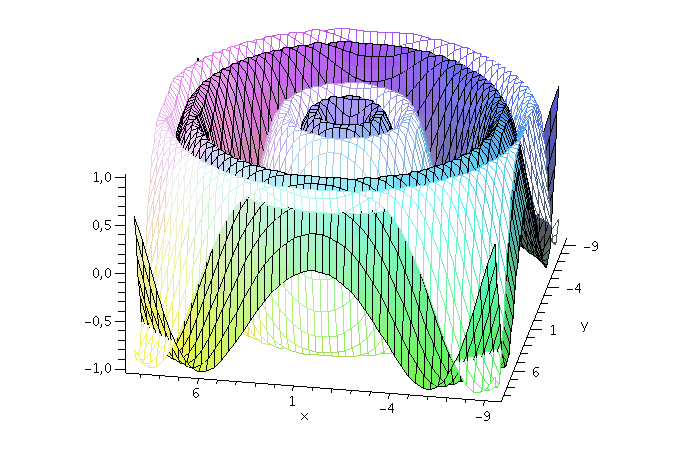
Wie nehmen im folgenden z.B. an, dass die Energie und der Impuls des Teilchens festgelegt sind und setzen die Amplitude auf eins (z.B. A=1, kx=2, ky=1 und omega=10). Der Real- und Imaginärteil der Wellenfunktion hat zur Zeit t=0 dann das folgende Aussehen ( Realteil=blau und Imaginärteil=rot): 

>

setA:=1: setk[x]:=x/sqrt(x^2+y^2): setk[y]:=y/sqrt(x^2+y^2): setomega:=8: sett:=0: subs({k[x]=setk[x],k[y]=setk[y]},lambda=2*Pi/sqrt(k[x]^2+k[y]^2)); PReal:=plot3d(Re(subs({A=setA,k[x]=setk[x],k[y]=setk[y],omega=setomega,t=sett},psi)),x=-3*Pi..3*Pi,y=-3*Pi..3*Pi,numpoints=2500): PIm:=plot3d(Im(subs({A=setA,k[x]=setk[x],k[y]=setk[y],omega=setomega,t=sett},psi)),x=-3*Pi..3*Pi,y=-3*Pi..3*Pi,numpoints=2500,style=wireframeopaque): display(PReal,PIm,axes=boxed,orientation=[100, 50]);

 

Betrachten wir die zeitliche Entwicklung der Materiewelle von t=0 bis t=1, so ergibt sich die folgende Animation: 

>

AnReal:=animate3d(Re(subs({A=setA,k[x]=setk[x],k[y]=setk[y],omega=setomega},psi)),x=-3*Pi..3*Pi,y=-3*Pi..3*Pi,t=0..1,numpoints=2500): AnIm:=animate3d(Im(subs({A=setA,k[x]=setk[x],k[y]=setk[y],omega=setomega},psi)),x=-3*Pi..3*Pi,y=-3*Pi..3*Pi,t=0..1,numpoints=2500,style=wireframeopaque): display(AnReal,AnIm,axes=framed,orientation=[100, 50]);

 

Die Phasengeschwindigkeit der Welle berechnet sich wie folgt 

>	Phase:=k[x]*x(t)+k[y]*y(t)-omega*t; Eq1:=diff(Phase,t)=0; Eq2:=(Eq1+omega); subs({k[x]=setk[x],k[y]=setk[y],omega=setomega},Eq2);

 

 

 

 

	(3.11)

 

Endliche Wellenpakete 

Um die Beschreibung der de Broglieschen Materiewellen auf räumlich begrenzte Teichen anwenden zu können, müssen wir zu endlichen Wellenpaketen übergehen. Wellenpakete werden als eine Überlagerung harmonischer Wellen dargestellt, die sich hinsichtlich ihrer Wellenlänge und Fortpflanzungsgeschwindigkeit unterscheiden. Wir betrachten im folgenden eine spezielle Art eines Wellenpaketes, das sog. Gaußsche Wellenpaket in einer Dimension (x-Richtung).  

>	restart: with(plots):

 

Das Wellenpaket sei zur Zeit t=0 durch folgenden Ausdruck gegeben: 

>	psi:=A*exp(-1/(4*sigma^2)*x^2+I*k0*x);

 

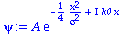(4.1)

 

Diese Materiewelle ist räumlich begrenzt, so dass wir die zunächst willkürlich gesetzte Amplitude A durch die Normierungseigenschaft festlegen können. Wie nehmen im folgenden z.B. an, dass sigma=0.5 und k0=4 sei und berechnen uns mittels der Normierungseigenschaft (Teilchen muß mit einer Wahrscheinlichkeit von Eins irgendwo im Raum zu finden sein) die Amplitude A: 

>	setk0:=4: setsigma:=2: EqNorm:=int(conjugate(subs({k0=setk0,sigma=setsigma},psi))*subs({k0=setk0,sigma=setsigma},psi),x=-infinity..infinity)=1; LoesA:=solve(subs(conjugate(A)=A,EqNorm),A);

 

 

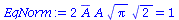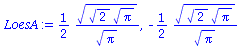	(4.2)

 

Der allgemeine analytische Ausdruck der Normierungskonstanten ist A=1/sqrt(sigma*sqrt(2*Pi)). Überprüfung: 

>	evalf(subs(sigma=setsigma,1/(sqrt(sigma*sqrt(2*Pi))))); evalf(LoesA[1]);

 

 

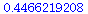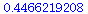	(4.3)

 

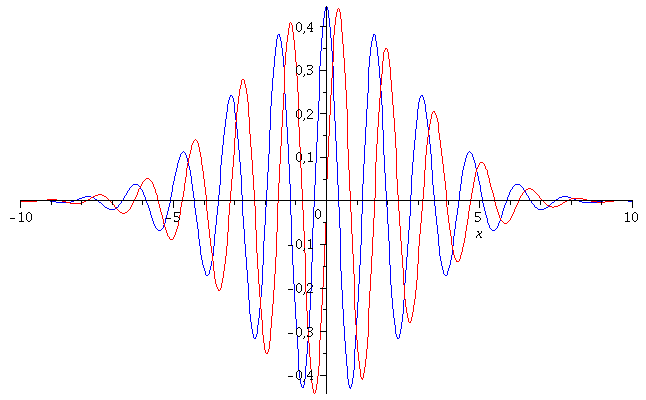
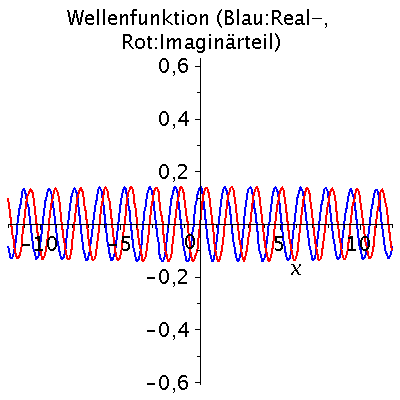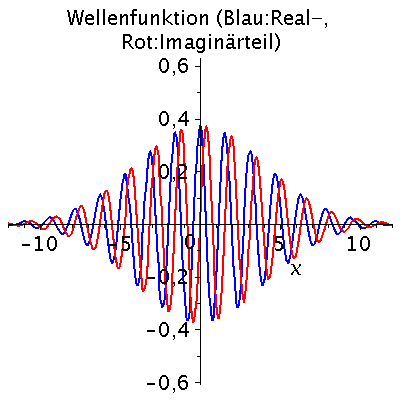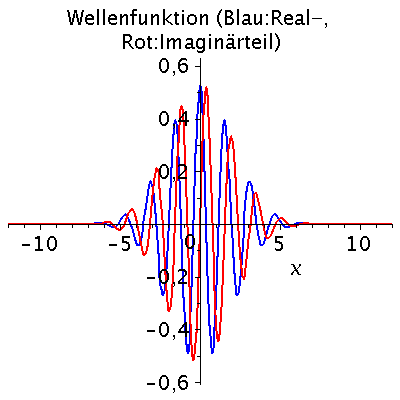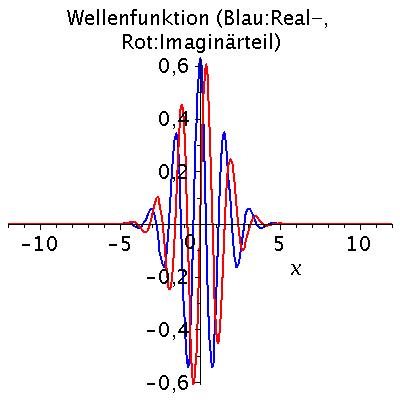
Der Real- und Imaginärteil der Wellenfunktion hat zur Zeit t=0 dann das folgende Aussehen ( Realteil=blau und Imaginärteil=rot): 

>	setA:=LoesA[1]: PReal:=plot(Re(subs({A=setA,k0=setk0,sigma=setsigma},psi)),x=-10..10,color=blue,numpoints=700): PIm:=plot(Im(subs({A=setA,k0=setk0,sigma=setsigma},psi)),x=-10..10,color=red,numpoints=700): display(PReal,PIm);

 

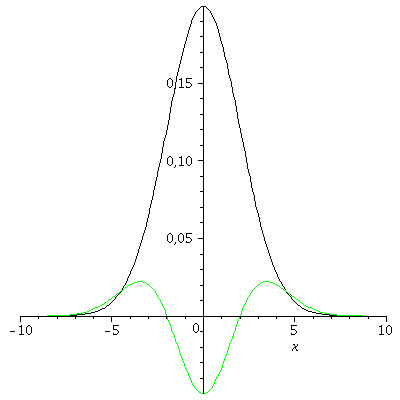
Die Wahrscheinlichkeit das Teilchen am Ort x zu finden ist durch die Wahrscheinlichkeitsdichte gegeben. Die Quadratwurzel der Varianz (die Standardabweichung sigma) kann man an den Wendestellen der Wahrscheinlichkeitsdichte ablesen (grüne Kurve). 

>	psi0:=subs({A=setA,k0=setk0,sigma=setsigma},psi): rho0:=expand(conjugate(psi0)*psi0): P1:=plot(rho0,x=-10..10,color=black): P2:=plot(Re(eval(diff(rho0,x,x))),x=-10..10,color=green): display(P1,P2);

 

Diese Materiewelle setzt sich aus einer Überlagerung von ebenen Wellen unterschiedlichster Frequenzen zusammen. Das zugehörige Frequenzspektrum der Gaußwelle erhalten wir mittels seiner Fouriertransformierten, wobei ein Normierungsfaktor (1/sqrt(2*Pi)) zusätzlich eingefügt wird. 

>	1/sqrt(2*Pi)*int(Psi(x)*exp(-I*k*x),x=-infinity..infinity)=simplify(1/sqrt(2*Pi)*int(psi0*exp(-I*k*x),x=-infinity..infinity));

 

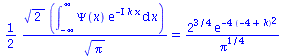(4.4)

 

Einfachere Berechnung: Die Fouriertransformation ist in Maple schon vordefiniert. 

>	with(inttrans): FourPsi:=1/sqrt(2*Pi)*fourier(psi0,x,k);

 

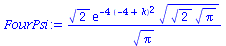(4.5)

 

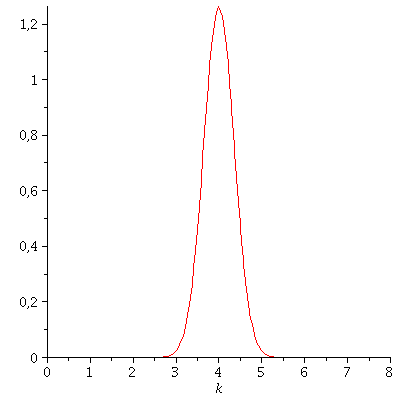
Stellen wir diese Fouriertransformierte als Funktion der Wellenzahl k dar so erhält man das folgende Bild: 

>	plot(FourPsi,k=0..8);

 

Das Quadrat dieser Fouriertransformierten ist wieder auf 1 normiert: 

>	int(FourPsi^2,k=-infinity..infinity);

 

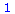(4.6)

 

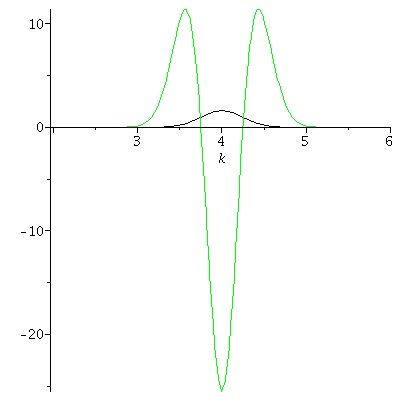
Die Quadratwurzel der Varianz der Impulsverteilung (die Standardabweichung sigma_k) kann man an den Wendestellen der Fouriertransformierten ablesen. Analytisch erhält man den folgenden Zusammenhang: sigma_k^2=1/(4*sigma^2) 

>	evalf(4+sqrt(1/(4*setsigma^2))); evalf(4-sqrt(1/(4*setsigma^2))); P1:=plot(FourPsi^2,k=2..6,color=black): P2:=plot(diff(FourPsi^2,k,k),k=2..6,color=green): display(P1,P2);

 

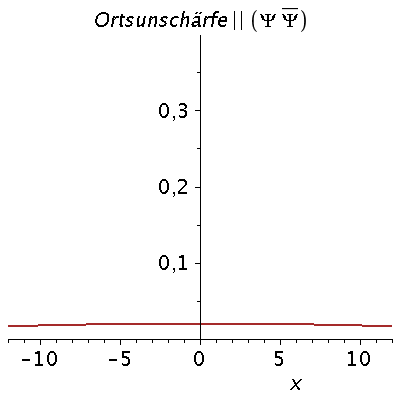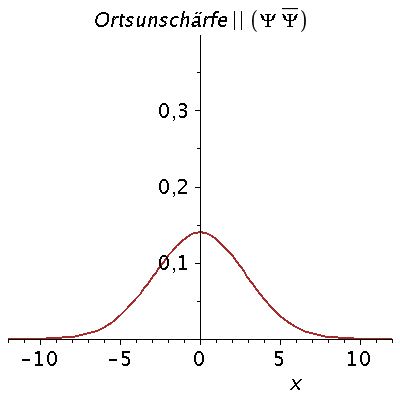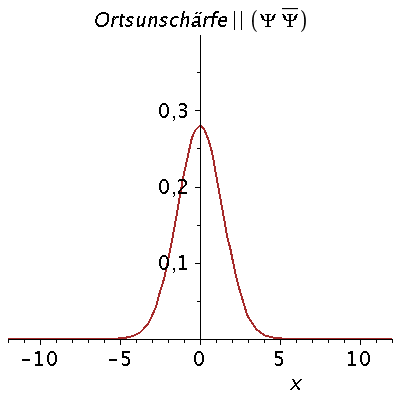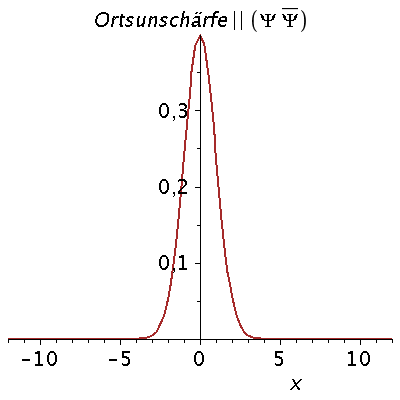
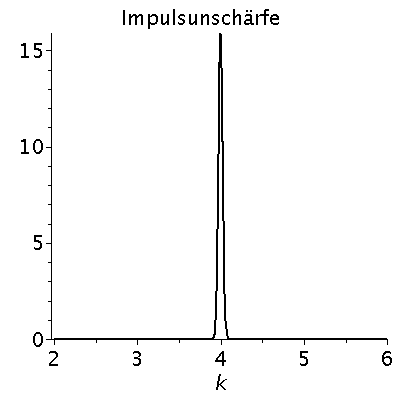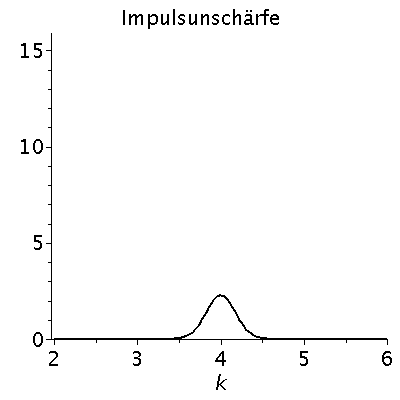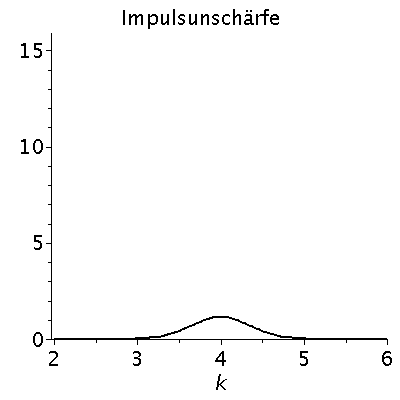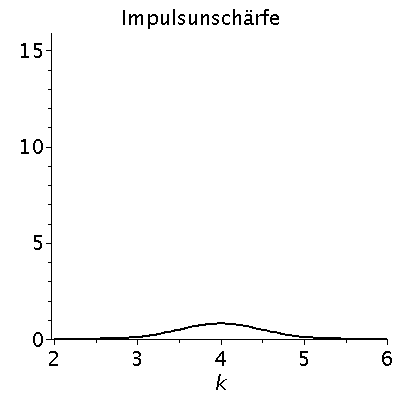
Das kontinuierliche Frequenzspektrum zeigt die Gaußsche Normalverteilung, wobei der Wert k0 der Erwartungswert und sigma_k^2 die Varianz der Verteilung ist. Aufgrund der Verbindung der Wellenzahl k mit dem Impuls des Teilchens p=hq*k, zeigt diese Verteilung also auch eine gewisse Impulsunschärfe des Teilchens. Diese Impulsunschärfe ist durch die Varianz sigma^2 quantifiziert, die ihrerseits auch die Ortsunschärfe des Gaußsche Wellenpaketes bestimmt. Wir wollen im folgenden die Auswirkungen dieser Unschärfe-Beziehung zwischen Ort und Impuls des Teilchens veranschaulichen: 

>

for i from 1 by 1 to 20 do setk0:=4: setsigma:=1/(0.05*i): EqNorm:=int(conjugate(subs({k0=setk0,sigma=setsigma},psi))*subs({k0=setk0,sigma=setsigma},psi),x=-infinity..infinity)=1: LoesA:=solve(subs(conjugate(A)=A,EqNorm),A): setA:=LoesA[1]: PReal:=plot(Re(subs({A=setA,k0=setk0,sigma=setsigma},psi)),x=-12..12,color=blue,thickness=2): PIm:=plot(Im(subs({A=setA,k0=setk0,sigma=setsigma},psi)),x=-12..12,color=red,thickness=2): POrt:=display(PReal,PIm,title="Wellenfunktion (Blau:Real-, Rot:Imaginärteil)",titlefont = [HELVETICA, 16]): FourPsi:=1/sqrt(2*Pi)*fourier(subs({A=setA,k0=setk0,sigma=setsigma},psi),x,k): PImpuls:=plot(FourPsi^2,k=2..6,color=black,title="Impulsunschärfe",titlefont = [HELVETICA, 16],thickness=2); rho:=conjugate(subs({A=setA,k0=setk0,sigma=setsigma},psi))*subs({A=setA,k0=setk0,sigma=setsigma},psi): Prho:=plot(rho,x=-12..12,color=brown,title=cat(Ortsunschärfe,Psi*conjugate(Psi)),titlefont = [HELVETICA, 16],thickness=2): Ani[i]:=display(Matrix(1,3,[[POrt,Prho,PImpuls]])); od:

 

>	display([seq(Ani[i],i=1..20)],insequence=true);

 

>