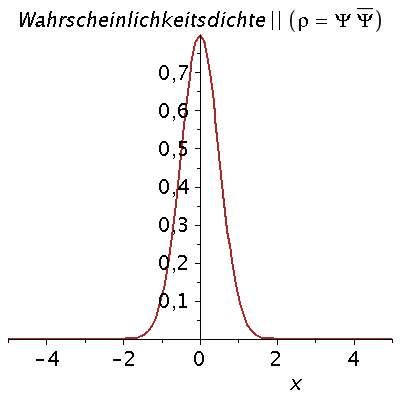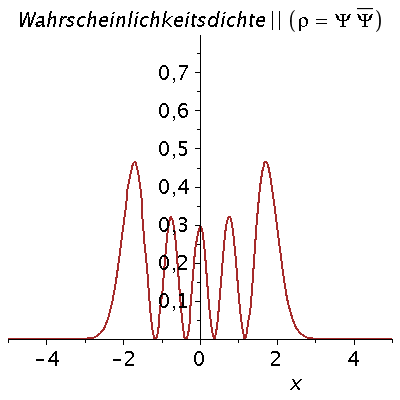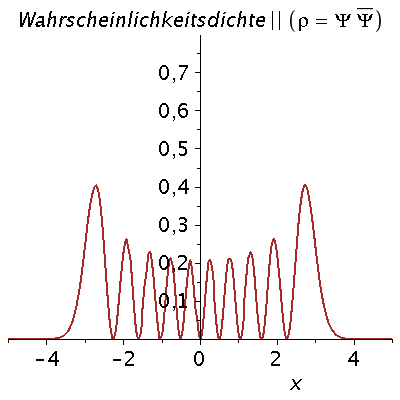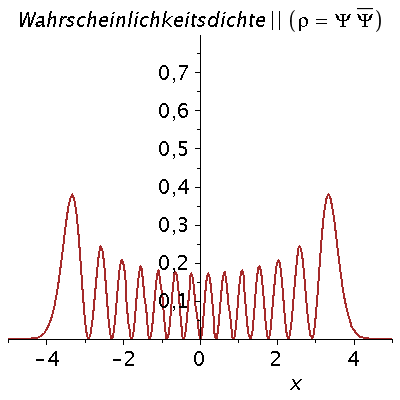Der harmonische Oszillator in der Quantenmechanik (Superposition von Zuständen und Zeitentwicklung) 

>	restart: with(plots): with(StringTools):

 

Die Energie-Eigenzustände eines quantenmechanischen Teilchens, welcher in einem Potentialtopf parabolische Gestalt gebunden ist, besitzen das folgende Aussehen: 

>	psi:=(m*omega/(Pi*hbar))^(1/4)*1/(sqrt(2^n*n!))*HermiteH(n, u)*exp(-u^2/2);

 

(1.1)

 

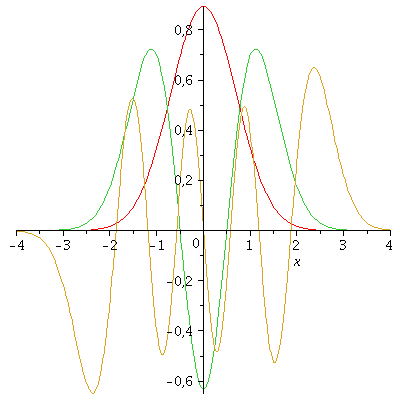
Wir setzen im Folgenden omega=2, m=1,k=4 , Rück-Transformieren die Variable u=sqrt(omega)*x und stellen uns die Zustände für n=0, n=2 und n=7 dar:  

>	psi0:=subs({n=0,omega=2, u=sqrt(2)*x,m=1,hbar=1},psi); psi1:=subs({n=2,omega=2, u=sqrt(2)*x,m=1,hbar=1},psi); psi2:=subs({n=7,omega=2, u=sqrt(2)*x,m=1,hbar=1},psi); plot({psi0,psi1,psi2},x=-4..4);

 

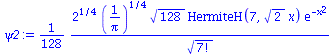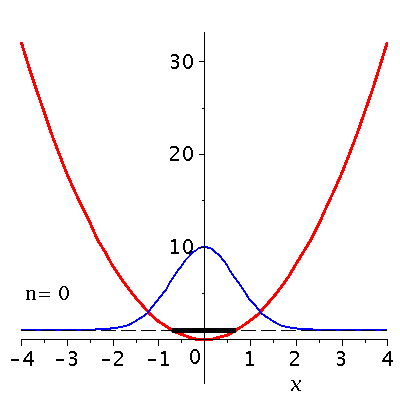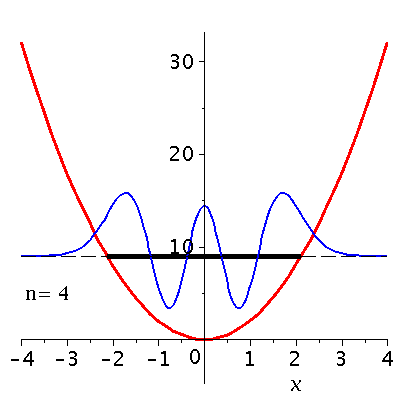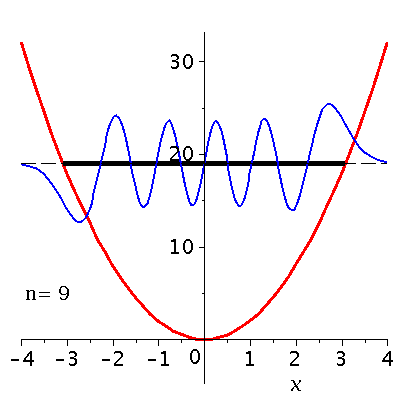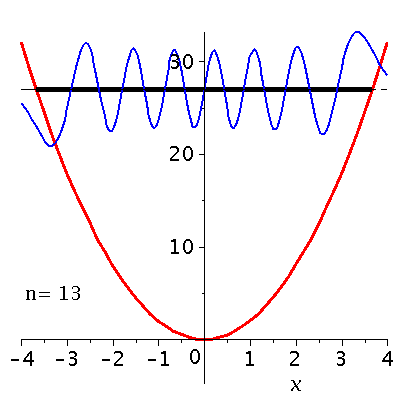
Veranschaulichung der ersten 13 Zustände im Potential: 

>

V:=k/2*x^2: setomega:=2: setk:=4: setm:=1: nend:=13: PlotPot:=plot(subs({k=setk},V),x=-4..4,thickness=3,titlefont = [HELVETICA, 16]): for nn from 0 by 1 to nend do setn:=nn: PSI[setn]:=subs({omega=setomega,n=setn,u=sqrt(setomega)*x,m=setm,hbar=1},psi); PlotPSI[setn]:=plot(PSI[setn],x=-4..4,thickness=2,color=blue); Energie[setn]:=subs({omega=setomega,n=setn},(n+1/2)*omega); PlotPSI1[setn]:=plot(10*PSI[setn]+Energie[setn],x=-4..4,thickness=2,color=blue); PlotEnergie[setn]:=plot(Energie[setn],x=-solve(subs({k=setk},V)=Energie[setn])[2]..solve(subs({k=setk},V)=Energie[setn])[2],thickness=5,color=black): PlotEnergie1[setn]:=plot(Energie[setn],x=-4..4,thickness=1,color=black,linestyle=3): rho[setn]:=conjugate(PSI[setn])*PSI[setn]: Prho[setn]:=plot(rho[setn],x=-5..5,thickness=2,color=brown,title=cat(Wahrscheinlichkeitsdichte,rho=Psi*conjugate(Psi)),titlefont = [HELVETICA, 16]); Ptext:=textplot([-4,5, Join(["n=",convert(setn,string)])], align =RIGHT,color=black,font = [TIMES, ROMAN, 15]): Ani[setn]:=display(Matrix(2,1,[display(Prho[setn]),display(PlotPot,PlotEnergie[setn],PlotPSI1[setn],PlotEnergie1[setn],Ptext)])); od:

 

>	display([seq(Ani[i],i=0..nend)],insequence=true);

 

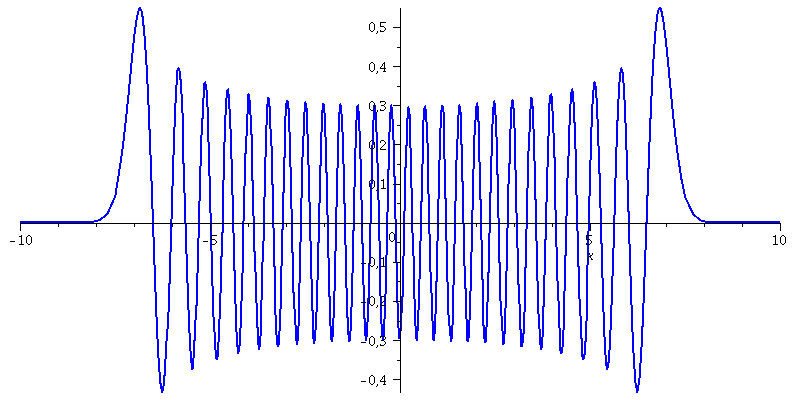
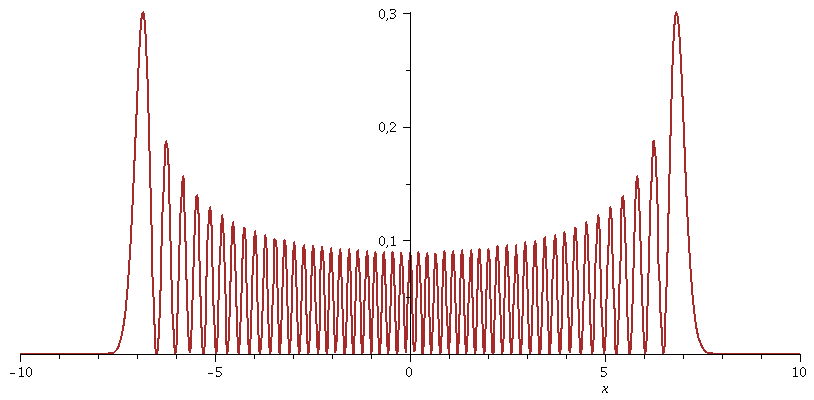
Für sehr große n geht die Wahrscheinlichkeitsdichte in den klassischen Grenzfall über (hier n=50): 

>	n1:=50; PSI[n1]:=subs({omega=setomega,n=n1,u=sqrt(setomega)*x,m=setm,hbar=1},psi): plot(PSI[n1],x=-10..10,thickness=2,color=blue); plot(PSI[n1]*PSI[n1],x=-10..10,thickness=2,color=brown,numpoints=200);

 

Die Zeitentwicklung eines stationären Eigenzustandes (z.B. n=2) erfolgt mittels 

>	nn:=2; PSI[nn]:=subs({omega=setomega,n=nn,u=sqrt(setomega)*x,m=setm,hbar=1},psi): Energie[nn]:=subs({omega=setomega,n=nn},(n+1/2)*omega); PSIT:=PSI[nn]*exp(-I*t*Energie[nn]);

 

 

 

	(1.2)

 

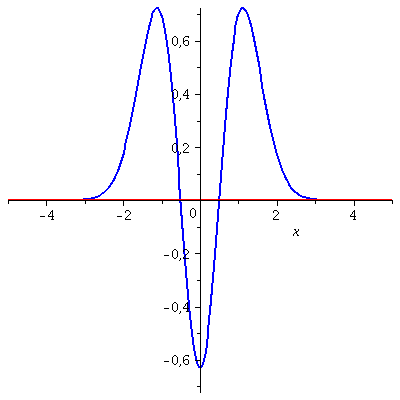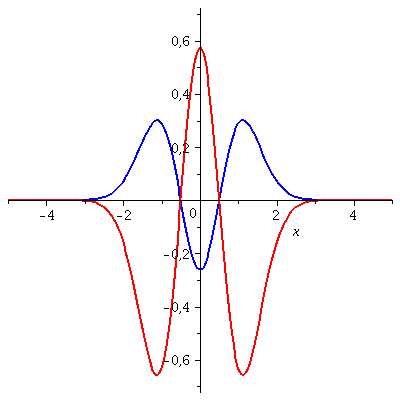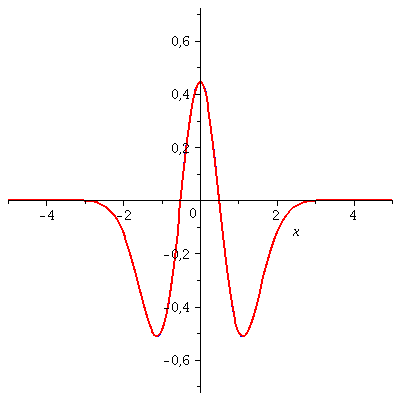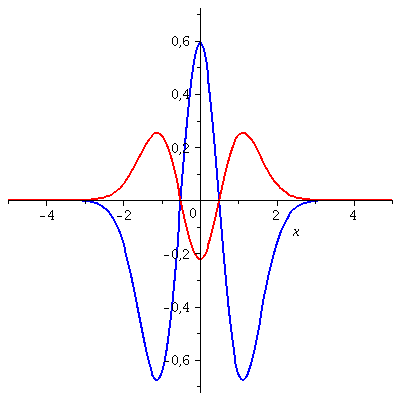
Die folgende Animation zeigt die zeitliche Entwicklung des Real- und Imaginärteils des Eigenzustandes mit n=2 für t=[0 , 0.7]: 

>	P1:=animate(Re(PSIT),x=-5..5,t=0..0.7,color=blue,thickness=2,numpoints=200,frames=50): P2:=animate(Im(PSIT),x=-5..5,t=0..0.7,color=red,thickness=2,numpoints=200,frames=50): display(P1,P2);

 

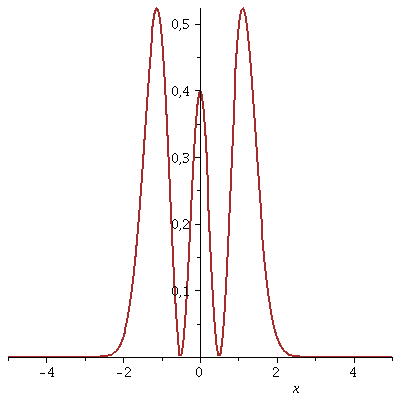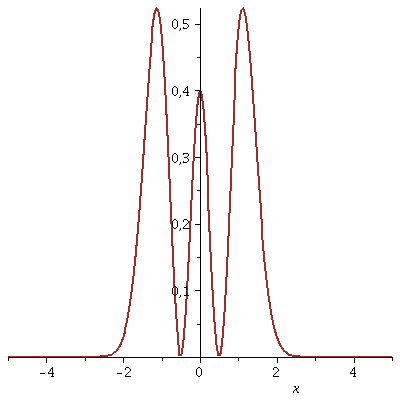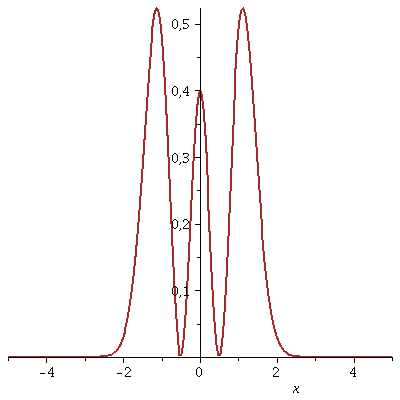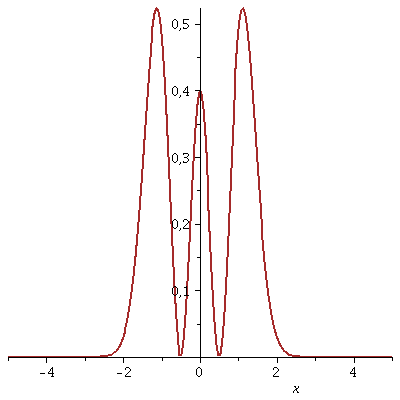
Die Wahrscheinlichkeitsdichte is jedoch zeitunabhängig: 

>	animate(Re(conjugate(PSIT)*PSIT),x=-5..5,t=0..0.7,thickness=2,color=brown,numpoints=200,frames=50);

 

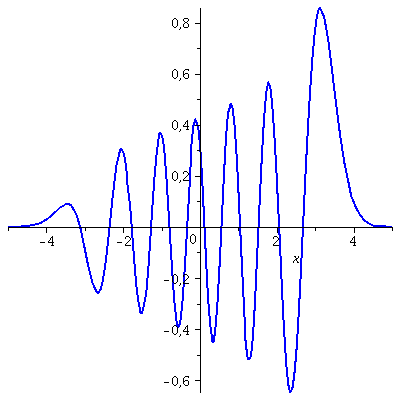
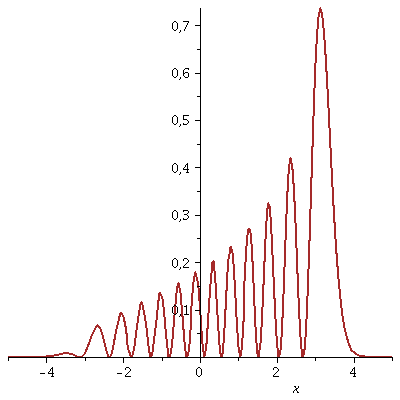
Betrachten wir die Linearkombination (Superposition) zweier Eigenzustände (z.B. n=11 und n=12). Die Zustandsfunktion (blaue Kurve) und die Wahrscheinlichkeitsdichte (braune Kurve) ist in der folgenden Abbildung dargestellt: 

>

n1:=11; n2:=12; PSI[n1]:=subs({omega=setomega,n=n1,u=sqrt(setomega)*x,m=setm,hbar=1},psi): PSI[n2]:=subs({omega=setomega,n=n2,u=sqrt(setomega)*x,m=setm,hbar=1},psi): c1:=1/sqrt(2); c2:=sqrt(1-c1^2); PSISup:=c1*PSI[n1]+c2*PSI[n2]; xmittel=evalf(int(PSISup*x*PSISup,x=-infinity...infinity)); plot(PSISup,x=-5..5,thickness=2,color=blue); plot(PSISup*PSISup,x=-5..5,thickness=2,color=brown);

 

Die Zeitentwicklung eines solchen Zustandes erfolgt mittels 

>	PSISupt:=c1*PSI[n1]*exp(-I*t*Energie[n1])+c2*PSI[n2]*exp(-I*t*Energie[n2]);

 

(1.3)

 

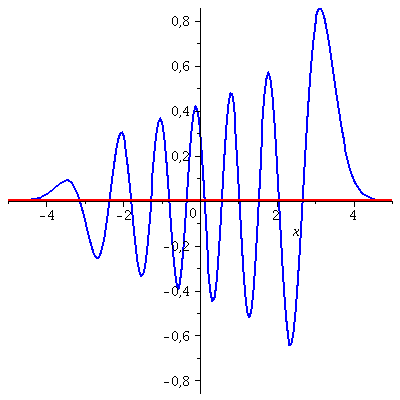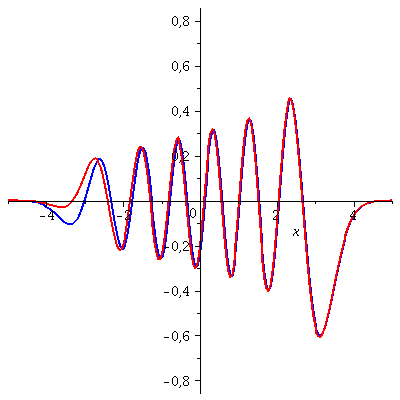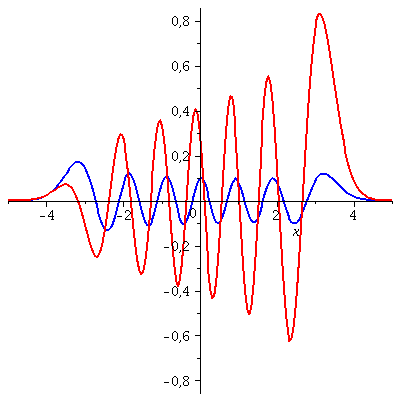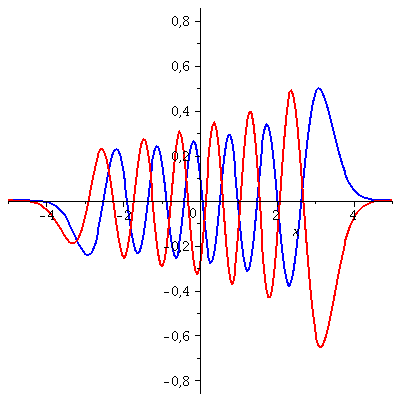
Die folgende Animation zeigt die zeitliche Entwicklung des Real- und Imaginärteils dieses Zustandes für t=[0 , 0.3] 

>	P1:=animate(Re(PSISupt),x=-5..5,t=0..0.3,color=blue,thickness=2,numpoints=200,frames=50): P2:=animate(Im(PSISupt),x=-5..5,t=0..0.3,color=red,thickness=2,numpoints=200,frames=50): display(P1,P2);

 

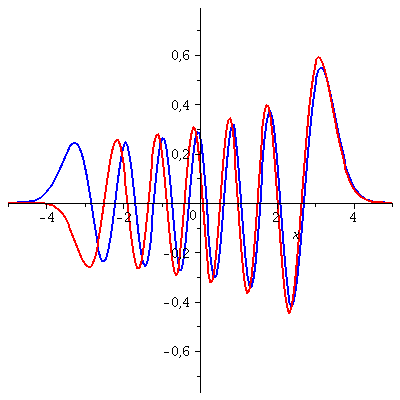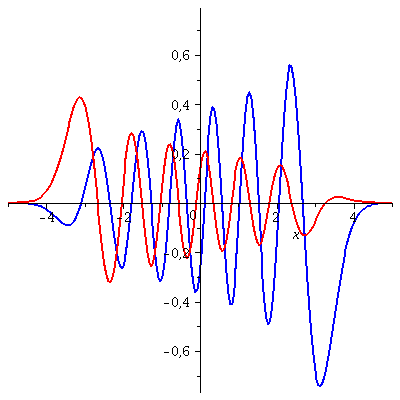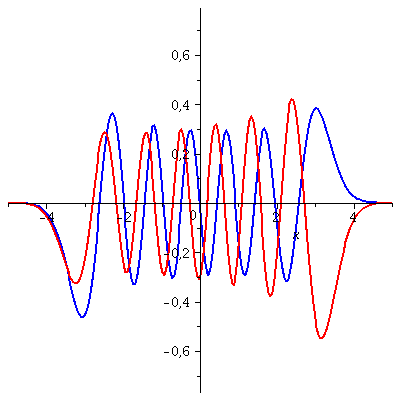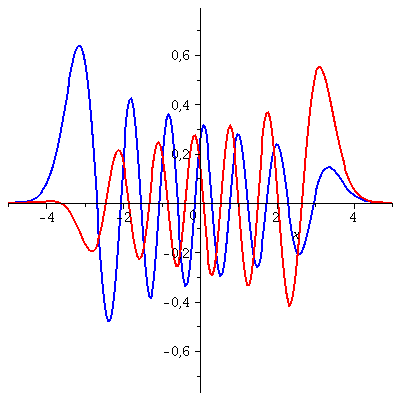
Die folgende Animation zeigt die zeitliche Entwicklung des Real- und Imaginärteils dieses Zustandes für eine spätere Zeitspanne t=[3.5 , 4] 

>	P1:=animate(Re(PSISupt),x=-5..5,t=3.5..4,color=blue,thickness=2,numpoints=200,frames=50): P2:=animate(Im(PSISupt),x=-5..5,t=3.5..4,color=red,thickness=2,numpoints=200,frames=50): display(P1,P2);

 

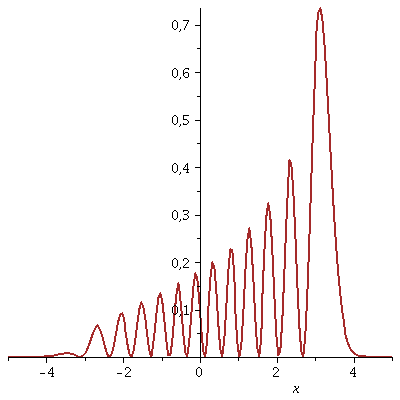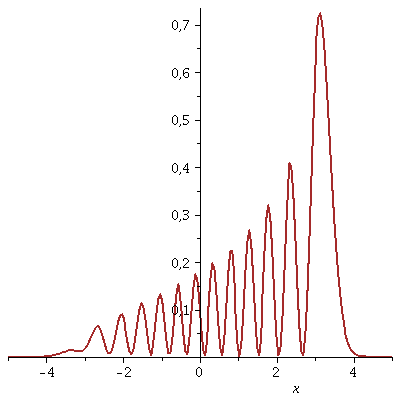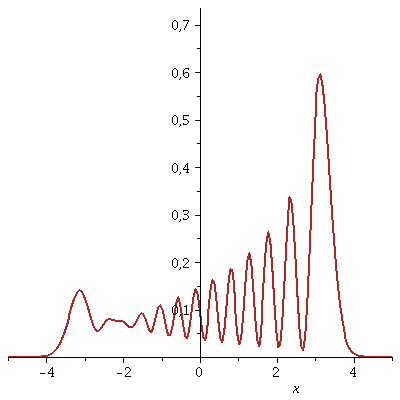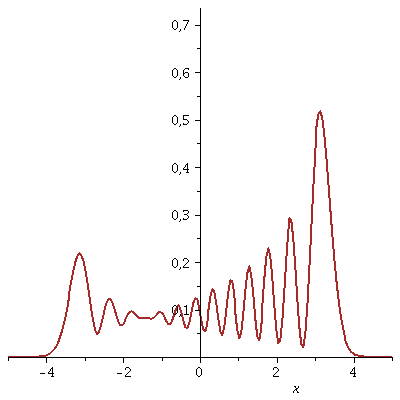
Die Wahrscheinlichkeitsdichte pendelt im Potentialtopf hin und her t=[0 , 10]: 

>	animate(Re(conjugate(PSISupt)*PSISupt),x=-5..5,t=0..10,thickness=2,color=brown,numpoints=200,frames=50);

 

>